衍射光栅及其特性
光学衍射光栅的原理与应用

光学衍射光栅的原理与应用光学衍射光栅是一种利用光的衍射现象进行光学分析和测量的重要光学元件。
它的原理基于光波在通过光栅时会发生衍射现象,从而产生一系列衍射光束,这些光束之间的干涉和衍射效应可以被用来进行光学分析和测量。
本文将介绍光学衍射光栅的原理、分类以及应用领域。
## 一、光学衍射光栅的原理光学衍射光栅的原理基于光的波动性质。
当平行入射的光线照射到光栅上时,光波会在光栅的周期性结构上发生衍射,形成一系列衍射光束。
这些衍射光束的强度和方向取决于光栅的周期、衍射角度以及入射光的波长等因素。
光学衍射光栅根据其结构可以分为振动光栅和位相光栅两种类型。
振动光栅是通过周期性地改变光栅的折射率或透射率来实现衍射效应,而位相光栅则是通过改变光栅的光程差来实现衍射效应。
不同类型的光栅在应用中具有各自的优势和特点。
## 二、光学衍射光栅的应用光学衍射光栅在光学领域有着广泛的应用,主要包括光谱分析、波长测量、光学成像等方面。
### 1. 光谱分析光学衍射光栅在光谱仪中被广泛应用。
通过光栅的衍射效应,可以将入射光线分散成不同波长的光束,形成光谱。
利用光栅的衍射特性,可以对光谱进行分辨、测量和分析,从而获得样品的光谱信息,广泛应用于化学分析、光谱学研究等领域。
### 2. 波长测量光学衍射光栅也被用于波长的精确测量。
通过测量衍射光束的角度或位置,可以计算出入射光的波长,实现对光波长的准确测量。
这在光学实验和精密测量中具有重要意义,例如在激光技术、光通信等领域的应用中发挥着关键作用。
### 3. 光学成像光学衍射光栅还可以用于光学成像。
通过设计特定结构的光栅,可以实现对光场的调控和成像,例如产生特定形状的光斑、实现光学信息的编码和解码等。
这些应用在光学显微镜、光学信息处理等领域有着重要的应用前景。
## 三、结语光学衍射光栅作为一种重要的光学元件,具有广泛的应用前景和研究价值。
通过深入理解光学衍射光栅的原理和特性,可以更好地发挥其在光学分析、测量和成像等方面的作用,推动光学技术的发展和创新。
大学物理实验报告系列之衍射光栅
【实验名称】衍射光栅【实验目的】1.观察光栅的衍射光谱,理解光栅衍射基本规律。
2.进一步熟悉分光计的调节和使用。
3.学会测定光栅的光栅常数、角色散率和汞原子光谱部分特征波长。
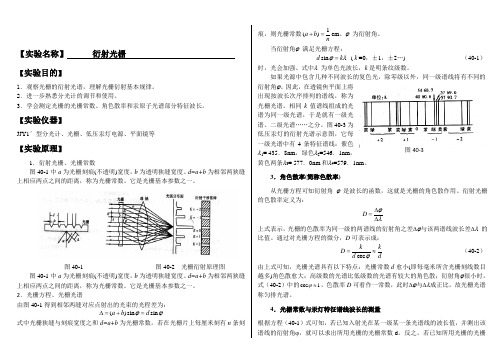
【实验仪器】JJY1′型分光计、光栅、低压汞灯电源、平面镜等【实验原理】1.衍射光栅、光栅常数图40-1中a为光栅刻痕(不透明)宽度,b为透明狭缝宽度。
d=a+b为相邻两狭缝上相应两点之间的距离,称为光栅常数。
它是光栅基本参数之一。
图40-1 图40-2 光栅衍射原理图图40-1中a为光栅刻痕(不透明)宽度,b为透明狭缝宽度。
d=a+b为相邻两狭缝上相应两点之间的距离,称为光栅常数。
它是光栅基本参数之一。
2.光栅方程、光栅光谱由图40-1得到相邻两缝对应点射出的光束的光程差为:ϕϕsinsin)(dba=+=∆式中光栅狭缝与刻痕宽度之和d=a+b为光栅常数,若在光栅片上每厘米刻有n条刻痕,则光栅常数nba1)(=+cm。
ϕ为衍射角。
当衍射角ϕ满足光栅方程:λϕkd=sin( k =0,±1,±2…) (40-1)时,光会加强。
式中λ为单色光波长,k是明条纹级数。
如果光源中包含几种不同波长的复色光,除零级以外,同一级谱线将有不同的衍射角ϕ。
因此,在透镜焦平面上将出现按波长次序排列的谱线,称为光栅光谱。
相同k值谱线组成的光谱为同一级光谱,于是就有一级光谱、二级光谱……之分。
图40-3为低压汞灯的衍射光谱示意图,它每一级光谱中有4条特征谱线:紫色λ1= 435.8nm,绿色λ2=546.1nm,黄色两条λ3= 577.0nm和λ4=579.1nm。
3.角色散率(简称色散率)从光栅方程可知衍射角ϕ是波长的函数,这就是光栅的角色散作用。
衍射光栅的色散率定义为:λϕ∆∆=D上式表示,光栅的色散率为同一级的两谱线的衍射角之差∆ϕ与该两谱线波长差∆λ的比值。
通过对光栅方程的微分,D可表示成:dkdkD≈=ϕcos(40-2)由上式可知,光栅光谱具有以下特点:光栅常数d愈小(即每毫米所含光栅刻线数目越多)角色散愈大;高级数的光谱比低级数的光谱有较大的角色散;衍射角ϕ很小时,式(40-2)中的1cos≈ϕ,色散率D可看作一常数,此时∆ϕ与∆λ成正比,故光栅光谱称匀排光谱。
11大学物理实验光栅衍射

三、数据处理
计算绿光、黄1和黄2三种波长成分的衍射角 及不确定度,正确表示结果。 (分光计测量角度时,B类不确定度取1分) 以绿光的衍射角计算光栅常数d及其不确定度, 正确表示结果(绿光波长为546.1nm) 。
cos d 2 sin
使用上一步计算出的光栅常数和两条黄线的 衍射角计算黄光的波长,并与已知值(p369) 比较,计算定值误差。
光栅衍射
衍射光栅是利用多缝衍射原理使光发生色散的 光学元件,由大量相互平行、等宽、等间距的 狭缝或刻痕所组成。由于光栅具有较大的色散 率和较高的分辨本领,它已被广泛地装配在各 种光谱仪器中。
光栅按不同分类方法可分为透射型和反射型光 栅或振幅型和位相型光栅,本实验使用的是透 射型振幅光栅。
一、实验原理
注意,测量之前务必把望远镜与外刻度盘固 定在一起。
测量衍射角 以绿光为例,转动望远镜,使-1级与分划板 垂线重合,读角位置θ1和θ′1,再测+1级角位 置θ2和θ′2,则1级绿光的衍射角θ为:
1 1 2 1 2 4
测量时,从最右端的黄2光开始,依次测黄2、 黄1,绿光,· · · · · · 直到最左端的黄2光,重复 测量三次。
1、光栅分光原理 光栅透光部分宽为a, 不透光部分宽为b, d=a+b称为光栅常数。
a
d
b
波长为λ的单色平行光垂直照射光栅时,出射角 θ满足如下光栅方程时,得到衍射主极大。
d sin k
(k 0,1,2)
光栅常数d,波长λ以及衍射角θ三个量,已知其 中两个,则第三个可由光栅方程求得。
Leabharlann 黄123 1
黄2
2 3
本实验用分光计的准直管获得平行光,垂直照 射光栅后的衍射图样通过望远镜的物镜聚焦到 分划板上,进行观察和读数。
衍射光栅实验报告

衍射光栅实验报告一、实验目的:1.了解光栅的分光特性2.测量光栅常量二、实验用具:分光仪、平面透射光栅、平面反射镜、低压汞灯三、实验原理:光栅是在空间上具有周期性的栅状物,并作为衍射元件的光学元件。
从产生衍射的机制上,光栅可分为振幅型和相位型两种。
振幅型光栅是利用栅状物的透过率(或反射率)对入射光振幅在空间上进行调制,相位型光栅则是利用栅状物对入射光的相位在空间上进行调制。
通常在光谱仪器中所用的光栅是振幅型的。
振幅型光栅多为面光栅。
根据振幅型光栅的形状又可分为平面光栅和凹面光栅。
目前常用的栅状物透过率有正弦型(理想的全息光栅)和二元型(平行、等宽、等间距的刻痕)两种。
振幅型光栅又分透射和反射两种类型。
本实验使用的是透射型的全息光栅。
二元光栅是平行等宽、等间距的多狭缝,它的分光原理如图所示狭缝S处于透镜L1的焦平面上,并认为它是无限细的;G是衍射光栅,它有N个宽度为a的狭缝,相邻狭缝间不透明部分的宽度为b。
如果自透镜L1出射的平行光垂直照射在光栅上,透镜L2将与光栅法线成θ角的光会聚在焦平面上的P点。
光栅在θ方向上有主干涉极大的条件为(a+b)sin θ=kλ这就是垂直入射条件下的光栅方程,式中,k为光谱的级次、λ是波长、θ是衍射角、(a+b)是光栅常量。
光栅常量通常用d表示,d=a+b。
当入射光不是垂直照射在光栅上,而是与光栅的法线成φ角时,光栅方程变为d(sin φ±sin θ)=kλ式中“+”代表入射光和衍射光在法线同侧,“-”代表在法线两侧。
光栅的衍射角θ仍定义为与光栅表面法线的夹角。
在复色光以相同的入射角照射到光栅,不同波长的光对应有不同的θ角,也就是说在经过光栅后,不同波长的光在空间角方向上被分开了,并按一定的顺序排列。
这就是光栅的分光原理。
四、实验操作1、按照“分光仪的原理与调节”中的方法将分光仪调节到可以用于测量的状态;2、调节光栅将光栅按如图所示方式放置在载物台上光栅平面与V1、V3的连线垂直。
光栅的制作及其衍射特性研究

光栅的制作及其衍射特性的研究实验原理1.光的干涉原理当两束相干的平面波以一定的角度相遇时,在他们相遇的区域内便会产生干涉,其干涉图样在某一平面内是一系列平行等距的干涉条纹,其强度分布则是按余弦规律而变化,即干涉图样的强度分布是121212I =I I 2cos()A A ϕϕ++-(1)式中的211I A =、222I A =,1A 、2A 是两列平面波的振幅,1ϕ、2ϕ是对应的空间相位函数。
当两束相干光的相位差为π2的整数倍时,即 122n ϕϕπ-=012n =±±、、……(1)式便描述了两束相干光干涉所形成的峰值强度面的轨迹,如图1所示。
若能用记录介质将此干涉图样记录下来并经过适当处理,则就获得了一块全息光栅。
1. 全息光栅基本参数的控制(1) 全息光栅空间频率(周期)的控制如图2所示,波长为λ的Ⅰ、Ⅱ两束相干光与P 平面法线的夹角分别为1θ和2θ, 它们之间的夹角为22θθθ+=。
这两束相干的平行光相干叠加时所产生的干涉图样是平行等距的、明暗相间的直条纹,条纹的间距d 可由下式决定:)(21cos )(21sin 21sin sin 212121θθθθθθλ-+=-=d (2)当两束对称入射,即12=/2θθθ=时2sin2θλ=d (3)当θ很小时有/d λθ=(4)若所制光栅的空间频率较低时,两光束的之间的夹角不大,就可以根据(4)式估算光栅的空间频率。
具体做办法是:把透镜L 放在Ⅰ、Ⅱ两光束的重合区,则两光束在透镜后焦面上会聚成两个亮点,若两个亮点之间的距离为X ,透镜的焦距为f ,则有0/X f θ=(5)将(5)带入(4)式得到图1两束平行相遇所形成的干涉/d f X λ=(6)即光栅的空间频率为01//v d X f λ==如图2所示,将白屏P 放在透镜L 的后焦面上,根据亮点的距离0X 估算光栅的空间频率v0X f vλ=(7)(2) 全息光栅的槽形控制由于全息光栅是通过记录相干光场的干涉图形而制成的,因此,其光栅的周期结构与两个因素有关:干涉图样的本身周期结构;记录干涉图样的条件。
光栅衍射光强分布特点

光栅衍射光强分布特点
光栅衍射是指光通过光栅后发生的衍射现象。
光栅由许多平行的狭缝或条纹构成,当光线通过光栅时,会发生衍射现象。
光栅衍射的光强分布特点如下:
1. 衍射级次分布规律性强:光栅衍射光强分布在一定条件下会出现明显的衍射规律,即不同衍射级次的亮暗条纹交替出现。
这是由于光通过光栅时,被不同的狭缝或条纹衍射后形成的干涉等效光束在空间中形成干涉图样。
2. 衍射极大点相对尖锐:在光栅衍射中,主极大点的光强较大且集中,其附近的辅极大点的光强逐渐变弱。
这是因为在主极大点处,干涉光束相位差为整数倍的波长,各个衍射光束叠加相长,光强叠加得到最大值。
3. 衍射极小点位置规律性强:在光栅衍射中,各级次的衍射极小点位置与入射光波长、光栅常数及衍射级次有关。
不同级次的衍射极小点位置之间存在数学关系,可以通过光栅常数和入射角的关系进行描述。
4. 栅常数越小,衍射角越大:光栅衍射中,光栅常数表示光栅上相邻两个狭缝或条纹的距离。
当光栅常数减小时,会导致衍射角增大,光强分布中的亮条纹变得更加密集。
总之,光栅衍射的光强分布具有规律性、集中性和分布规律性强等特点。
这些特点使得光栅衍射成为研究波动光学、光学仪器等领域的重要实验方法和基础理论。
12-4 衍射光栅及光栅光谱解析
光栅衍射 光强曲线 单缝衍射 轮廓线
0
sin
Hale Waihona Puke 单缝衍射对缝间干涉调制的特例:缺级
若衍射角θ同时满足条件
1, 2,(缝间干涉主极大) d sin k , k 0, 2, 3,(单缝衍射暗纹) a sin k , k 1,
则每缝出射的光线因各缝自身的单缝衍射而相消, 因而尽管各缝间的干涉是加强,但仍为暗纹。 ——这一现象叫缺级
7
6
l
二. 光栅衍射图样的形成
光栅平面 透镜L S 观察屏 透镜L p · 0 f f
*
那么光栅的衍射条纹是不是把N个缝的衍射 条纹直接叠加就可以了呢?下面我们看一些在 实验室拍的单缝和光栅衍射的照片。
单缝和不同缝数光栅的衍射条纹
N 1
N 5
N 2
N 6
N 3
N 20
单缝衍射与光栅衍射条纹光强分布的比较
d km a
N、a、d和λ对条纹的影响 光栅方程
Flash
d sin k , (k 0,1,2,)
主极大半角宽度
半
主极大间隔
Nd
d
k 1, sin k 1 sin k
三 衍射光谱
入射光为白光时, k不同,按波长分开形成光谱. 不同,
缺级满足的关系 从
d sin k 和 a sin k
得
d k a k
d k k (k 1,2,3) a
则 2,4,6 缺级
缺级满足关系
如果
d 2 a
问:缺级是否一定从存在? 光栅条纹的特点四:可能缺级
例:双缝衍射的结果讨论
衍射光栅特性实验报告

一、实验目的1. 理解衍射光栅的工作原理及其在光谱分析中的应用。
2. 掌握使用衍射光栅测定光波波长和光栅常数的实验方法。
3. 深入理解光栅衍射公式及其适用条件。
4. 分析衍射光栅的色散率、光谱特性等关键参数。
二、实验原理衍射光栅是利用多缝衍射原理使光发生色散的光学元件。
光栅由一组数目极多、平行等距、紧密排列的等宽狭缝构成,分为透射光栅和平面反射光栅。
当一束单色光垂直照射在光栅上时,各狭缝的光线因衍射而向各方向传播,经透镜会聚相互产生干涉,并在透镜的焦平面上形成一系列明暗条纹。
光栅衍射公式为:\[ d \sin \theta = m \lambda \]其中,\( d \) 为光栅常数(即相邻两狭缝间距),\( \theta \) 为衍射角,\( m \) 为衍射级数,\( \lambda \) 为光波波长。
三、实验仪器1. 分光计2. 平面透射光栅3. 低压汞灯(连镇流器)4. 白色光源5. 硅光电池6. 毫米刻度尺四、实验步骤1. 将分光计调整至水平状态,确保光栅垂直于光路。
2. 打开低压汞灯,调节光源与光栅的距离,使光束垂直照射在光栅上。
3. 通过分光计观察衍射光谱,记录不同衍射级数 \( m \) 对应的衍射角\( \theta \)。
4. 利用光栅衍射公式计算光波波长 \( \lambda \) 和光栅常数 \( d \)。
5. 改变光栅常数,观察衍射光谱的变化,分析色散率、光谱特性等参数。
五、实验结果与分析1. 计算光波波长和光栅常数:\[ \lambda = \frac{d \sin \theta}{m} \]\[ d = \frac{\lambda}{m \sin \theta} \]根据实验数据,计算得到光波波长和光栅常数,并与理论值进行比较。
2. 分析色散率:色散率 \( D \) 表示为:\[ D = \frac{d \sin \theta}{\theta} \]随着衍射级数 \( m \) 的增加,色散率 \( D \) 呈线性增加,说明光栅的色散率较高。
