2011年—2019年高考全国卷(1卷、2卷、3卷)理科数学试题分类汇编——1.集合
2011年—2019年高考全国卷(1卷、2卷、3卷)理科数学试题分类汇编——13.概率、统计
2011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编13．排列组合、概率统计一、选择题(2019·全国卷Ⅰ，理6)我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是（ ）A ．516B ．1132C ．2132D ．1116 (2019·全国卷Ⅱ，理5)演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，不变的数字特征是（ ）A ．中位数B ．平均数C ．方差D ．极差(2019·全国卷Ⅲ，理3)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著，某中学为了解本校学生阅读四大名著的情况，随机调查了100名学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（ ）A ．0．5B ．0．6C ．0．7D ．0．8(2018·新课标Ⅰ，理3)某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：则下列选项中不正确的是：A ．新农村建设后，种植收入减少。
B. 新农村建设后，其他收入增加了一倍以上。
C. 新农村建设后，养殖收入增加了一倍。
D.新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半。
(2018·新课标Ⅰ，理10)下图来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC 的斜边BC ，直角边AB ，AC ，ABC △的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ，在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为1p ，2p ，3p ，则（ ）A ．12p p =B ．13p p =C ．23p p =D ．123p p p =+（2018·新课标Ⅱ，理8）我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30723=+．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（ ）A ．112B ．114C ．115D ．118（2018·新课标Ⅲ，理8）某群体中的每位成品使用移动支付的概率都为p ，各成员的支付方式相互独立，设X 为该群体的10位成员中使用移动支付的人数， 2.4DX =，()()46P X P X =<=，则p =（ ）A ．0.7B ．0.6C ．0.4D ．0.3（2017·新课标Ⅰ，2）如图，正方形ABCD 内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（ ）A ．14B ．π8C ．12D ．π4（2017·新课标Ⅱ，6）安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（ ）A ．12种B ．18种C ．24种D ．36种（2017·新课标Ⅲ，3）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图，根据该折线图，下列结论错误的是（ ）.A ．月接待游客量逐月增加B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7，8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳（2016·新课标Ⅰ，4）某公司的班车在30:7，00:8，30:8发车，小明在50:7至30:8之间到达发车站乘坐班车，且到达发车丫的时候是随机的，则他等车时间不超过10分钟的概率是（A ）31 （B ）21 （C ）32 （D ）43 （2016·新课标Ⅱ，5）如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（ ）A ．24B ．18C ．12D ．9（2016·新课标Ⅱ，10）从区间[0，1]随机抽取2n 个数x 1，x 2，…，x n ，y 1，y 2，…，y n ，构成n 个数对11(,)x y ，22(,)x y ，…，(,)n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为（ ）A ．4n mB ．2n mC ．4m nD ．2m n（2016·新课标Ⅲ，4）某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A 点表示十月的平均最高气温约为15C ，B 点表示四月的平均最低气温约为5C .下面叙述不正确的是（ ）A. 各月的平均最低气温都在0C 以上B. 七月的平均温差比一月的平均温差大C. 三月和十一月的平均最高气温基本相同D. 平均最高气温高于20C 的月份有5个（2015·新课标Ⅰ，4）投篮测试中，每人投3次，至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（ ）（A ）0.648 （B ）0.432 （C ）0.36 （D ）0.312（2015·新课标Ⅱ，3）根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A ．逐年比较，2008年减少二氧化硫排放量的效果最显著.B ．2007年我国治理二氧化硫排放显现成效.C ．2006年以来我国二氧化硫年排放量呈减少趋势.D ．2006年以来我国二氧化硫年排放量与年份正相关.G •F •E•（2014·新课标Ⅰ，5）4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率（）A.18B.38C.58D.78（2014·新课标Ⅱ，5）某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A．0.8 B．0.75 C．0.6 D．0.45（2013·新课标Ⅰ，3）为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是()．A．简单随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样（2012·新课标Ⅰ，2）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（）A．12种B．10种C．9种D．8种（2011·新课标Ⅰ，4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）（A）13（B）12（C）23（D）34(2019·(2019·(2018·（2017·X （2013·（2012·3三、解答题(2019·全国卷Ⅰ，理21)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得1-分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得1-分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X ．（1）求X 的分布列；（2）若甲药、乙药在试验开始时都赋予4分，(0,1,,8)i p i =表示“甲药的累计得分为i 时，最终认为甲药比乙药更有效”的概率，则00p =，81p =，11i i i i p ap bp cp -+=++(1,2,,7)i =，其中(1)a P X ==-，(0)b P X ==，(1)c P X ==．假设0.5α=，0.8β=．(i)证明：1{}i i p p +-(0,1,2,,7)i =为等比数列；(ii)求4p ，并根据4p 的值解释这种试验方案的合理性．(2019·全国卷Ⅱ，理18)11分制乒乓球比赛，每赢一球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10：10平后，甲先发球，两人又打了X个球该局比赛结束．（1）求P（X=2）；（2）求事件“X=4且甲获胜”的概率．(2019·全国卷Ⅲ，理17)为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同、摩尔浓度相同．经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比，根据试验数据分别得到如下直方图：记C为事件：“乙离子残留在体内的百分比不低于5．5”，根据直方图得到P（C）的估计值为0．70．（1）求乙离子残留百分比直方图中a，b的值；（2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值代表）．(2018·新课标Ⅰ，理20) 某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品，检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为()<<，且各件产品是否p p01为不合格品相互独立．p；⑴记20件产品中恰有2件不合格品的概率为()f p，求()f p的最大值点⑵现对一箱产品检验了20件，结果恰有2件不合格品，以⑴中确定的p作为p的值．已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用．（i）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为X，求EX；（ii）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？（2018·新课标Ⅱ，理18）下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测改地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型①：30.413.5y t =-+：根据2010年至2016年的数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型②：9917.5y t =+．（1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；（2）你认为用哪个模型得到的预测值更可靠？并说明理由．（2018·新课标Ⅲ，理18）某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：⑴根据茎叶图判断哪种生产方式的效率更高？并说明理由；⑵求40名工人完成生产任务所需时间的中位数m，并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表：超过m不超过m第一种生产方式第二种生产方式⑶根据⑵中的列表，能否有99%的把握认为两种生产方式的效率有差异？附：()()()()()22n ad bcKa b c d a c b d-=++++，()20.0500.0100.0013.8416.63510.828P K kk≥．（2017·新课标Ⅰ，19）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N (μ,σ2)．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数，求 P (X ≥1)及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性；（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：经计算得16119.9716i i x x ===∑，0.212s ==≈，其中x i 为抽取的第i 个零件的尺寸，i =1,2, (16)0．（2017·新课标Ⅱ，18）淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比学|科网，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg）某频率直方图如下：（1）设两种养殖方法的箱产量相互独立，记A表示事件：旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A的概率；箱产量＜50kg 箱产量≥50kg 旧养殖法新养殖法22()()()()()n ad bcKa b c d a c b d-=++++（2017·新课标Ⅲ，18）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[)2025，，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率.（1）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；（2）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？最高气温[)1015，[)1520，[)2025，[)2530，[)3035，[)3540，天数 2 16 36 25 7 4（2016·新课标Ⅰ，19）某公司计划购买2台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图： 以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X 表示2台机器三年内共需更换的易损零件数，n 表示购买2台机器的同时购买的易损零件数．（Ⅰ）求X 的分布列；（Ⅱ）若要求5.0)(≥≤n X P ，确定n 的最小值；（Ⅲ）以购买易损零件所需费用的期望值为决策依据，在19=n 与20=n 之中选其一，应选用哪个？（2016·（2016·新课标Ⅲ，18）下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图.(1)由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； (2)建立y 关于t 的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量. 附注：参考数据：719.32i i y ==∑，7140.17i i i t y ==∑721()0.55ii yy =-=∑7≈2.646.参考公式：2211()()()(y y)nii nnii i i tt y y r tt ==--=--∑∑∑，回归方程y a bt =+中斜率和截距的最小二乘估计公式分别为：121()()()nii i nii tt y y b tt ==--=-∑∑，a y bt =-（2015·新课标Ⅰ，19）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费i x和年销售量i y （1,2,,8i=）数据作了初步处理，得到下面的散点图及一些统计量的值.x y w821()iix x=-∑821()iiw w=-∑81()()i iix x y y=--∑81()()i iiw w y y=--∑46.6 563 6.8 289.8 1.6 1469 108.8表中i iw x=，8118iiw w==∑（Ⅰ）根据散点图判断，y a bx=+与y c d x=+哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程；（III）已知这种产品的年利润z与x，y的关系为0.2z y x=-，根据（Ⅱ）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？（ii）年宣传费x为何值时，年利润的预报值最大？附：对于一组数据1122(,),(,),,(,)n nu v u v u v，其回归直线v uαβ=+的斜率和截距的最小二乘估计分别为121()()()ni iiniiu u v vu uβ==-=--∑∑，v uαβ=-.（2015·新课标Ⅱ，18）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：A 地区 62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89B 地区 73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：满意度评分低于70分 70分到89分不低于90分 满意度等级不满意满意非常满意记事件C ：“A 地区用户的满意度等级高于B 地区用户的满意度等级”，假设两地区用户的评价结果相互独立，根据所给数据，以事件发生的频率作为相应事件发生的概率，求C 的概率．（2014·新课标Ⅰ，18）从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：(Ⅰ)求这500件产品质量指标值的样本平均数x 和样本方差2s （同一组数据用该区间的中点值作代表）； （Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z 服从正态分布2(,)N μδ，其中μ近似为样本平均数x ，2δ近似为样本方差2s .(i)利用该正态分布，求(187.8212.2)P Z <<；（ii ）某用户从该企业购买了100件这种产品，记X 表示这100件产品中质量指标值为于区间（187.8,212.2）的产品件数，利用（i ）的结果，求EX .附：15012.2.若Z ～2(,)N μδ，则()P Z μδμδ-<<+=0.6826，(22)P Z μδμδ-<<+=0.9544.（2014·新课标Ⅱ，19）某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：（Ⅰ）求y关于t的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.（2012·新课标Ⅰ、Ⅱ，18）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理。
2011年—2019历年高考全国卷(1卷、2卷、3卷)理科数学试题分类汇编9.三角函数与解三角形
2011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编9．三角函数与解三角形一、选择题(2019·全国卷Ⅰ，理11)关于函数()sin |||sin |f x x x =+有下述四个结论：①f (x )是偶函数②f (x )在区间（2π，π）单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是（ ） A ．①②④B ．②④C ．①④D ．①③(2019·全国卷Ⅱ，理9)下列函数中，以2π为周期且在区间(4π，2π)单调递增的是（ ）A ．f (x )=│cos 2x │B ．f (x )=│sin 2x │C ．f (x )=cos│x │D ．f (x )= sin │x │(2019·全国卷Ⅱ，理10)已知(0)2πα∈，，2sin 2cos21αα=+，则sin α=（ ）A ．15B C D (2019·全国卷Ⅲ，理12)设函数()sin(0)f x x ωω=+>，已知f (x )在[0,2π]有且仅有5个零点，下述四个结论：①f (x )在(0,2π)有且仅有3个极大值点；②f (x )在(0,2π)有且仅有2个极小值点；③f (x )在(0,)10π单调递增；④ω的取值范围是1229[,)510．其中所有正确结论的编号是（ ） A ．①④B ．②③C ．①②③D ．①③④（2018·新课标Ⅱ，6）在ABC △中，cos2C =1BC =，5AC =，则AB =（ ）A ．BCD ．（2018·新课标Ⅲ，理4）若1sin 3α=，则cos2α=（ ）A ．89B ．79C ．79-D ．89-（2018·新课标Ⅲ，理9）ABC △的内角A B C ，，的对边分别为a ，b ，c ，若ABC ∆的面积为2224a b c +-，则C =（ ）A ．2π B ．3π C ．4π D ．6π（2017·新课标Ⅰ，9）已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结正确的是（ ） A ．把C 1上各点的横坐标伸长到原来2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2（2017·新课标Ⅲ，6）设函数()πcos 3f x x ⎛⎫=+⎪⎝⎭，则下列结论错误的是（ ）. A ．()f x 的一个周期为2-πB ．()y f x =的图像关于直线83x π=对称 C ．()f x +π的一个零点为6x π=D ．()f x 在π,2⎛⎫π⎪⎝⎭单调递减 （2016·新课标Ⅰ，12）已知函数)2,0)(sin()(πϕωϕω≤>+=x x f ，4π-=x 为)(x f 的零点，4π=x 为)(x f y =图像的对称轴，且)(x f 在)365,18(ππ单调，则ω的最大值为（ ）A ．11B ．9C ．7D ．5（2016·新课标Ⅱ，7）若将函数y =2sin 2x 的图像向左平移12π个单位长度，则平移后图象的对称轴为（ ） A ．()26k x k Z ππ=-∈ B ．()26k x k Z ππ=+∈ C ．()212k x k Z ππ=-∈D ．()212k x k Z ππ=+∈（2016·新课标Ⅱ，9）若3cos()45πα-=，则sin 2α =（ ） A ．725B ．15C ．15-D ．725-（2016·新课标Ⅲ，5）若3tan 4α=，则2cos 2sin 2αα+=（ ） A.6425 B. 4825 C. 1 D. 1625（2016·新课标Ⅲ，8）在ABC △中，π4B =，BC 边上的高等于13BC ,则cos A =（ ）A.31010 B. 1010 C.1010- D. 31010- （2015·新课标Ⅰ，2）sin 20cos10cos160sin10-=（ ）A ．32-B ．32C ．12-D ．12（2015·新课标Ⅰ，8）函数()f x =cos()x ωϕ+的部分图象如图所示，则()f x 的单调递减区间为（ ）A ．13(,),44k k k ππ-+∈Z B ．13(2,2),44k k k ππ-+∈Z C ．13(,),44k k k -+∈Z D ．13(2,2),44k k k -+∈Z（2014·新课标Ⅰ，6）如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为（ ）（2014·新课标Ⅰ，8）设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则（ ） A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=（2014·新课标Ⅱ，4）钝角三角形ABC 的面积是12，AB =1，BC =2，则AC =（ ）A ．5B ．5C ．2D ．1（2012·新课标Ⅰ，9）已知0ω>，函数()sin()4f x x πω=+在（2π，π）上单调递减，则ω的取值范围是（ ）A ．[12，54] B ．[12，34] C ．（0，12] D ．（0，2]（2011·新课标Ⅰ，5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=（ ）A ．45-B ．35-C ．35D ．45（2011·新课标Ⅰ，11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（ ）A ．()f x 在(0,)2π单调递减B ．()f x 在3(,)44ππ单调递减C ．()f x 在(0,)2π单调递增D ．()f x 在3(,)44ππ单调递增二、填空题(2019·全国卷Ⅱ，理15)ABC △的内角,,A B C 的对边分别为,,a b c ．若π6,2,3b ac B ===，则ABC △的面积为__________．（2018·新课标Ⅰ，理16）已知函数x x x f 2sin sin 2)(+=，则)(x f 的最小值是 .（2018·新课标Ⅲ，理15）函数()cos 36f x x π⎛⎫=+ ⎪⎝⎭在[]0π，的零点个数为________． （2018·新课标Ⅱ，理15）已知sin cos 1αβ+=，cos sin 0αβ+=，则()sin αβ+=__________．（2017·新课标Ⅱ，14）函数()23sin 4f x x x =+-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是 ． （2016·新课标Ⅱ，13）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若cos 45A =，1cos 53C =，a = 1，则b = .（2016·新课标Ⅲ，14）函数sin y x x =-的图像可由函数sin y x x =的图像至少向右平移______个单位长度得到.（2015·新课标Ⅰ，16）在平面四边形ABCD 中，75A B C ∠=∠=∠=，2BC =，则AB 的取值范围是 .（2014·新课标Ⅰ，16）已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，a =2，且(2)(sin sin )()sin b A B c b C +-=-，则ABC ∆面积的最大值为 . （2014·新课标Ⅱ，14）函数()sin(2)2sin cos()f x x x ϕϕϕ=+-+的最大值为_________.（2013·新课标Ⅰ，15）设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝__________.（2013·新课标Ⅱ，15）设θ为第二象限角，若1tan()42πθ+=，则sin cos θθ+=_________.（2011·新课标Ⅰ，16）在ABC 中，60,B AC ==2AB BC +的最大值为 ．三、解答题(2019·全国卷Ⅰ，理17)ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，设22(sin sin )sin sin sin B C A B C -=-．（1）求A ；（22b c +=，求sin C ．(2019·全国卷Ⅲ，理18)△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，已知sin =sin 2A Ca b A +． （1）求B ；（2）若△ABC 为锐角三角形，且c =1，求△ABC 面积的取值范围．(2018·新课标Ⅰ，理17)在平面四边形ABCD 中，o ADC 90=∠，oA 45=∠，2=AB ，5=BD .（1）求ADB ∠cos ；（2）若22=DC ，求BC .（2017·新课标Ⅰ，17）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ；（2）若6cos B cos C =1,a =3,求△ABC 的周长（2017·新课标Ⅱ，17）ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2BA C +=． （1）求cosB ；（2）若6a c += , ABC ∆面积为2，求.b ．（2017·新课标Ⅲ，17）ABC △的内角,,A B C 的对边分别为,,a b c ，已知sin 0A A +=，a =2b =．（1）求c ；（2）设D 为BC 边上一点，且 AD AC ⊥，求ABD △的面积．（2016·新课标Ⅰ，17）ABC ∆内角C B A ,,的对边分别为c b a ,,，已知c A b B a C =+)cos cos (cos 2． （Ⅰ）求C ；（Ⅱ）若7=c ，ABC ∆的面积为233，求ABC ∆周长．（2015·新课标Ⅱ，17）在∆ABC 中，D 是BC 上的点，AD 平分∠BAC ，∆ABD 面积是∆ADC 面积的2倍．（Ⅰ）求 sin sin B C ∠∠；（Ⅱ） 若AD =1，DC ，求BD 和AC 的长．（2013·新课标Ⅰ，17）如图，在△ABC 中，∠ABC ＝90°，AB BC ＝1，P 为△ABC 内一点，∠BPC＝90°.(1)若PB ＝12，求P A ；(2)若∠APB ＝150°，求tan ∠PBA .（2013·新课标Ⅱ，17）在△ABC 内角A 、B 、C 的对边分别为a ，b ，c ，已知a=bcosC+csinB . （Ⅰ）求B ；（Ⅱ）若b=2，求△ABC 面积的最大值.（2012·新课标Ⅰ，17）已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，cos sin 0a C C b c --=．（1）求A ；（2）若2a =，△ABC b ，c ．2011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编9．三角函数与解三角形（逐题解析版）一、选择题(2019·全国卷Ⅰ，理11)关于函数()sin |||sin |f x x x =+有下述四个结论：①f (x )是偶函数②f (x )在区间（2π，π）单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是（ ） A ．①②④B ．②④C ．①④D ．①③【答案】C 解析：因为()sin sin()sin sin ()f x x x x x f x -=-+-=+=，所以()f x 是偶函数，①正确；因为52,(,)632ππππ∈，而52()()63f f ππ<，所以②错误， 画出函数()f x 在[],ππ-上的图像，很容易知道()f x 有3零点，所以③错误， 结合函数图像，可知()f x 的最大值为2，④正确，故答案选C. (2019·全国卷Ⅱ，理9)下列函数中，以2π为周期且在区间(4π，2π)单调递增的是（ ）A ．f (x )=│cos 2x │B ．f (x )=│sin 2x │C ．f (x )=c os│x │D ．f (x )= sin │x │【答案】A 解析：f （x ）＝sin|x |不是周期函数，可排除D 选项； f （x ）＝cos|x |的周期为2π，可排除C 选项；f （x ）＝|sin2x |在处取得最大值，不可能在区间（，）单调递增，可排除B ．方法2：对于A ，如图，以()1cos4cos22x f x x +==12T π=，且在区间,42ππ⎛⎫⎪⎝⎭单调递增；A 对.对于B ，如图，以()1cos4sin 22x f x x -==12T π=，且在区间,42ππ⎛⎫⎪⎝⎭单调递减；B 错. 对于C ，()cos cos f x x x ==，2T π=，C 错对于D ，()()()sin 0sin sin 0x x f x x x x ≥⎧⎪==⎨-≤⎪⎩，如图，不是周期函数， D 错；故选A.(2019·全国卷Ⅱ，理10)已知(0)2πα∈，，2sin 2cos21αα=+，则sin α=（ ）A ．15B ．5 C ．3 D ．25【答案】B 解析：24sin cos 2cos ααα=()cos 2sin cos 0ααα⇒-= ，0,2πα⎛⎫∈ ⎪⎝⎭，1tan 2α∴=，5sin α=.(2019·全国卷Ⅲ，理12)设函数()sin()(0)5f x x πωω=+>，已知f (x )在[0,2π]有且仅有5个零点，下述四个结论：①f (x )在(0,2π)有且仅有3个极大值点；②f (x )在(0,2π)有且仅有2个极小值点；③f (x )在(0,)10π单调递增；④ω的取值范围是1229[,)510．其中所有正确结论的编号是（ ） A ．①④B ．②③C ．①②③D ．①③④【答案】D【基本解法】令05wx π+=，得05x wπ=-<，令52wx ππ+=，得3010x wπ=>， 设()f x 的正零点从小到大一次为()i x i Z +∈由图可知（1）正确； 极小值个数 可能是2个或3个，故（2）错误令555wx ππ+=，解得5245x πω=令665wx ππ+=，解得6295x πω=，解不等式562x x π≤<，得1229510ω≤<，（4）正确 010x π<<时，(,)55105w wx ππππ+∈+29(,)(0,)5101052ππππ⊆⨯+⊆故()f x 在(0,)10π单调递增 ，故（3）正确。
2011—2019年高考真题全国卷1理科数学分类汇编——6.数列
2011—2019年高考真题全国卷1理科数学分类汇编——6.数列一、选择题【2019，9】.记n S 为等差数列{}n a 的前n 项和.已知40S =，55a =，则（ ）A.25n a n =-B.310n a n =-C.228nS n n =- D.2122n S n n=- 【2018,4】记n S 为等差数列{}n a 的前n 项和.若3243S S S =+，12a =，则=5a （ ） A ．12- B ．10-C ．10D ．12【2017，4】记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为（ ）A ．1B ．2C ．4D ．8【2017，12】几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16 ，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推．求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂．那么该款软件的激活码是（ ）A ．440B ．330C ．220D ．110【2016，3】已知等差数列}{n a 前9项的和为27，810=a ，则=100a （ ）A ．100B ．99C ．98D ．97【2013，7】设等差数列{a n }的前n 项和为S n ，若S m －1＝－2，S m ＝0，S m ＋1＝3，则m ＝( )．A ．3B ．4C ．5D ．6【2013，12】设△A n B n C n 的三边长分别为a n ，b n ，c n ，△A n B n C n 的面积为S n ，n ＝1,2,3，….若b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝2n n c a +，c n ＋1＝2n nb a +，则( )． A ．{S n }为递减数列 B ．{S n }为递增数列C ．{S 2n －1}为递增数列，{S 2n }为递减数列D ．{S 2n －1}为递减数列，{S 2n }为递增数列 【2013，14】若数列{a n }的前n 项和2133n n S a =+，则{a n }的通项公式是a n ＝__________． 【2012，5】已知{n a }为等比数列，472a a +=，568a a =-，则110a a +=（ ）A ．7B ．5C ．－5D ．－7二、填空题【2019，14】记nS 为等比数列{}n a的前n 项和，若113a =，246a a =，则5S = .【2018,14】记n S 为数列{}n a 的前n 项和.若21n n S a =+，则6S =_____________．【2016，15】设等比数列}{n a 满足1031=+a a ，542=+a a ，则12n a a a L 的最大值为 ．【2012，16】数列{n a }满足1(1)21nn n a a n ++-=-，则{n a }的前60项和为__________．三、解答题【2015，17】n S 为数列{}n a 的前n 项和．已知n a ＞0，2243nn n a a S +=+．（Ⅰ）求{}n a 的通项公式；（Ⅱ）设11n n n b a a +=错误!未找到引用源。
2011年—2018年新课标全国卷(1卷、2卷、3卷)理科数学试题分类汇编——1
2011年—2018年新课标全国卷(1卷、2卷、3卷)理科数学试题分类汇编——1.集合2011年至2018年的新课标全国卷理科数学试题分类汇编中，集合与简易逻辑是一个重要的考点。
下面是一些选择题的例子：1.已知集合A={x|x^2-x-2>0}，则C∪A=（）A。
{x|-1<x<2}B。
{x|-1≤x≤2}C。
{x|x2}D。
{x|x≤-1}∪{x|x≥2}2.已知集合A={(x,y)|x^2+y^2≤3，x∈Z，y∈Z}，B={[1,2]}，则A∩B的元素个数为（）A。
9B。
8C。
5D。
43.已知集合A={x|x-1≥0}，B={[1,2]}，则A∩B=（）A。
{[ ]}B。
{[1]}C。
{[1,1,2]}D。
{[2]}4.已知集合A={x|x<1}，B={x|x^3<1}，则A∩B=（）A。
{x|x<0}B。
{x|x≤0}C。
{x|x>1}D。
∅5.已知集合A={1,2,4}，B={x|(x+1)(x-2)<0，x∈Z}，则A∩B=（）A。
{1}B。
{1,2}C。
{0,1,2,3}D。
{-1,0,1,2,3}6.已知集合S={x|(x-2)(x-3)≥0}，T={x|x>0}，则S∩T=（）A。
[2,3]B。
(-∞,2]∪[3,+∞)C。
[3,+∞)D。
(0,2]∪[3,+∞)7.命题p：∃n∈N，n>2，则¬p为（）A。
∀n∈N，n>2B。
∃n∈N，n≤2C。
∀n∈N，n≤2D。
∃n∈N，n=2以上内容由XXXXXX收集整理，欢迎研究交流）2015·新课标Ⅱ，1）已知集合A={-2，-1，2}，B={x|(x-1)(x+2)<0}，求A∩B。
解：首先求出B的解析式为B={x|-2<x<1}，然后将A和B的元素进行比较，得到A∩B={-1}，因此选项A.{-1，0}为正确答案。
2014·新课标Ⅰ，1）已知集合A={x|x22x3≥0}，B={x|x-2≤x<2}，求A∩B。
2011-2019年新课标全国卷2理科数学试题分类汇编——10.立体几何
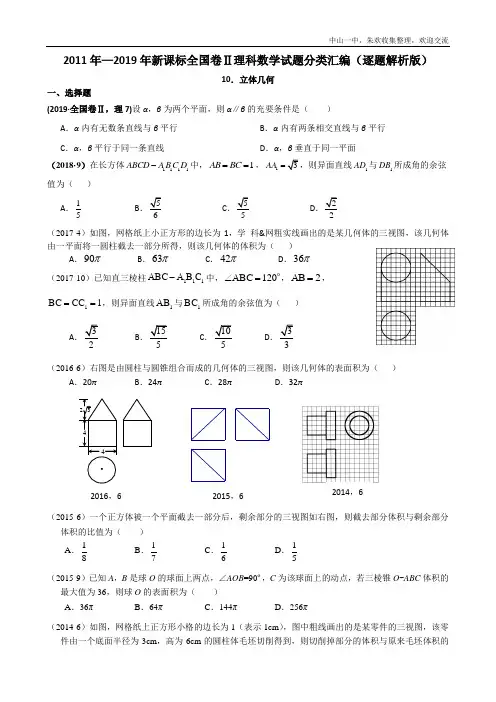
2011年—2019年新课标全国卷Ⅱ理科数学试题分类汇编（逐题解析版）10．立体几何一、选择题(2019·全国卷Ⅱ，理7)设α，β为两个平面，则α∥β的充要条件是（ ） A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线D ．α，β垂直于同一平面（2018·9）在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（ ）A ．15BCD（2017·4）如图，网格纸上小正方形的边长为1，学 科&网粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）A ．90πB ．63πC ．42πD ．36π （2017·10）已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（ ）ABCD（2016·6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ）A ．20πB ．24πC ．28πD ．32π（2015·6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ） A ．81 B ．71 C ．61 D ．51 （2015·9）已知A ，B 是球O 的球面上两点，∠AOB =90º，C 为该球面上的动点，若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为（ ） A ．36πB ．64πC ．144πD ．256π（2014·6）如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的2016，62015，62014，6比值为（ ） A ．1727B ．59C ．1027D ．13（2014·11）直三棱柱ABC -A 1B 1C 1中，∠BCA =90º，M ，N 分别是A 1B 1，A 1C 1的中点，BC =CA =CC 1，则BM 与AN 所成的角的余弦值为（ ） A ．110B ．25CD（2013·4）已知,m n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l m ⊥，l n ⊥，l α⊄，l β⊄，则（ ） A .α // β且l // αB .αβ⊥且l β⊥C .α与β相交，且交线垂直于lD .α与β相交，且交线平行于l（2013·7）一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（ ）（2012·7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ） A. 6B. 9C. 12D. 18（2012·11）已知三棱锥S -ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC =2，则此棱锥的体积为（ ） A.62B.63C. 32D. 22 （2011·6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（ ）A. B. C. D.二、填空题(2019·全国卷Ⅱ，理16)中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）B. C. D.（2018·新课标Ⅱ，理16）已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45︒．若SAB △的面积为_________． （2016·14）α、β是两个平面，m 、n 是两条直线，有下列四个命题： （1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n . （3）如果α∥β，m ⊂α，那么m ∥β.（4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 . (填写所有正确命题的编号.)（2011·15）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,AB BC ==则棱锥O -ABCD的体积为 .三、解答题(2019·全国卷Ⅱ，理17)如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值．（2018·新课标Ⅱ，20）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．（2017·19）如图，四棱锥P -ABCD 中，侧面PAD 为等比三角形且垂直于底面ABCD ，12AB BC AD ==，o 90BAD ABC ∠=∠=， E 是PD 的中点.（1）证明：直线//CE 平面PAB ；（2）点M 在棱PC 上，且直线BM 与底面ABCD 所成锐角为o 45 ，求二面角M -AB -D 的余弦值（2016·19）如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB =5，AC =6，点E ，F 分别在AD ，CD 上，AE =CF =54，EF 交BD 于点H . 将△DEF 沿EF 折到△D ´EF的位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ； （Ⅱ）求二面角B D A C '--的正弦值.OBAFDH E D '（2015·19）如图，长方体ABCD-A1B1C1D1中AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形.（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；（Ⅱ）求直线AF与平面α所成角的正弦值.（2014·18）如图，四棱锥P -ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB // 平面AEC ； （Ⅱ）设二面角D -AE -C 为60º，AP =1，ADE -ACD 的体积.（2012·19）如图，直三棱柱ABC -A 1B 1C 1中，121AA BC AC ==，D 是棱AA 1的中点，DC 1⊥BD . （Ⅰ）证明：DC 1⊥BC ；（Ⅱ）求二面角A 1-BD -C 1的大小.（2011·18）如图，四棱锥P -ABCD 中，底面ABCD 为平行四边形，∠DAB =60°，AB =2AD ，PD ⊥底面ABCD . （Ⅰ）证明：P A ⊥BD ；（Ⅱ）若PD =AD ，求二面角A -PB -C 的余弦值.C B ADC 1 A 1 B 12011年—2018年新课标全国卷Ⅱ理科数学试题分类汇编10．立体几何（逐题解析版）一、选择题(2019·全国卷Ⅱ，理7)设α，β为两个平面，则α∥β的充要条件是（ ） A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线D ．α，β垂直于同一平面【答案】B 解析：对于A ，α内有无数条直线与β平行，α∩β或α∥β； 对于B ，α内有两条相交直线与β平行，α∥β； 对于C ，α，β平行于同一条直线，α∩β或α∥β； 对于D ，α，β垂直于同一平面，α∩β或α∥β． 故选：B ．（2018·新课标Ⅱ，9）在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（ ）A ．15B C D ．2【答案】C 解析：法一：由几何关系可知：112EF B D ==，AE ，1AF =，由余弦定理可知：cos θ解法二：坐标法：由几何关系可知：(1B D =，点A 的坐标为(，点1D 的坐标为()1,1,0(10,1,AD = ，cos θ==解法三：补型法（以右补为例）：由几何关系可知：BD ，2DG =，1B G =cos θ=.（2017·4）B 【解析】从三视图可知：一个圆柱被一截面截取一部分而剩余的部分，剩下的体积分上下两部分阴影的体积，下面阴影的体积为V Sh =，3r =，4h =，∴ 136V π=；上面阴影的体积2V 是上面部分体积3V 的一半，即2312V V =，3V 与1V 的比为高的比（同底），即3132V V =，213274V V π==，故总体积02163V V V π=+=.方法2：354V Sh π==，其余同上，故总体积02163V V V π=+=.（2017·10）B 【解析】解法一：在边1BB ﹑11B C ﹑11A B ﹑AB 上分别取中点E ﹑F ﹑G ﹑H ，并相互连接. 由三角形中位线定理和平行线平移功能，异面直线1AB 和1BC 所成的夹角为FEG ∠或其补角，通过几何关系求得EF =FG =FH =，利用余弦定理可求得异面直线1AB 和1BC .解法二：补形通过补形之后可知：1BC D ∠或其补角为异面直线1AB 和1BC 所成的角，通过几何关系可知：1BC =1C D =，BD 1AB 和1BC .解法三：建系建立如左图的空间直角坐标系，()0,2,1A ，()10,0,0B ，()0,0,1B，11,02C ⎫-⎪⎪⎝⎭，∴ 131,12BC ⎛⎫=-- ⎪⎪⎝⎭，()10,2,1B A =，∴1111cos 5B A BC B A BC θ⋅===⋅ （2016·6）C 解析：几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h ．由图得2r =， 2π4πc r ==，由勾股定理得：4l ==，21π4π16π8π28π2S r ch cl =++=++=表，故选C ．（2015·6）D 解析：由三视图得，在正方体ABCD -A 1B 1C 1D 1中，截去四面体A -A 1B 1D 1，如图所示，设正方体棱长为a ，则11133111326A AB D V a a -=⨯=，故剩余几何体体积为3331566a a a -=，所以截去部分体积与剩余部分体积的比值为，故选D.（2015·9）C 解析：如图所示，当点C 位于垂直于面AOB 的直径端点时，三棱锥O ABC -的体积最大，设球O 的半径为R ，此时2311136326O ABC C AOB V V R R R --==⨯⨯==，故R=6，则球O 的表面积为24144S R ππ==，故选C ．（2014·6）C 解析：原来毛坯体积为π·32·6=54π (cm 2)，由三视图得，该零件由左侧底面半径为2cm ，高为4cm 的圆柱和右侧底面半径为3cm ，高为2cm 的圆柱构成，所以该零件的体积为：π·32·2+π·22·4=34π (cm 2)，则切削掉部分的体积为54π-34π =20π(cm 2)，所以切削掉部分的体积与原来毛坯体积的比值为20105427ππ=.（2014·11）C 解析：取BC 的中点P ，连结NP 、AP ， ∵M ，N 分别是A 1B 1，A 1C 1的中点，∴四边形NMBP为平行四边形，∴BM //PN ，∴所求角的余弦值等于∠ANP 的余弦值，不妨令BC=CA =CC 1=2，则AN =APNP =，∴222222||||||cos 2||||AN NP AP ANP AN NP +-∠=⨯⋅=. 【另解】如图建立坐标系，令AC =BC =C 1C =2，则A (0, 2, 2)，B (2, 0, 2)，M (1,1,0)，N (0,1,0)，(1,1,2)(0,1,2),BMAN ∴=--=--，cos 10||||BM AN θBM AN ⋅===⋅（2013·4）D 解析：因为m ⊥α，l ⊥m ，l ⊄α，所以l ∥α. 同理可得l ∥β. 又因为m ，n 为异面直线，所以α与β相交，且l 平行于它们的交线．故选D.（2013·7）A 解析：如图所示，该四面体在空间直角坐标系O －xyz的图像为右图，1ACB1A1C1BN MP1-x1-x 2则它在平面zOx上的投影即正视图为右图，故选A.（2012·7）B 解析：由三视图可知，此几何体为底面是斜边为6的等腰直角三角形（俯视图），高为3的三棱锥，故其体积为113932V =⨯⨯=.（2012·11）A 解析：易知点S 到平面ABC 的距离是点O 到平面ABC 的距离的2倍.显然O -ABC 是棱长为113O ABC V -==2S ABC O ABC V V --=. （2011·6）D 解析：条件对应的几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的. 故选D.二、填空题(2019·全国卷Ⅱ，理16)中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）【命题意图】考查空间想象能力，数学抽象概括能力.【答案】261 解析：该半正多面体共有8+8+8+2＝26个面，设其棱长为x ，则x x x ＝1，解得x 1．（2018·新课标Ⅱ，理16）已知圆锥的顶点为S ，母线SA ，SB所成角的余弦值为78，SA 与圆锥底面所成角为45︒．若SAB △的面积为_________． 【答案】解析：由面积的关系可知：SA SB ==由几何关系可知：SOAO ==侧面积S SA l =⋅，2l OA π==，侧面积S SA l =⋅=（2016·14）【答案：②③④】（2011·15）设ABCD 所在的截面圆的圆心为M ，则AM =，OM 22=，1623O ABCD V -=⨯⨯=三、解答题(2019·全国卷Ⅱ，理17)如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值．17．解：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知190BEB ∠=︒．由题设知11Rt Rt ABE A B E ≅△△，所以45AEB ∠=︒， 故AE AB =，12AA AB =．以D 为坐标原点，DA 的方向为x 轴正方向，||DA 为单位长，建立如图所示的空间直角坐标系D -xyz ，则C （0，1，0），B （1，1，0），1C （0，1，2），E （1，0，1），(1,1,1)CE =-，1(0,0,2)CC =．设平面EBC 的法向量为n =（x ，y ，x ），则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--．设平面1ECC 的法向量为m =（x ，y ，z ），则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩所以可取m =（1，1，0）．于是1cos ,||||2⋅<>==-n m n m n m ．所以，二面角1B EC C --．（2018·新课标Ⅱ，20）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．解析：（1）连接OB ，由几何关系可知：PO =2OB =，因为 22216PO OB PB +==，所以2POB π∠=，所以 PO OB ⊥，因为 =PB PA ，OA OC =，所以 PO AC ⊥， 因为 ACOB O =，所以PO ABC ⊥平面.解法二：常规解法（二线法，以AB 边中点为例，三垂线定理） 在AB 边去中点N ，连接PN 、ON ，因为 PA PB =，所以 PA AB ⊥在ABC ∆中，由勾股定理可知：AB BC ⊥，在ABC ∆中，AO OC =，AN NB =，所以 ON BC ， 所以 AB ON ⊥，因为 ONPN N =，所以 AB PNO ⊥平面，所以 AB PO ⊥由几何关系可知：PO AC ⊥，因为 ACON O =，所以PO ABC ⊥平面.以O 为坐标原点，OB 的方向为x 轴的正方向，建立空间直角坐标系O xyz -.由题意的可知：()0,0,0O ，()2,0,0B ，()0,2,0A -，()0,2,0C ，(P ，(AP =.取平面 PAC 的法向量()2,0,0OB =. 设(),2,0M a a -（02a <≤），则(),4,0AM a a =-.设平面PAM 的法向量为(),,n x y z =，由0AP n ⋅=，0AM n ⋅=，()2040y ax a y ⎧+=⎪⎨+-=⎪⎩可取))4,n a a =--所以cos ,OB n <>==4a =-（舍去），43a =所以 平面PAM 的法向量为43n ⎛⎫=- ⎪ ⎪⎝⎭，因为 (0,2,PC =-，所以 cos ,PC n <>=所以PC 与平面PAM .（2017·19）如图，四棱锥P -ABCD 中，侧面PAD 为等比三角形且垂直于底面ABCD ，12AB BC AD ==，o 90BAD ABC ∠=∠=， E 是PD 的中点.（1）证明：直线//CE 平面PAB ；（2）点M 在棱PC 上，且直线BM 与底面ABCD 所成锐角为o 45 ，求二面角M -AB -D 的余弦值【基本解法1】（1）证明：取PA 中点为F ，连接EF 、AF ，因为90BAD ABC ∠=∠=︒，12BC AD =所以BC 12AD ，因为E 是PD 的中点，所以EF12AD ，所以EF BC ， 所以四边形EFBC 为平行四边形，所以//EC BF ，因为BF ⊂平面PAB ，EC ⊄平面PAB ，所以直线//CE 平面PAB ，（2）取AD 中点为O ，连接OC OP 、，因为△PAD 为等边三角形，所以PO ⊥AD ，因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，PO ⊂平面PAD ， 所以PO ⊥平面ABCD ，因为AO BC ，所以四边形OABC 为平行四边形，所以//AB OC ， 所以OC AD ⊥，以,,OC OD OP 分别为,,x y z 轴建立空间直角坐标系，如图设1BC =，则(0,0,3),(0,1,0),(1,1,0),(1,0,0)P A B C --，所以(1,0,PC =， 设(,,)M x y z ，则(,,3)PM x y z =-，(1,0,0)AB =，因为点M 在棱PC 上，所以(01)PM PC λλ=≤≤，即(,,(1,0,x y z λ-=，所以()M λ，所以()BM λ=-， 平面ABCD 的法向量为(0,0,1)n =， 因为直线BM 与底面ABCD 所成角为45︒，所以|||sin 45||cos ,|2||||(BM nBM n BM n λ⋅︒=<>===，解得1λ=-(BM =-， 设平面MAB 的法向量为(,,)m x y z =，则00AB m x BM m x y z ⎧⋅==⎪⎨⋅=-+=⎪⎩， 令1z =，则(0,m=，所以cos ,||||6m n m n <>==⋅， 所以求二面角M AB D --的余弦值5. （2016·19）如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB =5，AC =6，点E ，F 分别在AD ，CD 上，AE =CF =54，EF 交BD 于点H . 将△DEF 沿EF 折到△D ´EF 的位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ； （Ⅱ）求二面角B D A C '--的正弦值.解析：⑴证明：∵54AE CF ==，∴AE CF AD CD=，∴EF AC ∥．∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF DH'⊥．∵6AC =，∴3AO =； 又5AB =，AO OB ⊥，∴4OB =，∴1AEOH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+，∴'D H OH ⊥．又∵OH EF H =I ，∴'D H ⊥面ABCD ．⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，，()430AB =uu u r，，，()'133AD =-uuur ，，，()060AC =uuu r，，，设面'ABD 法向量()1n x y z =，，u r，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩u r uu u r u r uuu r得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩， ∴()1345n =-u r ，，．同理可得面'AD C 的法向量()2301n =u u r ，，， OBAFDHED '中山一中，朱欢收集整理，欢迎交流∴1212cos n n n n θ⋅===u r u u r u r u u r，∴sin θ． （2015·19）如图，长方体ABCD -A 1B 1C 1D 1中AB =16，BC =10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E =D 1F =4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形. （Ⅰ）在图中画出这个正方形（不必说出画法和理由）； （Ⅱ）求直线AF 与平面α所成角的正弦值.（2015·19）解析：（Ⅰ）交线围成的正方形EHGF 如图：（Ⅱ）作EM AB ⊥，垂足为M ，则14AM A E ==，18EM AA ==因为EHGF 为正方形，所以EH EF =10BC ==，于是6MH ==，所以10AH =，以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所以的空间直角坐标系D xyz -，则(10,0,0)A ，(10,10,0)H ，(10,4,8)E ，(0,4,8)F ，(10,0,0)FE =，(0,6,8)HE =-，设(,,)n x y z =是平面EHGF 的法向量，则0n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩，即100680x y z =⎧⎨-+=⎩，所以可取(0,4,3)n =，又(10,4AF =-，故||5|c o s ,|||||n AF n AF n AF ⋅<>==AF 与平面EHGF（2014·18）如图，四棱锥P -ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB // 平面AEC ；（Ⅱ）设二面角D -AE -C 为60º，AP =1，AD E -ACD 的体积.解析：（Ⅰ）证明：连结BD 交AC 于点O ，连结OE ．∵底面ABCD 为矩形，∴点O 为BD 的中点，又E 为PD 的中点，∴//OE PB ，∵OE ⊂平面AEC ，PB ⊄平面AEC ，∴PB //平面AEC .（Ⅱ）以A 为原点，直线AB 、AD 、AP 分别为x 、y 、z 轴建立空间直角坐标系，设AB a =，则(,0)D ，(0,0,0)A，1(0,)22E，(C a ，∴1(0,)22AE =，(AC a =，设(,,)n x y z =是平面AEC 的法向量，则PBCDEA310220n AE yz n AC ax ⎧⋅=+=⎪⎨⎪⋅=+=⎩，解得：y x z⎧=⎪⎨⎪=⎩，令x =得(3,,n a=--，又∵(,0,0)AB a =是平面AED 的一个法向量，∴1|cos ,|cos602AB n <>===， 解得32a =，∴111||||||322EA C DV A D C D A P -=⨯⨯⨯⨯11333228=⨯⨯⨯.解析：（Ⅰ）连结AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，连结DF ，则BC 1∥DF . 因为DF ⊂平面A 1CD ，BC 1⊄平面A 1CD ，所以BC 1 // 平面A 1CD .（Ⅱ）由AC ＝CB ＝2AB 得，AC ⊥BC . 以C 为坐标原点，CA uu r 的方向为x 轴正方向，建立如图所示的空间直角坐标系C －xyz . 设CA ＝2，则D (1,1,0)，E (0,2,1)，A 1(2,0,2)，CD uuu r ＝(1,1,0)，CE uur＝(0,2,1)，1CA uuu r ＝(2,0,2)．设n ＝(x 1，y 1，z 1)是平面A 1CD 的法向量，则10CD CA ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu r n n ，即11110,220.x y x z +=⎧⎨+=⎩可取n ＝(1, -1, -1)． 同理，设m 是平面A 1CE 的法向量，则10CE CA ⎧⋅=⎪⎨⋅=⎪⎩m m uur uuu r，可取m ＝(2, 1, -2)． 从而cos 〈n ，m 〉＝||||3=·n m n m ，故sin 〈n ，m 即二面角D －A 1C －E 的正弦值为3（2012·19）如图，直三棱柱ABC -A 1B 1C 1中，121AA BC AC ==，D 是棱AA 1的中点，DC 1⊥BD . （Ⅰ）证明：DC 1⊥BC ； （Ⅱ）求二面角A 1-BD -C 1的大小.C B ADC 1 A 1 B 114．解析：（Ⅰ） 证明：设112AC BC AA a ===，直三棱柱111C B A ABC -，1DC DC ∴==， 12CC a =，22211DC DC CC ∴+=，1DC DC ∴⊥. 又1DC BD ⊥Q ，1DC DC D =I ，1DC ∴⊥平面BDC . BC ⊂Q 平面BDC ，1DC BC ∴⊥.（Ⅱ）由 (Ⅰ)知，1DC a=，1BC =，又已知BD DC ⊥1，BD ∴=. 在Rt ABD △中，B D a =，,90AD a DAB =∠=o，AB ∴=. 222AC BC AB ∴+=，AC BC ∴⊥.<法一>取11A B 的中点E ，则易证1C E ⊥平面1B D A ，连结DE ，则1C E ⊥BD ，已知BD DC ⊥1，BD ∴⊥平面1DC E ，BD ∴⊥DE ，1C DE ∴∠是二面角11C BD A --平面角.在1Rt C DE △中，1111sin 2C E C DE C D ∠===，130C DE ∴∠=. 即二面角11C BD A --的大小为30.<法二>以点C 为坐标原点，为x 轴，CB 为y 轴,1CC 为z 轴,建立空间直角坐标系C xyz -.则()()()()11,0,2,0,,0,,0,,0,0,2A a a B a D a a C a . (),,DB a a a =--uu u r ，()1,0,DC a a =-uuu r,设平面1DBC 的法向量为1111(,,)n x y z =r ，则11111100n DB ax ay az n DC ax az ⎧⋅=-+-=⎪⎨⋅=-+=⎪⎩uuu r r uuur r ，不妨令11x =，得112,1y z ==，故可取1(1,2,1)n =r.同理,可求得平面1DBA 的一个法向量2(1,1,0)n =r.设1n r 与2n r 的夹角为θ，则1212cos ||||n n n n θ⋅===⋅r rr r , 30θ∴=. 由图可知，二面角的大小为锐角，故二面角11C BD A --的大小为30.（2011·18）如图，四棱锥P -ABCD 中，底面ABCD 为平行四边形，∠DAB =60°，AB =2AD ，PD ⊥底面ABCD . （Ⅰ）证明：P A ⊥BD ；（Ⅱ）若PD =AD ，求二面角A -PB -C 的余弦值.15．解析：（Ⅰ）因为602DAB AB AD ∠=︒=，，由余弦定理得B D A D=，从而BD 2+AD 2= AB 2，故BD ⊥AD ，又PD ⊥底面ABCD ，可得BD ⊥PD ，所以BD ⊥平面P AD ，故 P A ⊥BD .（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D -xyz ，则(1,0,0)A，(0B，(C -，(0,0,1)P. (AB =-uu u r，1)PB =-，u u r C BADC 1A 1B 1(1,0,0)BC =-uu u r ，设平面P AB 的法向量为n =(x , y , z )，则00AB PB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu rn n ，即00x z ⎧-=⎪-=，因此可取=n ，设平面PBC 的法向量为m ，则0PB BC ⎧⋅=⎪⎨⋅=⎪⎩uuruu ur m m ，可取(0,3)=-m，cos ,<>==m n A-PB-C的余弦值为。
(完整word版)2011年-2019年全国二卷理科数学函数与导数分类汇编,推荐文档.docx
2011 年— 2019 年新课标全国卷Ⅱ理科数学试题分类汇编7．函数与导数一、选择题（ 2019·4） 2019 年 1 月 3 日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就，实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系．为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日 L 2 点的轨道运行． L 2 点是平衡点， 位于地月连线的延长线上．设地球质量为 M １ ，月球质量为 M ２ ，地月距离为 R ， L 2 点到月球的距离为r ，根据牛顿运动定律和万有引力定律，r 满足方程：M 1M 2(R r )M 1.设r 的值(R r ) 2r 23，由于RR很小，因此在近似计算中333 453 3 ，则 r 的近似值为(1)2A ．M2RB ．M 2 RM 12M 1C ． 3 3M 2 RD ． 3M 2 RM 13M 1（ 2019·6）若 a>b ，则A ． ln(a- b)>0B ． 3a <3bC ．a 3- b 3>0D ． │a │ >b ││（2019·12）设函数 f ( x) 的定义域为 R ，满足 f (x 1)2 f (x) ，且当 x (0,1] 时，f (x)x(x 1) ．若对任意 x ( , m] ，都有 f ( x)8，则 m 的取值范围是9A ．,9B ．,743C ．,5D ．,823（2018·3）函数 e x e xf ( x)2的图象大致为x（2018·11）已知f (x) 是定 域 ( ,) 的奇函数， 足f (1 x) f (1 x) ．若 f (1)2 ，f (1) f (2) f (3) Lf (50)A ． 50B ． 0C ． 2D ． 50（2017·11）若 x2 是函数 f ( x) ( x 2 ax1)e x 1` 的极 点， f ( x) 的极小 （）A. 1B. 2e 3C. 5e 3D.1（ 2016·12）已知函数f ( x)( x R ) 足 f ( x)2 f (x) ，若函数 yx 1与 yf (x) 像的x交点 ( x 1 , y 1 ) ， (x 2 , y 2 ) ，⋯， ( x m , y m ) ，m( x i y i )（）i 1A ． 0B ．mC ． 2mD ．4m（2015·5） 函数 f ( x)1 log2 (2x) ( x1) 2) f (l og 2 12) （）2x1( x， f (1)A ． 3B ． 6C ．9D ． 12（ 2015·10）如 ， 方形 ABCD 的 AB=2，BC=1，O 是 AB 的中点，点 P 沿着 BC ，CD 与DA 运 ， ∠ BOP=x. 的 像大致（将 点 P 到 A ， B 两点距离之和表示 x 的函数 f （ x ）， f （ x ））A ．B ．C ．D ．（ 2015·12）函 数f ( x) 是 奇 函 数f (x)(xR) 的函 数 ， f (1)0 ， 当x>0，xf ( x)f (x)0 ， 使得f (x) >0 成立的x 的取 范 是（）A ． ( , 1) U (0,1)B ． (1,0)U (1, )C ． (, 1)U ( 1,0)D ． (0,1)U (1,)（ 2014·8）设曲线 y=ax- ln(x+1)在点 (0,0)处的切线方程为 y=2x ，则 a=（ ）A ． 0B ． 1C ．2D ． 3（2014·12）设函数 f ( x)3 sinx，若存在 f (x) 的极值点 x 0 满足 x 02[ f ( x 0 )] 2 m 2 ，则mm 的取值范围是（ ）A ． ( , 6) U (6,+ )B ． (, 4) U (4,+ )C ．( , 2) U (2,+)D ． (, 1)U (4,+)（2013·8）设 a log 3 6 ， b log 5 10 ， c log 7 14 ，则（）A. c b aB. b c aC. a c bD. a b c（2013·10）已知函数 f (x)32bxc ，下列结论中错误的是（）xaxA. x 0R, f (x 0 )B. 函数 y f (x) 的图像是中心对称图形C. 若 x 0 是 f ( x) 的极小值点，则 f (x) 在区间 ( , x 0 ) 单调递减D. 若 x 0 是 f ( x) 的极值点，则f ( x 0 ) 0（2012·10）已知函数 f ( x)1，则 yf ( x) 的图像大致为（）ln( x 1)xy y y y 1111o 1xo 1xo 1xo 1xA.B.C.D.（2012·12）设点 P 在曲线 y1 e x 上，点 Q 在曲线 y ln(2 x) 上，则 | PQ |的最小值为（）2A. 1 ln 2B.2 (1 ln 2)C. 1 ln 2D. 2(1 ln 2)（2011·2）下列函数中，既是偶函数又在 （ 0，+ ））x 2单调递增的函数是（． y x 3 ． y | x | 1 ． y 1 ． y 2 |x|A B CD（2011·9）由曲线 yx ，直线 y x2 及 y 轴所围成的图形的面积为（）A ．10B ． 4C ．16D ． 633（2011·12）函数 y1 的图像与函数 y2sin x,( 2 x4) 的图像所有交点的横坐标之x 1和等于（）A ． 2B ． 4C ．6D ． 8二、填空题（· ）已知 f ( x) 是奇函数，且当 x 0时，ax8 ，则 a2019 14f (x)e . 若 f (ln 2)__________．（2018·13）曲线 y 2ln( x 1) 在点 (0, 0) 处的切线方程为__________ ．（2014·15）已知偶函数 f (x)在[0, +∞)单调递减， f (2)=0. 若 f (x- 1)>0，则 x 的取值范围是_________.（2016·16）若直线 y = kx+b 是曲线 y = lnx+2 的切线，也是曲线 y = ln(x+1)的切线，则 b =.三、解答题（2019·20）已知函数x1 f x ln x.x 1（1）讨论 f(x)的单调性，并证明 f(x)有且仅有两个零点；（ 2）设 x0是 f(x)的一个零点，证明曲线 y=lnx 在点 A(x0，lnx0)处的切线也是曲线y e x的切线 .（2018·21）已知函数 f (x)e x ax2 ．（ 1）若 a 1 ，证明：当x ≥ 0时， f ( x) ≥ 1；（ 2）若 f(x) 在 (0, )只有一个零点，求 a ．（2017·21）已知函数f ( x)ax2ax x ln x, 且 f (x)0 .（ 1）求 a；（ 2）证明：f ( x)存在唯一的极大值点x0，且 e 2 f (x0 ) 2 2.（2016·21）（Ⅰ）讨论函数f (x)x 2 e x的单调性，并证明当 x >0时，( x 2) e x x 2 0 ；x2e x ax a( x 0)有最小值 .设 g (x)的最小值为h( a) ，（Ⅱ）证明：当 a [0,1) 时，函数 g( x)=x2求函数 h( a) 的值域.（2015·21）设函数 f (x) e mx x2mx .（Ⅰ）证明： f (x)在（ - ∞， 0）单调递减，在（0， +∞）单调递增；（Ⅱ）若对于任意 x1,， x2∈ [- 1，1]，都有｜ f(x1)- f (x2)｜≤e- 1，求 m 的取值范围．（2014·21）已知函数 f (x)e x e x2x .（Ⅰ）讨论 f ( x)的单调性；（Ⅱ）设 g ( x) f (2 x)4bf (x) ，当x0 时，g( x)0 ，求b的最大值；（Ⅲ）已知 1.41422 1.4143，估计 ln2 的近似值（精确到0.001） .（2013·21）已知函数 f (x)e x ln( x m) .（Ⅰ）设 x0 是 f (x) 的极值点，求m ，并讨论 f ( x)的单调性；（Ⅱ）当 m 2 时，证明 f (x)0 .x 112（2012·21）已知函数f ( x) f (1)e f (0) x x .（Ⅰ）求 f (x) 的解析式及单调区间；（Ⅱ）若 f (x) 1 x2ax b ，求 (a1)b 的最大值.2（ 2011·21）已知函数f ( x)a ln x b，曲线y f (x)在点(1, f (1))处的切线方程为x 1 xx 2 y 30 .（Ⅰ）求a、 b 的值；（Ⅱ）如果当 x0 ，且 x 1 时， f (x)ln x k，求 k 的取值范围 .x 1x。
2011—2019年高考真题全国卷1理科数学分类汇编——5.平面向量
2011—2019年高考真题全国卷1理科数学分类汇编——5.平面向量一、选择题【2019，7】已知非零向量,a b r r 满足2a b =r r ，且()a b b -⊥r r r ，则a r 与b r 的夹角为（ ）A.6π B.3π C.23π D.56π 【2018，6】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =u u u r （ ）A ．3144AB AC -u u u r u u u r B ．1344AB AC -u u u r u u u r C ．3144AB AC +u u u r u u u rD ．1344AB AC +u u u r u u u r 【2015，7】设D 为ABC ∆错误!未找到引用源。
所在平面内一点3BC CD =u u u r u u u r ，则（ ）A ．1433AD AB AC =-+u u u r u u u r u u u r B ．1433AD AB AC =-u u u r u u u r u u u r C ．4133AD AB AC =+u u u r u u u r u u u r D ．4133AD AB AC =-u u u r u u u r u u u r 【2011，10】已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦ 其中的真命题是（ ）A ．14,P PB ．13,P PC ．23,P PD ．24,P P二、填空题【2017，13】已知向量a ，b 的夹角为60°，|a |=2， | b |=1，则| a +2 b |= ．【2016，13】设向量a )1,(m =，b )2,1(=，且|a +b ||2=a ||2+b 2|，则=m ．【2014，15】已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+u u u r u u u r u u u r ，则AB u u u r 与AC uuu r 的夹角为 ． 【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t )b ．若b ·c ＝0，则t ＝__________．【2012，13】已知向量a r ，b r 夹角为45°，且||1a =r ，|2|10a b -=r r ||b =r _________．5．平面向量（解析版）一、选择题【2019，7】已知非零向量,a b r r 满足2a b =r r ，且()a b b -⊥r r r ，则a r 与b r 的夹角为（ ）A.6π B.3π C.23π D.56π 【解析】设a r 与b r 的夹角为θ，∵()a b b -⊥r r r ∴2()cos a b b a b b θ-⋅=-r r r r r r =0∴1cos =2θ ∴=3πθ.选B【2018，6】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =u u u r （ ）A ．3144AB AC -uu u r uu u r B ．1344AB AC -u u u r u u u r C ．3144AB AC +u u u r u u u r D ．1344AB AC +u u u r u u u r【解析】选A【2015，7】设D 为ABC ∆错误!未找到引用源。
2011-2019年高考数学全国Ⅲ卷理科真题分类整理分析
年份
题目
答案
2015 年 （3）设命题 P： ∃ n∈N， n2 > 2n ，则 ¬ P 为
C
全国 2
理 （A） ∀ n∈N, n2 > 2n （B） ∃ n∈N, n2 ≤ 2n
（C） ∀ n∈N, n2 ≤ 2n （D） ∃ n∈N, n2 = 2n
二、复数小题：4 年 4 考，每年 1 题，以四则运算为主，偶尔与其他知识交汇，难度较小．一般 涉及考查概念：实部、虚部、共轭复数、复数的模、对应复平面的点坐标等．
B
A．3
B．2
C．1
D．0
2016 年 （1）设集合 S = {x (x− 2)(x− 3) ≥ 0}, T = {x | x > 0} ，则 S I T=
D
(A) [2，3]
(C) [3,+ ∞ ）
(B)（- ∞ ，2] U [3,+ ∞ ） (D)（0，2] U [3,+ ∞ ）
2
2．简易逻辑小题：4 年 0 考．这个考点包含的小考点较多，并且容易与函数，不等式、数列、三 角函数、立体几何交汇，热点就是“充要条件”；难点：否定与否命题；冷点：全称与特称，思想： 逆否．要注意，这类题可以分为两大类，一类只涉及形式的变换，比较简单，另一类涉及命题真 假判断，比较复杂．下面举一个全国 1 卷的例子．
2011-2019 年高考数学全国Ⅲ卷理 科真题分类整理分析
全国卷类型
使用地区
甲卷（新课标 II 卷） 甘肃、青海、内蒙古、黑龙江、吉林、辽宁、宁夏、新疆、陕西、重庆
乙卷（新课标 I 卷） 福建、河南、河北、山西、江西、湖北、湖南、广东、安徽、山东
丙卷（新课标 III 卷） 云南、广西、贵州、四若 z = 1+ 2i ，则 4i = zz −1
2011—2019年高考真题全国卷1理科数学分类汇编——1.集合与常用逻辑用语
2011—2019年高考真题全国卷1理科数学分类汇编——1.集合与常用逻辑用语一、选择题【2019，1】已知集合}24|{<<-=x x M ，}06|{2<--=x x x N ，则=N M I （ ）A.}34|{<<-x xB.}24|{-<<-x xC. }22|{<<-x xD. }32|{<<x x【2018，2】已知集合{}02|2>--=x x x A ，则=A C R ( )A.{}21|<<-x xB.{}21|≤≤-x xC.{}{}2|1|>-<x x x x YD.{}{}2|1|≥-≤x x x x Y【2017，1】已知集合{}1A x x =<，{}31x B x =<，则（ ）A ．{|0}AB x x =<I B ．A B =R UC ．{|1}A B x x =>UD ．A B =∅I【2016，1】设集合}034{2<+-=x x x A ，}032{>-=x x B ，则A B =I （ ）A ．)23,3(-- B ．)23,3(- C ．)23,1( D ．)3,23( 【2015，3】设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n =【2014，1】已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( ) A ．[-2,-1] B ．[-1,2） C ．[-1,1] D ．[1,2）【2013，1】已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( )A ．A ∩B ＝ B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ）A ．3B ．6C ．8D ．101．集合与常用逻辑用语（解析版）一、选择题【2019，1】已知集合}24|{<<-=x x M ，}06|{2<--=x x x N ，则=N M I （ ）A.}34|{<<-x xB.}24|{-<<-x xC. }22|{<<-x xD. }32|{<<x x【解析】由题知,}32|{<<-=x x N ,又}24|{<<-=x x M ,则}22|{<<-=x x N M I ，故选C .【2018，2】已知集合{}02|2>--=x x x A ，则=A C R ( )A.{}21|<<-x xB.{}21|≤≤-x xC.{}{}2|1|>-<x x x x YD.{}{}2|1|≥-≤x x x x Y 【解析】因为2{20}=-->A x x x ，所以2{|20}=--R ≤A x x x ð{|12}=-≤≤x x ，故选B ． 【2017，1】已知集合{}1A x x =<，{}31x B x =<，则（ ）A ．{|0}AB x x =<I B ．A B =R UC ．{|1}A B x x =>UD ．A B =∅I【解析】{}1A x x =<，{}{}310x B x x x =<=<，∴{}0A B x x =<I ，{}1A B x x =<U ，故选A 【2016，1】设集合}034{2<+-=x x x A ，}032{>-=x x B ，则A B =I （ ）A ．)23,3(-- B ．)23,3(- C ．)23,1( D ．)3,23( 【解析】{}13A x x =<<，{}32302B x x x x ⎧⎫=->=>⎨⎬⎩⎭．故332A B x x ⎧⎫=<<⎨⎬⎩⎭I ．故选D ． 【2015，3】设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = 解析：命题p 含有存在性量词（特称命题），是真命题（如3n =时），则其否定（p ⌝）含有全称量词（全称命题），是假命题，故选C ．.【2014，1】已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( ) A .[-2,-1] B .[-1,2） C .[-1,1] D .[1,2）【解析】∵{|13}A x x x =≤-≥或，B={}22x x -≤<，∴A B ⋂={}21x x -≤≤，选A.【2013，1】已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( )A ．A ∩B ＝ B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B解析：∵x (x －2)＞0，∴x ＜0或x ＞2，∴集合A 与B 可用图象表示为：由图象可以看出A ∪B ＝R ，故选B. 【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ）A ．3B ．6C ．8D ．10【解析】由集合B 可知，x y >，因此B={（2，1），（3，2），（4，3），（5，4），（3，1），（4，2），（5，3），（4，1），（5，2），（5，1）}，B 的元素10个，所以选择D ．。
2011—2020年十年新课标全国卷高考数学分类汇编——1
2011—2020年十年新课标全国卷高考数学分类汇编——1.集合2011年至2020年的新课标全国卷数学试题共包含8套全国卷，包括全国Ⅰ卷、Ⅱ卷、Ⅲ卷、新高考Ⅰ卷和新高考Ⅱ卷。
本资料根据全国卷的特点编写，共包含14个专题，包括集合、复数、逻辑、数学文化、新定义、平面向量、不等式、数列、三角函数与解三角形、解析几何、概率与统计、程序框图、坐标系与参数方程、不等式选讲。
通过掌握各种题型，可以把握全国卷命题的灵魂。
集合与简易逻辑是数学试题中的一个重要专题。
以下是一些选择题的例子：2020年新高考Ⅰ卷第一题：设集合A={x|1≤x≤3}，B={x|2<x<4}，则A∪B=（）A．{x|2<x≤3} B．{x|2≤x≤3} C．{x|1≤x<4} D．{x|1<x<4}2020年全国卷Ⅰ理科第二题：设集合A={x|x2–4≤0}，B={x|2x+a≤0}，且A∩B={x|–2≤x≤1}，则a=（）A．–4 B．–2 C．2 D．42020年全国卷Ⅰ文科第一题：已知集合A={x|x23x40}，B={4,1,3,5}，则B={x|1<x<4}。
2020年全国卷Ⅱ理科第一题：已知集合U={−2，−1.1，2，3}，A={−1.1}，B={1，2}，则CUAA．{−2，3} B．{−2，2，3} C．{−2，−1.3} D．{−2，−1.2，3}2020年全国卷Ⅱ文科第一题：已知集合A={x||x|1，x∈Z}，则A∩B={–2，2}。
2020年全国卷Ⅲ理科第一题：已知集合A{(x,y)|x,y N*,y x}，B{(x,y)|x y8}，则A∩B中元素的个数为3.2020年全国卷Ⅲ文科第一题：已知集合A1，2，3，5，7，11，B x|3x15，则A∩B中元素的个数为4.2019·全国卷Ⅰ，理1)已知集合M={x|-4<x<2}，N={x|x^2-x-6<0}，则M的正确表示为A。
2011-2019年新课标全国卷2理科数学试题分类汇编——12.概率、统计
2011年—2018年新课标全国卷Ⅱ理科数学试题分类汇编（逐题解析版）12．排列组合、概率统计一、选择题(2019·全国卷Ⅱ，理5)演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，不变的数字特征是（ ）A ．中位数B ．平均数C ．方差D ．极差（2018·8）我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30723=+．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（ ） A ．112B ．114C ．115D ．118（2017·6）安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（ ）A ．12种B ．18种C ．24种D ．36种 （2016·5）如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（ ）A ．24B ．18C ．12D ．9（2016·10）从区间[0，1]随机抽取2n 个数x 1，x 2，…，x n ，y 1，y 2，…，y n ，构成n 个数对11(,)x y ，22(,)x y ，…，(,)n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为（ ）A ．4nmB ．2n mC ．4mnD ．2mn（2015·3）根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A ．逐年比较，2008年减少二氧化硫排放量的效果最显著.B ．2007年我国治理二氧化硫排放显现成效.C ．2006年以来我国二氧化硫年排放量呈减少趋势.D．2006年以来我国二氧化硫年排放量与年份正相关.（2014·5）某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A．0.8 B．0.75 C．0.6 D．0.45（2012·2）将2名教师，4名学生分成两个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由一名教师和2名学生组成，不同的安排方案共有（）A. 12种B. 10种C. 9种D. 8种（2011·4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）A．13B．12C．23D．34二、填空题(2019·全国卷Ⅱ，理13)我国高铁发展迅速，技术先进．经统计，在经停某站的高铁列车中，有10个车次的正点率为0．97，有20个车次的正点率为0．98，有10个车次的正点率为0．99，则经停该站高铁列车所有车次的平均正点率的估计值为__________．（2017·13）一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X表示抽到的二等品件数，则D X=．（2016·15）有三张卡片，分别写有1和2，1和3，2和3. 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是.（2013·14）从n个正整数1，2，…，n中任意取出两个不同的数，若取出的两数之和等于5的概率为114，则n=______.（2012·15）某一部件由三个电子元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作. 设三个电子元件的使用寿命（单位：小时）服从正态分布N(1000，502)，且各元件能否正常工作互相独立，那么该部件的使用寿命超过1000小时的概率为.三、解答题(2019·全国卷Ⅱ，理18)11分制乒乓球比赛，每赢一球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10：10平后，甲先发球，两人又打了X 个球该局比赛结束．（1）求P（X=2）；（2）求事件“X=4且甲获胜”的概率．（2018·18）下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测改地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型①：30.413.5y t =-+：根据2010年至2016年的数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型②：9917.5y t =+． （1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； （2）你认为用哪个模型得到的预测值更可靠？并说明理由．（2017·18）淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg ）某频率直方图如下：（1）设两种养殖方法的箱产量相互独立，记A 表示事件：旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A 的概率；（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：22()()()()()n ad bc K a b c d a c b d -=++++（2016·18）某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上年度的出险次数的关联如下：（Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；（Ⅲ）求续保人本年度的平均保费与基本保费的比值.（2015·18）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：记事件C ：“A 地区用户的满意度等级高于B 地区用户的满意度等级”，假设两地区用户的评价结果相互独立，根据所给数据，以事件发生的频率作为相应事件发生的概率，求C 的概率．（2014·19）某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121ˆnii i ni i tty y btt==--=-∑∑，ˆˆa y bt=-.（2012·18）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花做垃圾处理. （Ⅰ）若花店某天购进16枝玫瑰花，求当天的利润y （单位：元）关于当天需求量n （单位：枝，n ∈N ）的函数解析式；（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：以100天记录的各需求量的频率作为各需求量发生的概率.（i ）若花店一天购进16枝玫瑰花，X 表示当天的利润（单位：元），求X 的分布列、数学期望及方差； （ii ）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.t（2011·19）某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：A配方的频数分布表B配方的频数分布表（Ⅰ）分别估计用A配方，B配方生产的产品的优质品率；（Ⅱ）已知用B配方生成的一件产品的利润y(单位：元)与其质量指标值t的关系式为2(94)2(94102)4(102),t<y,t<,t-⎧⎪=≤⎨⎪≥⎩，从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望.（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）2011年—2018年新课标全国卷Ⅱ理科数学试题分类汇编12．排列组合、概率统计（解析版）一、选择题(2019·全国卷Ⅱ，理5)演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，不变的数字特征是（ ）A ．中位数B ．平均数C ．方差D ．极差【答案】A 解析：根据题意，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分，7个有效评分与9个原始评分相比，最中间的一个数不变，即中位数不变．（2018·新课标Ⅱ，8）我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30723=+．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（ ） A ．112B ．114C ．115D ．118【答案】C 解析：30以内的素数有10个，满足和为30的素数对有3对，概率为2103314515C ==，选C. （2017·6）【解析】解法一：将三人分成两组，一组为三个人，有336A =种可能，另外一组从三人在选调一人，有133C =种可能；两组前后在排序，在对位找工作即可，有222A =种可能；共计有36种可能. 解法二：工作分成三份有246C =种可能，在把三组工作分给3个人有336A =可能，共计有36种可能. （2016·5）B 解析：E F →有6种走法，F G →有3种走法，由乘法原理知，共6318⨯=种走法，故选B ．（2016·10）C 解析：由题意得：()()12i i x y i n =⋅⋅⋅，，，，在如图所示方格中，而平方和小于1的点均在如图所示的阴影中，由几何概型概率计算公式知π41m n=，∴4πmn=，故选C ．（2015·3）D 解析：由柱形图可知，从2006年以来，我国二氧化硫排放量呈下降趋势，所以二氧化硫排放量与年份负相关，故选D.（2014·5）A 解析：设 A =“某一天的空气质量为优良”，B =“随后一天的空气质量为优良”，则()0.6(|)0.8()0.75P AB P B A P A ===. （2012·2）A 解析：只需选定安排到甲地的1名教师2名学生即可，共有1224C C 种安排方案.（2011·4）A 解析：每个同学参加的情形都有3种，故两个同学参加一组的情形有9种，而参加同一组的情形只有3种，所求的概率为P =3193=，故选A. 二、填空题(2019·全国卷Ⅱ，理13)我国高铁发展迅速，技术先进．经统计，在经停某站的高铁列车中，有10个车次的正点率为0．97，有20个车次的正点率为0．98，有10个车次的正点率为0．99，则经停该站高铁列车所有车次的平均正点率的估计值为__________． 【答案】0.98 解析：0.98200.97100.99100.9840⨯+⨯+⨯=.（2017·13）1.96【解析】随机变量()100,0.02∽B X ，()()1 1.96D X np p =-=.（2016·15）(1,3)解析：由题意得：丙不拿（2，3），若丙（1，2），则乙（2，3），甲（1，3）满足； 若丙（1，3），则乙（2，3），甲（1，2）不满足，故甲（1，3）.（2013·14）8解析：从1，2，…，n 中任取两个不同的数共有2C n 种取法，两数之和为5的有(1,4)，(2,3)，共2种，所以221C 14n =，即24111142n n n n ==(-)(-)，亦即n 2-n -56=0，解得n =8.（2012·15）38解析：由已知可得，三个电子元件使用寿命超过1000小时的概率均为12，所以该部件的使用寿命超过1000小时的概率为2113[1(1)]228--⨯=. 三、解答题(2019·全国卷Ⅱ，理18)11分制乒乓球比赛，每赢一球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10：10平后，甲先发球，两人又打了X 个球该局比赛结束．（1）求P （X =2）；（2）求事件“X =4且甲获胜”的概率．18．解：（1）X =2就是10：10平后，两人又打了2个球该局比赛结束，则这2个球均由甲得分，或者均由乙得分．因此P （X =2）=0.5×0.4+（1–0.5）×（1–0.4）=0.5．（2）X =4且甲获胜，就是10：10平后，两人又打了4个球该局比赛结束，且这4个球的得分情况为：前两球是甲、乙各得1分，后两球均为甲得分．因此所求概率为[0.5×（1–0.4）+（1–0.5）×0.4]×0.5×0.4=0.1．【解答】解：（1）设双方10：10平后的第k 个球甲获胜为事件A k （k ＝1，2，3，…）， 则P （X ＝2）＝P （A 1A 2）+P （）＝P （A 1）P （A 2）+P （）P （）＝0.5×0.4+0.5×0.6＝0.5． （2）P （X ＝4且甲获胜）＝P （A 2A 2A 4）+P （）＝P （）P （A 2）P （A 3）P （A 4）+P （A 1）P （）P （A 3）P （A 4）＝（0.5×0.4+0.5×0.6）×0.5×0.4＝0.1．（2018·新课标Ⅱ，18）下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测改地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型①：30.413.5y t =-+：根据2010年至2016年的数据（时间变量t 的值依次为127⋅⋅⋅，，，）建立模型②：9917.5y t =+． （1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； （2）你认为用哪个模型得到的预测值更可靠？并说明理由．解析：（1）利用模型①,该地区2018年的环境基础设施投资额的预测值为ˆ30.413.519226.1y=-+⨯=(亿元).利用模型②,该地区2018年的环境基础设施投资额的预测值为ˆ9917.59256.5y=+⨯=(亿元). （2）利用模型②得到的预测值更可靠. 理由如下：（ⅰ）从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线30.413.5y t =-+上下.这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加，2010年至2016年的数据对应的点位于一条直线的附近，这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型ˆ9917.5yt =+可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.（ⅱ）从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理.说明利用模型②得到的预测值更可靠. 以上给出了2种理由，考生答出其中任意一种或其他合理理由均可得分.（2017·18）淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg ）某频率直方图如下：（1）设两种养殖方法的箱产量相互独立，记A 表示事件：旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A 的概率；22()()()()()n ad bc K a b c d a c b d -=++++（2017·18）解析：（Ⅰ）旧养殖法的箱产量低于50kg 的频率为0.012×5+0.014×5+0.024×5+0.034×5+0.040×5=0.62，由于两种养殖方法的箱产量相互独立，于是P （A ）=0.62×0.66=0.4092（Ⅱ）旧养殖法的箱产量低于50kg 的有100×0.62=62箱，不低于50kg 的有38箱，新养殖法的箱产量不低于50kg 的有100×0.66=66箱，低于50kg 的有34箱，得到2×2列联表如下：所以22200(62663438)122515.7059610410010078K ⨯⨯-⨯==≈⨯⨯⨯ 2 6.635K ∴>，所以有99%的把握认为箱产量与养殖方法有关。
2011—2019年高考真题全国卷1理科数学分类汇编——8.立体几何
2011—2019年高考真题全国卷1理科数学分类汇编——8.立体几何一、选择题【2019.12】已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为 A ．68π B ．64π C ．62πD ．6π【2018,7】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为（ ） A ．172B ．52C ．3D ．2【2018，12】已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（ ） A ．334B ．233C ．324D ．32【2017，7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ） A ．10 B ．12 C ．14 D ．16【2016，11】平面α过正方体1111D C B A ABCD -的顶点A ，//α平面11D CB ，αI 平面ABCD m =，I α平面n A ABB =11，则n m ,所成角的正弦值为A ．23 B ．22 C ．33 D ．31 【2016，6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是328π，则它的表面积是（ ） A ．π17 B ．π18 C ．π20 D ．π28【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1．62立方尺，圆周率约为3，估算出堆放的米约有（）A．14斛B．22斛C．36斛D．66斛【2015，11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为1620π+，则r=（）A．1 B．2 C．4 D．8【2015年，11题】【2014年，12题】【2013年，6题】【2014，12】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为（）A．62B．42C．6 D．4【2013，6】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为()A．500π3cm3B．866π3cm3 C．1372π3cm3D．2048π3cm3【2013，8】某几何体的三视图如图所示，则该几何体的体积为()．A．16＋8π B．8＋8π C．16＋16π D．8＋16π【2013年，8】 【2012年，7】 【2011年，6】 【2012，7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）A ．6B ．9C ．12D ．15【2012，11】已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC =2，则此棱锥的体积为（ ） A ．26B ．36C ．23D ．22【2011，6】在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（ ）二、填空题【2011，15】已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,23AB BC ==,则棱锥O ABCD -的体积为 ．三、解答题【2019年高考全国Ⅰ卷理数】如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ；（2）求二面角A −MA 1−N 的正弦值．【2018,18】如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥.（1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值.【2017，18】如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o（1）证明：平面P AB ⊥平面P AD ；（2）若P A =PD =AB =DC ,90APD ∠=o ,求二面角A -PB -C 的余弦值．【2016，18】 如图，在以F E D C B A ,,,,,为顶点的五面体中，面ABEF 为正方形，︒=∠=90,2AFD FD AF ，且二面角E AF D --与二面角F BE C --都是︒60．（Ⅰ）证明：平面⊥ABEF 平面EFDC ；（Ⅱ）求二面角A BC E --的余弦值．【2015，18】如图，四边形ABCD 为菱形，120ABC ∠=o，,E F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，2BE DF =，AE EC ⊥．ABCDE F（I ）证明：平面AEC ⊥平面AFC ；（II ）求直线AE 与直线CF 所成角的余弦值．【2014，19】如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥．(Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC ，求二面角111A A B C --的余弦值．【2013，18】如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°．(1)证明：AB ⊥A 1C ；(2)若平面ABC ⊥平面AA 1B 1B ，AB ＝CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值．【2012，19】如图，直三棱柱ABC －A 1B 1C 1中，AC=BC=21AA 1，D 是棱AA 1的中点，DC 1⊥BD ． （1）证明：DC 1⊥BC ；（2）求二面角A 1－BD －C 1的大小．A 1【2011，18】如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD．(Ⅰ)证明：P A⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值．C7．立体几何（解析版）一、选择题1．【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为 A ．68π B ．64π C ．62πD ．6π【答案】D【解析】解法一：,PA PB PC ABC ==Q △为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CE AC C EF =∴⊥I 平面PAC ，∴PB ⊥平面PAC ，2APB PA PB PC ∴∠=90︒,∴===，P ABC ∴-为正方体的一部分，22226R =++=，即364466,π62338R V R =∴=π=⨯=π，故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC Q △为边长为2的等边三角形，3CF ∴=，又90CEF ∠=︒，213,2CE x AE PA x ∴=-==， AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =Q ，D \为AC 的中点，1cos 2AD EAC PA x∠==，2243142x x x x+-+∴=， 22122122x x x ∴+=∴==，，，2PA PB PC ∴===， 又===2AB BC AC ，,,PA PB PC ∴两两垂直，22226R ∴=++=，62R ∴=，344666338V R ∴=π=π⨯=π，故选D.8．【2018年理新课标I 卷】已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为A. 334B. 233C. 324D. 32 【答案】A详解：根据相互平行的直线与平面所成的角是相等的，所以在正方体ABCD-A1B1C1D1中，平面AB1D1与线AA1,A1B1,A1D1所成的角是相等的，所以平面AB1D1与正方体的每条棱所在的直线所成角都是相等的，同理平面C1BD 也满足与正方体的每条棱所在的直线所成角都是相等，要求截面面积最大，则截面的位置为夹在两个面AB1D1与C1BD 中间的，且过棱的中点的正六边形，且边长为22，所以其面积为S=6×34⋅(22)2=334，故选A.点睛：该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.+【2018年理新课标I 卷】某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为A. 217B. 25C. 3D. 2 【答案】B【解析】分析：首先根据题中所给的三视图，得到点M 和点N 在圆柱上所处的位置，点M 在上底面上，点N 在下底面上，并且将圆柱的侧面展开图平铺，点M 、N 在其四分之一的矩形的对角线的端点处，根据平面上两点间直线段最短，利用勾股定理，求得结果.详解：根据圆柱的三视图以及其本身的特征，可以确定点M 和点N 分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，所以所求的最短路径的长度为42+22=25，故选B.【2017，7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）A ．10B ．12C ．14D ．16（7）【解析】由三视图可画出立体图，该立体图平面内只有两个相同的梯形的面，()24226S =+⨯÷=梯，6212S =⨯=全梯，故选B ；【2016，11】平面α过正方体1111D C B A ABCD -的顶点A ，//α平面11D CB ，αI 平面ABCD m =，I α平面n A ABB =11，则n m ,所成角的正弦值为A ．23 B ．22 C ．33 D ．31 【解析】如图所示：αAA 1B1DC1D 1∵11CB D α∥平面，∴若设平面11CB D I 平面1ABCD m =，则1m m ∥ 又∵平面ABCD ∥平面1111A B C D ，结合平面11B D C I 平面111111A B C D B D = ∴111B D m ∥，故11B D m ∥，同理可得：1CD n ∥故m 、n 的所成角的大小与11B D 、1CD 所成角的大小相等，即11CD B ∠的大小． 而1111B C B D CD ==（均为面对交线），因此113CD B π∠=，即113sin CD B ∠=． 故选A ．【2016，6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是328π，则它的 表面积是（ ）A ．π17B ．π18C ．π20D ．π28【解析】：原立体图如图所示：是一个球被切掉左上角的18后的三视图表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S ⨯⨯⨯⨯πππ，故选A ． 【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（ ）A ．14斛B ．22斛C ．36斛D ．66斛解析：284R π=，圆锥底面半径16R π=，米堆体积21320123V R h ππ==，堆放的米约有221.62V≈，选B ．.【2015，11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示. 若该几何体的表面积为1620π+，则r =（ ）A ．1B ．2C ．4D ．8解析：由正视图和俯视图知，该几何体是半球和半个圆柱的组合体，圆柱的半径与球的半径都r ，圆柱的高为2r ，其表面积为2222142225416202r r r r r r r r πππππ⨯+⨯++⨯=+=-，解得2r =，故选B ．. 【2014，12】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为（ ）A .62B .42C .6D .4【解析】如图所示，原几何体为三棱锥D ABC -， 其中4,42,25AB BC AC DB DC =====，()24246DA =+=，故最长的棱的长度为6DA =，选C【2013，6】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )A ．500π3cm 3 B ．866π3cm 3 C ．1372π3cm 3 D ．2048π3cm 3解析：设球半径为R ，由题可知R ，R －2，正方体棱长一半可构成直角三角形，即△OBA 为直角三角形，如图．BC ＝2，BA ＝4，OB ＝R －2，OA ＝R ，由R 2＝(R －2)2＋42，得R ＝5， 所以球的体积为34500π5π33=(cm 3)，故选A. 【2013，8】某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π 答案：A解析：由三视图可知该几何体为半圆柱上放一个长方体，由图中数据可知圆柱底面半径r ＝2，长为4，在长方体中，长为4，宽为2，高为2，所以几何体的体积为πr 2×4×12＋4×2×2＝8π＋16.故选A.【2012，7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）A ．6B ．9C ．12D ．15【解析】由三视图可知，该几何体为三棱锥A-BCD ， 底面△BCD 为 底边为6，高为3的等腰三角形，侧面ABD ⊥底面BCD ， AO ⊥底面BCD ， 因此此几何体的体积为11(63)3932V =⨯⨯⨯⨯=，故选择B ．【2012，11】已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC =2，则此棱锥的体积为（ ） A ．26B ．36C ．23D ．22【解析】如图所示，根据球的性质，知⊥1OO 平面ABC ，则C O OO 11⊥．在直角C OO 1∆中，1=OC ，331=C O ， ODA所以36)33(122121=-=-=C O OC OO ． 因此三棱锥S －ABC 的体积6236433122=⨯⨯⨯==-ABC O V V ，故选择A ．【2011，6】在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（ ）解析：条件对应的几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的．故选D 二、填空题【2011，15】已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,23AB BC ==,则棱锥O ABCD -的体积为 ．解析：设ABCD 所在的截面圆的圆心为M,则AM=221(23)6232+=,OM=224(23)2-=，16232833O ABCD V -=⨯⨯⨯=.三、解答题【2019年高考全国Ⅰ卷理数】如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点． （1）证明：MN ∥平面C 1DE ； （2）求二面角A −MA 1−N 的正弦值． 【答案】（1）见解析；（2）10. 【解析】（1）连结B 1C ，ME ． 因为M ，E 分别为BB 1，BC 的中点，所以ME ∥B 1C ，且ME =12B 1C ． 又因为N 为A 1D 的中点，所以ND =12A 1D ． 由题设知A 1B 1=P DC ，可得B 1C =P A 1D ，故ME =P ND ， 因此四边形MNDE 为平行四边形，MN ∥ED ． 又MN ⊄平面EDC 1，所以MN ∥平面C 1DE ． （2）由已知可得DE ⊥DA ．以D 为坐标原点，DA uuu r的方向为x 轴正方向，建立如图所示的空间直角坐标系D −xyz ，则(2,0,0)A ，A 1(2，0，4)，(1,3,2)M ，(1,0,2)N ，1(0,0,4)A A =-u u u r ，1(1,3,2)A M =--u u u u r，1(1,0,2)A N =--u u u u r ，(0,3,0)MN =-u u u u r．设(,,)x y z =m 为平面A 1MA 的法向量，则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r m m ， 所以32040x y z z ⎧-+-=⎪⎨-=⎪⎩，．可取(3,1,0)=m ．设(,,)p q r =n 为平面A 1MN 的法向量，则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u ur ，．n n 所以3020q p r ⎧-=⎪⎨--=⎪⎩，．可取(2,0,1)=-n ．于是2315cos ,||25⋅〈〉===⨯‖m n m n m n ， 所以二面角1A MA N --的正弦值为10． 13．【2018年理新课标I 卷】如图，四边形ABCD 为正方形，E,F 分别为AD,BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF⊥BF . （1）证明：平面PEF⊥平面ABFD ； （2）求DP 与平面ABFD 所成角的正弦值. 【答案】(1)证明见解析.(2) 34.(2)结合题意，建立相应的空间直角坐标系，正确写出相应的点的坐标，求得平面ABFD 的法向量，设DP 与平面ABFD 所成角为θ，利用线面角的定义，可以求得sinθ=|HP⋅DP|HP|⋅|DP||=343=34，得到结果. 详解：（1）由已知可得，BF ⊥PF ，BF ⊥EF ，又PF∩EF=F ，所以BF ⊥平面PEF . 又BF⊂平面ABFD ，所以平面PEF ⊥平面ABFD .（2）作PH ⊥EF ，垂足为H .由（1）得，PH ⊥平面ABFD .以H 为坐标原点，HF 的方向为y 轴正方向，|BF|为单位长，建立如图所示的空间直角坐标系H −xyz .由（1）可得，DE ⊥PE .又DP =2，DE =1，所以PE =3.又PF =1，EF =2，故PE ⊥PF .可得PH=32,EH=32.则H(0,0,0),P(0,0,32),D(-1,-32,0),DP=(1,32,32), HP=(0,0,32)为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ，则sinθ=|HP⋅DP|HP|⋅|DP||=343=34. 所以DP 与平面ABFD 所成角的正弦值为34.点睛：该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的证明以及线面角的正弦值的求解，属于常规题目，在解题的过程中，需要明确面面垂直的判定定理的条件，这里需要先证明线面垂直，所以要明确线线垂直、线面垂直和面面垂直的关系，从而证得结果；对于线面角的正弦值可以借助于平面的法向量来完成，注意相对应的等量关系即可.【2017，18】如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o （1）证明：平面P AB ⊥平面P AD ；（2）若P A =PD =AB =DC ,90APD ∠=o ,求二面角A -PB -C 的余弦值．【解析】（1）证明：∵90BAP CDP ∠=∠=︒，∴PA AB ⊥，PD CD ⊥， 又∵AB CD ∥，∴PD AB ⊥，又∵PD PA P =I ，PD 、PA ⊂平面PAD ， ∴AB ⊥平面PAD ，又AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ． （2）取AD 中点O ，BC 中点E ，连接PO ，OE ，∵AB CD ，∴四边形ABCD 为平行四边形，∴OEAB ，由（1）知，AB ⊥平面PAD ，∴OE ⊥平面PAD ， 又PO 、AD ⊂平面PAD ，∴OE PO ⊥，OE AD ⊥， 又∵PA PD =，∴PO AD ⊥，∴PO 、OE 、AD 两两垂直，∴以O 为坐标原点，建立如图所示的空间直角坐标系O xyz -，设2PA =，∴()002D -，、()220B ，、(002P ，，、()202C -，， ∴(022PD =-u u u r ，、222PB =u u u r，，、()2200BC =-u u u r，，设()n x y z =r ,,为平面PBC 的法向量，由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u r ，得2220220x y z x ⎧+=⎪⎨-=⎪⎩， 令1y =，则2z =，0x =，可得平面PBC 的一个法向量(012n =r,,，∵90APD ∠=︒，∴PD PA ⊥，又知AB ⊥平面PAD ，PD ⊂平面PAD ，∴PD AB ⊥，又PA AB A =I ，∴PD ⊥平面PAB ，即PD u u u r是平面PAB 的一个法向量，(022PD =-u u u r ,,，∴3cos 23PD n PD n PD n ⋅===⋅u u u r ru u u r r u u u r r ,，由图知二面角A PB C --为钝角，所以它的余弦值为3． 【2016，18】 如图，在以F E D C B A ,,,,,为顶点的五面体中，面ABEF 为正方形，︒=∠=90,2AFD FD AF ，且二面角E AF D --与二面角F BE C --都是︒60． （Ⅰ）证明：平面⊥ABEF 平面EFDC ；（Ⅱ）求二面角A BC E --的余弦值．【解析】：⑴ ∵ABEF 为正方形，∴AF EF ⊥，∵90AFD ∠=︒，∴AF DF ⊥，∵=DF EF F I∴AF ⊥面EFDC ，AF ⊂面ABEF ，∴平面ABEF ⊥平面EFDC⑵ 由⑴知60DFE CEF ∠=∠=︒，∵AB EF ∥，AB ⊄平面EFDC ，EF ⊂平面EFDC ∴AB ∥平面ABCD ，AB ⊂平面ABCD ∵面ABCD I 面EFDC CD = ∴AB CD ∥，∴CD EF ∥ ∴四边形EFDC 为等腰梯形以E 为原点，如图建立坐标系，设FD a =，()()000020E B a ，，，，()302202a C A a a ⎛⎫⎪ ⎪⎝⎭，，，，， ()020EB a =uu r ，，，322a BC a ⎛⎫=- ⎪ ⎪⎝⎭uu u r ，，，()200AB a =-uu u r ，，，设面BEC 法向量为()m x y z =u r ，，，00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩u r uu r u r uu u r ，即1111203202a y a x ay z ⋅=⎧⎪⎨⋅-⋅=⎪⎩，111301x y z ===-，，)301m =-u r ，ABCDE F设面ABC 法向量为()222n x y z =r，，，=00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩r uu u r r uu u r .即2222320220a x ay az ax ⎧-+=⎪⎨⎪=⎩ 222034x y z ===，，，()034n =r，，，设二面角E BC A --的大小为θ.219cos 31316m n m n⋅===-+⋅+⋅u r r u r r θ，∴二面角E BC A --的余弦值为219-【2015，18】如图，四边形ABCD 为菱形，120ABC ∠=o ，,E F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，2BE DF =，AE EC ⊥.（I ）证明：平面AEC ⊥平面AFC ； （II ）求直线AE 与直线CF 所成角的余弦值.解：（Ⅰ）证明：连接BD ，设BD AC G =I ，连接EG ，FG ，EF . 在菱形ABCD 中，不妨设1GB =，由120ABC ∠=o ，可得3AG GC ==，由BE ⊥平面ABCD ，AB BC =，可知AE EC =.又AE EC ⊥，所以3EG =，且EG AC ⊥.在Rt EBG ∆中，可得2BE =,故22DF =.在Rt FDG ∆中，可得6FG =.在直角梯形BDFE 中，由2BD =，2BE =，22DF =，可得322EF =.因为222EG FG EF +=，所以EG FG ⊥，又AC FG G =I ，则EG ⊥平面AFC . 因为EG ⊂平面AEC ，所以平面AFC ⊥平面AEC . ……6分（Ⅱ）如图，以G 为坐标原点，分别以,GB GC u u u r u u u r 的方向为x 轴，y 轴正方向，||GB u u u r为单位长度，建立空间直角坐标系G xyz -，由（Ⅰ）可得(0,3,0)A -，(1,0,2)E ，2(1,0,)2F -，(0,3,0)E ，(1,3,2)AE =u u u r ，2(1,3,)2CF =--u u u r .故3cos ,3||||AE CF AE CF AE CF ⋅<>==-u u u r u u u ru u u r u u u r u u ur u u u r . 所以直线AE 与直线CF 所成的角的余弦值为33. ……12分 【2014，19】如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥. (Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC求二面角111A A B C --的余弦值.【解析】：(Ⅰ)连结1BC ，交1B C 于O ，连结AO ．因为侧面11BB C C 为菱形，所以1B C 1BC ⊥，且O 为1B C 与1BC 的中点．又1AB B C ⊥，所以1B C ⊥平面ABO ，故1B C AO ⊥又 1B O CO =，故1AC AB =（Ⅱ）因为1AC AB ⊥且O 为1B C 的中点，所以AO=CO 又因为AB=BC ，所以BOA BOC ∆≅∆ 故OA ⊥OB ，从而OA ，OB ，1OB 两两互相垂直．以O 为坐标原点，OB 的方向为x 轴正方向，OB 为单位长，建立如图所示空间直角坐标系O-xyz ． 因为0160CBB ∠=，所以1CBB ∆为等边三角形．又AB=BC ，则30,0,3A ⎛⎫ ⎪ ⎪⎝⎭，()1,0,0B ，130,,03B ⎛⎫ ⎪ ⎪⎝⎭，30,,03C ⎛⎫- ⎪ ⎪⎝⎭ 1330,,33AB ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，1131,0,,A B AB ⎛⎫==- ⎪ ⎪⎝⎭u u u u r u u u r 1131,,0B C BC ⎛⎫==-- ⎪ ⎪⎝⎭u u u u r u u u r 设(),,n x y z =r是平面的法向量，则11100n AB n A B ⎧=⎪⎨=⎪⎩r u u u r g r u u u ur g ，即33030y z x z ⎧-=⎪⎨⎪-=⎪⎩所以可取()1,3,3n =r设m u r 是平面的法向量，则111100m A B n B C ⎧=⎪⎨=⎪⎩u r u u u u rg r u u u u rg，同理可取(1,m =u r 则1cos ,7n m n m n m ==r u rr u r g r u r g ，所以二面角111A A B C --的余弦值为17.【2013，18】如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°.(1)证明：AB ⊥A 1C ；(2)若平面ABC ⊥平面AA 1B 1B ，AB ＝CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值． 证明：(1)取AB 的中点O ，连结OC ，OA 1，A 1B .因为CA ＝CB ，所以OC ⊥AB .由于AB ＝AA 1，∠BAA 1＝60°，故△AA 1B 为等边三角形，所以OA 1⊥AB . 因为OC ∩OA 1＝O ，所以AB ⊥平面OA 1C . 又A 1C ⊂平面OA 1C ，故AB ⊥A 1C . (2)解：由(1)知OC ⊥AB ，OA 1⊥AB .又平面ABC ⊥平面AA 1B 1B ，交线为AB ，所以OC ⊥平面AA 1B 1B ，故OA ，OA 1，OC 两两相互垂直．以O 为坐标原点，OA u u u r 的方向为x 轴的正方向，|OA u u u r|为单位长，建立如图所示的空间直角坐标系O －xyz .由题设知A (1,0,0)，A 1(0，3，0)，C (0,0，3)，B (－1,0,0)．则BC uuu r ＝(1,0，3)，1BB u u u ＝1AA u u r ＝(－1，3，0)，1AC u u u r＝(0，3-，3)． 设n ＝(x ，y ，z )是平面BB 1C 1C 的法向量，则10,0,BC BB ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即30,30.x z x y ⎧+=⎪⎨-+=⎪⎩可取n ＝(3，1，－1)． 故cos 〈n ，1AC u u u r 〉＝11A C A C⋅u u u ru u u r n n ＝10-. 所以A 1C 与平面BB 1C 1C 所成角的正弦值为105. 【2012，19】如图，直三棱柱ABC －A 1B 1C 1中，AC=BC=21AA 1，D 是棱AA 1的中点，DC 1⊥BD ． （1）证明：DC 1⊥BC ；（2）求二面角A 1－BD －C 1的大小．【解析】（1）在Rt DAC ∆中，AD AC =，得：45ADC ︒∠=，同理：1114590A DC CDC ︒︒∠=⇒∠=，得：1DC DC ⊥．又DC 1⊥BD ，DC BD D =I ， 所以1DC ⊥平面BCD ．而BC ⊂平面BCD ，所以1DC BC ⊥．（2）解法一：（几何法）由11,DC BC CC BC BC ⊥⊥⇒⊥面11ACC ADA 1B 1CABC 1BC AC ⇒⊥．取11A B 的中点O ，连接1C O ，OD ． 因为1111AC B C =，所以111C O A B ⊥，因为面111A B C ⊥面1A BD ，所以1C O ⊥面1A BD ，从而1C O BD ⊥，又DC 1⊥BD ，所以BD ⊥面1DC O ，因为OD ⊂平面1DC O ，所以BD OD ⊥． 由BD OD ⊥，BD ⊥DC 1，所以1C DO ∠为二面角A 1－BD －C 1的平面角． 设12AA a =，AC BC a ==，则122aC O =，12CD a =，在直角△1C OD ，1C O OD ⊥，1112C O CD =， 所以130C DO ︒∠=． 因此二面角11C BD A --的大小为30︒．解法二：（向量法）由11,DC BC CC BC BC ⊥⊥⇒⊥面11ACC ABC AC ⇒⊥．又1C C ⊥平面ABC ，所以1C C AC ⊥，1C C BC ⊥，以C 点为原点，CA 、CB 、CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系C xyz -．不妨设AA 1=2，则AC=BC=21AA 1=1， 从而A 1（1，0，2），D （1，0，1）， B （0，1，0），C 1（0，0，2），所以1(0,0,1)DA =u u u u r ，(1,1,1)DB =--u u u r ， 1(1,0,1)DC =-u u u u r．设平面1A BD 的法向量为1111(,,)n x y z =u r， 则11n DA ⊥u r u u u u r ，1n DB ⊥u r u u u r ，所以111100z x y z =⎧⎨-+-=⎩，即1110z x y =⎧⎨=⎩，令11y =，则1(1,1,0)n =u r ．设平面1C BD 的法向量为2222(,,)n x y z =≤u u r ，则21n DC ⊥u u r u u u u r ，2n DB ⊥u u r u u u r， 所以2222200x z x y z -+=⎧⎨-+-=⎩，即22222x z y z =⎧⎨=⎩，令21z =，则2(1,2,1)n =u u r ．所以121212cos ,2||||n n n n n n ⋅<>===⋅u r u u ru r u u r u r u u r 12,30n n <>=︒u r u u r ．因为二面角11C BD A --为锐角，因此二面角11C BD A --的大小为30︒．【2011，18】如图，四棱锥P-ABCD 中，底面ABCD 为平行四 边形，∠DAB=60°,AB=2AD ,PD ⊥底面ABCD . (Ⅰ)证明：P A ⊥BD ；(Ⅱ)若PD =AD ，求二面角A-PB-C 的余弦值．解：（I ）因为60DAB ∠=︒，2AB AD =，由余弦定理得BD =.从而222BD AD AB +=，故BD AD ⊥. 又PD ⊥底面ABCD ，可得BD PD ⊥. 所以BD ⊥平面PAD . 故PA BD ⊥.（II ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D xyz -，则()1,0,0A，()B，()C -，()0,0,1P，()AB =-u u u r，()1PB =-u u u r，()1,0,0BC =-u u u r设平面PAB 的法向量为(),,x y z =n ，则00AB PB ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u rn n，即x z ⎧-⎪-=因此可取=n .设平面PBC 的法向量为m ，则00PB BC ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u rm m ，可取(0,1,m =-. cos ,〈〉==m n 故二面角A PB C --的余弦值为.。
2011到历年高考数学真题(全国卷整理版)
参考公式:如果事件A 、B 互斥，那么 球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件A 、B 相互独立,那么 其中R 表示球的半径 ()()()P A B P A P B = 球的体积公式 如果事件A 在一次试验中发生的概率是p ，那么 334V R π=n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(0,1,2,)k kn k n n P k C p p k n -=-=…2012年普通高等学校招生全国统一考试一、选择题1、 复数131ii-++= Ａ ２+I B 2－I C １＋2ｉ D 1- 2ｉ2、已知集合A={1.3.}，B ＝｛１，m} ，AB ＝A ， 则ｍ=Ａ B 0或3 C 1 D 1或３ 3 椭圆的中心在原点,焦距为4 一条准线为ｘ=-4 ，则该椭圆的方程为A 216x +212y =1 Ｂ 212x +28y ＝1 C 28x ＋24y =1 Ｄ 212x +24y =１４ 已知正四棱柱ＡＢCD － Ａ1B 1C 1D 1中 ,AB=２，C Ｃ１= E 为CC １的中点，则直线AC 1与平面BE Ｄ的距离为Ａ 2 BC Ｄ 1（5）已知等差数列{a n ｝的前n 项和为Ｓn ，a 5＝5，S ５=15,则数列的前1００项和为(A)100101(Ｂ）99101(C)99100(D）101100（6)△ＡBC中,AB边的高为CD,若a·b＝0，｜ａ|＝１,｜b|＝2,则(Ａ)(Ｂ)(C)(D)(７)已知α为第二象限角,ｓｉnα＋sｉnβ=3,则coｓ2α＝(Ａ) -3(Ｂ）-9(C) 9(Ｄ）3(８）已知F１、F2为双曲线C：x²-ｙ²＝2的左、右焦点，点P在Ｃ上，｜PF1|=|2PF２|，则cos∠Ｆ1PＦ2=(A)14(B)35(Ｃ)34(Ｄ)45（９）已知ｘ=lnπ,y=loｇ5２,12z=e,则(A)x<y<z (B)z＜ｘ＜y (Ｃ)z<y<x(Ｄ）ｙ<ｚ＜x(10) 已知函数y=ｘ²-3x+ｃ的图像与x恰有两个公共点,则c＝(A)-2或2 （B）－9或3 （Ｃ)-1或１（D）－３或1(1１)将字母a，a,b,b,c,c,排成三行两列,要求每行的字母互不相同，梅列的字母也互不相同,则不同的排列方法共有（Ａ)12种（B)1８种（Ｃ）24种(D）36种(１2)正方形ABCD的边长为1,点Ｅ在边ＡB上，点F在边BC上,AＥ＝BF＝73。
2011年—2019年高考全国卷(1卷、2卷、3卷)理科数学试题分类汇编——14.坐标系与参数方程
2011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编14．坐标系与参数方程（逐题解析版）(2019·全国卷Ⅰ，理22)[选修4—4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩，（t 为参数）．以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为2cos sin 110ρθθ++=． （1）求C 和l 的直角坐标方程； （2）求C 上的点到l 距离的最小值．(2019·全国卷Ⅱ，理22) [选修4-4：坐标系与参数方程]（10分）在极坐标系中，O 为极点，点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上，直线l 过点(4,0)A 且与OM 垂直，垂足为P ． （1）当0=3θπ时，求0ρ及l 的极坐标方程； （2）当M 在C 上运动且P 在线段OM 上时，求P 点轨迹的极坐标方程．(2019·全国卷Ⅲ，理22) [选修4-4：坐标系与参数方程]（10分）如图，在极坐标系Ox 中，(2,0)A ，(2,)4B π，3(2,)4C π，(2,)D π，弧AB ，BC ，CD ，所在的圆的圆心分别是(1,0)，(1,)2π，(1,)π，曲线M 1是弧AB ，曲线M 2是弧BC ，曲线M 3是弧CD ． （1）分别写出M 1，M 2，M 3的极坐标方程；（2）曲线M 由M 1，M 2，M 3构成，若点P 在M 上，且|OP |=3，求P 的极坐标．（2018·新课标Ⅰ，理22）在直角坐标系xOy 中，曲线1C 的方程为2y k x =+。
以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为22cos 30ρρθ+-=（I ）求2C 的直角坐标方程；（II ）若1C 与2C 有且仅有三个公共点，求1C 的方程。
2011年—2018年新课标全国卷(1卷、2卷、3卷)理科数学试题分类汇编——4.简易逻辑、推理与证明
4．简易逻辑、推理与证明一、选择题（2017，新课标Ⅱ，7）甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（ ）A ．乙可以知道四人的成绩B ．丁可以知道四人的成绩C ．乙、丁可以知道对方的成绩D ．乙、丁可以知道自己的成绩（2015，新课标Ⅰ，3）设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = （2011·新课标Ⅱ，10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题中真命题是（ ）12:+10,3P πθ⎡⎫>⇔∈⎪⎢⎣⎭a b 22:1,3P πθπ⎛⎤+>⇔∈ ⎥⎝⎦a b 3:10,3P πθ⎡⎫->⇔∈⎪⎢⎣⎭a b 4:1,3P πθπ⎛⎤->⇔∈ ⎥⎝⎦a b A ． P 1，P 4B ．P 1，P 3C ．P 2，P 3D ．P 2，P 4二、填空题（2014，新课标Ⅰ，14）甲、乙、丙三位同学被问到是否去过A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一个城市.由此可判断乙去过的城市为 .4．简易逻辑、推理与证明（解析版）一、选择题（2017，新课标Ⅱ，7）甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（ ）A ．乙可以知道四人的成绩B ．丁可以知道四人的成绩C ．乙、丁可以知道对方的成绩D ．乙、丁可以知道自己的成绩【解析】D 解法一：假设法：甲看乙﹑丙成绩，甲不知道自己的成绩，那么乙﹑丙成绩中有一人为优，一人为良；乙已经知道自己的成绩要么良，要么优，丙同样也是，当乙看到丙的成绩，一定知道自己的成绩，但是丙一定不知道自己的成绩；而丁同学也知道自己的成绩要么良，要么优，只有看到甲的成绩，才能判断自己的成绩，丁同学也一定知道自己的成绩，故只有乙﹑丁两位同学知道自己的成绩.（2015，新课标Ⅰ，3）设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n =【答案】C 解析：命题p 含有存在性量词（特称命题），是真命题（如3n =时），则其否定（p ⌝）含有全称量词（全称命题），是假命题，故选C ．.（2011·新课标Ⅱ，10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题中真命题是（ ）12:+10,3P πθ⎡⎫>⇔∈⎪⎢⎣⎭a b 22:1,3P πθπ⎛⎤+>⇔∈ ⎥⎝⎦a b 3:10,3P πθ⎡⎫->⇔∈⎪⎢⎣⎭a b 4:1,3P πθπ⎛⎤->⇔∈ ⎥⎝⎦a b A ． P 1，P 4 B ．P 1，P 3 C ．P 2，P 3 D ．P 2，P 4【答案】A 解析：由||1+=>a b 得1cos 2θ>-2[0,)3πθ⇒∈.由||1-==>a b 得1cos 2θ<(,]3πθπ⇒∈，故选A. 二、填空题 （2014，新课标Ⅰ，14）甲、乙、丙三位同学被问到是否去过A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一个城市.由此可判断乙去过的城市为 .【答案】A 解析：∵丙说：三人同去过同一个城市，甲说没去过B 城市，乙说：我没去过C 城市∴三人同去过同一个城市应为Ａ，∴乙至少去过Ａ，若乙再去城市B ，甲去过的城市至多两个，不可能比乙多，∴可判断乙去过的城市为Ａ.。
2011年—2019年高考全国卷(1卷、2卷、3卷)理科数学试题分类汇编——7.二项式定理
7．二项式定理一、选择题(2019·全国卷Ⅲ，理4)24(12)(1)x x ++的展开式中3x 的系数为（ ）A ．12B ．16C ．20D ．24（2018·新课标Ⅲ，理5）522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为（ ）A ．10B ．20C ．40D ．80（2017·新课标Ⅰ，6）621(1)(1)x x++展开式中2x 的系数为（ ） A ．15 B ．20 C ．30 D ．35（2017·新课标Ⅲ，4）()()52x y x y +-的展开式中33x y 的系数为（ ）.A ．80-B ．40-C ．40D ．80（2015·新课标Ⅰ，10）()52x x y ++的展开式中，52x y 的系数为（ ）A ．10B ．20C ．30D ．60（2013·新课标Ⅰ，9）设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b .若13a ＝7b ，则m ＝( )A ．5B ．6C ．7D ．8（2013·新课标Ⅱ，5）已知5(1)(1)ax x ++的展开式中2x 的系数为5，则a =（ ）A .4-B .3-C .2-D .1-（2011·新课标Ⅰ，8）51()(2)ax x x x+-的展开式中各项系数的和为2，则该展开式中常数项为（ ）A ．-40B ．-20C ．20D ．40 二、填空题（2016·新课标Ⅰ，14）5(2x 的展开式中，3x 的系数是_______．（用数字填写答案）（2015·新课标Ⅱ，15）4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =_______． （2014·新课标Ⅰ，13）8()()x y x y -+的展开式中22x y 的系数为 ．(用数字填写答案) （2014·新课标Ⅱ，13）10()x a +的展开式中，7x 的系数为15，则a =________.7．二项式定理（解析版）一、选择题(2019·全国卷Ⅲ，理4)24(12)(1)x x ++的展开式中3x 的系数为（ ）A ．12B ．16C ．20D ．24【答案】A 解析：()41x +的通项公式为kk n k k x C T -+=141，利用通项公式求出x x C T 4131411==+，331341341x x C T ==+，24(12)(1)x x ++的展开式中x 3的系数：12424=+⨯，故选A法二：利用组合的性质，()()42121x x++展开式中x 3的系数为1211211133311411334=⨯⨯⨯⨯+⨯⨯⨯⨯C C C C（2018·新课标Ⅲ，理5）522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为（ ）A ．10B ．20C ．40D ．80【答案】C 解析：25103552()()2rrr r r r C x C x x--=⋅⋅，当2r =时，1034r -=，此时系数22552240r r C C ==.故选C.（2017·新课标Ⅰ，6）621(1)(1)x x++展开式中2x 的系数为（ ） A ．15 B ．20 C ．30 D ．35【解析】()()()66622111+1111x x x x x ⎛⎫+=⋅++⋅+ ⎪⎝⎭，对()61x +的2x 项系数为2665C 152⨯==， 对()6211x x⋅+的2x 项系数为46C =15，∴2x 的系数为151530+=，故选C ； （2017·新课标Ⅲ，4）()()52x y x y +-的展开式中33x y 的系数为（ ）.A ．80-B ．40-C ．40D ．80解析 由二项式定理可得，原式展开中含33x y 的项为()()()()2332233355C 2C 240x x y y x y x y ⋅-+⋅-=，则33x y 的系数为40，故选C.（2015·新课标Ⅰ，10）()52x x y ++的展开式中，52x y 的系数为（ ）A ．10B ．20C ．30D ．60解析：在25()x x y ++的5个因式中，2个取因式中2x 剩余的3个因式中1个取x ，其余因式取y ，故52x y 的系数为21253230C C C =.另解：5252()()x x y x x y ⎡⎤++=++⎣⎦，含2y 的项223235()T C x x y =+，其中23()x x +中含5x 的项为141533C x x C x =，所以52x y 的系数为215330C C =，故选C ．（2013·新课标Ⅰ，9）设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b .若13a ＝7b ，则m ＝( )A ．5B ．6C ．7D ．8答案：B解析：由题意可知，a ＝2C mm ，b ＝21C mm +，又∵13a ＝7b ，∴2!21!13=7!!!1!m m m m m m ()(+)⋅⋅(+)， 即132171m m +=+.解得m ＝6.故选B. （2013·新课标Ⅱ，5）已知5(1)(1)ax x ++的展开式中2x 的系数为5，则a =（ ）A .4-B .3-C .2-D .1-（2013·5）D 解析：因为(1＋x )5的二项展开式的通项为5C r rx (0≤r ≤5，r ∈Z )，则含x 2的项为225C x ＋ax ·15C x ＝(10＋5a )x 2，所以10＋5a ＝5，a ＝－1. 故选D.（2011·新课标Ⅰ，8）51()(2)ax x x x+-的展开式中各项系数的和为2，则该展开式中常数项为（ ）A ．-40B ．-20C ．20D ．40 解析 1.令x=1得a=1.故原式=511()(2)x x x x +-．511()(2)x x x x+-的通项521552155(2)()(1)2r r r r r r r r T C x x C x ----+=-=-，由5-2r=1得r=2,对应的常数项=80，由5-2r=-1得r=3,对应的常数项=-40，故所求的常数项为40 ，选D解析2.用组合提取法,把原式看做6个因式相乘，若第1个括号提出x,从余下的5个括号中选2个提出x ，选3个提出1x ；若第1个括号提出1x ，从余下的括号中选2个提出1x，选3个提出x. 故常数项=223322335353111(2)()()(2)X C X C C C X X X X⋅⋅-+⋅-⋅=-40+80=40 二、填空题（2016·新课标Ⅰ，14）5(2x 的展开式中，3x 的系数是_______．（用数字填写答案）【解析】：设展开式的第1k +项为1k T +，{}0,1,2,3,4,5k ∈，∴()5552155C 2C 2k kkkkkk T x x---+==．当532k -=时，4k =，即454543255C 210T x x --==，故答案为10．（2015·新课标Ⅱ，15）4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =_______．（2015·15）3解析：由已知得4234(1)1464x x x x x +=++++，故4()(1)a x x ++的展开式中x 的奇数次幂项分别为4ax ，34ax ，x ，36x ，5x ，其系数之和为441+6+1=32a a ++，解得3a =．（2014·新课标Ⅰ，13）8()()x y x y -+的展开式中22x y 的系数为 ．(用数字填写答案) 【解析】：8()x y +展开式的通项为818(0,1,,8)r r r r T C x y r -+==，∴777888T C xy xy ==，626267828T C x y x y ==，∴8()()x y x y -+的展开式中27x y 的项为7262782820x xy y x y x y -=-，故系数为-20．（2014·新课标Ⅱ，13）10()x a +的展开式中，7x 的系数为15，则a =________. （2014·13）12解析：∵10110r r r r T C x a -+=，∴107r -=，即3r =，∴373741015T C x a x ==，解得12a =.。
全国Ⅰ,Ⅱ,Ⅲ卷2011-2018年高考分类分析理科数学
A. 1, 0
B. 0,1
C. 1, 0,1
D.0,1, 2
2
2014 年 1. 设集合 M 0,1, 2, N x | x2 3x 2≤0 ，则 M N =
A. 1
B. 2
C. 0,1
D. 1,2
2013 年 1．已知集合 M x x 12 4, x R , N 1,0,1, 2,3，则 M N
A.[2，3]
B.（- ，2] [3,+ ）
C. [3,+ ）
D.（0，2] [3,+ ）
Ⅱ卷 2．已知集合 A x ，y x2 y 2≤3，x Z ，y Z ，则 A 中元素的个数为
2018 年 A．9
B．8
C．5
D．4
2017 年 2.设集合 A 1, 2, 4 ， B x x2 4x m 0 ．若 A B {1}，则 B
D.x | x 1x | x 2
2017 年 1.已知集合 A={x|x<1}，B={x| 3x 1 }，则 A． A B {x | x 0} B． A B R C． A B {x | x 1}
D． A B
2016 年 1.设集合 A {x | x2 4x 3 0} ， B {x | 2x 3 0} ，则 A B
A．1, 3
B． 1, 0
C． 1, 3
D． 1, 5
2016 年 2.已知集合 A 1,2,3， A x x 1x 2 0, x Z，则 A B
A. 1
B. 1,2
C. 0,1,2,3
D. 1,0,1,2,3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2011年—2019年全国卷(Ⅰ、Ⅱ、Ⅲ卷)理科数学试题分类汇编1．集合与简易逻辑一、选择题(2019·全国卷Ⅰ，理1)已知集合}242{60{}M x x N x x x =-<<=--<，，则M N =（ ） A ．}{43x x -<< B ．}42{x x -<<-C ．}{22x x -<<D ．}{23x x << (2019·全国卷Ⅱ，理1)设集合2{|560}A x x x =-+>，{|10}B x x =-<，则A ∩B =（ ）A ．(,1)-∞B ．(2,1)-C ．(3,1)--D ．(3,)+∞(2019·全国卷Ⅲ，理1)已知集合{}1,0,1,2A =-，{}2|1B x x =≤，则AB =（ ） A ．{1,0,1}- B ．{0,1}C ．{1,1}-D ．{0,1,2} (2018·新课标Ⅰ，理2)已知集合{}02|2>--=x x x A ，则=A C U （ ） A ．{}21|<<-x x B. {}21|≤≤-x x C.{}{}2|1|>-<x x x x D. {}{}2|1|≥-≤x x x x (2018·新课标Ⅱ，理2)已知集合(){}223A x y x y x y =+∈∈Z Z ，≤，，，则A 中元素的个数为（ ） A ．9 B ．8C ．5D ．4 （2018·新课标Ⅲ，理1）已知集合{}|10A x x =-≥，{}012B =，，，则A B =（ ） A ．{}0 B ．{}1 C ．{}12， D ．{}012，， （2017，新课标Ⅰ，1）已知集合{}1A x x =<，{}31x B x =<，则（ ）A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅（2017·新课标Ⅱ，2）设集合{}1,2,4A =，{}240x x x m B =-+=．若{}1A B =，则B =（ ） A ．{}1,3- B ．{}1,0 C ．{}1,3 D ．{}1,5 （2017·新课标Ⅲ，1）已知集合A ={}22(,)1A x y x y =+=，{}(,)B x y y x ==，则A B 中元素的个数为（ ）A ．3B ．2C ．1D ．0 （2016，新课标Ⅰ，1）设集合}034{2<+-=x x x A ，}032{>-=x x B ，则AB =（ ） A ．)23,3(--B ．)23,3(-C ．)23,1(D ．)3,23(（2016·新课标Ⅱ，2）已知集合A ={1，2，3}，B ={x |(x +1)(x -2)<0，x ∈Z }，则A B =（ ）A ．{1}B ．{1，2}C ．{0，1，2，3}D ．{-1，0，1，2，3}（2016·新课标Ⅲ，1）设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ，则ST =（ ） A. []2,3 B. (][),23,-∞+∞ C. [)3,+∞ D. (][)0,23,+∞（2015·新课标Ⅰ，3）设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = （2015·新课标Ⅱ，1）已知集合A ={-2，-1，0，2}，B ={x |(x -1)(x +2)<0}，则A ∩B =（ ）A ．{-1，0}B ．{0，1}C ．{-1，0，1}D ．{0，1，2}（2014·新课标Ⅰ，1）已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( ) A .[-2,-1] B .[-1,2） C .[-1,1] D .[1,2）（2014·新课标Ⅱ，1）设集合M ={0, 1, 2}，N ={}2|320x x x -+≤，则MN =（ ） A ．{1}B ．{2}C ．{0，1}D ．{1，2} （2013·新课标Ⅰ，1）已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( ) A ．A ∩B ＝ B ．A ∪B ＝R C ．B ⊆A D ．A ⊆B（2013·新课标Ⅱ，1）已知集合M ={x|(x -1)2 < 4, x ∈R }，N ={-1，0，1，2，3}，则M ∩ N =（ ）A .{0, 1, 2}B .{-1, 0, 1, 2}C .{-1, 0, 2, 3}D .{0, 1, 2, 3}（2012·新课标Ⅰ，1）已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ）A ．3B ．6C ．8D ．10（2012·新课标Ⅱ，1）已知集合A ={1, 2, 3, 4, 5}，B ={(x ,y )| x ∈A , y ∈A , x -y ∈A }，则B 中所含元素的个数为（ ）A. 3B. 6C. 8D. 10（2011·新课标Ⅱ，10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题中真命题是（ ）12:+10,3P πθ⎡⎫>⇔∈⎪⎢⎣⎭a b 22:1,3P πθπ⎛⎤+>⇔∈ ⎥⎝⎦a b 3:10,3P πθ⎡⎫->⇔∈⎪⎢⎣⎭a b 4:1,3P πθπ⎛⎤->⇔∈ ⎥⎝⎦a b A ． P 1，P 4 B ．P 1，P 3 C ．P 2，P 3D ．P 2，P 42011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编1．集合与常用逻辑用语（解析版）一、选择题(2019·全国卷Ⅰ，理1)已知集合}242{60{}M x x N x x x =-<<=--<，，则M N =（ ） A ．}{43x x -<< B ．}42{x x -<<- C ．}{22x x -<< D ．}{23x x <<【答案】C 解析：{}23N x x =-<<，则MN ={}22x x -<<． (2019·全国卷Ⅱ，理1)设集合2{|560}A x x x =-+>，{|10}B x x =-<，则A ∩B =（ ）A ．(,1)-∞B ．(2,1)-C ．(3,1)--D ．(3,)+∞【答案】A 解析：{}23A x x x =<>或，{}1B x x =<，则(),1A B =-∞-.故选A.(2019·全国卷Ⅲ，理1)已知集合{}1,0,1,2A =-，{}2|1B x x =≤，则A B =（ ） A ．{1,0,1}- B ．{0,1} C ．{1,1}- D ．{0,1,2}【答案】A 解析：因为{}11B x x =-≤≤，所以{}1,0,1A B =-．(2018·新课标Ⅰ，理2)已知集合{}02|2>--=x x x A ，则=A C U （ ） A ．{}21|<<-x x B. {}21|≤≤-x x C.{}{}2|1|>-<x x x x D. {}{}2|1|≥-≤x x x x 【答案】B 解析：21022>-<⇒>--x x x x 或，即{}21|>-<=x x x A 或，∴=A C U {}21|≤≤-x x 故选B.(2018·新课标Ⅱ，理2)已知集合(){}223A x y x y x y =+∈∈Z Z ，≤，，，则A 中元素的个数为（ ） A ．9 B ．8C ．5D ．4 【答案】A 解析：① 当1x =-时，101y =-共有三个解；② 当0x =时， 101y =-共有三个解 ③ 当1x =时， 101y =-共有三个解；综上所述：共有9个整数点，分别为()()()()()()()()()-1,1-1,0-1,10-10,00,11-11,01,1、、、，、、、，、、，选A.（2018·新课标Ⅲ，理1）已知集合{}|10A x x =-≥，{}012B =，，，则A B =（ ） A ．{}0 B ．{}1 C ．{}12， D ．{}012，， 【答案】C 解析：∵{|10}{|1}A x x x x =-≥=≥，{0,1,2}B =，∴{1,2}A B =.故选C.（2017，新课标Ⅰ，1）已知集合{}1A x x =<，{}31x B x =<，则（ ）A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅【答案】A 解析：{}1A x x =<，{}{}310x B x x x =<=<，∴{}0AB x x =<，{}1A B x x =<，选A. （2017·新课标Ⅱ，2）设集合{}1,2,4A =，{}240x x x m B =-+=．若{}1A B =，则B =（ ）A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,5【答案】C 解析：∵ {}1AB =， ∴ 1是方程240x x m -+=的一个根，即3m =，∴ {}2430B x x x =-+=，故{}1,3B =，选C.（2017·新课标Ⅲ，1）已知集合A ={}22(,)1A x y x y =+=，{}(,)B x y y x ==，则AB 中元素的个数为（ ）A ．3B ．2C ．1D ．0 【答案】B 解析 A 表示圆221x y +=上所有点的集合，B 表示直线y x =上所有点的集合，故A B 表示两直线与圆的交点，由图可知交点的个数为2，即A B 元素的个数为2.故选B.（2016，新课标Ⅰ，1）设集合}034{2<+-=x x x A ，}032{>-=x x B ，则AB =（ ） A ．)23,3(-- B ．)23,3(- C ．)23,1( D ．)3,23(【答案】D 解析：{}13A x x =<<，{}32302B x x x x ⎧⎫=->=>⎨⎬⎩⎭．故332A B x x ⎧⎫=<<⎨⎬⎩⎭．故选D ． （2016·新课标Ⅱ，2）已知集合A ={1，2，3}，B ={x |(x +1)(x -2)<0，x ∈Z }，则A B =（ ）A ．{1}B ．{1，2}C ．{0，1，2，3}D ．{-1，0，1，2，3}【答案】C 解析：()(){}120Z B x x x x =+-<∈，，∴{}01B =，，∴{}0123A B =，，，，故选C ．（2016·新课标Ⅲ，1）设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ，则ST =（ ） A. []2,3 B. (][),23,-∞+∞ C. [)3,+∞ D. (][)0,23,+∞【答案】D 解析：易得(][),23,S =-∞+∞，(][)0,23,S T ∴=+∞，选D（2015，3）设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n =【答案】C 解析：命题p 含有存在性量词（特称命题），是真命题（如3n =时），则其否定（p ⌝）含有全称量词（全称命题），是假命题，故选C ．.（2015·新课标Ⅱ，1）已知集合A ={-2，-1，0，2}，B ={x |(x -1)(x +2)<0}，则A ∩B =（ ）A ．{-1，0}B ．{0，1}C ．{-1，0，1}D ．{0，1，2}【答案】A 解析：由已知得{}21B x x =-<<，故，故选A.（2014·新课标Ⅰ，1）已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( ) A .[-2,-1] B .[-1,2） C .[-1,1] D .[1,2）【答案】A 解析：∵{|13}A x x x =≤-≥或，B={}22x x -≤<，∴A B ⋂={}21x x -≤≤，选A. （2014·新课标Ⅱ，1）设集合M ={0, 1, 2}，N ={}2|320x x x -+≤，则MN =（ ）A ．{1}B ．{2}C ．{0，1}D ．{1，2} 【答案】D 解析：∵2={|320}{|12}N x x x x x -+≤=≤≤，∴{1,2}M N =.（2013·新课标Ⅰ，1）已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( )A ．A ∩B ＝ B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B【答案】B 解析：∵x (x －2)＞0，∴x ＜0或x ＞2，∴集合A 与B 可用图象表示为：由图象可以看出A ∪B ＝R ，故选B. （2013·新课标Ⅱ，1）已知集合M ={x|(x -1)2 < 4, x ∈R }，N ={-1，0，1，2，3}，则M ∩ N =（ ）A .{0, 1, 2}B .{-1, 0, 1, 2}C .{-1, 0, 2, 3}D .{0, 1, 2, 3}【答案】A 解析：解不等式(x -1)2<4，得-1<x <3，即M ＝{x |-1<x <3}．而N ＝{-1, 0, 1, 2, 3}，所以M ∩N ＝{0, 1, 2}，故选A.（2012·新课标Ⅰ，1）已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ）A ．3B ．6C ．8D ．10【答案】D 解析：由集合B 可知，x y >，因此B={（2，1），（3，2），（4，3），（5，4），（3，1），（4，2），（5，3），（4，1），（5，2），（5，1）}，B 的元素10个，所以选择D ．（2012·新课标Ⅱ，1）已知集合A ={1, 2, 3, 4, 5}，B ={(x ,y )| x ∈A , y ∈A , x -y ∈A }，则B 中所含元素的个数为（ ）A. 3B. 6C. 8D. 10【答案】D 解析：要在1，2，3，4，5中选出两个，大的是x ，小的是y ，共2510C =种选法.（2011·新课标Ⅱ，10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题中真命题是（ ）12:+10,3P πθ⎡⎫>⇔∈⎪⎢⎣⎭a b 22:1,3P πθπ⎛⎤+>⇔∈ ⎥⎝⎦a b 3:10,3P πθ⎡⎫->⇔∈⎪⎢⎣⎭a b 4:1,3P πθπ⎛⎤->⇔∈ ⎥⎝⎦a b A ． P 1，P 4 B ．P 1，P 3 C ．P 2，P 3 D ．P 2，P 4【答案】A 解析：由||1+=>a b 得1cos 2θ>-2[0,)3πθ⇒∈.由||1-=a b 得1cos 2θ<(,]3πθπ⇒∈，故选A.。