结构化学基础习题答案_周公度_第4版
结构化学基础习题答案_周公度_第4版

【1.15】已知在一维势箱中粒子的归一化波函数为()n n x x l πϕ=1,2,3n =⋅⋅⋅ 式中l 是势箱的长度,x 是粒子的坐标)x l <,求粒子的能量,以及坐标、动量的平均值。
解:(1)将能量算符直接作用于波函数,所得常数即为粒子的能量:222n222h d n πx h d n πx ˆH ψ(x )-)-)8πm d x l 8πm d x l ==(sin )n n n x l l l πππ=⨯-22222222()88n h n n x n h x m l l ml ππψπ=-⨯= 即:2228n h E ml =(2)由于ˆˆx ()(),x n n x c x ψψ≠无本征值,只能求粒子坐标的平均值:()()x l x n sin l x l x n sin l x x ˆx x l *ln l*n d 22d x 000⎰⎰⎰⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==ππψψ()x l x n cos x l dx l x n sin x l l l d 22122002⎰⎰⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=ππ2000122sin sin d 222l l l x l n x l n x x x l n l n l ππππ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎣⎦⎰ 2l =(3)由于()()ˆˆp,p x n n x x c x ψψ≠无本征值。
按下式计算p x的平均值:()()1*ˆd x n x n p x px x ψψ=⎰0d 2n x ih d n x x l dx l πππ⎛=- ⎝⎰20sin cos d 0l nih n x n x x l l l ππ=-=⎰【1.20】若在下一离子中运动的π电子可用一维势箱近似表示其运动特征:估计这一势箱的长度 1.3l nm =,根据能级公式222/8n E n h ml =估算π电子跃迁时所吸收的光的波长,并与实验值510.0nm 比较。
结构化学基础习题答案_周公度_第版

【1.3】金属钾的临阈频率为5.464×10-14s -1,如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时,发射光电子的最大速度是多少?解:2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kg υ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长: (a )质量为10-10kg ,运动速度为0.01m·s -1的尘埃;(b )动能为0.1eV 的中子; (c )动能为300eV 的自由电子。
解:根据关系式: (1)34221016.62610J s6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅34-11 (2) 9.40310mh p λ-==⨯ 34(3) 7.0810mh p λ-==⨯【1.7】子弹(质量0.01kg ,速度1000m ·s -1),尘埃(质量10-9kg ,速度10m ·s -1)、作布郎运动的花粉(质量10-13kg ,速度1m ·s -1)、原子中电子(速度1000 m ·s -1)等,其速度的不确定度均为原速度的10%,判断在确定这些质点位置时,不确定度关系是否有实际意义?解:按测不准关系,诸粒子的坐标的不确定度分别为: 子弹:343416.2610 6.63100.01100010%h J sx mm v kg m s ---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃:3425916.62610 6.6310101010%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉:34201316.62610 6.631010110%h J sx mm v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子:3463116.626107.27109.10910100010%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅ 【1.9】用不确定度关系说明光学光栅(周期约610m -)观察不到电子衍射(用100000V 电压加速电子)。
《结构化学》第三章习题答案

《结构化学》第三章习题答案3001 ( A, C )3002 H ab =∫ψa [-21∇2- a r 1 - br 1 +R 1 ] ψb d τ =E H S ab + R 1 S ab - ∫a r 1ψa ψb d τ= E H S ab + K因 E H = -13.6e V , S ab 为正值,故第一项为负值; 在分子的核间距条件下, K 为负值。
所以 H ab 为负值。
3003 ∫ψg ψu d τ=(4 - 4S 2)-1/2∫(ψa s 1+ψb s 1)((ψa s 1-ψb s 1)d τ = (4 - 4S 2)-1/2∫[ψa s 12 -ψb s 12 ] d τ= (4 - 4S 2)-1/2 [ 1 - 1 ] = 0故相互正交。
3004 ( C )3006 描述分子中单个电子空间运动状态的波函数叫分子轨道。
两个近似 (1) 波恩 - 奥本海默近似 ( 核质量 >> 电子质量 )(2) 单电子近似 (定态)3007 单个电子3008 (B)3009 (1) 能级高低相近(2) 对称性匹配(3) 轨道最大重叠3010 不正确3011 (B)3012 ψ= (0.8)1/2φA + (0.2)1/2φB3013 能量相近, 对称性匹配, 最大重叠> , < 或 < , >3014 正确3015 不正确3016 σ π π δ30173018 z3019 (C)3020 π3021 σ轨道: s -s , s -p z , s -d z , p z –p z , p z -2z d , 2z d -2z d ,π轨道p x –p x ,p x –d xz ,p y –p y ,p y –d yz ,d yz –d yz ,d xz –d xzδ轨道:d xy -d xy , d 22y x -- d 22y x -3022 σ δ π 不能 不能3023 (B)3024 原子轨道对 分子轨道p z -d xy ×p x -d xz πd 22y x -- d 22y x - δ2z d -2z d σp x –p x π3025 1σ22σ21π43σ2 , 3 , 反磁3026 d xy , δ3027 p y , d xy3028 C 2 ( 1σg )2( 1σu )2( 1πu )2+2 s -p 混杂显著.因1σu 为弱反键,而1σg 和1πu 均为强成键,故键级在2-3之间.3029 N 2: (1σg )2(1σu )2(1πu )4(2σg )2O 2: σ2s 2σ2s σ2pz 2π2px 2π2py 2π2px *π2py *1或 ( 1σg )2(1σu )22σg 2(1πu )4(1πg )23030 ( 1σg )2( 1σu )2( 1πu )4( 2σg )2的三重键为 1 个σ键 (1σg )2,2个π键 (1πu )4,键级为 3( 1σu )2和(2σg )2分别具有弱反键和弱成键性质, 实际上成为参加成键作用很小的两对孤对电子,可记为 :N ≡N: 。
(完整版)结构化学基础习题答案_周公度_第4版

【1.3】金属钾的临阈频率为5.464×10-14s -1,如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时,发射光电子的最大速度是多少?解:2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kg υ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦g g134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯g g【1.4】计算下列粒子的德布罗意波的波长: (a )质量为10-10kg ,运动速度为0.01m ·s -1的尘埃;(b ) 动能为0.1eV 的中子; (c )动能为300eV 的自由电子。
解:根据关系式: (1)34221016.62610J s6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅34 (2) 9.40310mh p λ-==⨯3411(3) 7.0810mh p λ--==⨯【1.7】子弹(质量0.01kg ,速度1000m ·s -1),尘埃(质量10-9kg ,速度10m ·s -1)、作布郎运动的花粉(质量10-13kg ,速度1m ·s -1)、原子中电子(速度1000 m ·s -1)等,其速度的不确定度均为原速度的10%,判断在确定这些质点位置时,不确定度关系是否有实际意义?解:按测不准关系,诸粒子的坐标的不确定度分别为: 子弹:343416.2610 6.63100.01100010%h J sx mm v kg m s ---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃:3425916.62610 6.6310101010%h J sx mm v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉:34201316.62610 6.631010110%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子:3463116.626107.27109.10910100010%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅ 【1.9】用不确定度关系说明光学光栅(周期约610m -)观察不到电子衍射(用100000V 电压加速电子)。
结构化学基础习题答案周公度第版

01.量子力学基础知识【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm,这是Li原子由电子组态(1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红光的频率、波数以及以k J·mol-1为单位的能量。
解:811412.99810m s4.46910s670.8mcνλ--⨯⋅===⨯【1.3】金属钾的临阈频率为5.464×10-14s-1,如用它作为光电极的阴极当用波长为300nm的紫外光照射该电池时,发射光电子的最大速度是多少?解:212hv hv mv =+【1.4】计算下列粒子的德布罗意波的波长:(a)质量为10-10kg,运动速度为0.01m·s-1的尘埃;(b)动能为0.1eV的中子;(c)动能为300eV的自由电子。
解:根据关系式:(1)34221016.62610J s6.62610m10kg0.01m shmvλ----⨯⋅===⨯⨯⋅【1.6】对一个运动速度cυ(光速)的自由粒子,有人进行了如下推导:结果得出12m mυυ=的结论。
上述推导错在何处?请说明理由。
解:微观粒子具有波性和粒性,两者的对立统一和相互制约可由下列关系式表达:式中,等号左边的物理量体现了粒性,等号右边的物理量体现了波性,而联系波性和粒性的纽带是Planck 常数。
根据上述两式及早为人们所熟知的力学公式:知①,②,④和⑤四步都是正确的。
微粒波的波长λ服从下式:式中,u是微粒的传播速度,它不等于微粒的运动速度υ,但③中用了/u vλ=,显然是错的。
在④中,E hv=无疑是正确的,这里的E是微粒的总能量。
若计及E中的势能,则⑤也不正确。
【1.7】子弹(质量0.01kg,速度1000m·s-1),尘埃(质量10-9kg,速度10m·s-1)、作布郎运动的花粉(质量10-13kg,速度1m·s-1)、原子中电子(速度1000 m·s-1)等,其速度的不确定度均为原速度的10%,判断在确定这些质点位置时,不确定度关系是否有实际意义?解:按测不准关系,诸粒子的坐标的不确定度分别为:子弹:343416.26106.63100.01100010%h J sx m m v kg m s---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃:3425916.626106.6310101010%h J sx m m v kg m s----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉:34201316.62610 6.631010110%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子:3463116.626107.27109.10910100010%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅【1.8】电视机显象管中运动的电子,假定加速电压为1000V ,电子运动速度的不确定度υ∆为υ的10%,判断电子的波性对荧光屏上成像有无影响?解:在给定加速电压下,由不确定度关系所决定的电子坐标的不确定度为:34102/10%3.8810h x m m eV m mυ--==⨯==⨯这坐标不确定度对于电视机(即使目前世界上最小尺寸最小的袖珍电视机)荧光屏的大小来说,完全可以忽略。
结构化学问答题

问答题( 附答案)103. 5 分第一过渡系列二价金属离子在八面体弱场作用下和在八面体强场作用下,离子半径变化规律有何不同,简述之。
104. 5 分正八面体络合物MA6中的三个配位体A 被三个B 取代,所生成的络合物MA3B3有多少种异构体?这些异构体各属什么点群?105. 5 分作图证明CO 是个强配位体。
106. 5 分试用分子轨道理论阐明X-,NH3和CN-的配体场强弱的次序。
107. 5 分分别推测下列两对络合物中,哪一个络合物的d-d跃迁能量较低:(1)Pt(NH3)42+ , Pd(NH3)42+(2)Co(CN)63-, Ir(CN)63-108. 5 分配位离子[FeF6]3-的分子轨道中最高占有轨道是哪一个?---------------------------- ( )(A)t2g(B)t2g*(C)t1u(D)e g*109. 5 分试写出[CoF6]3-分子轨道中的电子组态。
110. 5 分Fe3+与强场配体形成的配位离子呈八面体构型稳定还是呈四面体构型稳定?为什么?111. 5 分试判断下列配位离子为高自旋构型还是低自旋构型,并写出d电子的排布:(a)Fe(H2O)62+(b)Fe(CN)64-(c)Co(NH3)63+(d)Cr(H2O)62+(e)Mn(CN)64-112. 5 分已知[Ni(CN)4]2-是反磁性的,试用晶体场理论推测配位离子的几何构型。
113. 5 分已知FeF63-中d轨道分裂能为167.2?kJ,成对能为351.12?kJ,配位离子的磁矩为μ,试用分子轨道理论讨论配位离子的电子构型并验证磁矩值。
5.9B114. 5 分试解释为什么d7~ d10组态的过渡金属原子或离子难以形成稳定的八面体配合物。
115. 5 分为什么在过渡元素的配位离子中,八面体构型远较四面体构型多?116. 5 分什么是Jahn-Teller 效应?用它解释Cu(en)32+在水溶液中逐级稳定常数(K1,K2和K3)的特点。
结构化学习题答案

结构化学习题 答案第八章 金属晶体结构8001(C)8002非。
8003非。
六方晶系只有简单六方一种点阵型式,六方晶胞中所含的两个球,均属一个结构基元。
80041:2:18005(E)80060,0,0; 1/3,2/3,1/2 (或 0,0,0; 2/3,1/3,1/2)8007(1) 63,6 简单六方。
(2) 0,0,0; 1/3,2/3,1/2。
(3) (N A ·34πr 3)/0.7405 = 13.95 cm 3 (4) d 002= 2×1.633×160/2 pm = 522.6/2 pm = 261.3 pm8008面; 面8009(1) (1/3,2/3,1/4); (1/3,2/3,3/4);(2) (2/3,1/3,1/8); (2/3,1/3,7/8); (0,0,3/8); (0,0,5/8)8010分子占据面积πr 2; 平行四边形面积 2r ×2r ×sin60°rr r 22866.02⨯⨯π = 0.9078011布拉格角: 34.27°; 40.56°; 66.83°;指标: 111; 200; 220 。
8012(1) a = 352.4 pm(2) d =V N nM A /=2432310524.31002.6/70.584-⨯⨯⨯ g▪cm -3 = 8.906 g▪cm -3 (3) 略8013A 1型堆积为立方面心结构,第一对谱线的衍射指标为111a = 362.0 pmr = 128.0 pm立方面心,每个晶胞中有4个Cu 原子, d = 8.89 g ·cm -38014r = 143 pm; θ= 19.3°8015a = 400.4 pmr = 141.6 pmA 1堆积每个晶胞中有4个Al 原子, d = 2.793 g ·cm -38016(1) r = 138.4 pm(2) 最多能得到(100)的4级衍射8017体心点阵8018r =41(3×4292)1/2= 185.8 pm8019d (110)=330×sin45°pm = 233.3 pmsin θ=0.660, θ=41.3°8020d = 21.45 g ·cm -3r = 138.7 pm8021a = 405.0 pm8021r =41(2×405.02)1/2 pm = 143.2 pm8022a =b =2×146 pm = 292 pmc =292×1.633 pm = 477 pm8023对于体心立方,只能出现h +k +l =偶数之衍射线,即只出现(110),(200), (211),(220), (310),(222),(231),(004)等。
结构化学基础习题答案周公度第版
λ/nm
v /1014s-1
312.5 9.59
365.0 8.21
404.7 7.41
546.1 5.49
Ek/10-19J
3.41
2.56
1.95
0.75
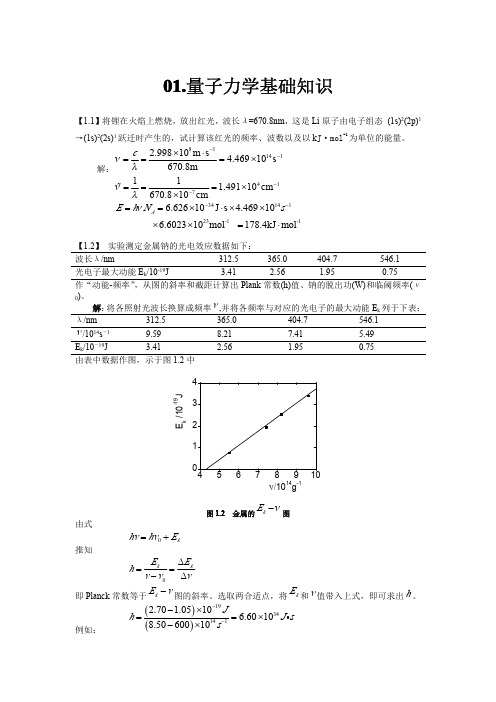
由表中数据作图,示于图 1.2 中
4
Ek /10-19J
3
2
1
0 4 5 6 7 8 9 10 ν/1014g-1
图 1.2 金属的 Ek −ν 图
由式
hv = hv0 + Ek
推知
h = Ek = ∆Ek v − v0 ∆v
即 Planck 常数等于 Ek − v 图的斜率。选取两合适点,将 Ek 和 v 值带入上式,即可求出 h 。
例如:
h
=
(2.70 −1.05) ×10−19 J (8.50 − 600)×1014 s−1
=
6.60×1034 J is
( ) ( ) n 和 n' 皆为正整数,因而 n − n' 和 n + n' 皆为正整数,所以积分:
l
∫ψ n ( x)ψ n' ( x) dτ = 0
0
ψ
根据定义,
n
(
x
)
ψ
和
n'
(
x)
互相正交。
【1.15】已知在一维势箱中粒子的归一化波函数为
ϕn ( x) =
2 sin nπ x ll
n = 1, 2,3⋅⋅⋅
压加速电子)。
解:解法一:根据不确定度关系,电子位置的不确定度为:
△x
=
h △ px
h =
h/λ
= 1.226 ×10−9 i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【1.3】金属钾的临阈频率为5.464×10-14s -1,如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时,发射光电子的最大速度是多少?解:2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kg υ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦g g134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯g g【1.4】计算下列粒子的德布罗意波的波长: (a )质量为10-10kg ,运动速度为0.01m ·s -1的尘埃;(b ) 动能为0.1eV 的中子; (c )动能为300eV 的自由电子。
解:根据关系式: (1)34221016.62610J s6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅34 (2) 9.40310mh p λ-==⨯3411(3) 7.0810mh p λ--==⨯【1.7】子弹(质量0.01kg ,速度1000m ·s -1),尘埃(质量10-9kg ,速度10m ·s -1)、作布郎运动的花粉(质量10-13kg ,速度1m ·s -1)、原子中电子(速度1000 m ·s -1)等,其速度的不确定度均为原速度的10%,判断在确定这些质点位置时,不确定度关系是否有实际意义?解:按测不准关系,诸粒子的坐标的不确定度分别为: 子弹:343416.2610 6.63100.01100010%h J s x mm v kg m s ---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃:3425916.62610 6.6310101010%h J sx mm v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉:34201316.62610 6.631010110%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子:3463116.626107.27109.10910100010%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅ 【1.9】用不确定度关系说明光学光栅(周期约610m -)观察不到电子衍射(用100000V 电压加速电子)。
解:解法一:根据不确定度关系,电子位置的不确定度为:99 1.22610/1.226101.22610x h h x p h m λ---===⨯=⨯=⨯V V这不确定度约为光学光栅周期的10-5倍,即在此加速电压条件下电子波的波长约为光学光栅周期的10-5倍,用光学光栅观察不到电子衍射。
解法二:若电子位置的不确定度为10-6m ,则由不确定关系决定的动量不确定度为:3462816.62610106.62610x h J s p x mJ s m ----⨯∆==∆=⨯g g g 在104V2315.40210p m J s m υ--==⨯g g由Δp x 和p x 估算出现第一衍射极小值的偏离角为:2812315arcsin arcsin 6.62610arcsin 5.40210arcsin100x xop p J s m J s m θθ-----∆==⎛⎫⨯ ⎪⨯⎝⎭≈g g B g g B这说明电子通过光栅狭缝后沿直线前进,落到同一个点上。
因此,用光学光栅观察不到电子衍射。
【1.11】2axxeϕ-=是算符22224d a x dx ⎛⎫- ⎪⎝⎭的本征函数,求其本征值。
解:应用量子力学基本假设Ⅱ(算符)和Ⅲ(本征函数,本征值和本征方程)得:22222222244ax d d a x a x xe dx dx ψ-⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭()2222224ax axd xe a x xe dx --=- ()22222222232323242444ax ax ax ax ax ax ax d e ax e a x e dxaxe axe a x e a x e -------=--=--+-266axaxe a ψ-=-=-因此,本征值为6a -。
【1.13】im e φ和cos m φ对算符d i d φ是否为本征函数?若是,求出本征值。
解:im im d ie ie d φφφ=,im im me φ=-所以,im e φ是算符d i d φ的本征函数,本征值为m -。
而()cos sin sin cos di m i m m im m c m d φφφφφ=-=-≠g所以cos m φ不是算符d id φ的本征函数。
【1.14】证明在一维势箱中运动的粒子的各个波函数互相正交。
证:在长度为l 的一维势箱中运动的粒子的波函数为:()n x ψ01x <<n =1,2,3,……令n 和n()()()()()()()()()()()()()()00002sin sin sin sin 222sinsin sin sin lnn l l ln xx x d dx ln x n x dxl l ln n n n x x l l l n n n n l l n n n n x x l l n n n n n n n n n n n n πψψτππππππππππππππ==⎡⎤-+⎢⎥⎢⎥=-⎢⎥-+⨯⨯⎢⎥⎣⎦⎡⎤-+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦-+=--+⎰⎰gn 和n 皆为正整数,因而()n n -和()n n +皆为正整数,所以积分: ()()0lnn x x d ψψτ=⎰根据定义,()n x ψ和()n x ψ互相正交。
【1.15()n n x x l πϕ 1,2,3n =⋅⋅⋅式中l 是势箱的长度,x 是粒子的坐标()0x l <<,求粒子的能量,以及坐标、动量的平均值。
解:(1)将能量算符直接作用于波函数,所得常数n n πx ˆH ψ(x )cos )l = =)x = 即:228n E ml =(2)由于ˆˆx()(),x n n x c x ψψ≠无本征值,只能求粒子坐标的平均值:()()x l x n sin l x l x n sin l x x ˆx x l *l n l *n d 22d x 000⎰⎰⎰⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛==ππψψ()x l x n cos x l dx l x n sin x l l l d 22122002⎰⎰⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=ππ2000122sin sin d 222l l l x l n x l n x x x l n l n l ππππ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎣⎦⎰ 2l =(3)由于()()ˆˆp,p x n n x x c x ψψ≠无本征值。
按下式计算p x 的平均值:()()1*ˆd x n x n p x px x ψψ=⎰d 2n x ih d n xx l dx l πππ⎛=- ⎝⎰20sin cosd 0l n x n x x l l l ππ=-=⎰【1.19】若在下一离子中运动的π电子可用一维势箱近似表示其运动特征: 估计这一势箱的长度1.3l nm =,根据能级公式222/8n E n h ml=估算π电子跃迁时所吸收的光的波长,并与实验值510.0nm 比较。
H 33解:该离子共有10个π电子,当离子处于基态时,这些电子填充在能级最低的前5个π型分子轨道上。
离子受到光的照射,π电子将从低能级跃迁到高能级,跃迁所需要的最低能量即第5和第6两个分子轨道的的能级差。
此能级差对应于棘手光谱的最大波长。
应用一维势箱粒子的能级表达式即可求出该波长:22222652226511888hch h h E E E ml ml ml λ∆==-=-=()22318193481189.109510 2.997910 1.31011 6.626210506.6mcl h kg m s m J snmλ----=⨯⨯⨯⨯⨯⨯=⨯⨯=g g实验值为510.0nm ,计算值与实验值的相对误差为-0.67%。
【1.20】已知封闭的圆环中粒子的能级为:22228n n h E mR π=0,1,2,3,n =±±±⋅⋅⋅式中n 为量子数,R 是圆环的半径,若将此能级公式近似地用于苯分子中66π离域π键,取R=140pm ,试求其电子从基态跃迁到第一激发态所吸收的光的波长。
解:由量子数n 可知,n=0为非简并态,|n|≥1都为二重简并态,6个π电子填入n=0,1,1-等3个轨道,如图1.20图1.20苯分子66π能级和电子排布()22122418hhcE E E mR πλ-∆=-==()()()()22223110813498389.11101.40102.998103 6.6261021210212mR c h kg m m sJ s m nmπλπ-----=⨯⨯⨯⨯⨯⨯=⨯⨯=⨯=g g实验表明,苯的紫外光谱中出现β,Γ和α共3个吸收带,它们的吸收位置分别为184.0nm,208.0nm 和263.0nm ,前两者为强吸收,后面一个是弱吸收。
由于最低反键轨道能级分裂为三种激发态,这3个吸收带皆源于π电子在最高成键轨道和最低反键之间的跃迁。
计算结果和实验测定值符合较好。
【1.21()/)/)x x a xa ϕππ=-是否是一维势箱中粒子的一种可能状态?若是,其能量有无确定值?若有,其值为多少?若无,求其平均值。
解:该函数是长度为a 能状态函数()1/)x x a ψπ和()2/)x x a ψπ都是一维势箱中粒子的可能状态(本征态),根据量子力学基本假设Ⅳ(态叠加原理),它们的线性组合也是该体系的一种可能状态。
因为()()()1223H x H x x ψψψ∧∧=-⎡⎤⎣⎦()()1223H x H x ψψ∧∧=-()()22122242388h hx x ma ma ψψ=⨯-⨯≠ 常数()x ψ⨯所以,()x ψ不是H ∧的本征函数,即其能量无确定值,可按下述步骤计算其平均值。
将()x ψ归一化:设()x ψ=()c x ψ,即:()()()222200aaax dx c x dx c x dxψψψ==⎰⎰⎰2202ax x c dxa a ππ⎛⎫=- ⎪ ⎪⎝⎭⎰ 2131c== 2113c=()x ψ所代表的状态的能量平均值为:()()0a E x H x dxψψ∧=⎰222202238am x xh d a a dx πππ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎰223x x dx a a ππ⎛⎫- ⎪ ⎪⎝⎭ 2222222233200015292sin sin sin sin 2a a ac h x c h x x c h x dx dx dx ma a ma a a ma a ππππ=-+⎰⎰⎰ 222225513c h hma ma ==也可先将()1x ψ和()2x ψ归一化,求出相应的能量,再利用式2i i E c E =∑求出()x ψ所代表的状态的能量平均值:222222222224049888h h c h E c c ma ma ma =⨯+⨯=22401813h ma =⨯22513h ma =【2.9】已知氢原子的200exp zp r r a a ϕ⎫⎡⎤-⎪⎢⎥⎭⎣⎦cos θ,试回答下列问题:(a)原子轨道能E=?(b)轨道角动量|M|=?轨道磁矩|μ|=?(c)轨道角动量M 和z 轴的夹角是多少度?(d)列出计算电子离核平均距离的公式(不算出具体的数值)。
