材料力学习题解答
材料力学习题及答案
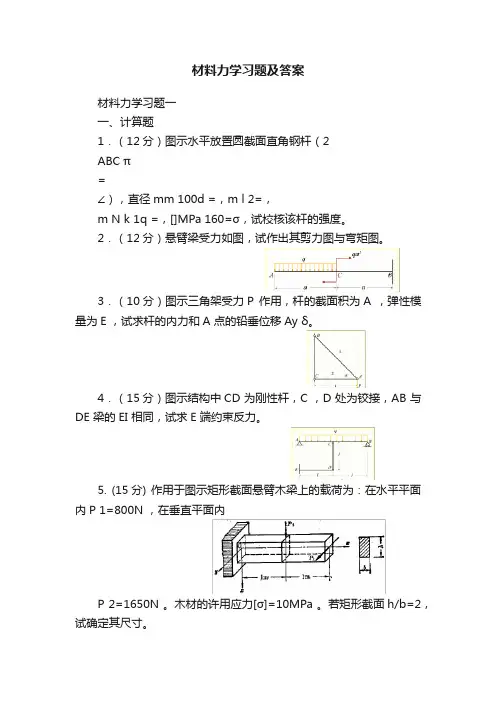
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学习题答案

材料力学习题答案1(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--材料力学习题答案1试求图各杆1-1、2-2、3-3 截面上的轴力,并作轴力图。
解:(a) ()1140302050F kN -=+-=,()22302010F kN -=-=,()3320F kN -=-(b) 11F F -=,220F F F -=-=,33F F -=(c) 110F -=,224F F -=,3343F F F F -=-=轴力图如题2. 1 图( a) 、( b ) 、( c) 所示。
作用于图示零件上的拉力F=38kN ,试问零件内最大拉应力发生在哪个截面上 并求其值。
解 截面1-1 的面积为()()21502220560A mm =-⨯=截面2-2 的面积为()()()2215155022840A mm =+-=因为1-1截面和2-2 截面的轴力大小都为F ,1-1截面面积比2-2 截面面积小,故最大拉应力在截面1-1上,其数值为:()3max 11381067.9560N F F MPa A A σ⨯====冷镦机的曲柄滑块机构如图所示。
镦压工件时连杆接近水平位置,承受的镦压力F=1100kN 。
连杆截面是矩形截面,高度与宽度之比为 1.4hb=。
材料为45钢,许用应力[]58MPa σ=,试确定截面尺寸h 及b 。
解 连杆内的轴力等于镦压力F ,所以连杆内正应力为F Aσ=。
根据强度条件,应有[]F F A bh σσ==≤,将1.4h b=代入上式,解得()()0.1164116.4b m mm ≥== 由 1.4h b=,得()162.9h mm ≥所以,截面尺寸应为()116.4b mm ≥,()162.9h mm ≥。
在图示简易吊车中,BC 为钢杆,AB为木杆。
木杆AB 的横截面面积21100A cm =,许用应力[]17MPa σ=;钢杆BC 的横截面面积216A cm =,许用拉应力[]2160MPa σ=。
材料力学习题册参考答案

材料力学习题册参考答案材料力学习题册参考答案(无计算题)第1章:轴向拉伸与压缩一:1(ABE )2(ABD )3(DE )4(AEB )5(C )6(CE)7(ABD )8(C )9(BD )10(ADE )11(ACE )12(D )13(CE )14(D )15(AB)16(BE )17(D )二:1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三:1:钢铸铁 2:比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =, EAFl l =5.强度,刚度,稳定性;6.轴向拉伸(或压缩);7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形,加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案:1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <;< 剪切挤压答案:一:1.(C ),2.(B ),3.(A ),二:1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章:扭转一:1.(B ) 2.(C D ) 3.(C D ) 4. (C ) 5. (A E ) 6. (A )7. (D )8. (B D ) 9.(C ) 10. (B ) 11.(D ) 12.(C )13.(B )14.(A ) 15.(A E )二:1错 2对 3对 4错 5错 6 对三:1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路(剪力流)第3章:平面图形的几何性质一:1.(C ),2.(A ),3.(C ),4.(C ),5.(A ),6.(C ),7.(C ),8.(A ),9.(D )二:1). 1;无穷多;2)4)4/5(a ; 3),84p R I π=p 4z y I 16R I I ===π4)12/312bh I I z z ==;5))/(/H 6bh 6BH W 32z -= 6)12/)(2211h b bh I I I I z y z y +=+=+;7)各分部图形对同一轴静矩8)两轴交点的极惯性矩;9)距形心最近的;10)惯性主轴;11)图形对其惯性积为零三:1:64/πd 114; 2.(0 , 14.09cm )(a 22,a 62)3: 4447.9cm 4, 4:0.00686d 4 ,5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章:弯曲内力一:1.(A B )2.(D )3.(B )4.(A B E )5.(A B D )6.(ACE ) 7.(ABDE ) 8.(ABE )9. (D ) 10. (D ) 11.(ACBE ) 12.(D ) 13.(ABCDE )二:1错 2错 3错 4对 5错 6对 7对三:1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章:弯曲应力一:1(ABD)2.(C )3.(BE )4.(A )5.(C )6.(C )7.(B )8.(C )9.(BC )二:1对 2错 3错 4 对 5 错 6错 7 对三:1.满足强度要求更经济、更省料2. 变成曲面,既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章:弯曲变形一:1(B ),2(B ),3(A ),4(D ),5(C ),6(A ),7(C ),8(B ),9(A )10(B ),11(A )二:1对2错3错4错5错6对7错8错9错10对11错12对三:1.(转角小量:θθtan ≈)(未考虑高阶小量对曲率的影响)2. 挠曲线采用近似微分方程导致的。
材料力学习题解答

解: (3) 梁可简化, 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
(逆时针)
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解: (4) 梁可简化,为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7.试用叠加法计算图示各梁C点旳挠度。
解: (1) 梁可简化, 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
(逆时针)
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI (向下)
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
材料力学完整课后习题答案

习题2-2一打入基地内的木桩如图所示,杆轴单位长度的摩擦力fkx2,试做木桩的后力图。
解:由题意可得:l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ,其横截面面尺寸如图所示。
荷载 F 1000kN ,材料的密度2.35kg / m 3 ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积: A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7 图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:Fdx l F F l dx d l ,l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ,r 2 1 x r1 2 x 1 ,r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ,d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ,2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此,l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。
材料力学课后习题答案
材料力学课后习题答案1. 弹性力学。
1.1 问题描述,一根钢丝的弹性模量为200GPa,其截面积为0.01m²。
现在对这根钢丝施加一个拉力,使其产生弹性变形。
如果拉力为2000N,求钢丝的弹性变形量。
解答:根据胡克定律,弹性变形量与拉力成正比,与材料的弹性模量和截面积成反比。
弹性变形量可以用以下公式计算:$$。
\delta = \frac{F}{AE}。
$$。
其中,$\delta$表示弹性变形量,F表示拉力,A表示截面积,E表示弹性模量。
代入已知数据,可得:$$。
\delta = \frac{2000N}{0.01m² \times 200GPa} = 0.001m。
$$。
所以,钢丝的弹性变形量为0.001m。
1.2 问题描述,一根长为1m,截面积为$10mm^2$的钢棒,两端受到拉力为1000N的作用。
求钢棒的伸长量。
解答:根据胡克定律,钢棒的伸长量可以用以下公式计算:$$。
\delta = \frac{F \cdot L}{AE}。
$$。
其中,$\delta$表示伸长量,F表示拉力,L表示长度,A表示截面积,E表示弹性模量。
代入已知数据,可得:$$。
\delta = \frac{1000N \times 1m}{10mm² \times 200GPa} = 0.005m。
$$。
所以,钢棒的伸长量为0.005m。
2. 塑性力学。
2.1 问题描述,一块金属材料的屈服强度为300MPa,现在对其施加一个拉力,使其产生塑性变形。
如果拉力为500MPa,求金属材料的塑性变形量。
解答:塑性变形量与拉力成正比,与材料的屈服强度无关。
塑性变形量可以用以下公式计算:$$。
\delta = \frac{F}{A}。
$$。
其中,$\delta$表示塑性变形量,F表示拉力,A表示截面积。
代入已知数据,可得:$$。
\delta = \frac{500MPa}{300MPa} = 1.67。
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学课后习题答案详细
N1 N 2 0.5F 0.5 20 10(kN )
10
(2)求 C 点的水平位移与铅垂位移。 变形协调图
A
点的铅垂位移:l1
N1l EA1
10000N 1000mm 210000N / mm2 100mm2
0.476mm
B 点的铅垂位移: l2
材料可认为符合胡克定律,其弹性模量 E 10GPa 。如不计柱的自重,试求:
(1)作轴力图;
(2)各段柱横截面上的应力;
(3)各段柱的纵向线应变;
(4)柱的总变形。
解:(1)作轴力图
N AC 100kN NCB 100 160 260(kN )
轴力图如图所示。
(2)计算各段上的应力
第二章 轴向拉(压)变形
[习题 2-1] 试求图示各杆 1-1 和 2-2 横截面上的轴力,并作轴力图。 (a) 解:(1)求指定截面上的轴力
N11 F N 22 2F F F
(2)作轴力图 轴力图如图所示。
(b) 解:(1)求指定截面上的轴力
N11 2F N 22 2F 2F 0
如以 表示斜截面与横截面的夹角,试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
上的正应力和切应力,并用图表示其方
向。
解:斜截面上的正应力与切应力的公式
为:
5
0 cos 2
0 2
sin 2
式中, 0
N A
10000 N 100mm 2
100MPa ,把
示。
由平平衡条件可得:
X 0
N EG N EA cos 0
(完整版)材料力学课后习题答案
xx8-1 试求图示各杆的轴力,并指出轴力的最大值。
取 1-1 截面的左段;(2) (3) F N1取 2-2 截面的右段;F R用截面法求内力,取1-1、2-2、 3-3 截面;(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2;kN 取 2-2 截面的左段;取 3-3 截面的右段;轴力最大值: 用截面法求内力,取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面;38-2 解:8-5 (2) (2) 取 1-1 截面的右段; 取 2-2 截面的右段F ;N112kN 22kN(5) 轴力最大值: 试画出 8-1所示各杆的轴力图。
(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆,承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用, 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ,如欲使 AB 与 BC 段横截面上的正应力相同,试求载荷 F 2 之值。
(2) 求 1-1、 2-2 截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷 F=10 kN 作用,杆的横截面面积 A=1000 mm 2,粘接面的方位 角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
l 1l 2解: (1) 用截面法求 AB 、 BC 段的轴力;(2) 分段计F 算个杆向变形;FAC 杆缩短。
2F8-22 图示桁架,杆 1与A 杆 2的横截面面积与材料均相B 同,在节点 A 处承受C 载荷 F 作用。
从解: 8-6 解: (1) 用截面法求出 F 11-1、2-2 截面的轴力;(2) 求 1-1、 2-2 截面的正应A 力 ,利用正应力相B 同 ;题 8-5 图所示圆截面杆,已知载荷 1F 1=200 kN ,F 2=1020 kN ,CAB 段的直径 d 1=40 mm ,如 欲使 AB 与 BC 段横截面上的正应力相同,试求 BC 段的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)求结构的许可载荷。
(2)求结构能承受的最大载荷。
1
解: (1)载荷靠近右端最危险。( [1][2])F N 1 x
2
FN 2
FN1 0 FN2 F
C
FF
FB
(2)
FN2 A
F A[2]
结构的许可载荷为:[F]A[L2]
(2)假设载荷作用在靠近左端距离为x地方结构承受的载荷最大。
wC
Bl2
l1F EN1lAW(1EA)l
l2
FN2l Wl
2EA 2EA
xW C
W
w C l1 2 l22 W (1 2 E )l A W l [2(1)]2W EA l
(2
)
Wl 2EA
wCma x(2)02W EA lW EA l载荷靠近1号杆作用.
w Cmi n(2)12W EA l 2W EA l载荷靠近2号杆作用.
不计刚性梁的重量。求刚性梁上 D点的竖向位移和水平位移。
解: 拉杆的拉力为:
m 0 C
1 FNaF2a 2
FN 2F
l FNa 2Fa EA EA
wD
2l
2
2Fa EA
A
a
FN B
90
l
a C
D
vD wD
F
uD
a
uD
wD 2
2Fa EA
(向右)
vD
wD 2
2Fa EA
(向下)
32**. 如图所示结构, AB是刚性梁,横截面为 A80mm2的钢索绕过无 摩擦的滑轮。载荷 F20kN ,钢索的弹性模量 E30GP,a不计刚性 梁的重量。试求钢索横截面上的应力以及刚性梁上 C 点的竖向位移。
N3
P
协调方程: L2 2L3L1
物理方程:
L1
N1a EA
L2
N2a EA
L3
2 N3a EA
补充方程: N22N3N1
C
D
N2 2
a
A N11 B
3
N3
a
a
F
L3 L1
L2
45
2L3 L1
N1
2 1P 2
N2
3 2
2
P
N3 (1
2 )P 2
36.如图所示杆件两端固定,分别受集中轴向载荷 F
a
FN2 A2
[]W
FN 2
[ ]W
[
2 ]
F
W
a
2
FN 2
[ ]W 1.4
150103 8 10
a84mm
3 .9mm
25. 图示结构横梁 AB, BC均为刚性梁,1号杆和2号杆的截
面直径分别为 d1 10mmd2 20mm,不计横梁 AB, BC
的重量, 试求两杆截面上的应力。
解: 将结构从中间铰处拆开,由 右边梁的平衡有:
4.4mm
14.34MPawC 4.4mm
33. 如图所示很长的直钢缆须考虑其自重的影响,设钢缆材料的
密度为 ,弹性模量为 E,许用应力为 [ ] ,截面面积为
A,在其下端受有载荷 F的作用,试计算钢缆所允许的
长度以及其总伸长量。
O
解: 采用叠加法求解
载荷引起的应力和伸长:
F
F A
LF
FL EA
自重引起的应力和伸长: FNqgAx 总应力:
R0
FN 2
2m 2
F10kN
R0
A
D
B
C
FN1
2m 1 1m
1m R0 1.5m
FN1 F FN2 2F
(1)
FN1 A1
4F
d12
43 .114 011020 3 12.37MPa
(2)
FN2 A2
8F
d22
83 .114 02100 23 63.7MPa
(1) 12.73MP拉 a( 应力) (2) 63.7MP拉 a( 应力)
2[(75)2 18
1]
32 .7MPa [ ]
活塞杆安全。
27*. 如图所示结构,直径 D80mm 、高度 H3m的立柱 OD 由三根钢缆同步拉紧固定在竖直方向,钢缆下端均匀固定在 R2m
的圆周上。每根钢缆由80根直径 d1mm的钢丝制成,忽略钢缆中可能
存在的预应力,如果钢缆还能承受的拉应力为 20M 0 Pa,则尽可能
(1)
FN1 A1
[1]
A1
FN 1
[ 1 ]
d12 FN1 4 [ 1 ]
d1
4 FN 1 420103 17.8mm
[ 1 ]
3.1480
A
B
W
d1 18mm
当载荷移动到B处时2号杆最危险。
(2)
FN2 A2
[2]
d 22
4
FN 2
[ 2 ]
FN1 0 FN2 W
d2
4FN 2
[ 2 ]
距离为 a。不计刚性梁 AB的重量。(1)横梁中点C的最大和
最小竖向位移是多少?(2)球体放在何处,才不会使其沿 AB 梁滚动?
解:假设载荷作用在靠近左端距离为x地方.
WxFN2a
FN2
Wx a
W
(
x) a
F N 1 W F N 1 W (1 )
11 F N 1
EA
Hale Waihona Puke l1Aa FN 2 2
2EA
ES 200GP,a 木材的许用应力 [W]12MPa,弹性模量
EW 10GPa,每根角钢的横截面面积为 A30.68mm 2
求结构的许可载荷 [F]?
F
解: 一次超静定问题。
平衡方程: FW4FS F
物理方程:
W
FW L EW AW
S
FS L ES AS
几何方程: W S
250
L 250
F
补充方程: FS FW
F N2co4s 5F N1 FN2sin 45 F
F
1 FN1
45 2
FN 2
FN1 F(拉) FN2 2F(压)
(1)
FN1 A1
[]St
A1
FN 1
[ ]St
d 2 FN1
4
[ ]St
d 4 FN1
4F
450103 19.9mm
[ ]St
[ ]St
3.14160
d20mm
(2)
ES AS EW AW
FS
ESAS EWAW
FW
FW
E E W SA AW S 210 0 2 0 35 02 .60 80.1 FW 10FS
FS
F 14
FS
F S FW
FS FS
FW
5F 7
37.如图所示,木制杆件的四个棱边分别用四个 4m 04 m m 04 m mm
的等边角钢加固,角钢的许用应力 [S]16M 0 P,a 弹性模量
3 5
F
FN 2
6 5
F
max FA N2
6F[]
5A
Fmax
5A[]
6
5d 2[
24
]
53.14202160 24
41 .810 3N 41.8kN
Fmax41.8kN
35.如图所示桁架结构,各杆的抗拉刚度均为 EA,载荷 F为已知。试求各杆中的轴力。
解: 平衡方程:
N1
2 2
N3
N2
2 2
ES 200GP,a 木材的许用应力 [W]12MPa,弹性模量
EW 10GPa,每根角钢的横截面面积为 A30.68mm 2
求结构的许可载荷 [F]?
F
解:
F FS 14
5F FW 7
WF AW W
5F 7AW
[W]
L
F 7AW[W]
5
725 2 0 12 10 5 13 0 0 N 10k5N 0 5
30aE FNA dx0a
qxdx EA
当: F 2qa
qa
2
(拉伸)
2EA
F 2qa
FA
F 3
5qa(拉力) 6
Fmax
F 3
5qa 6
Fmax
2F 3
qa 6
37.如图所示,木制杆件的四个棱边分别用四个 4m 04 m m 04 m mm
的等边角钢加固,角钢的许用应力 [S]16M 0 P,a 弹性模量
l11co3s0
l22co3s0 wC1 222 c l1 o3 sl2 0
钢缆的伸长是: l l1 l22 w Cco 3 s0L2c4o60s0 0160m0m
l TL EA
wC
2E
ATc oL3s02131 .0 514 0 37 180 3 01c6o30s0 0c3o.83s50
l2
FN2l Wl
2EA 2EA
( x )
a
球不会滚动则要求: l1 l2
11 EA
l1
A
FN1 a
FN 2 2
2EA
wC
Bl2
xW C
W(1)l Wl
W
EA 2EA
1
2
2 3
x 2a 3
球放在离右边三分之一的距离处时,球不会滚动。
31.如图所示结构, CD是刚性梁,拉杆 AB的抗拉刚度为 EA
ma xF m Aa x42D .5T 2ma x20 D d 20 2
ax20(0D d)2
200( 1 )2 80
6.25MPa
