中考数学类比探究(一)——直角、平行(习题及答案).
中考数学几何结构之直角、平行(讲义及答案).
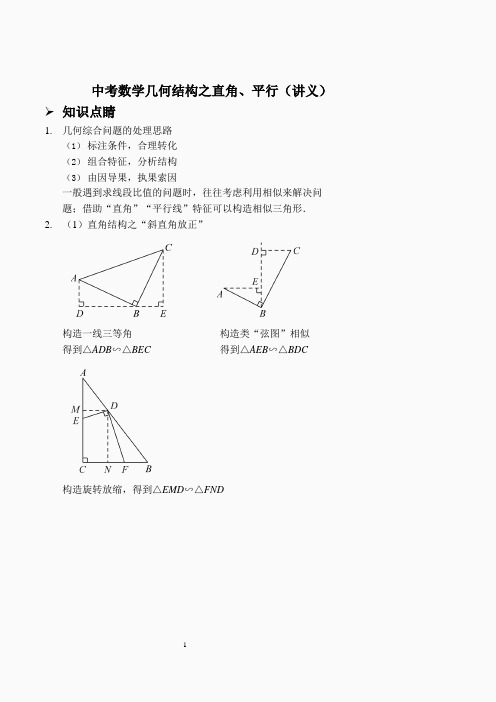
中考数学几何结构之直角、平行(讲义)➢知识点睛1.几何综合问题的处理思路(1)标注条件,合理转化(2)组合特征,分析结构(3)由因导果,执果索因一般遇到求线段比值的问题时,往往考虑利用相似来解决问题;借助“直角”“平行线”特征可以构造相似三角形.2.(1)直角结构之“斜直角放正”构造一线三等角构造类“弦图”相似得到△ADB∽△BEC 得到△AEB∽△BDC构造旋转放缩,得到△EMD∽△FND(2)直角结构之“十字模型”特征:①正方形;②BF⊥CE 特征:①矩形;②BF⊥CE结论:BF=CE 结论:BF=AB CE BC特征:①矩形;②EF⊥GH结论:EF=AB GH BC3.平行结构之“作平行,得相似”(构造X 型、A 型)➢精讲精练1.如图,在梯形ABCD 中,AB∥CD,∠B=∠C=90°,点E 在BC 边上,AB=3,CD=2,BC=7.若∠AED=90°,则CE= .2.如图,已知矩形ABCD 的顶点A,D 分别落在x 轴、y 轴上,OD=2OA=6,AD:AB=3:1,则点C 的坐标是()A.(2,7) B.(3,7) C.(3,8) D.(4,8)3.如图,将三角板放在矩形ABCD 上,使三角板的一边恰好经过点B,三角板的直角顶点E 落在矩形对角线AC 上,另一边交CD 于点F.若AB=3,BC=4,则EF.EB第3 题图第4 题图4.如图,直角梯形ABCD 中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC 绕点D 逆时针方向旋转90°并缩短,恰好使连接AE,则△ADE 的面积是.DE=23CD,5.如图,在Rt△ABC 中,∠ABC=90°,AB=3,BC=4,将Rt△MPN 的直角顶点P 放置在AC 上,PM 交AB 于点E,PN 交BC 于点F,当PE=2PF 时,AP= .6.在矩形ABCD 中,AE⊥BD 于点E,点P 是边AD 上一点,PE⊥EC.若AB=1,BC=2,则AP 的长为.7.如图,在Rt△ACB 中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD 于H,点O 是AB 的中点,连接OH,则OH= .8.如图,已知矩形ABCD 中,AB=3,BC=4,点M,N 分别在边AD,BC 上,沿着MN 折叠矩形ABCD,使点A,B 分别落在E,F 处,且点F 在线段CD 上(不与两端点重合),过点M作MH⊥BC 于点H,连接BF,则△MHN∽;折痕MN的长度的取值范围为.9.如图,在矩形ABCD 中,AB=6 cm,BC=12 cm,AM=5 cm,点P 为BC 上一动点,把矩形ABCD 对折,折痕分别交AD,BC 于E,F,连接DF.若点A 关于PM 的对称点A′落到DF 上,则线段MP 的长度为.10.如图,在等腰Rt△ABC 中,∠C=90°,AC=15,点E 在边CB上,CE=2EB,点D 在边AB 上,CD⊥AE,垂足为F,过点B 作BG∥AC,交CD 的延长线于点G,则AD 的长为.11.如图,在△ABC 中,点D,E,F 分别在AB,BC,AC 边上,DE∥AC,EF∥AB.设AF1.FC 2①若BC=12,则线段BE 的长为;②若△EFC 的面积是20,则△ABC 的面积为.12.如图,E,F 是平行四边形ABCD 对角线AC 上两点,1AE=CF=4AC.连接DE,DF 并延长,分别交AB,BC 于点G,H,连接GH,则CH=AD,CH=,BHAG=GB ,S△A DG =.S△BGH13.如图,在△ABC 中,D 在AC 边上,AD:DC=1:2,O 是BD的中点,连接AO 并延长交BC 于E,则BE:EC=()A.1:2 B.1:3 C.1:4 D.2:35 【参考答案】1. 1 或 62. A3. 434. 25. 36. 127.8. △BCF ;3<MN < 15 49. 2 10. 9 cm 或3 cm11. ①4;②45.12. 1 ; 1 3 2 13. B; 1 ; 3 2 43 5 510 2。
类比探究(一)——直角、平行(习题)

类比探究(一)——直角、平行(习题)1. 如图1,在□ABCD 中,点E 是BC 边的中点,点F 是线段AE 上一点,BF的延长线交射线CD 于点G .(1)尝试探究:如图1,若3AFEF=,则CD CG 的值是______. (2)类比延伸:如图2,在原题的条件下,若AFm EF=(m >0),则CD CG 的值是_______(用含m 的代数式表示),试写出解答过程. (3)拓展迁移:如图3,在梯形ABCD 中,DC ∥AB ,点E 是BC 延长线上一点,AE 和BD 相交于点F .若AB a CD =,BCb BE=(a >0,b >0),则AF EF 的值是________(用含a ,b 的代数式表示).GF DC BA图1GF E DBA图2ADCEFB图32. 如图1,一副直角三角板满足AB =BC ,AC =DE ,∠ABC =∠DEF =90°,∠EDF =30°.【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P ,边EF 与边BC 交于点Q .【探究】在旋转过程中,(1)如图2,当1CEEA =时,EP 与EQ 满足怎样的数量关系?并给出证明.(2)如图3,当2CEEA=时,EP 与EQ 满足怎样的数量关系?并给出证明.(3)根据你对(1),(2)的探究结果,试写出当CEm EA=时,EP 与EQ 满足的数量关系式为________________.A (D )C (E )BF图1QPDEFB C A图2Q PDE F B CA图33. 在△ABC 中,已知D 是BC 边的中点,G 是△ABC 的重心,过点G 的直线分别交AB ,AC 于点E ,F .(1)如图1,当点E 与点B 重合时,AGGD=_______. (2)如图2,当EF ∥BC 时,求证:1=+AFCFAE BE .(3)如图3,当EF 和BC 不平行,且点E ,F 分别在线段AB ,AC 上时,(2)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由. 提示:①过点A 作AM ∥BC ,交EF 于点M ,直线FE 交BC 于N ;②NB +NC =2ND .(4)如图4,当点E 在AB 的延长线上或点F 在AC 的延长线上时,(2)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.AB (E )CDFG图1ABCD EF G 图2GFE D CBA图3ABCD EFG图4【参考答案】1. (1)32; (2)2m ;(3)ab .2. (1)EP =EQ ,证明略;(2)EP =12EQ ,证明略;(3)EP =1mEQ .3. (1)2;(2)证明略;(3)(2)中的结论仍然成立,证明略; (4)(2)中的结论不成立,理由略.。
类比探究(一)——直角、平行(讲义及答案).

类比探究(一)课前预习如图,在△4BC 中,AF:FB=2:3,延长BC 至点D,使得BC=2CD, 则竺=EC ----------提示:求比例,找相似.利用平行线构造“A 型”或“X 型” 相似是我们常用的一种做法.如图,AB=4.射线和AB 相互垂直,点D 是AS 上的一个 动点,点E 在射线BM 上,2BE 二DB ,作EF 丄DE 并截取EF=DE, 连接AF 并延长交射线BM 于点C.设BE 二X, BC=y,则y 关 于X 的函数解析式是( )12.V.V-I8-V提示:斜放置的直角特征, 整合信息.知识点睛类比探究问题的处理思路(1)根题干条件,结合 _________________ 先解决第一问. <2)尝试类比解决下一问,探索过程中确定 ___________.直角.平行(讲义)A)' =- B. )' = - C. )' = -D.可考虑构造一线三等角,利用相似 X- 3x X-4 2x①如果能类比,根条件变化,则确定________________ .②如果不能类比,分析两问间关系,__________________ ,并尝试、验证.注:类比过程中,往往要在不变结构的框架下去思考分析,有时也会进行适当的探索来解决图形变化过程中产生的一些新问题.比如在第3问,会需要根据前2问发现的不变结构去补全图形.>精讲精练I现有矩形ABCD和一个以0为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC, CD交于点M, N.(1)如图1,当AB二AD且点0与点A重合时,则0M与ON 的数量关系是___________ ;⑵ 如图2,当An=AD且点0在矩形的内部(含边界)时,若OM=ON,请探究点0在移动过程中可形成什么图形?⑶ 如图3,当点O在矩形的对角线BD上时,若BC=7,CD二竺,BO=5,则(1)中的结论是否成立?3⑷ 如图4,在平面直角坐标系中,已知点A(0, 4^疗),点B(l, JJ),且ZABC=90%若点Q到y轴的距离为4,请直接写出满足题意的点C的坐标.备用图2在△ABC 中,ZABC=90。
类比探究(一)——平行、直角(讲义及答案)

类比探究(一)——平行、直角(讲义)➢知识点睛1.类比探究一般会围绕一个不变结构进行考查.常见结构有:平行结构、直角结构、旋转结构、中点结构.2.类比是解决类比探究问题的主要方法.往往会类比字母、类比辅助线、类比结构、类比思路来解决类比探究问题.3.常见结构:①平行结构②直角结构③旋转结构④中点结构平行夹中点(类)倍长中线中位线➢精讲精练1.如图,△ABC 中,点E,P 在边AB 上,且AE=BP,过点E,P 作BC 的平行线,分别交AC 于点F,Q,记△AEF 的面积为S1,四边形EFQP 的面积为S2,四边形PQCB 的面积为S3.(1)①若EP=2AE,则EF:PQ:BC= ;②求证:EF+PQ=BC.(2)若S1+S3=S2,求PE的值.AE(3)若S3-S1=S2,直接写出PE的值.AE2.在△ABC 中,AD 为BC 边上的中线,E 为AD 上一动点,设DE=nEA,连接CE 并延长交AB 于点F.FB (1)如图1,当∠BAC=90°,∠B=30°,DE=EA 时,求FA 的值;FB (2)如图2,当△ABC 为锐角三角形,DE=EA 时,求FA 的值;FB (3)如图3,当△ABC 为锐角三角形,DE=nEA 时,求FA 的值.3.在正方形ABCD 中,对角线AC 与BD 交于点O;在Rt△PMN中,∠MPN=90°.(1)如图1,若点P 与点O 重合且PM⊥AD,PN⊥AB,分别交AD,AB 于点E,F,请直接写出PE 与PF 的数量关系.(2)将图1 中的Rt△PMN 绕点O 顺时针旋转角度α(0°<α<45°).①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由.②如图3,旋转后,若Rt△PMN 的顶点P 在线段OB 上移动(不与点O,B 重合),当BD=3BP 时,猜想此时PE 与PF 的数量关系,并给出证明.③当BD=m·BP 时,请直接写出PE 与PF 的数量关系.(3)在(2)②的条件下,当∠DPM=15°时,连接EF,若正方形的边长为9 ,请直接写出线段EF 的长.34.在等腰直角三角形ABC 中,∠BAC=90°,AB=AC,直线MN过点A 且MN∥BC.以点 B 为一锐角顶点作Rt△BDE,∠BDE=90°,且点D 在直线MN 上(不与点A 重合).如图1,DE 与AC 交于点P,易证:BD=DP.(1)在图2 中,DE 与CA 的延长线交于点P,则BD=DP 是否成立?如果成立,请给予证明;如果不成立,请说明理由.(2)在图3 中,DE 与AC 的延长线交于点P,BD 与DP 是否相等?请直接写出你的结论,无需证明.【参考答案】1. (1)①1:3:4 ②证明略(2)2(3) (3)2. (1)2(2)2 (3)2n 3. (1)PE =PF(2)①成立,证明略;②PE =2PF ,证明略;③PE =(m -1)PF (3) 6 4. (1)成立,证明略(2)相等2 5。
【中考数学必备专题】类比探究之图形运动(含答案)[1]
![【中考数学必备专题】类比探究之图形运动(含答案)[1]](https://img.taocdn.com/s3/m/eb50796e7e21af45b307a818.png)
类比探究之图形运动一、探究题(共2道,每道50分)1.已知:在中,,动点绕的顶点逆时针旋转,且,连结.过、的中点、作直线,直线与直线、分别相交于点、.(1)如图1,当点旋转到的延长线上时,点恰好与点重合,证明(提示取的中点,连结、,根据三角形中位线定理和平行线的性质即可证明).(2)当点旋转到图2或图3中的位置时,与有何数量关系?请分别写出猜想,并证明.答案:图2:∠AMF=∠ENB图3:∠AMF+∠ENB=180°证明:如图2,取AC的中点H,连接HE、HF∵F是DC的中点,H是AC的中点∴HF∥AD,HF=AD∴∠AMF=∠HFE同理,HE∥CB,HE=CB,∴∠ENB=∠HEF又∵∴HF=HE∴∠HEF=∠HFE∴∠ENB=∠AMF如图3,取AC的中点H,连接HE、HF∵F是DC的中点,H是AC的中点∴HF∥AD,HF=AD∴∠AMF+∠HFE=180°同理,HE∥CB,HE=CB,∴∠ENB=∠HEF又∵∴HF=HE∴∠HEF=∠HFE∴∠AMF+∠BNE=180°解题思路:两题思路基本相同,都需要作出两条辅助线,两次运用中位线定理解答.试题难度:三颗星知识点:平行线的性质2.正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.答案:(1)AP=EF,AP⊥EF,理由如下:连接AC,则AC必过点O,延长FO交AB于M;∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,∴四边形OECF是正方形,∴OM=OF=OE=AM,∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,∴△AMO≌△FOE,∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,故AP=EF,且AP⊥EF.(2)题(1)的结论仍然成立,理由如下:延长AP交BC于N,延长FP交AB于M;∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,∴四边形MBEP是正方形,∴MP=PE,∠AMP=∠FPE=90°;又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,∴AM=PF,∴△AMP≌△FPE,∴AP=EF,∠APM=∠FPN=∠PEF∵∠PEF+∠PFE=90°,∠FPN=∠PEF,∴∠FPN+∠PFE=90°,即AP⊥EF,故AP=EF,且AP⊥EF.(3)题(1)(2)的结论仍然成立;如图,延长AB交PF于H,证法与(2)完全相同.解题思路:(1)连接AC,则AC必过O点,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FOE,则AO=EF,且∠AOM=∠FOC=∠OFE=45°,由此可证得AP⊥EF.(2)方法与①类似,延长FP交AB于M,延长AP交BC于N,易证得四边形MBEP是正方形,可证得△APM≌△FEP,则AP=EF,∠APM=∠FEP;而∠APM=∠FPN=∠PEF,且∠PEF与∠PFE互余,故∠PFE+∠FPN=90°,由此可证得AP⊥EF,所以(1)题的结论仍然成立.(3)解题思路和方法同(2).试题难度:四颗星知识点:全等三角形的判定与性质。
中招考试几何类比探究题集锦一参考答案

中招考试几何类比探究题集锦(附参考答案)参考答案与试题解析一.解答题(共11小题)1.在△ABC中,AB=AC,∠BAC=2∠DAE=2α.(1)如图1,若点D关于直线AE的对称点为F,求证:△ABD≌△ACF;(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;(3)如图3,若α=45°,点E在BC的延长线上,请直接写出DE2,BD2,CE2三者之间的等量关系.【解答】解:(1)∵点D关于直线AE的对称点为F,∴EF=DE,AF=AD,∠DAE=∠EAF=α∴∠CAE+∠CAF=α∵∠BAC=2∠DAE=2α.∴∠BAD+∠CAE=∠BAC﹣∠DAE=α,∴∠BAD=∠CAF,在△ABD和△ACF中,第1页(共33页)第2页(共33页)∴△ABD ≌△ACF (SAS ),(2)由(1)知,△ABD ≌△ACF (SAS ),∴CF=BD ,∠ACF=∠B ,∵AB=AC ,∠BAC=2α,α=45°,∴△ABC 是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB +∠ACF=45°+45°=90°,在Rt △CEF 中,由勾股定理得,EF 2=CF 2+CE 2,∴DE 2=BD 2+CE 2,(3)DE 2=BD 2+CE 2;理由:如图,∵∠BAC=2∠DAE=2α.∴∠DAE=α,∵点D 关于直线AE 的对称点为F ,∴EF=DE ,AF=AD ,∠DAE=∠EAF=α∴∠CAF=∠EAF +∠CAE=α+∠CAE∴∠BAD=∠BAC ﹣∠DAC=2α﹣∠DAC=2α﹣(∠DAE ﹣∠CAE )=2α﹣(α﹣∠CAE)=α+∠CAE∴∠BAD=∠CAF,在△ABD和△ACF中,∴△ABD≌△ACF(SAS),∴CF=BD,∠ACF=∠B,∵AB=AC,∠BAC=2α,α=45°,∴△ABC是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB+∠ACF=45°+45°=90°,在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,∴DE2=BD2+CE2,2.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF 均为等第3页(共33页)边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.【解答】解:(1)DE=BD+CE.理由如下:如图1,∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD在△ABD和△CAE中,,∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;(2)如图2,∵∠BDA=∠AEC=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,第4页(共33页)∴∠CAE=∠ABD,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;(3)DF=EF.理由如下:由(2)知,△ADB≌△CAE,BD=EA,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE,∵BF=AF在△DBF和△EAF中,,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,第5页(共33页)∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.∴DF=EF.3.(1)问题发现如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:①∠ACE的度数为60°;②线段AC、CD、CE之间的数量关系为AC=CD+CE.(2)拓展探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC 上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.(3)解决问题如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.第6页(共33页)【解答】解:(1)①∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠B=60°,故答案为:60°;②线段AC、CD、CE之间的数量关系为:AC=CD+CE;理由是:由①得:△BAD≌△CAE,∴BD=CE,∵AC=BC=BD+CD,∴AC=CD+CE;故答案为:AC=CD+CE;(2)∠ACE=45°,AC=CD+CE,理由是:如图2,∵△ABC和△ADE均为等腰直角三角形,且∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,第7页(共33页)∴△ABD≌△ACE,∴BD=CE,∠ACE=∠B=45°,∵BC=CD+BD,∴BC=CD+CE,∵在等腰直角三角形ABC中,BC=AC,∴AC=CD+CE;(3)如图3,过A作AC的垂线,交CB的延长线于点F,∵∠BAD=∠BCD=90°,AB=AD=2,CD=1,∴BD=2,BC=,∵∠BAD=∠BCD=90°,∴∠BAD+∠BCD=180°,∴A、B、C、D四点共圆,∴∠ADB=∠ACB=45°,∴△ACF是等腰直角三角形,由(2)得:AC=BC+CD,∴AC===.第8页(共33页)4.【探究发现】如图1,△ABC是等边三角形,∠AEF=60°,EF交等边三角形外角平分线CF所在的直线于点F,当点E是BC的中点时,有AE=EF成立;【数学思考】某数学兴趣小组在探究AE、EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点E是直线BC上(B,C除外)任意一点时(其它条件不变),结论AE=EF仍然成立.假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任意一点”;“点E是线段BC延长线上的任意一点”;“点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并证明AE=EF.【拓展应用】当点E在线段BC的延长线上时,若CE=BC,在备用图2中画出图形,并运用上述结论求出S△ABC :S△AEF的值.【解答】证明:第一种情况:点E是线段BC上的任意一点,可作三种辅助线:方法一:如图1,在AB上截取AG,使AG=EC,连接EG,第9页(共33页)∵△ABC是等边三角形,∴AB=BC,∠B=∠ACB=60°.∵AG=EC,∴BG=BE,∴△BEG是等边三角形,∠BGE=60°,∴∠AGE=120°.∵FC是外角的平分线,∠ECF=120°=∠AGE.∵∠AEC是△ABE的外角,∴∠AEC=∠B+∠GAE=60°+∠GAE.∵∠AEC=∠AEF+∠FEC=60°+∠FEC,∴∠GAE=∠FEC.在△AGE和△ECF中,∴△AGE≌△ECF(ASA),∴AE=EF;方法二:在CA上截取CG=CE,连结GE,证明类似方法一;方法三:延长FC到G,使CG=CE,连结EG,易证△CEG是等边三角形,第10页(共33页)∴CE=EG,∠G=∠ACB=60°,∠CEG=∠AEF=60°,∴∠CEG+∠CEF=∠AEF+∠CEF,即∠GEF=∠AEC,∴△GEF≌△CEA,∴AE=EF.第二种情况:点E是线段BC延长线上的任意一点如图2,可作三种辅助线:①在CF上截取CG=CE,连接GE②延长AC到G,使CG=CE,连结EG;③或延长BA到G,使BG=BE,连结EG.第②种添加辅助线的方法证明如下:证明:延长AC到G,使CG=CE,连结EG,易证△CEG为等边三角形,∴∠G=∠ECF=60°,EG=CE,又∠AEG=∠CEG+∠AEC=60°+∠AEC,∠CEF=∠AEF+∠AEC=60°+∠AEC,第11页(共33页)∴∠AEG=∠CEF,∴△AEG≌△FEC,∴AE=EF.第三种情况:点E是线段BC反向延长线上的任意一点如图3,可作三种辅助线:①延长AB到G,使BG=BE,连结EG;②延长CF到G,使CG=CE,连结EG;③在CE上截取CG=CF,连结GF现就第①种添加辅助线的方法证明如下:证明:延长AB到G,使BG=BE,连结EG,易证△BEG为等边三角形,∴∠G=∠ECF=60°,第12页(共33页)∵∠AEB+∠BAE=∠ABC=60°,∠AEB+∠CEF=∠AEF=60°,∴∠BAE=∠CEF,∵AB=BC,BG=BE,∴AB+BG=BC+BE,即AG=CE,∴△AEG≌△EFC,∴AE=EF.拓展应用:如图4:作CH⊥AE于H点,∴∠AHC=90°.由数学思考得AE=EF,又∵∠AEF=60°,∴△AEF是等边三角形,∴△ABC∽△AEF.第13页(共33页)∵CE=BC=AC,△ABC是等边三角形,∴∠CAH=30°,AH=EH.∴CH=AC,AH=AC,AE=AC,∴.∴==.5.问题情境:在Rt△ABC中,AB=BC,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,将三角板绕点O旋转.(1)操作发现:当点O为AC中点时:①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF与EF之间存在的等量关系:AE2+CF2=EF2(无需证明);②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接EF,判断①中的结论是否成立.若成立,请证明;若不成立,请说明理由;第14页(共33页)(2)类比延伸:当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,若=,请直接写出=.【解答】解:(1)①猜想:AE2+CF2=EF2,连接OB,如图1,∵AB=BC,∠ABC=90°,O点为AC的中点,∴OB=AC=OC,∠BOC=90°,∠ABO=∠BCO=45°.∵∠EOF=90°,∴∠EOB+∠BOF=∠FOC+∠BOF.∴∠EOB=∠FOC,在△OEB和△OFC中,,∴△OEB≌△OFC(ASA).∴BE=CF,又∵BA=BC,∴AE=BF.在Rt△EBF中,∵∠EBF=90°,∴BF2+BE2=EF2,∴AE2+CF2=EF2;故答案为:AE2+CF2=EF2;第15页(共33页)②成立.证明:连结OB.如图2,∵AB=BC,∠ABC=90°,O点为AC的中点,∴OB=AC=OC,∠BOC=90°,∠ABO=∠BCO=45°.∵∠EOF=90°,∴∠EOB=∠FOC.在△OEB和△OFC中,,∴△OEB≌△OFC(ASA).∴BE=CF,又∵BA=BC,∴AE=BF.在Rt△EBF中,∵∠EBF=90°,∴BF2+BE2=EF2,∴AE2+CF2=EF2;(2)=,如图3,过点O作OM⊥AB于M,ON⊥BC于N.∵∠B=90°,第16页(共33页)∴∠MON=90°,∵∠EOF=90°,∴∠EOM=∠FON.∵∠EMO=∠FNO=90°,∴△OME∽△ONF,∴=,∵△AOM和△OCN为等腰直角三角形,∴△AOM∽△OCN,∴=,∵=,∴=,故答案为.第17页(共33页)第18页(共33页)6.阅读发现:(1)如图①,在Rt △ABC 和Rt △DBE 中,∠ABC=∠DBE=90°,AB=BC=3,BD=BE=1,连结CD ,AE .易证:△BCD ≌△BAE .(不需要证明) 提出问题:(2)在(1)的条件下,当BD ∥AE 时,延长CD 交AE 于点F ,如图②,求AF 的长.解决问题:(3)如图③,在Rt △ABC 和Rt △DBE 中,∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,连结CD ,AE .当∠BAE=45°时,点E 到AB 的距离EF 的长为2,求线段CD的长为 .【解答】(2)解:如图②中,AB与CF交于点O.由(1)可知:△BCD≌△BAE,∴∠OAF=∠OCB,CD=AE,∵∠AOF=∠COB,∴∠AFO=∠CBO=90°,∴CF⊥AE,∵BD∥AE,∴BD⊥CF,在RT△CDB中,∵∠CDB=90°,BC=3,BD=1,∴CD=AE==2,∵∠BDF=∠DFE=∠DBE=90°,∴四边形EFDB是矩形,∴EF=BD=1,∴AF=AE﹣EF=2﹣1.(3)解:在RT△ABC,RT△EBD中,∵∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,∴AB=BC,BE=BD,∴==,∵∠ABC=∠EBD=90°,∴∠ABE=∠DBC,∴△ABE∽△CBD,∴==,第19页(共33页)第20页(共33页)在RT △AEF 中,∵∠AFE=90°,∠EAF=45°,EF=2,∴AF=EF=2,AE=2,∴=,∴CD=.故答案为.7.如图1,两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是DE∥AC;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是S1=S2.(2)猜想论证当△DEC绕点C旋转到如图3所示的位置时,请猜想(1)中S1与S2的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)拓展探究已知∠ABC=60°,BD平分∠ABC,BD=CD,BC=9,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请求相应的BF的长.【解答】解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,第21页(共33页)∴△ACD是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;故答案为:DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,根据等边三角形的性质,△ACD的边AC、AD上的高相等,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2=×2×2=2;故答案为:S1=S2;(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,,第22页(共33页)∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF1=S△BDE;过点D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,∵BF1=DF1,∠F1BD=∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB=×60°=30°,∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,第23页(共33页)∵在△CDF1和△CDF2中,,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD=×60°=30°,又∵BD=4,∴BE=×6÷cos30°=3÷=2,∴BF1=2,BF2=BF1+F1F2=2+2=4,故BF的长为2或4.8.问题解决:如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D 重合),压平后得到折痕MN.当时,求的值.类比归纳:第24页(共33页)在图(1)中,若,则的值等于;若,则的值等于;若(n 为整数),则的值等于.(用含n的式子表示)联系拓广:如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D 重合),压平后得到折痕MN,设,则的值等于.(用含m,n的式子表示)【解答】解:(1)方法一:如图(1﹣1),连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.∴MN垂直平分BE,∴BM=EM,BN=EN.∵四边形ABCD是正方形,∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.∵,∴CE=DE=1.第25页(共33页)设BN=x,则NE=x,NC=2﹣x.在Rt△CNE中,NE2=CN2+CE2.∴x2=(2﹣x)2+12,解得x=,即BN=.在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,∴AM2+AB2=DM2+DE2.设AM=y,则DM=2﹣y,∴y2+22=(2﹣y)2+12,解得y=,即AM=(6分)∴.方法二:同方法一,BN=.如图(1﹣2),过点N做NG∥CD,交AD于点G,连接BE.∵AD∥BC,∴四边形GDCN是平行四边形.∴NG=CD=BC.同理,四边形ABNG也是平行四边形.∴AG=BN=∵MN⊥BE,∴∠EBC+∠BNM=90度.∵NG⊥BC,∴∠MNG+∠BNM=90°,第26页(共33页)∴∠EBC=∠MNG.在△BCE与△NGM中,∴△BCE≌△NGM,EC=MG.∵AM=AG﹣MG,AM=﹣1=.∴.(2)如图1,当四边形ABCD为正方形时,连接BE,=,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n﹣x)2+12,x=;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,∴NH=EC=1,AM=BH=BN﹣NH=﹣1=则:==.故当=,则的值等于;若=,则的值等于;第27页(共33页)(3)若四边形ABCD为矩形,连接BE,=,不妨令CD=n,则CE=1;又==,则BC=mn,同样的方法可求得:BN=,BE⊥MN,易证得:△MHN∽△BCE.故=,=,HN=,故AM=BH=BN﹣HN=,故==.故答案为:;;;.第28页(共33页)第29页(共33页)9.阅读理解:如图1,在直角梯形ABCD 中,AB ∥CD ,∠B=90°,点P 在BC 边上,当∠APD=90°时,易证△ABP ∽△PCD ,从而得到BP•PC=AB•CD ,解答下列问题.(1)模型探究:如图2,在四边形ABCD 中,点P 在BC 边上,当∠B=∠C=∠APD 时,结论BP•PC=AB•CD 仍成立吗?试说明理由;(2)拓展应用:如图3,M 为AB 的中点,AE 与BD 交于点C ,∠DME=∠A=∠B=45°且DM 交AC 于F ,ME 交BC 于G .AB=,AF=3,求FG 的长.【解答】解:(1)∵∠APC=∠APD +∠CPD ,∠APC=∠BAP +∠B (三角形外角定理),∠B=∠APD (已知),∴∠BAP=∠CPD,又∵∠B=∠C,∴△ABP∽△PCD∴=,∴BP•PC=AB•CD;(2)∵∠AFM=∠DME+∠E(三角形外角定理),∠DME=∠A(已知),∴∠AFM=∠A+∠E(等量代换),又∠BMG=∠A+∠E(三角形外角定理),∴∠AFM=∠BMG.∵∠A=∠B,∴△AMF∽△BGM.当∠A=∠B=45°时,∠ACB=180°﹣∠A﹣∠B=90°,即AC⊥BC且AC=BC.∵M为AB的中点,∴AM=BM=,AC=BC=4.又∵△AMF∽△BGM,∴,∴BG===,又∵,CF=4﹣3=1,∴.第30页(共33页)10.基本模型如下图,点B、P、C在同一直线上,若∠B=∠1=∠C=90°,则△ABP∽△PCD成立,(1)模型拓展如图1,点B、P、C在同一直线上,若∠B=∠1=∠C,则△ABP∽△PCD成立吗?为什么?(2)模型应用①如图2,在等腰梯形ABCD中,AD∥BC,AD=1,AB=2,BC=4,在BC上截取BP=AD,作∠APQ=∠B,PQ交CD于点Q,求CQ的长;②如图3,正方形ABCD的边长为1,点P是线段BC上的动点,作∠APQ=90°,PQ交CD于Q,当P在何处时,线段CQ最长?最长是多少?【解答】解:(1)成立,∵∠A=180°﹣(∠B+∠APB),第31页(共33页)∠CPD=180°﹣(∠1+∠APB),∠B=∠1,∴∠A=∠CPD,∵∠B=∠C,∴△ABP∽△PCD;(2)①∵四边形ABCD是等腰梯形,∴∠B=∠C,∵∠B=∠APQ,∴∠B=∠APQ=∠C,由(1)知,△ABP∽△PCD,∴=,∴=,∴CQ=;②设BP=x,CQ=y.∵∠B=∠APQ=90°,∴△ABP∽△PCQ,∴=,即=,∴y=﹣x2+x=﹣(x﹣)2+,第32页(共33页)∴当x=时,y=,最大即当P是BC的中点时,CQ最长,最长为.第33页(共33页)。
九年级数学中考压轴题类比探究问题(附答案)

专题四中考压轴试题——类比探究题多重训练1.类比探究题,一般在中考试卷第22题,分三个问题解答,属几何综合题;2.第(1)问比较简单,但一定要注意解题时所作的“工作”:①添加了什么样的辅助线?(线段的截长补短、旋转某一角度、作平行线或者连接等)②解题所用的知识点有哪些?(如全等三角形、相似三角形、勾股定理列方程等)③解题时先做了什么后做了什么?④解题的整体思路是什么?(如由SAS推出全等,再由全等得到边相等,然后再由线段间的等量代换得出结论,即贯穿解题全过程的思路)3.第(2)问题体现了“类比”的思想,即几乎“照搬”第(1)问题的解题全过程,即添加辅助线、所用知识点、解题全思路,包括添加的字母有时都可以保持一致;4.既然是类比,就必须注意在三个不同的问题中,哪些条件自始至终没有变化,这就是本题的“核心条件”,也是解题的关键。
5.第(3)问题往往让学生直接写出结果,不需证明,有时和前面的结论一致,有时是一个变化的结论,所以要根据前两个问题,大胆猜测。
1.在正方形ABCD中,点M、N分别在AD、CD上,如图1,若∠MBN=45°,求证:MN=AM+CN⑴如图2,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上,若∠MBN= ∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?写出猜想并证明.⑵如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN= ∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?写出猜想并证明.(2)2.(1)如图1,已知正方形ABCD和正方形CGEF(CG>BC),B、C、G在同一条直线上,M为线段AE的中点。
探究:线段MD、MF的关系,并证明。
(2)若将正方形CGEF绕点C顺时针旋转,使得正方形CGEF的对角线CE在正方形ABCD的边BC的延长线上,M为AE的中点。
中考数学类比探究实战演练(一)(含答案)

学生做题前请先回答以下问题问题1:类比探究的处理思路是什么?问题2:类比迁移的具体操作是什么?问题3:想一想类比探究问题常见的不变结构有哪些,处理方式是什么?以下是问题及答案,请对比参考:问题1:类比探究的处理思路是什么?答:①类比上一问,迁移解决下一问;②依据不变结构,分析特征解决问题.问题2:类比迁移的具体操作是什么?答:类比字母、类比辅助线、类比思路、类比结构.问题3:想一想类比探究问题常见的不变结构有哪些,处理方式是什么?答:类比探究中常见不变结构及处理方式分别为:①旋转结构,找等腰结构,借助全等整合条件;②中点结构,作倍长,通过全等转移边和角;③平行结构,找相似,转比例;④直角结构,作横平竖直的线,找全等或相似.中考数学类比探究实战演练(一)一、单选题(共6道,每道4分)1.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在BC边上,∠BAD=75°,∠CAD=30°,AD=2,BD=2CD,求AC的长.(1)小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).请回答:∠ACE的度数为_____,AC的长为_____.( )A. B.C. D.答案:C解题思路:见第2题中解析试题难度:三颗星知识点:探究应用2.(上接第1题)(2)参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2DE,则BC的长为( )A.6B.C. D.答案:C解题思路:试题难度:三颗星知识点:探究应用3.已知正方形ABCD中,O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD 于点F,连接PB.(1)如图1,当点P在线段AO上时(不与点A,O重合),过点P作PE⊥PB,交CD于点E,则DF,EF之间有怎样的数量关系?线段PA,PC,CE之间有怎样的一个等量关系?请给出证明过程.(2)如图2,当点P在线段OC上时(不与点O,C重合),过点P作PE⊥PB,交直线CD 于点E,(1)中的两个结论是否仍成立?若不成立,写出相应的结论.(所写结论均不必证明)(建议学生打印做题,并在做完之后对比解题思路中的过程,推敲里面是如何踩点得分的)(1)中DF,EF之间的数量关系是( )A. B.C.DF=EFD.答案:C解题思路:见第6题中解析试题难度:三颗星知识点:中考数学几何中的类比探究4.(上接第3题)(1)中线段PA,PC,CE之间的一个等量关系为( )A. B.C. D.答案:D解题思路:见第6题中解析试题难度:三颗星知识点:中考数学几何中的类比探究5.(上接第3,4题)(2)中DF,EF之间的数量关系是( )A. B.C.DF=EFD.答案:C解题思路:见第6题中解析试题难度:三颗星知识点:中考数学几何中的类比探究6.(上接第3,4,5题)(2)中线段PA,PC,CE之间的一个等量关系为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学类比探究(一)——直角、平行(习题)
1. 如图 1,在□ABCD 中,点 E 是 BC 边的中点,点 F 是线段
AE 上一点,BF 的延长线交射线 CD 于点 G . (1) 尝试探究:如图 1,若 AF = 3 ,则 CD 的值是 .
EF CG
(2) 类比延伸:如图 2,在原题的条件下,若 AF = m (m > EF
0),则 CD 的值是 (用含 m 的代数式表示),试写出
CG
解答过程.
(3) 拓展迁移:如图 3,在梯形 ABCD 中,DC ∥AB ,点 E
是 BC 延长线上一点,AE 和 BD 相交于点 F .若 AB = a , CD BC = b (a >0,b >0),则 AF 的值是 (用含 a ,b
BE EF
的代数式表示).
2.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=
∠DEF=90°,∠EDF=30°.
【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P,边EF 与边BC 交于点Q.
【探究】在旋转过程中,
(1)如图2,当CE
=1时,EP 与EQ 满足怎样的数量关系?EA
并给出证明.
(2)如图3,当CE
= 2 时,EP 与EQ 满足怎样的数量关系?EA
并给出证明.
(3)根据你对(1),(2)的探究结果,试写出当CE
=m时,EA
EP 与EQ 满足的数量关系式为.
3.在△ABC 中,已知D 是BC 边的中点,G 是△ABC 的重心,
过点G 的直线分别交AB,AC 于点E,F.
(1)如图1,当点E 与点B 重合时,
AG
=
GD
(2)如图2,当EF∥BC 时,求证:
BE
+
CF
.
= 1 .
AE AF
(3)如图3,当EF 和BC 不平行,且点E,F 分别在线段
AB,AC 上时,(2)中的结论是否成立?如果成立,请给出
证明;如果不成立,请说明理由.
提示:①过点 A 作AM∥BC,交EF 于点M,直线FE 交BC 于N;②NB+NC=2ND.
(4)如图4,当点E 在AB 的延长线上或点F 在AC 的延长
线上时,(2)中的结论是否成立?如果成立,请给出证明;
如果不成立,请说明理由.
【参考答案】 1. 1 3 ( ) ; 2
(2) m ;
2
(3) a b .
2. (1)EP =EQ ,证明略;
(2) EP = 1 2
EQ ,证明略; (3) EP = 1 EQ . m
3. (1)2;
(2)证明略;
(3)(2)中的结论仍然成立,证明略;
(4)(2)中的结论不成立,理由略.。
