应用统计学大作业
应用统计学作业答案

第1章导论作业1指出下面的变量哪一个属于分类变量:A、年龄B、工资C、汽车产量D、购买商品时的方式(现金、信用卡、支票)我的答案:D得分:4.3分2指出下面哪个变量属于顺序变量:A、年龄B、工资C、汽车产量D、员工对企业某项改革措施的态度(赞成、中立、反对)我的答案:D得分:4.3分3指出下面哪一个变量属于数值型变量:A、年龄B、性别C、企业类型D、员工对企业某项改革措施的态度(赞成、中立、反对)我的答案:A得分:4.3分4一名统计学专业的学生为了完成其统计作业,在《统计年鉴》中找到了2006年城镇家庭的人均收入。
这一数据属于:A、分类数据B、顺序数据C、截面数据D、时间序列数据我的答案:C得分:4.3分5下列不属于描述统计问题的是:A、根据样本信息对总体进行的推断了解数据分布的特征C、分析感兴趣的总体特征D、利用图、表或其他数据汇总工具分析数据我的答案:A得分:4.3分6某大学的一位研究人员希望估计该大学本科生平均每月的生活费支出,为此,他调查了200名学生,发现他们每月平均生活费支出是500元。
该研究人员感兴趣的总体是:A、该大学的所有学生B、该校所有大学生的总生活费支出C、该大学所有的在校本科生D、所调查的200名学生我的答案:C得分:5.4分7某大学的以为研究人员希望估计该大学本科生平均每月的生活费支出,为此,他调查了200名学生,发现他们每月平均生活费支出是500元。
该研究人员感兴趣的参数是:A、该大学的所有学生人数B、该大学所有本科生的月平均生活费支出C、该大学所有本科生的月生活费支出D、所调查的200名学生的月平均生活费支出我的答案:B得分:4.3分8某大学的以为研究人员希望估计该大学本科生平均每月的生活费支出,为此,他调查了200名学生,发现他们每月平均生活费支出是500元。
该研究人员感兴趣的统计量是:A、该大学的所有学生人数B、该大学所有本科生的月平均生活费支出该大学所有本科生的月生活费支出D、所调查的200名学生的月平均生活费支出我的答案:D得分:4.3分9在下列叙述中,采用推断统计方法的是:A、用饼图描述某企业职工的学历构成B、从一个果园中采摘36个橘子,利用这36个橘子的平均重量估计果园中橘子的平均总量C、一个城市在1月份的平均汽油价格D、反映大学生统计学成绩的条形图我的答案:B得分:4.3分10一项民意调查的目的是想确定年轻人愿意与其父母讨论的话题。
应用统计实验报告期末大作业

.专业整理.应用统计调查报告调查概述(一)调查背景与目的为了更好地做好课程的教学方案,提高同学们实际应用能力,特进行本次调查。
(二)小组分工说明组长:韩嘉楠组员:陈旭东来锦涛分工说明:分配与安排工作由组长韩嘉楠负责,由来锦涛负责录入问卷数据与基本的数据汇总;全员共同参与对调查数据进行研究分析,其中由来锦涛负责用图形展示数据的分布情况,研究数据的分布特征,陈旭东负责求总体均值和总体方差的置信区间,韩嘉楠负责对分类变量检验和度量和方差分析研究;韩嘉楠负责撰写调查报告。
一、报告主体数据的分布情况和特征1.这次总共调查了57个人,51%女,49%男。
.专业整理.频 率百 分比有效 百分比累积 百分比有很3154.454.454.4效重要57人中有比较一部分人觉得这门课程比较重要,但是也有一部分人觉得不■男重要|4~51%比1■ urn第1题3.对于这门课的合理程度只有1 , 75%的人觉得不合理4.对于这个考核方式大部分趋于认为这个基本合理不同性别的在第4题上面的看法分布可知,不同性别在第4题上面的看法分布差异无统计学意义,尚可以认为不同性别在第4题上的看法分布相同。
8对于对生产管理影响较大的工作是什么的问题。
大部分认为重要的是生产规划你认为财务主管哪些工作对企业经营影响最大N 有效57缺失0 均值92.60 均值的标准误42.019 中值 1.55a 众数 1 标准差317.236 方差100638.852 偏度 3.426 偏度的标准误.316 峰度10.163 峰度的标准误.623 全距1233 极小值 1 极大值1234 百分位数10b,c20253040 1.0750 1.55 ■生*规划■]恵卩羞叫■生产调鹰■严開开炊9.营销管理最重要的工作这个问题第9题关于ERP 实践对专业知识的学习和掌握有什么作用这个问题 自由度2 0.05平均 2.157895 标准误差 0.060229中位数 2 众数 2标准差0.454716n=57, 1-a = 90% ,za/2=1.645。
应用统计学大作业

2.3 调查Leabharlann 法根据本调研的特点,本次调查方法为: ① 调研采用问卷式; (/jq/6789388.aspx) ② 利用问卷星的形式在朋友圈等社交平台转发问卷链接进行网络在线调查。
4
2.4 问卷设计
问卷问题的设置具体包括以下几个步骤: ①在结合主题的基础上,初步确定了问卷的调查方向以及问卷中应涉及的问题; ②参照现有的有关大学生外卖订餐情况的统计报告,制定原始的调查问卷; ③经过再次多方面分析,对问卷的问题设置及排序进行调整; ④进行问卷的预发放工作,通过反馈的关于问卷的问题设置意见,对问卷进行进 步修改; ⑤发放问卷,以朋友圈转发调查问卷为主。
由于男生样本数为 25,女生样本数为 40,总体方差未知,且没有理由判定 σ1 =σ22,,故认为σ12≠σ22。当总体方差未知时,用样本方差 S12 与 S22 分别估计 总体方差和σx1-x2。公式为:
x
1
x2
2 s12 s2 n n2 1
注:令外卖订餐次数“每周 1-2 次”=1.5, “每周 3-4 次”=3.5, “每周 5-6 次”=5.5, “每周 7-8 次”=7.5, “每周 8 次以上”=8.5
6
建立假设:性别对外卖订餐次数没有影响。 H0 : µ1-µ2 = 0 没有显著差别 H1 : µ1-µ2 ≠ 0
2
有显著差别
目录
1.确定研究问题............................................................................................................ 3 1.1 研究背景.......................................................................................................... 3 2.调查设计.................................................................................................................... 3 2.1 调查目的.......................................................................................................... 3 2.2 调查对象.......................................................................................................... 4 2.3 调查方法.......................................................................................................... 4 2.4 问卷设计.......................................................................................................... 5 2.5 问卷内容.......................................................................................................... 5 3.调查组织与实施........................................................................................................ 5 3.1 调查组织.......................................................................................................... 5 3.2 调查结果.......................................................................................................... 6 4.数据处理与原因分析................................................................................................ 6 4.1 外卖订餐原因的单因素分析.......................................................................... 6 4.1.1 性别对外卖订餐次数的影响的假设性分析....................................... 6 4.1.2 年级对外卖订餐次数的影响............................................................... 8 4.1.3 餐饮支出对外卖订餐次数的影响..................................................... 10 4.1.4 是否有人陪伴吃饭对订外卖意愿的影响......................................... 12 4.1.5 选择外卖订餐的时间......................................................................... 12 4.1.6 选择外卖的原因................................................................................. 13 4.1.7 不选择外卖的原因............................................................................. 14 4.1.8 在哪种天气下更容易选择外卖......................................................... 15 4.1.9 每次外卖订餐支出情况..................................................................... 16 5.调查方案的优缺点分析........................................................................................... 16 附录.............................................................................................................................. 17 附录 1:北京交通大学选修课缺课情况调查问卷............................................ 17 附录 2:原始数据................................................................................................ 19
应用统计方法(大作业)
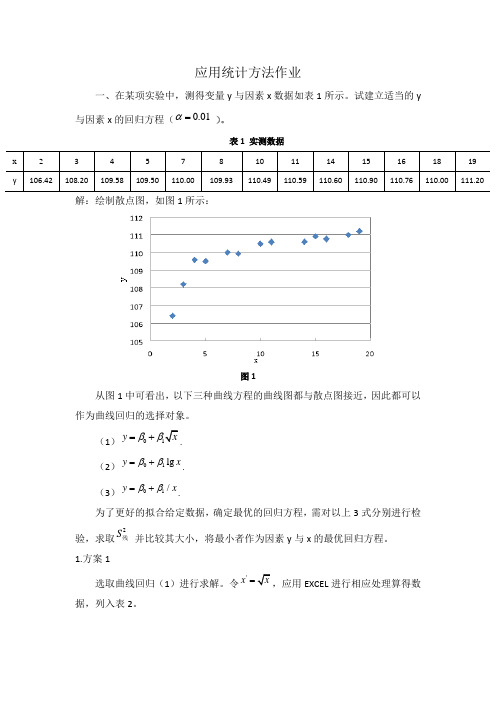
应用统计方法作业一、在某项实验中,测得变量y 与因素x 数据如表1所示。
试建立适当的y 与因素x 的回归方程(0.01α= )。
表1 实测数据x 2 3 4 5 7 8 10 11 14 15 16 18 19 y106.42108.20109.58109.50110.00109.93110.49110.59110.60110.90110.76110.00111.20解:绘制散点图,如图1所示:图1从图1中可看出,以下三种曲线方程的曲线图都与散点图接近,因此都可以作为曲线回归的选择对象。
(1)0y x ββ=+. (2)01lg y x ββ=+.(3)01/y xββ=+.为了更好的拟合给定数据,确定最优的回归方程,需对以上3式分别进行检验,求取2S 残并比较其大小,将最小者作为因素y 与x 的最优回归方程。
1.方案1选取曲线回归(1)进行求解。
令'x x =EXCEL 进行相应处理算得数据,列入表2。
表2 方案1数据处理计算由表2得:''13''2111.6670()i x x i l x x ==-=∑1321()21.2105yy i i l y y ==-=∑'13''1()()13.9389i i x y i l x x y y ==--=∑由此得: µ'''113.938911.667194701.x y x x l l β===¶µ'011.1947109.9362 3.0424=106.3014y x ββ=-=⨯- 故所求的回归方程为:$'106.3014 1.1947y x =+进行变量还原得回归方程:$106.3014y =+检验假设H 01:10β=.'21= 1.194713.938916.6528x y S l β=⨯=回2221.210516.6528 4.5577yy S l S =-=-=回残2216.652840.1915/11 4.5577/11S F S ===回残对给定的0.01α=,查F(1,11)表(附表5)得临界值9.65λ=。
应用统计学作业

上市公司定向增发旳长期财务绩效实证研究一、本文以~已实行定向增发旳43家深市A股上市公司为样本, 综合选用10个财务指标进行因子分析, 构造并检查样我司增发前一年、当年及后三年旳财务绩效评价模型, 来研究定向增发前后五年间增发公司旳财务绩效均值与否有明显变化。
二、指标体系旳设计(1)为了尽量全面地反映上市公司旳财务状况和经营业绩, 本文从偿债能力、营运能力、赚钱能力、发展能力和钞票流量能力五个方面选用了10个财务指标来考察杨我司旳绩效。
(2)偿债能力指标, 选用流动比率、速动比率、资产负债率。
(3)营运能力指标, 选用流动资产周转率、总资产周转率。
(4)赚钱能力指标, 选用每股收益、净资产收益率。
三、发展能力指标, 选用资本积累率。
四、钞票流量能力指标, 选用营业收入钞票比率、每股经营活动钞票净流量。
五、研究措施及构建模型由于至今整体经济环境和证券市场等客观因素波动较大, 因此, 本文选用因子分析法, 从而在一定限度上消除外在客观因素旳影响。
使用因子分析法对所选用旳10个财务指标进行降维, 共得到4个公因子, 再以各公因子旳负荷量与因子得分相乘, 得到财务绩效综合得分模型:F i =a1F i1+a2F i2+a3F i3+a4F i4六、式中F i为第i家公司旳综合得分, a j为各因子旳方差比例, F ij表达公共因子第i家公司第j个因子旳得分。
七、实证分析1、指标趋同化解决。
指标趋同化解决是指将指标正向化, 即把逆指标转化为正指标, 本文采用倒数旳措施将其转换为正指标。
所选用旳10个指标中只有资产负债率为逆指标。
因此取资产负债率倒数进行分析。
2、因子分析合用性检查。
进行因子分析前一方面对样本数据进行KMO检查和Barlett球形检查。
3、由上表可知KMO值为0.437, 可以接受进行因子分析;Barlett球形检查旳明显性为0.000, 适合进行因子分析。
4、财务绩效综合得分模型表1 旋转成分矩阵由表1可以看出, 旋转后因子变量在较多变量上均有较高旳载荷。
应用统计学作业(专)

1、统计调查的种类(1)按调查对象包括的范围不同可分为全面调查和非全面调查全面调查是对被调查对象中所有的单位全部进行调查,其主要目的是要取得总体的全面、系统、完整的总量资料。
如普查。
全面调查要耗费大量的人力、物力、财力和时间。
非全面调查是对被调查对象中一部分单位进行调查。
如重点调查、典型调查、抽样调查和非全面统计报表等。
全面调查和非全面调查是以调查对象所包括的单位范围不同来区分的,而不是以最后取得的结果是否反映总体特征的全面资料而言的。
(2)按登记时间是否连续,可分为经常性调查与一次性调查经常性调查,是随着调查对象在时间上的发展变化,而随时对变化的情况进行连续不断的登记。
其主要目的是获得事物全部发展过程及其结果的统计资料。
一次性调查:是不连续登记的调查,它是对事物每隔一段时期后在一定时点上的状态进行登记。
其主要目的是获得事物在某一时点上的水平、状况的资料。
一次性调查又分为定期和不定期两种。
定期调查是每隔一段固定时期进行一次调查,不定期调查是时间间隔不完全相等,而且间隔很久才调查一次。
(3)按调查的组织方式不同,可分为统计报表制度和专门调查统计报表制度:它是按照国家统一规定的调查要求与文件(指标、表格形式、计算方法等)自下而上的提供统计资料的一种报表制度。
专门调查:是为了某一特定目的而专门组织的统计调查。
包括:普查、抽样调查、重点调查、典型调查等。
①普查:普查是专门组织一次性的全面调查,用来调查属于一定时点或时期内的社会经济现象的总量。
普查要遵循以下几点:a.确定普查的标准时间:普查的标准时间是指登记调查单位项目所依据的统计时点。
所有的调查资料都必须是反映这一时点上的情况。
例如,我国第四人口普查,1990年7月1日零时为普查登记的标准时点。
凡是在这个时点以前死亡和这个时点以后出生的,都不能计入这次普查的人口数内。
这样才可避免所登记的生重复或遗漏。
b.普查的登记工作应在整个普查范围内同时进行,以保证普查资料的实效性、准确性,避免资料的搜集工作拖的太久。
应用统计学大作业
学院:经济管理学院班级:食品经济管理(1)班姓名:张从容学号:0846112日期:2010年6月应用统计学大作业题目:校友捐赠是高等学校收入的重要来源。
如果学校的管理人员能确定影响捐赠的校友所占比例增长的因素,他们就可能制定使学校收入增长的政策。
研究表明,对与老师的沟通交往感到比较满意的学生,他们很可能更容易毕业。
于是人们可能猜测,人数比较少的班级和比较低的学生—教师比可能有一个比较高的令人满意的毕业率,随后又可能引起给予学校捐赠的校友所占比例的增长。
EXCEL文件Alumin给出了48所美国国立大学的有关统计数据。
“学生教师比”是注册学生人数除以全体教师人数,单位是倍;“捐赠校友的比例”是给予学校捐赠的校友所占的百分比。
要求:1、对这些数据做出数值和图示的概述2、利用回归分析求出估计的回归方程,使这个方程在学生人数少于20人的班级所占的比例已知时,能被用来预测给予学校捐赠的校友所占的比例。
3、利用回归分析求出估计的回归方程,使这个方程在学生教师比已知时,能被用来预测给予学校捐赠的校友所占的比例。
4、从你的分析中,你能得到什么结论或提出什么建议吗?案例数据:答:1/1) 首先制作学生人数少于20人的学生比例的图表:102030405060708090Boston CollegeCalifornia Institute ofCollege of William and MaryDartmouth CollegeGeorgetown UniversityLehigh University Northwestern UniversityRice UniversityTulane University U. of California-IrvineU. of California-Santa BarbaraU. of Illinois-Urbana Champaign U. of Notre DameU. of Southern CaliforniaU. of WashingtonWake Forest University数值和图示的概述:如果设学生人数少于20人班级的比例为x ,则755.7291666=x 。
应用统计学大作业
应用统计学大作业在当今数字化和信息化的时代,数据无处不在。
从社交媒体的互动到医疗保健的记录,从金融市场的交易到科学研究的成果,数据以惊人的速度积累和增长。
而应用统计学作为一门处理、分析和解释数据的学科,发挥着至关重要的作用。
它不仅帮助我们从海量的数据中提取有价值的信息,还为决策提供了坚实的依据。
应用统计学的应用领域广泛而多样。
在商业领域,企业利用统计学来分析市场趋势、消费者行为和销售数据,以制定营销策略、优化生产流程和预测需求。
例如,一家电商公司可以通过分析用户的浏览和购买历史,了解不同产品的受欢迎程度,从而调整商品推荐和库存管理。
在医学领域,统计学有助于评估新药物的疗效、研究疾病的发病机制和预测疾病的流行趋势。
研究人员通过对大量病例数据的分析,能够确定治疗方法的有效性和安全性,为医疗决策提供科学依据。
教育领域也是应用统计学的重要舞台。
学校可以通过分析学生的考试成绩、学习行为和家庭背景等数据,评估教学质量,发现学生的学习困难,制定个性化的教育方案。
在社会科学中,统计学被用于研究人口趋势、社会现象和民意调查,为政策制定提供参考。
要进行有效的数据分析,首先需要收集合适的数据。
数据的收集方法多种多样,包括问卷调查、实验观测、数据库查询等。
然而,无论采用哪种方法,都需要确保数据的准确性和代表性。
不准确或有偏差的数据可能导致错误的结论和决策。
在收集到数据后,接下来的关键步骤是数据的整理和预处理。
这包括检查数据的完整性、纠正错误、处理缺失值和异常值等。
例如,如果在一份调查问卷中发现大量缺失的回答,就需要考虑这些缺失值对分析结果的影响,并采取适当的方法进行处理,如删除含有缺失值的样本或通过其他变量进行推测填补。
数据分析的方法众多,常见的有描述性统计分析和推断性统计分析。
描述性统计分析主要用于概括和描述数据的特征,如均值、中位数、标准差、频率分布等。
通过这些统计量,我们可以对数据有一个初步的了解。
例如,通过计算学生考试成绩的平均分和标准差,可以了解学生整体的学习水平和成绩的离散程度。
统计学大作业
宁波大红鹰学院工商管理分院《应用统计学》实验(践)报告专业:工商管理专业班级:学生姓名:同组人员:无任课老师:黄涛2017年6月12日目录实验(一) SPSS安装 (2)实验(二)统计数据的搜集与整理 (6)实验(三)统计数据的图表描述 (9)实验四统计数据的度量 (16)实验五统计抽样与参数估计 (19)实验六相关与回归分析 (24)实验七统计数据的动态分析 (33)实验八统计指数分析 (35)实验(一) SPSS安装一、实验名称:SPSS安装二、实验目的:学会安装spss软件及有关操作三、实验步骤:SPSS的安装和启动在启动SPSS软件之前,需要先在计算机上进行安装。
其安装方法主要有两种:一是直接使用SPSS安装光盘进行安装;二是通过网络下载SPSS安装程序进行安装。
本小节使用第二种方法详细介绍SPSS的安装步骤(以IBM SPSS 19.0为例)。
1.打开计算机,找到已经下载到计算机上的SPSS安装程序。
如图一图一2.单击该图标,按照顺序下去,直到出现如下界面,单击“下一步”,则弹出对话框;个人用户选择第一个“单个用户许可证”,如果图二所示。
图二3.单击“下一步”,切换到用户协议对话框。
在该对话框中接受用户协议,然后单击“下一步”,如图三所示。
图三4.单击“下一步”,显示客户信息。
在该对话框中填写好用户姓名与单位,然后单击“下一步”,如图四所示。
图四5.单击“下一步”,语言选择。
选择“英语”,然后单击“下一步”,如图五所示。
图五6.在弹出的对话框中是选择文件安装位置,如图六所示。
在该对话框中单击“更改”,可调整软件的安装位置。
图七7.在选择文件安装对话框中单击“下一步”,在弹出的对话框中单击“安装”即可,如图七所示。
图七8.此时则弹出正在安装的界面,如图八所示。
图八9.在以上安装程序完后,则弹出授权许可证的对话框。
把框中的勾去掉,单击“确定”,如图九所示。
图九10.此时则弹出产品授权对话框,选择“启用以用于临时使用”按钮,单击“下一步”,如图十所示。
应用统计大作业 哈工大
《应用统计》大作业——2013年秋季学期题目:大学生手机话费消费调查院系:机电学院工业工程系班号: 1108401姓名:王震宇学号: 1100800609时间:10月6日第一节:引言在这个信息高速社会,手机在我们生活中扮演不可或缺的角色,时下大学生几乎人手一部手机。
在此,我们将对大学生在手机话费消费做一次详细调查。
以了解大学生每月手机话费消费情况和大学生手机话费消费观念。
第二节:调查方案一、调查目的:分析研究大学生的话费消费情况及影响大学生话费消费的各项因素,从而为大学生的话费消费提供相关建议。
二、调查对象哈尔滨工业大学在校大学生采用的随机抽取人员进行调查,由于此次调查的时间和经费有限,调查的人数为100人,男生为主。
三、调查的时间2013年9月26日——9月30日四、调查的内容此次调查采用问卷调查。
第三节:调查结果及分析一、大学生每月手机话费费用根据市场调查所得到的信息的统计,我们得到表一:每月手机话费频数百分比50元以内61 61%50—100元32 32%100—150元 5 5%150元以上 2 2%1020304050607050元以下50-100元100-150元150元以上对上述数据进行描述统计,可得关于大学生手机话费的各项指标如表二平均 49.00 中位数 40.98 众数 33.89 方差 1173.75 标准差34.26二、通信运营商的选择表三, 大学生通信运营商选择的频数分布表通信运营商 频数 百分比 移动 68 68% 联通 15 15% 电信 17 17% 其他0%众数为移动。
目前移动的动感地带仍然在学生群体中广泛使用,它的卖点主要是服务和价格。
移动联通电信其他扇面 5三、大学生选择此通信运营商的原因表四 大学生选择此通信运营商原因的频数分布表 选择此通信运营商的原因频数 百分比 套餐优惠 4141% 通话质量好 9 9% 随大流 39 39% 其他1111%1020304050套餐优惠通话质量好随大流其他条形图 3条形图 2条形图 1从表三和表四来看,哈工大学生绝大多数选择了移动,而他们选择该运营商的原因是随大流和套餐优惠,这也难怪,移动退出的套餐确实比较实惠,而且它有庞大的短号网,我相信这是最吸引人的地方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院:经济管理学院班级:食品经济管理(1)班姓名:张从容学号:0846112日期:2010年6月应用统计学大作业题目校友捐赠是高等学校收入的重要来源。
如果学校的管理人员能确定影响捐赠的校友所占比例增长的因素,他们就可能制定使学校收入增长的政策。
研究表明,对与老师的沟通交往感到比较满意的学生,他们很可能更容易毕业。
于是人们可能猜测,人数比较少的班级和比较低的学生一教师比可能有一个比较高的令人满意的毕业率,随后又可能引起给予学校捐赠的校友所占比例的增长。
EXCEL文件Alumin给出了48所美国国立大学的有关统计数据。
“学生教师比”是注册学生人数除以全体教师人数,单位是倍;“捐赠校友的比例”是给予学校捐赠的校友所占的百分比。
要求:1、对这些数据做出数值和图示的概述2、利用回归分析求出估计的回归方程,使这个方程在学生人数少于20人的班级所占的比例已知时,能被用来预测给予学校捐赠的校友所占的比例。
3、利用回归分析求出估计的回归方程,使这个方程在学生教师比已知时,能被用来预测给予学校捐赠的校友所占的比例。
4、从你的分析中,你能得到什么结论或提出什么建议吗?案例数据:从图表(饼图)中可以得出这样的结论,学生和老师人数之间的比例平均在 11倍左右,也就是说平均为一个老师带 11个学生,而且各学校之间的差异也不是很大(最大值为23,最小值为3 )。
答:1/1)首先制作学生人数少于20人的学生比例的图表Wake Forest Uni versityU. of Washi ngtonU. of Southern CaliforniaU. of Notre DameU. of Illi no is-Urba na Champaig n U. of Califor ni a-Sa nta BarbaraU. of Califor ni a-Irvi neTula ne Uni versityRice Un iversityNorthwester n Uni versityLehigh Uni versity Georgetow n Uni versity Dartmouth CollegeCollege of William and MaryCalifornia In stitute ofBost on College数值和图示的概述:二 Yale Un iversity^Washi ngton Uni versity-St. Louis Wake Forest Uni versity .Vanderbuilt University -j U. of Wisco nsin-Madiso n □ U. of Washi ngton U. of Virgi nia .U. of Texas-Austi n□ U. of Southern California 叵 U. of Rochester□ U. of Penn sylva nia □ U. of Notre Dame□ U. of North Caroli na-Chapel Hill ■ U. of Michiga n-Ann Arbor 厂 U. of Illi no is-Urba na Champaig n □ U. of Florida一 U. of Chicago—U. of California-Sa nta Barbara_U. of California-San Diego —U. ofCalifornia-Los An geles -U. of California-Irvi ne _ U. of California-Davis_U. of California-Berleley— Tula ne Uni versity — Tufts Un iversityI . Stanford University Rice University如果设学生人数少于 20人班级的比例为 x ,则x 55.72916667。
从图表(条形图)中可以看出,学生人数少于 20人的学校的比例都很高,平均水平在 50%以上,约等于55.73%,最高达到了 77%,最小值为29%,可以看出美国大学班级学生人数 基本都在20人以下,班级人数比较少。
1/2)其次制作学生教师比例的图表:_10数值和图示的概述:口 Boston College .Brandeis University 口Brown University 口 California Institute of Technology .Carnegie Mellon University 口 Case Western Reserve Univ. .College of William and Mary 口 ColumbiaUniversity .Cornell University .Dartmouth College 口 Duke University 口 EmoryUniversity .Georgetown University .Harvard University .John Hopkins University .Lehigh University■ Massachusetts Inst. of Technology 口 NewYork University口 Northwestern University 口 Pennsylvania State Univ. 口 Princeton University 口 RiceUniversity□ Stanford University 口 TuftsUniversity .Tulane University 口I U. of California-Berleley U. of Calirornia-Davis如果设学生与教师的比例为x ,则x 11.54166667。
_821137 131615815195238 4 720199 1212 13.-121820191/3)最后制作捐赠校友比例的图表:数值和图示的概述:如果设捐赠校友比例的比例为x ,则 x 29.27083333。
从图表(柱状图)中可以看出各学校之间的校友捐赠情况差异很大,最大值为 67%,最小值为7%。
捐赠校友比例eaelQC npaxoyusrevliu m I K eraeoLadna ma _____L fo eaBl& eKb^LPLS 9IQ &SnlKnn^^f o *Lsn — s- -enaLYSIVaD - arnrofla^ fo uselenHA SOL - arobTlau fo uarrDIHb alnao - arnrD — ___ E fo ua=u"oil FtoroDrurt nA - naor-nc^M f o urATSRncaR f o ufo uSIUOL +KO - yLrsrRffliu nQtuzt/xa—Bost on CollegeLT Brandeis University —I Brown UniversitypCalifor nia In stitute of Tech no logy □ Carnegie Mello n Un iversity l_ Case Wester n Reserve Univ. □ College of William and Mary I Columbia University■ Corn ell Un iversity U Dartmouth College 厂 Duke Un iversity厂 Emory University□ Georgetow n Un iversity ■ Harvard Un iversity □ Joh n Hopk ins Uni versity ■ Lehigh Uni versity-Massachusetts In st. of Tech no logy一 New York Un iversity_Northwester n Uni versity一 Penn sylva nia State Un iv.— Princeton University一 Rice Un iversity— Sta nford Uni versity_Tufts Un iversity— Tula ne Uni versity I . U. of California-Berleley U. of California-Davis(1)画散点图,判断是否相关。
⑵ 求相关系数,求联系的密切程度。
(1)根据学生人数少于 20人的班级比例与校友捐赠的比例制作出散点图:学生人数少于20班级的比例与校友捐赠的比例的线性关系图学校人数少于20人班级的比例从图表(散点图)中可以看到,两者之间是相关的,且相关性较大。
2)设方程为y a bx ,学生少于20人班级的比例为 X ,校友捐赠比例为 y ,利用EXCEL 求出a,b 的值:SLVMARY OLTPtT鶴二烦回归统计R. 0 645MR Square C 416S&4Adjusted R 0.4C4l^标楷误鑫 10观皿曲l£方差分折dfSS MS F iigrn& an< e F回归分折l 3539 7M M3S7M 32 SS5S9 -J23E-074951107 64竹总计47 B491.479■a C ozfficienEs 标禮课差t Stal P-Vahie Leu 更S 下限卒小止限9土0%lntcrcqx6.565472 1.12490J66+31 -20,^17 5.S2954-20.W17 5.82J542 V0J657769 Qlir050.4263S 0.8SS65- 0 425ES 0SS8657可求出方程:y 7.38607 0.657769X r 0.4169显著相关所以,由这个回归方程可以看出两者之间的关系,即每增加 1%少于20人班级的比例,就会增加0.657769%的校友捐赠比例,r 0,所以两者之间正相关。
OOOOOOOOO 87654321例比友校赠捐*系列1(1)画散点图,判断是否相关。
⑵ 求相关系数,求联系的密切程度。
(1)根据教师与学生人数的比例与校友捐赠的比例制作出散点图:学生教师比与捐赠校友的比例线性相关图从图表(散点图)中可以看到,两者之间是相关的,且相关性较大。
2)设方程为y bx a ,学生少于20人班级的比例为x,校友捐赠比例为y,利用EXCEL求出a,b的值:可求出方程:y 2.05715x 53.01383 r 0.742 显著相关所以,由这个回归方程可以看出两者之间的关系,即每增加学生教师1倍,校友捐赠的比例就会减少2.05715% r 0,所以两者之间负相关。
