工程力学23 梁的正应力计算
工程力学中的应力和应变分布的计算方法

工程力学中的应力和应变分布的计算方法工程力学是工程领域中研究物体在作用力下产生的应力和应变的学科。
在工程设计和结构分析中,准确计算应力和应变分布是至关重要的,它们对于评估结构的安全性和可靠性具有重要意义。
本文将介绍工程力学中常用的应力和应变分布的计算方法。
一、应力的计算方法1. 线性结构的应力计算方法在线性结构中,应力可以通过应力=力/截面积的公式进行计算。
对于受压或受拉的杆件,应力等于施加在杆件上的力除以杆件的截面积。
对于弯曲杆件,应力的计算需要考虑弯矩和截面惯性矩的影响。
根据梁的弯矩公式,弯曲杆件上的应力等于弯矩乘以截面离轴距离除以截面惯性矩。
2. 非线性结构的应力计算方法对于非线性结构,如塑性材料或复合材料,应力的计算方法会更加复杂。
在这种情况下,常常需要使用数值模拟方法,如有限元分析,来计算应力分布。
有限元分析通过将结构划分为有限数量的小单元,并在每个小单元上进行应力计算,然后将结果汇总得到整个结构上的应力分布。
二、应变的计算方法1. 线性结构的应变计算方法在工程力学中,应变定义为物体长度或体积的变化与原始长度或体积之比。
对于受压或受拉的线性结构,应变计算可以通过应变=位移/原始长度的公式进行。
位移是杆件两端的距离差,原始长度是杆件未受力时的长度。
2. 非线性结构的应变计算方法对于非线性结构,应变的计算方法也会更加复杂。
类似于应力计算,可以使用有限元分析等数值模拟方法来计算非线性结构上的应变分布。
有限元分析可以考虑材料的非线性特性,如材料的应力-应变曲线,从而得到更精确的应变分布。
三、常见应力和应变分布形式1. 拉伸和压缩应力分布在拉伸和压缩加载下,线性材料的应力分布呈现均匀分布。
即在整个截面上应力大小相等。
但对于非线性材料,应力分布可能呈现不均匀分布,尤其是在接近临界点时。
2. 弯曲应力分布在弯曲结构中,线性材料的应力分布呈现最大值位于中性轴线处,随着距离中性轴线的增加而逐渐减小。
对于非线性材料,应力分布也会受到材料特性的影响,可能不呈现对称的形式。
工程力学选择填空复习
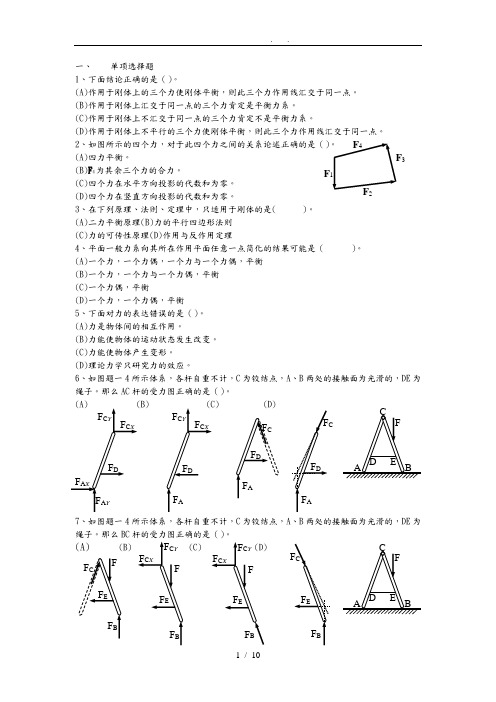
一、 单项选择题1、下面结论正确的是()。
(A)作用于刚体上的三个力使刚体平衡,则此三个力作用线汇交于同一点。
(B)作用于刚体上汇交于同一点的三个力肯定是平衡力系。
(C)作用于刚体上不汇交于同一点的三个力肯定不是平衡力系。
(D)作用于刚体上不平行的三个力使刚体平衡,则此三个力作用线汇交于同一点。
2、如图所示的四个力,对于此四个力之间的关系论述正确的是()。
(A)四力平衡。
(B)F 4为其余三个力的合力。
(C)四个力在水平方向投影的代数和为零。
(D)四个力在竖直方向投影的代数和为零。
3、在下列原理、法则、定理中,只适用于刚体的是( )。
(A)二力平衡原理(B)力的平行四边形法则 (C)力的可传性原理(D)作用与反作用定理4、平面一般力系向其所在作用平面任意一点简化的结果可能是( )。
(A)一个力,一个力偶,一个力与一个力偶,平衡 (B)一个力,一个力与一个力偶,平衡 (C)一个力偶,平衡(D)一个力,一个力偶,平衡 5、下面对力的表达错误的是()。
(A)力是物体间的相互作用。
(B)力能使物体的运动状态发生改变。
(C)力能使物体产生变形。
(D)理论力学只研究力的效应。
6、如图题一4所示体系,各杆自重不计,C 为铰结点,A 、B 两处的接触面为光滑的,DE 为绳子。
那么AC 杆的受力图正确的是()。
7、如图题一4所示体系,各杆自重不计,C 为铰结点,A、B 两处的接触面为光滑的,DE 为绳子。
那么BC 杆的受力图正确的是()。
(A)F 4 F 1 F 2F 38、下列结论中正确的是()(A)材料力学主要研究各种材料的力学问题(B)材料力学主要研究各种材料的力学性质(C)材料力学主要研究杆件受力后变形与破坏的规律(D)材料力学主要研究各种材料中力与材料的关系9、柔索对物体的约束反力,作用在连接点,方向沿柔索( )(A)指向该被约束体,恒为拉力(B)背离该被约束体,恒为拉力(C)指向该被约束体,恒为压力(D)背离该被约束体,恒为压力10、已知力P=40kN,S=20kN,物体与地面的静摩擦系数f=0.5,动摩擦系数f′= 0.4 ,则物体的摩擦力的大小为()。
梁的应力计算公式全部解释

梁的应力计算公式全部解释应力是材料受力时产生的内部力,它是描述材料内部抵抗外部力的能力的物理量。
在工程领域中,计算材料的应力是非常重要的,可以帮助工程师设计和选择合适的材料,以确保结构的安全性和稳定性。
梁的应力计算公式是计算梁在受力时产生的应力的公式,它可以帮助工程师了解梁在不同条件下的应力情况,从而进行合理的设计和分析。
梁的应力计算公式是由弹性力学理论推导而来的,它可以根据梁的几何形状、受力情况和材料性质来计算梁的应力。
在工程实践中,梁的应力计算公式通常包括弯曲应力、剪切应力和轴向应力三种类型的应力。
下面将分别对这三种类型的应力计算公式进行详细解释。
1. 弯曲应力计算公式。
梁在受到外部力的作用时,会产生弯曲应力。
弯曲应力是由于梁在受力时产生的弯曲变形所引起的,它可以通过以下公式进行计算:σ = M c / I。
其中,σ表示梁的弯曲应力,单位为N/m^2;M表示梁的弯矩,单位为N·m;c表示梁截面内的距离,单位为m;I表示梁的惯性矩,单位为m^4。
弯曲应力计算公式可以帮助工程师了解梁在受力时产生的弯曲应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的弯曲应力计算公式进行计算。
2. 剪切应力计算公式。
梁在受到外部力的作用时,会产生剪切应力。
剪切应力是由于梁在受力时产生的剪切变形所引起的,它可以通过以下公式进行计算:τ = V Q / (I b)。
其中,τ表示梁的剪切应力,单位为N/m^2;V表示梁的剪力,单位为N;Q 表示梁的截面偏心距,单位为m;I表示梁的惯性矩,单位为m^4;b表示梁的截面宽度,单位为m。
剪切应力计算公式可以帮助工程师了解梁在受力时产生的剪切应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的剪切应力计算公式进行计算。
3. 轴向应力计算公式。
梁在受到外部力的作用时,会产生轴向应力。
轴向应力是由于梁在受力时产生的轴向变形所引起的,它可以通过以下公式进行计算:σ = N / A。
杆件正应力怎么求计算公式

杆件正应力怎么求计算公式杆件正应力的计算公式。
在工程力学中,杆件正应力是指在杆件内部由外部加载引起的正向拉伸或压缩应力。
正应力的计算是工程设计中非常重要的一部分,它可以帮助工程师确定杆件是否能够承受外部加载,并且可以帮助工程师选择合适的材料和尺寸来设计结构。
杆件正应力的计算公式可以通过简单的力学原理推导得出。
在这篇文章中,我们将介绍杆件正应力的计算公式,并且讨论一些实际应用中的例子。
杆件正应力的计算公式可以表示为:σ = P / A。
其中,σ表示杆件的正应力,P 表示施加在杆件上的外部力,A 表示杆件的横截面积。
这个公式的推导可以通过简单的力学原理来进行。
当一个外部力 P 作用在杆件上时,杆件内部会产生一个与外部力方向相反的内部应力。
根据牛顿第三定律,这个内部应力的大小与外部力的大小相等,方向相反。
而杆件的横截面积 A 则可以用来表示内部应力的分布情况。
因此,杆件的正应力可以表示为外部力 P 与横截面积 A 的比值。
在实际应用中,杆件正应力的计算可以通过这个简单的公式来进行。
例如,当一个钢杆承受一个拉力时,我们可以通过测量钢杆的横截面积和外部拉力来计算钢杆的正应力。
这个计算可以帮助工程师确定钢杆是否能够承受这个拉力,并且可以帮助工程师选择合适的钢材来设计结构。
除了上面提到的简单拉力的情况,杆件正应力的计算公式也可以应用在其他复杂的情况中。
例如,在梁的设计中,梁的横截面积不是均匀的,因此我们可以通过积分的方法来计算梁的正应力分布。
这个计算可以帮助工程师确定梁在不同位置的正应力大小,并且可以帮助工程师选择合适的梁的尺寸和材料来设计结构。
除了简单的拉力和梁的设计,杆件正应力的计算公式也可以应用在其他工程结构的设计中。
例如,在桥梁的设计中,我们可以通过计算桥梁的正应力来确定桥梁的承载能力,并且可以帮助工程师选择合适的桥梁的尺寸和材料来设计结构。
总之,杆件正应力的计算公式是工程设计中非常重要的一部分。
通过这个简单的公式,工程师可以确定杆件是否能够承受外部加载,并且可以帮助工程师选择合适的材料和尺寸来设计结构。
工程力学梁的正应力强度条件及其应用1
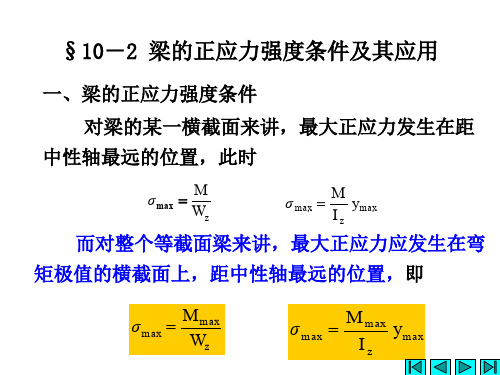
ymax
对矩形截面
Wz
bh3 12 h2
bh2 6
Wz
bh2 6
对圆形截面
Wz
d 4
d
64 2
d 3
32
Wz
d 3
32
各种型钢的截面惯性矩Iz和弯曲截面系数Wz的 数值,可以在型钢表中查得。
为了保证梁能安全的工作,必须使梁横截面上的
最大正应力不超过材料的许用应力,所以梁的正应力
强度条件为
σmax
M max Wz
σ
二、三种强度问题的计算
σmax
M max Wz
σ
(1)强度校核 (2)选择截面 (3)确定许用荷载
σmax
M max Wz
σ
Wz
M max σ
M max Wz σ
例题10-2 一矩形截面简支木梁如图所示,已知l=4m, b=140mm,h=210mm,q=2kN/m,弯曲时木材的许 用正应力[σ]=10MPa,校核该梁的强度。
σc,max
MC Iz
y1
2.7 103 0.072 0.573105
33.9 106 Pa
33.9MPa [σc]
由以上分析知该梁满足强度要求。
例题10−4 如图所示的简支梁由工字钢制成,钢的 许用应力[σ ]=150MPa,试选择工字钢的型号。
解:先画出弯矩图如图b所示。 梁的最大弯矩值为
y1
1.8103 0.072 0.573105
22.5106 Pa
22.5MPa
工程力学弯曲应力和内力知识点总结
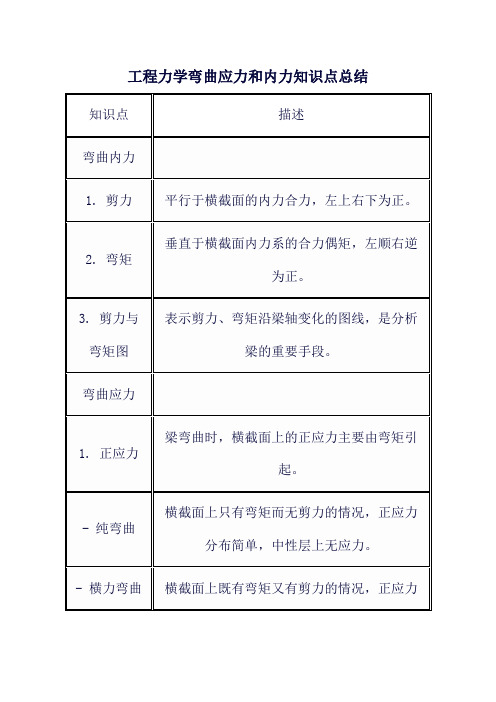
2. 单向受力假设
纵向纤维互不挤压,只受单向拉压。
计算方法
1. 正应力计算公式
适用于弹性变形范围内的长直梁,具体公式依据材料力学原理推导得出。
2. 切应力计算公式
复杂且因截面形状而异,需根据具体情况分析。
应用实例
1. 简支梁
一端固定铰支、另一端可动铰支的梁,是工程中常见的梁类型。
2. 悬臂梁
一端固定、另一端自由的梁,受力分析较为复杂。
3. 外伸梁
具有一个或两个外伸部分的简支梁,需考虑外伸部分的影响。
工程力学弯曲应力和内力知识点总结
知识点
描述
弯曲内力
1. 剪力
平行于横截面的内力合力,左上右下为正。
2. 与弯矩图
表示剪力、弯矩沿梁轴变化的图线,是分析梁的重要手段。
弯曲应力
1. 正应力
梁弯曲时,横截面上的正应力主要由弯矩引起。
- 纯弯曲
横截面上只有弯矩而无剪力的情况,正应力分布简单,中性层上无应力。
- 横力弯曲
横截面上既有弯矩又有剪力的情况,正应力分布复杂,需考虑切应力的影响。
2. 切应力
由剪力引起,横截面上的切应力分布规律因截面形状而异。
中性层与中性轴
1. 中性层
梁内一层纤维既不伸长也不缩短,此层纤维称为中性层。
2. 中性轴
中性层与横截面的交线,为应力分布分析的基准线。
应力假设
1. 平面假设
土木工程力学基础单选题100道及答案

土木工程力学基础单选题100道及答案1. 力的三要素是()A. 大小、方向、作用点B. 大小、方向、作用线C. 大小、作用点、作用线D. 方向、作用点、作用线答案:A2. 两个力的大小相等,方向相反,作用在同一直线上,则这两个力()A. 一定平衡B. 不一定平衡C. 一定不平衡D. 无法确定答案:B3. 作用在刚体上的力,可以沿其作用线(),而不改变该力对刚体的作用效果。
A. 任意移动B. 任意转动C. 任意滑动D. 任意拉伸答案:A4. 约束反力的方向总是与约束所能阻止的物体的运动趋势的方向()A. 相同B. 相反C. 垂直D. 平行答案:B5. 光滑接触面约束的约束反力总是沿接触面的()指向被约束物体。
A. 切线方向B. 法线方向C. 任意方向D. 无法确定答案:B6. 由两个物体组成的物体系统,共受到()个未知约束力。
A. 3B. 4C. 5D. 6答案:D7. 平面汇交力系平衡的几何条件是()A. 力多边形自行封闭B. 力的代数和为零C. 合力为零D. 合力矩为零答案:A8. 平面汇交力系平衡的解析条件是()A. 力多边形自行封闭B. 力的代数和为零C. 合力为零D. 合力矩为零答案:B9. 平面力偶系平衡的条件是()A. 力偶系中各力偶矩的代数和为零B. 力偶系中各力偶矩的矢量和为零C. 力偶系中各力的代数和为零D. 力偶系中各力的矢量和为零答案:A10. 力对物体的转动效应,取决于()A. 力的大小B. 力的方向C. 力臂的大小D. 力的大小和力臂的乘积答案:D11. 平面一般力系向作用面内一点简化,得到一个主矢和一个主矩。
当主矢等于零,主矩不等于零时,力系简化结果为()A. 合力B. 合力偶C. 平衡D. 无法确定答案:B12. 平面一般力系向作用面内一点简化,得到一个主矢和一个主矩。
当主矢不等于零,主矩等于零时,力系简化结果为()A. 合力B. 合力偶C. 平衡D. 无法确定答案:A13. 平面一般力系向作用面内一点简化,得到一个主矢和一个主矩。
工程力学中的梁受力分析

工程力学中的梁受力分析在工程力学中,梁受力分析是一项关键的研究内容。
梁作为一种常见的结构元素,承载着重要的功能和责任。
了解梁的受力情况对于设计和分析工程结构至关重要。
本文将探讨工程力学中的梁受力分析的原理和方法。
一、梁的基本概念与类型在工程力学中,梁是指一种主要受弯曲和剪切力作用的结构元素。
梁通常由直线段或曲线段组成,通过支座进行支撑。
根据结构形式和受力特点,梁可以分为多种类型,如简支梁、悬臂梁、连续梁等。
这些不同类型的梁受力特点和分析方法各有差异。
二、受力分析的基本原理梁的受力分析基于力的平衡原理和材料的力学性质。
在进行受力分析时,需要考虑以下几个方面的因素:1. 外力作用:包括点载荷、均布载荷、集中力矩等,这些外力对梁的任一截面都会产生作用力和力矩。
2. 内力分布:外力作用下,梁内部会产生应力和应变,从而导致内力的产生和分布。
内力包括弯矩、剪力和轴力等。
3. 材料特性:梁所使用的材料具有一定的力学性质,如弹性模量、抗弯强度等。
在受力分析中,需要将这些材料特性考虑进去。
基于以上几个方面的考虑,进行梁的受力分析可以采用多种方法,如弯矩法、剪力法、位移法等。
下面将介绍其中两种常用的方法。
三、弯矩法弯矩法是一种常见的梁受力分析方法,它基于弯矩对梁的受力分布进行分析。
1. 绘制弯矩图:根据梁所受外力的类型和分布,可以计算出梁上各个截面的弯矩大小和分布情况。
一般来说,梁受弯曲力作用导致的弯矩在梁的上表面和下表面呈现相反方向的分布。
2. 寻找最大弯矩:在弯矩图中,寻找出最大的正弯矩和最大的负弯矩,即最大正应力和最大剪应力所在的位置。
这些位置通常对应梁中的关键截面。
3. 结构分析:在找到最大弯矩所在的位置后,可以根据受力平衡原理,进行截面力的计算和受力分析。
比如,可以计算出截面上的剪力和轴力等。
四、剪力法剪力法是另一种常用的梁受力分析方法,它基于剪力对梁的受力分布进行分析。
1. 绘制剪力图:根据梁所受外力的类型和分布,可以计算出梁上各个截面的剪力大小和分布情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M.y
Iz
(Flexure Formula)
该式为等直梁纯弯曲时横截面上任一点处正应力的计算公式
式中: M
横截面上的弯矩(bending moment in the beam)
Iz
横截面对中性轴的惯性矩 (moment of inertia of the
工 程力 学
ENGINEERING MECHANICS 梁的正应力计算
工 程力 学
ENGINEERING MECHANICS
1、实验( Experiment)
纯弯曲梁加载过程
工 程力 学
ENGINEERING MECHANICS
(1)变形现象(Deformation phenomenon )
纵向线 各纵向线段弯成弧线,且靠近顶 端的纵向线缩短,靠近底端的纵 向线段伸长
横截面上内力系为垂直于横截面的空间平 行力系
这一力系简化,得到三个内力分量
FN
A dFN
dA 0
A
(1)
M y
A dM y
zdA 0
A
(2)
Mz
A dMZ
ydA
A
M(3)
Mz z
O
x
My
y
dFN dA
dM y z dA dMz y dA
工 程力 学
ENGINEERING MECHANICS
M
所以 E y
?
?
应力分布规律
z
O
x
y
直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴的距离
成正比
待解决问题
? 中性轴的位置
中性层的曲率半径ρ
工 程力 学
ENGINEERING MECHANICS
工 程力 学
ENGINEERING MECHANICS
4、静力关系 (Static relationship)
工 程力 学
ENGINEERING MECHANICS
工 程力 学
ENGINEERING MECHANICS
2、变形几何关系( Deformation geometric relation )
工 程力 学
ENGINEERING MECHANICS
dx
图(a)
dx
o o
zb
o yx b
y
图(b)
d
o’
b’ z
y
o’
x
b’
图(c)
应变分布规律 直梁纯弯曲时纵向纤维的应变与它到中性层的距离成正比
工 程力 学
ENGINEERINGINEERING MECHANICS
3、物理关系(Physical relationship)9
Hooke’s Law E
cross section of the beam)
y
求应力的点到中性轴的距离 (distance from the neutral
axis of the beam to the fibers)
工 程力 学
ENGINEERING MECHANICS
谢 谢 观 赏!
横向线 各横向线仍保持为直线,相对转 过了一个角度,仍与变形后的纵 向弧线垂直
工 程力 学
ENGINEERING MECHANICS
(2)提出假设 ( Assumptions)
(a) 平面假设 变形前为平面的横截面变形后仍保持为平面且垂直于变形后的梁 轴线.
(b) 单向受力假设 纵向纤维不相互挤压,只受单向拉压.
将应力表达式代入(1)式,得
Sz
ydA 0
A
中性轴通过横截面形心
将应力表达式代入(2)式,得
I yz
yzdA 0
A
自然满足
将应力表达式代入(3)式,得
M yE ydA M E y2dA
A
A
E
M Iz
1M
E Iz
工 程力 学
ENGINEERING MECHANICS
工 程力 学
工 程力 学
ENGINEERING MECHANICS
推论(Inference):
横截面的转动将使梁的凹边的纵向线段缩短,凸边的纵向线段伸长,由于 变形的连续性,中间必有一层纵向线段 无长度改变。此层称为 中性层 (Neutral surface)。中性层与横截面的交线称为 中性轴( neutral axis).
