图形组合
图形组合思维绘画图解教案

图形组合思维绘画图解教案教案标题:图形组合思维绘画图解教案教学目标:1. 培养学生的图形组合思维能力。
2. 提高学生的绘画技巧和表现能力。
3. 增强学生的观察力和创造力。
教学准备:1. 教师准备:白板、彩色粉笔、绘画工具、绘画纸、范例图。
2. 学生准备:铅笔、橡皮擦、彩色铅笔或颜料。
教学步骤:引入活动:1. 引导学生观察周围的事物,并询问他们对图形组合的理解和认识。
2. 引导学生思考图形组合在绘画中的作用,并与他们分享一些相关的艺术作品。
知识讲解:1. 介绍不同的图形组合方式,如重叠、连接、排列等,并通过范例图示给学生展示。
2. 解释每种图形组合方式的特点和表现效果,并鼓励学生提出自己的观点和想法。
示范演示:1. 在白板上示范一个简单的图形组合绘画,解释每个步骤的绘画技巧和注意事项。
2. 鼓励学生跟随示范进行绘画,同时提供个别指导和帮助。
实践练习:1. 学生使用自己准备的绘画工具和纸张,选择一个他们感兴趣的主题进行图形组合绘画。
2. 学生根据自己的创意和想法,运用所学的图形组合方式进行绘画,并尽量展现个人风格和表现力。
3. 教师在学生绘画过程中巡视指导,鼓励学生尝试不同的图形组合方式,并提供必要的帮助和建议。
展示与分享:1. 学生完成绘画后,组织一个小组展示和分享活动。
2. 学生可以互相欣赏和评价彼此的作品,同时分享自己的创作过程和体会。
3. 教师提供积极的反馈和鼓励,同时指出学生在图形组合思维和绘画技巧方面的进步和发展。
总结回顾:1. 教师与学生一起总结本节课学到的知识和技巧。
2. 强调图形组合思维在绘画中的重要性,并鼓励学生在日常生活中多加观察和实践。
3. 鼓励学生继续探索和发展自己的绘画技巧和创作能力。
扩展活动:1. 鼓励学生在课后继续进行图形组合绘画的实践,并分享他们的作品和体会。
2. 提供更多的图形组合绘画技巧和范例,以拓展学生的创作思路和表现方式。
评估方式:1. 教师观察学生的参与程度和绘画表现,并给予积极的反馈和评价。
中班数学《图形组合》

中班数学《图形组合》前言在幼儿园末期,孩子开始对数学有了初步的认识。
对于幼儿来说,数学是一个有趣的学科,他们开始了解数字、形状和大小之间的关系。
其中,图形组合是幼儿数学中的重要部分。
本篇文档将介绍中班数学《图形组合》的相关内容。
什么是图形组合?图形组合是一项基本的数学技能,可以帮助孩子们培养逻辑思维能力和创造力。
图形组合包括将两个或多个图形组合成一个更大的图形,或将一个图形分解为两个或多个小的部分。
例如,如果有两个正方形,可以将它们组合成一个更大的正方形,也可以将一个正方形拆分为两个小正方形。
图形组合的分类图形组合可以分为两种类型:平面组合和空间组合。
平面组合平面组合,顾名思义,是将两个或多个平面图形组合成一个更大的平面图形。
在幼儿园中,平面组合通常通过拼图进行。
拼图可以帮助幼儿们熟悉各种形状,并培养他们的想象和创造力。
在拼图中,孩子需要将多个形状组合成一个整体,这不仅可以帮助他们认识形状,还可以帮助他们建立对空间关系的理解。
空间组合空间组合是将两个或多个三维图形组合成一个更大的三维图形。
这种组合需要基本的几何知识,如面积、体积等。
在中班,孩子们开始学习基本的几何知识,例如认识球、圆锥、圆柱和棱锥等形状,并了解它们的性质和特征。
图形组合在生活中的应用图形组合不仅在学校中有用,也在生活中有广泛的应用。
例如,在家庭装修中,需要将不同的瓷砖组合在一起来创造一个美丽的图案。
在建筑中,需要将不同的构件组合在一起来构造一个坚固的建筑。
除此之外,图形组合还可以在艺术中应用。
例如,在绘画中,艺术家可以将不同的形状组合在一起来创造独特、美丽的画作。
总结图形组合是幼儿数学的一个重要部分,通过将不同的形状组合在一起,可以帮助孩子们培养逻辑思维能力和创造力。
平面组合和空间组合是图形组合的两种类型,在幼儿园中,孩子们可以通过拼图来熟悉各种形状,并建立对空间关系的理解。
图形组合不仅在学校中有用,也在生活中有广泛的应用,例如在家庭装修、建筑和艺术中。
小学数学课件几何图形的拼接与组合

实践操作的注意事项
准备工具:确保 有足够的几何图 形拼接材料和工 具,如剪刀、胶 水等。
明确目标:在开 始拼接前,明确 要制作的几何图 形组合的目标, 避免盲目操作。
观察图纸:仔细 阅读并理解拼接 图纸的指示,按 照步骤进行操作。
注意安全:使用 工具时要小心, 避免受伤。同时, 也要注意拼接材 料的质量,确保 安全无毒。
几何图形拼接与组合的教学建议
针对不同年龄段学生的教学策略
低年龄段:注重培养观察力和想象力,通过拼接简单的几何图形激发兴趣。 中年龄段:加强空间思维训练,教授组合图形的规律和技巧,培养解决问题的能力。 高年龄段:引入复杂组合图形,鼓励学生自主探究和尝试,培养创新思维和实践能力。 针对不同学生的特点和需求,个性化指导,因材施教,提高教学效果。
结合生活实际进行教学
选取生活中的 几何图形作为 教学素材,如 圆形、三角形
等。
引导学生观察 生活中的几何 图形,培养几
何思维。
通过拼接与组 合几何图形, 解决生活中的 实际问题,如 拼装玩具、设
计图案等。
鼓励学生动手 操作,感受几 何图形的拼接 与组合之美。
注重评价与反馈
及时给予学生反馈,指出拼接与组合过程中的优点和不足 设计评价量表,让学生了解自己的学习进度和需要改进的地方 鼓励学生自我评价,培养其独立思考和判断能力 收集学生作品,进行展示和交流,促进互相学习和进步
小学数学课件几何图形的拼 接与组合
汇报人:XX
汇报时间:20XX/XX/XX
YOUR LOGO
目录
CONTENTS
1 单击添加目录项标题 2 几何图形拼接与组合的概念 3 几何图形拼接与组合的方法 4 几何图形拼接与组合的应用 5 几何图形拼接与组合的实践操作 6 几何图形拼接与组合的教学建议
组合图形(一)

三角形面积:
S ah 2
阴影部分的面积:
(19.625-12.5)×2=14.25(平方厘米)
答:阴影部分的面积是14.25平方厘米。
点击关注,学习更多知识!
2 2
练习三
主讲:拓老师
已知下面图形的两条线段长2厘米,并互相 垂直,求阴影部分的面积。
正方形的面积: 2×2=4(平方厘米) 四分之一圆面积: 3.14×22÷4=3.14(平方厘米) 阴影部分的面积: 4-3.14=0.86(平方厘米) 答:阴影部分的面积是0.86平方厘米。
主讲:拓老师
组合图形(一)
点击关注,学习更多知识!
例题一
主讲:拓老师
如图,长方形的面积是8平方厘米,长方 形的长宽比是2:1,求这个组合图形的面积。
解:设宽为x厘米,长为2x厘米, 2x×x=8 x=2
·宽为2厘米,长为4厘米,
长方形面积:
S ab
半圆面积:
S r2 2
3.14×(4÷2)2÷2+8 =14.28(平方厘米)
117.75-60°÷360°×3.14×(15-7)2 ≈84.26(平方厘米) 答:阴影部分的面积是84.26平方厘米。
扇形面注,学习更多知识!
主讲:拓老师
总结
先把组合图形分成几个简单的图形,再 把每个简单图形的面积相加或相减,就是所 求的组合图形的面积;或将组合图形添补成 基本图形再进行求解。
半圆面积:
S r2 2
组合图形的面积:
9+14.13=23.13(平方厘米)
答:这个组合图形的面积是23.13
平方厘米。
点击关注,学习更多知识!
例题二
主讲:拓老师
求下面图形阴影部分的面积。(单位:厘米)
第3讲:组合图形面积

组合图形面积(一)知识梳理:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1、切实掌握有关简单图形的概念、公式,牢固建立空间观念;2、仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3、适当采用增加辅助线等方法帮助解题;4、采用割、补、分解、代换等方法,可将复杂问题变得简单。
典型例题:例1:一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习:已知,一个等腰直角三角形,最长的边是16厘米,这个等腰直角三角形的面积是多少平方厘米?例2:求四边形ABCD的面积。
(单位:厘米)练习:已知一个五边形的三条边的长和四个角的度数,如图所示,那么,它的面积是多少?例3:已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
练习:如下图、已知大正方形的边长是12厘米,求中间最小正方形的面积。
例4:正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习:如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.长方形的面积是多少?例5:正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
练习:如图,在长方形ABCD中,BD长18cm,AB长15cm,E是BC中点,F是CD中点,求三角形AEF的面积例6:四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
例7:下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习:如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
图形的拆分和组合

图形的拆分和组合
汇报人:XXX
目录
CONTENTS
01 图形的拆分
02 图形的组合
03 图形的拆分与组合 的应用
04 图形的拆分与组合 的技巧
05 图形的拆分与组合 的注意事项
图形的拆分
拆分定义
拆分:将图形分解 成多个部分或元素
目的:便于理解和 处理图形
方法:使用几何工 具或算法进行分解
拆分实例
圆形拆分:将圆形 分为两个半圆
正方形拆分:将正 方形分为四个等边 三角形
长方形拆分:将长 方形分为两个矩形
三角形拆分:将三 角形分为三个等边 三角形
提高图形的灵活性和可塑性
拆分意义
便于对图形进行修改和优化
增强图形的视觉效果和表现力
便于对图形进行复制和粘贴,提高工作效率
图形的组合
图形的拆分与组合的技 巧
色彩搭配
色彩对比:使用对比色来突出重点,如红绿、蓝黄等 色彩协调:使用相近色或同色系来保持整体和谐,如蓝绿、红橙等 色彩平衡:注意色彩的分布和比例,避免过于单调或杂乱 色彩渐变:使用渐变色来增加层次感和立体感,如从浅到深、从冷到暖等
旋转:将图形围绕某个点 旋转一定角度
形状变化
基本概念:点、 线、面、体、颜 色、纹理等
技术方法:几何建 模、光照模型、纹 理映射、动画技术 等
艺术创作
抽象画:通过图形的拆分与组合, 创造出独特的艺术风格
拼贴画:将不同的图形进行拆分 与组合,形成独特的视觉效果
插画设计:利用图形的拆分与组 合,设计出独特的插画作品
海报设计:通过图形的拆分与组 合,设计出独特的海报作品
遵循美学原则
保持图形的简洁性和统一性 注意图形的比例和布局 避免过度装饰和复杂化 考虑图形的色彩搭配和视觉效果
六上数学组合图形
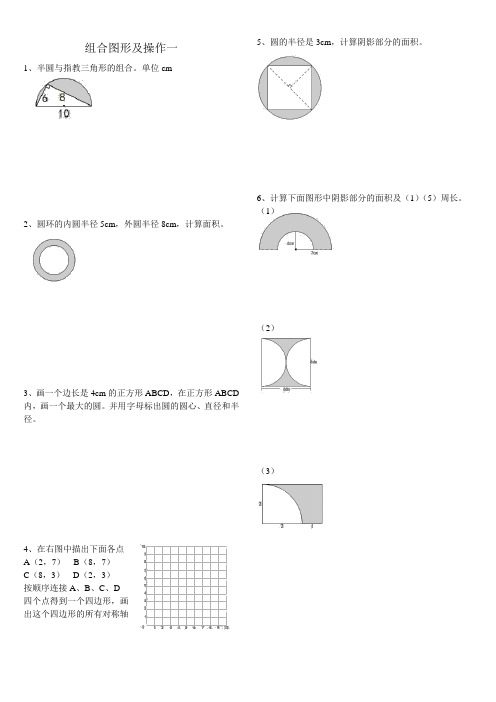
组合图形及操作一1、半圆与指教三角形的组合。
单位cm2、圆环的内圆半径5cm,外圆半径8cm,计算面积。
3、画一个边长是4cm的正方形ABCD,在正方形ABCD 内,画一个最大的圆。
并用字母标出圆的圆心、直径和半径。
4、在右图中描出下面各点A(2,7)B(8,7)C(8,3)D(2,3)按顺序连接A、B、C、D四个点得到一个四边形,画出这个四边形的所有对称轴5、圆的半径是3cm,计算阴影部分的面积。
6、计算下面图形中阴影部分的面积及(1)(5)周长。
(1)(2)(3)(4)(5)(6)(7)(8)7、求运动场周长和面积8、正方形的面积是8cm²。
阴影部分的面积是多少平方厘米?9、如果所示,下水道圆形井盖半径是40cm,底座是一个边长超过井盖直径16cm的正方形带孔的框。
这个井盖底座的面积有多少平方厘米?10、圆形花坛周长是25.12m。
在花坛周围修一条宽为1m 的圆环形小路,小路的面积是多少平方米?11、一匹马被栓在一棵树下,拴马的绳子长8米,如果将绳子再放出一米,马儿能多吃多大面积的草?12、用15.7m长的篱笆靠墙围了一个半圆形的鸡舍,这个鸡舍的面积是多少平方米?如果将圆的半径增加1米,鸡舍的面积增加多少?13、如图所示,线段AB=4cm,求阴影部分面积和周长。
14、如图,正方形的面积是2cm²,求圆面积。
15、下面两个圆中的直角等腰三角形的面积都是5cm²,求圆面积。
16、图中圆与长方形面积相等,长方形的长是6.28m,阴影部分的面积是多少平方米?17、如图,钢管的厚度是0.8cm,内圆直径是5dm,它的横截面面积是多少平方厘米?(得数保留两位小数)18、操作题:以01为圆心画一个直径为5cm的圆,用字母标出圆的直径和半径。
以02为圆心画一个半径4cm的圆,与圆01形成一个只有一条对称轴的图形,并在圆02中画出一个圆心角为150°的扇形。
计算圆01和圆02的面积差。
图形的分割与组合

再考虑形状.如果能将图12—4先分成两个面积相等、形状相同的图形,然后再将其中的一个再分成两个面积相等、形状相同的图形,那么达到目的了.
图形的分割与组合
图形的分割与组合是几何学中一个非常有趣味的课题,研究图形的分割与组合问题不仅可以增强几何图形的直观感觉和判断能力,丰富对图形的想象力,提高数学的思维能力,而且还有一定的实用价值,对工厂里的下料、工艺美术的图案设计都有一定的用处.
例1将图12—1所示的图形分成两块,然后拼成一个正方形.
除了上面的几种分法外,还可以这样想,因为6=1+5=2+4=3+3。所以对
余下的三角形分成五个面积相等的小三角形。对6=2+4而言,可先从原三角形
分出的三角形和剩下的三角形分别分成2个和4个面积相等的小三角形,对6=3+3可采用与上面类似的方法进行分割。
解法1将三角形的任一边六等分,再将分点与这边相对的顶点用线段连接起来,见图10-1。
第一种,将图10-4中不规则的那块图形,按图10-5中虚线所示分成三块,拼得的正方形见图10-6。
第二种,将图10-4中的长方形图形,按图10-7中虚线所示分成三块,拼得的正方形见图10-8。
例3有一块长24米、宽15米的长方形地毯,现在要把它移到长20米、宽18米的新房间里去。问是否可以找到一种剪裁法,把长方形地毯分成形状与面积都一样的两块,拼合后正好能铺满新房间的地面?
解:按图12—9中的粗线将长方形分成两块,然后错位对齐,即可拼成新的长方形,见图12—10.
例4图12—11是一块正中间开有长方形孔的长方形木板,尺寸如图所示(单位:厘米).把它锯成两块,拼成一个面积为100平方厘米的桌面,如何切分.
