(完整版)立体几何常见题型归纳,推荐文档
高中立体几何知识点及经典题型

高中立体几何知识点及经典题型立体几何是高中数学中的重要部分,它研究了在三维空间内的几何形体。
本文将介绍高中立体几何的主要知识点和经典题型。
知识点以下是高中立体几何的主要知识点:1. 空间几何基础:点、线、面的概念及性质。
2. 参数方程和一般式方程:用参数或方程表示几何体的方法。
3. 立体图形的投影:点、直线、平面在投影中的表现形式。
4. 空间几何中的平行与垂直:直线、平面之间的平行关系及垂直关系。
5. 直线与面的位置关系:直线与平面之间的交点、垂线、倾斜角等概念。
6. 空间角的性质:二面角、棱锥、棱台等形体的角度关系。
7. 空间几何中的直线及曲线:空间中直线与曲线的方程及性质。
8. 空间立体角:球、球台、球扇等形体的角度关系。
9. 空间的切线:曲线在空间中的切线方程及其性质。
10. 空间的幂:圆、球及其他形体的幂的概念和性质。
经典题型以下是高中立体几何的经典题型:1. 求直线与平面的位置关系问题:例如,给定一直线和一个平面,求它们之间的交点、垂直线、倾斜角等。
2. 求空间角的问题:例如,给定两个平面的交线,求二面角的度数。
3. 求直线与曲线的位置关系问题:例如,给定一条直线和一个曲面,求它们之间的位置关系。
4. 求切线和法平面的问题:例如,给定一个曲线和一个点,求曲线在该点处的切线方程及法平面方程。
5. 求空间形体的幂问题:例如,给定一个球和一个平面,求平面关于球的幂及其性质。
以上只是一些经典的立体几何题型,通过解答这些题目,可以加深对立体几何知识的理解和运用。
希望本文对高中立体几何知识点和题型的介绍能够帮助到你。
祝你在学习立体几何时取得好成绩!。
高考数学立体几何题型大全总结

高考数学立体几何题型大全总结1. 空间直线和面的位置关系题型:
- 确定直线和平面的位置关系
- 求平面与直线的交点、垂足等
2. 空间向量题型:
- 确定向量的方向、模长和坐标
- 求向量的数量积、向量积和混合积
3. 空间几何体积题型:
- 确定几何体的形状和大小
- 求立体图形的表面积和体积
4. 立体几何相似题型:
- 确定几何体的相似性质
- 求相似多面体的比例
5. 立体几何坐标题型:
- 确定三维空间内点的坐标
- 求点、线、面的距离
参考内容:
- 教材《高等数学》(第七版)同济大学出版社;
- 教材《高等代数与解析几何》(第三版)高等教育出版社;- 网络资源《高考数学立体几何通关攻略》、《高考数学立体几何考点详解》等。
立体几何题型汇总及详细答案

(2)若 , , ,试求该几何体的体积V.
9.在长方体 中, ,
(1) 求证: ∥面 ;
(2)证明: ;
(3)一只蜜蜂在长方体 中飞行,求它飞入三棱锥 内的概率.
10. 如图甲,在平面四边形ABCD中,已知
, ,现将四边形ABCD沿BD折起,
使平面ABD 平面BDC(如图乙),设点E、F分别为棱
10.(2008江苏模拟)一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
(1)求证:
(2)当FG=GD时,在棱AD上确定一点P,使得GP//平面FMC,并给出证明.
立体几何中的动点问题
1.(2011五校联考)已知四边形 为矩形, 、 分别是线段 、
的中点, 平面
17.如图6,已知正三棱柱ABC—A1B1C1中,D是BC的中点。
(1)求证:平面AB1D⊥平面B1BCC1;
(2)求证:A1C//平面AB1D。
18.如图,已知 平面 , 平面 ,△ 为等边三角形,
, 为 的中点.
(1)求证: 平面 ;
(2)求证:平面 平面 ;
19.如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90.E为BB1的中点,D点在AB上且DE= .
39.(2008中山市)如图,四棱锥P—ABCD中, PA 平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,E为PC中点.
(I) 求证:平面PDC 平面PAD;
(II) 求证:BE//平面PAD.
40.(2008华南师大附中) 如图,已知棱柱ABCD—A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1,F为棱AA1的中点,M为线段BD1的中点。
高三高考数学总复习《立体几何》题型归纳与汇总

(3)当 PA// 平面 BDE 时, PA 平面 PAC ,且平面 PAC 平面 BDE DE ,可得 PA//DE .由 D 是 AC 边的中 点知, E 为 PC 边的中点.故而 ED 1 PA 1, ED∥PA ,因为 PA 平面 ABC ,所以 ED 平面 BDC .
2
由 AB BC 2 ,AB BC ,D 为 AC 边中点知,BD CD 2. 又 BD AC ,有 BD DC ,即 BDC 90.
3 【解析】(1)∵ PA PD, N 为 AD 的中点,∴ PN AD, ∵底面 ABCD为菱形, BAD 60 ,∴ BN AD, ∵ PN BN N ,∴ AD 平面 PNB . (2)∵ PN PD AD 2 , ∴ PN NB 3 , ∵平面 PAD 平面 ABCD,平面 PAD 平面 ABCD AD , PN AD, ∴ PN 平面 ABCD, ∴ PN NB ,
【易错点】 外接球球心位置不好找 【思维点拨】 应用补形法找外接球球心的位置
题型四 立体几何的计算
例 1 如图,已知三棱锥的底面是直角三角形,直角 边边长分别为 3 和 4 ,过直角顶点的侧棱长为 4 ,且 垂直于底面,该三棱锥的主视图是 ( )
【答案】 B 【解析】显然由空间直角坐标系可知,该几何体在 xoy 面内的点保持不动,在 y 轴上的点在 xoy 面内的射影为坐标原 点,所以该几何体的主视图就是其在面 xoy 面的表面图形,即主视图应为高为 4 ,底面边长为 3 的直角三角形.故选 B.
以 PA BD . (2)因为 AB BC , AB BC , D 为线段 AC 的中点,所以在等腰 Rt△ABC 中, BD AC .又 由(1)可知, PA BD,PA AC A,所以 BD 平面 PAC .由 E 为线段 PC 上一点,则 DE 平面 PAC ,
立体几何常见重要题型归纳(学生版)
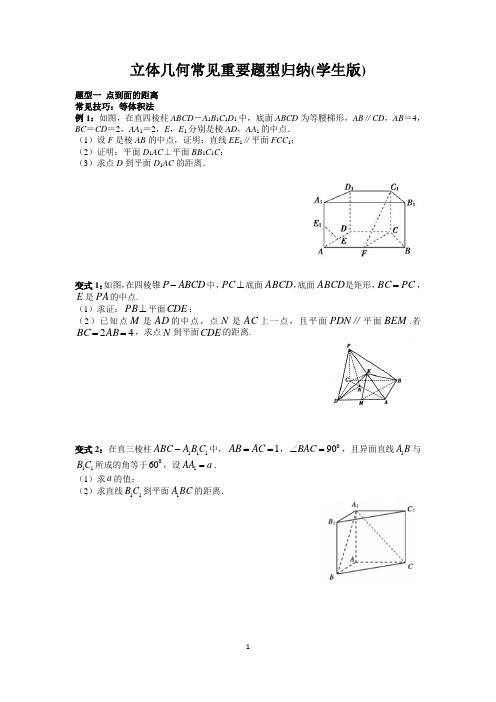
立体几何常见重要题型归纳(学生版)题型一 点到面的距离 常见技巧:等体积法例1:如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,AB =4,BC =CD =2,AA 1=2,E ,E 1分别是棱AD ,AA 1的中点. (1)设F 是棱AB 的中点,证明:直线EE 1∥平面FCC 1; (2)证明:平面D 1AC ⊥平面BB 1C 1C ; (3)求点D 到平面D 1AC 的距离.变式1:如图,在四棱锥P A B C D -中,⊥PC 底面ABCD ,底面ABCD 是矩形,PC BC =,E 是PA 的中点.(1)求证:⊥PB 平面CDE ;(2)已知点M 是AD 的中点,点N 是AC 上一点,且平面∥PDN 平面BEM .若42==AB BC ,求点N 到平面CDE 的距离.变式2:在直三棱柱111A B C A B C -中,1A B A C ==,090B A C ∠=,且异面直线1A B 与11B C 所成的角等于060,设1A A a =.(1)求a 的值;(2)求直线11B C 到平面1A B C 的距离.变式3:如图,A B 是O ⊙的直径,点C 是O ⊙上的动点,P A 垂直于O ⊙所在的平面A B C . (Ⅰ)证明:P A C ⊥平面P B C ;(Ⅱ)设1P AA C ==,,求三棱锥AP B C-的高.变式4:在三棱锥P A B C -中,底面A B C 为直角三角形,A B B C =,P A ⊥平面A B C . (1)证明:B C P B ⊥;(2)若D 为A C 的中点,且4,P A A B ==,求点D 到平面P B C 的距离.变式5:如图,在三棱柱111A B C A B C -中,1A A ⊥平面A B C ,12A B A A ==,A C =3B C =,M ,N 分别为11B C 、1A A 的中点.(1)求证:平面1A B C ⊥平面11A A C C ;(2)求证://M N 平面1A B C ,并求M 到平面1A B C 的距离.变式6:如图6,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,C D=,直线C D⊥平面A B C.A B是直径,1(1)证明:A C B D⊥;(2)在D B上是否存在一点M,使得O M∥平面D A C,若存在,请确定点M的位置,并证明之;若不存在,请说明理由;(3)求点C到平面A B D的距离.题型二线面角常见技巧:1、定义法;2、等体积法例2:如图,在四棱锥P A B C D-中,底面A B C D是平行四边形,A D C A D A C O∠===为A C的中点,P O⊥平面A B C D,2,45,1,=为B D的P O M中点.(1)证明: A D⊥平面P A C;(2)求直线A M与平面A B C D所成角的正切值.变式1:在四棱锥P A B C D-中,底面A B C D为矩形,P A⊥面A B C D,4==,P A A DA B=,以A C为直径的球面交P D于M点.2(1)求证:面A B M⊥面P C D;(2)求C D与面A C M所成角的正弦值.变式2:如图,在长方体1111A B C D A B C D -中,已知11A D A A ==,2A B =,点E 是A B 的中点.(1)求证:11D E A D ⊥;(2)求直线1B C 与平面1D E D 所成角的大小.变式3:如下图,已知四棱锥P A B C D -中,底面A B C D 为菱形,P A ⊥平面A B C D ,60A B C ∠=,E ,F 分别是B C ,P C 的中点. (I )证明:A E ⊥平面P A D ;(II )取2A B =,在线段P D 上是否存在点H ,使得E H 与平面P A D 所成最大角的正切值为2,若存在,请求出H 点的位置;若不存在,请说明理由.变式4:如图,四棱锥C D P -A B ,底面C D A B 是C 60∠A B =的菱形,侧面D P A 是边长为2的正三角形,O 是AD 的中点, M 为C P 的中点. (1)求证:C D P ⊥A ;(2)若PO 与底面ABCD 垂直,求直线DM 与平面C P A 所成的角的正弦值.变式5:已知等腰直角三角形RBC ,其中, 2==BC RB .点A 、D 分别是RB 、RC 的中点,现将△RAD 沿着边AD 折起到△PAD 位置, 使PA ⊥AB ,连结PB 、PC .(Ⅰ)求证:BC ⊥PB(Ⅱ)求PC 与平面ABCD 所成角的余弦值变式6:如图,在三棱锥P A B C -中,A B C ∆是等边三角形,D 是A C 的中点,P A P C =,二面角P A C B --的大小为60. (1)求证:平面P B D ⊥平面P A C ;(2)求A B 与平面P A C 所成角的正弦值.变式7:如图,棱柱111C B A ABC -中,四边形B B AA 11是菱形,四边形11B BCC 是矩形,60,2,1,1=∠==⊥AB A AB CB BC AB .(1)求证:平面111ABB A B CA 平面⊥; (2)求点1C 到平面CB A 1的距离;(3)求直线C A 1与平面11B BCC 所成角的正切值.A C 1B 1CBA 1题型三 锥体体积常用技巧:选择合适的底面例3:如图,在三棱锥P A B C -中,2PA PB AB ===,3B C =,90A B C ∠=︒,平面P A B ⊥平面A B C ,D ,E 分别为A B ,A C 中点. (1)求证://D E 平面P B C ; (2)求证:A B P E ⊥;(3)求三棱锥P B E C -的体积.变式1:如图,三棱柱111A B C A B C -中,112A B A C A A B C ====,01160A A C ∠=,平面1A B C ⊥平面11A A C C ,1A C 与1A C 相交于点D .(1)求证:1B D A C ⊥;(2)若E 在棱1B C 上,且满足//D E 面A B C ,求三棱锥1E A C C -的体积变式2:如图,在平行四边形A B C D 中,1,2A B B C ==,3C B A π∠=,A B E F 为直角梯形,//B E A F ,2B A F π∠=,2B E =,3A F =,平面A B C D ⊥平面A B E F .(1)求证:A C ⊥平面A B E F ; (2)求三棱锥D A E F -的体积.变式3:如图,在四棱锥P A B C D -中,P D ⊥平面A B C D ,底面A B C D 是菱形,60B A D ∠=,2A B =,P D =O 为A C 与B D 的交点,E 为棱P B 上一点.(Ⅰ)证明:平面E A C ⊥平面P B D ;(Ⅱ)若//P D 平面E A C ,求三棱锥P E A D -的体积.变式4:如图,在三棱锥ABC S -中,⊥SA 底面ABC , 90=∠ABC ,且AB SA =, 点M 是S B 的中点,SC AN ⊥且交SC 于点N . (1)求证:⊥SC 平面AMN ;(2)当1A B B C ==时,求三棱锥SAN M -的体积.题型4 二面角常用技巧:1、定义法;2、垂线法;3、垂面法例4:四棱锥A B C D E -中,底面B C D E 为矩形,侧面A B C ⊥底面B C D E ,2B C =,C D =A B A C =.(1)证明:A D C E ⊥;(2)设C E 与平面A B E 所成的角为45,求二面角C A D E --的余弦值的大小.变式1:如图,三棱柱111C B A ABC -的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是3,D 是AC 的中点。
立体几何7大题型汇编

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
立体几何大题15种题型全归纳

【题型一】 平行1:四边形法证线面平行【典例分析】如图,在正方体中,E ,F 分别是,CD 的中点.(1)求证:平面;(2)求异面直线与所成角的余弦值.【答案】(1)证明见解析;(2(1)在正方体中,取中点G ,连接FG ,,如图,而F 是CD 的中点,则,,又E 是的中点,则,, 因此,,,四边形是平行四边形,有,而平面,平面,平面.【经验总结】基本规律1.利用平移法做出平行四边形2.利用中位线做出平行四边形【变式演练】1.如图所示,在四棱锥P -ABCD 中,PC ⊥底面ABCD ,,,,E 是PB 的中点.(1)求证:平面PAD ;(2)若,求三棱锥P -ACE 的体积.【答案】(1)证明见解析(2) 【分析】(1)取PA 的中点F ,连接EF ,DF ,利用平行四边形证明,再由线面平行的判定定理即可得证;(2)根据等体积法知,即可由棱锥体积公式求解.(1)取PA 的中点F ,连接EF ,DF ,∵点E ,F 分别为PB ,PA 的中点,1111ABCD A B C D -1AA //EF 11A CD 1ED 1A C 1111ABCD A B C D -1CD 1GA 1//FG DD 112FG DD =1AA 11//A E DD 1112A E DD =1//A E FG 1A E FG =1FGA E 1//EF GA EF ⊄11A CD 1GA ⊂11A CD //EF 11A CD AB AD ⊥//AB CD 222AB AD CD ===//CE 2PC =13//EC DF P ACE E ACP V V --=∴,,∴四边形EFDC 是平行四边形,∴,又∵平面PAD ,平面PAD ,∴平面PAD ;2.如图,在四棱锥中,面,,且,,,,为的中点.(1)求证:平面;(2)求平面与平面所成二面角的余弦值;(3)在线段上是否存在一点,使得直线与平面若存在求出的值,若不存在说明理由. 【答案】(1)证明见解析(2)(3)存在, (1)证明:取CP 中点F ,连接NF 、BF ,因为F ,N 分为PC ,PD 的中点,则,且, 又,且,,所以四边形NABF 是平行四边形, ,又面PBC ,面PBC 。
(完整版)高中数学立体几何经典常考题型

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角,求空间角一般都可以建立空间直角坐标系,用空间向量的坐标运算求解.【例1】如图,在△ABC中,∠ABC=,O为AB边上一点,且3OB=3OC=2AB,已知PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.(1)求证:平面PBD⊥平面COD;(2)求直线PD与平面BDC所成角的正弦值.(1)证明 ∵OB=OC,又∵∠ABC=,∴∠OCB=,∴∠BOC=.⊥∴CO AB.又PO⊥平面ABC,⊥OC⊂平面ABC,∴PO OC.又∵PO,AB⊂平面PAB,PO∩AB=O,∴CO⊥平面PAB,即CO⊥平面PDB.又CO⊂平面COD,∴平面PDB⊥平面COD.(2)解 以OC,OB,OP所在射线分别为x,y,z轴,建立空间直角坐标系,如图所示.设OA=1,则PO=OB=OC=2,DA=1.则C(2,0,0),B(0,2,0),P(0,0,2),D(0,-1,1),∴PD=(0,-1,-1),BC=(2,-2,0),BD=(0,-3,1).设平面BDC的一个法向量为n=(x,y,z),∴∴令y=1,则x=1,z=3,∴n=(1,1,3).设PD与平面BDC所成的角为θ,则sin θ===.即直线PD与平面BDC所成角的正弦值为.【类题通法】利用向量求空间角的步骤间标.第一步:建立空直角坐系第二步:确定点的坐标.线)坐标.第三步:求向量(直的方向向量、平面的法向量计夹(或函数值).第四步:算向量的角将夹转为间.第五步:向量角化所求的空角查关键错题规.第六步:反思回顾.看点、易点和答范【变式训练】 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(1)证明:EF∥B1C.(2)求二面角EA1DB1的余弦值.(1)证明 由正方形的性质可知A1B1AB DC∥∥,且A1B1=AB=DC,所以四边形A1B1CD为平行四边形,从而B1C A∥1D,又A1D⊂面A1DE,B1C⊄面A1DE,于是B1C∥面A1DE.又B1C⊂面B1CD1,面A1DE∩面B1CD1=EF,所以EF∥B1C.(2)解 因为四边形AA1B1B,ADD1A1,ABCD均为正方形,所以AA1⊥AB,AA1⊥AD,AB⊥AD且AA1=AB=AD.以A为原点,分别以AB,AD,AA1为x轴,y轴和z轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),B1(1,0,1),D1(0,1,1),而E点为B1D1的中点,所以E点的坐标为.设平面A1DE的一个法向量n1=(r1,s1,t1),而该面上向量A1E=,A1D=(0,1,-1),由n1⊥A1E,n1⊥A1D得r1,s1,t1应满足的方程组(-1,1,1)为其一组解,所以可取n1=(-1,1,1).设平面A1B1CD的一个法向量n2=(r2,s2,t2),而该面上向量A1B1=(1,0,0),A1D=(0,1,-1),由此同理可得n2=(0,1,1).所以结合图形知二面角EA1DB1的余弦值为==.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现,常涉及线、面平行、垂直位置关系的探究或空间角的计算问题,是高考命题的热点,一般有两种解决方式:(1)根据条件作出判断,再进一步论证;(2)利用空间向量,先假设存在点的坐标,再根据条件判断该点的坐标是否存在.【例2】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.(1)证明 因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,所以AB⊥平面PAD,所以AB⊥PD.又PA⊥PD,AB∩PA=A,所以PD⊥平面PAB.(2)解 取AD的中点O,连接PO,CO.因为PA=PD,所以PO⊥AD.因为PO⊂平面PAD,平面PAD⊥平面ABCD,所以PO⊥平面ABCD.因为CO⊂平面ABCD,所以PO⊥CO.因为AC=CD,所以CO⊥AD.如图,建立空间直角坐标系O-xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD的一个法向量为n=(x,y,z),则即令z=2,则x=1,y=-2.所以n=(1,-2,2).又PB=(1,1,-1),所以cos〈n,PB〉==-.所以直线PB与平面PCD所成角的正弦值为.(3)解 设M是棱P A上一点,则存在λ∈0,1],使得AM=λAP.因此点M(0,1-λ,λ),BM=(-1,-λ,λ).因为BM⊄平面PCD,所以要使BM∥平面PCD,则BM·n=0,即(-1,-λ,λ)·(1,-2,2)=0,解得λ=.所以在棱P A上存在点M,使得BM∥平面PCD,此时=.应设,把要成立的作件结论当条,据此列方对断问题,先假存在【类题通法】(1)于存在判型的求解规围内”等.标,是否有定范的解程或方程组,把“是否存在”化问题转为“点的坐是否有解对问题,通常借助向量,引进参数,合已知和列出等式综结论,解出参数.(2)于位置探究型【变式训练】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠P AD=45°,E为P A的中点.(1)求证:DE∥平面BPC;(2)线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出二面角F-PC-D的余弦值;若不存在,请说明理由.(1)证明 取PB的中点M,连接EM和CM,过点C作CN⊥AB,垂足为点N.∵CN⊥AB,DA⊥AB,∴CN∥DA,又AB∥CD,∴四边形CDAN为平行四边形,∴CN=AD=8,DC=AN=6,在Rt△BNC中,BN===6,∴AB=12,而E,M分别为P A,PB的中点,∴EM∥AB且EM=6,又DC∥AB,∥且EM=CD,四边形CDEM为平行四边形,∴EM CD∥∵⊂平面PBC,DE⊄平面PBC,∴DE CM.CM∴DE∥平面BPC.(2)解 由题意可得DA,DC,DP两两互相垂直,如图,以D为原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系D-xyz,则A(8,0,0),B(8,12,0),C(0,6,0),P(0,0,8).假设AB上存在一点F使CF⊥BD,设点F坐标为(8,t,0),则CF=(8,t-6,0),DB=(8,12,0),由CF·DB=0得t=.又平面DPC的一个法向量为m=(1,0,0),设平面FPC的法向量为n=(x,y,z).又PC=(0,6,-8),FC=.由得即不妨令y=12,有n=(8,12,9).则cos〈n,m〉===.又由图可知,该二面角为锐二面角,故二面角F-PC-D的余弦值为.题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起,使其成为空间图形,这类问题称为立体几何中的折叠问题,折叠问题常与空间中的平行、垂直以及空间角相结合命题,考查学生的空间想象力和分析问题的能力.【例3】如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD 上,AE=CF=,EF交BD于点H.将△DEF沿EF折到△D′EF的位置,OD′=.(1)证明:D′H⊥平面ABCD;(2)求二面角B-D′A-C的正弦值.(1)证明 由已知得AC ⊥BD ,AD =CD .又由AE =CF 得=,故AC ∥EF .因此EF ⊥HD ,从而EF ⊥D ′H .由AB =5,AC =6得DO =BO ==4.由EF ∥AC 得==.所以OH =1,D ′H =DH =3.于是D ′H 2+OH 2=32+12=10=D ′O 2,故D ′H ⊥OH .又D ′H ⊥EF ,而OH ∩EF =H ,所以D ′H ⊥平面ABCD .(2)解 如图,以H 为坐标原点,HF 的方向为x 轴正方向,建立空间直角坐标系H -xyz .则H (0,0,0),A (-3,-1,0),B (0,-5,0),C (3,-1,0),D ′(0,0,3),AB =(3,-4,0),AC =(6,0,0),AD′=(3,1,3).设m =(x 1,y 1,z 1)是平面ABD ′的一个法向量,则即所以可取m =(4,3,-5).设n =(x 2,y 2,z 2)是平面ACD ′的一个法向量,则即所以可取n =(0,-3,1).于是cos 〈m ,n 〉===-.sin 〈m ,n 〉=.因此二面角B -D ′A -C 的正弦值是.【类题通法】立体几何中的折叠问题,是翻折前后形中面位置系和度量系的化关键搞清图线关关变情况,一般地翻折后在同一平面上的性不生化还个质发变,不在同一平面上的性生化个质发变.【变式训练】如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =,AB =BC =1,AD =2,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置,如图2.(1)证明:CD⊥平面A1OC;(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.(1)证明 在题图1中,因为AB=BC=1,AD=2,E是AD的中点,∠BAD=,所以BE⊥AC.即在题图2中,BE⊥OA1,BE⊥OC,从而BE⊥平面A1OC.又CD∥BE,所以CD⊥平面A1OC.(2)解 由已知,平面A1BE⊥平面BCDE,又由(1)知,BE⊥OA1,BE⊥OC,所以∠A1OC为二面角A1-BE-C的平面角,所以∠A1OC=.如图,以O为原点,OB,OC,OA1分别为x轴、y轴、z轴正方向建立空间直角坐标系,因为A1B=A1E=BC=ED=1,BC∥ED,所以B,E,A1,C,得BC=,A1C=,CD=BE=(-,0,0).设平面A1BC的一个法向量n1=(x1,y1,z1),平面A1CD的一个法向量n2=(x2,y2,z2),平面A1BC与平面A1CD的夹角为θ,则得取n1=(1,1,1);得取n2=(0,1,1),从而cos θ=|cos〈n1,n2〉|==,即平面A1BC与平面A1CD夹角的余弦值为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(8)直线 l 与平面 、 所成角相等,则 ∥ .( )
(9)垂直于同一平面的两个平面平行. (
) (10)垂直于同一直线的两个平面平
行. ( )
(11)垂直于同一平面的两条直线平行. ( )
(12)若直线 a 与平面 平行,则 内必存在无数条直线与 a 平行. ( )
(13)有两个侧面是矩形的棱柱是直棱柱. ( )(14)各侧面都是正方形的棱柱一定是
例 3、如图,四棱锥 P—ABCD 的底面 ABCD 为正方形,PD⊥底面 ABCD,PD=AD. 求证:(1)平面 PAC⊥平面 PBD;
(2)求 PC 与平面 PBD 所成的角;
例 4、如图,正三棱柱 ABC A1B1C1 的所有棱长都为 2 , D 为 CC1 中点. A
(Ⅰ)求证: AB1 ⊥平面 A1BD ;
(2)在平面内射影是直线的图形一定是直线. ( )
(3)直线 a 与平面 内一条直线平行,则 a ∥ .( )
(4)两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. ( )
(5)平行于同一直线的两个平面平行. (
) (6)平行于同一个平面的两直线平
行. ( )
(7)直线 a 与平面 内一条直线相交,则 a 与平面 相交. ( )
(Ⅱ)求二面角 A A1D B 的正弦值;
C
(Ⅲ)求点 C 到平面 A1BD 的距离.
B
A1
D
C1
B1
SO⊥底面 ABC,AC= 2r,则球的体积与三棱锥体积之比是____________ 例 5、如图所示,已知球 O 的面上四点 A、B、C、D,DA⊥平面 ABC,AB⊥BC,DA=AB=BC= 3,则球 O 的体积等于____________
例 6、表面积为 2 3 的正八面体的各个顶点都在同一个球面上,则此球的体积为
例 2、如图,已知矩形 ABCD 中,AB=10,BC=6,将矩形沿对角线 BD 把△ABD 折起,使
A 移到 A1 点,且 A1 在平面 BCD 上的射影 O 恰好在 CD
上.
(Ⅰ)求证: BC A1D ; (Ⅱ)求证:平面 A1BC 平面 A1BD ; (Ⅲ)求三棱锥 A1 BCD 的体积.
C1
A1
B1
C
A
B
例3
例4
例5
例 5、如图,三棱柱的侧棱长为 2,底面是边长为 1 的正三角形, AA1 面A1B1C1 ,正视图 是长为 2,宽为 1 的矩形,则该三棱柱的侧视图(或左视图)的面积为____________ 考点 3 球
例 1、在三棱锥 A BCD 中,侧棱 AB 、 AC 、 AD 两两垂直, ABC 、 ACD 、
______________ 例 7、棱长为 2 的正四面体的四个顶点都在同一个球面上, 若过该球球心的一个截面 如图 1,则图中三角形(正四面体的截面)的面积是______________ 例 8、用与球心距离为 1 的平面去截球,所得的截面面积为 π,则球的体积为
图1
__________ 考点 4 平行与垂直 例 1、如图(1)是一正方体的表面展开图,MN 和 PB 是两条面对角线,请在图(2)的 正方体中将 MN 和 PB 画出来,并就这个正方体解决下面问题. (1)求证:MN//平面 PBD; (2)求证:AQ⊥平面 PBD; (3)求二面角 P—DB—M 的正切值.
例 2、对于平面 和共面的直线 m 、 n, 下列命题中真命题是
(
)
(A)若 m , m n, 则 n∥ (B)若 m∥, n∥, 则 m∥n
(C)若 m , n∥, 则 m∥n (D)若 m 、 n 与 所成的角相等,则 m∥n
辨析:
(1)两条异面直线在同一平面内射影一定是相交的两条直线.( )
2
2 正视 图
1
2 左视 图
1
2 俯视 图 (例 3 图)
例 3、一个几何体的三视图 如图所示,
于( )
1 Aa3
则这个几何体的体积等
5 D.6a3
例 4、一个五面体的三视图如图,正(主)视图与侧(左)视图都是等腰直角三角形,俯视图 为直角梯形,部分边长如图所示,则此五面体的体积为________.
立体几何常见题型归纳
考点 1 概念辨析
例 1、设 m,n 是两条不同的直线, , , 是三个不同的平面,给出下列四个说法:
① m , n // m n ;② // , // , m m ;③ m // , n // m // n
④ , // ,说法正确的序号是:_________________
正棱柱. ( )
考点 2 三视图 例 1、下图是一个多面体的三视图,则其全面积为__________ 例 2、如图,一个空间几何体的正(主)视图、侧(左)视图都是面积为
3 2 ,且一个内角为 60°的菱形,俯视图为正方形,那么这个几何体的
表面积为__________ 例 3、已知某个几何体的三视图如下,根据图中标出的尺寸(单位: cm),那么可得这个几何体的体积是_________
ADB 的面积分别为
2
、
3
、
6
,则该三棱锥外接球的表面积_____________
222
例 2、正方体的内切球与其外接球的体积之比为________,正四面体外接球与内切球半径
之比为________ 例 3、已知球面上的三个点 A、B、C,且 AB=6,BC=8,AC=10,球半径 R=15,则球 心到平面 ABC 的距离是_____________ 例 4、已知三棱锥 S—ABC 的各顶点都在一个半径为 r 的球面上,球心 O 在 AB 上,
