逐差法和Origin 7.0在大学物理实验数据处理中的比较
物理实验技术中的实验数据处理软件推荐评述
物理实验技术中的实验数据处理软件推荐评述在物理实验中，实验数据的处理是不可或缺的一部分。
随着科技的发展，越来越多的实验数据处理软件涌现出来，为研究人员提供了更加方便和高效的工具。
本文将对物理实验数据处理中的几种常用软件进行评述和推荐。
首先，我们来介绍一款被广泛应用的实验数据处理软件- Origin。
Origin软件功能强大，可以实现数据导入、处理、分析和可视化等多种功能。
它提供了丰富的绘图工具，可以创建各种类型的图表和图像，方便用户直观地展示实验结果。
同时，Origin还提供了强大的统计功能，可以进行统计分析和拟合曲线，并给出相应的拟合参数和误差。
此外，Origin还支持脚本编程和自动化操作，使得用户可以自定义处理过程，提高数据处理的效率。
其次，我们来介绍一款专门用于光学实验数据处理的软件- MATLAB。
MATLAB是一种高级的计算机编程语言和环境，被广泛应用于科学计算和工程领域。
在光学实验中，MATLAB可以通过强大的数学和信号处理工具，对实验数据进行处理和分析。
例如，通过傅里叶变换，可以将光学信号从时域转换到频域，进一步研究光的频谱特性。
此外，MATLAB还具备强大的图像处理和显示功能，可以进行图像滤波、边缘检测和图像增强等操作，方便用户观察和分析实验图像。
另外，我们还推荐一款专业的电子实验数据处理软件- LabVIEW。
LabVIEW是一种用于控制、测试和测量的实验室编程环境。
它拥有友好的图形化编程界面，使得用户无需掌握复杂的编程语言即可进行数据处理。
LabVIEW支持多种硬件设备的连接和控制，可以实现实验仪器的自动化测量和数据采集。
同时，LabVIEW还提供了丰富的分析工具和函数库，方便用户进行数据分析和可视化。
由于其功能的强大和可扩展性，LabVIEW在电子实验中得到了广泛的应用和推广。
除了以上几款软件外，还有一些其他的实验数据处理软件也值得一提。
例如Python编程语言，凭借其简单易学和强大的科学计算库（如NumPy和SciPy），被很多科研人员用于实验数据分析和建模。
逐差法和Origin7.0软件在驻波法测超声波波速的实验数据处理中的比较
目前 常见 用 Ｅ ｃｌ ｘｅ 等软 件处 理实 验数 据 。虽
收稿日期 ： ０ ９０ －８ ２ ０ －５ ０ 基金项 目： 湖北 省教育厅 教学科研项 目（ ：５ ３ ０ Ｎｏ ０ ０ ５ ）
逐 差法和 Ｏｒ ｉ ． 软件 在驻波法测超声 波波速的实验数据处理 中的比较 ｉ ｎ７ ０ ｇ
８ 柑ｎ３ 。 一
似 的平 面声 波 ； ｚ Ｓ 为超 声 波接 收器 ， 波 传至 它 的 声
接收 面上 时 ， 再被 反射 ． Ｓ 和 Ｓ 当 的 表 面互 相 平 行时 ， 波就 在两个 平 面 间来 回反 射 ， 声 当两个平 面
来说 ， 使用 逐差 法进 行数 据处 理 要满 足 两个条 件 ：
优点 。
个重要 的环节 ， 数据处理 的好坏将直 接影 响到实
验 的结果 与结论 。学生在数 据处理 的过程 中 ， 以 可
养成严谨的科学态度和扎实的工作作风。但是， 当 学生已经掌握了一定的数据处理能力后 ， 仍然要求 其进行大量的繁琐、 精确度往往很低 的数据处理 ， 会使学生丧失学习兴趣 ， 学习效率降低。随着计算 机进一步 发展和一些强 大的数据处 理软件 的推 出 ，
较后得出用 Ｏｒ ｉ ． ｉ ｎ７ ０软件对此 实验数据处理也是一种很好 的选择 。 ｇ
中图分类号 ： ２ １ １ Ｏ ． ４
文献标识码 ： Ａ
众所周知， 大学物理实验课程是理工科院校的
一
然 Ｅ ｃｌ ｘｅ软件具有数据处理、 曲线拟合功能 ， 但对 非线性数据处理拟合等方面不能提供很多相关信
秦平力 ， 李端 勇， 张
（ 汉工 程 大学 ， 北 武 湖 武汉
昱
４０７ ３ ０ ４）
摘
物理实验技术中的数据处理算法和计算工具推荐
物理实验技术中的数据处理算法和计算工具推荐在物理实验中，数据处理是非常重要且不可或缺的步骤。
通过对实验数据的精确处理和分析，我们能够从中得出科学结论并验证理论模型。
为了提高数据处理的准确性和效率，使用适当的算法和计算工具非常重要。
本文将推荐几种常用的数据处理算法和计算工具，旨在帮助物理实验者提高数据处理和分析的水平。
一、数据处理算法1. 平均值算法：在实验中，我们通常需要重复测量同一物理量多次。
这时，计算平均值可以减小因外界干扰引起的误差，提高测量结果的精度。
平均值算法是将所有测量结果相加，然后除以测量次数。
2. 标准差算法：标准差是测量数据分散程度的一种指标。
它可以告诉我们测量结果的可靠性和精确性。
标准差算法是将每个测量结果与平均值的差的平方相加，然后除以测量次数的平方根。
3. 最小二乘法：最小二乘法用于拟合实验数据和理论模型之间的关系。
它通过最小化实际观测值与理论预测值之间的残差平方和，找到最佳拟合线或曲线。
4. 傅里叶变换：傅里叶变换是将一个函数或信号从时域转换到频域的一种数学方法。
在物理实验中，傅里叶变换广泛应用于信号分析、频谱分析和图像处理等领域。
二、计算工具推荐1. MATLAB：MATLAB是一种非常强大的科学计算软件，它提供了丰富的功能和工具箱，可以用于各种数据处理和分析任务。
MATLAB具有友好的界面和易于使用的语法，可以对实验数据进行快速处理、绘图和分析。
2. Python：Python是一种流行的编程语言，也被广泛应用于科学计算和数据处理。
Python拥有丰富的科学计算库，如NumPy和SciPy，可以支持各种数据处理算法和方法。
3. Origin：Origin是一种专业的数据分析和图形绘制软件，它可以用于各种科学数据的处理和分析。
Origin具有强大的绘图功能和可定制性，可以生成高质量的图形和图表。
4. Excel：Excel是一种常见的电子表格软件，它也可以用于简单的数据处理和分析。
逐差法和Origin7.0软件在大学物理实验数据处理中的比较
图 １ 光 杠 杆 原 理
本文 以该 软件 用 于拉伸 法 测金 属丝 杨 氏模 量 的实 验数 据处 理过 程 为例 ， 与逐差 法进 行 比较 ， 并 使用 Ｏｒ ｉ ． 软 件 能完成 实 验数据 的准确 快速 ｉ ｎ７ ０ ｇ
处理 与分 析 。
△ 一 Ｌ
表 ３ 其 它 数 据 测 量
螺旋测微器零点读数 ：． ０ ； ０ ０ ０ｍｍ 游标 卡尺零 点读数 ０ ０ ．０ｃ
２ 实 验 数 据
本 实 验采 用 ＹＮＣ １杨 氏模 量 测定 仪 ， 始实 一 原
Ｄ 一 （５ ． １ ０ ２± ０ ５ ｃ ． ） ｍ
Ｌ 一 （ ８ Ｏ± ０ ０５ ｍ ６ ．２ ． ）ｃ ｚ 一 （ ６． ０± ０ ０２ ７ ６ ． ）ｍｍ
Ｏｒ ｉ ａ ｉ ｎＬ ｂ公 司推 出 的软件 Ｏｒ ｉ ７ ０在这 一 问 ｇ ｉｎ ． ｇ
本 实验采 用 图光杠 杆法 测得 △ Ｌ值 ， 图 １ 见 。
题上 能够 提供 迅速 、 确 的信息 和参 数 以及 图形 。 准 因此 它在 教学 、 科研 、 工程技 术 等领域 具 有广 泛 的
明， 利用 Ｏｒ ｉ７０软件处理实验数据 ， ｉｎ． ｇ 具有简洁 、 快捷 与直观等特点 ， 避免了人为因素所造成的误差 ， 在 物 理实验数据处理过程 中有显 著的应用 价值 。 关 键 词： 逐差 法 ； ｉｉ７ ０软件 ； Ｏｒ ｎ ． ｇ 不确定度 ； 数据处理
文献标志码 ： Ａ 中 图 分 类 号 ： —９ ０４３
．
ｄ 一 ± △ａ
兀 ¨
Ｊ
可得到拟合直线方程 Ｙ—Ｂ Ｘ＋Ａ， 并从其斜
率 ｋ中求 出 Ｅ 值 。
ｄＴ （ ｍ ） ａ ｒ
大学物理实验---声速的测定数据处理
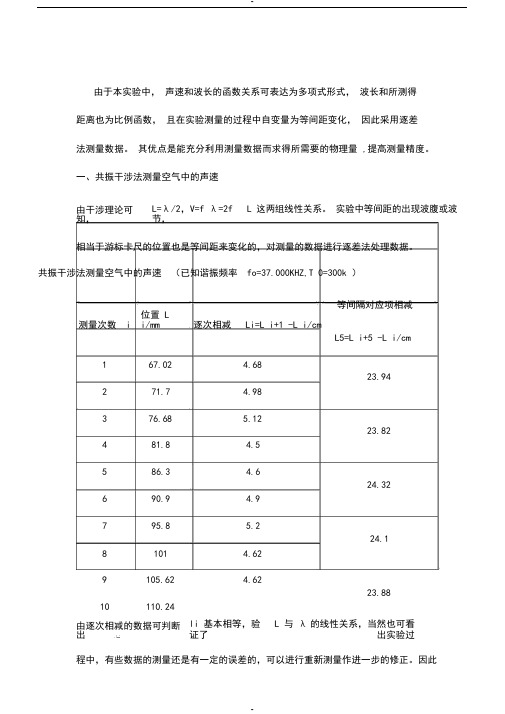
由于本实验中，声速和波长的函数关系可表达为多项式形式，波长和所测得距离也为比例函数，且在实验测量的过程中自变量为等间距变化，因此采用逐差法测量数据。
其优点是能充分利用测量数据而求得所需要的物理量 ,提高测量精度。
一、共振干涉法测量空气中的声速由干涉理论可知，L=λ/2，V=f λ=2f L 这两组线性关系。
实验中等间距的出现波腹或波节，相当于游标卡尺的位置也是等间距来变化的，对测量的数据进行逐差法处理数据。
共振干涉法测量空气中的声速（已知谐振频率fo=37.000KHZ,T 0=300k ）等间隔对应项相减测量次数 i 位置 Li/mm 逐次相减 Li=L i+1 -L i/cmL5=L i+5 -L i/cm1 67.02 4.6823.94 2 71.7 4.983 76.68 5.1223.82 4 81.8 4.55 86.3 4.624.32 6 90.9 4.97 95.8 5.224.1 8 101 4.629 105.62 4.6223.88 10 110.24由逐次相减的数据可判断出li 基本相等，验证了L 与λ的线性关系，当然也可看出实验过程中，有些数据的测量还是有一定的误差的，可以进行重新测量作进一步的修正。
因此有L 平均 =??× ??????， L 平均 =4.802 mm, ??λ平均=2× ×3×4.802×1-3= 355.348 m/s ，并且此速度是在温度T0 =300 K测V=f =2fL 37 10得。
二、相位比较法测量空气中的声速实验中采用测量两个相同李萨如图像的位置点来测量波长。
选取的李萨如图形是?? = π时的斜直线，比较容易判断，减小实验误差，测得的数据进行逐差法处理。
相位比较法测量空气中的声速等间隔对应项相减测量次数 i 位置 Li/mm 逐次相减 li=li+1 -li/cml5=li+5 -l i/cm1 65.59.5446.7 2 75.049.663 84.79.3647.08 4 94.069.745 103.88.947.02 6 112.79.37 122 9.7246.96 8 131.72 9.429 141.14 9.3647.2 10 150.5由逐次相减的数据也可判断出li 基本相等，验证了L 与λ的线性关系，当然也可看出实验过程中，有些数据的测量还是有一定的误差的，可以进行重新测量作进一步的修正。
数据处理软件Origin在物理化学实验数据处理中的应用
数据处理软件Origin在物理化学实验数据处理中的应用许劲毅指导老师：沈雪松桂林医学院摘要：应用软件Origin在计算机上对实验数据进行处理(作相图,线性拟合，非线性拟合等)，能提高试验数据处理的准确性和规范性,并能及时了解和判断学生实验结果的正确性和精密度。
关键字：Origin 线性拟合直线回归相图物理化学实验中常见的数据处理有：①公式计算；②相图绘制；③线性拟合；④非线性拟合；⑤求斜率或截距。
在学生实验中，经常要对数据进行定量处理,用手工绘图.例如；在二组分体系相图的绘制中，必须先进行标准曲线的手工绘制,再在标准曲线上进行量取这样手工的数据处理误差大,效率低。
随着计算机技术的发展对实验数据的处理也应计算机化。
一个专门的数据处理软件Origin7.0，可对物理化学实验的数据处理有很大帮助，能提高试验数据处理的准确性和规范性，可提高数据处理的效率.在学生实验中，可很快知道其实验是否成功,而且大大减少实验数据处理的误差。
1. Origin软件的介绍1.1数据作图Origin可绘制散点图，点线图,柱行图，条形三角图以及双Y轴图形等，在物化实验中通常用散点图，点线图及双Y轴图形。
1.2线性拟合当用散点图或用点线图作出曲线后，用菜单栏中的Analysis中的Fit linear或Tools菜单中的Liner Fit可对曲线进行线性拟合.结果记录中显示曲线的公式,斜率,截距和相对误差等。
在处理数据时，可对散点图或点线图的形状选择合适的函数进行拟合。
2. 应用介绍2.1 相图绘制2.1.1二元组分T-X相图的绘制2.1.1.1 苯－乙醇二组分T-X相图的绘制2.1.1.1.1作二元组分的标准曲线下表苯-乙醇溶液折光率测定数据.苯的摩尔分数折光率10% 1.373420% 1.387550% 1.429070% 1.457090% 1.48502.1.1.1.2线性拟合.将数据输入Origin 数据表中，作苯组分-折光率的散点图，再进行选择Analysis菜单中的Fit linea，对该数点图进行线性拟合.得到曲线类的为y=B+Ax, B= -9.75602，A= 7.17622 R(相关系数)=1，SD(标准偏差)=9.95047E-4，P(R2=0的概率)<0.0001表明拟合效果最佳,拟合函数式为y=7.17622x-9.75602。
大学物理实验中数据处理方法的实例分析
∃ ( # U-
# Ui ) 2
n n ! ( - 1) 2 2
0. 075, u B ( U) = 0. 029( V)
2 u2 A ( U) + u B ( U) = uB ( U) = 0. 030( V)
uA ( I ) = 0, uB ( I ) = 0. 00029( A) , u c ( I ) = 0. 00029( A) , u cR = 0. 6( ) R ∀ u c ( R ) = 99. 7 ∀ 0. 6( ) 1 3 4 最小二乘法 尽管 Excel 中具有用回归即直接用最小二乘法处理数据的功能 , 但数据的分析中有很多结果我们不需要 , 112
而且处理数据的过程很快不便于了解 , 故把公式推出后 , 只采用 Excel 的计算功能。根据表 1 的数据 , 计算如 下: R =
∃ UiI i = 100 2 ∃ Ii
41
uA ( R ) =
∃ Ii ∃ Ii
∃ ( Ui -
R Ii ) 2 = 0. 34 , u B ( I ) = 0. 00029( A) , uB ( U) = 0. 029( V) n( n - 1 )
根据常用函数的不确定度传递公式 uB( R ) = R u B ( U) U
2
+
uB ( I ) I
2
, uB ( R ) = 0. 82( ) , u c ( R ) = 0. 89( )
测量结果: R ∀ uc ( R ) = 100. 3 ∀ 0. 9( )
2
几种方法的比较
列表法是物理实验处理数据中最常用的一种方法 , 此方法使测量数据表达清晰、 条理化 , 便于检查数据和 发现问题、 减少和避免差错, 有助于反映出各物理量之间的对应关系 , 列表格没有统一的格式 , 可让学生尽个人 能力发挥[ 3] , 但对于一些实验不便计算出它的不确定度( 例如本实验测量的数据 , 不能估算 A 类不确定度 ) , 这 种方法比较适合初学者; 作图法把数据间的函数关系形象直观化 , 有利于发现个别不服从规律的数据 , 通过描 点作图具有取平均的效果 , 从曲线图较容易地得出某些实验结果 , 但在手工绘制图线时有一定的主观随意性 , 此方法适合于测量结果要求不高、 定性测量、 不要求估算不确定度的实验或者是利用图线确定函数关系和省略 某些因素影响的实验 , 如用惯性秤测量物体的质量、 伏安测二极管特性的实验; 逐差法处理数据具有充分利用 测量数据的特点 , 比作图法处理数据得到的实验结果精确 , 比最小二乘法处理数据过程简单 , 但逐差法处理数 据有其局限性, 适用于自变量等间距变化, 与因变量之间的函数关系最好为线性关系, 如非线性函数关系变化 后, 原来各个数据是等精度的 , 经过函数变换后可能成为非等精度的 , 而且部分随机误差无法相互抵消, 因而随 机误差对逐差法处理数据仍有较大的影响 [ 4] ; 对于许多复杂和测量要求高的实验, 往往采用最小二乘法处理 实验数据 , 因为最小二乘法是以误差理论为依据, 在诸数据处理方法中, 误差最小、 精确性最好 过程中计算繁杂。
物理实验技术中的数据处理软件及其使用方法
物理实验技术中的数据处理软件及其使用方法在物理实验中，数据处理是一个关键的环节。
通过对实验数据的处理和分析，我们可以得到更准确的结果和更深入的理解。
为了提高实验数据处理的效率和准确性，科研人员和学生们常常会使用各种数据处理软件来辅助实验数据的处理和分析。
本文将介绍几种常用的物理实验数据处理软件及其使用方法。
一、Excel数据处理软件Excel是一种功能强大的电子表格软件，它可以用于各种实验数据的处理和分析。
使用Excel进行数据处理的第一步是将实验数据输入到工作表中。
在Excel中，每个数据都可以对应一个单元格，可以在单元格中输入数字、文字、公式等内容。
在输入完实验数据后，可以通过Excel提供的各种函数和公式进行数据处理，如求平均值、方差、标准差等统计数据。
此外，Excel还可以进行图表绘制，通过绘制折线图、柱状图等图表，我们可以更直观地观察和分析实验数据之间的关系。
二、Origin数据分析软件Origin是一种专业的数据分析和绘图软件，特别适合物理实验中大量数据的处理和分析。
与Excel相比，Origin具有更强大的数据处理功能和分析工具。
使用Origin进行数据处理的第一步是导入实验数据。
Origin支持多种数据格式的导入，如文本文件、Excel文件、LabVIEW等。
导入数据后，可以通过Origin提供的各种功能进行数据处理和分析，如拟合曲线、求解微分方程、图像处理等。
此外，Origin还可以进行数据可视化，绘制各种专业的图表和曲线，方便进行数据的观察和分析。
三、MATLAB数据处理软件MATLAB是一种广泛应用于科学计算和工程领域的高级数学软件。
在物理实验中，MATLAB可以用于数据处理、信号处理、图像处理等各个方面。
使用MATLAB进行数据处理的第一步是将实验数据导入到MATLAB的工作空间中。
导入数据后，可以通过MATLAB提供的各种函数和工具进行数据处理和分析，如求积分、傅里叶变换、小波变换等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1）
本实验采用图光杠杆法测得ΔL值（见图1）
(2)
将（2）代入式（1）得
（3）
1.1逐差法求
应用加重和减重的对称测量法测量，消除弹性滞后效应引起的系统误差。
多次测量 （4）
1.2用Origin 7.0软件求
把（3）上式改写为 （5）
用origin7.0软件作图处理数据，作出 ～ 的关系图。
Abstract:This paperdescribles that theyoung's modulus’s data is measured by thegradual deduction methodand theOrigin 7.0 software.The results showthat, the way ,usingthesoftwareto process theexperiment’sdata, havesimple, quicklyand intuitive features. And it can avoid the errors caused by man-made factors.Inthephysics experiment data processing, it also hassignificant application value.
6 结论
通过Origin7.0软件处理用拉伸法测金属丝的杨氏模量实验的数据，并与教材使用的逐差法处理实验数据进行比较，充分体现了用计算机软件处理实验数据简化了数据处理过程，提高了实验结果的准确度，也避免了人为因素所造成的误差，在物理实验数据处理过程中有显著的应用价值。
参考文献
[1]钱萍，申江主编 物理实验数据的计算机处理[M]北京：化学工业出版社，2007.2.
RSDNP
0.999930.014238<0.0001
A为截距以及截距的标准偏差SA；B为斜率以及斜率的标准偏差SB；R为相关系数；P为
Probability (that R is zero)R=0的置信概率；N为数据点的个数；SD为拟合变量Y的标准偏差SY。R的平方值代表拟合曲线的确定系数，用来检验拟合方程是否符合变量间的规律及拟合曲线的精度如何。 值越接近1，说明实测数据点越靠近拟合曲线,趋势线越可靠。从表5中可以得出 =0.99986。因此这直线拟合非常可靠。从表5中可以看出，拟合的直线方程为：Y=0.02+0.45643X
=( )cm
表2 金属丝直径测量数据
金属丝直径
未加载时 加满载时
± （mm）
1 2 1 2
(mm)
(mm)
(mm)
0.601 0.601 0.599 0.599
0.601 0.601 0.600 0.600
0.602 0.601 0.596 0.598
表3其它数据测量
螺旋测微器零点读数：0.000mm ;游标卡尺零点读数0.00cm
逐差法和Origin7.0软件在大学物理实验数据处理中的比较
摘要本文用逐差法和Origin7.0软件分别对拉伸法测金属丝杨氏模量的实验数据进行处理，结果表明,利用Origin7.0软件处理实验数据,具有简洁、快捷与直观等特点,避免了人为因素所造成的误差，在物理实验数据处理过程中有显著的应用价值。
关键词逐差法；Origin7.0软件；不确定度；பைடு நூலகம்据处理
4.4用Origin7.0处理实验数据结果（标准值： ）
拟合的直线方程为：Y=0.02+0.45643X
得 将有关数据代入得：
杨氏模量
百分差：
相对不确定度
5两种数据处理方法的结果比较
用逐差法和Origin7.0软件处理结果进行比较得到： ；
。逐差法产生较大的误差，是因为实验数据的取样个数对处理结果会产生极大影响。另外,从上面的数据处理的过程来看，用逐差法进行数据处理较繁杂并费时。同样的数据,用Origin 7.0软件进行数据能得到比较精确的实验结果,而且计算量不大,并且直观、快捷、高效。从这个角度来说,用Origin 7.0软件对拉伸法测金属丝杨氏模量的实验进行数据处理是不错的选择。
4.2调用绘图窗口绘制散点图
全选所有输入的实验数据后,点击菜单Plot的Scatter,能得到数据散点图Graph1，将鼠标放在Graph1上的坐标轴上双击,弹出一个对话框,在这个对话框中设置相应坐标轴参数(如图3)。
4.3执行Fit Linear(线性拟合)得到拟合直线
绘出散点图后，选择Analysis菜单中的Fit Linear如图4，即可对该图形进行线性拟合，Graph1中新增一条拟合出来的直线如图5。
3.000
4.000
5.000
6.000
7.000
（cm)
0.00
0.48
0.96
1.39
1.84
2.30
2.76
3.21
4.1数据输入Origin7.0的工作表
将表4中的数据分别在Origin7.0的Worksheet中输入,将表4 作为X轴， 作为Y轴得到
如图2所示的窗口。
图2实验数据输入图 图3 - 散点图
3.000
0.00 0.00 0.00
0.47 0.49 0.48
0.94 0.98 0.96
1.38 1.40 1.39
1.84
1.82
1.80
1.82
4
5
6
7
4.000
5.000
6.000
7.000
1.83 1.85 1.84
2.29 2.31 2.30
2.77 2.75 2.76
3.21 3.21 3.21
大学物理实验测得的数据，必须经过科学的分析和处理，才能揭示出各物理量之间的关系。我们把从获得原始数据起到得出结论为止的加工过程称为数据处理。目前大多数大学物理实验教材中对于实验数据的处理方法有：逐差法、列表法、作图法、最小二乘法。在实验教学中，一般将测量的实验数据选用某种处理方法，来计算实验结果及测量误差分析。不管用那种方法处理实验数据处理,既繁琐又枯燥，又占用学生大量的课外时间,成为教师和大学生头痛的事情。随着现代教育的发展,大量的实验数据和图像都可以通过计算机应用软件进行分析和处理。利用先进的计算机软件对大量的实验数据进行成批的数据处理能够提高学生的学习效率,使学生从繁琐的数据推导和计算中解脱出来。而美国Origin Lab公司推出的软件Origin 7.0在这一问题上能够提供迅速、准确的信息和参数以及图形。因此它在教学、科研、工程技术等领域具有广泛的应用。[1] [3]
图5线性拟合图
4.4结果在Results Log窗口中
同时弹出结果窗口Result s Log,显示拟合结果见表5。
表5数据拟合参数
Linear Regression for Data1_A:Y= A + B*X
ParameterValueError
A0.020.00918
B0.456430.0022
本文以该软件用于拉伸法测金属丝杨氏模量的实验数据处理过程为例,并与逐差法进行比较，使用Origin 7.0软件能完成实验数据的准确快速处理与分析。
1实验原理[2]
一根均匀的金属丝，长度为L，截面积为S，在受到沿长度方向的外力F的作用时发生形变，伸长ΔL。根据胡克定律，在弹性限度内，其应力F/S与应变ΔL/L成正比，即
key words：gradual deduction method;Origin 7.0 sof tware;undefined degree;process data
令 ； ； ；
可得到拟合直线方程 ，并从其斜率ｋ中求出E值。
2实验数据
本实验采用YNC-1杨氏模量测定仪，原始实验来自教学用的教师示范报告, 实验数据及部分数据处理见表1、表2及表3。
表1望远镜中直尺读数记录
i
Mi(kg)
直尺读数(cm)
(cm)
加砝码 减砝码 平均
0
1
2
3
0.000
1.000
2.000
金属丝伸长量
3.2计算金属丝直径 及不确定度计算：
3.3计算杨氏模量 及 的不确定度：
相对不确定度
3.4逐差法处理数据结果（标准值： ）
杨氏模量E=（2.02 0.13）
百分差：
相对不确定度
4用Origin 7.0处理实验数据[3]
从表1中可得到 与 之间关系数据表4
(kg)
0.000
1.000
2.000
[2]杨述武，赵立竹，沈国土主编， 普通物理实验1，力学、热学部分[M]北京：高等教育出版社，2007.12.
[3]刘芬,王爱芳,孙大鹏,杨田林Origin软件在大学物理实验数据处理中的应用[J].
实验科学与技术2010.01.
The Comparison of Gradual Deduction Method and Origin 7. 0In College Physics Experiment Data Processing
(150.2 0.5) cm
(68.20 0.05) cm
(76.60 0.02) mm
3逐差法处理实验数据
逐差法是数据处理中的一种常用方法。一般来说,使用逐差法进行数据处理要满足两个条件：(1)函数具有 的线性或有多项形式；(2)自变量是等间距变化。本实验通常采用逐差法来处理实验数据。
3.1用逐差法求 ， 的不确定度计算：