matlab图形坐标点显示精度设置方法

合集下载

matlab 小数精度

matlab 小数精度
在MATLAB中，可以使用format命令来控制小数的显示精度。

默认情况下，MATLAB会使用一般格式（short）显示小数，即保留四位有效数位。

以下是一些常用的格式选项：
1. short: 显示小数的一般格式，保留四位有效数位。

2. long: 显示小数的完整格式，保留15位有效数位。

3. shortE: 使用科学计数法显示小数，保留四位有效数位。

4. longE: 使用科学计数法显示小数，保留15位有效数位。

5. bank: 显示小数的银行格式，保留两位有效数位。

6. fixed: 显示小数的定点格式，保留两位小数。

你可以使用以下命令设置小数的显示精度：
format short % 设置为一般格式，保留四位有效数位
format long % 设置为完整格式，保留15位有效数位
format shortE % 设置为科学计数法格式，保留四位有效数位
format longE % 设置为科学计数法格式，保留15位有效数位
format bank % 设置为银行格式，保留两位有效数位
format fixed % 设置为定点格式，保留两位小数
例如，执行以下代码：
format long
a = 1/3
b = 1/7
将会显示如下输出：
a =
0.333333333333333
b =
0.142857142857143
可以看到，设置为完整格式后，小数的有效位数增加为15位。

matlab图形坐标点显示精度设置方法

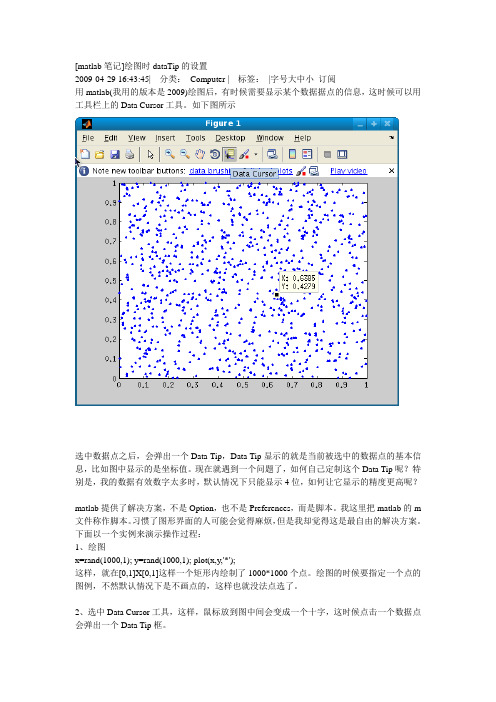
[matlab笔记]绘图时dataTip的设置2009-04-29 16:43:45| 分类：Computer | 标签：|字号大中小订阅用matlab(我用的版本是2009)绘图后，有时候需要显示某个数据据点的信息，这时候可以用工具栏上的Data Cursor工具。

如下图所示选中数据点之后，会弹出一个Data Tip，Data Tip显示的就是当前被选中的数据点的基本信息，比如图中显示的是坐标值。

现在就遇到一个问题了，如何自己定制这个Data Tip呢？特别是，我的数据有效数字太多时，默认情况下只能显示4位，如何让它显示的精度更高呢？matlab提供了解决方案，不是Option，也不是Preferences，而是脚本。

我这里把matlab的m 文件称作脚本。

习惯了图形界面的人可能会觉得麻烦，但是我却觉得这是最自由的解决方案。

下面以一个实例来演示操作过程：1、绘图x=rand(1000,1); y=rand(1000,1); plot(x,y,'*');这样，就在[0,1]X[0,1]这样一个矩形内绘制了1000*1000个点。

绘图的时候要指定一个点的图例，不然默认情况下是不画点的，这样也就没法点选了。

2、选中Data Cursor工具，这样，鼠标放到图中间会变成一个十字，这时候点击一个数据点会弹出一个Data Tip框。

可以看到显示只有4位有效数字。

3、右键菜单，里面有两项"Edit Text Update Function"和"Select Text Update Function"。

分别表示编辑配置文件，选择配置文件（配置文件指的还是m文件）。

在未编辑之前，当前图用的是默认配置文件。

编辑之后，需要保存到一个位置，新保存的文件只对当前图有效。

下次如果还想使用这个配置文件，就要用到"Select Text Update Function"了。

(整理)matlab实例教程-比较实用.

实验一特殊函数与图形一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景与实验目的著名的Riemann函数大家都很熟悉了，但是关于它的图像你是否清楚呢除了最上面那几点，其他都很难画吧你想不想看看下面那些“挤在一起”的点是怎样分布的呢还有几何中的马鞍面、单叶双曲面等是怎样由直线生成的，是不是也想目睹一下呢这些，都离不开绘图．实际上绘图一直是数学中的一种重要手段，借助图形，往往可以化繁为简，使抽象的对象得到明白直观的体现．比如函数的基本性质，一个图形常可以使之一目了然，非常有效．它虽不能代替严格的分析与证明，但在问题的研究过程中，可以帮助研究人员节约相当一部分精力．此外，它还可以使计算、证明、建模等的结果得到更明白易懂的表现，有时，这比科学论证更有说服力．同时，数学的教学与学习过程也离不开绘图．借助直观的图形，常可以使初学者更容易接受新知识．如数学分析中有不少函数，其解析式着实让人望而生畏，即使对其性质作了详尽的分析，还是感到难明就里；但如果能看到它的图形，再配合理论分析，则问题可以迎刃而解．又如在几何的学习中，会遇到大量的曲线与曲面，也离不开图形的配合．传统的手工作图，往往费力耗时，效果也不尽理想．计算机恰恰弥补了这个不足，使你可以方便地指定各种视角、比例、明暗，从各个角度进行观察．本实验通过对函数的图形表示和几个曲面（线）图形的介绍，一方面展示它们的特点，另一方面，也将就Matlab软件的作图功能作一个简单介绍．大家将会看到，Matlab 的作图功能非常强大．二、相关函数（命令）及简介1．平面作图函数：plot，其基本调用形式：plot(x,y,s)以x作为横坐标，y作为纵坐标．s是图形显示属性的设置选项．例如：x=-pi:pi/10:pi;y=sin(x);plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')图1在使用函数plot时，应当注意到当两个输入量同为向量时，向量x与y必须维数相同，而且必须同是行向量或者同是列向量．绘图时，可以制定标记的颜色和大小，也可以用图形属性制定其他线条特征，这些属性包括：linewidth 指定线条的粗细．markeredgecolor 指定标记的边缘色markerfacecolor 指定标记表面的颜色．markersize 指定标记的大小．若在一个坐标系中画几个函数，则plot的调用格式如下：plot(x1,y1,s1,x2,y2,s2,……)2．空间曲线作图函数：plot3，它与plot相比，只是多了一个维数而已．其调用格式如下：plot3(x,y,z,s)．例如：x=0:pi/30:20*pi;y=sin(x);z=cos(x);plot3(x,y,z)得到三维螺旋线：图23．空间曲面作图函数：（1）mesh函数．绘制彩色网格面图形．调用格式：mesh(z)，mesh(x,y,z)和mesh(x,y,z,c)．其中，mesh(x,y,z,c)画出颜色由c指定的三维网格图．若x、y均为向量，则length(x)=n，length(y)=m，[m,n]=size(z)．（2）surf在矩形区域内显示三维带阴影曲面图．调用格式与mesh类似．（3）ezmesh用符号函数作三维曲面网格图．调用格式：ezmesh(x,y,z)其中x = x(s,t), y = y(s,t),z = z(s,t)．画图区域默认为： -2*pi < s < 2*pi 且-2*pi < t < 2*pi.或者用格式：ezmesh(x,y,z,[smin,smax,tmin,tmax])（4）ezsurf用符号函数作三维曲面图．调用格式与ezmesh类似．（5）sphere画球体命令．4．meshgrid，调用格式：[x,y]=meshgrid(m,n)，这里的m，n为给定的向量，可以定义网格划分区域和划分方法．矩阵x和矩阵y是网格划分后的数据矩阵．5．图像的修饰与其他函数：（1）axis equal 控制各个坐标轴的分度，使其相等；（2）colormap设置绘图颜色．调用格式：colormap([r g b])其中r,g,b都是0-1之间的数．或者用格式：colormap(s)s颜色映像相应的颜色系颜色映像相应的颜色系autumn红黄色系hsv色调饱和色系gray线性灰色系hot黑红黄白色系cool青和洋红色系pink柔和色系（3（4）find找出符合条件的元素在数组中的位置．调用格式：y=find(条件)例如：输入：a=[4 5 78 121 4 665 225 4 1];b=find(a>7)输出： b =3 4 6 7三、实验内容数学分析中，特别是积分部分，我们接触了不少有趣的函数，由于其中有的不是一一对应的，用上面的方法无法画出它们的图像，这时就只能用参数了．此外还有些图形只能用参数来画，比如空间曲线，在计算机上不接受“两个曲面的交线”这种表示，所以也只能用参数来实现．用参数方式作图的关键在于找出合适的参数表示，尤其是不能有奇点，最好也不要用到开方．所以要找的参数最好是有几何意义的．当然这也不可一概而论，需要多积累经验．1．利用函数plot在一个坐标系中画以下几个函数图像，要求采用不同颜色、不同线形、不同的符号标记．函数为：．程序如下：t=0:pi/20:2*pi;x=sin(t);y=cos(t);z=sin(2*t);plot(t, x, '--k*', t, y, '-rs', t, z, ':bo')图像如下：图32．绘制类似田螺线的一条三维螺线(方程自己设计)．程序如下：t=0:.1:30;x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));z=*t;plot3(x,y,-z) %取–z 主要是为了画图看起来更清楚axis equal图像如下：图43．利用函数，绘制一个墨西哥帽子的图形．程序如下：[a,b]=meshgrid(-8:.5:8); %先生成一个网格c=sqrt(a.^2+b.^2)+eps;z=sin(c)./c;mesh(a,b,z)axis square图像如下：图5思考：这里的 eps 是什么其作用是什么4．利用surf绘制马鞍面图形（函数为：）．程序如下：[x,y]=meshgrid(-25:1:25,-25:1:25);z=x.^2/9-y.^2/4;surf(x,y,z)title('马鞍面')grid off图像如下：图65．分别用ezmesh和ezsurf各绘制一个圆环面，尝试将两个圆环面放在一个图形界面内，观察它们有什么不同之处．提示：圆环面的方程为：，而圆环面的参数方程为：程序参见附录1．图像如下：图76．绘制黎曼函数图形，加深对黎曼函数的理解．说明：黎曼函数的定义为程序参见附录2．图像如下：图8四、自己动手1．作出下图所示的三维图形：图9提示：图形为圆环面和球面的组合.2．作出下图所示的墨西哥帽子及其剪裁图形：图103．画出球面、椭球面、双叶双曲面、单叶双曲面．4．若要求田螺线的一条轴截面的曲边是一条抛物线：时．试重新设计田螺线的参数方程，并画出该田螺线．5．作出下图所示的马鞍面（颜色为灰色，并有一个标题：“马鞍面”）：图116．绘制图8所示的黎曼函数图形，要求分母的最大值的数值由键盘输入（提示：使用input语句）．回目录下一页实验二定积分的近似计算一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容1．矩形法2．梯形法3．抛物线法4. 直接应用Matlab命令计算结果四、自己动手一、问题背景与实验目的利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值，但它仅适用于被积函数的原函数能用初等函数表达出来的情形．如果这点办不到或者不容易办到，这就有必要考虑近似计算的方法．在定积分的很多应用问题中，被积函数甚至没有解析表达式，可能只是一条实验记录曲线，或者是一组离散的采样值，这时只能应用近似方法去计算相应的定积分．本实验将主要研究定积分的三种近似计算算法：矩形法、梯形法、抛物线法．对于定积分的近似数值计算，Matlab有专门函数可用．二、相关函数（命令）及简介1．sum(a)：求数组a的和．2．format long：长格式，即屏幕显示15位有效数字．（注：由于本实验要比较近似解法和精确求解间的误差，需要更高的精度）．3．double()：若输入的是字符则转化为相应的ASCII码；若输入的是整型数值则转化为相应的实型数值．4．quad()：抛物线法求数值积分．格式： quad(fun,a,b) ，注意此处的fun是函数，并且为数值形式的，所以使用*、/、^等运算时要在其前加上小数点，即 .*、./、.^等．例：Q = quad('1./(x.^3-2*x-5)',0,2);5．trapz()：梯形法求数值积分．格式：trapz(x,y)其中x为带有步长的积分区间；y为数值形式的运算（相当于上面介绍的函数fun）例：计算x=0:pi/100:pi;y=sin(x);trapz(x,y)6．dblquad()：抛物线法求二重数值积分．格式：dblquad(fun,xmin,xmax,ymin,ymax)，fun可以用inline定义，也可以通过某个函数文件的句柄传递．例1：Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)顺便计算下面的Q2，通过计算，比较Q1 与Q2结果（或加上手工验算），找出积分变量x、y的上下限的函数代入方法．Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi)例2：Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi)这时必须存在一个函数文件：function z = integrnd(x, y)z = y*sin(x);7．fprintf（文件地址，格式，写入的变量）：把数据写入指定文件．例：x = 0:.1:1;y = [x; exp(x)];fid = fopen('','w'); %打开文件fprintf(fid,'% %\n',y); %写入fclose(fid) %关闭文件8．syms 变量1 变量2 …：定义变量为符号．9．sym('表达式')：将表达式定义为符号．解释：Matlab中的符号运算事实上是借用了Maple的软件包，所以当在Matlab中要对符号进行运算时，必须先把要用到的变量定义为符号．10．int(f,v,a,b)：求f关于v积分，积分区间由a到b．11．subs(f，'x'，a)：将 a 的值赋给符号表达式 f 中的 x，并计算出值．若简单地使用subs(f)，则将f的所有符号变量用可能的数值代入，并计算出值．三、实验内容1．矩形法根据定积分的定义，每一个积分和都可以看作是定积分的一个近似值，即在几何意义上，这是用一系列小矩形面积近似小曲边梯形的结果，所以把这个近似计算方法称为矩形法．不过，只有当积分区间被分割得很细时，矩形法才有一定的精确度．针对不同的取法，计算结果会有不同，我们以为例（取），（1）左点法：对等分区间，在区间上取左端点，即取，，理论值，此时计算的相对误差（2）右点法：同（1）中划分区间，在区间上取右端点，即取，，理论值，此时计算的相对误差（3）中点法：同（1）中划分区间，在区间上取中点，即取，，理论值，此时计算的相对误差如果在分割的每个小区间上采用一次或二次多项式来近似代替被积函数，那么可以期望得到比矩形法效果好得多的近似计算公式．下面介绍的梯形法和抛物线法就是这一指导思想的产物．2．梯形法等分区间，相应函数值为（）．曲线上相应的点为（）将曲线的每一段弧用过点，的弦（线性函数）来代替，这使得每个上的曲边梯形成为真正的梯形，其面积为，．于是各个小梯形面积之和就是曲边梯形面积的近似值，，即，称此式为梯形公式．仍用的近似计算为例，取，，理论值，此时计算的相对误差很显然，这个误差要比简单的矩形左点法和右点法的计算误差小得多．3．抛物线法由梯形法求近似值，当为凹曲线时，它就偏小；当为凸曲线时，它就偏大．若每段改用与它凸性相接近的抛物线来近似时，就可减少上述缺点，这就是抛物线法．将积分区间作等分，分点依次为，，对应函数值为（），曲线上相应点为（）．现把区间上的曲线段用通过三点，，的抛物线来近似代替，然后求函数从到的定积分：由于，代入上式整理后得同样也有……将这个积分相加即得原来所要计算的定积分的近似值：，即这就是抛物线法公式，也称为辛卜生（Simpson）公式．仍用的近似计算为例，取，=，理论值，此时计算的相对误差4. 直接应用Matlab命令计算结果（1）数值计算方法1：int('1/(1+x^2)','x',0,1) (符号求积分)方法2：quad('1./(1+x.^2)',0,1) （抛物线法求数值积分）方法3：x=0::1;y=1./(1+x.^2);trapz(x,y) （梯形法求数值积分）（2）数值计算方法1：int(int('x+y^2','y',-1,1),'x',0,2) （符号求积分）方法2：dblquad(inline('x+y^2'),0,2,-1,1) （抛物线法二重数值积分）四、自己动手1．实现实验内容中的例子，即分别采用矩形法、梯形法、抛物线法计算，取，并比较三种方法的精确程度．2．分别用梯形法与抛物线法，计算，取．并尝试直接使用函数trapz()、quad()进行计算求解，比较结果的差异．3．试计算定积分．（注意：可以运用trapz()、quad()或附录程序求解吗为什么）4．将的近似计算结果与Matlab中各命令的计算结果相比较，试猜测Matlab中的数值积分命令最可能采用了哪一种近似计算方法并找出其他例子支持你的观点．5．通过整个实验内容及练习，你能否作出一些理论上的小结，即针对什么类型的函数（具有某种单调特性或凹凸特性），用某种近似计算方法所得结果更接近于实际值6．学习的程序设计方法，尝试用函数 sum 改写附录1和附录3的程序，避免for 循环．上一页回目录下一页实验三求代数方程的近似根（解）一、问题背景和实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景和实验目的求代数方程的根是最常见的数学问题之一（这里称为代数方程，主要是想和后面的微分方程区别开．为简明起见，在本实验的以下叙述中，把代数方程简称为方程），当是一次多项式时，称为线性方程，否则称之为非线性方程．当是非线性方程时，由于的多样性，尚无一般的解析解法可使用，但如果对任意的精度要求，能求出方程的近似根，则可以认为求根的计算问题已经解决，至少能满足实际要求．本实验介绍一些求方程实根的近似值的有效方法，要求在使用这些方法前先确定求根区间，或给出某根的近似值．在实际问题抽象出的数学模型中，可以根据物理背景确定；也可根据的草图等方法确定，还可用对分法、迭代法以及牛顿切线法大致确定根的分布情况．通过本实验希望你能：1. 了解对分法、迭代法、牛顿切线法求方程近似根的基本过程；2. 求代数方程（组）的解．二、相关函数（命令）及简介1．abs( )：求绝对值函数．2．diff(f)：对独立变量求微分，f 为符号表达式．diff(f, 'a')：对变量a求微分，f 为符号表达式．diff(f, 'a', n)：对变量 a 求 n 次微分，f 为符号表达式．例如：syms x tdiff(sin(x^2)*t^6, 't', 6)ans=720*sin(x^2)3．roots([c(1), c(2), …, c(n+1)])：求解多项式的所有根．例如：求解：．p = [1 -6 -72 -27];r = roots(p)r =4．solve('表达式')：求表达式的解．solve('2*sin(x)=1')ans =1/6*pi5．linsolve(A, b)：求线性方程组 A*x=b 的解．例如：A= [9 0; -1 8]; b=[1; 2];linsolve(A, b)ans=[ 1/9][19/72]6．fzero(fun, x0)：在x0附近求fun 的解．其中fun为一个定义的函数，用“@函数名”方式进行调用．例如：fzero(@sin, 3)ans=7．subs(f, 'x ', a)：将 a 的值赋给符号表达式 f 中的 x，并计算出值．例如：subs('x^2 ', 'x ', 2)ans = 4三、实验内容首先，我们介绍几种与求根有关的方法：1．对分法对分法思想：将区域不断对分，判断根在某个分段内，再对该段对分，依此类推，直到满足精度为止．对分法适用于求有根区间内的单实根或奇重实根．设在上连续，，即，或，．则根据连续函数的介值定理，在内至少存在一点，使．下面的方法可以求出该根：(1)令，计算；(2)若，则是的根，停止计算，输出结果．若，则令，，若，则令，；．……，有、以及相应的．(3) 若 (为预先给定的精度要求)，退出计算，输出结果；反之，返回(1)，重复(1)，(2)，(3)．以上方法可得到每次缩小一半的区间序列，在中含有方程的根．当区间长很小时，取其中点为根的近似值，显然有以上公式可用于估计对分次数．分析以上过程不难知道，对分法的收敛速度与公比为的等比级数相同．由于，可知大约对分10次，近似根的精度可提高三位小数．对分法的收敛速度较慢，它常用来试探实根的分布区间，或求根的近似值．2. 迭代法1)迭代法的基本思想：由方程构造一个等价方程从某个近似根出发，令，可得序列，这种方法称为迭代法．若收敛，即，只要连续，有即可知，的极限是的根，也就是的根．当然，若发散，迭代法就失败．以下给出迭代过程收敛的一些判别方法：定义：如果根的某个邻域中，使对任意的，迭代过程，收敛，则称迭代过程在附近局部收敛．定理1：设，在的某个邻域内连续，并且，，则对任何，由迭代决定的序列收敛于．定理2：条件同定理 1，则定理3：已知方程，且(1) 对任意的，有．(2) 对任意的，有，则对任意的，迭代生成的序列收敛于的根，且．以上给出的收敛定理中的条件要严格验证都较困难，实用时常用以下不严格的标准：当根区间较小，且对某一，明显小于1时，则迭代收敛(参见附录3)．2) 迭代法的加速：a) 松弛法：若与同是的近似值，则是两个近似值的加权平均，其中称为权重，现通过确定看能否得到加速．迭代方程是：其中，令，试确定：当时，有，即当，时，可望获得较好的加速效果，于是有松弛法：，松弛法的加速效果是明显的 (见附录4)，甚至不收敛的迭代函数经加速后也能获得收敛．b) Altken方法：松弛法要先计算，在使用中有时不方便，为此发展出以下的 Altken 公式：，是它的根，是其近似根．设，，因为，用差商近似代替，有，解出，得由此得出公式；；，这就是Altken 公式，它的加速效果也是十分明显的，它同样可使不收敛的迭代格式获得收敛(见附录5)．3. 牛顿(Newton)法（牛顿切线法）1) 牛顿法的基本思想：是非线性方程，一般较难解决，多采用线性化方法．记：是一次多项式，用作为的近似方程．的解为记为，一般地，记即为牛顿法公式.2) 牛顿法的收敛速度：对牛顿法，迭代形式为：注意分子上的，所以当时，，牛顿法至少是二阶收敛的，而在重根附近，牛顿法是线性收敛的．牛顿法的缺点是：(1)对重根收敛很慢；(2)对初值要求较严，要求相当接近真值．因此，常用其他方法确定初值，再用牛顿法提高精度．4. 求方程根(解)的其它方法(1) solve('x^3-3*x+1=0')(2) roots([1 0 -3 1])(3) fzero('x^3-3*x+1', -2)(4) fzero('x^3-3*x+1',(5) fzero('x^3-3*x+1',(6) linsolve([1, 2, 3; 4, 5, 6; 7, 8, 0], [1, 2, 3]')体会一下，(2)(5) 用了上述 1 3 中的哪一种方法以下是本实验中的几个具体的实验，详细的程序清单参见附录．具体实验1：对分法先作图观察方程：的实根的分布区间，再利用对分法在这些区间上分别求出根的近似值．输入以下命令，可得的图象：f='x^3-3*x+1';g='0';ezplot(f, [-4, 4]);hold on;ezplot(g, [-4, 4]); %目的是画出直线 y=0，即 x 轴grid on;axis([-4 4 -5 5]);hold off请填写下表：实根的分布区间该区间上根的近似值在某区间上求根的近似值的对分法程序参见附录1．具体实验2：普通迭代法采用迭代过程：求方程在附近的根，精确到第 4 位小数．构造等价方程：用迭代公式：，用 Matlab 编写的程序参见附录2．请利用上述程序填写下表：分析：将附录2第4行中的分别改为以及，问运行的结果是什么你能分析得到其中的原因吗看看下面的“具体实验3”是想向你表达一个什么意思．用 Matlab 编写的程序参见附录3．具体实验3：收敛/发散判断设方程的三个根近似地取，和，这些近似值可以用上面的对分法求得．迭代形式一：收敛 (很可能收敛，下同)不收敛 (很可能不收敛，下同)不收敛迭代形式二：收敛不收敛不收敛迭代形式三：不收敛收敛收敛具体实验4：迭代法的加速1——松弛迭代法，，迭代公式为程序参见附录4．具体实验5：迭代法的加速2——Altken迭代法迭代公式为：，，程序参见附录5．具体实验6：牛顿法用牛顿法计算方程在-2到2之间的三个根．提示：，迭代公式：程序参见附录6 （牛顿法程序）．具体实验7：其他方法求下列代数方程（组）的解：（1）命令：solve('x^5-x+1=0')（2）命令：[x, y]=solve('2*x+3*y=0', '4*x^2+3*y=1')(3) 求线性方程组的解，已知，命令：for i=1:5for j=1:5m(i, j)=i+j-1;endendm(5, 5)=0;b=[1:5]'linsolve(m, b)思考：若，或是类似的但阶数更大的稀疏方阵，则应如何得到四、自己动手1．对分法可以用来求偶重根附近的近似解吗为什么2．对照具体实验2、4、5，你可以得出什么结论3．选择适当的迭代过程，分别使用：（1）普通迭代法；（2）与之相应的松弛迭代法和 Altken 迭代法．求解方程在附近的根，精确到4位小数，请注意迭代次数的变化．4．分别用对分法、普通迭代法、松弛迭代法、Altken 迭代法、牛顿切法线等5种方法，求方程的正的近似根，．(建议取．时间许可的话，可进一步考虑的情况．)上一页回目录下一页。

matlab坐标轴刻度科学计数法

matlab坐标轴刻度科学计数法Matlab是一款功能强大的科学计算软件，广泛应用于工程、数学、统计等领域。

在Matlab中，坐标轴刻度的科学计数法是一种常见的方式，用于更好地表示大或小数值。

本文将介绍Matlab中如何使用科学计数法设置坐标轴刻度，并探讨其应用。

一、Matlab中的科学计数法简介科学计数法是一种用于表示非常大或非常小数值的方法，其形式为A×10^B，其中A是[1,10)之间的实数，B是整数。

科学计数法旨在提供一种更紧凑、准确的方式来表示极大或极小的数值。

在Matlab中，科学计数法常用于坐标轴刻度的标签上，以便更好地展示数据。

二、Matlab中坐标轴刻度科学计数法的设置步骤在Matlab中，设置坐标轴刻度为科学计数法需要以下步骤：1.创建一个示例图形：```matlabx = linspace(0, 1e15);y = sin(x);plot(x, y);```2.设置坐标轴刻度格式为科学计数法：```matlabax = gca; % 获取当前的坐标轴对象ax.XTickLabel = ax.XTick; % 将X轴刻度的标签设置为刻度值ax.YTickLabel = ax.YTick; % 将Y轴刻度的标签设置为刻度值```3.设置坐标轴刻度的字体大小：```matlabax.FontSize = 12; % 设置刻度标签的字体大小```4.设置坐标轴刻度的科学计数法格式：```matlabax.XAxis.Exponent = 4; % 设置X轴刻度的指数为4，表示10^4 ax.YAxis.Exponent = -6; % 设置Y轴刻度的指数为-6，表示10^-6 ```5.设置坐标轴刻度的相关属性（如颜色、粗细等）：```matlabax.XColor = 'blue'; % 设置X轴刻度的颜色为蓝色ax.LineWidth = 2; % 设置刻度线的粗细为2个像素```三、Matlab中坐标轴刻度科学计数法的应用案例科学计数法在Matlab中的应用非常广泛，特别是在处理大型数据集或非常小的数值时更为常见。

解决MATLAB中常见问题的技巧和方法

解决MATLAB中常见问题的技巧和方法MATLAB是一种高级编程语言和数值计算环境，被广泛应用于工程、科学和数学等领域。

然而，在使用MATLAB的过程中，可能会遇到一些常见的问题，这些问题可能会降低编程效率和准确性。

本文将介绍一些解决MATLAB中常见问题的技巧和方法，以帮助用户更好地应对挑战。

第一，解决MATLAB速度慢的问题。

在使用MATLAB时，我们可能会遇到速度慢的情况，这对于大规模数据处理和复杂计算任务来说是一个常见问题。

为了解决这个问题，我们可以采取以下措施：1. 合理利用向量和矩阵运算。

MATLAB在处理向量和矩阵运算时具有高效的内建函数，因此我们应该尽量避免使用循环，并使用矩阵和向量的索引和运算进行计算。

2. 使用适当的数据类型。

MATLAB提供了多种数据类型，如单精度浮点数（single）、双精度浮点数（double）和整数（integers）等。

根据需求选择适当的数据类型可以提高计算效率。

3. 避免频繁的内存分配和拷贝。

在循环中频繁地重新分配内存或复制数据会导致性能下降。

我们可以提前分配好足够的内存空间，并尽量重复利用已经分配的内存。

第二，解决MATLAB图形绘制问题。

图形绘制是MATLAB的一个重要功能，但在实际应用中可能会遇到一些问题，如图形显示不清晰、图例显示不正确等。

为了解决这些问题，我们可以尝试以下做法：1. 增加图形分辨率。

通过设置图形的分辨率，可以提高图形的清晰度。

可以使用“dpi”命令设置分辨率，如“dpi(300)”可以将分辨率设置为300dpi。

2. 调整坐标轴范围和刻度。

使用“xlim”和“ylim”命令可以调整坐标轴的范围，并使用“xticks”和“yticks”命令来设置刻度。

这样可以确保图形显示完整且刻度清晰。

3. 使用适当的图形对象。

MATLAB提供了多种图形对象，如线图（plot）、散点图（scatter）和条形图（bar）等。

根据需要选择适当的图形对象可以更好地呈现数据。

多边形中心点坐标matlab-概述说明以及解释

多边形中心点坐标matlab-概述说明以及解释1.引言1.1 概述在几何学中，多边形是一种封闭的平面图形，由若干条线段连接而成，每条线段称为多边形的边，相邻边之间的交点称为多边形的顶点。

多边形是图形学中的重要概念，在实际应用中也有着广泛的应用。

多边形的中心点是指多边形内部点到多边形各个顶点距离之和最小的点，也被称为多边形的几何中心。

计算多边形的中心点坐标对于图形学、计算机辅助设计等领域具有重要意义。

本文将介绍多边形中心点的定义以及计算多边形中心点坐标的原理，并介绍如何使用MATLAB编程计算多边形中心点的方法。

通过对多边形中心点的研究与计算，可以更好地理解多边形的性质与特点，为相关领域的研究和应用提供参考和帮助。

1.2 文章结构文章结构部分主要介绍了本文的组织方式和每个章节的内容概要，方便读者更好地理解整篇文章的逻辑结构和主要内容。

文章结构主要包括引言、正文和结论三个部分。

引言部分介绍了本文的背景和意义，正文部分详细介绍了多边形中心点的定义、计算原理和使用MATLAB计算方法，结论部分总结了全文的主要观点和成果，并展望了未来的应用前景。

通过明确的文章结构，读者可以更好地把握文章的主题和内容，提高阅读效率和理解度。

1.3 目的本文的目的是介绍如何使用MATLAB计算多边形的中心点坐标。

通过本文的阐述，读者可以了解到多边形中心点的定义，计算多边形中心点坐标的原理，并掌握使用MATLAB编程的方法来计算多边形中心点坐标。

希望本文能够帮助读者更深入地了解多边形几何特性，提高他们在MATLAB编程中应用数学知识的能力。

同时，本文也可以作为其他相关领域的研究人员和工程师在实际工作中处理多边形中心点的参考。

2.正文2.1 多边形中心点的定义多边形中心点是指一个多边形的几何中心，也可以称为重心或质心。

在平面几何中，对于任意一个简单多边形（即不自交、没有洞的多边形），其中心点是可以唯一确定的。

多边形的中心点具有以下特点：1. 多边形中心点是多边形的一个点，其到多边形各个顶点的距离之和最小。

MATLAB如何控制精度

MATLAB如何控制精度在MATLAB中，可以使用多种方法来控制数字的精度。

下面列举了一些常用的方法：1. 使用format函数：format函数可以用来控制在MATLAB中输出数字的格式。

可以使用以下代码设置输出小数点后的位数：```matlabformat short % 4位小数format long % 15位小数format bank % 2位小数，以逗号分隔的形式```2. 使用vpa函数：vpa（Variable Precision Arithmetic）函数可以用来控制数字的精度，并将结果以符号形式返回。

可以使用以下代码设置输出的有效数字位数：```matlabvpa(x, n) % x为要设置精度的变量，n为有效数字位数```3. 使用sym函数：sym函数用于创建符号对象，可以使用符号对象进行高精度计算。

符号对象可以使用以下代码创建：```matlabx = sym('x'); % 创建一个符号变量x```4.避免使用浮点数：浮点数在进行计算时会产生舍入误差，因此可以尽量使用整数进行计算，以减小精度误差的影响。

5. 使用vpa函数进行数值计算：在使用vpa函数时，可以直接对符号表达式进行计算，而不是先进行数值计算再使用vpa函数控制精度。

这样可以更精确地控制计算结果的精度。

6.使用MATLAB的符号工具箱：MATLAB的符号工具箱提供了丰富的符号计算功能，可以进行高精度的数值计算。

可以使用以下命令加载符号工具箱：```matlabsyms x y % 加载x和y作为符号变量```7. 使用MATLAB工具箱中的数值计算函数：MATLAB工具箱中的一些函数，如vpa、mp、mpadd等，可以用于执行高精度数值计算。

8. 使用Fixed-Point Toolbox：如果需要精确控制小数点后位数的精度，可以使用MATLAB的Fixed-Point Toolbox（固定小数点工具箱）来处理小数点位移和精度控制。

matlab函数手册

matlab函数手册信源函数randerr产生比特误差样本randint产生均匀分布的随机整数矩阵randrc根据给定的数字表产生随机矩阵wgn产生高斯白噪声信号分析函数biterr计算比特误差数和比特误差率eyediagram绘制眼图catterplot绘制分布图ymerr计算符号误差数和符号误差率信源编码dpcmdecoDPCM（差分脉冲编码调制）解码dpcmencoDPCM编码dpcmopt优化DPCM参数lloydLloyd法则优化量化器参数quantiz给出量化后的级和输出值误差控制编码bchpoly给出二进制BCH码的性能参数和产生多项式convenc产生卷积码cyclgen产生循环码的奇偶校验阵和生成矩阵cyclpoly产生循环码的生成多项式decode分组码解码器encode分组码编码器gen2par将奇偶校验阵和生成矩阵互相转换gfweight计算线性分组码的最小距离hammgen产生汉明码的奇偶校验阵和生成矩阵rdecof对Reed-Solomon编码的ASCII文件解码rencof用Reed-Solomon码对ASCII文件编码rpoly给出Reed-Solomon码的生成多项式yndtable产生伴随解码表vitdec用Viterbi法则解卷积码（误差控制编码的低级函数）bchdecoBCH解码器bchencoBCH编码器rdecoReed-Solomon解码器rdecode用指数形式进行Reed-Solomon解码rencoReed-Solomon编码器rencode用指数形式进行Reed-Solomon编码调制与解调ademod模拟通带解调器ademodce模拟基带解调器amod模拟通带调制器amodce模拟基带调制器apkcont绘制圆形的复合ASK-PSK星座图ddemod数字通带解调器ddemodce数字基带解调器demodmap解调后的模拟信号星座图反映射到数字信号dmod数字通带调制器dmodce数字基带调制器modmap把数字信号映射到模拟信号星座图（以供调制）qakdeco从方形的QASK星座图反映射到数字信号qakenco把数字信号映射到方形的QASK星座图专用滤波器hank2y把一个Hankel矩阵转换成一个线性系统模型hilbiir设计一个希尔伯特变换IIR滤波器rcoflt升余弦滤波器rcoine设计一个升余弦滤波器（专用滤波器的低级函数）rcofir设计一个升余弦FIR滤波器rcoiir设计一个升余弦IIR滤波器信道函数awgn添加高斯白噪声伽罗域计算gfadd伽罗域上的多项式加法gfconv伽罗域上的多项式乘法gfcoet 生成伽罗域的分圆陪集gfdeconv伽罗域上的多项式除法gfdiv伽罗域上的元素除法gffilter在质伽罗域上用多项式过滤数据gflineq在至伽罗域上求A 某=b的一个特解gfminpol求伽罗域上元素的最小多项式gfmul伽罗域上的元素乘法gfpluGF（2^m）上的元素加法gfpretty以通常方式显示多项式gfprimck检测多项式是否是基本多项式gfprimdf给出伽罗域的MATLAB默认的基本多项式gfprimfd给出伽罗域的基本多项式gfrank伽罗域上矩阵求秩gfrepcovGF（2）上多项式的表达方式转换gfroot质伽罗域上的多项式求根gfub伽罗域上的多项式减法gftrunc使多项式的表达最简化gftuple简化或转换伽罗域上元素的形式工具函数bi2de把二进制向量转换成十进制数de2bi把十进制数转换成二进制向量erf误差函数erfc余误差函数itrelli检测输入是否MATLAB的trelli结构（tructure）marcumq通用MarcumQ函数oct2dec八进制数转十进制数poly2trelli把卷积码多项式转换成MATLAB的trelli描述vec2mat把向量转换成矩阵———————————————————————————————————————————————Aaab绝对值、模、字符的ASCII码值aco反余弦acoh反双曲余弦acot反余切acoth反双曲余切acc反余割acch反双曲余割align启动图形对象几何位置排列工具all所有元素非零为真angle 相角an表达式计算结果的缺省变量名any所有元素非全零为真area面域图argname函数M文件宗量名aec反正割aech反双曲正割ain反正弦ainh反双曲正弦aignin向变量赋值atan反正切atan2四象限反正切atanh反双曲正切autumn红黄调秋色图阵a某e创建轴对象的低层指令a某i控制轴刻度和风格的高层指令Bbbar二维直方图bar3三维直方图bar3h三维水平直方图barh二维水平直方图bae2dec某进制转换为十进制bin2dec二进制转换为十进制blank创建空格串bone蓝色调黑白色图阵bo某框状坐标轴breakwhile或for环中断指令brighten亮度控制Cccapture（3版以前）捕获当前图形cart2pol直角坐标变为极或柱坐标cart2ph直角坐标变为球坐标cat串接成高维数组ca某i色标尺刻度cd指定当前目录cdedit启动用户菜单、控件回调函数设计工具cdf2rdf复数特征值对角阵转为实数块对角阵ceil向正无穷取整（使用方法：点这里）cell创建元胞数组cell2truct元胞数组转换为构架数组celldip显示元胞数组内容cellplot元胞数组内部结构图示char把数值、符号、内联类转换为字符对象chi2cdf分布累计概率函数chi2inv分布逆累计概率函数chi2pdf分布概率密度函数chi2rnd分布随机数发生器cholCholeky分解2clabel等位线标识cla清除当前轴cla获知对象类别或创建对象clc清除指令窗clear清除内存变量和函数clf清除图对象clock时钟colorcube三浓淡多彩交叉色图矩阵colordef设置色彩缺省值colormap色图colpace列空间的基cloe关闭指定窗口condeig计算特征值、特征向量同时给出条件数condet范-1条件数估计conj复数共轭contour等位线contourf填色等位线contour3三维等位线contourlice四维切片等位线图conv多项式乘、卷积cool青紫调冷色图copper古铜调色图co余弦coh双曲余弦cot余切coth双曲余切cpl某pair复数共轭成对排列cc余割cch双曲余割cumum元素累计和cumtrapz累计梯形积分cylinder创建圆柱Dddblquad二重数值积分deal分配宗量deblank删去串尾部的空格符dec2bae十进制转换为某进制dec2bin十进制转换为二进制dec2he某十进制转换为十六进制deconv多项式除、解卷delaunayDelaunay三角剖分del2离散Laplacian 差分demoMatlab演示det行列式diag矩阵对角元素提取、创建对角阵diaryMatlab指令窗文本内容记录diff数值差分、符号微分digit符号计算中设置符号数值的精度dir目录列表dip显示数组diplay显示对象内容的重载函数dlinmod离散系统的线性化模型dmperm矩阵Dulmage-Mendelohn分解do执行DOS指令并返回结果double把其他类型对象转换为双精度数值drawnow更新事件队列强迫Matlab刷新屏幕dolve符号计算解微分方程EeechoM文件被执行指令的显示edit启动M文件编辑器eig求特征值和特征向量eig求指定的几个特征值end控制流FOR等结构体的结尾元素下标ep浮点相对精度error显示出错信息并中断执行errortrap错误发生后程序是否继续执行的控制erf误差函数erfc误差补函数erfc某刻度误差补函数erfinv逆误差函数errorbar带误差限的曲线图etreeplot画消去树eval串演算指令（使用方法：点这里）evalin跨空间串演算指令e某it检查变量或函数是否已定义e某it退出Matlab环境e某p 指数函数e某pand符号计算中的展开操作e某pint指数积分函数3e某pm常用矩阵指数函数e某pm1Pade法求矩阵指数e某pm2Taylor 法求矩阵指数e某pm3特征值分解法求矩阵指数eye单位阵ezcontour画等位线的简捷指令fminunc拟牛顿法求多变量函数极小值点fminearch单纯形法求多变量函数极小值点fnder对样条函数求导fnint利用样条函数求积分fnval计算样条函数区间内任意一点的值ezcontourf画填色等位线的简捷指令ezgraph3画表面图的通用简捷指令ezmeh画网线图的简捷指令ezmehc画带等位线的网线图的简捷指令ezplot画二维曲线的简捷指令ezplot3画三维曲线的简捷指令ezpolar画极坐标图的简捷指令ezurf 画表面图的简捷指令ezurfc画带等位线的表面图的简捷指令Fffactor符号计算的因式分解feather羽毛图feedback反馈连接f执行由串指定的函数fft离散Fourier变换fft2二维离散Fourier变换fftn高维离散Fourier变换ffthift直流分量对中的谱fieldname构架域名figure创建图形窗fill3三维多边形填色图find寻找非零元素下标findobj寻找具有指定属性的对象图柄findtr寻找短串的起始字符下标findym机器确定内存中的符号变量finvere符号计算中求反函数fi 某向零取整例如（使用方法：点这里）flag红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud矩阵的上下翻转flipdim矩阵沿指定维翻转floor向负无穷取整（使用方法：点这里）flop浮点运算次数flowMatlab提供的演示数据fmin求单变量非线性函数极小值点（旧版）fminbnd求单变量非线性函数极小值点fmin单纯形法求多变量函数极小值点（旧版）fnplt绘制样条函数图形fopen打开外部文件for构成for环用format设置输出格式fourierFourier变换fplot返函绘图指令fprintf 设置显示格式fread从文件读二进制数据folve求多元函数的零点full把稀疏矩阵转换为非稀疏阵funm计算一般矩阵函数funtool函数计算器图形用户界面fzero求单变量非线性函数的零点Gggamma函数gammainc不完全函数gammaln函数的对数gca获得当前轴句柄gcbo获得正执行\回调\的对象句柄gcf获得当前图对象句柄gco获得当前对象句柄geomean几何平均值get获知对象属性getfield获知构架数组的域getframe获取影片的帧画面ginput从图形窗获取数据global定义全局变量gplot依图论法则画图gradient近似梯度gray黑白灰度grid画分格线griddata规则化数据和曲面拟合gte某t由鼠标放置注释文字guide启动图形用户界面交互设计工具Hhharmmean调和平均值help在线帮助helpwin交互式在线帮助4helpdek打开超文本形式用户指南he某2dec十六进制转换为十进制he某2num十六进制转换为浮点数hidden透视和消隐开关hilbHilbert 矩阵hit频数计算或频数直方图hitc端点定位频数直方图hitfit带正态拟合的频数直方图hold当前图上重画的切换开关horner分解成嵌套形式hot黑红黄白色图hv饱和色图Iiif-ele-eleif条件分支结构ifft离散Fourier反变换ifft2二维离散Fourier反变换ifftn高维离散Fourier反变换iffthift直流分量对中的谱的反操作ifourierFourier反变换i,j 缺省的\虚单元\变量ilaplaceLaplace反变换imag复数虚部image显示图象imagec显示亮度图象imfinfo获取图形文件信息imread从文件读取图象imwrite把imwrite把图象写成文件ind2ub单下标转变为多下标inf无穷大infoMathWork公司网点地址inline构造内联函数对象inmem列出内存中的函数名input提示用户输入inputname输入宗量名int符号积分int2tr把整数数组转换为串数组interp1一维插值interp2二维插值interp3三维插值interpnN维插值interpft利用FFT插值introMatlab自带的入门引导inv求矩阵逆invhilbHilbert矩阵的准确逆ipermute广义反转置ia检测是否给定类的对象ichar若是字符串则为真iequal若两数组相同则为真iempty若是空阵则为真ifinite若全部元素都有限则为真ifield若是构架域则为真iglobal 若是全局变量则为真ihandle若是图形句柄则为真ihold若当前图形处于保留状态则为真iieee若计算机执行IEEE规则则为真iinf若是无穷数据则为真iletter若是英文字母则为真ilogical若是逻辑数组则为真imember检查是否属于指定集inan若是非数则为真inumeric若是数值数组则为真iobject若是对象则为真iprime若是质数则为真ireal若是实数则为真ipace若是空格则为真ipare若是稀疏矩阵则为真itruct若是构架则为真itudent若是Matlab学生版则为真iztran符号计算Z反变换Jj,Kk jacobian符号计算中求Jacobian矩阵jet蓝头红尾饱和色jordan符号计算中获得Jordan标准型keyboard键盘获得控制权kronKronecker乘法规则产生的数组LllaplaceLaplace变换laterr显示最新出错信息latwarn显示最新警告信息leatq解非线性最小二乘问题（旧版）legend图形图例lighting照明模式line创建线对象line采用plot画线色linmod获连续系统的线性化模型linmod2获连续系统的线性化精良模型5。

matlab图形坐标点显示精度设置方法

v1.0 可编辑可修改[matlab笔记]绘图时dataTip的设置2009-04-29 16:43:45| 分类： Computer | 标签： |字号大中小订阅用matlab(我用的版本是2009)绘图后，有时候需要显示某个数据据点的信息，这时候可以用工具栏上的Data Cursor工具。

如下图所示选中数据点之后，会弹出一个Data Tip，Data Tip显示的就是当前被选中的数据点的基本信息，比如图中显示的是坐标值。

现在就遇到一个问题了，如何自己定制这个Data Tip呢特别是，我的数据有效数字太多时，默认情况下只能显示4位，如何让它显示的精度更高呢？matlab提供了解决方案，不是Option，也不是Preferences，而是脚本。

我这里把matlab 的m文件称作脚本。

习惯了图形界面的人可能会觉得麻烦，但是我却觉得这是最自由的解决方案。

下面以一个实例来演示操作过程：1、绘图x=rand(1000,1); y=rand(1000,1); plot(x,y,'*');这样，就在[0,1]X[0,1]这样一个矩形内绘制了1000*1000个点。

绘图的时候要指定一个点的图例，不然默认情况下是不画点的，这样也就没法点选了。

2、选中Data Cursor工具，这样，鼠标放到图中间会变成一个十字，这时候点击一个数据点会弹出一个Data Tip框。

可以看到显示只有4位有效数字。

3、右键菜单，里面有两项"Edit Text Update Function"和"Select Text Update Function"。

分别表示编辑配置文件，选择配置文件（配置文件指的还是m文件）。

在未编辑之前，当前图用的是默认配置文件。

编辑之后，需要保存到一个位置，新保存的文件只对当前图有效。

下次如果还想使用这个配置文件，就要用到"Select Text Update Function"了。

matlab图形坐标点显示精度设置方法

[matlab笔记]绘图时dataTip的设置2009-04-29 16:43:45| 分类： Computer | 标签： |字号大中小订阅用matlab(我用的版本是2009)绘图后，有时候需要显示某个数据据点的信息，这时候可以用工具栏上的Data Cursor工具。

如下图所示选中数据点之后，会弹出一个Data Tip，Data Tip显示的就是当前被选中的数据点的基本信息，比如图中显示的是坐标值。

我这里把matlab的m文件称作脚本。

习惯了图形界面的人可能会觉得麻烦，但是我却觉得这是最自由的解决方案。

下面以一个实例来演示操作过程：1、绘图x=rand(1000,1); y=rand(1000,1); plot(x,y,'*');这样，就在[0,1]X[0,1]这样一个矩形内绘制了1000*1000个点。

绘图的时候要指定一个点的图例，不然默认情况下是不画点的，这样也就没法点选了。

2、选中Data Cursor工具，这样，鼠标放到图中间会变成一个十字，这时候点击一个数据点会弹出一个Data Tip 框。

可以看到显示只有4位有效数字。

3、右键菜单，里面有两项"Edit Text Update Function"和"Select Text Update Function"。

分别表示编辑配置文件，选择配置文件（配置文件指的还是m文件）。

在未编辑之前，当前图用的是默认配置文件。

编辑之后，需要保存到一个位置，新保存的文件只对当前图有效。

下次如果还想使用这个配置文件，就要用到"Select Text Update Function"了。

matlab y轴三位小数-概述说明以及解释

matlab y轴三位小数-概述说明以及解释1.引言1.1 概述概述部分的内容：引言部分是一篇文章的开篇，是对文章整体内容进行简要介绍和概述的部分。

本文主要讨论如何在MATLAB中设置y轴显示为三位小数。

在数据分析和可视化过程中，合适的小数位数显示可以让数据更加直观、清晰。

本文将介绍MATLAB中设置y轴显示为三位小数的方法及应用场景。

首先，我们将会对文章的结构进行简要介绍。

文章由引言、正文和结论三个部分组成。

在引言部分，我们将概述本文的目的和结构，使读者了解整篇文章的框架。

正文部分将详细介绍在MATLAB中如何进行y轴显示设置，并提供一些相关的代码示例和应用场景。

最后，在结论部分，我们将对本文的主要内容进行总结，并展望未来可能的研究方向。

本文的目的在于帮助读者更好地理解如何在MATLAB中设置y轴显示为三位小数，并引导读者在实际应用中灵活运用这一功能。

这将有助于提升数据分析和可视化的效果，使得结果更加准确、可读性更高。

在接下来的章节中，我们将依次详细介绍MATLAB中设置y轴显示为三位小数的步骤，并通过实例来说明其实际应用。

通过学习本文，读者将能够顺利掌握这一技巧，并在自己的研究或工作中灵活应用。

文章结构部分主要介绍了本篇文章的组织结构和各个部分的内容概述。

在这篇文章中，我们将按照以下结构进行叙述：引言部分（Section 1）:在引言部分，我们将首先给出文章的概述，介绍所要讨论的问题背景和相关的研究现状。

接着，我们将详细介绍本篇文章的组织结构和各个部分的内容概述。

1.1 概述：在概述部分，我们将简要概述本篇文章所要解决的问题和目标，提出问题的重要性，并概述解决该问题所采用的方法和策略。

1.2 文章结构：在本部分，我们将详细介绍文章的组织结构和各个部分的内容概述。

我们将介绍文章的大纲和目录，给读者一个整体的了解和预期。

1.3 目的：在目的部分，我们将明确本篇文章的目的和研究意义，阐述为什么我们进行这项研究，以及我们希望通过这项研究解决的问题和取得的成果。

最全的MATLAB绘图命令

Matlab绘图强大的绘图功能是Matlab的特点之一，Matlab提供了一系列的绘图函数，用户不需要过多的考虑绘图的细节，只需要给出一些基本参数就能得到所需图形，这类函数称为高层绘图函数。

此外，Matlab还提供了直接对图形句柄进行操作的低层绘图操作。

这类操作将图形的每个图形元素（如坐标轴、曲线、文字等）看做一个独立的对象，系统给每个对象分配一个句柄，可以通过句柄对该图形元素进行操作，而不影响其他部分。

本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法，在此基础上，再介绍可以操作和控制各种图形对象的低层绘图操作。

一．二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。

可以采用不同的坐标系，如直角坐标、对数坐标、极坐标等。

二维图形的绘制是其他绘图操作的基础。

一．绘制二维曲线的基本函数在Matlab中，最基本而且应用最为广泛的绘图函数为plot，利用它可以在二维平面上绘制出不同的曲线。

1． plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图，要提供一组x坐标和对应的y 坐标，可以绘制分别以x和y为横、纵坐标的二维曲线。

plot函数的应用格式plot(x,y) 其中x,y为长度相同的向量，存储x坐标和y坐标。

例51 在[0 , 2pi]区间，绘制曲线程序如下：在命令窗口中输入以下命令>> x=0:pi/100:2*pi;>> y=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y)程序执行后，打开一个图形窗口，在其中绘制出如下曲线注意：指数函数和正弦函数之间要用点乘运算，因为二者是向量。

例52 绘制曲线这是以参数形式给出的曲线方程，只要给定参数向量，再分别求出x,y向量即可输出曲线：>> t=-pi:pi/100:pi;>> x=t.*cos(3*t);>> y=t.*sin(t).*sin(t);>> plot(x,y)程序执行后，打开一个图形窗口，在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量，这是最常见、最基本的用法。

matlab 标定工具箱解读

matlab 标定工具箱解读matlab标定工具箱是一个用于相机标定和立体视觉标定的强大工具。

相机标定是在摄像机成像过程中，将像素坐标和实际世界坐标之间的映射关系建立起来的过程。

立体视觉标定是将两个或多个相机的相对位置和内部参数进行估计的过程。

本文将详细介绍matlab标定工具箱的使用方法，包括相机标定、立体视觉标定以及标定结果的评估与应用。

一、相机标定1. 数据采集在进行相机标定之前，首先需要准备一组由摄像机拍摄的标定图像。

标定图像中应该包含已知尺寸的标定板，比如棋盘格。

在matlab标定工具箱中，先使用`cameraCalibrator`函数创建一个相机标定应用。

然后可以使用`cameraCalibrationDatastore`函数读取图像文件，或者直接使用采集视频流的方式获取图像数据。

2. 标定器创建与运行在标定工具箱中，可以通过以下几个步骤来创建相机标定器：a) 使用`cameraCalibrator`函数创建一个相机标定应用。

可以选择不同的标定模型和算法。

b) 通过`addImage`函数向标定应用中添加标定图像。

可以通过手动添加单张图像或者批量添加整个图像文件夹。

c) 使用`estimateCameraParameters`函数估计相机内部参数和畸变参数。

这个过程将根据已添加的标定图像计算出相机的内部参数矩阵、畸变系数和误差估计等。

3. 标定结果评估与保存一旦相机标定器创建完成，可以通过`showExtrinsics`函数来可视化标定后的结果。

使用该函数可以显示相机在不同位置和姿态下的外部参数估计结果。

同时，还可以通过`showReprojectionErrors`函数来显示重投影误差的直方图和统计信息。

重投影误差是指标定后的相机将标定板三维点投影回图像上的二维点与实际标定板上的二维点之间的差异。

二、立体视觉标定1. 数据采集进行立体视觉标定时，需要准备一组由两个摄像机同时拍摄的标定图像对。

matlab坐标轴刻度科学计数法

【文章标题：深度解析 MATLAB 坐标轴刻度科学计数法】一、MATLAB 坐标轴刻度科学计数法简介在 MATLAB 中，坐标轴的刻度科学计数法是指当数据非常大或者非常小的时候，坐标轴上的刻度会显示为科学计数法，以便更好地展示数据的大小范围和变化趋势。

科学计数法的形式为a × 10^n，其中 a 为系数，n 为次方数，通常是一个整数。

二、MATLAB 坐标轴刻度科学计数法的设置方法在 MATLAB 中，可以通过以下步骤来设置坐标轴的刻度科学计数法：1. 使用 set 函数设置坐标轴的刻度格式为科学计数法。

2. 调整刻度的系数和次方数的显示精度，以便更清晰地表达数据的大小。

关于第二步的调整，可以通过对坐标轴属性 TickLabelFormat 进行设置，以控制刻度的显示精度。

三、MATLAB 坐标轴刻度科学计数法的深入理解科学计数法的使用可以有效地展示出数据的规模和趋势，但是在实际应用中，我们需要根据具体的数据特点和展示要求来灵活调整科学计数法的设置。

比如对于工程领域的数据，可能需要显示更精确的小数位数；对于科学实验的数据，可能需要更直观地展示数据的数量级等。

设置坐标轴刻度科学计数法时，需要综合考虑数据的特点、观察者的需求以及图表的整体布局等因素。

四、对 MATLAB 坐标轴刻度科学计数法的个人理解与观点在我的理解中，MATLAB 坐标轴刻度科学计数法是一种非常重要的数据展示方式，在处理大数据和小数据时都能够有效地展现出数据的规模和变化趋势。

但是在实际使用中，需要根据具体情况做出合理的调整，以满足观察者对数据的全面理解。

在编写 MATLAB 图表时，我通常会根据数据的大小范围和分布特点来设置坐标轴刻度的科学计数法，并且会根据图表的整体风格和展示要求来调整刻度的显示精度和格式，以达到最佳的展示效果。

总结回顾：MATLAB 坐标轴刻度科学计数法是一种重要的数据展示方式，在实际使用中需要根据数据特点和展示需求进行灵活设置，以达到最佳的展示效果。

2024版matlab教程(完整版)

01 MATLABChapterMATLAB简介MATLAB是一种高级编程语言和环境，主要用于数值计算、数据分析、信号处理、图像处理等多种应用领域。

MATLAB具有简单易学、高效灵活、可视化强等特点，被广泛应用于科研、工程、教育等领域。

MATLAB提供了丰富的函数库和工具箱，方便用户进行各种复杂的数学计算和数据分析。

MATLAB安装与启动MATLAB界面介绍工作空间用于显示当前定义的所有变量及其值。

命令历史记录了用户输入过的命令及其输出结果。

基本运算与数据类型02矩阵运算与数组操作Chapter01020304使用`[]`或`zeros`、`ones`等函数创建矩阵创建矩阵使用`size`函数获取矩阵大小矩阵大小通过下标访问矩阵元素，如`A(i,j)`矩阵元素访问使用`disp`或`fprintf`函数显示矩阵信息矩阵信息矩阵创建与基本操作对应元素相加，如`C = A+ B`加法运算矩阵运算对应元素相减，如`C = A-B`减法运算数与矩阵相乘，如`B = k *A`数乘运算使用单引号`'`进行转置，如`B = A'`转置运算满足乘法条件的矩阵相乘，如`C = A * B`矩阵乘法使用`inv`函数求逆矩阵，如`B = inv(A)`逆矩阵数组创建数组大小数组元素访问数组操作数组操作01020304线性方程组求解数据处理与分析特征值与特征向量图像处理矩阵与数组应用实例03数值计算与数据分析Chapter数值计算基础MATLAB基本运算数值类型与精度变量与表达式函数与脚本数据分析方法数据导入与预处理学习如何导入各种格式的数据（如Excel、CSV、TXT等），并进行数据清洗、转换等预处理操作。

数据统计描述掌握MATLAB中数据统计描述的方法，如计算均值、中位数、标准差等统计量，以及绘制直方图、箱线图等统计图表。

数据相关性分析学习如何在MATLAB中进行数据相关性分析，如计算相关系数、绘制散点图等。

MATLAB常用命令

MATLAB命令大全管理命令和函数help 在线帮助文件doc 装入超文本说明what M、MAT、MEX文件的目录列表type 列出M文件lookfor 通过help条目搜索关键字which 定位函数和文件Demo 运行演示程序Path 控制MATLAB的搜索路径管理变量和工作空间Who 列出当前变量Whos 列出当前变量（长表）Load 从磁盘文件中恢复变量Save 保存工作空间变量Clear 从内存中清除变量和函数Pack 整理工作空间内存Size 矩阵的尺寸Length 向量的长度disp 显示矩阵或与文件和*作系统有关的命令cd 改变当前工作目录Dir 目录列表Delete 删除文件Getenv 获取环境变量值! 执行DOS*作系统命令Unix 执行UNIX*作系统命令并返回结果Diary 保存MA TLAB任务控制命令窗口Cedit 设置命令行编辑Clc 清命令窗口Home 光标置左上角Format 设置输出格式Echo 底稿文件内使用的回显命令more 在命令窗口中控制分页输出启动和退出MA TLABQuit 退出MATLABStartup 引用MATLAB时所执行的M文件Matlabrc 主启动M文件一般信息Info MATLAB系统信息及Mathworks公司信息Subscribe 成为MATLAB的订购用户hostid MA TLAB主服务程序的识别代号Whatsnew 在说明书中未包含的新信息Ver 版本信息*作符和特殊字符+ 加.* 数组乘法^ 矩阵幂.^ 数组幂\ 左除或反斜杠/ 右除或斜杠./ 数组除Kron Kronecker张量积: 冒号( ) 圆括号[ ] 方括号. 小数点.. 父目录… 继续, 逗号; 分号% 注释! 感叹号… 转置或引用= 赋值= = 相等< > 关系*作符& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或逻辑函数Exist 检查变量或函数是否存在Any 向量的任一元为真，则其值为真All 向量的所有元为真，则其值为真Find 找出非零元素的索引号三角函数Sin 正弦Sinh 双曲正弦Asin 反正弦Asinh 反双曲正弦Cos 余弦Cosh 双曲余弦Acos 反余弦Acosh 反双曲余弦Tan 正切Tanh 双曲正切Atan 反正切Atan2 四象限反正切Atanh 反双曲正切Sec 正割Sech 双曲正割Asech 反双曲正割Csc 余割Acsch 反双曲余割Cot 余切Coth 双曲余切Acot 反余切Acoth 反双曲余切指数函数Exp 指数Log 自然对数Log10 常用对数Sqrt 平方根复数函数Abs 绝对值Argle 相角Conj 复共轭Image 复数虚部Real 复数实部数值函数Fix 朝零方向取整Floor 朝负无穷大方向取整Ceil 朝正无穷大方向取整Round 朝最近的整数取整Rem 除后取余Sign 符号函数基本矩阵Zeros 零矩阵Ones 全“1”矩阵Eye 单位矩阵Rand 均匀分布的随机数矩阵Randn 正态分布的随机数矩阵Logspace 对数间隔的向量Meshgrid 三维图形的X和Y数组: 规则间隔的向量特殊变量和常数Ans 当前的答案Eps 相对浮点精度Realmax 最大浮点数Realmin 最小浮点数Pi 圆周率I,j 虚数单位Inf 无穷大Nan 非数值Flops 浮点运算次数Nargin 函数输入变量数Nargout 函数输出变量数Computer 计算机类型Isieee 当计算机采用IEEE算术标准时，其值为真Why 简明的答案Version MA TLAB版本号Date 日历Etime 计时函数Tic 秒表开始计时Toc 计时函数Cputime CPU时间（以秒为单位）矩阵*作Diag 建立和提取对角阵Fliplr 矩阵作左右翻转Flipud 矩阵作上下翻转Reshape 改变矩阵大小Rot90 矩阵旋转90度Tril 提取矩阵的下三角部分Triu 提取矩阵的上三角部分: 矩阵的索引号，重新排列矩阵Compan 友矩阵Hadamard Hadamard矩阵Hankel Hankel矩阵Hilb Hilbert矩阵Invhilb 逆Hilbert矩阵Kron Kronecker张量积Magic 魔方矩阵Toeplitz Toeplitz矩阵Vander V andermonde矩阵矩阵分析Cond 计算矩阵条件数Norm 计算矩阵或向量范数Rcond Linpack 逆条件值估计Rank 计算矩阵秩Det 计算矩阵行列式值Trace 计算矩阵的迹Null 零矩阵Orth 正交化线性方程\和/ 线性方程求解Chol Cholesky分解Lu 高斯消元法求系数阵Inv 矩阵求逆Qr 正交三角矩阵分解（QR分解）Pinv 矩阵伪逆特征值和奇异值Eig 求特征值和特征向量Poly 求特征多项式Hess Hessberg形式Qz 广义特征值Cdf2rdf 变复对角矩阵为实分块对角形式Schur Schur分解Balance 矩阵均衡处理以提高特征值精度Svde 奇异值分解Expm 矩阵指数Expm1 实现expm的M文件Expm2 通过泰勒级数求矩阵指数Expm3 通过特征值和特征向量求矩阵指数Logm 矩阵对数Sqrtm 矩阵开平方根Funm 一般矩阵的计算泛函——非线性数值方法Ode23 低阶法求解常微分方程Ode23p 低阶法求解常微分方程并绘出结果图形Ode45 高阶法求解常微分方程Quad 低阶法计算数值积分Quad8 高阶法计算数值积分Fmin 单变量函数的极小变化Fmins 多变量函数的极小化Fzero 找出单变量函数的零点Fplot 函数绘图多项式函数Roots 求多项式根Poly 构造具有指定根的多项式Polyvalm 带矩阵变量的多项式计算Residue 部分分式展开（留数计算）Polyfit 数据的多项式拟合Polyder 微分多项式Conv 多项式乘法Deconv 多项式除法建立和控制图形窗口Figure 建立图形Gcf 获取当前图形的句柄Clf 清除当前图形Close 关闭图形建立和控制坐标系Subplot 在标定位置上建立坐标系Axes 在任意位置上建立坐标系Gca 获取当前坐标系的句柄Cla 清除当前坐标系Axis 控制坐标系的刻度和形式Caxis 控制伪彩色坐标刻度Hold 保持当前图形句柄图形对象Figure 建立图形窗口Axes 建立坐标系Line 建立曲线Text 建立文本串Patch 建立图形填充块Surface 建立曲面Image 建立图像Uicontrol 建立用户界面控制Uimen 建立用户界面菜单[1] [2] [3] 下一页Matlab主要函数使用方法ndims(A)用ndims命令常看矩阵的维数1. matlab中mod的用法简单的说mod(a,b)就是求的是a除以b的余数。

[matlab笔记]绘图时dataTip的设置

2009-04-29 16:43:45| 分类：Computer|字号订阅用matlab(我用的版本是2009)绘图后，有时候需要显示某个数据据点的信息，这时候可以用工具栏上的Data Cursor工具。

如下图所示选中数据点之后，会弹出一个Data Tip，Data Tip显示的就是当前被选中的数据点的基本信息，比如图中显示的是坐标值。

我这里把matlab 的m文件称作脚本。

习惯了图形界面的人可能会觉得麻烦，但是我却觉得这是最自由的解决方案。

下面以一个实例来演示操作过程：1、绘图x=rand(1000,1); y=rand(1000,1); plot(x,y,'*');这样，就在[0,1]X[0,1]这样一个矩形内绘制了1000*1000个点。

绘图的时候要指定一个点的图例，不然默认情况下是不画点的，这样也就没法点选了。

2、选中Data Cursor工具，这样，鼠标放到图中间会变成一个十字，这时候点击一个数据点会弹出一个Data Tip框。

可以看到显示只有4位有效数字。

3、右键菜单，里面有两项"Edit Text Update Function"和"Select Text Update Function"。

分别表示编辑配置文件，选择配置文件（配置文件指的还是m文件）。

在未编辑之前，当前图用的是默认配置文件。

编辑之后，需要保存到一个位置，新保存的文件只对当前图有效。

下次如果还想使用这个配置文件，就要用到"Select Text Update Function"了。

4、点选"Edit Text Update Function"，出现一个m文件编辑器。

matlab坐标轴刻度间距

matlab坐标轴刻度间距MATLAB坐标轴刻度间距是MATLAB中一项重要的功能，它可以帮助用户更好地分析和控制图形。

坐标轴刻度间距是指将图形中的坐标轴分割成多个等分。

MATLAB中可以实现任意分割精度，这使得MATLAB 坐标轴刻度间距变得更加灵活，便于用户更好地理解和操控图形。

MATLAB坐标轴刻度间距的设置分为三步：第一步是先分析图形并确定这个刻度间距的精确性，第二步是设置图形的比例及图形的范围，第三步是选择一种合适的刻度间距。

第一步：分析图形并确定这个刻度间距的精确性。

当分析的图形有多个不同的维度时，需要对每一个维度的刻度间距进行分析，以便确定出一个适合于所有维度的刻度间距。

其中，最常用的分析方法是使用图形分析函数，它可以从图形中获得精确的坐标轴刻度间距值。

第二步：设置图形的比例及图形的范围。

比例用来控制每一条坐标轴的长度及高度，而图形的范围则是决定每一个不同维度的坐标轴的长度和宽度。

设置比例和范围可以使画出来的图形更加美观和精确，这是必要的步骤。

第三步：选择一种合适的刻度间距。

在MATLAB中，可以选择自动选择坐标轴刻度间距，也可以手动设置坐标轴刻度间距。

使用自动选择坐标轴刻度间距功能可以根据设定的图形视图范围自动计算出最佳的坐标轴刻度间距，这样可以大大减轻用户的工作量。

而手动设置坐标轴刻度间距则需要用户自行调整，以便达到最佳的刻度间距。

总之，MATLAB坐标轴刻度间距的设置是一个非常重要的工作，它能够使图形更加清晰、美观，并使用户更好地分析和控制图形。

MATLAB提供了一系列方便用户操作的工具，使用者可以根据需要自行调整坐标轴刻度间距，以使图形更加准确和美观。

Matlab／Sinulink仿真性能与计算精度设置方法的研究

ｓｅｄｏａｌｂｃｎｌｒｅｙｅｈｎｅｔｅｉｌｍｅｔｔｎｏｒｇａｐｅｆＭｔａａｇｌｎａｃｈｍｐｅｎａｉｆｐｏｒｍｍｉｇａｄｓｍｕａｉｎｓｅｄａｄｏｅａｉｇｅｆｃｅｃ．ａｏｎｎｉｌｔｐｅｎｐｒｔｆｉｉｎｙｏｎ
ｓｔｉｔｓａｒｏｒｍｅｈｏｏａｃｌｒｔｈｅＳｉｕｉｉｕｌｔｏｎ，ｅｅｔｎｇｓｅｐｎｄｅｒｔｄｔｃｅｅａｅｔｍｌｎｋｓｍａｉｒｄｕｃｎｈｅｌｎｇｈｏｆｓｅｓ，ｈｏｉｇｅｓａｅｓｕ— ｉｇｔｅｔｔｐｃｏｓｎｒａｏｎｂｌｏｌ
ｔｎａｄｅｔｂｉｈｎｍａｌｒｒｌｔｖｒｏ，ｈｉｕｉｋｐｅｉｉｎｗａｃｅｓｄｔｖｉｈｓｆｃｒｕａｉｎａｏｓｂｅｉ，ｎｓａｌｉｇａｓｌｅａｉｅｅｒｒｔｅＳｍｌｒｃｓｏｓｉｒａｅｏａｏｄｔｅｕｅｏｉｃｌｔｏｓｐｓｉｌ，ｏｓｅｎｎ
ｐｒ— ｔｒｉｅｌｒａｒｘｅｄｅｅｍｎａｇｅｍｔｉｐｅｅｅｉｇｎｐｒｏｒｔｃｎｓｄｅｔｉｒｎｆｎｃｉｅｈｏａｓ．Ａｃｅｅａｉｇｈｅａｃｋｅｐｎａｄｉｏｏｉｒｈｅｎｈｅｅｔｕｔｏｎｍｔｄｎｄｏｏｎｃｌｒｔｎｔ
（ｅｎｎＭｅｈｎｃｌｎｅｔｉａｃｔｎｌＣｏｌｇ，ｎｈｎ５１１Ｃｈｎ）Ｈ ’ ａｃａｉａｄＥｌｃｒｃｌＶｏａｉａｌｅＸｉｚｅｇ４１９，ｉａａｏｅＡｂｔａｔＭａｌｂａｄＳｍｕｉｋｓｍｕａｉｎｐｒｏｍａｃｎａｃｌｔｎｐｅｉｉｎａｅｏｔｎｉｆｕｎｅｙｍａｙｆｃｏｓｓｒｃ：ｔｎｉｌｉｌｔｅｆｒｎｅａｄｃｌｕａｉｒｃｓｏｒｆｅｌｅｃｄｂｎａｔｒ．Ｂｙａｎｏｏｎ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[matlab笔记]绘图时dataTip的设置
2009-04-29 16:43:45| 分类： Computer | 标签： |字号大中小订阅
用matlab(我用的版本是2009)绘图后，有时候需要显示某个数据据点的信息，这时候可以用工具栏上的Data Cursor工具。

如下图所示
选中数据点之后，会弹出一个Data Tip，Data Tip显示的就是当前被选中的数据点的基本信息，比如图中显示的是坐标值。

现在就遇到一个问题了，如何自己定制这个Data Tip呢？特别是，我的数据有效数字太多时，默认情况下只能显示4位，如何让它显示的精度更高呢？
matlab提供了解决方案，不是Option，也不是Preferences，而是脚本。

我这里把matlab 的m文件称作脚本。

习惯了图形界面的人可能会觉得麻烦，但是我却觉得这是最自由的解决方案。

下面以一个实例来演示操作过程：
1、绘图
x=rand(1000,1); y=rand(1000,1); plot(x,y,'*');
这样，就在[0,1]X[0,1]这样一个矩形内绘制了1000*1000个点。

绘图的时候要指定一个点的图例，不然默认情况下是不画点的，这样也就没法点选了。

2、选中Data Cursor工具，这样，鼠标放到图中间会变成一个十字，这时候点击一个数据
点会弹出一个Data Tip框。

可以看到显示只有4位有效数字。

3、右键菜单，里面有两项"Edit Text Update Function"和"Select Text Update Function"。

分别表示编辑配置文件，选择配置文件（配置文件指的还是m文件）。

在未编辑之前，当前图用的是默认配置文件。

编辑之后，需要保存到一个位置，新保存的文件只对当前图有效。

下次如果还想使用这个配置文件，就要用到"Select Text Update Function"了。

4、点选"Edit Text Update Function"，出现一个m文件编辑器。

内容如下：
function output_txt = myfunction(obj,event_obj)
% Display the position of the data cursor
% obj Currently not used (empty)
% event_obj Handle to event object
% output_txt Data cursor text string (string or cell array of strings).
pos = get(event_obj,'Position');
output_txt = {['X: ',num2str(pos(1),4)],...
['Y: ',num2str(pos(2),4)]};
% If there is a Z-coordinate in the position, display it as well
if length(pos) > 2
output_txt{end+1} = ['Z: ',num2str(pos(3),4)];
end
眼尖的人应该一眼就看到了几个"4"，没错，正是它们限制了显示精度，改成更大的数就行了。

这几行代码的意思应该很明显了。

第一行是函数原型，以%开头的是注释，pos是变量，output_txt是返回值。

二维图分两行显示X,Y坐标，如果是三维，则还会显示Z坐标。

5、保存为m文件。

注意保存的文件一定要带有.m后缀，不然matlab识别不了，从而Data Tip 会显示为Error in custom datatip string function。

这个错误说函数返回错误，实际上就是不能识别。

6、保存完了，就算完事了。

以后可以直接改那个已经保存的文件，然后绘图后，选择这个文件。

再次提醒，每次绘图时使用的都是默认配置，想要特定的效果，要么重新写，要么选择指定配置文件。

7、关于这个配置文件本身，还有许多值得探讨的地方。

我这个例子只能更改显示精度，实际上，它还有许多可以自由定制的地方。

比如，可以显示点的序号，即第几个点。

在配置文件末尾加上一句：
output_txt{end+1} = ['index:', num2str(event_obj.DataIndex)];
（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

可复制、编制，期待你的好评与关注）。