电容放电和充电时间计算
放电时间计算公式
放电时间计算公式1. 基本公式。
- 对于电容通过电阻放电的电路，其放电时间的计算公式为t =RC×ln(V_0)/(V)，其中t是放电时间，R是放电电阻（单位为欧姆Ω），C是电容（单位为法拉F），V_0是电容初始电压，V是放电过程中某一时刻的电压。
- 当电容放电到初始电压的36.8%（即V = 0.368V_0）时，此时的时间t=τ = RC，这里τ被称为时间常数。
2. 推导过程（简单理解）- 根据电容的电压 - 电流关系i = C(dv)/(dt)，在放电电路中，根据欧姆定律i=(v)/(R)（这里v是电容两端电压）。
- 所以(v)/(R)=-C(dv)/(dt)（负号表示放电，电流方向与充电时相反）。
- 对这个微分方程进行求解，分离变量得到(dv)/(v)=-(1)/(RC)dt。
- 两边积分∫_V_0^V(dv)/(v)=-(1)/(RC)∫_0^tdt，解得ln(V)/(V_0)=-(t)/(RC)，即t = RC×ln(V_0)/(V)。
1. 公式。
- 对于电池以恒定电流I放电，电池容量为Q（单位为安时Ah），则放电时间t=(Q)/(I)。
- 例如，一个电池容量为10Ah，以2A的恒定电流放电，那么放电时间t=(10)/(2) = 5h。
2. 注意事项。
- 实际电池放电过程中，由于电池内阻的存在，随着放电的进行，电池电压会逐渐降低，当电压降低到一定程度（例如，对于铅酸蓄电池，电压降低到终止电压时），就不能再继续放电了。
而且电池的容量也会受到放电率（电流大小）、温度等因素的影响，所以这个公式是在理想恒流放电且不考虑电池老化等其他因素的情况下的简单计算。
RC电路充放电时间的计算(含计算公式)
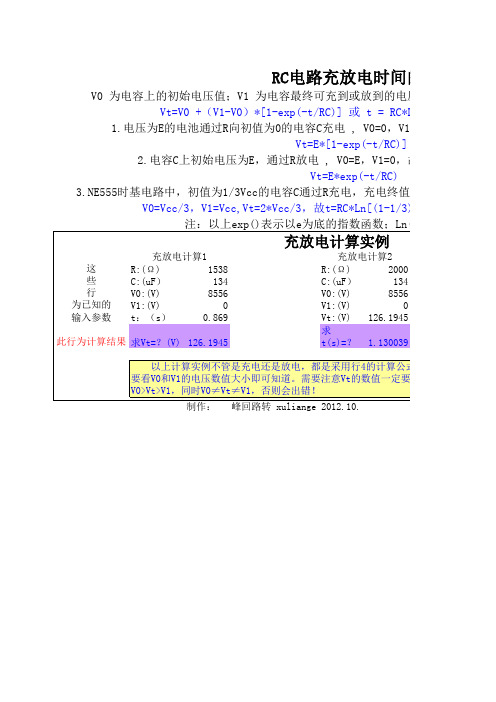
V0 为电容上的初始电压值；V1 为电容最终可充到或放到的电压值；Vt 为t时刻 Vt=V0 +（V1-V0）*[1-exp(-t/RC)] 或 t = RC*Ln[(V1 - V0)/(V1 1.电压为E的电池通过R向初值为0的电容C充电 , V0=0，V1=E，故充到t时刻 Vt=E*[1-exp(-t/RC)] 2.电容C上初始电压为E，通过R放电 , V0=E，V1=0，故放到t时刻电容上 Vt=E*exp(-t/RC) 3.NE555时基电路中，初值为1/3Vcc的电容C通过R充电，充电终值为Vcc，问充到2/ V0=Vcc/3，V1=Vcc,Vt=2*Vcc/3，故t=RC*Ln[(1-1/3)/(1-2/3)]=RC*Ln 注：以上exp()表示以e为底的指数函数；Ln()是e为底的对数函
充放电计算实例
这 些 行 为已知的 输入参数 此行为计算结果 充放电计算1 R:(Ω ) 1538 C:(uF） 134 V0:(V) 8556 V1:(V) 0 t：（s） 0.869 求Vt=？(V) 126.1945 充放电计算2 R:(Ω ) 2000 C:(uF） 134 V0:(V) 8556 V1:(V) 0 Vt:(V) 126.1945 求t(s)=？ 1.130039
以上计算实例不管是充电还是放电，都是采用行4的计算公式，至于是计算的是 要看V0和V1的电压数值大小即可知道。需要注意Vt的数值一定要介于V0和V1之间方可 V0>Vt>V1，同时V0≠Vt≠V1，否则会出错！ 制作： 峰回路转 xuliange 2012.10.
电时间的计算
放到的电压值；Vt 为t时刻电容上的电压值。则: t = RC*Ln[(V1 - V0)/(V1 - Vt)] V0=0，V1=E，故充到t时刻电容上的电压为： (-t/RC)] ，V1=0，故放到t时刻电容上的电压为： -t/RC) 充电终值为Vcc，问充到2/3Vcc需要的时间是多少？ n[(1-1/3)/(1-2/3)]=RC*Ln2 =0.693RC 函数；Ln()是e为底的对数函数
RC电路充放电时间的计算
RC电路充放电时间的计算RC电路是由电阻(R)和电容(C)组成的电路，充放电时间是指电容器上电压从0V充电到一定电压或从一定电压放电到0V所花费的时间。
1.充电时间的计算：在RC电路中，电压(V)会通过电阻和电容器进行充电。
充电时，电容器的电压会随时间逐渐上升，直到趋于稳定。
在一个理想的RC电路中，充电时间可以通过以下公式计算：t = R * C * ln(V_batt / (V_batt - V_c))其中，t是充电时间，R是电阻的阻值，C是电容器的电容量，V_batt是电源电压，V_c是电容器上的电压。
2.放电时间的计算：在RC电路中，电容器中存储的电能会通过电阻耗散，电容器的电压会随时间逐渐下降，直到趋于0V。
在一个理想的RC电路中，放电时间可以通过以下公式计算：t = R * C * ln(V_c / V_0)其中，t是放电时间，R是电阻的阻值，C是电容器的电容量，V_c是电容器上的电压，V_0是初始电压。
需要注意的是，以上的公式是基于理想的条件得出的，实际的电路中可能存在一些非理想因素，如电路的电阻、电容等元件的精确值与理论值之间的差异，以及电池的内阻等因素。
此外，还需要注意的是，在实际的RC电路中，电容器上的电压不会严格上升到电源电压或严格下降到0V，而是逐渐接近这些值。
因此，我们可以定义充电时间为电容器上电压达到电源电压的时间的约90%。
同样，放电时间可以定义为电容器上电压从电源电压下降到初始电压的时间的约90%。
总之，充放电时间的计算可以通过RC电路的电阻、电容、电源电压和初始电压，结合以上的计算公式，得出结果。
需要注意的是，公式是基于理想条件下得出的，实际的电路中可能存在一些不可忽略的非理想因素。
电容充放电公式总结
电容充放电公式总结一、电源U 通过电阻R 给电容C 充电：A ）充电过程中电源输出的瞬时功率：dtCdU UdtdQ U UIP ctt ===B ）整个过程中电源输出的能量：2CUdUCUdt dtCdU Udt P W Ucct U ====⎰⎰⎰∞∞C ）电容上最终存储的能量：221CUdU UCdt dtCdUUW UcCcCC ===⎰⎰∞D ）整个过程中电阻上消耗的能量（221CUW W W C U R =-=）：221)()(CUdUU U Cdt dtCdU UU dt dtCdUUWCUc cCcRR=-=-==⎰⎰⎰∞∞E ）电容两端电压随时间的变化关系推导：⎪⎪⎪⎩⎪⎪⎪⎨⎧===-dt dQ I C Q U R I U U tCt C dtCQ U dQ RdtdQ RCQ U =-⇒=-⇒两边求不定积分，用初始条件：0,000==Q t)1()1ln(RCt eCU Q RCt CUQ dtdQ QCURC --=⇒=--⇒=-⎰⎰极板电压随时间变化的函数)1(RCt CeU CQ U--==F ）电容充电时间计算公式：Ut UU U RC t CC --=)()0(ln理论上，只有当时间t 趋向无穷大时，极板上的电荷和电压才达到稳定，充电才结束。
但实际中，由于RCt e--1很快趋向1，故经过很短的一段时间后，电容器极板间电荷和电压的变化已经微乎其微，这时可以认为已达到平衡，充电结束。
● 整个过程中电阻上消耗的能量也可这样计算：()2222022222102CU t t eRC R Udt eRU dt RUe dt RU Ut RUW RC tRCt RCt CR==∞=⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫ ⎝⎛=-==-∞-∞-∞⎰⎰⎰二、不难理解，两端电压为U 的电容C 对R 放电时，电容上所存储的能量221CU最终都消耗在电阻R 上。
RC电路充放电时间的计算(含计算公式)
RC电路充放电时间的计算（含计算公式）RC电路是一种由电阻和电容器组成的电路，又称为电容电阻电路。
在RC电路中，电容器可以通过电阻进行充电和放电。
充放电时间是指电容器从零电压充电到达一定电压或从一定电压放电到零电压所需的时间。
1.RC电路的充电时间计算：假设一个RC电路，电容器的电压从0V充电到Vo需要的时间记为t。
首先，根据基尔霍夫电压定律，电压满足以下方程：V=Vo(1-e^(-t/RC))其中，R为电阻的阻值（单位为Ω），C为电容器的电容值（单位为F），e为自然对数的底数。
当时间t趋近于无穷大时，电压V趋近于Vo，即电容器充电完全。
因此，我们可以令V≈Vo，得到方程：1-e^(-t/RC)≈1即e^(-t/RC)≈0取对数得到：-t/RC ≈ ln(0)其中，ln(0)无定义。
因此，当-t/RC足够小的时候，我们可以近似地认为电容器充电的时间t满足以下公式：t≈RC2.RC电路的放电时间计算：假设一个RC电路，电容器的电压从Vo放电到0V需要的时间记为t。
根据基尔霍夫电压定律，电压满足以下方程：V=Vo*e^(-t/RC)当时间t趋近于无穷大时，电压V趋近于0V，即电容器放电完全。
因此，我们可以令V≈0V，得到方程：0=Vo*e^(-t/RC)移项化简得到：e^(-t/RC)=0取对数得到：-t/RC = ln(0)其中，ln(0)无定义。
因此，当-t/RC足够小的时候，我们可以近似地认为电容器放电的时间t满足以下公式：t≈RC综上所述，RC电路的充电时间和放电时间的近似计算公式都为：t≈RC需要注意的是，以上的计算公式是在假设无电流流过电阻时成立的。
如果电阻上有电流流过，则需要考虑电流对电压的影响，进而得到更精确的计算结果。
rc时间计算公式
RC 时间常常被用于描述电路中的电压或电流变化速度。
在一个简单的RC 电路中，R 代表电阻值（单位为欧姆），C 代表电容值（单位为法拉），而RC 时间常被定义为电容充电或放电到达其初始值的时间。
计算RC 时间的公式如下:
RC 充电时间常数（τ）：τ = R × C
- 电容充电时间(t)：当电容充电到达63.2%（即1 - 1/e, 其中e 是自然对数的底数）所需的时间。
t = τ × ln(2)
- 电容放电时间(t)：当电容放电到达36.8%（即1/e）所需的时间。
t = τ × ln(2)
请注意，这些公式是基于简化的模型，假设电路是理想的完美条件。
在实际情况下，可能还需要考虑其他因素，例如电压源的特性和导线电阻等。
此外，RC 时间在不同的领域和应用中也具有不同的含义和计算方式。
如在信号处理中，RC 时间常使用于描述带通滤波器的截止频率，其计算方式为1/(2πRC)。
因此，具体使用的场景和定义会对应有所差异。
电容放电和充电时间计算
电容放电和充电时间计算1.电容放电时间计算：电容放电是指将电容器中的电荷释放出来的过程。
当电容器上的电压突然从一个值变为另一个值时，电容器会放出全部或部分的电荷。
以下是电容放电时间的计算公式：τ=R×C其中τ代表电容放电的时间常数，单位为秒（s）；R代表电路中的电阻，单位为欧姆（Ω）；C代表电路中的电容，单位为法拉（F）。
根据上述公式，我们可以计算出电容放电的时间。
例如，假设电路中的电阻为100欧姆，电容为0.1法拉，则电容放电的时间为：τ=100Ω×0.1F=10s因此，在这个例子中，电容放电的时间为10秒。
2.电容充电时间计算：电容充电是指将电流通过电容器充入的过程。
当电容器上的电压逐渐上升到一个稳定的值时，我们可以计算出电容充电的时间。
以下是电容充电时间的计算公式：τ=R×C与电容放电时间的计算公式相同，电容充电时间也可以用上述公式计算。
例如，假设电路中的电阻为100欧姆，电容为0.1法拉，则电容充电的时间为：τ=100Ω×0.1F=10s同样地，在这个例子中，电容充电的时间也为10秒。
放电曲线：充电曲线：在实际测量中，我们可以通过示波器等仪器来观察充电和放电曲线，并使用计算机软件进行计算和分析。
总结：电容放电和充电时间的计算可以通过简单的公式来进行。
根据电路中的电阻和电容参数，我们可以计算出电容放电和充电的时间常数。
但需要注意的是，实际的电容充电和放电过程是逐渐进行的，我们可以通过测量充电和放电曲线来分析电路中的电容行为，并使用计算机软件进行进一步的计算和分析。
电容放电和充电时间的计算对于电路设计和分析非常重要，它们的准确计算可以帮助我们预测电容器在电路中的行为，并优化电路的性能。
电容放电和充电时间计算
充电时间计算: 设：V O 为电容器两端的初始电压值
V a 为电容器两端充满时电压值
V t 为电容器两端任意时刻t 时的电压值
那么：
r t \ V t=V°+(V max-乂卜 e 帝
l 丿
若，电压为E 的电池通过电阻R 向初值为0的电容C 充电，此时V°=0， 充电极限V max 二E
故，任意时刻t ，电容上的电压为:
若，已知某时刻电容上的电压V t ，根据常数可以计算出时间t 公式涵义： 完全充满时，V 接近E ,时间t 无穷大;
当t 二RC 时，电容电压=0.63E ；
当t =2RC 时，电容电压 =0.86E ；
当t =3RC 时，电容电压 -0.96E ；
当t =4RC 时，电容电压 -0.98E ；
当t =5RC 时，电容电压 =0.99E ； 可见，经过3~5个RC 后，充电过程基本结束。
例: V 。
=0V ，乂 =325V , V max=375V ，，C = 0.l4F 求 t
375
t =1 106 0.1 106 In 0.20S
放电时间计算：
已知，初始电压为E 的电容C 通过电阻R 放电，V °=E , Vmax = O ；
那么，
375 - 325
电容器放电时任意时刻t，电容两端电压V t为：
丄E
V t^E^e RC= t =RC ・ln
V t
例: V。
=375V，V t=22V，R =1MC，C=O.14F 求t
t =1 106 0.1 106 In 竺=0.28S
22。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
设：O V 为电容器两端的初始电压值
m a x
V 为电容器两端充满时电压值 t V 为电容器两端任意时刻t 时的电压值
那么：
()⎪⎪⎭
⎫ ⎝⎛-⨯-+=-RC t o o t e V V V V 1max 若，电压为E 的电池通过电阻R 向初值为0的电容C 充电，此时0=o V ，充电极限E V =max
故，任意时刻t ，电容上的电压为：
⎪⎪⎭
⎫ ⎝⎛-∙=⇒⎪⎪⎭⎫ ⎝⎛-=-t RC t t V E E RC t e E V ln 1 若，已知某时刻电容上的电压t V ，根据常数可以计算出时间t 。
公式涵义：
完全充满时，t V 接近E ,时间t 无穷大； 当RC t =时，电容电压E 63.0=；
当RC t 2=时，电容电压E 86.0=；
当RC t 3=时，电容电压E 96.0=；
当RC t 4=时，电容电压E 98.0=；
当RC t 5=时，电容电压E 99.0=；
可见，经过RC 个5~3后，充电过程基本结束。
例：F C V V V t μ1.01M R 375V 325V V 0max O =Ω====，，，，，求t
S t 20.0325
375375ln 101.010166=-⨯⨯⨯⨯=
已知，初始电压为E 的电容C 通过电阻R 放电，0max O ==V E V ，； 那么，电容器放电时任意时刻t ，电容两端电压t V 为： t
RC t
t V E
RC t e E V ln ∙=⇒∙=-
例：F C V V t μ1.01M R 22V V 375O =Ω===，，，，求t S t 28.022375
ln 101.010166=⨯⨯⨯⨯=。