1.2.3《简单几何体的直观图》课件(新人教版A必修2)
合集下载
2021版高中数学人教A版必修2课件:1.2.3 空间几何体的直观图

-7-
1.2.3 空间几何体的直观图
目标导航
12
知识梳理
重难聚焦
典例透析
【做一做2】 在空间几何体中,平行于z轴的线段AB=10 cm,则在
直观图中对应的线段A'B'= cm.
解析:由于平行于z轴的线段在直观图中保持原长度不变,则 A'B'=AB=10 cm.
答案:10
-8-
1.2.3 空间几何体的直观图
目标导航
பைடு நூலகம்
知识梳理
重难聚焦
典例透析
12
1.斜二测画法的作图技巧 剖析:(1)在已知图形中建立直角坐标系,理论上是在任何位置建 立直角坐标系都行,但在实际作图时,一般建立特殊的直角坐标系, 尽量以原有直线为坐标轴,或以图形中互相垂直的直线为坐标轴, 或以图形的对称中心为坐标原点等. (2)原图中与x轴或y轴或z轴平行的线段在直观图中依然与x'轴或 y'轴或z'轴平行;原图中不与坐标轴平行的线段可以先画出线段的 端点再连线,画端点时作坐标轴的平行线为辅助线;原图中的曲线 段可以通过取一些关键点,利用上述方法作出直观图中的相应点后, 用平滑的曲线连接而成.
-13-
1.2.3 空间几何体的直观图
目标导航
知识梳理
重难聚焦
典例透析
题型一 题型二 题型三 题型四
【变式训练1】 按图示的建系方法,画出水平放置的正五边形 ABCDE的直观图.
画法:(1)如图①,作AG⊥x轴于点G,作DH⊥x轴于点H. (2)如图②,画相应的x'轴与y'轴,两轴相交于点O',使∠x'O'y'=45°.
-18-
1.2.3 空间几何体的直观图
高一数学(人教A版)立体图形的直观图-2ppt课件

点.
A
O
Bx
例题 已知圆锥的底面半径为1cm,轴长为2cm,画出
它的直观图.
(4)成图.连接SA,SB,整理得到圆锥的直观图.
zS
S
A
O
Bx
O
例题 画一个球的直观图.
球的直观图画法:画球的直观图,一般需要画出球的轮廓 线,它是一个圆.同时还经常画出经过球心的截面圆,它 们的直观图是椭圆,用以衬托球的立体性.
取线段 BD,使BODO1.5,连接 AB,
y
AD,CB,CD 就得到底面的直观图.
D
AO
Cx
B
练习 已知一直棱柱的底面是菱形,两条对角线
AC,BD相交于点O,且 AC 8,BD 6.侧棱长为
4,画出这个几何体的直观图.
(3)画侧棱.在 z 轴正半轴上取 一 点 O , 使 OO , 过 点 A,B,C,D分别作 z 轴的平行线, 并在这些平行线上分别截取长度
z A
B O
C
Ay
BO
Cx
(4)成图.连接 A,B,C,整理就得到正三棱柱的直观
图.
z A
A
B
C
B
C
Ay
BO
Cx B
A
C
【小结】
画法: 画轴
画底面 画侧棱
成图
事实上,现实世界中的物体表示的几何体,还有柱、 锥、台、球等简单几何体,以及大量的简单组合体.对 于这些立体图形,我们如何画出它的直观图呢?下面举 例说明.
六棱柱的直观图.
z
A F
E D
B C
A F
E D
B C
F
AO
B
y
E
Dx
人教A版高中数学必修二课件1.2.3 空间几何体的直观图3

x′轴的平行线 l,在 l 上沿 x′轴正方向取点 C′使得 D′C′=DC.连接 B′C′,如图②. (3)所得四边形O′B′C′D′就是直角梯形OBCD的直观图.如图③.
方法技能
在画水平放置的平面图形的直观图时,选取适当的直角坐标系是关键, 一般要使平面多边形尽可能多的顶点在坐标轴上,以便于画点.原图 中不平行于坐标轴的线段可以通过作平行于坐标轴的线段来完成.
(2)画底面.作水平放置的三角形(俯视图)的直观图△ABC. (3)画侧棱.过A,B,C各点分别作z轴的平行线,并在这些平行线上分别截 取线段AA′,BB′,CC′,且AA′=BB′=CC′.(侧视图中矩形的高) (4)成图,顺次连接A′,B′,C′,并加以整理(擦去辅助线,将遮挡部分用虚线 表示),得到的图形就是所求的几何体的直观图.
即时训练1-1:用斜二测画法画如图所示边长为4 cm的水平放置的正三角 形的直观图.
解:(1)如图①所示,以BC边所在的直线为x轴,以BC边上的高线AO所在 的直线为y轴.建立平面直角坐标系.
解:(2)画对应的 x′轴、y′轴, 使∠x′O′y′=45°. 在 x′轴上截取 O′B′=O′C′=OB=OC=2 cm,
(2)画底面.按x′轴、y′轴画正五边形的直观图ABCDE. (3)画侧棱.过点A,B,C,D,E分别作z′轴的平行线,并在这些平行线上分别 截取AA′,BB′,CC′,DD′,EE′都等于正视图的高. (4)成图.顺次连接A′,B′,C′,D′,E′,去掉辅助线,改被挡部分为虚线,如图② 所示.
方法技能
(3)原图的面积 S 与直观图的面积 S′之间的关系为 S=2 2 S′.
即时训练 3-1:等腰梯形 ABCD 中,上底 CD=1,腰 AD=CB= 2 ,下底 AB=3,以下 底所在直线为 x 轴,则由斜二测画法画出的直观图 A′B′C′D′的面积
方法技能
在画水平放置的平面图形的直观图时,选取适当的直角坐标系是关键, 一般要使平面多边形尽可能多的顶点在坐标轴上,以便于画点.原图 中不平行于坐标轴的线段可以通过作平行于坐标轴的线段来完成.
(2)画底面.作水平放置的三角形(俯视图)的直观图△ABC. (3)画侧棱.过A,B,C各点分别作z轴的平行线,并在这些平行线上分别截 取线段AA′,BB′,CC′,且AA′=BB′=CC′.(侧视图中矩形的高) (4)成图,顺次连接A′,B′,C′,并加以整理(擦去辅助线,将遮挡部分用虚线 表示),得到的图形就是所求的几何体的直观图.
即时训练1-1:用斜二测画法画如图所示边长为4 cm的水平放置的正三角 形的直观图.
解:(1)如图①所示,以BC边所在的直线为x轴,以BC边上的高线AO所在 的直线为y轴.建立平面直角坐标系.
解:(2)画对应的 x′轴、y′轴, 使∠x′O′y′=45°. 在 x′轴上截取 O′B′=O′C′=OB=OC=2 cm,
(2)画底面.按x′轴、y′轴画正五边形的直观图ABCDE. (3)画侧棱.过点A,B,C,D,E分别作z′轴的平行线,并在这些平行线上分别 截取AA′,BB′,CC′,DD′,EE′都等于正视图的高. (4)成图.顺次连接A′,B′,C′,D′,E′,去掉辅助线,改被挡部分为虚线,如图② 所示.
方法技能
(3)原图的面积 S 与直观图的面积 S′之间的关系为 S=2 2 S′.
即时训练 3-1:等腰梯形 ABCD 中,上底 CD=1,腰 AD=CB= 2 ,下底 AB=3,以下 底所在直线为 x 轴,则由斜二测画法画出的直观图 A′B′C′D′的面积
1.2.3空间几何体的直观图 课件(人教A必修2) 2

2 结 A′B′, A′C′, 则三角形 A′B′C′即 为正三角形 ABC 的直观图, 如图所示.
栏目 导引
第一章 空间几何体
思考:你能用上述方法画水平放置的正五边形的直观图吗?
y A
E
B
o
x
A`
E` B`
D`
C`
D
C
栏目 导引
第一章 空间几何体
思考:你能用上述方法画水平放置的正五边形的直观图吗?
第一章 空间几何体
做一做 2.利用斜二测画法画边长为3 cm的正方形的 直观图, 正确的是图中的( )
答案: C
栏目 导引
第一章 空间几何体
典题例证·技法归纳
题型探究 题型一 水平放置的平面图形的直观图
例1 用斜二测画法画边长为2 cm的水平放 置的正三角形的直观图.
栏目 导引
第一章 空间几何体
新知初探·思维启动
1. 斜二测画法 我们常用斜二测画法画空间图形及水平放置 的平面多边形的直观图. 斜二测画法是一种特 殊的____平__行__投__影____画法. 2. 平面图形直观图的画法 斜二测画法的步骤:
栏目 导引
第一章 空间几何体
(1).在已知图形中取互相垂直的x轴和y轴, 两轴相交于点 O. 画直观图时, 把它们画成对应的x′轴和y′轴, 两 轴交于点O′, 且使∠x′O′y′=4_5_°__(_或__1_3_5_°__)____, 它们确定的平面表示_水__平__面_________. (2).已知图形中平行于x轴或y轴的线段, 在直观图中分别 画成__平__行______于x′轴或y′轴的线段. (3).已知图形中平行于x轴的线段, 在直观图中保持 _原__长__度__不__变__, 平行于y轴的线段, 长度为原来的_一_半___.
栏目 导引
第一章 空间几何体
思考:你能用上述方法画水平放置的正五边形的直观图吗?
y A
E
B
o
x
A`
E` B`
D`
C`
D
C
栏目 导引
第一章 空间几何体
思考:你能用上述方法画水平放置的正五边形的直观图吗?
第一章 空间几何体
做一做 2.利用斜二测画法画边长为3 cm的正方形的 直观图, 正确的是图中的( )
答案: C
栏目 导引
第一章 空间几何体
典题例证·技法归纳
题型探究 题型一 水平放置的平面图形的直观图
例1 用斜二测画法画边长为2 cm的水平放 置的正三角形的直观图.
栏目 导引
第一章 空间几何体
新知初探·思维启动
1. 斜二测画法 我们常用斜二测画法画空间图形及水平放置 的平面多边形的直观图. 斜二测画法是一种特 殊的____平__行__投__影____画法. 2. 平面图形直观图的画法 斜二测画法的步骤:
栏目 导引
第一章 空间几何体
(1).在已知图形中取互相垂直的x轴和y轴, 两轴相交于点 O. 画直观图时, 把它们画成对应的x′轴和y′轴, 两 轴交于点O′, 且使∠x′O′y′=4_5_°__(_或__1_3_5_°__)____, 它们确定的平面表示_水__平__面_________. (2).已知图形中平行于x轴或y轴的线段, 在直观图中分别 画成__平__行______于x′轴或y′轴的线段. (3).已知图形中平行于x轴的线段, 在直观图中保持 _原__长__度__不__变__, 平行于y轴的线段, 长度为原来的_一_半___.
人教A版必修二高一数学《1.2.3空间几何体的直观图1》课件.pptx

上分别截取2cm长的线段AA,BB,CC,DD.
Z
D
C y
A
D
BQ C
MO N x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的AB直CD观图ABCD
4 成图.顺次连接A,B,C,D,并加以整理
去掉辅助线,将被遮挡住的部分改为虚线 ,
就可得到长方体的直观图.
D
A
▪ 把空间图形画在平面内,使得既富有 立体感,又能表达出图形各主要部分 的位置关系和度量关系的图形.
D
A
C
B
D A
C B
例1.用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中,取AD所在的直线为X轴,
对称轴MN所在直线为Y轴,两轴交于点O。画相应 的X轴和Y轴,两轴相交于点O,使xOy=45
例3.已知几何体的三视图,用斜二测画法画出 它的直观图
▪ 由三视图可知:
该几何体是怎么
的一个组合体?
·
O
·O
▪ 如何画出一个圆 柱的直观图?
·
O
·
O
正视图
▪ 如何画出一个圆
侧视图
锥的直观图?
▪ 思考三视图与直
·
观图有何关系?
俯视图
·Z
y
O y x
Ox
练习
1.已知一四边形ABCD的水平放置的直观 图是一个边长为2的正方形,请画出这个 图形的真实图形。
y
F ME
y
A
O Dx
O
x
B NC
2以O为中心,在X上取AD=AD,在y轴上取
MN= 1 MN.以点N为中心,画BC平行于x轴, 2
Z
D
C y
A
D
BQ C
MO N x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的AB直CD观图ABCD
4 成图.顺次连接A,B,C,D,并加以整理
去掉辅助线,将被遮挡住的部分改为虚线 ,
就可得到长方体的直观图.
D
A
▪ 把空间图形画在平面内,使得既富有 立体感,又能表达出图形各主要部分 的位置关系和度量关系的图形.
D
A
C
B
D A
C B
例1.用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中,取AD所在的直线为X轴,
对称轴MN所在直线为Y轴,两轴交于点O。画相应 的X轴和Y轴,两轴相交于点O,使xOy=45
例3.已知几何体的三视图,用斜二测画法画出 它的直观图
▪ 由三视图可知:
该几何体是怎么
的一个组合体?
·
O
·O
▪ 如何画出一个圆 柱的直观图?
·
O
·
O
正视图
▪ 如何画出一个圆
侧视图
锥的直观图?
▪ 思考三视图与直
·
观图有何关系?
俯视图
·Z
y
O y x
Ox
练习
1.已知一四边形ABCD的水平放置的直观 图是一个边长为2的正方形,请画出这个 图形的真实图形。
y
F ME
y
A
O Dx
O
x
B NC
2以O为中心,在X上取AD=AD,在y轴上取
MN= 1 MN.以点N为中心,画BC平行于x轴, 2
人教A版必修二数学课件:1-2-3空间几何体的直观图30张PPT.ppt

▪ [点评] 1°z′轴画法应使∠z′O′x′=90°
▪ 2°在z轴上(或平行于z轴的直线上)的线段 在直观图中保持长度不变.
▪ 3°几何体中,位于底面(xOy平面)以外的 点,常常先向xOy平面投影,找出在xOy平 面上的对应点,再在直观图中画出.
图(1)
图(2)
▪ 过B作BC∥AD,过D作DC∥AB,使BC与 DC交于点C,则四边形ABCD即为A′B′C′D′ 的实际图形.
▪ [例4] 利用下图所示的三视图,画出它的 直观图.
▪ [分析] 由正视图和俯视图知该几何体为 柱体,由侧视图知,该几何体是一横放的 三棱柱.
▪ [解析] 该几何体是一个三棱柱,直观图 如下图所示
(2)在 y′轴正半轴上,截取 O′A′=12OA,负半轴上 截取 O′D′=12OD,过 D′作直线 l∥x′轴,在 l 截取 D′B′=DB,D′C′=DC,连结 A′B′,A′C′.
(3)过 O′点作与 x′轴垂直的 z′轴,在 z′轴正半轴 上截取 O′P′=OP=2,连结 P′A′,P′B′,P′C′, 则 P′-A′B′C′,即为此三棱锥的直观图.
▪ [例3] 如图(1)的平行四边形A′B′C′D′ 为一个平面图形的直观图,其中∠D′A′B′ =45°.请画出它的实际形状.
▪ [解析] 在图(1)中建立如图所示的坐标系 x′A′y′,再建一个直角坐标系xAy,如图(2) 所示.
▪ 在x轴上截取线段AB=A′B′,在y轴上截取 线段AD,使AD=2A′D′.
②在图 2 中,以 O′为中点,在 x′轴上取 A′D′= AD,在 y′轴上取 M′N′=12MN,以点 N′为中点画 B′C′平行于 x′轴,并且等于 BC;再以 M′为中点画 E′F′平行于 x′轴,并且等于 EF.
人教A版高中数学必修二 1.2.3 空间几何体的直观图课件(共PPT20张)

(二) 空间几何体的直观图的画法
思考1:对于柱、锥、台等几何体的直观图,可用斜二测画法
或椭圆模板画出一个底面,我们能否再用一个坐标确定底面
外的点的位置?
Z
y
o
x
例2.用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm 的长方体ABCD-A′B′C′D′的直观图.
D′ A′
D A
C′ B′
点
P和Q作x轴的平行线z ,设它们的交点分别为A,B,z C,D,四边形
ABCD
y
y
就是长方体的底面ABCD.
D QC
O
x
MO N x
AP B
(3)画侧棱.过A,B,C,D各点分别作z轴的平行线,并在这些平行 线上分别截取2 cm长的线段AA′,BB′,CC′,DD′.
Z
D
A D
MO
C y
B
Q
C
Nx
C B
联想水平放置的平 面图形的画法,并注意 高的处理.
画法:(1)画轴.画x轴、y轴、z轴,三轴交于点O,使∠xoy=45°,
∠xoz=90°.
(2)画底面.以点O为中心,在x轴上取线段MN,使MN4=____cm;在
y
1.5
轴上取线段PQ,使PQ=_____cm,分别过点M和N作y轴的平行线,O
D x
B N C
B NC
注意:水平放置的线段长不变,垂直放置的线段长变为原来 的一半.
(3)连接A'B',C'D', D'E',F'A', 并擦去辅助线x′轴和y′轴,便 获得正六边形ABCDEF水平放置的直观图A'B'C ' D' E 'F '.
人教版高中数学必修二1.3.1空间几何体的直观图课件
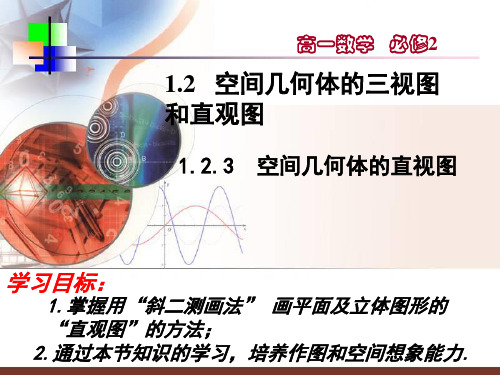
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F ME
A
O Dx
B NC
y
F M E
A
O
D x
B N C
方法总结
水平放置的平面图形的直观图的作法 1.斜二测画法:画多边形
(1)在已知图形中取互相垂直的x轴和y轴,两轴相交 于o点.画直观图时,把它画成对应的x′轴、y′轴,使
xOy=45 或135 ,它确定的平面表示水平平面。
Z
y
D QC
MO N x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
3画侧棱.过A,B,C,D,各点分别作z轴的平行线,并在这些平行线
上分别截取2cm长的线段AA,BB,CC,DD.
Z
D
C y
A
B
M D O Q NC x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
1画轴.画x轴,y轴,z轴,三轴交于点O,使xOy=45 ,
xOz 90 .
Z
y
O
x
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
2画底面.以O为中心,在x轴上取线段MN,使MN= 4 cm;在y
轴上取线段PQ,使PQ=1.5 cm;分别过点M 和N作y轴的平行 线,过点P和Q作x轴的平行线,设它们的交点分别为A,B, C,D,四边形ABCD就是长方形的底面ABCD
典例分析
用斜二测画法画水平放置的平面图形的直观图 例1.用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中,取AD所在的直线为X轴,
y
F ME
A
O Dx
B NC
y
F M E
A
O
D x
B N C
方法总结
水平放置的平面图形的直观图的作法 1.斜二测画法:画多边形
(1)在已知图形中取互相垂直的x轴和y轴,两轴相交 于o点.画直观图时,把它画成对应的x′轴、y′轴,使
xOy=45 或135 ,它确定的平面表示水平平面。
Z
y
D QC
MO N x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
3画侧棱.过A,B,C,D,各点分别作z轴的平行线,并在这些平行线
上分别截取2cm长的线段AA,BB,CC,DD.
Z
D
C y
A
B
M D O Q NC x
AP B
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
1画轴.画x轴,y轴,z轴,三轴交于点O,使xOy=45 ,
xOz 90 .
Z
y
O
x
例3.用斜二测画法画长,宽,高分别是 4cm,3cm,2cm的长方体的直观图.
2画底面.以O为中心,在x轴上取线段MN,使MN= 4 cm;在y
轴上取线段PQ,使PQ=1.5 cm;分别过点M 和N作y轴的平行 线,过点P和Q作x轴的平行线,设它们的交点分别为A,B, C,D,四边形ABCD就是长方形的底面ABCD
典例分析
用斜二测画法画水平放置的平面图形的直观图 例1.用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中,取AD所在的直线为X轴,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识探究(二):空间几何体的直观图的画法
思考1:对于柱、锥、台等几何体的直观 图,可用斜二测画法或椭圆模板画出一 个底面,我们能否再用一个坐标确定底 面外的点的位置?
z y
o
x
思考2:怎样画长、宽、高分别为4cm、 3cm、2cm的长方体ABCD-A′B′C′D′的 直观图?
D′
z
C′
A′ D
y B′
1.建立斜坐标系 2.原图中平行于x轴的,直观图 中平行于x’轴,长度不变。 3.原图中平行于y轴的,直观图 中平行于y’轴,长度减半。
画等腰梯形的直观图
结论
(1)角的直观图还是角; (2)原图中相等的角直观图中不一定相等; (3)相等的线段不一定再相等; (4)平行的线段仍平行;
思考3:画一个水平放置的平面图形的直 观图,关键是确定直观图中各顶点的位 置,我们可以借助平面坐标系解决这个 问题. 那么在画水平放置的直角梯形的 直观图时应如何操作?
y
D
C
y′ C′
D′
A
Bx
ห้องสมุดไป่ตู้
A′
B′ x′
思考6:斜二测画法可以画任意多边形水 平放置的直观图,如果把一个圆水平放 置,看起来像什么图形?在实际画图时 有什么办法?
y
y
F ME
A
O
Dx
O
x
B NC
2以O为中心,在X上取AD=AD,在y轴上取
MN=1MN.以点N为中心,画BC平行于x轴, 2
并且等于BC;再以M为中心,画EF平行于x轴,
并且等于EF.
y
F ME
A
O
D
x
y
F M E
A
O B N C
D x
B NC
3 连 接 A B , C D , E F , F A , 并 擦 去 辅 助 线 x 轴 和 y 轴 ,
一.水平放置的平面图形的直观图 例1.用斜二测画法画水平放置的六边形的直观图
1在 六 边 形 A B C D E F 中 , 取 AD所 在 的 直 线 为 X轴 ,
对 称 轴 M N 所 在 直 线 为 Y轴 ,两 轴 交 于 点 O 。 画 相 应
的 X轴 和 Y轴 , 两 轴 相 交 于 点 O ,使 xO y=45
便 获 得 正 六 边 形 A B C D E F 水 平 放 置 的 直 观 图 A B C D E F
y
F ME
A
O
Dx
B NC
y
F M E
A
O B N C
D x
y FM E
x
A
o
D
BN C
y′
F′ M E′
A′
o′
D′ x′
B′ N C′
F′
E′
A′ D′
B′
C′
用斜二测画法画直观图
知识探究(一):水平放置的平面图形的画法
思考1:把一个矩形水平放置,从适当的 角度观察,给人以平行四边形的感觉, 如图.比较两图,其中哪些线段之间的位 置关系、数量关系发生了变化?哪些没 有发生变化?
思考2:把一个直角梯形水平放置得其直 观图如下,比较两图,其中哪些线段之 间的位置关系、数量关系发生了变化? 哪些没有发生变化?
Q
C
o
x
A
PB
D′ A′
D
A
C′ B′
C
B
思考3:怎样画底面是正三角形,且顶点 在底面上的投影是底面中心的三棱锥?
C
A
B
zS
y C
M
A
o Bx
S
C
A
B
思考4:画棱柱、棱锥的直观图大致可分 几个步骤进行?
画轴 → 画底面 → 画侧棱 → 成图
思考5:已知一个几何体的三视图如下, 这个几何体的结构特征如何?试用斜二 测画法画出它的直观图.
1.2.3《简单几何体的直观图》课件(新人教版A必修 2)
在此添加副标题
北京奥运会场馆图
问题提出
1.把一本书正面放置,其视觉效果 是一个矩形;把一本书水平放置,其视 觉效果还是一个矩形吗?这涉及水平放 置的平面图形的画法问题.
2.对于柱体、锥体、台体及简单的组 合体,在平面上应怎样作图才具有强烈 的立体感?这涉及空间几何体的直观图 的画法问题.
正视图 侧视图 俯视图
z
y′
A′
B′
o′
x′
y
A
oB x
理论迁移
例 如图,一个平面图形的水平放 置的斜二测直观图是一个等腰梯形,它 的底角为45°,两腰和上底边长均为1, 求这个平面图形的面积.
D
C
D
C
S 2 2
A
B
A
B
让学生摆出来、画出来、做出来
