【原创】《立体图形的整理和复习》课件
合集下载
立体图形整理与复习PPT课件
第30页/共32页
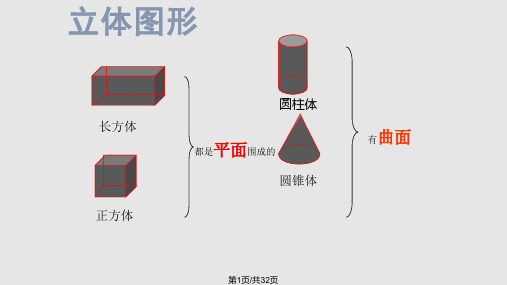
1、把一个底面半径是3分米,高是5分 米的圆柱削成一个最大的圆锥,这个 圆锥的体积是多少? 2、一个圆柱形油桶,从里面量底面半 径是2分米,高5分米。这个油桶的表 面积是多少平方分米?
3、一个圆锥的底面周长是62.8厘米,
第31页/共32页
谢谢您的观看!
第32页/共32页
第29页/共32页
达标测试
(1)做一个圆柱形铁皮罐头盒,求需要多 少铁皮,是求它的(表面积 ),罐头盒周围 贴商标纸, 求商标纸的面积是求它的 (侧面积 ) 。
(2)做一只圆柱形通风管要用多少铁皮, 是求它的(侧面积)。
(3)下雨时,给打谷场上的圆锥形谷堆盖上 塑料防雨布,所需防雨布的最小面积是指圆 锥的(侧面积 )。
相等。这个圆锥的高是圆柱的高的( 3 )倍。
(3)一个正方体的棱长5厘米,这个正方体的棱长
总和是(60 )厘米。
第22页/共32页
我会判断:
1)一个圆柱形水桶的体积就是它的容ห้องสมุดไป่ตู้。
…………………………………………( )
×
2)正方体的棱长扩大2倍,体积就扩大8倍。…………………………………( )
3)圆锥的体积等于圆柱体积的 ,它们一定等底等高。…………………………
有两个底面,是相等的两个圆。 有一个侧面,是个曲面,沿高展开一般是个长 方形。 有无数条高,每条高长度都相等。
有一个底面,是个圆形。 有一个侧面,是个曲面,展开是个扇形。 有一个顶点。 有一条高。
第2页/共32页
表面积: 立体图形所有面的面积之和。 体 积: 物体所占空间的大小。
第3页/共32页
立体图形的表面积和体积有什么 区别?
小明把一铁块放在底面直径是20厘米 的圆柱形容器里清洗,这时水深30厘 米,拿出铁块后,水面下降了3厘米。 你能求出铁块的体积吗?
1、把一个底面半径是3分米,高是5分 米的圆柱削成一个最大的圆锥,这个 圆锥的体积是多少? 2、一个圆柱形油桶,从里面量底面半 径是2分米,高5分米。这个油桶的表 面积是多少平方分米?
3、一个圆锥的底面周长是62.8厘米,
第31页/共32页
谢谢您的观看!
第32页/共32页
第29页/共32页
达标测试
(1)做一个圆柱形铁皮罐头盒,求需要多 少铁皮,是求它的(表面积 ),罐头盒周围 贴商标纸, 求商标纸的面积是求它的 (侧面积 ) 。
(2)做一只圆柱形通风管要用多少铁皮, 是求它的(侧面积)。
(3)下雨时,给打谷场上的圆锥形谷堆盖上 塑料防雨布,所需防雨布的最小面积是指圆 锥的(侧面积 )。
相等。这个圆锥的高是圆柱的高的( 3 )倍。
(3)一个正方体的棱长5厘米,这个正方体的棱长
总和是(60 )厘米。
第22页/共32页
我会判断:
1)一个圆柱形水桶的体积就是它的容ห้องสมุดไป่ตู้。
…………………………………………( )
×
2)正方体的棱长扩大2倍,体积就扩大8倍。…………………………………( )
3)圆锥的体积等于圆柱体积的 ,它们一定等底等高。…………………………
有两个底面,是相等的两个圆。 有一个侧面,是个曲面,沿高展开一般是个长 方形。 有无数条高,每条高长度都相等。
有一个底面,是个圆形。 有一个侧面,是个曲面,展开是个扇形。 有一个顶点。 有一条高。
第2页/共32页
表面积: 立体图形所有面的面积之和。 体 积: 物体所占空间的大小。
第3页/共32页
立体图形的表面积和体积有什么 区别?
小明把一铁块放在底面直径是20厘米 的圆柱形容器里清洗,这时水深30厘 米,拿出铁块后,水面下降了3厘米。 你能求出铁块的体积吗?
【原创】《立体图形的整理和复习》课件

S侧
3个面。 侧面沿高 都 展开后是 有 长方形。 圆 和 曲 2个面。侧 面 面是曲面 , 。 展开后是扇 形。
S表=2S底+S侧
V V长=abh 柱 sh V正= a3
V柱= sh
1
V锥= sh
3
体体
圆 柱
圆 锥
特征
表面积
(立体图形所有面的面积总和)
体积(所占空间的大小) 容积(所能容纳的物体的体积)
相对的4条
棱长度相等
,相对面是 6个 完全相同的
S表
面, 长方形。 8个
S表=(ab+ah+bh)×2
顶点 , 12条 棱。
12条棱长 度相等 ,6 个面是完全 相同的正方
2S底 +
形。
S表=6a2
S表=2S底+S侧
V柱= sh
2个面底面 是圆,侧 面展开是 扇形
1
V锥= sh
3
棱长
棱长
棱长
上底面 下底面
上底面 下底面
上底面 下底面
柱体
上底面
上底面
上底面
下底面
下底面
下底面
柱体体积=底面积 × 高 V=sh
哪些立体图形的体积也可以用V=sh来计算呢?
底面积
高
高
长方体体积=底面积×高 圆柱体积=底面积×高
5cm
有一个无盖的玻璃鱼缸
6 5 10 (单位:分米)
①鱼缸的占地面积是多少平方分米?
10×5=50dm²
②制作这个鱼缸需要多少平方分米的 玻璃?
10×6×2+5×6×2+10×5=230dm²
③这个鱼缸最多能装多少升水?
10×5×6=300dm³=300L
《立体图形的整理和复习》优质课教学课件

V=sh
圆锥的体积是与它等底等高的圆柱体积的 1 , 3
圆柱的体积是与它等底等高的圆锥的体积的3倍。
图形
体积
h
长方a体 b
V=abh
a aa
r h
V=a3 V=sh
V=sh
h r
圆锥体
V= 1/3 sh
过关检测
判断: (1)一个直角三角形,绕它的一条直角边旋转一周,能形成一个圆锥。( ) (2)把一段圆柱形木材削成一个最大的圆锥,削去的部分是原来的2/3( ) (3)圆柱的底面半径扩大为原来的2倍,高不变,它的体积也扩大为原来的2倍
(1)准备给客厅的四周墙壁和顶面贴墙 纸,门窗、电视墙等10m2不贴,实际贴 的面积是多少平方米?
(2)装修时所选的木料是直径4dm,长 3m的圆木,自己加工,大约需要5根求所 需木料的体积?
通过这节课的学习, 你有什么收获?
2、李师傅要制40根长方体通风管,管 口是边长为20 厘米的正方形,管长1 米,一共需要多少平方米的铁皮?
3、 把一块棱长是10厘米的正方体 铁块铸成一个底面直径是20厘米的 圆锥形铁块。这个圆锥铁块的高约 是多少?(得数保留整厘米数.)
4、 王老师前不久买了一套新房,客厅长6m,宽4m,高3m。请同 学们帮他算一算装修所需要的部分材料:
长方形(也有可 面的面
12 条
8 个
能有两个相对的 积相等 面是正方形)
相对的棱长度相等
6个面都是相等 6个面 12条棱的长
的正方形
的面积 度都相等
都相等
正方 体是 特殊 的长 方体
圆柱和圆锥各有什么特点, 它们之间有什么关系?
图形
o
圆柱 h
or
圆锥 h
圆锥的体积是与它等底等高的圆柱体积的 1 , 3
圆柱的体积是与它等底等高的圆锥的体积的3倍。
图形
体积
h
长方a体 b
V=abh
a aa
r h
V=a3 V=sh
V=sh
h r
圆锥体
V= 1/3 sh
过关检测
判断: (1)一个直角三角形,绕它的一条直角边旋转一周,能形成一个圆锥。( ) (2)把一段圆柱形木材削成一个最大的圆锥,削去的部分是原来的2/3( ) (3)圆柱的底面半径扩大为原来的2倍,高不变,它的体积也扩大为原来的2倍
(1)准备给客厅的四周墙壁和顶面贴墙 纸,门窗、电视墙等10m2不贴,实际贴 的面积是多少平方米?
(2)装修时所选的木料是直径4dm,长 3m的圆木,自己加工,大约需要5根求所 需木料的体积?
通过这节课的学习, 你有什么收获?
2、李师傅要制40根长方体通风管,管 口是边长为20 厘米的正方形,管长1 米,一共需要多少平方米的铁皮?
3、 把一块棱长是10厘米的正方体 铁块铸成一个底面直径是20厘米的 圆锥形铁块。这个圆锥铁块的高约 是多少?(得数保留整厘米数.)
4、 王老师前不久买了一套新房,客厅长6m,宽4m,高3m。请同 学们帮他算一算装修所需要的部分材料:
长方形(也有可 面的面
12 条
8 个
能有两个相对的 积相等 面是正方形)
相对的棱长度相等
6个面都是相等 6个面 12条棱的长
的正方形
的面积 度都相等
都相等
正方 体是 特殊 的长 方体
圆柱和圆锥各有什么特点, 它们之间有什么关系?
图形
o
圆柱 h
or
圆锥 h
立体图形的复习整理ppt课件全

可编辑课件
68
3、一个底面周长为31.4厘米的 圆柱,如果把它的高增加2厘米, 它的表面积增加多少?
2厘米
C=31.4可厘编辑课件米
69
根据所给的条件,也可以自 己添加条件,你能提出什么样的 问题?
2分米
6分米
2分米 可编辑课件
70
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
③在池内的侧面和池底抹一层水泥,水泥
面的面积是多少平 方米?
可编辑课件
15
有两种生日蛋糕:
20厘米 12 厘 米
12厘米
15厘米 20厘米
(1)如果两者的价格一样,你会选哪个? 你是怎样判断的?
(2)如果在蛋糕外面涂一层奶油,哪个
涂的比较多?
可编辑课件
16
(1)学校修整校园,把一个长40米,宽15米, 深0 .2米的沙坑填平。现有一个近似圆锥形的 土堆,测得它的周长是56.52米,高0. 9米。 这堆土够不够?
相对的 面的两 个的面 积相等
6个面都是 6 个面 相等的正方 的面积
每一组互
相平行的 四条棱的 长度相等
正方 体是
特殊
12条棱的 长度都相
的长 方体
形
形
都相等 等
可编辑课件
4
长方体
正方体
可编辑课件
5
圆柱、圆锥有什么特点?
2.圆柱、圆锥的特征:
特征
名称 图形
底面
侧面
高
圆柱 圆锥
o
h or
上下底面 是完全相 同的两个 圆
可编辑课件
19
左
back
上
后后
立体图形的复习整理PPT

等体积法
对于涉及体积计算的立体几何问题,可以采用等体积法。 通过将立体图形分成若干部分,利用体积守恒定律,将问 题转化为求解平面图形面积的问题。
分割法
对于复杂的立体图形,可以采用分割法。将复杂的立体图 形分割成若干个简单的立体图形,分别求解后再进行综合 。
常见题型解析
求体积和表面积
求角度和距离
这类问题需要利用体积和表面积的计算公 式,结合题目的具体条件进行求解。
分类
01
02
03
平面图形
由直线段构成的二维图形, 如三角形、四边形等。
曲面图形
由曲面构成的立体图形, 如球体、圆柱体等。
立体图形
由平面和曲面构成的立体 图形,如长方体、圆锥体 等。
立体图形的特点
占据三维空间
立体图形存在于三维空间中,具有长、 宽、高三个维度。
具有大小和形状
立体图形具有确定的大小和形状,可 以通过测量和计算得到其面积、体积 等几何量。
分解
将一个复杂的立体图形分解成若干个简单的小立体图形,有助于理 解和分析其结构。
应用
组合与分解在几何学、建筑学、机械工程等领域有广泛应用,如建 筑设计、机械零件的组装与拆卸等。
立体图形的创意设计
创意设计
01
通过运用几何学原理和美学原则,可以设计出各种具有创意的
立体图形。
实例
02
建筑设计中的立体造型、雕塑艺术中的立体造型、玩具设计中
立体图形的对称性
对称轴
有些立体图形具有对称性,可以通过对称轴进行对称。对称 轴是穿过立体图形中心的一条直线,将立体图形分成两个完 全相同的部分。
对称面
有些立体图形具有对称面,可以通过对称面进行对称。对称 面是一个平面,将立体图形分成两个完全相同或镜像的部分 。
六年级数学下册立体图形复习与整理ppt

正方体
圆柱
圆锥
回顾与整理
后面
左面
下面
前面 上面
右面
长方体的表面积= (上 面 + 前 面 + 侧 面 )×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
回顾与整理
正方体的表面积=一个面的面积×6
S=a2 × 6
回顾与整理
圆柱的表面积:
底面
底面周长
高
底面
圆柱的侧面积=底面周长×高
不用计算,你能很快比较出谁的体积最大吗?
二、练习与应用
一、火眼金睛辨对错 ① 圆柱的侧面展开一定是长方形。 (
×)
√
)
② 这面小旗旋转一周产生的图形是圆锥体。 (
③ 一根长24厘米的铁丝制作成一个正方体框架, 棱长是3厘米。 (
×)
练习与应用
二、把两个棱长是4厘米的正方体木块粘合成一个 长方体,这个长方体的表面积是多少平方厘米?
三、应用与反思
想一想,刚才我们在解决这两道题时有什么共同之处?
2cm
40cm 40cm
40cm 40cm
不规则图形
转化
规则图形
和同学们分享你的收获吧!
方法一、(8×4+8×4+4×4)×2=160(平方厘米) 方法二、8×4×4 + 4×4×2=160(平方厘米) 方法三、4×4×10=160(平方厘米) 方法四、4×4×12- 4×4×2=160(平方厘米)
练习与应用
三、李老师做一件冰雕作品,要将两个棱长为60厘米的正方体冰块 分别雕成最大的圆柱和圆锥。它们的体积各是多少立方分米? 圆柱的体积:
圆柱的表面积=底面积×2 + 侧面积 S=ch+2 ∏ r2
立体图形的总复习ppt课件
8
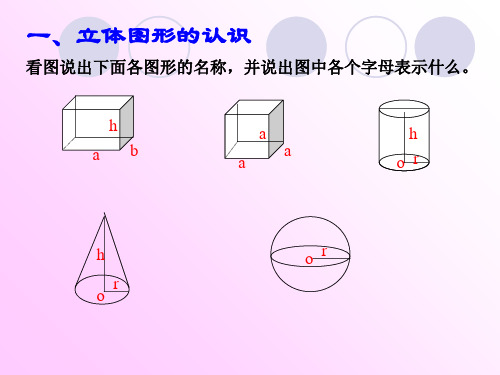
12
6
长
方 体
个 条个
8
12
6
正
方 体
个条 个
不同点
面的形状
面积
至少有四 个面是长方 形
相对的 面的面积 相等
6个面都 是相等的 正方形
6个面 的面积 都相等
关系 棱长
每一 组互相 平行的 四条棱 正方体 的长度 是特殊 相等 的长方
体 12条 棱的长 度都相 等
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
2、如果一个圆柱的侧面积展开是一个正方形,那么这 个圆柱的高等于它的底面( C )
A:半径 B:直径
C:周长
3、等底等体积的圆柱和圆锥,圆锥的高是18厘米那么 圆柱的高是( C )厘米
A:54
B:18
C:6
4、把一个棱长3分米的正方体,切削成最大的圆柱体,
求这个圆柱体的侧面积的算式是( )A
A:3.14 × 3 × 3
• (1)每相邻的两个体积单位之间的进率是
1000。( √ )
1
• (2)圆锥的体积是圆柱的 3 。( × )
• (3) 一个正方体的棱长是6分米,它的表面积与
体积一样大。(× )
• (4)两个圆柱的体积相等,它们的形状完全相
同。( × ) • (5)等底等高的长方体与圆柱体的体积相等。
(√ )
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
人教版一年级数学上册第3单元 认识立体图形《整理复习》课件

3. 教材第70页例2。 要想把积木搭得又稳又高,一般把( 长方体 )和
新 课 ( 正方体 )搭在下面,把( 圆柱 )和( 球 )搭 先 知 在上面。
4. 教材第71页例3。
新
2个完全相同的正方体可以拼成一个( 长方体 );2
课 个完全相同的圆柱可以拼成一个( 圆柱 );4个完全相
先
知 同的长方体可以拼成一个( 长方体或正方体 )。
( 6 )个
3.把立体图形①放在立体图形②上面,所组成的 立体图形是哪个?
✔ 所组成的是立体图形⑤。
这节课有什么收获呢?
认识立体图形的特征
通过拼搭活动进一步认识立体图形
1.从教材72页练一练中选取; 2.从课时练中选取。
板书设计
认识立体图形
长方体
正方体
圆柱
球
长方体和正方体摆放时较稳定,球和横放 的圆柱易滚动。
2. 高的(
搭一搭。在搭得最稳的( )里画“√”。
○ )里画“ ”,最
○ ( ) (
√) (
)
3. 数一数,填一填。
( 4 )个 ( 4 )个
( 3 )个 ( 1 )个
4. 填。
哪两种图形可以组成左边的形状?选一选,填一
④ ③
5. 接着摆什么?圈一圈。
(1)
(
)
(2)
(
)
2. 我会按规律,圈一圈。(4 分) (1) (2)
3. 我会按要求,圈一圈。 (1)圈出能搭成左边图形的一组。(2 分)
(2)先摆一个 把摆在
,在 的左边摆一个 ,再 的上面。(圈出正确的摆法)(2 分)
四、我挑战,我会想。(共24 分) 1. 认一认,圈一圈。(找出每组中的不同图形)(6 分) (1) (2) (3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V=sh
1
圆锥的体积是与它等底等高的圆柱体积的 ,
3
圆柱的体积是与它等底等高的圆锥的体积的3倍。
侧面积
侧面积
表面积=侧面积+2个底面积 侧面积=底面周长×高
侧面积
要制作一个长和宽都是30厘米,高是5厘米的长 方体框架,求需要多少铁丝,就是求它的( 2 );在 框架外面糊上一层纸,就是求它的( 3 );要在纸盒 的四周贴上标签,就是求( 1 );这个长方体的纸盒 占有多大的空间,就是求( 4 );这个长方体纸盒能 装多少沙,就是求( 5 )。
体体
圆 柱
圆 锥
特征) 容积(所能容纳的物体的体积)
相对的4条
棱长度相等
,相对面是 6个 完全相同的
S表
面, 长方形。 8个
S表=(ab+ah+bh)×2
顶点 , 12条 棱。
12条棱长 度相等 ,6 个面是完全 相同的正方
2S底 +
形。
S表=6a2
2厘米=0.2分米 10×5×0.2=10dm³
⑤如果要把这个体积是10dm³的长方体铁块熔铸 成一个底面积是2.5dm²的圆柱,圆柱的高是多少?
10÷2.5=4dm
⑥如果要把这个圆柱形铁块熔铸成一个与它等 底的圆锥,圆锥的高是多少?
4×3=12dm
今天这节课你有什么收获?
图形
长 方 体
柱
正 方
5cm
有一个无盖的玻璃鱼缸
6 5 10 (单位:分米)
①鱼缸的占地面积是多少平方分米?
10×5=50dm²
②制作这个鱼缸需要多少平方分米的 玻璃?
10×6×2+5×6×2+10×5=230dm²
③这个鱼缸最多能装多少升水?
10×5×6=300dm³=300L
④在这个鱼缸里放入了一个长方体铁块后,水面上升 了2厘米,这个长方体铁块的体积是多少?
人教版小学数学六年级下册
立体图形的整理和复习
小组交流,要求:
1.说说你是用什么方式来整理立体图形的知识? 2.你围绕哪几个方面进行整理? 3.你最想和同学分享哪个知识点?
图形
长 方 体
正柱
方
体体
圆 柱
圆 锥
特征
表面积
体积(所占空间的大小)
容积 (立体图形所有面的面积总和)
(所能容纳的物体的体积)
S侧
3个面。 侧面沿高 都 展开后是 有 长方形。 圆 和 曲 2个面。侧 面 面是曲面 , 。 展开后是扇 形。
S表=2S底+S侧
V V长=abh 柱 sh V正= a3
V柱= sh
1
V锥= sh
3
妈妈生日快到了,雯雯精心挑选了一个漂亮的水杯送给 妈妈。水杯的底面直径是6cm,高15cm。(厚度忽略不计) (1)这只水杯最多能装多少毫升的水?
3.14X(6÷2) 2 ×15=423.9(立方厘米) =423.9毫升
(2)水杯中部的装饰带宽5cm, 它的面积是多少平方厘米?
3.14X 6×5=94.2(平方厘米) 15cm
1.侧面积 2.棱长总和 3.表面积 4.体积 5.容积
1、只列式不计算,求表面积和体积。
7分米
3
3
.
分
2米 4
表面积=(4X2+4X3+2X3)X2 表面积=3.14X 32 ×2+3.14 ×3 ×2 ×7
体积=4X2X3
体积= 3.14 × 32 ×7
妈妈生日 快到了,雯雯 精心挑选了一 个漂亮的水杯 送给妈妈。
S表=2S底+S侧
V柱= sh
2个面底面 是圆,侧 面展开是 扇形
1
V锥= sh
3
棱长
棱长
棱长
上底面 下底面
上底面 下底面
上底面 下底面
柱体
上底面
上底面
上底面
下底面
下底面
下底面
柱体体积=底面积 × 高 V=sh
哪些立体图形的体积也可以用V=sh来计算呢?
底面积
高
高
长方体体积=底面积×高 圆柱体积=底面积×高
相对的
6个 面, 8个 顶点 ,
棱相等,
相对面是完 S表=(ab+ah+bh)×2
全相同的长
方形 。 12条棱相
S表=
12 条 棱。
等 ,6个 面是完全 相同的正
2S +S S表=6a2 底
侧
方形。
V长=abh
V柱= sh
V正= a3
都有 圆和 曲面.
3个面底面 是两个完 全相同的 圆,侧面 沿高展开 是长方形
1
圆锥的体积是与它等底等高的圆柱体积的 ,
3
圆柱的体积是与它等底等高的圆锥的体积的3倍。
侧面积
侧面积
表面积=侧面积+2个底面积 侧面积=底面周长×高
侧面积
要制作一个长和宽都是30厘米,高是5厘米的长 方体框架,求需要多少铁丝,就是求它的( 2 );在 框架外面糊上一层纸,就是求它的( 3 );要在纸盒 的四周贴上标签,就是求( 1 );这个长方体的纸盒 占有多大的空间,就是求( 4 );这个长方体纸盒能 装多少沙,就是求( 5 )。
体体
圆 柱
圆 锥
特征) 容积(所能容纳的物体的体积)
相对的4条
棱长度相等
,相对面是 6个 完全相同的
S表
面, 长方形。 8个
S表=(ab+ah+bh)×2
顶点 , 12条 棱。
12条棱长 度相等 ,6 个面是完全 相同的正方
2S底 +
形。
S表=6a2
2厘米=0.2分米 10×5×0.2=10dm³
⑤如果要把这个体积是10dm³的长方体铁块熔铸 成一个底面积是2.5dm²的圆柱,圆柱的高是多少?
10÷2.5=4dm
⑥如果要把这个圆柱形铁块熔铸成一个与它等 底的圆锥,圆锥的高是多少?
4×3=12dm
今天这节课你有什么收获?
图形
长 方 体
柱
正 方
5cm
有一个无盖的玻璃鱼缸
6 5 10 (单位:分米)
①鱼缸的占地面积是多少平方分米?
10×5=50dm²
②制作这个鱼缸需要多少平方分米的 玻璃?
10×6×2+5×6×2+10×5=230dm²
③这个鱼缸最多能装多少升水?
10×5×6=300dm³=300L
④在这个鱼缸里放入了一个长方体铁块后,水面上升 了2厘米,这个长方体铁块的体积是多少?
人教版小学数学六年级下册
立体图形的整理和复习
小组交流,要求:
1.说说你是用什么方式来整理立体图形的知识? 2.你围绕哪几个方面进行整理? 3.你最想和同学分享哪个知识点?
图形
长 方 体
正柱
方
体体
圆 柱
圆 锥
特征
表面积
体积(所占空间的大小)
容积 (立体图形所有面的面积总和)
(所能容纳的物体的体积)
S侧
3个面。 侧面沿高 都 展开后是 有 长方形。 圆 和 曲 2个面。侧 面 面是曲面 , 。 展开后是扇 形。
S表=2S底+S侧
V V长=abh 柱 sh V正= a3
V柱= sh
1
V锥= sh
3
妈妈生日快到了,雯雯精心挑选了一个漂亮的水杯送给 妈妈。水杯的底面直径是6cm,高15cm。(厚度忽略不计) (1)这只水杯最多能装多少毫升的水?
3.14X(6÷2) 2 ×15=423.9(立方厘米) =423.9毫升
(2)水杯中部的装饰带宽5cm, 它的面积是多少平方厘米?
3.14X 6×5=94.2(平方厘米) 15cm
1.侧面积 2.棱长总和 3.表面积 4.体积 5.容积
1、只列式不计算,求表面积和体积。
7分米
3
3
.
分
2米 4
表面积=(4X2+4X3+2X3)X2 表面积=3.14X 32 ×2+3.14 ×3 ×2 ×7
体积=4X2X3
体积= 3.14 × 32 ×7
妈妈生日 快到了,雯雯 精心挑选了一 个漂亮的水杯 送给妈妈。
S表=2S底+S侧
V柱= sh
2个面底面 是圆,侧 面展开是 扇形
1
V锥= sh
3
棱长
棱长
棱长
上底面 下底面
上底面 下底面
上底面 下底面
柱体
上底面
上底面
上底面
下底面
下底面
下底面
柱体体积=底面积 × 高 V=sh
哪些立体图形的体积也可以用V=sh来计算呢?
底面积
高
高
长方体体积=底面积×高 圆柱体积=底面积×高
相对的
6个 面, 8个 顶点 ,
棱相等,
相对面是完 S表=(ab+ah+bh)×2
全相同的长
方形 。 12条棱相
S表=
12 条 棱。
等 ,6个 面是完全 相同的正
2S +S S表=6a2 底
侧
方形。
V长=abh
V柱= sh
V正= a3
都有 圆和 曲面.
3个面底面 是两个完 全相同的 圆,侧面 沿高展开 是长方形
