统计学答案第八章
统计学答案第八章

三、选择题1 某厂生产的化纤纤度服从正态分布,纤维的纤度的标准均值为1.40。
某天测得25根纤维的纤度的均值=1。
39,检验与原来设计的标准均值相比是否有所变化,要求的显著性水平为α=0.05,则下列正确的假设形式是()。
A.H0:μ=1.40,H1:μ≠1.40 B。
H0:μ≤1。
40,H1:μ>1。
40C。
H0:μ〈1.40,H1:μ≥1。
40 D。
H0:μ≥1.40,H1:μ〈1。
402 某一贫困地区估计营养不良人数高达20%,然而有人认为这个比例实际上还要高,要检验该说法是否正确,则假设形式为().A. H0:π≤0。
2,H1:π〉0。
2B. H0:π=0.2,H1:π≠0。
2C。
H0:π≥0.3,H1:π〈0.3 D。
H0:π≥0。
3,H1:π<0.33 一项新的减肥计划声称:在计划实施的第一周内,参加者的体重平均至少可以减轻8磅。
随机抽取40位参加该项计划的样本,结果显示:样本的体重平均减少7磅,标准差为32磅,则其原假设和备择假设是().A. H0:μ≤8,H1:μ>8 B。
H0:μ≥8,H1:μ〈8C. H0:μ≤7,H1:μ〉7 D。
H0:μ≥7,H1:μ<74 在假设检验中,不拒绝原假设意味着()。
A。
原假设肯定是正确的B。
原假设肯定是错误的C.没有证据证明原假设是正确的D.没有证据证明原假设是错误的5 在假设检验中,原假设和备择假设()。
A.都有可能成立B。
都有可能不成立C.只有一个成立而且必有一个成立D。
原假设一定成立,备择假设不一定成立6 在假设检验中,第一类错误是指().A。
当原假设正确时拒绝原假设B。
当原假设错误时拒绝原假设C。
当备择假设正确时拒绝备择假设 D.当备择假设不正确时未拒绝备择假设7 在假设检验中,第二类错误是指().A.当原假设正确时拒绝原假设B.当原假设错误时未拒绝原假设C。
当备择假设正确时未拒绝备择假设D。
当备择假设不正确时拒绝备择假设8 指出下列假设检验哪一个属于右侧检验()。
统计学概论课后答案第8章统计指数习题解答.

167第八章 对比分析与统计指数思考与练习4. 指出下列哪一个数量加权算术平均数指数,恒等于综合指数形式的拉 氏数量指标指数(C )。
C. d.6. 编制数量指标综合指数所采用的同度量因素是( a ) a .质量指标b .数量指标C •综合指标d •相对指标7. 空间价格指数一般可以采用( C )指数形式来编制。
a .拉氏指数 b.帕氏指数 C.马埃公式d.平均指数二、问答题:1.报告期与基期相比,某城一、选择题:1.某企业计划要求本月每万元产值能源消耗率指标比去年同期下降 实际降低了2.5%,则该项计划的计划完成百分比为( d )。
d. 102.6%5%a. 50.0%b. 97.4%c. 97.6% 2. 下列指标中属于强度相对指标的是(a..产值利润率 C.恩格尔系数3. 编制综合指数时, a .指数化指标 b. b. d.应固定的因素是( b基尼系数 人均消费支出C )。
个体指数c.同度量因素 d.被测定的因素S k q q 。
P 1 」2k q q 1 p 1S k q q o P 0 」 S k q q t p o;b. --------- ; c. -------- ; d. -------- a .S q 。
P 1送 q i P i S q o P o Z q i P o 5.之所以称为同度量因素,是因为:它可使得不同度量单位的现象总体转化为数量上可以加总; 客观上体现它在实际经济现象或过程中的份额 ;是我们所要测定的那个因素; 它必须固定在相同的时期。
(a )。
a .市居民消费价格指数为110%,居民可支配收入增加了20 %,试问居民的实际收入水平提高了多少?解:(1+20% /110%-100%=109.10%-100%=9.10%2.某公司报告期能源消耗总额为28.8万元,与去年同期相比,所耗能源的价格平均上升了20%那么按去年同期的能源价格计算,该公司报告期能源消耗总额应为多少?解:28.8 -(1+20%)=24 万元3.编制综合指数时,同度量因素的选择与指数化指标有什么关系?同度量因素为什么又称为权数?它与平均指数中的权数是否一致?解:(略)4.结构影响指数的数值越小,是否说明总体结构的变动程度越小?一般说来,当总体结构发生什么样的变动时,结构影响指数就会大于1。
统计学课后答案(第3版)第8章方差分析习题答案

第八章 方差分析习题答案一、单选1.D ;2.B ;3.A ;4.C ;5.C ;6.C ;7.C ;8.A ;9.B ;10.A二、多选1.ACE ;2.ABD ;3.BE ;4.AD ;5.BCE6.ABCD ;7.ABCDE ;8.ABCE ;9.ACD ;10.ABD三、计算分析题1、运用EXCEL 进行单因素方差分析,有:方差分析:单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 1.21 0.242 2.45E-05列 2 5 1.38 0.276 0.00226列 3 5 1.31 0.262 1.35E-05方差分析差异源 SS df MS F P-value F crit 组间 0.00292 2 0.00146 1.906005 0.191058 3.885294 组内 0.009192 12 0.000766总计 0.012112 14由于P 值=1.906005>05.0=α,不拒绝原假设,没有证据表明3个总体的均值之间有显著差异。
(或用F 值判断,有同样结论)2、运用EXCEL 进行单因素方差分析,有:方差分析:单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 222 44.4 28.3列 2 5 150 30 10列 3 5 213 42.6 15.8方差分析差异源 SS df MS F P-value F crit 组间 615.6 2 307.8 17.06839 0.00031 3.885294 组内 216.4 12 18.03333总计 832 14由于由于P 值=0.00031<05.0=α,拒绝原假设,表明3个总体的均值之间有显著差异。
(或用F 值判断,有同样结论)进一步用LSD 方法见教材P2063、(1)按行依次为:420、2、1.478(第一行);27、142.07(第二行);4256(第三行)。
(2)由于P 值=0.245946>05.0=α,不拒绝原假设,没有证据表明3种方法组装产品数量有显著差异。
统计学罗文宝主编 第八章时间序列分析单选题多选题参考答案

第八章 时间序列分析二、单项选择题1.根据时期数列计算序时平均数应采用( C )。
A 、几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法2.间隔相等的时点数列计算序时平均数应采用(D )。
A.几何平均法B.加权算术平均法C.简单算术平均法D.首末折半法3.数列中各项数值可以直接相加的时间数列是(B )。
A.时点数列B.时期数列C.平均指标动态数列D.相对指标动态数列4.时间数列中绝对数列是基本数列,其派生数列是(D )。
A. 时期数列和时点数列B. 绝对数时间数列和相对数时间数列C. 绝对数时间数列和平均数时间数列D.相对数时间数列和平均数时间数列5.下列数列中哪一个属于动态数列( D )。
A.学生按学习成绩分组形成的数列B.工业企业按地区分组形成的数列C.职工按工资水平高低排列形成的数列D.出口额按时间先后顺序排列形成的数列6.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为(B )。
7.说明现象在较长时期内发展的总速度的指标是(C )。
A 、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度8.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为(A )。
A.(102%×105%×108%×107%)-100%B. 102%×105%×108%×107%C. 2%×5%×8%×7%D. (2%×5%×8%×7%)-100%4201193195190+++、A 3193195190++、B 1422011931952190-+++、C 422011931952190+++、D9.平均发展速度是( C )。
A.定基发展速度的算术平均数B.环比发展速度的算术平均数C.环比发展速度的几何平均数D.增长速度加上100%10.若要观察现象在某一段时期内变动的基本趋势,需测定现象的( C )。
大学统计学第八章课后题答案
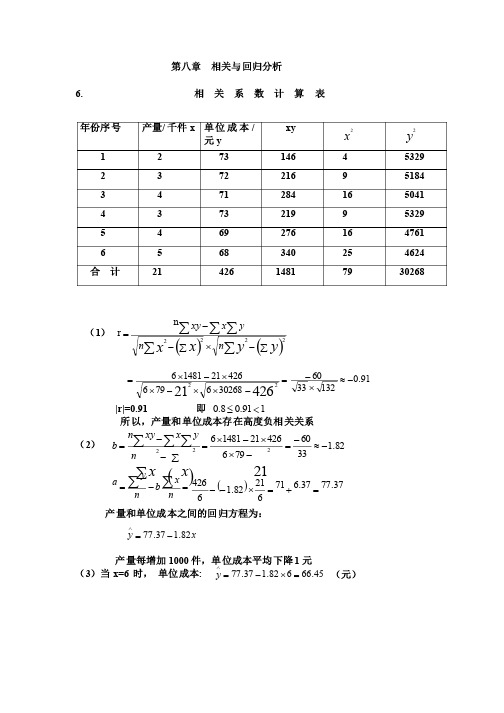
第八章 相关与回归分析 6. 相 关 系 数 计 算 表 (1) ()()åååååå-´å--=y yx x n n yx xy 2222nr 91.0132336030268679642621148164262122-»´-=-´´-´´-´= |r|=0.91 即 191.08.0<£ 所以,产量和单位成本存在高度负相关关系(2) ()82.133********211481621222-»-=-´´-´=å--=ååååx x n y x xy n b =-=åånx b ny a ()37.7737.67162182.16426=+=´-- 产量和单位成本之间的回归方程为: x y 82.137.77-=Ù 产量每增加1000件,单位成本平均下降1元 (3)当x=6 时, 单位成本: 45.66682.137.77=´-=Ùy (元) 年份序号 产量/千件x 单位成本/元y xy x 2 y 2 1 2 73 146 4 5329 2 3 72 216 9 5184 3 4 71 284 16 5041 4 3 73 219 9 5329 5 4 69 276 16 4761 6 5 68 340 25 4624 合 计 21 426 1481 79 30268 7. 相 关 系 数 计 算 表 序号 汽车使用年限/年x 年维修费用/元y xy x 2 y 2 1 2 400 800 4 160000 2 2 540 1080 4 291600 3 3 520 1560 9 270400 4 4 640 2560 16 409600 5 4 740 2960 16 547600 65 600 3000 25 360000 7 5 800 4000 25 640000 86 700 4200 36 490000 9 6 760 4560 36 577600 10 6 900 5400 36 810000 11 8 840 6720 64 705600 12 9 1080 9720 81 1166400 合 计 608520465603526428800()()åååååå-´å--=y yx x n n yx xy 2222n r=89.045552006244752064288001235212852060465601285206022»´=-´´-´´-´|r|=0.89 即 189.08.0<£所以,汽车使用年限与其维修费用间存在高度正相关关系(2) ()15.766244752035212852060465601260222==-´´-´=å--=ååååxx n y x xy n b =-=åån x b n y a 25.32975.380710126015.76128520=-=´- 汽车使用年限与其维修费用的回归方程为: x y 15.7625.329+=Ù(3) 当x=15时, 维修费用为: 5.14711515.7625.329=´+=Ùy8. (1) 相 关 系 数 计 算 表 序号 母亲身高/厘米x 女儿身高/厘米y xy x 2y 21 158 159 25122 24964 25281 2 159 160 25440 25281 256003 160 160 25600 25600 256004 161 163 26243 25921 265695 161 159 25599 25921 252816 155 154 23870 24025 237167 162 159 25758 26244 25281 8 157 158 24806 24649 24964 9 162 160 25920 26244 25600 10 150 157 23550 22500 24649 合计1585 1589251908251349252541()()åååååå-´å--=yy x x n n y x xy 2222nr=158915852225254110251349101589158525190810-´´-´´-´655.0»|r|=0.655 所以,母亲与女儿之间的关系为显著正相关(2) ()41.012655152513491015891585251908101585222»=-´´-´=å--=ååååxx n y x xy n b =-=åånx b n y a 915.93985.649.15810158541.0101589=-=´- 母亲与女儿之间的回归方程为: x y 41.0915.93+=Ù(3) 当x=170时, 女儿的身高为: 615.16317041.0915.93=´+=Ùy 9.(1) 由题知 n=9 å=546x å=260y å=16918xy 343622=åx()92.01114210302343629260546169189546222»=-´´-´=å--=ååååx x n yx xy n b =-=åånx b ny a 92.26954692.09260-=´-银行存款余额的直线回归方程: x y 92.092.26+-=Ù(2) 当x=400时,银行存款余额08.34140092.092.26=´+-=Ùy。
管理统计学习题参考答案第八章

第八章1. 解:(1)假设检验的基本思想是,样本平均数与总体平均数出现差异不外乎两种可能:一是改革后的总体平均长度不变,但由于抽样的随机性使样本平均数与总体平均数之间存在抽样误差;二是由于工艺条件的变化,使总体平均数发生了显著的变化。
因此,可以这样推断:如果样本平均数与总体平均数之间的差异不大,未超出抽样误差范围,则认为总体平均数不变;反之,如果样本平均数与总体平均数之间的差异超出了抽样误差范围,则认为总体平均数发生了显著的变化。
根据样本平均数的抽样分布定理,有x Z σx μ±=或Z /σμx x ≤-。
当0=Z 时,表明样本均值等于总体均值,即μx =;当Z 很大时,表明样本均值离总体均值很远,即∆很大。
后一种情况是小概率事件。
在正常情况下,小概率事件是不会发生的,那么在一次抽样中小概率事件居然发生了,我们就有理由认为样本均值是不正常的,它与原总体相比,性质已经发生变化,应该拒绝接受原假设。
(2)假设检验的一般步骤包括:① 提出原假设和备择假设;对每个假设检验问题,一般可同时提出两个相反的假设:原假设和备择假设。
原假设又称零假设,是正待检验的假设,记为H 0;备择假设是拒绝原假设后可供选择的假设,记为H 1。
原假设和备择假设是相互对立的,检验结果二者必取其一。
接受H 0,则必须拒绝H 1;反之,拒绝H 0则必须接受H 1。
② 选择适当的统计量,并确定其分布形式;不同的假设检验问题需要选择不同的统计量作为检验统计量。
在例中,我们所用的统计量是Z ,在H 0为真时,N Z ~(0,1)。
③选择显著性水平α,确定临界值;显著性水平表示H 0为真时拒绝H 0的概率,即拒绝原假设所冒的风险,用α表示。
假设检验就是应用了小概率事件实际不发生的原理。
这里的小概率就是指α。
但是要小到什么程度才算小概率? 对此并没有统一的标准。
通常取α=0.1,0.05,0.01。
给定了显著性水平α,就可由有关的概率分布表查得临界值,从而确定H 0的接受区域和拒绝区域。
统计学贾俊平_第四版课后习题答案第八章

姓名:潘方 学号:1106026 班级:金融一班8.2 解:根据题目的分析,本题采用左单侧检验:已知:μ0=700,x =680,σ=60, n=36,α=0.05则z α=1.645 其过程为: H 0:μ≥700 H 1:μ<700 x z ==-2 因为|z|>|z α|,Z 值位于拒绝域,故拒绝原假设,说明这批产品不合格。
因为2=Z ,且为左单侧检验,则()05.0022750132.0977249868.01=<=-=αP8.4 解:由excel 计算得:x =99.9778 S =1.21221H 0:μ=100 H 1:μ≠100 x t =-0.055 这是一个双侧检验,当α=0.05,自由度n -1=9时,得()29t α=2.262。
因为t <|2t α|,t 值位于接受区域,故接受原假设,说明打包机工作正常。
因为|Z|=0.055,且为双侧检验,由excel 得: P=0.95734>(α=0.05)8.9解:该题样本为,大样本,方差2σ已知、且不等,因此采用z 统计量 已知, 05.0=α、即96.12/=αZ ,811=n , 642=n ,σA=63*63 2σB=57*57 0:211≠-μμH 0:210=-μμH , ()()96.15.0645781630102010702222<≈+--=+---=BB A AB A B A n n x x Z σσμμ 因为|z|<|z α|,Z 值位于接受区域,故接受原假设,两厂生产材料抗压强度相同。
因为5.0=Z ,则()=-⨯=691462461.012P 0.617075078()05.0=>α8.13 解:此题为两个总体比例之差的假设H 0:π1≥π2;H 1:π1<π 2 α=0.05,即z α=1.6451100021==n n ,00945.0110001041==p ,01718.0110001892==pp p d z --=0.009450.017180--=-5 因为|z|>|z α|,Z 值位于拒绝域,故拒绝原假设,说明用阿司匹林可以降低心脏病发生率。
人大版统计学习题加答案 第八章 指数

统计指数分析练习题一、填空题1. 是表明社会现象复杂经济总体的数量对比关系的相对数。
2. 指数按其指标的作用不同,可分为 和 。
3.总指数的编制方法,其基本形式有两种:一是 ,二是 。
4. 编制质量指标综合指数,一般是以 为同度量因素,并将其固定在 。
5. 编制数量指标综合指数,一般是以 为同度量因素,并将其固定在 。
二、选择1.设p 表示商品的价格,q 表示商品的销售量,1011q p q p ∑∑说明了( )。
A 在基期销售量条件下,价格综合变动的程度B 在报告期销售量条件下,价格综合变动的程度C 在基期价格水平下,销售量综合变动的程度D 在报告期价格水平下,销售量综合变动的程度2.某市居民以相同的人民币在物价上涨后少购商品15%,则物价指数为( )。
A 17.6% B 85% C 115% D 117.6%3. 某商店报告期与基期相比,商品销售额增长6.5%,商品销售量增长6.5%,则商品价格( )。
A 增长13%B 增长6.5%C 增长1%D 不增不减4.某种产品报告期与基期比较产量增长26%,单位成本下降32%,则生产费用支出总额为基期的( )。
A 166.32%B 85.68%C 185%D 54%5.某商店本年同上年比较,商品销售额没有变化,而各种商品价格上涨了7%,则商品销售量增的百分比为( )。
A -6.54%B –3%C 6.00%D 14.29% 三、判断题1.指数的实质是相对数,它能反映现象的变动和差异程度。
( ) 2.在实际应用中,计算价格指数通常以基期数量指标为同度量因素。
( ) 3.某企业职工人数比去年减少2%,而全员劳动生产率比去年提高5%,则企业总产值增长了7%。
( )4.拉氏价格指数和派氏价格指数计算结果不同,是因为拉氏价格指数主要受报告期商品结构的影响,而派氏价格指数主要受基期商品结构的影响。
( )5.如果各种商品的销售量平均上涨5%,销售价格平均下降5%,则销售额不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、选择题1某厂生产的化纤纤度服从正态分布,纤维的纤度的标准均值为1.40.某天测得25根纤维的纤度的均值x=1.39,检验与原来设计的标准均值相比是否有所变化,要求的显著性水平为α=0。
05,则下列正确的假设形式是()。
A。
H0:μ=1.40,H1:μ≠1。
40 B. H0:μ≤1.40,H1:μ〉1.40C。
H0:μ<1.40,H1:μ≥1.40 D. H0:μ≥1.40,H1:μ〈1。
402某一贫困地区估计营养不良人数高达20%,然而有人认为这个比例实际上还要高,要检验该说法是否正确,则假设形式为()。
A。
H0:π≤0.2,H1:π>0.2 B. H0:π=0.2,H1:π≠0.2C. H0:π≥0.3,H1:π<0。
3 D。
H0:π≥0.3,H1:π<0.33 一项新的减肥计划声称:在计划实施的第一周内,参加者的体重平均至少可以减轻8磅。
随机抽取40位参加该项计划的样本,结果显示:样本的体重平均减少7磅,标准差为32磅,则其原假设和备择假设是()。
A。
H0:μ≤8,H1:μ〉8 B。
H0:μ≥8,H1:μ〈8C.H0:μ≤7,H1:μ>7 D. H0:μ≥7,H1:μ〈74 在假设检验中,不拒绝原假设意味着()。
A。
原假设肯定是正确的B。
原假设肯定是错误的C。
没有证据证明原假设是正确的 D.没有证据证明原假设是错误的5 在假设检验中,原假设和备择假设()。
A。
都有可能成立B。
都有可能不成立C。
只有一个成立而且必有一个成立D.原假设一定成立,备择假设不一定成立6在假设检验中,第一类错误是指()。
A。
当原假设正确时拒绝原假设 B。
当原假设错误时拒绝原假设C.当备择假设正确时拒绝备择假设 D。
当备择假设不正确时未拒绝备择假设7在假设检验中,第二类错误是指()。
A。
当原假设正确时拒绝原假设 B.当原假设错误时未拒绝原假设C.当备择假设正确时未拒绝备择假设 D.当备择假设不正确时拒绝备择假设8 指出下列假设检验哪一个属于右侧检验()。
A。
H0:μ=μ0, H1:μ≠μ0 B。
H0:μ≥μ0, H1:μ<μ0C.H0:μ≤μ0, H1:μ〉μ0 D.H0 :μ>μ0, H1:μ≤μ09 指出下列假设检验哪一个属于左侧检验()。
A. H0:μ=μ0, H1:μ≠μ0B. H0:μ≥μ0 ,H1:μ<μ0C. H0:μ≤μ0, H1:μ>μ0 D. H0:μ〉μ0,H1:μ≤μ010指出下列假设检验哪一个属于双侧检验().A。
H0:μ=μ0, H1:μ≠μ0 B.H0:μ≥μ0, H1:μ〈μ0C 。
H 0:μ≤μ0, H1:μ〉μ0 D. H 0:μ〉μ0, H 1:μ≤μ011 指出下列假设检验形式的写法哪一个是错误的()。
A 。
H 0:μ=μ0, H 1:μ≠μ0 B. H 0:μ≥μ0 , H 1:μ<μ0C 。
H 0:μ≤μ0, H 1:μ>μ0 D. H 0:μ>μ0, H 1:μ≤μ012 如果原假设H 0为真,所得到的样本结果会像实际观测结果那么极端或更极端的概率称为()。
A.临界值 B .统计量 C.P 值 D .事先给定的显著性水平13 P值越小().A.拒绝原假设的可能性越小 B 。
拒绝原假设的可能性越大C .拒绝备择假设的可能性越大 D.不拒绝备择假设的可能性越小14 对于给定的显著性水平α,根据P 值拒绝原假设的准则是()。
A 。
P=αB .P 〈αC .P>αD 。
P=α=015 在假设检验中,如果所计算出的P值越小,说明检验的结果()。
A.越显著 B 。
越不显著 C.越真实 D.越不真实16 在大样本情况下,检验总体均值所使用的统计量是().A.0x Z n μσ-= B 。
02x Z nμσ-= C. 0x t s n μ-= D. 0x Z s n μ-= 17 在小样本情况下,当总体方差未知时,检验总体均值所使用的统计量是(). A.0x Z n μσ-= B. 02x Z nμσ-= C. 0x t s n μ-=D. 0x Z s n μ-=18 在小样本情况下,当总体方差已知时,检验总体均值所使用的统计量是(). A.x Z= B. 02x Z n μσ-= C. 0x t s n μ-= D. 0x Z s nμ-=19 检验一个正态总体的方差时所使用的分布为().分布 D.F分布A。
正态分布B。
t分布C.220一种零件的标准长度5cm,要检验某天生产的零件是否符合标准要求,建立的原假设和备择假设应为()。
A。
H0:μ=5,H1:μ≠5 B。
H0:μ≠5,H1:μ=5C.H0:μ≤5,H1:μ>5 D. H0:μ≥5,H1:μ<521 一项研究表明,中学生中吸烟的比例高达30%,为检验这一说法是否属实,建立的原假设和备择假设应为()。
A. H0:μ=30%,H1:μ≠30% B.H0:π=30%,H1:π≠30%C.H0:π≥30%,H1:π<30% D.H0:π≤30%,H1:π>30%22 一项研究表明,司机驾车时因接打手机而发生事故的比例超过20%,用来检验这一结论的原假设和备择假设应为()。
A. H0:π=20%,H1:π≠20% B.H0:π≠20%,H1:π=20%C. H0:π≥20%,H1:π<20%D. H0:π≤20%,H1:π>20%23某企业每月发生事故的平均次数为5次,企业准备制定一项新的安全生产计划,希望新计划能减少事故次数.用来检验这一计划有效性的原假设和备择假设应为().A. H0:μ=5,H1:μ≠5 B. H0:μ≠5,H1:μ=5C. H0:μ≤5,H1:μ〉5 D. H0:μ≥5,H1:μ<524环保部门想检验餐馆一天所用的快餐盒平均是否超过600个,建立的原假设和备择假设应为().A. H0:μ=600,H1:μ≠600B。
H0:μ≠600,H1:μ=600C. H0:μ≤600,H1:μ>600D.H0:μ≥600,H1:μ<60025 随机抽取一个n=100的样本,计算得到x=60,s=15,要检验假设H0:μ=65,H1:μ≠65,检验的统计量为().A.-3.33 B.3.33 C.-2。
36 D.2。
3626 随机抽取一个n=50的样本,计算得到x-=60,s=15,要检验假设H0:μ=65,H1:μ≠65,检验的统计量为()。
A。
-3.33 B。
3.33 C.—2.36 D.2。
3627 若检验的假设为H0:μ=μ0,H1:μ≠μ0,则拒绝域为()。
A.z>zαB。
z〈— zαC.z> zα/2或z〈- zα/2D.z> zα或z〈- zα28 若检验的假设为H0:μ≥μ0,H1:μ〈μ0,则拒绝域为()。
A.z〉zαB。
z<— zα C.z〉zα/2或z<— zα/2 D.z> zα或z〈- zα29 若检验的假设为H0:μ≤μ0,H1:μ>μ0,则拒绝域为()。
A.z>zα B.z<- zα C.z> zα/2或z<— zα/2 D.z〉 zα或z<- zα30 设zc为检验统计量的计算值,检验的假设为H0:μ≤μ0,H1:μ〉μ0,当z c=1.645时,计算出的P值为()。
A.0.025 B.0。
05 C。
0.01 D。
0.002531设zc为检验统计量的计算值,检验的假设为H0:μ≤μ0,H1:μ〉μ0,当zc=2.67时,计算出的P值为()。
A.0.025 B。
0.05 C。
0。
003 8 D。
0.002 532一家汽车生产企业在广告中宣称“该公司的汽车可以保证在2年或24 000公里内无事故”,但该汽车的一个经销商认为保证“2年”这一项是不必要的,因为汽车车主在2年内行驶的平均里程超过24000公里。
假定这位经销商要检验假设H0:μ≤24 000,H1:μ〉24 000,取显著性水平为α=001,并假设为大样本,则此项检验的拒绝域为()。
A.z〉2。
33 B。
z〈-2.33 C.|z|〉2。
33D。
z=2.3333 一家汽车生产企业在广告中宣称“该公司的汽车可以保证在2年或24 000公里内无事故”,但该汽车的一个经销商认为保证“2年”这一项是不必要的,因为汽车车主在2年内行驶的平均里程超过24 000公里。
假定这位经销商要检验假设H0:μ≤24 000,H1:μ〉24000,抽取容量n=32个车主的一个随机样本,计算出两年行驶里程的平均值=24 517公里,标准差为s=1 866公里,计算出的检验统计量为()。
A。
z=1。
57B.z=—1.57 C。
z=2。
33 D。
z=—2.3334 由49个观测数据组成的随机样本得到的计算结果为∑x=50.3,∑x2=68,取显著性水平α=0。
01,检验假设H0:μ≥1。
18,H1:μ〈1.18,得到的检验结论是().A.拒绝原假设B.不拒绝原假设C.可以拒绝也可以不拒绝原假设 D.可能拒绝也可能不拒绝原假设35 一项研究发现,2000年新购买小汽车的人中有40%是女性,在2005年所作的一项调查中,随机抽取的120个新车主中有57人为女性,在α=0.05的显著性水平下,检验2005年新车主中女性的比例是否有显著增加,建立的原假设和备择假设为H0:π≤40%,H1:π>40%,检验的结论是()。
A.拒绝原假设B。
不拒绝原假设C.可以拒绝也可以不拒绝原假设D。
可能拒绝也可能不拒绝原假设36 从一个二项总体中随机抽出一个n=125的样本,得到p=0.73,在α=0。
01的显著性水平下,检验假设H0:π=0。
73, H1:π≠0.73,所得的结论是()。
A.拒绝原假设 B。
不拒绝原假设C.可以拒绝也可以不拒绝原假设 D.可能拒绝也可能不拒绝原假设37 从正态总体中随机抽取一个n=25的随机样本,计算得到x=17,s2=8,假定σ20=10,要检验假设H0:σ2=σ20,则检验统计量的值为()。
A.2χ=19.2 B.2χ=18。
7 C。
2χ=30.38 D。
2χ=39.638 从正态总体中随机抽取一个n=10的随机样本,计算得到x=231.7,s=15.5,假定σ20=50,在α=0.05的显著性水平下,检验假设H0:σ2≥20, H1:σ2〈20,得到的结论是()。
A.拒绝H0 B.不拒绝H0C。
可以拒绝也可以不拒绝H0 D.可能拒绝也可能不拒绝H039 一个制造商所生产的零件直径的方差本来是0。
00156。
后来为削减成本,就采用一种费用较低的生产方法。
从新方法制造的零件中随机抽取100个作样本,测得零件直径的方差为0.00211。
在α=0.05的显著性水平下,检验假设H0:σ2≤0。
