用-全等三角形的判定(总复习)ppt课件
合集下载
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三 角形中。
②分析要证两个三角形全等,已有什么条件,还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E,BC=ED AF⊥CD 求证:点F是CD的中点
分析:要证CF=DF可以考虑CF 、 DF所在的两个三角形全等,为此可 添加辅助线构建三角形全等 ,如何 添加辅助线呢?
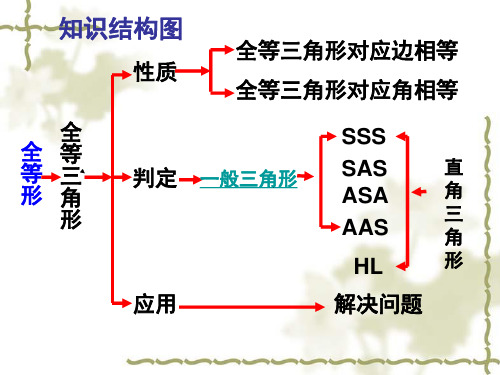
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上,△ABD,△BCE都是等边 三角形,AE交BD于F,DC交BE于G,求证:BF=BG。
AB
=
DB
∠ABE = ∠ DBC
BE=BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3: 已知一边一角(边与角相邻):
找夹这个角的另一边
AD=CB (SAS)
找夹这条边的另一角
∠ACD=∠CAB(ASA)
找边的对角
∠D=∠(B AAS)
15
如图,已知∠B= ∠E,要识别△ABC≌ △AED,需 要添加的一个条件是--------------
A
D
C
E
思路4:
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中,AE < AB+BE=AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA, CD过点E,则AB与AC+BD相等吗?请说明理由。
C A
∵ QD⊥OA,QE⊥OB,QD=QE(已知). ∴点Q在∠AOB的平分线上.(到角的两边的距
离相等的点在角的平分线上)
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等
全等三角形判定ppt课件

若两个三角形全等,则它们的周长也 相等。
对应角相等
在全等三角形中,任意两个对应 的角都相等。
若两个三角形全等,则它们的内 角和也相等,且均为180度。
可以通过测量两个三角形的三个 内角来判断它们是否全等。
面积相等
若两个三角形全等,则它们的面积也相等。 可以通过计算两个三角形的面积来判断它们是否全等。
1 2
定义
两边和它们的夹角分别相等的两个三角形全等。
图形语言
若a=a',∠B=∠B',b=b',则⊿ABC≌⊿A'B'C'。
3
符号语言
∵a=a',∠B=∠B',b=b',∴⊿ABC≌⊿A'B'C'( SAS)。
角边角判定法(ASA)
01
02
03
定义
两角和它们的夹边分别相 等的两个三角形全等。
图形语言
实例1
证明两个三角形全等并求出未知 边长
实例2
利用全等三角形判定方法证明两个 四边形面积相等
实例3
利用全等三角形判定方法解决一个 实际问题,如测量一个不可直接测 量的距离
06
总结与展望
判定全等三角形的方法总结
三边分别相等的两个三角形全等。这是最基本的判定 方法,通过比较三角形的三边长度来确定两个三角形
证明过程
可以通过AAS(角角边)全等条件进行证明,即 如果两个三角形有两个角和其中一个角的对边分 别相等,则这两个三角形全等。这也是一种常用 的全等三角形判定方法。
实际应用举例
在实际应用中,角角边判定法常用于解决与角度 和边长有关的问题。例如,在建筑设计中,如果 需要确保两个建筑结构的角度和边长完全相等, 就可以利用角角边判定法来进行验证。
用全等三角形的判定总复习ppt课件

7.如图(5)∠CAE=∠BAD,∠B=∠D,
AC=AE,△ABC与△ADE全等吗?为什么?
B
解:∵ ∠CAE=∠BAD(已知)
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量,和相等) 即∠BAC=∠DAE
在△ABC和△ADE中,
∠B=∠D(已知)
∠BAC=∠DAE(已证)
AC=AE(已知)
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
分析:现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
要使△ABD≌△ACD, • 根据“SAS”需要添加条件 AB=AC ; • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
D
C
; ;
友情提示:添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
8
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
12
D
E
M
N
B
C
创造条件! ? 6
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
《三角形全等的判定》全等三角形PPT课件

好的△ ′′′剪下来,放到△ 上,它们全等吗?
画一个△ ′′′,使′′ = ,′’ =
,∠′ = ∠:
(1)画∠′ = ∠;
(2)在射线′上截取′′ = ,在
射线′上截取′′ = ;
(3)连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说,三角形的两
⫽ .
∠4. 求证:∠5 = ∠6.
∵ ∠1 = ∠2,∠3 = ∠4, = ,
根据易证△ ≌△ ,
∴有 = ,
又∵ ∠3 = ∠4, = ,
则可根据判定△ ≌△ ,
故∠5 = ∠6.
知识梳理
例4:如图,、交于点,、为上两点, = , =
就全等了.如果满足斜边和一条直角边分别相等,这两个直
角三角形全等吗?
教学新知
探索5:任意画出一个△,使∠=90°.再画一个 △ ′’’,使
∠′=90°,′′=,′′=.把画好的△′′′剪下来,放
到△上,它们全等吗?
画 一 个 △ ′′′ , 使 ∠′ = 90° , ′′ =
求证 = .
∵⊥,⊥
∴∠与∠都是直角
在R △ 和Rt △ 中,
=
=
∴ △ ≌ △ ()
∴ = .
知识梳理
知识点1:“边边边”(或“SSS”)
1.三边分别相等的两个三角形全等(可以简写成“边边边”
两个三角形全等吗?上述六个条件中,有些条件是相关的.
能否在上述六个条件中选择部分条件,简捷地判定两个三角
形全等呢?
探索1:先任意画出一个△ ABC.再画一个△ A′B′C′,使△ ABC与
△ A′B′C′满足上述六个条件中的一个(一边或一角分别
相等)或两个(两边、一边一角或两角分别相等).你
画一个△ ′′′,使′′ = ,′’ =
,∠′ = ∠:
(1)画∠′ = ∠;
(2)在射线′上截取′′ = ,在
射线′上截取′′ = ;
(3)连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说,三角形的两
⫽ .
∠4. 求证:∠5 = ∠6.
∵ ∠1 = ∠2,∠3 = ∠4, = ,
根据易证△ ≌△ ,
∴有 = ,
又∵ ∠3 = ∠4, = ,
则可根据判定△ ≌△ ,
故∠5 = ∠6.
知识梳理
例4:如图,、交于点,、为上两点, = , =
就全等了.如果满足斜边和一条直角边分别相等,这两个直
角三角形全等吗?
教学新知
探索5:任意画出一个△,使∠=90°.再画一个 △ ′’’,使
∠′=90°,′′=,′′=.把画好的△′′′剪下来,放
到△上,它们全等吗?
画 一 个 △ ′′′ , 使 ∠′ = 90° , ′′ =
求证 = .
∵⊥,⊥
∴∠与∠都是直角
在R △ 和Rt △ 中,
=
=
∴ △ ≌ △ ()
∴ = .
知识梳理
知识点1:“边边边”(或“SSS”)
1.三边分别相等的两个三角形全等(可以简写成“边边边”
两个三角形全等吗?上述六个条件中,有些条件是相关的.
能否在上述六个条件中选择部分条件,简捷地判定两个三角
形全等呢?
探索1:先任意画出一个△ ABC.再画一个△ A′B′C′,使△ ABC与
△ A′B′C′满足上述六个条件中的一个(一边或一角分别
相等)或两个(两边、一边一角或两角分别相等).你
全等三角形的判定ppt课件

全等三角形也是数学竞赛中常见 的考点之一,涉及到的知识点包
括边角关系、判定方法等。
02
全等三角形的判定方法
边边边定理
总结词
三边对应相等的两个三角形全等 。
详细描述
根据三角形的基本性质,如果两 个三角形的三边长度相等,则这 两个三角形必然全等。
边角边定理
总结词
两边对应相等且夹角相等的两个三角 形全等。
全等三角形的判定
• 全等三角形概述 • 全等三角形的判定方法 • 全等三角形的证明步骤 • 全等三角形在几何中的应用 • 全等三角形的实际应用案例
01
全等三角形概述
全等三角形的定义
定义
两个三角形全等,是指能够完全重合的两个三角形,即它们的形状相同,大小 也相同。
符号表示
记作△ABC≌△DEF或ABCDH≌EFGH。
全等三角形在几何中的其他应用
证明其ቤተ መጻሕፍቲ ባይዱ几何命题
通过证明两个三角形全等,可以证明一些其他几何命题,比如平 行线性质、勾股定理等。
研究三角形和多边形的性质
利用全等三角形研究三角形和多边形的性质,可以发现一些新的几 何定理和性质。
解决其他实际问题
利用全等三角形解决其他实际问题,比如面积计算、周长计算等。
THANKS
证明线段相等
总结词
全等三角形的对应边相等
详细描述
全等三角形的对应边也称为对应边。因此,全等三角形的对应边是相等的。这个性质常常被用来证明 两条线段相等。
证明线段垂直
总结词
全等三角形可以用来证明线段垂直
详细描述
在几何图形中,有时候需要证明某条线段与 另一条线段垂直。这时,可以利用全等三角 形的性质,通过证明两个三角形全等来证明 这两条线段垂直。
13.3 全等三角形的判定 - 第1课时课件(共18张PPT)

使用几何拼接条探究三个元素相等的三角形是否全等?1.用绿色、蓝色、橙色拼条为边长作2个三角形,把两个三角形比较,它们能重合吗?2.用红色、蓝色、黄色拼条为边长作2个三角形,把两个三角形比较,它们能重合吗?
三角相等:
三边相等:
基本事实一
如果两个三角形的三边对应相等,那么这两个三角形全等.
基本事实一可简记为“边边边”或“SSS”.
拓展提升
1.如图,已知AB=AE,AD=AC,BC=ED,BC,DE交于点O.求证:∠BAD=∠EAC.
证明:在△BAC和△EAD中,AB=AE,AC=AD,BC=ED.∴△BAC≌△EAD(SSS).∴∠BAC=∠EAD.∴∠BAC-∠DAC=∠EAD-∠DAC,即∠BAD=∠EAC.
归纳小结
能够完全重合的两个三角形叫做全等三角形.
全等三角形的性质:全等三角形的对应边相等,对应角相等.
探究一
新知探究
知识点1 边边边
通过作图探究一个元素相等能否判定两个三角形全等?
一条边相等:
一个角相等:
探究二
通过几何拼接条探究两个元素相等的三角形是否全等?
两条边相等:
两个角相等:
一边一角相等:
探究三
探究四
知识点2 三角形的稳定性
用拼接条制作三角形和四边形框架,并拉动它们,你发现了什么?
三角形的形状和大小是固定不变的,而四边形的会改变.
三角形所具有的这一性质叫做三角形的稳定性.四边形具有不稳定性.
在生活中,我们经常会看到应用三角形稳定性的例子.
在生活中,我们也经常会看到应用四边形不稳定性的例子.
随堂练习
1.已知:如图,AB=EF,AC=ED,BF=CD.求证:∠A=∠E.
证明:∵BF=CD,∴BF+FC=CD+FC∴BC=FD∵AB=EF,AC=ED∴△ABC≌△EFD(SSS)∴∠A=∠E.
三角相等:
三边相等:
基本事实一
如果两个三角形的三边对应相等,那么这两个三角形全等.
基本事实一可简记为“边边边”或“SSS”.
拓展提升
1.如图,已知AB=AE,AD=AC,BC=ED,BC,DE交于点O.求证:∠BAD=∠EAC.
证明:在△BAC和△EAD中,AB=AE,AC=AD,BC=ED.∴△BAC≌△EAD(SSS).∴∠BAC=∠EAD.∴∠BAC-∠DAC=∠EAD-∠DAC,即∠BAD=∠EAC.
归纳小结
能够完全重合的两个三角形叫做全等三角形.
全等三角形的性质:全等三角形的对应边相等,对应角相等.
探究一
新知探究
知识点1 边边边
通过作图探究一个元素相等能否判定两个三角形全等?
一条边相等:
一个角相等:
探究二
通过几何拼接条探究两个元素相等的三角形是否全等?
两条边相等:
两个角相等:
一边一角相等:
探究三
探究四
知识点2 三角形的稳定性
用拼接条制作三角形和四边形框架,并拉动它们,你发现了什么?
三角形的形状和大小是固定不变的,而四边形的会改变.
三角形所具有的这一性质叫做三角形的稳定性.四边形具有不稳定性.
在生活中,我们经常会看到应用三角形稳定性的例子.
在生活中,我们也经常会看到应用四边形不稳定性的例子.
随堂练习
1.已知:如图,AB=EF,AC=ED,BF=CD.求证:∠A=∠E.
证明:∵BF=CD,∴BF+FC=CD+FC∴BC=FD∵AB=EF,AC=ED∴△ABC≌△EFD(SSS)∴∠A=∠E.
三角形全等的判定ppt课件

∴△ABC≌△A1B1C1(AAS)
5.HL(H.L.) 在Rt△ABC与Rt△A1B1C1中,
AB=A1B1(已知)
BC=B1C1(已证) ∴△ABC≌△A1B1C1(HL)
例题精讲
例:已知:如图,点A,C,B,D在同一条直线上,
AC=BD,AM=CN,BM=DN 求证:AM∥CN,BM∥DN.
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
为BC边的中点,那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明:∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD(SSS)
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
证明:∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND(SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN,BM∥DN
例:如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,
AE=FC
求证:△ABC≌△FDE.
(2)全等三角形对应角相等
PART II 全等三角形的判定 1.SSS(S.S.S.) 在△ABC与△A1B1C1中,
AB=A1B1(已知) BC=B1C1(已知) AC=A1C1(已证)
∴△ABC≌△A1B1C1(SSS)
5.HL(H.L.) 在Rt△ABC与Rt△A1B1C1中,
AB=A1B1(已知)
BC=B1C1(已证) ∴△ABC≌△A1B1C1(HL)
例题精讲
例:已知:如图,点A,C,B,D在同一条直线上,
AC=BD,AM=CN,BM=DN 求证:AM∥CN,BM∥DN.
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
为BC边的中点,那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明:∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD(SSS)
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
证明:∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND(SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN,BM∥DN
例:如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,
AE=FC
求证:△ABC≌△FDE.
(2)全等三角形对应角相等
PART II 全等三角形的判定 1.SSS(S.S.S.) 在△ABC与△A1B1C1中,
AB=A1B1(已知) BC=B1C1(已知) AC=A1C1(已证)
∴△ABC≌△A1B1C1(SSS)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
如图小明线的段设A计B是方一案:个先池在塘池的塘长旁度取,一个能直 接现到在达想A测和量B处这的个点池C塘,连的结长A度C并,延在长至D点, 使连等水方A结于上法CCA较测=D,D量方,BC两用便不,点米连地方的尺结把便距测B池,C离出并塘你。D延的有E请的长长什你长至度么说,E明点测好这理,量的个由使长。B度C=就EC, 出来吗?想想看。
SSS(边边边) SAS(边角边) ASA(角边角) AAS(角角边)
有三边对应相 等的两个三角形 全等.
有两边和它们的 夹角对应相等的 两个三角形全等.
有两角和它们的夹 边对应相等的两个 三角形全等.
有两角和及其中 一个角所对的边对 应相等的两个三角 形全等.
.
3知识梳理:A来自ABC
SSA不能
A
判定全等
∴AE-FE=CF-EF(等量减等量,差相等)
即AF=CE
F
在△AFD和△CEB中,
AF=CE(已证)
∠AFD=∠CEB(已知)
B
DF=BE(已知)
∴△AFD≌△CEB (SAS)
.
D E
C
11
7.如图(5)∠CAE=∠BAD,∠B=∠D,
AC=AE,△ABC与△ADE全等吗?为什么?
B
解:∵ ∠CAE=∠BAD(已知)
为什么?
解答
C
8.“三月三,放风筝”如图(6)是小东同学自己
做的风筝,他根据AB=AD,BC=DC,不用度量,
就知道∠ABC=∠ADC。请用所学的知识给予说
明。
解答 .
D A
10
6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
A 解:∵AE=CF(已知)
∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应 边相等) ∴ ∠ABC=45 °.选DD
.
14、已知:ΔABC和ΔBDE是等边三角
形, 点D在AE的延长线上。
学习提示:公共边,公共角,
O B 图(3)C
对顶角这些都是隐含的边,角相等的条件!
.
8
二.添条件判全等
B
4、如图,已知AD平分∠BAC,A
要使△ABD≌△ACD, • 根据“SAS”需要添加条件 AB=AC ; • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
.
实际运用
9. 测量如图河的宽度,某人在河的对岸找到一参照物 树木A,视线 AB与河岸垂直,然后该人沿河岸 步行10步(每步约0.75M)到O处,进行标记, 再向前步行10步到D处,最后背对河岸向前步行20 步,此时树木A,标记O,恰好在同一视线上,则
河的宽度为 15 米。
A
B
O
D
.
14
C
如图是用两根长度相等的拉线固定电线杆的 示意图.其中一根拉到B,另一根拉到C。那么C、 B两端点到D的距离DC和DB的大小有何关系?说明 理由。
例、如图,已知AB=AC,AD=AE,AB、DC相交
于点M,AC、BE相交于点N,∠1=∠2,试说明:
(1) △ABE ≌ △ACD (2)AM=AN A
12
D
E
M
N
B
C
创造条件! ?
.
7
一、挖掘“隐含条件”判全等
AD
1.如图(1),AB=CD,AC=BD,则
△ABC≌△DCB吗?说说理由
B 图(1) C
2.如图(2),点D在AB上,点E在AC上, B
D
CD与BE相交于点O,且AD=AE,AB=AC.若 O
A
∠B=20°,CD=5cm,则 ∠C= 20°,BE= 5.说cm说理由.
E C 图(2)
3.如图(3),AC与BD相交于O,若
A
D
OB=OD,∠A=∠C,若AB=3cm3c,m 则
CD=
. 说说理由.
B
C
D
B D
.
.
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
.
分析:现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
第4讲 全等三角形的判定
.
1
知识点
定义:能够
的两个三角形
全 等
对应元素:对应_____、对应
、对应
。
三 性质:全等三角形的对应边
角 形
全等三角形的
、
、
。
也对应相等。
判定: 、
、
、
。
全等三角形的画图:
利用直尺和圆规,根据 、 、 的 方法都可画出与已知三角形全等的三角形。
.
三角形全等的4个种判定公理:
D
C
; ;
友情提示:添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
.
9
三、熟练转化“间接条件”判全等 A
D
6如图,AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
解答
FE
B
C
B
7.如图(5)∠CAE=∠BAD,∠B=∠D, E AC=AE,△ABC与△ADE全等吗?
AC=DC
A
B
∠ACB=∠DCE
BC=EC
C
△ACB≌△DCE(SAS)
E
D
. AB=DE
典型例题:
例8 :如图在 ΔABC中, AD⊥BC于D,BE⊥AC 于E,AD交BE于F, 若BF=AC,那么∠ABC 的大小是( )
A.40° B.50° C.60° D.45°B
A
1 FE 2 DC
解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和 ΔBDF中
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量,和相等) 即∠BAC=∠DAE
在△ABC和△ADE中, ∠B=∠D(已知) ∠BAC=∠DAE(已证)
AC=AE(已知)
∴△ABC≌ △ADE .
(AAS)
12
典型例题:
例6 :如图,已知,AB=CD, CE=DF,AE=BF, 则AE∥DF吗?为什么?
A
B
C
E
D
F
证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即 AC=BD.
在ΔACE和ΔBDF中 AC=BD(已证) CE=DF (已知) AE=BF (已知)
∴ ΔACE≌ΔBDF(SSS)
∴∠E=∠F(全等三角形的对 应角相等) ∴ AE∥DF(内错角相等,两 直线平行)
如图小明线的段设A计B是方一案:个先池在塘池的塘长旁度取,一个能直 接现到在达想A测和量B处这的个点池C塘,连的结长A度C并,延在长至D点, 使连等水方A结于上法CCA较测=D,D量方,BC两用便不,点米连地方的尺结把便距测B池,C离出并塘你。D延的有E请的长长什你长至度么说,E明点测好这理,量的个由使长。B度C=就EC, 出来吗?想想看。
SSS(边边边) SAS(边角边) ASA(角边角) AAS(角角边)
有三边对应相 等的两个三角形 全等.
有两边和它们的 夹角对应相等的 两个三角形全等.
有两角和它们的夹 边对应相等的两个 三角形全等.
有两角和及其中 一个角所对的边对 应相等的两个三角 形全等.
.
3知识梳理:A来自ABC
SSA不能
A
判定全等
∴AE-FE=CF-EF(等量减等量,差相等)
即AF=CE
F
在△AFD和△CEB中,
AF=CE(已证)
∠AFD=∠CEB(已知)
B
DF=BE(已知)
∴△AFD≌△CEB (SAS)
.
D E
C
11
7.如图(5)∠CAE=∠BAD,∠B=∠D,
AC=AE,△ABC与△ADE全等吗?为什么?
B
解:∵ ∠CAE=∠BAD(已知)
为什么?
解答
C
8.“三月三,放风筝”如图(6)是小东同学自己
做的风筝,他根据AB=AD,BC=DC,不用度量,
就知道∠ABC=∠ADC。请用所学的知识给予说
明。
解答 .
D A
10
6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
A 解:∵AE=CF(已知)
∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应 边相等) ∴ ∠ABC=45 °.选DD
.
14、已知:ΔABC和ΔBDE是等边三角
形, 点D在AE的延长线上。
学习提示:公共边,公共角,
O B 图(3)C
对顶角这些都是隐含的边,角相等的条件!
.
8
二.添条件判全等
B
4、如图,已知AD平分∠BAC,A
要使△ABD≌△ACD, • 根据“SAS”需要添加条件 AB=AC ; • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
.
实际运用
9. 测量如图河的宽度,某人在河的对岸找到一参照物 树木A,视线 AB与河岸垂直,然后该人沿河岸 步行10步(每步约0.75M)到O处,进行标记, 再向前步行10步到D处,最后背对河岸向前步行20 步,此时树木A,标记O,恰好在同一视线上,则
河的宽度为 15 米。
A
B
O
D
.
14
C
如图是用两根长度相等的拉线固定电线杆的 示意图.其中一根拉到B,另一根拉到C。那么C、 B两端点到D的距离DC和DB的大小有何关系?说明 理由。
例、如图,已知AB=AC,AD=AE,AB、DC相交
于点M,AC、BE相交于点N,∠1=∠2,试说明:
(1) △ABE ≌ △ACD (2)AM=AN A
12
D
E
M
N
B
C
创造条件! ?
.
7
一、挖掘“隐含条件”判全等
AD
1.如图(1),AB=CD,AC=BD,则
△ABC≌△DCB吗?说说理由
B 图(1) C
2.如图(2),点D在AB上,点E在AC上, B
D
CD与BE相交于点O,且AD=AE,AB=AC.若 O
A
∠B=20°,CD=5cm,则 ∠C= 20°,BE= 5.说cm说理由.
E C 图(2)
3.如图(3),AC与BD相交于O,若
A
D
OB=OD,∠A=∠C,若AB=3cm3c,m 则
CD=
. 说说理由.
B
C
D
B D
.
.
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
.
分析:现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
第4讲 全等三角形的判定
.
1
知识点
定义:能够
的两个三角形
全 等
对应元素:对应_____、对应
、对应
。
三 性质:全等三角形的对应边
角 形
全等三角形的
、
、
。
也对应相等。
判定: 、
、
、
。
全等三角形的画图:
利用直尺和圆规,根据 、 、 的 方法都可画出与已知三角形全等的三角形。
.
三角形全等的4个种判定公理:
D
C
; ;
友情提示:添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
.
9
三、熟练转化“间接条件”判全等 A
D
6如图,AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
解答
FE
B
C
B
7.如图(5)∠CAE=∠BAD,∠B=∠D, E AC=AE,△ABC与△ADE全等吗?
AC=DC
A
B
∠ACB=∠DCE
BC=EC
C
△ACB≌△DCE(SAS)
E
D
. AB=DE
典型例题:
例8 :如图在 ΔABC中, AD⊥BC于D,BE⊥AC 于E,AD交BE于F, 若BF=AC,那么∠ABC 的大小是( )
A.40° B.50° C.60° D.45°B
A
1 FE 2 DC
解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和 ΔBDF中
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量,和相等) 即∠BAC=∠DAE
在△ABC和△ADE中, ∠B=∠D(已知) ∠BAC=∠DAE(已证)
AC=AE(已知)
∴△ABC≌ △ADE .
(AAS)
12
典型例题:
例6 :如图,已知,AB=CD, CE=DF,AE=BF, 则AE∥DF吗?为什么?
A
B
C
E
D
F
证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即 AC=BD.
在ΔACE和ΔBDF中 AC=BD(已证) CE=DF (已知) AE=BF (已知)
∴ ΔACE≌ΔBDF(SSS)
∴∠E=∠F(全等三角形的对 应角相等) ∴ AE∥DF(内错角相等,两 直线平行)
