第四章习题参考答案

合集下载

电路与电子技术基础第四章习题答案

a b i (t ) iR(t) R + u(t) (a) 题图 4-3 i L (t ) L 0 -100V (b) 习题 4-4 电路及波形图 t 0 -10mA (c) t uL 10mA i
解：本题是求零输入响应，即在开关处于 a 时，主要是电感储能，当开关投向 b 后，讨论由电感的储能所引起的响应。所以对图(a)t≥0 时的电路可列出 di L L + Ri L = 0 t≥0 dt 及 iL(0)=i(t)=10(mA) 其解为： i L (t ) = 10e
而
t≥0
i R (t ) = −i L (t ) = −10e −10 t (mA)
7
t≥0
其波形图见图(b)、图(c)所示。 4-5 电路如题图 4-4 所示，开关接在 a 端为时已久，在 t=0 时开关投向 b 端，求 3Ω电 1Ω a b 阻中的电流。 i (t ) 解：因为 u c (0) = 3 × 2 = 6(V ) （注意：当稳态以后电容为开路，所以流过 1 3A Ω和电容串联支路的电流为零，因此电容两端的电压就是并联支路 2Ω支路两端的电压）当开关投向 b 时电流的初始值为
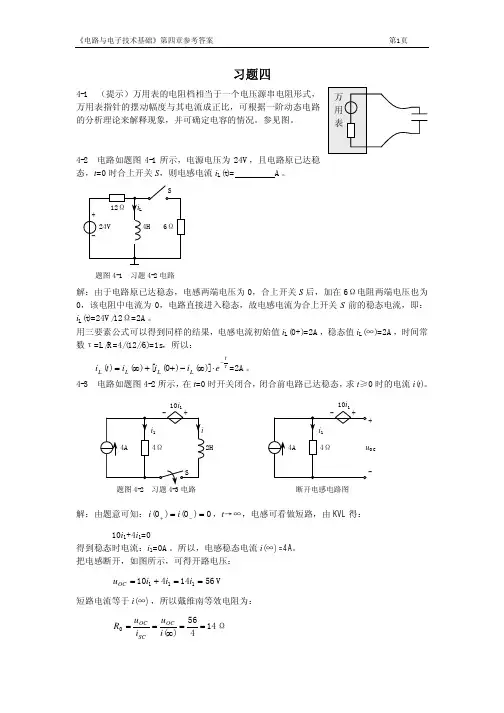
S 12Ω + 24V iL 4H 6Ω
题图 4-1
习题 4-2 电路
解：由于电路原已达稳态，电感两端电压为 0，合上开关 S 后，加在 6Ω电阻两端电压也为 0，该电阻中电流为 0，电路直接进入稳态，故电感电流为合上开关 S 前的稳态电流，即： iL(t)=24V/12Ω=2A。用三要素公式可以得到同样的结果，电感电流初始值 iL(0+)=2A，稳态值 iL(∞)=2A，时间常数τ=L/R=4/(12//6)=1s，所以：
当 t=0 时，开关打开，由于电感电流、电容电压均不跃变，有： i L (0 + ) = i L (0 − ) = 0.03( A) 1k u c (0 + ) = u c (0 − ) = 120(V ) 当 t≥0 时，根据基尔霍夫定律有

第四章制造费用核算练习题参考答案

第四章制造费用核算练习题参考答案一、某企业基本生产车间生产A、B两种产品，两种产品的生产工时分别为2500小时和3500小时。

某月生产工人工资为9000元，是按生产工时分配的；该月制造费用为18000元。

要求：根据以上资料分别按生产工时比例和工人工资比例分配制造费用。

解：1、按生产工时分配制造费用分配表车间名称：一车间 200×年×月根据“制造费用分配表”编制会计分录，登记有关账户。

借：基本生产成本——A 7500——B 10500贷：制造费用 180002、按工人工资比例分配制造费用分配表车间名称：一车间 200×年×月根据“制造费用分配表”编制会计分录，登记有关账户。

借：基本生产成本——A 7500——B 10500贷：制造费用 18000二、某企业基本生产车间全年计划制造费用为170000元，全年各种产品计划产量，甲产品20000件，乙产品18000件，单件产品工时定额，甲产品4小时，乙产品为5小时。

1月份实际产量分别为甲产品1200件，乙产品1000件，1月份实际制造费用为10000元，本年度实际制造用为160000元，假定年末已分配制造费用为165000元，其中甲产品负担80000元，乙产品负担85000元。

要求：根据以上资料采用计划分配率法分配制造费用，年终对计划制造费用与实际制造费用差异进行调整，并编制有关分录。

解：甲产品计划产量定额工时＝20000×4＝80000(小时)乙产品计划产量定额工时＝18000×5＝90000(小时)制造费用计划分配率＝170000/（90000+80000）＝1 根据以上资料，编制1月份“制造费用分配表”，如表5—6所示。

表5—6 制造费用分配表200×年1月根据“制造费用分配表”编制会计分录，登记有关账户。

借：基本生产成本——甲 4800——乙 5000贷：制造费用 9800年末差额分配率＝（160000-165000）/（80000+85000）＝－0.0303甲产品应负担差额＝80000×（－0.0303）＝－2424 (元)乙产品应负担差额＝85000×(－0.0303)＝－2576(元)借：基本生产成本——甲——乙贷：制造费用。

(仅供参考)信号与系统第四章习题答案

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
（f） x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图，确定满足下述情况的收敛域。
（1） f (t) 的傅里叶变换存在
（2） f (t )e 2t 的傅里叶变换存在
（3） f (t) = 0, t > 0
（4） f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。【逻辑推理】首先由零极点写出拉普拉斯变换式，再利用反变换求取其原信号，即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =

汇编第四章习题及参考答案

第四章习题及参考答案1. 在8086CPU中，如果SS的内容设置为1A4BH，堆栈的长度为100H字节，问：SP寄存器的初始化值为多少？SP初始指向哪个主存物理地址？参考答案：SP寄存器的初始化值为：100HSP初始指向的主存物理地址是：1A5B0H2.分别指出下列指令源操作数与目的操作数的寻址方式：(1)MOV ES, AX(2)ADD DS:[12H],AL(3)SUB BX,1200H(4)SHR AX,1(5)AND -28H[BP][DI], AX(6)MOV CX,LAB1[BX](7)SBB AX, [BX](8) OR DX,-360H[SI](9) ADC VAR1,CX(10) XOR [DI],AX参考答案：(1)寄存器，寄存器(2)直接，寄存器(3)寄存器，立即(4)寄存器，立即(5)基址变址，寄存器(6)寄存器，相对(7)寄存器，寄存器间接(8)寄存器，相对(9)直接，寄存器(10)寄存器间接，寄存器3.指出下列指令的语法是否错误，若错误请改正。

(1)MOV DS, 1234H(2)ADD AH，AL(3)SUB CS，AX(4)MOV BX,[BX][SI](5)ADC VAR1,[BP][DI](6) SBB [BX][BP],AX(7)PUSH 5678H(8)SHL [BP][SI]，CL(9)ROR AX,2(10)NEG AX,BX(11)LEA CS,AX(12)MOV AL,BX(13)ADD DS:200H,AX(14)AND [BX][BP]，AH(15)OR BH,-16H[BP](16)CLC AX(17)MUL AX,BX(18)DIV 12H参考答案：(1) 错误，立即数不能直接传送到段寄存器中(2) 正确(3) 错误，不能对CS直接操作(4) 正确(5) 错误，两个操作数不能同时都在存储器中(6) 错误, 基址变址寻址方式中不能两个寄存器都是基址寄存器(7) 错误，立即数不能作为源操作数直接压入堆栈(8) 错误，目的操作数没有明确指明是字还是字节(9) 错误，移位次数大于1时，需将其提前存入CL中(10) 错误，操作数个数错误(11) 错误，目的操作数只能是16位通用寄存器(12) 错误, 操作数位数不一致(13) 正确(14) 错误, 基址变址寻址方式中不能两个寄存器都是基址寄存器(15) 正确(16) 错误，操作数个数错误(17) 错误，操作数个数错误(18) 错误，源操作数不能是立即数4. MOV BX, 2345HMOV CX, 2HCLROL BX,0FFHAND BX,CMP BX,045H执行上述程序段后，（BX）= 14H , ZF= 0 . 5. XOR AX, AX5HMOV AL,9HMOV BL,BLADD AL,AAA执行上述程序段后，（AX）= 104H , CF= 1 .6. 假设（DS）=1234H,(SI)=124H,(12464)=30ABH,(12484H)=464H,有以下程序段：[SI]LEA SI,[SI]MOV AX,1200HMOV [SI+22H],[SI+20H]LDS SI,[SI]ADD AX,执行上述程序段后，（AX）= 6156H , (SI)= 464H .7. MOV AX, 0EF23H0B5A7HMOV BX,INC AXNEG AXDEC BXNEG BX执行上述程序段后，（AX）= 10DCH ,(BX)= 4A5AH .。

高分子化学-高化第四章答案

第四章离子聚合习题参考答案1．与自由基聚合相比，离子聚合活性中心有些什么特点？解答：离子聚合和自由基聚合的根本不同就是生长链末端所带活性中心不同。

离子聚合活性中心的特征在于：离子聚合生长链的活性中心带电荷，为了抵消其电荷，在活性中心近旁就要有一个带相反电荷的离子存在，称之为反离子，当活性中心与反离子之间得距离小于某一个临界值时被称作离子对。

活性中心和反离子的结合，可以是极性共价键、离子键、乃至自由离子等多种形式，彼此处于平衡状态：BA B+A B+A B AⅠ为极性共价物种，它通常是非活性的，一般可以忽略。

Ⅱ和Ⅲ为离子对，引发剂绝大多数以这种形式存在。

其中，Ⅱ称作紧密离子对，即反离子在整个时间里紧靠着活性中心。

Ⅲ称作松散离子对，即活性中心与反离子之间被溶剂分子隔开，或者说是被溶剂化。

Ⅳ为自由离子。

通常在一个聚合体系中，增长物种包括以上两种或两种以上的形式，它们彼此之间处于热力学平衡状态。

反离子及离子对的存在对整个链增长都有影响。

不仅影响单体的的聚合速度，聚合物的立体构型有时也受影响，条件适当时可以得到立体规整的聚合物。

2．适合阴离子聚合的单体主要有哪些，与适合自由基聚合的单体相比的些什么特点？解答：对能进行阴离子聚合的单体有一个基本要求：①适合阴离子聚合的单体主要有：（1）有较强吸电子取代基的烯类化合物主要有丙烯酸酯类、丙烯腈、偏二腈基乙烯、硝基乙烯等。

（2）有π-π共轭结构的化合物主要有苯乙烯、丁二烯、异戊二烯等。

这类单体由于共轭作用而使活性中心稳定。

（3）杂环化合物②与适合自由基聚合的单体相比的特点：（1）有足够的亲电结构，可以为亲核的引发剂引发形成活性中心，即要求有较强吸电子取代基的化合物。

如V Ac，由于电效应弱，不利于阴离子聚合。

（2）形成的阴离子活性中心应有足够的活性，以进行增长反应。

如二乙烯基苯，由于空间位阻大，可形成阴离子活性中心，但无法增长。

（3）不含易受阴离子进攻的结构，如甲基丙烯酸，其活泼氢可使活性中心失活。

计算机网络课后习题参考答案第四章

{第四章网络层1.网络层向上提供的服务有哪两种是比较其优缺点。

网络层向运输层提供“面向连接”虚电路（Virtual Circuit）服务或“无连接”数据报服务前者预约了双方通信所需的一切网络资源。

优点是能提供服务质量的承诺。

即所传送的分组不出错、丢失、重复和失序（不按序列到达终点），也保证分组传送的时限，缺点是路由器复杂，网络成本高；后者无网络资源障碍，尽力而为，优缺点与前者互易2.网络互连有何实际意义进行网络互连时，有哪些共同的问题需要解决网络互联可扩大用户共享资源范围和更大的通信区域[进行网络互连时，需要解决共同的问题有：不同的寻址方案不同的最大分组长度不同的网络接入机制不同的超时控制不同的差错恢复方法不同的状态报告方法不同的路由选择技术，不同的用户接入控制不同的服务（面向连接服务和无连接服务）不同的管理与控制方式3.作为中间设备，转发器、网桥、路由器和网关有何区别中间设备又称为中间系统或中继(relay)系统。

物理层中继系统：转发器(repeater)。

数据链路层中继系统：网桥或桥接器(bridge)。

、网络层中继系统：路由器(router)。

网桥和路由器的混合物：桥路器(brouter)。

网络层以上的中继系统：网关(gateway)。

4.试简单说明下列协议的作用：IP、ARP、RARP和ICMP。

IP协议：实现网络互连。

使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。

网际协议IP是TCP/IP体系中两个最主要的协议之一，与IP协议配套使用的还有四个协议。

ARP协议：是解决同一个局域网上的主机或路由器的IP地址和硬件地址的映射问题。

RARP：是解决同一个局域网上的主机或路由器的硬件地址和IP地址的映射问题。

（ICMP：提供差错报告和询问报文，以提高IP数据交付成功的机会因特网组管理协议IGMP：用于探寻、转发本局域网内的组成员关系。

地址分为几类各如何表示IP地址的主要特点是什么分为ABCDE 5类;每一类地址都由两个固定长度的字段组成，其中一个字段是网络号 net-id，它标志主机（或路由器）所连接到的网络，而另一个字段则是主机号 host-id，它标志该主机（或路由器）。

高等代数第四章矩阵练习题参考答案

第四章矩阵习题参考答案一、判断题1. 对于任意n 阶矩阵A ,B ,有A B A B +=+. 错.2. 如果20,A =则0A =. 错.如211,0,011A A A ⎛⎫==≠⎪--⎝⎭但.3. 如果2A A E +=,则A 为可逆矩阵.正确.2()A A E A E A E +=⇒+=,因此A 可逆,且1A A E -=+.4. 设,A B 都是n 阶非零矩阵,且0AB =,则,A B 的秩一个等于n ,一个小于n . 错.由0AB =可得()()r A r B n +≤.若一个秩等于n ,则该矩阵可逆,另一个秩为零,与两个都是非零矩阵矛盾.只可能两个秩都小于n . 5．C B A ,,为n 阶方阵,若,AC AB = 则.C B = 错.如112132,,112132A B C ⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭,有,AC AB =但B C ≠.6．A 为n m ⨯矩阵,若,)(s A r =则存在m 阶可逆矩阵P 及n 阶可逆矩阵Q ,使.000⎪⎪⎭⎫ ⎝⎛=sI PAQ 正确.右边为矩阵A 的等价标准形,矩阵A 等价于其标准形. 7．n 阶矩阵A 可逆,则*A 也可逆.正确.由A 可逆可得||0A ≠,又**||AA A A A E ==.因此*A 也可逆,且11(*)||A A A -=. 8．设B A ,为n 阶可逆矩阵,则.**)*(A B AB =正确.*()()||||||.AB AB AB E A B E ==又()(**)(*)*||*||*||||AB B A A BB A A B EA B AA A B E ====.因此()()*()(**)AB AB AB B A =.由B A ,为n 阶可逆矩阵可得AB 可逆,两边同时左乘式AB 的逆可得.**)*(A B AB =二、选择题1．设A 是n 阶对称矩阵,B 是n 阶反对称矩阵()T B B =-,则下列矩阵中为反对称矩阵的是B .A AB BA - B AB BA +C 2()ABD BABAD 为对称矩阵,B 为反对称矩阵,C 当,A B 可交换时为对称矩阵. 2. 设A 是任意一个n 阶矩阵,那么 A 是对称矩阵. A T A A B T A A - C 2A D T A A - 3．以下结论不正确的是 C .(A) 如果A 是上三角矩阵,则2A 也是上三角矩阵； (B) 如果A 是对称矩阵,则 2A 也是对称矩阵； (C) 如果A 是反对称矩阵,则2A 也是反对称矩阵； (D) 如果A 是对角阵,则2A 也是对角阵.4．A 是m k ⨯矩阵, B 是k t ⨯矩阵, 若B 的第j 列元素全为零,则下列结论正确的是BA AB 的第j 行元素全等于零； B AB 的第j 列元素全等于零；C BA 的第j 行元素全等于零；D BA 的第j 列元素全等于零； 5．设,A B 为n 阶方阵,E 为n 阶单位阵,则以下命题中正确的是D A 222()2A B A AB B +=++ B 22()()A B A B A B -=+-C 222()AB A B =D 22()()AE A E A E -=+- 6．下列命题正确的是B . A 若AB AC =,则B C = B 若AB AC =,且0A ≠,则B C = (C) 若AB AC =,且0A ≠,则B C = D 若AB AC =,且0,0B C ≠≠,则B C = 7. A 是m n ⨯矩阵,B 是n m ⨯矩阵,则 B. (A)当m n >时,必有行列式0AB ≠； (B)当m n >时,必有行列式0AB = (C)当n m >时,必有行列式0AB ≠； (D)当n m >时,必有行列式0AB =.AB 为m 阶方阵,当m n >时,(),(),r A n r B n ≤≤因此()r AB n m ≤<,所以0AB =.8．以下结论正确的是 C(A)如果矩阵A 的行列式0A =,则0A =； (B)如果矩阵A 满足20A =,则0A =；(C)n 阶数量阵与任何一个n 阶矩阵都是可交换的； (D)对任意方阵,A B ,有22()()A B A B A B -+=-9．设1234,,,αααα是非零的四维列向量,1234(,,,),*A A αααα=为A 的伴随矩阵,已知0Ax =的基础解系为(1,0,2,0)T ,则方程组*0A x =的基础解系为 C .A 123,,ααα.B 122331,,αααααα+++.C 234,,ααα.D 12233441,,,αααααααα++++.由0Ax =的基础解系为(1,0,2,0)T 可得12341310(,,,)0,2020αααααα⎛⎫ ⎪ ⎪=+= ⎪ ⎪⎝⎭.因此A,B 中向量组均为线性相关的,而D 显然为线性相关的,因此答案为C.由可得12,,αα34,αα均为*0A x =的解.10.设A 是n 阶矩阵,A 适合下列条件 C 时,n I A -必是可逆矩阵(A) n A A = B A 是可逆矩阵 C 0n A = (B) A 主对角线上的元素全为零11．n 阶矩阵A 是可逆矩阵的充分必要条件是 D(A)1A = B 0A = C T A A = D 0A ≠12．,,A B C 均是n 阶矩阵,下列命题正确的是 A(A) 若A 是可逆矩阵,则从AB AC =可推出BA CA = (B) 若A 是可逆矩阵,则必有AB BA = (C) 若0A ≠,则从AB AC =可推出B C = (D) 若B C ≠,则必有AB AC ≠13．,,A B C 均是n 阶矩阵,E 为n 阶单位矩阵,若ABC E =,则有C (A) ACB E = B BAC E = C BCA E = D CBA E =14．A 是n 阶方阵,*A 是其伴随矩阵,则下列结论错误的是 D (A) 若A 是可逆矩阵,则*A 也是可逆矩阵； (B) 若A 是不可逆矩阵,则*A 也是不可逆矩阵； (C) 若*0A ≠,则A 是可逆矩阵；Ｄ*.AA A = 15．设A 是5阶方阵,且0A ≠,则*A = Ｄ(A)A B 2A C 3A D 4A16．设*A 是()ij n n A a ⨯=的伴随阵,则*A A 中位于(,)i j 的元素为ＢA 1n jk ki k a A =∑ B 1n kj ki k a A =∑ C 1n jk ik k a A =∑ D 1nki kj k a A =∑应为A 的第i 列元素的代数余子式与A 的第j 列元素对应乘积和.17.设1111n n nn a a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 1111n n nn A A B A A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,其中ij A 是ij a 的代数余子式,则C(A)A 是B 的伴随 B B 是A 的伴随 C B 是A '的伴随 D 以上结论都不对18．设,A B 为方阵,分块对角阵00A C B ⎡⎤=⎢⎥⎣⎦,则*C = Ｃ (A)**00A CB ⎡⎤=⎢⎥⎣⎦ B **00A A C B B ⎡⎤=⎢⎥⎣⎦ C **00B AC A B ⎡⎤=⎢⎥⎣⎦ D **0A B A C A B B ⎡⎤=⎢⎥⎣⎦ 利用*||CC C E =验证.19．已知46135,12246A B ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦,下列运算可行的是 C (A) A B + B A B - C AB D AB BA -20．设,A B 是两个m n ⨯矩阵,C 是n 阶矩阵,那么 D21．对任意一个n 阶矩阵A ,若n 阶矩阵B 能满足AB BA =,那么B 是一个Ｃ(A)对称阵 B 对角阵 C 数量矩阵 D A 的逆矩阵与任意一个n 阶矩阵均可交换的矩阵为数量矩阵.22．设A 是一个上三角阵,且0A =,那么A 的主对角线上的元素Ｃ(A) 全为零 B 只有一个为零（C ）至少有一个为零 D 可能有零,也可能没有零23．设1320A⎡⎤=⎢⎥⎣⎦,则1A-= D(A)121136⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦B131136⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦C131126⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦D121136⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦24．设111222333a b cA a b ca b c⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,若111222333222a c bAP a c ba c b⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则P= B(A)100001020⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B100002010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C001020100⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦D200001010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦25．设(3)n n≥阶矩阵1111a a aa a aA a a aa a a⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,若矩阵A的秩为1,则a必为A(A)1 B-1 C11n-D11n-矩阵A的任意两行成比例.26. 设,A B为两个n阶矩阵,现有四个命题:①若,A B为等价矩阵,则,A B的行向量组等价;②若,A B的行列式相等,即||||,A B=则,A B为等价矩阵;③若0Ax=与0Bx=均只有零解,则,A B为等价矩阵;④若,A B为相似矩阵,则0Ax=与0Bx=解空间的维数相同.以上命题中正确的是 DA ①, ③.B ②, ④.C ②,③. D③,④.当APPB1-=时,,A B为相似矩阵;相似矩阵的秩相等;齐次线性方程组基础解系所含解的个数即为其解空间的维数;三、填空题1．设A 为三阶方阵,*A 为A 的伴随矩阵,有2A =,则11()2*3A A --=11*||2A A A A --==,111()33A A --=,因此11111311()2*34(1)32A A A A A A ------=-=-=-=-. 2．设,AB 为4阶方阵,且3A =,则1(3)A --= 1/27 , 21BA B -= 9 ; 3．设A 是一个m n ⨯矩阵,B 是一个n s ⨯矩阵,那么是()'AB 一个s m ⨯阶矩阵,它的第i 行第j 列元素为1njk ki k a b =∑.4.n 阶矩阵A 可逆A 非退化 ||0A ≠⇔ A 与单位矩阵等价 ⇔ A 可以表示为一系列初等矩阵的乘积 .4.三阶对角矩阵000000a A b c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则A 的伴随矩阵*A = 000000bc ac ab ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦. 5．设123023003A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则*1()A -=16A . 6．设0,1,2,i a i n ≠=,矩阵12100000000000n na a a a -⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦的逆矩阵为 111121100000000000n n a a a a -----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦. 7．设,A B 都是可逆矩阵,矩阵00A C B ⎡⎤=⎢⎥⎣⎦的逆矩阵为1100B A --⎡⎤⎢⎥⎣⎦.8．设121331,,342424A B C ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则(2)B A C -= ． 9．A 既是对称矩阵,又是反对称矩阵,则A 为零矩阵.10．设方阵111222333b x c A b x c b x c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,111222333b y c B b y c b y c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,且2,3A B =-=则行列式A B += 4 .11．设A 为m 阶方阵,B 为n 阶方阵,已知,A a B b ==,则行列式00A B=ab mn )1(-.将A 的各列依次与B 的各列交换,共需要交换mn 次,化为00A B12．设A 为n 阶方阵,且0A ≠,则在A 等价关系下的标准形为 n 阶单位矩阵 .13. 设12221311A a -⎛⎫⎪=- ⎪ ⎪⎝⎭a为某常数,B 为43⨯的非零矩阵,且0BA =,则矩阵B 的秩为 1 .由0BA =可得A 的各列为齐次线性方程组0Bx =的解,A 的前两列线性无关,因此0Bx =的基础解系至少有两个解,因此()1r B ≤.又B 为非零矩阵,因此()1r B ≥.即() 1.r B =四、解答下列各题 1．求解矩阵方程1 25461321X -⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;2 211113210432111X -⎛⎫-⎛⎫⎪= ⎪ ⎪⎝⎭ ⎪-⎝⎭; 3 142031121101X ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭;4 010100143100001201001010120X -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭解：11254635462231321122108X -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 212111132212104328/352/3111X --⎛⎫--⎛⎫⎛⎫ ⎪== ⎪ ⎪ ⎪--⎝⎭⎝⎭ ⎪-⎝⎭2．设033110123A ⎛⎫⎪= ⎪ ⎪-⎝⎭,2AB A B =+ ,求B 解：(2)A E B A -=.0332002332110020110123002121A E -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭.22A E -=,因此2A E -可逆.3．.设1P AP -=Λ,其中1411P --⎛⎫= ⎪⎝⎭,1002-⎛⎫Λ= ⎪⎝⎭,求11A . 解：1,A P P -=Λ4．设3级方阵,A B 满足124A B B E -=-,证明：2A E -可逆,并求其逆. 证明：124A B B E -=-两边同左乘以A 得到24B AB A =-.因此有(2)4A E B A -=.由A 可逆可得2A E -,且111(2).4A E BA ---=5．设A 是一个n 级方阵,且()R A r =,证明：存在一个n 级可逆矩阵P 使1PAP -的后n r -行全为零.证明：()R A r =,因此矩阵A 可以经过一系列行初等变换化为后n r -行全为零.也即存在初等矩阵11,,,m P P P ,使得21m P P P A 后n r -行全为零. 21mP P P P =,则PA 的后n r -行全为零.由矩阵乘法运算可得1PAP -的后n r -行全为零.6．设矩阵,m n n m A B ⨯⨯,且,m n AB E <=,证明：A 的行向量组线性无关. 证明：由,m n AB E <=可得()()m r AB r A m =≤≤,因此()r A m =.因此A 的行向量组线性无关.7．如果,2A A =称A 为幂等矩阵.设B A ,为n 阶幂等矩阵,证明：B A +是幂等矩阵的充要条件是0.AB BA +=证明：当B A +时幂等阵时, 因此0.AB BA +=反之,当0.AB BA +=时有 B A +是幂等矩阵.。

数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1．分析图4-1中所示的同步时序逻辑电路，要求：（1）写出驱动方程、输出方程、状态方程；（2）画出状态转换图，并说出电路功能。

CPY图4-12．由D触发器组成的时序逻辑电路如图4-2所示，在图中所示的CP脉冲及D作用下，画出Q0、Q1的波形。

设触发器的初始状态为Q0=0，Q1=0。

D图4-23．试分析图4-3所示同步时序逻辑电路，要求：写出驱动方程、状态方程，列出状态真值表，画出状态图。

CP图4-34．一同步时序逻辑电路如图4-4所示，设各触发器的起始状态均为0态。

（1）作出电路的状态转换表；（2）画出电路的状态图；（3）画出CP作用下Q0、Q1、Q2的波形图；（4）说明电路的逻辑功能。

图4-45．试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0，并说明它的功能（假设初态Q0Q1=00）。

CPQ1Q0CP图4-56．分析如图4-6所示同步时序逻辑电路的功能，写出分析过程。

Y图4-67．分析图4-7所示电路的逻辑功能。

（1）写出驱动方程、状态方程；（2）作出状态转移表、状态转移图；（3）指出电路的逻辑功能，并说明能否自启动；（4）画出在时钟作用下的各触发器输出波形。

CP图4-78．时序逻辑电路分析。

电路如图4-8所示：（1）列出方程式、状态表；（2）画出状态图、时序图。

并说明电路的功能。

1C图4-89．试分析图4-9下面时序逻辑电路：（1）写出该电路的驱动方程，状态方程和输出方程；（2）画出Q1Q0的状态转换图；（3）根据状态图分析其功能；1B图4-910.分析如图4-10所示同步时序逻辑电路，具体要求：写出它的激励方程组、状态方程组和输出方程，画出状态图并描述功能。

1Z图4-1011．已知某同步时序逻辑电路如图4-11所示，试：（1）分析电路的状态转移图，并要求给出详细分析过程。

（2）电路逻辑功能是什么，能否自启动？（3）若计数脉冲f CP频率等于700Hz，从Q2端输出时的脉冲频率是多少?CP图4-1112．分析图4-12所示同步时序逻辑电路，写出它的激励方程组、状态方程组，并画出状态转换图。

结构力学第四章作业参考答案

结构力学第四章习题参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1）求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2）把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2）把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

第四章习题答案

习题4.1选择填空1、选用差分放大电路的原因是 A 。

A 、克服温漂B 、提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ，将使电路的 B 。

A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。

4、设差放电路的两个输入端对地的电压分别为v i1和v i2，差模输入电压为v id ，共模输入电压为v ic ，则当v i1=50mV ，v i2=50mV 时，v id =_0mV __，v ic =_50mV __；当v i1=50mV ，v i2=-50mV 时，v id =_100mA __，v ic =_0mA__；当v i1=50mV ，v i2=0V 时，v id =_50mV __，v ic =_25mA __。

5、电流源常用于放大电路，作为_A ___（A.有源负载，B.电源，C.信号源），使得放大倍数__A __（A.提高，B.稳定）。

6、电压放大电路主要研究的指标是 a 、 b 、 c ；功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、（a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗）7、功率放大电路中，___甲类____功率放大电路导通角最大；_____乙类___功率放大电路效率较高。

（甲类、乙类、甲乙类） 8、甲类功放效率低是因为 B 。

A 、只有一个功放管B 、静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。

已知晶体管1T 和2T 的50=β，并设U BE (on )=0.7V,r bb ’=0,r ce =∞。

(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。

(2)求双端输出时的差模电压增益A ud ，差模输入电阻R id 和差模输出电阻R od 。

财务报表分析第四章-习题参考答案

财务报表分析第四章-习题参考答案第四章习题参考答案一、单项选择题1．B2．A3．A4．C5．A6．A二、多项选择题1．BCDE2．ABCD3．ABDE4．CDE5．BC6．CE7．ABCDE8．ACE三、判断题1．√2．√3．答案：解析：当企业的其他资产不变时，采用加速折旧法会提高资产周转率。

4．√5．答案：解析：资产周转次数越多，周转天数越短，说明资产的流动性相对越强，公司资产经营利用的效果相对越好。

6．√7．√四、名词解释1．营运能力，是指企业营运资产的效率与效益。

营运资产的效率通常指资产的周转速度。

营运资产的效益则指营运资产的利用效果。

2．资产结构，即公司各类资产的构成及其比例关系。

公司资产一般分为流动资产与长期资产，两种资产在经营过程中有不同的价值周转特征，因此，资产结构不仅能够反映公司资产周转能力，即公司资产的营运能力，而且对资产的价值实现也具有决定性影响，同时，在一定程度上与公司财务风险和经营风险相联系，并最终决定公司的可持续发展能力。

3．应收账款周转率，应收账款周转率是指公司一定时期赊销收入净额（营业收入）与应收账款平均余额的比率，用以反映公司应收账款的周转速度，即公司流动资产在一定时期内(通常为一年)周转的次数。

其计算公式为：应收账款周转率=营业收入/应收账款平均余额。

4．存货周转率，是公司产品营业成本与存货平均余额的比率，即公司的存货在一定时期内(通常为一年)周转的次数。

该指标反映公司存货规模是否合适，周转速度如何，也是衡量公司生产经营各环节中存货运营效率的综合性指标。

其计算公式为：存货周转率=营业成本/存货平均余额。

5.流动资产周转率，是指公司一定时期的营业收入与流动资产平均余额的比率，即公司流动资产在一定时期内(通常为一年)周转的次数。

流动资产周转率是反映公司流动资产运用效率的主要指标。

其计算公式为：流动资产周转率=营业收入/流动资产平均占用额。

6.固定资产周转率，是指公司一定时期的营业收入与固定资产平均净值的比率，它是反映公司固定资产运用状况，衡量固定资产利用效果的指标。

4教材习题参考答案第四章自由基共聚反应.doc

4.考虑当r1=r2=1; r1=r2=0; r1>0, r2=0及r1·r2=1等特殊情况下，d[M1] / d[M2] = f ( M1/M2 )及F1=f(f1)的函数关系和图像特征。
解：（1）r1 = r2 = 1
F1 = f1理想恒比共聚；共聚物组成为一对角线
（2）r1 = r2 = 0
F1 = 0.5交替共聚；图上为一条F1=0.5的水平线
∴原式可简化为F1＝(r1+1)/(r1+2+r2)由此式可计算出各种情况下的F1，再由1－F1算得F2
情况
1
2
3
4
5
6
7
8
9
F1
0.5
0.35
0.09
0.5
0.5
0.5
0.4
0.17
0.1
计算值与图中所查得的值相吻合
第四章自由基共聚合
计算题
1、氯乙烯—醋酸乙烯脂、甲基丙烯酸甲酯—苯乙烯两对单体共聚，若两体系中醋酸乙烯酯和苯乙烯的浓度均为15%（质量分数），根据文献报道的竞聚率，试求共聚物的起始组成。
解：1、对于氯乙烯—醋酸乙烯脂
r1=1.68 r2=0.23 M1=62.5 M2=86
= n1/(n1+n2) Nhomakorabeam1M2/(m1M2+m2M1)
W2= m2/(m1+m2) =15%所以m2=3/17m1
所以f1= m1M2/(m1M2+m2M1) =0.886
= 0.93
所以起始组成为F1=0.93 F2=0.07
教材习题参考答案第四章自由基共聚反应
思考题
1.无规、交替、接枝、嵌段共聚物的结构有何差异?举例说明这些共聚物名称中单体前后位置的规定?

算法分析习题参考答案第四章

第四章作业部分参考答案1．设有n 个顾客同时等待一项服务。

顾客i 需要的服务时间为n i t i ≤≤1,。

应该如何安排n 个顾客的服务次序才能使总的等待时间达到最小？总的等待时间是各顾客等待服务的时间的总和。

试给出你的做法的理由（证明）。

策略：对 1i t i n ≤≤进行排序，,21n i i i t t t ≤≤≤ 然后按照递增顺序依次服务12,,...,ni i i 即可。

解析：设得到服务的顾客的顺序为12,,...,n j j j ，则总等待时间为,2)1(121n n j j j j t t t n nt T +++-+=- 则在总等待时间T 中1j t 的权重最大，jn t 的权重最小。

故让所需时间少的顾客先得到服务可以减少总等待时间。

证明：设,21n i i i t t t ≤≤≤ ，下证明当按照不减顺序依次服务时，为最优策略。

记按照n i i i 21次序服务时，等待时间为T ，下证明任意互换两者的次序，T都不减。

即假设互换j i ,)(j i <两位顾客的次序，互换后等待总时间为T ~，则有.~T T ≥由于,))(())(()2)(2()1)(1(21n j i i i i i i t j t j n i t i n t n t n T +--++--++--+--=,))(())(()2)(2()1)(1(~21n i j i i i i i t j t j n i t i n t n t n T +--++--++--+--=则有.0))((~≥--=-i j i i t t i j T T同理可证其它次序，都可以由n i i i 21经过有限次两两调换顺序后得到，而每次交换，总时间不减，从而n i i i 21为最优策略。

2．字符h a ~出现的频率分布恰好是前8个Fibonacci 数，它们的Huffman 编码是什么？将结果推广到n 个字符的频率分布恰好是前n 个Fibonacci 数的情形。

第四章基本经济业务的核算练习题答案(2)

第四章基本经济业务的核算练习题答案一、单项选择题参考答案1．C。

其余三类企业均属于一般企业。

2．C。

销售商品属于企业经营活动交易和事项。

3．C。

从银行借款属于企业筹资活动交易和事项。

4．D。

产品生产与销售属于企业经营活动交易和事项。

5．B。

投资权益的获取属于企业对外投资活动交易和事项。

6．B。

与其他三项无关。

7．C。

与其他三项无关。

8．B。

固定资产损失应当视为投资活动产生的事项。

9．D。

法人资本金属于企业的投入资本按投资主体划分的组成内容。

10．C。

无形资产投资属于企业的投入资本按投资形式划分的组成内容。

11．C。

对外投资过程的交易或事项属于投资活动的交易或事项内容。

12．D。

进行产品生产属于企业经营活动的内容。

13．D。

固定资产购建属于企业投资活动的内容。

14．C。

发行企业债券属于企业资金筹集活动的内容。

15．B。

接受投资者投资属于资金筹集活动的交易和事项。

16．B。

流动性差属于权益性投资的特点。

17．D。

价值变动风险很小属于债权性投资的特点。

18．C。

“制造费用”账户属于资产（成本）类账户，与当期收入没有直接关系。

19．B。

“主营业务成本”账户属于费用（损益）类账户，与当期实现的收入有着直接关系。

该账户的结构为借增贷减，结转属于其发生额减少，应记入贷方，相应地记入“本年利润”账户的借方。

20．C。

“投资收益”账户属于收入（损益）类账户，与当期利润计算有着密切关系。

该账户的结构为贷增借减，结转属于其发生额减少，应记入借方，相应地记入“本年利润”账户的贷方。

21．B。

营业外收入属于企业的利得，按现行《企业会计准则》规定，应直接计入当期利润。

22．D。

“未分配利润”账户在期末结转后仍应有余额，反映当年留存的未分配利润。

二、多项选择题参考答案1．ABC。

其余两项属于特殊行业。

2．ABCDE。

以上五项均属于产品生产企业的主要交易或事项。

3．ABCE。

根据《公司法》规定，投资者的投资一般不予退还。

4．ABCDE。

第四章习题及参考答案

第四章抽样与抽样估计一、单项选择题1、实际工作中，小样本是指（）A、样本容量大于30的样本B、样本容量小于30的样本C、样本容量等于30的样本D、样本容量小于等于30的样本2、从5个字母中随机抽取2个字母作为样本，采用重复抽样，考虑顺序，则可能的样本个数为（）A、10个B、20个C、25个D、30个3、当总体方差未知，且样本容量小于30时，进行正态总体均值的区间估计应采用的临界值为（）A、F值B、Z值C、t值D、2x值4、当总体方差已知，无论样本容量n的大小如何，进行正态总体均值的区间估计应采用的临界值为（）A、F值B、Z值C、t值D、2x值5、在总体内部情况复杂、且各单位之间差异程度大、单位数又多的情况下，宜采用（）A、等距抽样B、整群抽样C、简单随机抽样D、类型抽样6、根据重复抽样的资料，甲单位工人工资方差为25，乙单位为100，乙单位抽的人数比甲单位多3倍，则抽样平均误差（）A、甲单位较大B、甲单位较大C、无法判断D、甲、乙单位相同7、某学校在全校学生中随机重复抽取100人调查身高，计算出抽样平均误差为5cm。

如果改用不重复抽样方法，在其他条件不变时，其抽样平均误差将会（）A、大于5cmB、小于5cmC、等于5cmD、不确定8、纯随机重复抽样条件下，样本容量扩大为原来的9倍，其它条件不变，则（）Ａ、抽样允许误差不变Ｂ、抽样允许误差缩小为原来的九分之一Ｃ、抽样允许误差缩小为原来的三分之一Ｄ、抽样允许误差增大为原来的九倍二、多项选择题1、影响抽样平均误差的因素主要有（）A、总体方差或标准差B、样本容量C、抽样方法D、抽样组织方式E、抽样的对象2、下列说法中错误的有（）A、抽样误差是不可避免的B、抽样误差是可以避免的C、抽样误差可以计算但不能加以控制机D、抽样误差是由于抽样的随机性而产生的样本估计量与总体参数之间的代表性误差 E、抽样误差是指登记性误差3、评价估计量的优劣常用下列三个标准（）A、一致性B、有效性C、合理性D、代表性E、无偏性4、抽样推断过程包括相互联系的三项内容（）A、随机抽样B、统计估计C、假设检验D、抽样精度E、置信度5、下列说法正确的有（）A、总体参数是唯一的、确定的，但又是未知的B、总体参数是随机变量C、样本统计量是随机变量D、样本统计量是唯一的、确定的E、样本所包含的总体单位个数称为样本容量6、概率抽样最基本的组织方式有（）A、简单随机抽样B、分层抽样C、等距抽样D、整群抽样E、配额抽样7、抽样估计中的抽样误差（）A、无法避免B、可以控制C、只能在估计结束才能知道D、可以计算E、不可控制8、抽样平均误差是指（）A、所有可能样本的样本指标与总体指标的平均离差B、所有可能样本的样本指标对总体指标的标准差C、已抽出样本的标准差D、等价于极限误差E、已抽出样本的平均差三、填空题1、概率抽样也叫随机抽样，是指按照原则抽取样本。

(完整版)第四章_复式记账法习题及参考答案

第四章复式记账法习题一、应掌握的名词记账方法复式记账法借贷记账法对应账户账户对应关系会计分录试算平衡二、填空题１．记账方法分为单式记账法和复式记账法两类。

２．借贷记账法是以“借”“贷”两个字作为记账符号的。

３．资产类账户的借方记录资产的增加，贷方记录资产的减少，期末余额一般在借方。

４．负债及所有者权益类账户的贷方记录负债及所有者权益的增加额，借方记录负债及所有者权益的减少额，期末余额一般在贷方。

５．借贷记账法的记账规则是有借必有贷，借贷必相等。

６．账户之间的应借应贷关系，称为账户的对应关系。

７．会计分录分为简单会计分录复合会计分录两种。

８．损益类账户期末一般无余额。

９．简单分录是指一借一贷的会计分录。

三、判断题１．所有经济业务的发生，都会引起会计等式两边发生变化。

（ B ）２．会计记账从产生开始，一直都是采用复式记账法。

（ B ）３．单式记账法是指所有的经济业务都记一笔账。

（ B ）４．复式记账法造成账户之间没有对应关系。

（ B ）５．借贷记账法账户的基本结构是：每一个账户的左边均为借方，右边均为贷方。

（ A ）６．一个账户的借方如果用来记录增加额，其贷方一定用来记录减少额。

（ A ）７．一般地说，各类账户的期末余额与记录增加额的一方都在同一方向。

（ A ）四、单项选择题１．复式记账法对每一项经济业务都以相等的金额，在（ D ）中进行登记。

Ａ．一个账户Ｂ．所有账户Ｃ．两个账户Ｄ．两个或两个以上的账户２．存在着对应关系的账户，称为（ D ）。

Ａ．平衡账户Ｂ．“Ｔ”字账户Ｃ．相关账户Ｄ．对应账户３．下列各项属于简单会计分录的有（ A ）会计分录。

Ａ．一借一贷Ｂ．一借多贷Ｃ．一贷多借Ｄ．多借多贷４．损益收入类账户期末应（ A ）。

Ａ．无余额Ｂ．借贷方都有余额Ｃ．借方有余额Ｄ．贷方有余额５．损益收入类账户的结构与所有者权益类账户的结构（ C ）。

Ａ．完全相反Ｂ．完全一致Ｃ．基本相同Ｄ．没有关系６．预付给供货单位的货款，可视同为一种（ D ）。

热学教程习题参考解(第四章)

《热学教程》习题参考答案第四章习题4-1. 电子管的真空度为1.333×103-Pa,设空气分子有效直径为3.0×1010-m,求27℃时空气分子的数密度n ,平均自由程λ和碰撞频率Z .(答: 3.2×1017m 3-，7.8 m ，60s 1-) 解：由nkT P =，可得)m (1021.3317-⨯==kTP n 分子平均自由程为)m (78.7212==n d πλ碰撞频率为 )s (2.6081-===λπμλRTvZ4-2. 求氦原子在其密度2.1×102-kg/m 3,原子的有效直径=d 1.9×1010-m 的条件下的平均自由程λ.(答:1.97×106-m)解：由n N mn A μρ==，可得 )m (1016.3324-⨯==μρA N n 分子平均自由程为)m (10972.12162-⨯==nd πλ 4-3. 试估算宇宙射线中的质子在海平面附近的平均自由程.(答：约m 102.16-⨯)4-4. 测得温度15℃和压强76cmHg 时氩原子和氖原子的平均自由程分别为Ar λ=6.7×108-m 和Ne λ=13.2×108-m ，试问：(1)氩原子和氖原子的有效直径各为多少？(2) 20℃和15cmHg 时Ar λ和-40℃和75cmHg 时Ne λ多大？(答(1)101063.3-⨯m,101059.2-⨯m;(2) 71045.3-⨯m,71080.1-⨯m)解：(1)由Pd kT n d 22221ππλ==，可得 )m (1063.321021Ar Ar -⨯=⎪⎪⎭⎫ ⎝⎛=λπP kT d)m (1059.221021Ne Ne -⨯=⎪⎪⎭⎫ ⎝⎛=λπP kT d(2)由分子平均自由程与温度及压强的关系)m (1045.3107.6288157629378Ar11212Ar2--⨯=⨯⨯⨯⨯==λλT P P T )m (1008.1102.13288757623378Ne11212Ne2--⨯=⨯⨯⨯⨯==λλT P P T 4-5. 高空的一片降雨云层,单位时间通过单位面积的降雨量为Q =10cm/hour 。

高等数学课后习题及参考答案(第四章)

高等数学课后习题及参考答案（第四章）习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231. (3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx xx 21;解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x m n m C x mn dx x dx x mn m m nm nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx xx 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224.(15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx xe e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532; 解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ;解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|C =2C ,C =3-2=1. 于是所求曲线的方程为 y =ln|x | 1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少？ (2)物体走完360m 需要多少时间？解设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e x ch x 都是x x e xsh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x e x ch x =e x (sh x ch x )x xx x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x e x sh x =e x (ch x sh x )x xx x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x xe d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332xdx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d xdx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2. (11)⎰-+dx e e xx 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ; 解 )sin cos (cos sin 1cos sin cos sin 33x x d x x dx x x x x +--=-+⎰⎰ C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx xx 239; 解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1.(23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a xa x a C t a t a +--=+-=222222arcsin 22sin 421. (35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+xdx 21;解C x x C t t dt t tdt t t x xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan . (40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x 23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d xx x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x x x x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233 ⎰⎰+-+-=dx x dx x x 3127)93(2 C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458; 解 ⎰⎰⎰--++++=--+dx xx x x dx x x dx x x x x 3223458)1(8 ⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解 ⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C xx dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222.8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u xu dx x221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u xu dx x221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17.⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dx x x )122(221111111令 C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4xx dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxxx x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx .解令u x x =-+311, 则1133-+=u u x , 232)1(6--=u udx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662.4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解 C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln .6.⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9.⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax ax axax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e ba ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e edx xx)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x x dx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12.16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a++=tan 1tan 31434C xa x ax a x a+-+-⋅=224322341)(31.17.⎰+241xxdx;解tdt t t tx x xdx 2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx . 24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444.25.⎰-416x dx;解⎰⎰⎰++-=+-=-dx x x dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx xxx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x e x23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x ex x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dx x x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x x C t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C ee x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xd e d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x xxxde e ee x )111(1 C e e e xx x x ++-++-=)1ln(ln 1C e e xe x x x++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ;解因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t t x dx x 2232/321sin cos sec sec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx x x xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。

线性代数习题答案4

a2 + b2 3 (a2 + b2 3)(a2 − b2 3) a22 − 3b22
a22 − 3b22
3,
a1 ± a2 , b1
± b2;
a1a2
+ 3b1b2 , a1b2
+ a2b1;
a1a2 a22
− 3b1b2 − 3b22
,
(a2b1 − a1b2 a22 − 3b22
)
都是有理数,故 K2 是数域.
x + y = (x1 + y1, x2 + y2 , x3 + y3 )T , 2(x1 + y1) + 3(x2 + y2 ) − (x3 + y3 ) = 0 ⇒ x + y ∈W4 , kx = (kx1, kx2 , kx3)T , 2(kx1) + 3(kx2 ) − (kx3) = 0 ⇒ kx ∈W4 故W4 对 R3 中的加法与数乘运算封闭, 它是 R3 的子空间. (5) W5 = {x ∈ R3 | 2x1 + 3x2 − x3 = 1}; 【解】W5 不是 R3 的子空间. 显然W5 中不含有零向量, 故W5 不是 R3 的子空间. (6) W6 = {x ∈ R3 | x1 − x22 = 0}.
=
a1a2 a22
+ b1b2 + b22
+
(a2b1 a22
− a1b2 ) + b22
i,
a1
± a2 , b1
± b2;
a1a2
− b1b2 , a1b2
+ a2b1;
a1a2 + b1b2 a22 + b22

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

'
3 ) 2
3 ' i (t ) i A (t ) iB (t ) 4 g1Vs cos(if t s l ) 2
可见混频器 B 的中频输出经过 90 度移相,在 M 处与 A 管中频同相迭加。外镜频抑制: 2 端口设外镜像频率信号为 vi (t ) Vi cos[(2 L S )t i ] 1 端口本振信号为 v L (t ) VL cos( L t L )
D1、D2、D3、D4 管混出的中频电流为：
i1 (t ) g1Vi cos(if t L i i2 (t ) g1Vi cos(if t L i

2 2
) )
i3 (t ) g1Vi cos(if t L i ) i4 (t ) g1Vi cos(if t L i ) iA (t ) i1 (t ) i2 (t ) 2 g1Vi cos(if t L i ) 2 iB (t ) i3 (t ) i4 (t ) 2 g1Vi cos(if t L i )
混频器 B 的中频输出经过 90 度移相得到

3 ' iB (t )Байду номын сангаас 2 g1Vi cos(if t L i ) 2
在 M 处 i (t ) i A (t ) iB (t ) 0 所以在 S L 时，中频移相器应该加在 B 端口，才能保证外来信号混出的中频在 M 处同相迭加，外来镜像干扰混出的中频在 M 处反同相相抵消。内镜频在射频口反相抵消: D1、D2、D3、D4 管混出的镜频电流为：
6．中频移相器应该加在 B 端口 vs (t ) Vs cos(s t s ) 设 2 端口信号电压
vL (t ) VL cos(Lt L ) 1 端口本振电压加到 D1、D2、D3、D4 管上的信号及本振电压分别为：
因为信源角频率>本振角频率，可得 D1、D2、D3、D4 产生的中频电流分别为：
在射频输入口处 i i (t ) iiA (t ) iiB (t ) 0
'
'
ii1 (t ) giVi cos(it 2 L i ) ii 2 (t ) g iVi cos(it 2 L i / 2) ii 3 (t ) giVi cos(it 2 L i ) ii 4 (t ) giVi cos(it 2 L i / 2) iiA (t ) ii1 (t ) ii 2 (t ) giVi cos(it 2 L i ) g iVi cos(it 2 L i / 2) iiB (t ) ii 3 (t ) ii 4 (t ) g iVi cos(it 2 L i ) g iVi cos(it 2 L i / 2)
混频器 A 的中频输出为：混频器 B 的中频输出为： iB (t ) iif 3 (t ) iif 4 (t ) 2 g1Vs cos(if t s L ) B 的中频输出经过移相器移相得到 iB (t ) 2 g1Vs cos(if t s l