第三章 词法分析和有穷自动机
《编译原理》第3章

NFA到相应的DFA的构造的基本思路是: DFA的每 一个状态对应NFA的一组状态. DFA使用它的状 态去记录在NFA读入一个输入符号后可能达到的 所有状态.
NFA M所能接受的符号串的全体记为L(M)
结论:
上一个符号串集V是正规的,当且仅当存 在一个上的不确定的有穷自动机M,使得 V=L(M)。
DFA是NFA的特例.对每个NFA N一定存在一个DFA M,使得 L(M)=L(N)。对每个NFA N存在着与之 等价的DFA M。 有一种算法,将NFA转换成接受同样语言的DFA.这 种算法称为子集法. 与某一NFA等价的DFA不唯一.
0
1
S P
Z
{P} {}
{P}
{S,Z} {Z}
{P}
• δ为S * 到S的子集(2 S)的一种映射
• 从NFA的矩阵表示中可以看出,表项通常是一状态的集合, 而在DFA的矩阵表示中,表项是一个状态
∑*上的符号串t被NFA M接受:
• 对于Σ*中的任何一个串t,若存在一条从某一初态 结点到某一终态结点的道路,且这条道路上所有 弧的标记字依序连接成的串(不理采那些标记为ε 的弧)等于t,则称t可为NFA M所识别(读出或接 受)。 • 若M的某些结点既是初态结点又是终态结点;或 者存在一条从某个初态结点到某个终态结点的道 路,其上所有弧的标记均为ε,那么空字ε可为M所 接受。
其中: δ(S,0)={P}
δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z} • 状态图表示
1 1 S 0 0,1 Z
P
1
• 矩阵表示
状态 输入
δ(S,0)={P} δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z}
编译原理第三章

例3.4 Z→ A→ B→
有正规文法G: 0A 0A | 0B 1A | ε
例3.5 A→ B→ C→
有正规文法G: aB | bB aC | a | b aB
例3.6 Z→ U→ V→
有正规文法G: Z=0(0|01)*0 U0 | V1 A=(a|b)(aa)*(a|b) Z1 | 1 Z=(10|01)(10|01)* Z0 | 0
A
B
r2 ε
A C
A
B
ε
B
r1
④R为复合正规式?
例3.12 3.13 P41
教学进度
3.4.4 NFA确定化为DFA
方法(子集法) 1、改造M为M’: ①引进新的初态结点X、终态结点Y; ②对M的状态转换图实施分裂(替换)
计算机科学与工程系
2、将M’进一步变换为DFA :
①状态子集T的闭包_CLOSURE(T) ②定义状态集Ta = _CLOSURE(J) ③从DFA的初态_CLOSURE({X})开始计算状态转换矩阵;直到 不再产生新的状态子集为止。
第三章
• • • • • •
词法分析与有穷自动机
计算机科学与工程系
词法分析器的功能与输出 单词符号的两种定义方式 正规表达式与有穷自动机 正规文法与有穷自动机 词法分析器的设计 词法分析程序自动构造工具LEX简介
教学进度
3.1 词法分析器的功能
计算机科学与工程系
词法分析:对字符串表示的源程序进行从左到右的扫描和 分解,根据语言的词法规则识别出一个个具有独立意义的 单词符号。
教学进度
3.3 单词符号的两种定义方式
单词符号结构的描述方法:
计算机科学与工程系
正规文法(3型文法)(regular grammar)
第三章 词法分析和有穷自动机
ε
ε
2
ε
6 b
ε
f
3.4.5 DFA的最小化(化简)
• 最少状态DFA 对于一个DFA M,存在一个最少状态DFA M’, 使得L(M’)=L(M)。 (a)没有多余状态 (b)没有两个状态是互相等价的 结论: 一个NFA 对应的DFA不惟一 但它对应的最小化DFA不计同构是惟一的
• 多余状态的例子 a
例
正规式 φ
ε
a a|b ab (a|b)(a|b) a* ba* (a|b)*
正规集 φ {ε } {a} L(a|b)=L(a) ∪ L(b)={a,b} L(ab)=L(a)L(b)={ab} {aa,ab,ba,bb} { ε ,a,aa,aaa,…} {b,ba,baa,baaa,…} {所有由a和b组成的字}
• 例 DFA M=({0,1,2,3},{a,b}, f ,0,{3}) 其中 f 为: f (0,a)=1 f (0,b)=2 f (1,a)=3 f (1,b)=2 f (2,a)=1 f (2,b)=3 f (3,b)=3 f (3,a)=3
3.4.1 确定有穷自动机(DFA) • DFA的表示方法 两种:矩阵和图形的方式 矩阵称为状态转换矩阵 图形称为状态转换图
• NFA M所接受字符串的集合称为NFA M所能 识别的语言,记为L(M)。 • NFA的确定化 DFA是NFA的特例
NFA M存在与之等价的DFA M’,L(M)=L(M’) 与某一NFA等价的DFA不惟一 正规式 NFA 正规文法 DFA
3.4.4 NFA 确定化
• 状态集合I的空闭包:ε -closure(I) 它是一个状态集合,包含 : ♠ I中任何状态q ♠ I中任何状态q经任意条空弧到达的任何状态 • 状态集合I的a弧转换:Ia 定义一个状态集J,J是I中所有状态经一条a 弧到达的状态的全体 Ia=ε -closure(J)
第三章词法分析及有穷自动机

U
④ 以识别符号为终止状态。
例:设有正规文法G[Z]: Z∷= U0|V1 U∷=Z1|1 V∷=Z0|0
(描述的语言为L(G)={01,10}+) 则状态转换图如下:
新增加开 始状态S
1 S
0
U 1
0
V
0 Z
1
以开始符号Z 作终态
例:标识符的转换图:
字 母 或 数 字
字 母
0
1
非 字 母 和 非 数 字 2
例:一种一类的单词输出形式 设保留字、标识符、常数、运算符、分界符
的种别码分别为1,2,3,4,5;将if a>1 then b:=10表示为一种一类的单词输出形式。
if a>1 then b:=10
(字符串表示 的源程序)
=>词法分析 器=>
(1, ’ if ’ )
(2,’ a ’ ) , (4,’ >’) (3,’1’ 的二进 制数)
2>根据状态转换图写词法分析程序 为每一个状态结点写一个过程或函数: 对N1结点: Procedure PN1
Begin
Ch:=getchar( );
If ch=”e” then PN5 Else if ch=”d” then PN2
Else if ch=” ·” then PN3 Else error
从开始状态出发到某一终止状态结点为止,所经过的路径 上的符号串,称能为该状态转换图所接收(识别)的符号 串。
如:标识符x26为上述转换图识别,识别路径为
x
2
6
0
1
1
1
非 字 母 和 非 数 字 2
2) 右线性正规文法构造状态转换图
① 右线性正规文法U ∷= a|aV构造状态转换图的步骤: ② 增加一个终止状态结点z(假定文法的词汇表中不含
北航计算机学院编译习题讲解

0
1
q3
q4
0
18
0
Start
A
1 B
1
0
1
C
D
E
1
0
1
{A} -
{B}
q0
{B} {B} {BC}
q1
{BC} {BD} {BC}
q2
{BD} {B} {BCE}
q3
{BCE} {BD} {BC}
q4
0
1
-
q1
q1
q2
q3
q2
q1
q4
q3
q2
2008年7月2日
19
0
q0
-
q1
q1
q2
q3
q3
2008年7月2日
17
01
q0 -- q1 q1 q2 q3 q2 q2 q3 q3 q4 q3 q4 q2 q5 q5 q4 q3
q0 q1 q2 q3 q4
01
q0 -- q1
q1 q2 q3
q2 q2 q3
q3 q4 q3
q4 q2 q5
q5 q4 q3
0
1
-
q1
q1
q2
பைடு நூலகம்q3
q2
q1
q4
q3
第三章:词法分析
3.1 词法分析的功能 3.2 词法分析程序的设计与实现
–状态图
3.3 词法分析程序的自动生成
–有穷自动机、LEX
2008年7月2日
1
补充
1 2
NFA
正则文法
4 3
5 6
正则表达式
DFA 最小化
2008年7月2日
编译原理第三章_有穷自动机

例 过河问题 分析(续)
初始状态:MWGC-φ;终止状态:φ-MWGC。 g
MWGC-φ
WC-MG
问题:
6
例 过河问题 状态转换图
起始 g
MWGC-φ g
g φ-MWGC
g
7
WC-MG
m
m MWC-G
w
w
c
C-MWG
c W-MGC
g
g
MGC-W c
MG-WC
w
m
c G-MWC
m
gg MWG-C
+dd. ddd;
输入符号串
数字 数字
SB
.
数字
+
A
H
-.
数字
.G
接收:若扫描完输入串, 且在一个终止状态上结 束。
数字 阻塞:若扫描结束但未 停止在终止状态上;或 者为能扫描完输入串 (如遇不合法符号)。
不完全描述:某些状态 对于某些输入符号不存 在转换。
练习:+34.567 .123 3.4.5
w
有穷自动机(FA)
数字系统:可以从一个状态移动到另一个状态;每次 状态转换,都上由当前状态及一组输入符号确定的;可以 输出某些离散的值集。
FA:一个状态集合;状态间的转换规则;通过读头来 扫描的一个输入符号串。
读头:从左到右扫描符号串。移动(扫描)是由状态 转换规则来决定的。
8
读头
一个FA的例子
(3)运行: 串f(,Q,且t1tt21)∈= Σf(,f(Qt1,t2t1∈), Σt2*),其中Q∈K, t1t2为输入字符
17
例3
题:试证abba可为例1的DFA M所识别(所接受)。
sun编译原理第3章词法分析与有穷自动机第4 8讲 优质课件

={a,b}*{aa,bb}{a,b}*
练习:若S=a|bb,则L((a|bb)*)=?
2019/11/24
信息学院 孙丽云
5
第3章 词法分析与有穷自动机
■正规式中运算的优先级
括号优先,* 次之,•(连接)再次之,| 最后 例:a|bc* ≌ a|(b(c*))
ab|c*d ≌ (ab)|((c*)d)
其中 U、W∈N t∈T 其中 U、W∈N t∈T
2019/11/24
信息学院 孙丽云
8
第3章 词法分析与有穷自动机
■正规文法到正规式的转换
(1)将正规文法中的每个非终结符表示成关于它的一 个正规式方程,获得一个联立方程组。 (2)依照求解规则:
若x=αx|β(或x=αx+β),则解为x=α*β; 若x=xα|β(或x=xα+β),则解为x=βα*; 以及正规式的分配律、交换律和结合律求关于文法 开始符号的正规式方程组的解. 这个解是关于该文法开始符号S的一个正规式,显然 它表示了由该正规文法所描述的语言。
信息学院 孙丽云
2
第3章 词法分析与有穷自动机
3.3 语言单词符号的两种定义方式 多数程序设计语言的单词符号都能用正规文法或正规 式来定义。
■ 正规式与正规集
设有字母表={a1,a2,…,an},在字母表上的正 规式和它所表示的正规集可用如下规则定义: (1) Φ是上的正规式,它所表示的正规集是Φ, 即空集{} (2)ε是上的正规式,它所表示的正规集是{ε} (3)ai是上的正规式,它所表示的正规集由单个符 号ai组成,即{ai}
③ (e1)*是上的一个正规式,它所表示的正规集为 L((e1)*) =L((e1))*
正规式描述了单词符号的构成规则,正规集是正规 式能描述的所有的单词的集合。
编译原理 第三章 有限自动机与词法分析器
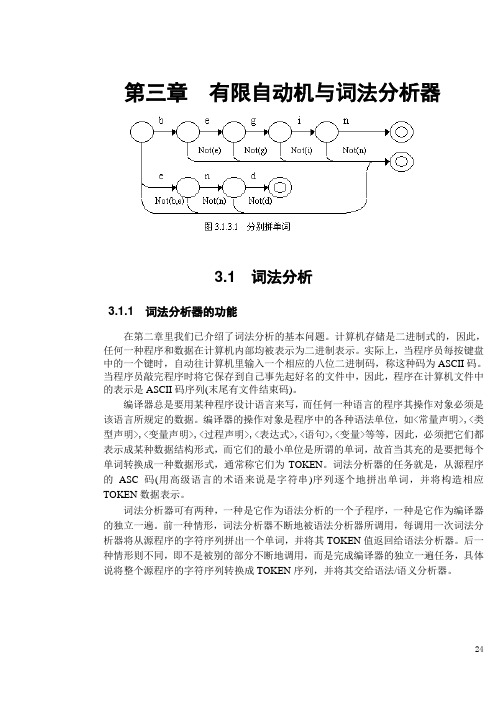
第三章有限自动机与词法分析器3.1词法分析3.1.1词法分析器的功能在第二章里我们已介绍了词法分析的基本问题。
计算机存储是二进制式的,因此,任何一种程序和数据在计算机内部均被表示为二进制表示。
实际上,当程序员每按键盘中的一个键时,自动往计算机里输入一个相应的八位二进制码,称这种码为ASCII码。
当程序员敲完程序时将它保存到自己事先起好名的文件中,因此,程序在计算机文件中的表示是ASCII码序列(末尾有文件结束码)。
编译器总是要用某种程序设计语言来写,而任何一种语言的程序其操作对象必须是该语言所规定的数据。
编译器的操作对象是程序中的各种语法单位,如<常量声明>,<类型声明>,<变量声明>,<过程声明>,<表达式>,<语句>,<变量>等等,因此,必须把它们都表示成某种数据结构形式,而它们的最小单位是所谓的单词,故首当其充的是要把每个单词转换成一种数据形式,通常称它们为TOKEN。
词法分析器的任务就是,从源程序的ASC码(用高级语言的术语来说是字符串)序列逐个地拼出单词,并将构造相应TOKEN数据表示。
词法分析器可有两种,一种是它作为语法分析的一个子程序,一种是它作为编译器的独立一遍。
前一种情形,词法分析器不断地被语法分析器所调用,每调用一次词法分析器将从源程序的字符序列拼出一个单词,并将其TOKEN值返回给语法分析器。
后一种情形则不同,即不是被别的部分不断地调用,而是完成编译器的独立一遍任务,具体说将整个源程序的字符序列转换成TOKEN序列,并将其交给语法/语义分析器。
实际的编译器一般都采用子程序方式,但是为了独立地介绍词法分析、语法分析和语义分析的概念和技术,我们将词法分析部分分离出来即作为独立一遍的词法处理器来介绍。
从实际的角度来说,这种方法有以下缺点:一是因为它要生成TOKEN列,自然多占用空间;二是因为要保存所有的TOKEN,需要耗费更多的时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设计词法分析程序
单词的描述工具
单词的识别系统
正规文法与正规式
有穷自动机
第三章 词法分析与有穷自动机
• 3.1 词法分析程序的功能
• 任务
从左到右扫描源程序,产生一个个单词符号。 • 通常词法分析程序作为语法分析程序的子程序
调用过程
字符串表示的 源程序
字符
词 法 分 析 器
• DFA M的矩阵表示
字符 0 1 2 3 a 1 3 1 3 b 2 2 3 3
状态
• DFA M的状态图表示
1 a 0 b 2 初态用箭头指出 终态双圈表示 b a a 3
a,b
b
3.4.1 确定有穷自动机(DFA) • Σ 上的符号串α 被 DFA M接受 从初态到某一终态结点通路上所有弧的标 记连接的字等于 α ,则称 α 可被M识别 (接受)。
例
正规式 φ
ε
a a|b ab (a|b)(a|b) a* ba* (a|b)*
正规集 φ {ε } {a} L(a|b)=L(a) ∪ L(b)={a,b} L(ab)=L(a)L(b)={ab} {aa,ab,ba,bb} { ε ,a,aa,aaa,…} {b,ba,baa,baaa,…} {所有由a和b组成的字}
例 NFA M=({S,P,F},{0,1}, f ,{S,P},{F}) 其中 f 为: f (S,0)={P} f (S,1)={S,F} f (P,1)={F} f (F,1)={P} f (F,0)={P}
1 1
0
F
1
{S,F} 1 {F} {P}
SS P 0 F
{P} 0,1
φ
P{P}
初态不惟一 后继状态不惟一
• 单词种别
• 一般用整数编码,对应五种单词,由具体的实 现系统来编码。 • 编码之后,语法分析可以对它进行识别。
• 单词自身的值
• 存放可以取到这个单词值的方法。 如: 标识符,自身值是它所在符号表的指针; 常数,自身值是其在常数表的指针; • 通过这个指针查到单词的值和属性,用于语义 分析。
• NFA M所接受字符串的集合称为NFA M所能 识别的语言,记为L(M)。 • NFA的确定化 DFA是NFA的特例
NFA M存在与之等价的DFA M’,L(M)=L(M’) 与某一NFA等价的DFA不惟一 正规式 NFA 正规文法 DFA
3.4.4 NFA 确定化
• 状态集合I的空闭包:ε -closure(I) 它是一个状态集合,包含 : ♠ I中任何状态q ♠ I中任何状态q经任意条空弧到达的任何状态 • 状态集合I的a弧转换:Ia 定义一个状态集J,J是I中所有状态经一条a 弧到达的状态的全体 Ia=ε -closure(J)
ε
ε
2
ε
6 b
ε
f
3.4.5 DFA的最小化(化简)
• 最少状态DFA 对于一个DFA M,存在一个最少状态DFA M’, 使得L(M’)=L(M)。 (a)没有多余状态 (b)没有两个状态是互相等价的 结论: 一个NFA 对应的DFA不惟一 但它对应的最小化DFA不计同构是惟一的
• 多余状态的例子 a
• ε -closure(I)例子 ε 5
a 1 a
6
ε
ε
2
a
3
ε
8
4
ε
7
I={1} , I={5}, I={1,5}
ε -closure(I)= {1,2} ε -closure(I)={5,6,2} ε -closure(I)= {1,2,5,6}
• I的a弧转换例子 ε 5
a 1 a
6
ε
ε
3.3.1 正规式与正规集
• 3 正规式等价 若两个正规式U和V所表示的正规集相同,则说 U和V等价。 记作:U=V
例 两个正规式等价
U=(a|b) U=b(ab)* U=(a|b)*
V=b|a V=(ba)*b V=(a*b*)*
3.3.1 正规式与正规集
• 4 正规式性质
设A,B和C均为正规式,则: ♣ A|B=B|A 或的交换律 ♣ A|(B|C)=(A|B)|C 或的结合律 ♣ A(BC)=(AB)C 连接的结合律 ♣ A(B|C)=AB|AC 分配律 (A|B)C=AC|BC 分配律 ε 是连接的恒等元素 ♣ ε A=A ε =A ♣ (A*)*=A* ♣ A*=AA*| ε =A|A*=(A| ε )*
语 单词符号 法 分 析 取下一个 器
单词符号
图 词法分析程序
3.2 单词符号及输出单词的形式
• 1 单词符号 程序语言中具有独立意义的最小单位。 一般分五种:
个数 不确定
关键字 标识符 常数 运算符 界符
个数 确定
3.2 单词符号及输出单词的形式
• 2 单词的机内表示 二元式: (单词种别,单词自身的值)
例 3.4 设有正规文法G[Z]: Z → 0A A → 0A|0B B → 1A| ε 求出该文法生成语言的正规式。 解得 正规文法G[Z]所生成语言的正规式是 0(0|01)*0
例3.5 设有正规文法G[A]: A → aB|bB B → aC|a|b C → aB 求该文法对应的正规式。
解得 G[A]所生成语言的正规式是: (a|b)(aa)*(a|b)
例 3.8 将R=(a|b)(aa)*(a|b)转换为正规文法。 S → (a|b)(aa)*(a|b)
解得G[S]: S → aA|bA A → aB|a|b B → aA
例 3.9 将R=l(l|d)*转换成正规文法
S → l(l|d)* 消去ε 得G[S]: S → l|lA A → l|d|lA|dA
3.3.1 正规式与正规集
• 1 正规式的递归定义 注:正规式中只包含3种运算符: 连接“•”,或“|”,闭包“*”。 优先级依次为:闭包-连接-或。 三种运算均是左结合的。
3.3.1 正规式与正规集
• 2 正规集 • 由正规式所表示的字集为这个正规式所对应的 正规集,也把它叫做正规式所定义的语言。 • 正规式U的正规集表示为L(U)。
• 例 if (a>1) b=100; 词法分析后的形式 if (2, ) ( (29, ) a (10,’a’) > (23, ) 1 (11,’1’) ) (30, ) b (10,’b’) = (17, ) 100 (11,’100’) ; (26, )
3.3 单词的两种定义方式
描述机制
• 正规文法(右线性文法和左线性文法) 机器易于识别 • 正规式 简洁清晰
a
A {1,2,4} C {1,2,4}
b
B B
A {1,2,4,5,6,f} D C {1,2,4,6,f} E
F {1,2,4,5,6,f} D F {1,2,4,5,6,f} D C {1,2,4,6,f} E
3.4.4 NFA 确定化-子集法
NFA N: i a 1 b DFA N’: a S b A b a B b D b a a 3 a 5 b a a C b b a E a F b 4 b a
3.4.2 非确定有穷自动机(NFA)
• α 被NFA M接受:从某一初态结点到某一终点 的通路上所有弧的标记连接成的字等于 α • 存在空转移的自动机一定是NFA • 如果某些结点既是初态又是终态,或 从某个初态到某个终态有空通路,则空字 ε 也 可被接受。
1
ε
2
ε
3
3.4.2 非确定有穷自动机(NFA)
• 例 DFA M=({0,1,2,3},{a,b}, f ,0,{3}) 其中 f 为: f (0,a)=1 f (0,b)=2 f (1,a)=3 f (1,b)=2 f (2,a)=1 f (2,b)=3 f (3,b)=3 f (3,a)=3
3.4.1 确定有穷自动机(DFA) • DFA的表示方法 两种:矩阵和图形的方式 矩阵称为状态转换矩阵 图形称为状态转换图
例 3.6 设有正规文法G[Z]: Z→ U0|V1 U→ Z1|1 V → Z0|0 求该文法对应的正规式。 解得 G[Z]所生成语言的正规式是: (10|01)(10|01)*
2 正规式转换到正规文法
Σ 上的正规式r转换到3)A→ab,可化为A→ aB,B →b (4)A→a*b,可化为A→ aA|b 不断应用(3),(4),直到每个产生式右部都只含有一个终结 符或 ε 为止。
解得G[S]: S → lA A → lA|dA| ε
去掉 ε 规则的算法
消去ε 规则的算法: (1)找出文法中在所有经过若干步能推出ε 的非终结符, 放入V中。 (2)按如下步骤构造新的P’: (a)若V中元素在某产生式右部,则将它变成两个产 生式:分别以ε 和它本身代入,将新生式加入P’ (b)其他产生式除去ε 也加入P’ (c)如果P中有产生式S →ε ,则引入新S’,将S’ → S|ε 加入P’
2
a
3
ε
8
4
ε
7
I={1,2}
J={5,3,4}
Ia= ε -closure(J)={2,3,4,5,6,7,8}
3.4.4 NFA 确定化-子集法
• NFA M=(Q, Σ , f ,S,Z) 转换成 DFA M’=(Q’, Σ ’ , f ’ ,S’,Z’) (1)字母表相同,令S’= ε -closure(S) (2) Q’, f ’ ,Z’ 由状态矩阵得出。
a 0 1 a 2 b 3 b a b 3 ab 1 a 2 a 5 a 6 4 0 b a b b a b 7 4 b 5
8
3.4.5 DFA的化简-分划法
• (1)首先将状态分成两个子集:终态和非终态 • (2)检查子集中的状态是否等价: 对输入字符是否落入现行的不同子集,是 的话就分化;直至没有新的分划。 • (3)最后在每个子集中选出一个代表,消去其他 等价状态。
