第三章 词法分析(3)
《编译原理》第3章

NFA到相应的DFA的构造的基本思路是: DFA的每 一个状态对应NFA的一组状态. DFA使用它的状 态去记录在NFA读入一个输入符号后可能达到的 所有状态.
NFA M所能接受的符号串的全体记为L(M)
结论:
上一个符号串集V是正规的,当且仅当存 在一个上的不确定的有穷自动机M,使得 V=L(M)。
DFA是NFA的特例.对每个NFA N一定存在一个DFA M,使得 L(M)=L(N)。对每个NFA N存在着与之 等价的DFA M。 有一种算法,将NFA转换成接受同样语言的DFA.这 种算法称为子集法. 与某一NFA等价的DFA不唯一.
0
1
S P
Z
{P} {}
{P}
{S,Z} {Z}
{P}
• δ为S * 到S的子集(2 S)的一种映射
• 从NFA的矩阵表示中可以看出,表项通常是一状态的集合, 而在DFA的矩阵表示中,表项是一个状态
∑*上的符号串t被NFA M接受:
• 对于Σ*中的任何一个串t,若存在一条从某一初态 结点到某一终态结点的道路,且这条道路上所有 弧的标记字依序连接成的串(不理采那些标记为ε 的弧)等于t,则称t可为NFA M所识别(读出或接 受)。 • 若M的某些结点既是初态结点又是终态结点;或 者存在一条从某个初态结点到某个终态结点的道 路,其上所有弧的标记均为ε,那么空字ε可为M所 接受。
其中: δ(S,0)={P}
δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z} • 状态图表示
1 1 S 0 0,1 Z
P
1
• 矩阵表示
状态 输入
δ(S,0)={P} δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z}
北航编译原理课件 03.词法分析

3. 词法分析程序算法
北京航空航天大学计算机学院
17
1.单词及内部表示 单词及内部表示: 单词及内部表示
单词名称
BEGIN END FOR DO IF THEN ELSE 标识符 常数(整 常数 整) : + * , ( ) :=
保留字和分界符采用一符一类
记忆符
BEGINSY ENDSY FORSY DOSY IFSY THENSY ELSESY IDSY INTSY COLONSY PLUSSY STARSY COMSY LPARSY RPARSY ASSIGNSY
字母、数字
标识符 无符号整数
单字符分界符
S S S
字母
标 数字
非字母数字
出口
数字
数
非数字
出口
+ * , 单界 ( ) :
其他字符 非=
出口
双字符分界符
北京航空航天大学计算机学院
S
冒号
=
双界
其他字符
出口 15
查保留字表 读字符
字母、数字
S
字母
标 数字
非字母数字
标识符
非数字
数字
数
无符号整数 单字符分界符
如:b{ab} = {ba}b {a|b} = {{a} {b}} = (a*b*)*
北京航空航天大学计算机学院 23
例:设 ∑ = { a,b },下面是定义在∑上的正则表达式和正则集合 正则表达式 ba* a(a|b)* (a|b)*(aa|bb)(a|b)* 正则集合
北京航空航天大学计算机学院
北京航空航天大学计算机学院 20
‘*’ : ‘,’ : ‘(’ : ‘)’ : ‘:’ :
第3讲词法分析

所有由 a 和 b 组成的串
(ab)(aabb)(ab)
}
2020/12/4
{ 上所有含有两个相继 的 a 或两个相继的 b 组成 的串
• 例 ={l,d},r=l(l d) 定义的正规集: {l,ll,ld,ldd,……}(标识符)
• 例4.3 ={d,.,e,+,-},则上的正规 式 d(.dd )(e(+- )dd )表示的 是无符号数的集合。其中d为0~9的数字 。
✓ 4。S∈K 是唯一的一个初态;
✓ 5。Z K 是一个终态集,终态也称可接受状态或结束状态。
2020/12/4
1. DFA 示 例
DFA M=({S,U,V,Q}, {a,b}, f, S, {Q})其中 f 定义为:
f(S,a)=U
f(V,a)=U
f(S,b)=V
f(V , b)=Q
f(U,a)=Q
3.3 有 穷 自 动 机
• 确定的有穷自动机(DFA) • 不确定的有穷自动机(NFA) • NFA DFA 的转换 • DFA的化简
2020/12/4
一、 DFA 的 定 义
• DFA定义:一个确定的有穷自动机(DFA)M是一 个五元组:M=(K,Σ,f,S,Z)其中:
✓ 1。K 是一个有穷集,状态集,它的每个元素称为一个状态;
对上的正规式 r , 存在一个 G=(VN,VT,P,S) 使得 L(G) = L(r) , 反之亦然。
2020/12/4
五、 正 规 文法 到 正 规 式
对上的正规式 r , 存在一个 G=(VN,VT,P,S) 使得 L(G) = L(r) , 反之亦然。
2020/12/4
• 1. 将 正 规 式 转 换 成 正 规 文 法
编译原理课件-词法分析

號等記號的文法
—— 正規文法
語法:借助於記號來描述語言的結構的文法
—— 上下文無關文法
21/76
二、記號的文法
識別字 常數
–整數 –無符號數
運算符 分界符 關鍵字
22/76
Wensheng Li BUPT @ 2008
識別字
識別字定義為“由字母打頭的、由字母或數字組成
的符號串”
正規運算式?
描述識別字集合的正規運算式:
9/76
Wensheng Li BUPT @ 2008
3.2 詞法分析程式的輸入與輸出
一、詞法分析程序的實現方法 二、設置緩衝區的必要性 三、配對緩衝區 四、詞法分析程序的輸出
10/76
Wensheng Li BUPT @ 2008
一、詞法分析程式的實現方法
利用詞法分析程序自動生成器
–從基於正規運算式的規範說明自動生成詞法分析程序。 –生成器提供用於根源程式字元流讀入和緩沖的若干副程
記號的屬性
詞法分析程式在識別出一個記號後,要把與之有關 的資訊作為它的屬性保留下來。 記號影響語法分析的決策,屬性影響記號的翻譯。 在詞法分析階段,對記號只能確定一種屬性
–識別字:單詞在符號表中入口的指針 –常數:它所表示的值 –關鍵字:(一符一種、或一類一種) –運算符:(一符一種、或一類一種) –分界符:(一符一種、或一類一種)
4/76
Wensheng Li BUPT @ 2008
3.1 詞法分析程式與語法分析程式的關係
詞法分析程式與語法分析程式之間的三種關係
–詞法分析程式作為獨立的一遍 –詞法分析程序作為語法分析程序的副程式 –詞法分析程序與語法分析程序作為協同程式
分離詞法分析程序的好處
第3章 词法分析(3)

3.4 正规式与有穷自动机的等价性
1. NFA M正规式R
在消结过程中,逐步用正规式来标记弧, 规则如下:
1.对于
1
2.对于
R1
2
R2
代之为
3
1
R1 R2
3
代之为 R1 R1| R2 1 2 1 2 R2 R2 3.对于 代之为 R1R2﹡R3 R 1 R 3 1 3 1 2 3
例如:有NFA M如图3.14,求其等价的正规式R。
a,b a 3
x ε 0 b 1 a|b a|b x ε 0
aa
a
4
ε
b
y (a|b)*(aa|bb)(a|b)* x y ε 2 a,b a|b aa(a|b) * y bb(a|b) *
4
ε y x
bb
2
ε
a|b
ε
0
3.4 正规式与有穷自动机的等价性
课堂练习 求以下NFA的正规式 a a 3 a 1 2 b
第一步
a
5 6 b
b
4
b
a
a
3
a
a
s
1 2
b
5 b
4 b
6 b
z
3.4 正规式与有穷自动机的等价性
第二步
a|b s 1 2
aa bb aa|bb 5
a|b
6
z
第三步
s
第四步
(a|b)*
2
5
(a|b)*
z
s
(a|b)*(aa|bb)(a|b)*
z
课堂讲解
• 【例5.12】第72页 • 【例5.13】第73页
编译原理chapter3 词法分析
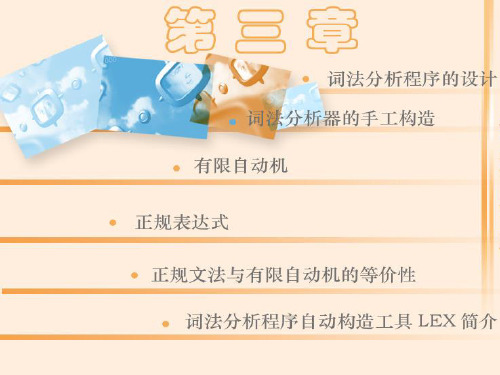
一 设计一个奇偶校验器
DFA是由集合,序列和函数定义的数学模型, 它对于 上的w,判定是可接受的还是不可 接受的。例如,设计一个DFA m ,奇偶校验 器,首先,w是由0,1组成的字符串,因此, 1. ={0 ,1}且w在一条输入带上。
0 1 0 1 1$
读头
精品文档
11
2. 状态集:它记忆已读入w子串的状态,m是 奇偶校验器,它应该记住,初始序列是奇数 个1还是偶数个1。因此,m有even和odd两个 状态. 3 .even为开始状态。
词法分析器
‘while’,‘i’,‘<>’,‘j’, ‘do’, ‘if’,‘i’,‘>’,‘j’,‘then’, 'i', ':=’ , 'i', ’-’ , 'j', 'else', 'j', ':=', 'j', '-', ‘i'
精品文档
4
词类和属性
computator n. Calcculating machine.
3.1.1 词法分析程序的功能 源程序 单词词序法列分析器
3.1.2 单词的词类和属性 (词类符号,单词的属性值)
3.1.3 词法分析程序作为一个独立子程序 (1)语法分析程序的子程序; (2)组 织成一遍扫描。
精品文档
3
While i<>j do if i>j then i:=i-j else j:=j-I
三 一个DFA有三种表示:
(1)象上面,用转换函数;
精品文档
14
转移矩阵
状态转换图
a
b
0
1
2
a
第三章词法分析
说明:*上的某些集合若不能用正规表达式表示,则该集合不是正规集。 如: ={a,b},L(G)={anbn| n0}就不是正规集,因为它不能用正规式表示。 (可以用上下文无关文法Z∷=aZb|ab|ε产生)可以证明,凡是由正规文 法所产生的语言一定是正规集,即可由正规式表示 。
18
第三章 词 法 分 析
§3.6正规表达式和有穷自动机
一、正规表达式和正规集的定义
1.非形式定义 2.递归定义
二、正规表达式的性质 三、正规文法、正规表达式与有穷自动机的关系 四、由正规表达式构造确定有穷自动机
1.由正规表达式e构造转换系统 2.由转换系统构造确定有穷自动机DFA(子集法) 3.由正规文法构造正规表达式
1.由正规表达式e构造转换系统 2.由转换系统构造确定有穷自动机DFA(子集法) 3.由正规文法构造正规表达式
五、确定有穷自动机的化简
1.等价和可区分的概念 2.确定有穷自动机的化简方法
2
§3.6正规表达式和有穷自动机
为什么引入正规表达式?
由正规文法构造状态转换图,再根据状态转换 图可以构造有穷自动机,往往很麻烦,但是, 对于一些复杂的正规文法,如果将其先转换成 正规表达式,再由正规表达式来产生有穷自动 机就方便得多。而且正规表达式的引入有助于 词法分析程序的自动生成,它还广泛应用于模 式识别和文献目录检索等。
五、确定有穷自动机的化简
1.等价和可区分的概念 2.确定有穷自动机的化简方法
16
第三章 词 法 分 析
§3.6正规表达式和有穷自动机
一、正规表达式和正规集的定义
1.非形式定义 2.递归定义
7.第三章词法分析(3)
0 1 D 1
0 A
1 0 C
A00B 1D B 1C 0D C 0 0B 1D
D 0D 1D
0, 1
图 3.9(a)DFA
右线性正规文法GR L(M)=0(10)* 非终结符D是无用的
例3.4 右线性正规文法GR NFA M’
A00B 1D 0 A 0 1 D 0,1 图3.9(b) GR导出的NFA
2015-3-29
Ch3.词法分析
29
状态的等价和可区别定义
定义: 设s, t S是两个不同的状态, 若对任何 α *, 从s (或t)出发能读出α而停于某个终 态,则称 s 和 t 是等价状态。否则,称 s 和 t 是可 区别的,即不等价的。 例如: 终态和非终态是可区别的,因为终态能 读出空字ε,而非终态不行。 又如: P51. 图 3.8 的 DFA 中的状态 1 和 2 是可区 别的,因为状态1能读出a而停于终态,但状态 2读出a后不能停于终态。 等价状态定义了状态集合上的等价关系。因此, 状态集合能被划分成等价类。
8
正规文法GR FA M
证明1: 设右线性文法 GR=(VT,VN, S, £) 构造 FA M = (Q, Σ, δ, Q0, F)
(1) GR增加一个新的终态符号 f , f VN , 令 Q={f}∪ VN , f及每个非终结符是一个状态 (2) 字母表∑= VT , 初态集Q0 ={S}, 终态集 F={f}
ε 1
A
1
0
q0
0
S
0
1
B
按变换方法画出箭弧 ( 产生式右部非终结符射向 左部非终结符),及弧 上的标记
第3章词法分析
例:语言L[G]={abn|n>=1},其正规文 语言L[G]={ab |n>=1},其正规文 法为G[A]: 法为G[A]: A→aB A→aB B→bB| B→bB| b 画出状态转换图
例:部分单词的状态图
Letter,digit
s
letter digit
其它 (IDN,入口) ,入口) digit 其它 (NUM,值) , (ASG,_) , ) =
3.2 状态转换图
•识别标识符的流程图 识别标识符的流程图 开始
出口 N N 数字 Y
字母 N 出口
Y
取字符
字母 Y
结点:状态用○表示;终态用◎表示 结点:状态用○表示;终态用◎ 有向弧 弧标记 初态 开始 1 letter 2 ── 箭头 ── 输入字符 Letter,d号的表示
• 常用单词种别 常用单词种别——分类 分类
–各关键字(保留字、基本字) 各关键字(保留字、基本字) 各关键字 –各种运算符 各种运算符 –各种分界符 各种分界符——各用一个种别码标识(特定符号类) 各用一个种别码标识( 各种分界符 各用一个种别码标识 特定符号类) –其它标识符 其它标识符——用一个种别码标示(非特定符号类) 用一个种别码标示( 其它标识符 用一个种别码标示 非特定符号类) –常数 常数——用一个种别码标示(非特定符号类) 用一个种别码标示( 常数 用一个种别码标示 非特定符号类)
• 例:文法 文法G[Z]: : • Z→ Z→Za| Aa| Bb • A→ A→Ba | a • B→ B→Ab| b • 画出状态转换图
2、从右线性正规文法出发,构造状态图 从右线性正规文法出发, 以每个非终结符为状态结点, 1. 以每个非终结符为状态结点 , 开始符号 对应初态S 对应初态S ; 2.增设一个终态 Z; 3. 对于规则 A→aB , 画从状态 A 到 B 的 A→aB, 弧,标为 a; A→a, 4. 对于规则 A→a , 画从状态 A 到终态 Z 的弧, 的弧,标为 a。
编译原理第二版第3章词法分析
1. ε和φ都是∑上的正规式,它所表示的正规集分
别为{ε}和Ф; 2. 任何a∈∑,a是∑上的正规式,它所表示的正 规集为{a}; 3. 假定e1和e2都是∑上的正规式,他们所表示的 正规集分别为L(e1)和L(e2),那么,以下也 都是正规式和他们所表示的正规集;
一、正规式与正规集的递归定义
3.2 单词符号及输出单词的形式
单词自身值
对常数,基本字,运算符,界符就是他们本 身的值 对标识符,将标识符的名字登记在符号表中, ‚自身值‛是指向该标识符所在符号表中位 置的指针。
假定基本字、运算符和界符都是一符一种 例:if(a>1) b=100; 词法分析后输出的单词序列是: (2, ) if (29, ) ( (10,‘a’) a (23, ) > (11,‘1’) 1 (30, ) ) (10,’b’) b (17, ) = (11,‘100’) 100 (26, ) ;
4. 仅由有限次使用上述三步定义的表达式才是∑上的 正规式,仅由这些正规式所表示的字集才是∑上 的正规集。
重点回顾
四、将正规文法转换成正规式 求非终结符的正规式 将正规文法中的每个非终结符表示成关 于它的一个正规式方程,获得一个联立 方程组 用代入法解正规式方程组 最后只剩下一个开始符号定义的正规式, 其中不含非终结符
3.3 语言单词符号的两种定义方式
作用: 描述单词的构成规则,基于这类描 述工具建立词法分析技术,进而实现词法 分析程序的自动构造。 工具有: 正规文法 正规式(Regular Expression)
多数程序设计语言的单词符号都能用正 规文法或正规式来定义。
3.3.1 正规文法
多数程序设计语言单词的语法都能用正 规文法(3型文法)描述 正规文法回顾 文法的任一产生式α →β 的形式都为 A→aB或A→a,其中A ,B∈VN ,a∈VT A→Ba或A→a,其中A ,B∈VN ,a∈ VT 正规文法描述的是VT*上的正规集
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章词法分析3.5 有穷自动机❑有穷自动机是一个更一般化的状态转换图,是一个语言的识别器(recognizer),对输入的串说“yes”or “no”❑确定的和不确定❑识别的语言恰好是正规表达式所能描述的语言❑介绍三类有穷自动机▪NFA▪ -NFA▪DFA3.5.1 不确定的有穷自动机❑不确定的有穷自动机(Non-Deterministic Finite Automata,简称NFA)是一个五元组M=(∑,S,δ,s0,F),其中:▪输入符号集合∑;▪状态集合S;▪转移函数δ:S⨯(∑⋃{ε})→P(S);•可以用转换图或转移表表示▪状态s0是开始状态,s∈S;▪F⊆S,接受状态(终止状态)集合。
S = { 0, 1, 2, 3 }s 0= 0F = { 3 }= { a, b }例3.14 识别语言(a|b)*abb 的NFA 转换图(Transition Diagrams )1starta0abb3b2输入符号ab 0{0, 1}{0}1∅{2}2∅{3}状态识别语言(a|b)*abb 的NFA 转换表(Transition Tables )1starta0abb3b2例,Input: ababb接受输入字符串ababb 的状态转移序列1starta0abb3b2?210000*********−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−ab abb aba bb a b a ACCEPT !Input: aabb练习3.5.3 找出所有标记为aabb 的路径1starta0εa,ba3b2000003221011100−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−bb a abb a a bbaa a,ba,bInput: aabb练习3.5.3 找出所有标记为aabb 的路径1startaa,ba3b2a,b a,b010120120123Input: aabb练习3.5.4 找出所有标记为aabb 的路径321030321010−→−−→−−→−−→−−→−−→−−→−−→−−→−−→−bb a a bb a aεε1starta 0εb 3b2aεεε定义❑一个NFA接受输入字符串x,当且仅当存在从初始状态到某个接受状态的路径,使得该路径的边上的标记恰好连成字符串x❑一个NFA接受(或定义)的语言是它接受的全体输入字符串的集合。
❑一个NFA接受(或定义)的语言是从初始状态到某个接受状态的所有路径上的标记串的集合。
例3.17识别aa *|bb *的NFA12startaabb34εε例,Input: aaa22210−→−−→−−→−−→−aaaε3.5.4 确定的有穷自动机❑确定的有穷自动机(Deterministic Finite Automata,, F),其中:简称DFA)是一个五元组M = (∑, S, δ, s▪输入字母表∑;▪状态集合S;▪转换函数δ: S⨯∑→S;▪初态s∈S;▪终态集合F⊆S;DFA是NFA的特例:1. 没有输入 上的转换;2. 对每个状态s和输入符号a,有且只有1条标记为a的边离开s。
Fig 3-24 模拟DFA的算法s←s0c ←nextchar;while c ≠eof dos ←move(s,c);c←nextcharend;if s is in F then return“yes”else return“no”例3.19 识别语言(a |b )*abb的DFAstart3b21b ababa a(How to get it?)例,Input: ababb321210−→−−→−−→−−→−−→−bb a b a构造DFA的一些例子Construct a DFA that accepts a language L over = {0,1} s.t.1.L is the set of all strings with three consecutive 0’s2.L is the set of all strings without three consecutive 0’sDFA -examples(a)Q ={q 0, q 1, q 2, q 3} ={0,1}F = {q 3}q 0q 1q 2q 30,1111startDFA -examples(b)Q ={q 0, q 1, q 2, q 3} ={0,1}F = {q 0, q 1, q 2}q 0q 1q 2q 30,1111start识别包含子串011的由0和1组成的符号串的NFA (0|1)*011 (0|1)*q 0q 1q 2q 311start11包含子串011的由0和1组成的符号串全体DFAq 0q 1q 2q 3110,11start不包含子串011的由0和1组成的符号串全体q 0q 1q 2q 3110,11start01*0*| 1*00*1(00*1)*或1*(0|01)*不包含子序列011的由0和1组成的符号串全体q 0q 1q 2q 3110,11start01*| 1*00* |1*00*10*或1*0*10* |构造一个DFA ,它接受的语言为{x | x {0,1}*,且当x 看成二进制数时,x 模3与同余0}。
q 210q 101q 01接受0和1的个数都是偶数的字符串的DFA31201111start 偶0偶1奇0奇1奇0偶1偶0奇13.6 从正则表达式到有限自动机3.6.1 从NFA到DFA的变换❑不确定的原因:多值转换函数▪对某个输入有多个转换▪ -转移NFA DFA子集构造法(Subset Construction)❑DFA的一个状态是NFA的一个状态集合❑读了输入a1a2…an后,NFA能到达的所有状态:s1,s2, …,s k,则DFA到达状态{s1,s2, …,s k}No input isconsumed NFA状态上的操作操作描述ε-Closure(s)s∈S,从状态s只经过ε-转换就可以到达的NFA状态集ε-Closure(T) T⊆S,从状态集T中的状态s只经过ε-转换就可以到达的NFA状态集move(T,a)从状态集T中的状态s只经过输入符号a-转换就可以到达的NFA状态集子集构造法❑DFA的初始状态ε-closur e(s),s0是NFA的初态❑其余状态由ε-closure(move(T,a))生成,其中T是由NFA的状态构成的状态集(也就是DFA的状态)▪∀t∈T, 计算ε-closure(move(t,a))19开始εab εab6782345εεεεε输入符号a b状态例3.2119开始εab εab6782345εεεεε输入符号a bA状态A = {0, 1, 2, 4, 7}计算ε-closure(0)19开始εab εab6782345εεεεε输入符号a bAB状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}计算ε-closure(move(A,a))ε-closure (move ({0,1,2,4,7},a))=ε-closure ({3,8})={1, 2, 3, 4, 6, 7, 8}19开始εab εab6782345εεεεε输入符号a bA BB状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}19开始εab εab6782345εεεεε输入符号a b A BCB状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}19开始εab εab6782345εεεεε输入符号a b A BCB C状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}19开始εab εab6782345εεεεε输入符号a b A B CB BC状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}19开始εab εab6782345εεεεε输入符号a b A B C B BDC状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}D = {1, 2, 4, 5, 6, 7, 9}19开始εab εab6782345εεεεε输入符号a b A B C B BDC D状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}D = {1, 2, 4, 5, 6, 7, 9}19开始εab εab6782345εεεεε输入符号a b A B C B B D C BCD状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}D = {1, 2, 4, 5, 6, 7, 9}19开始εab εab6782345εεεεε输入符号a b A B C B B D C B C DBC状态A = {0, 1, 2, 4, 7}B = {1, 2, 3, 4, 6, 7, 8}C = {1, 2, 4, 5, 6, 7}D = {1, 2, 4, 5, 6, 7, 9}B DstartaAab ba b C b a 19startεab εab6782345εεεεε输入符号a b A B C B B D C B C DBC状态Fig3-29 Algorithm For Subset Constructioninitially, ε-closure(s0)is only (unmarked) state in Dstates; while there is unmarked state T in Dstates do begin mark T;for each input symbol a do beginU:= ε-closure(move(T,a));if U is not in Dstates thenadd U as an unmarked state to Dstates;Dtran[T,a] := UendFig 3-30 Computation of ε-closurepush all states in T onto stack;initialize ε-closure(T) to T;while stack is not empty do beginpop the top element t off the stack;for each state u with edge from t to u labeled εdo if u is not in ε-closure(T)do beginadd u to ε-closure(T) ;push u onto stackend如果DFA的某个状态至少包含NFA的一个接受状态,那么,这个状态是DFA的一个接受状态。
