基于有限元理论的轮轨接触力学特性仿真研究
基于有限元的滚动轴承非线性接触分析
麓 翳
基 于 有 限元 的 滚 动 轴 承 非 线 性 接 触 分析
崔 波 程 珩
太原 00 2 ) 3 0 4 ( 原理工大学 机 械电子工程研 究所 山西 太
摘
要: 基于有 限元 分析软件A ss NY ,对滚 动轴承进 行非 线性接触 分析 ,得到其 受载过程 中的应 力和应 变分布情 况 将 计算结 果同赫 兹解 比较 ,二者较 为接
式 中, :00 3 3 . 6 p, 2
、
y是接 触 区尺寸 ,可 通过 图 表查 出 。对于轴 承钢 可 取值 为 l 。
赫 兹接触 应 力计算 式 表述 如下 : 最 大赫兹 接触 应 力:
p一
考
=
⑤
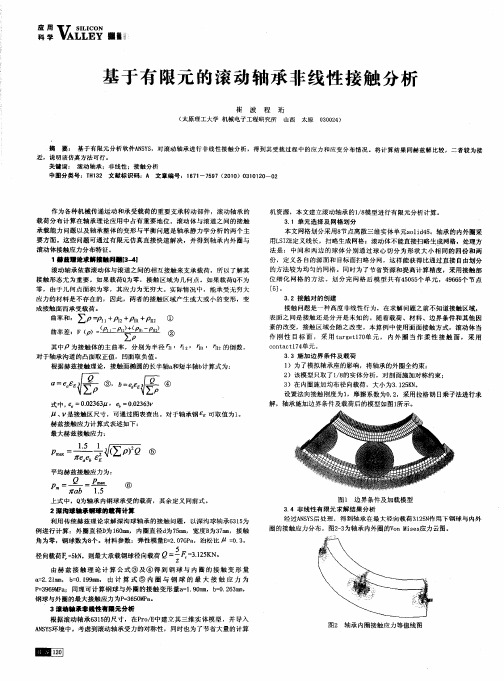
图1 边 界条件 及 加载模 型 3 4 非线性 有 限元 求解结 果分 析
cn at 7单 元 。 ot c 14
其 中 为接触 体 的 主 曲率 ,分 别 为半 径 , h,听2 , 对于轴 承沟 道 的凸面 取正 值 ,凹面 取 负值 。
3 3 施 加边界 条件 及载 荷 .
根 据赫 兹接 触理 论 ,接触 面椭 圆的 长 半轴瘌 短半 轴b 算式为 ; 计 a e£ 1E ③ , b=
本 文 网格划 分 采用 8 节点 离散 三维 实 体单元 s ld5 o i4 。轴承 的 内外 圈采 用 L IE S Z 定义线 长 ,扫略 生成 网格 ;滚 动体 不能 直接 扫略 生成 网格 ,处理 方
法 是 : 中 问 和 两边 的球 体 分 别通 过 球 心 切 分 为 形状 大 小 相 同 的 四份 和 两 份 , 定义 各 自的源 面 和 目标 面扫 略分 网,这 样 能获得 比通过 直接 自由划 分 的 方法 较 为均 匀 的网 格 。同 时为 了节 省 资源 和提 高计 算 精度 ,采 用接 触 部 位 细 化 网 格 的 方 法 。划 分完 网格 后 模 型 共 有 40 5 单元 ,46 5 节 点 5 5个 96 个
基于有限元法的齿轮强度接触研究分析

基于有限元法的齿轮强度接触研究分析随着科技的不断进步和人们对机械装置的需求日益迫切,齿轮的应用越来越广泛。
然而,齿轮在工作过程中难免会受到影响,如磨损、断裂等问题,这些问题需要进行有效的分析研究和解决。
基于有限元法的齿轮强度接触研究分析是一种有效的研究方法,本文将对该方法进行介绍和分析。
1.有限元法的基本原理及其在齿轮强度接触研究中的应用有限元法是一种数值分析方法,可用于复杂的结构应力分析和流体力学分析。
其基本思想是将连续体分割成多个有限的单元,并对每个单元的力学性质进行分析,通过单元之间的数学连接,推导出整个结构的力学特性。
在齿轮强度接触研究中,有限元法可用于齿轮的应力分析和接触特性的研究,以减少试验成本,提高研究效率。
2.齿轮强度接触研究分析的流程(1)建立数字模型:首先,建立齿轮数字模型,将齿轮模型分为齿轮齿面和花键齿面两个部分。
(2)有限元网格划分:将齿轮数字模型进行划分,将齿轮分为若干刚性单元或弹性单元。
(3)加载和边界条件:在有限元网格划分之后,对齿轮模型进行边界条件的设置和加载,如载荷、转速等。
(4)计算分析:进行计算分析,得出齿轮应力分布、接触压力、接触应力等参数。
(5)评价分析结果:根据计算分析得出的参数,对齿轮的强度进行评估和修正,并对齿轮材料的选择进行考虑。
3.有限元法在齿轮强度接触研究中的应用案例在有限元法的应用中,有利于通过理论计算和仿真模拟研究齿轮强度和接触特性的长期变化规律。
例如,在某钢轮齿轮接触强度研究中,使用有限元模拟软件分析齿轮强度,考虑两个因素:加载和齿形误差。
结果表明,齿形误差对齿轮强度有显著影响,而错误的安装和调整则会导致更高的齿轮应力。
另外,有限元分析还可以优化齿轮的设计,使其能够承受最大载荷。
4.总结和展望基于有限元法的齿轮强度接触研究分析,在齿轮制造和实际应用中发挥着重要的作用。
随着科技的不断发展和工业应用的需求,这种方法将在更广泛的范围内得到应用。
轮轨滚动接触弹塑性分析及疲劳损伤研究

轮轨滚动接触弹塑性分析及疲劳损伤研究一、本文概述《轮轨滚动接触弹塑性分析及疲劳损伤研究》是一篇针对轮轨系统滚动接触行为及其引发的弹塑性变形和疲劳损伤问题的综合性研究文章。
本文旨在通过理论分析和实验研究,深入探索轮轨滚动接触过程中的弹塑性力学特性,以及由此产生的疲劳损伤机制和预防措施。
文章将系统介绍轮轨滚动接触的基本理论,分析弹塑性变形对轮轨接触性能的影响,探讨疲劳损伤的产生机理和影响因素,并在此基础上提出优化轮轨设计和维护策略的建议。
本文的研究成果将为提高轮轨系统的运行安全性、稳定性和寿命提供理论支持和实际指导。
二、轮轨滚动接触弹塑性分析轮轨滚动接触弹塑性分析是理解轮轨系统动力学行为以及预测轮轨疲劳损伤的关键。
本章节将深入探讨轮轨滚动接触的弹塑性分析理论和方法。
在轮轨滚动接触过程中,由于轮轨材料的弹塑性特性,接触区域内的应力分布和变形情况十分复杂。
为了准确描述这一现象,我们需要引入弹塑性力学理论,该理论能够综合考虑材料的弹性变形和塑性变形。
在弹塑性分析中,材料的应力-应变关系不再是线性的,而是呈现出非线性特性。
当应力低于材料的弹性极限时,材料发生弹性变形,应力与应变之间遵循胡克定律;当应力超过弹性极限后,材料发生塑性变形,应力与应变之间的关系变得复杂,需要考虑材料的塑性流动和硬化行为。
对于轮轨滚动接触问题,通常采用有限元法或边界元法等数值方法进行求解。
这些方法能够考虑轮轨的几何形状、材料属性、接触条件等多种因素,从而得到接触区域内的应力分布、变形情况以及轮轨之间的接触力等关键信息。
在弹塑性分析中,还需要考虑材料的疲劳特性。
疲劳是指材料在循环应力或应变作用下,逐渐产生损伤并最终导致破坏的过程。
对于轮轨材料,疲劳损伤是一个重要的失效模式,因此,在弹塑性分析中,我们需要结合材料的疲劳特性,预测轮轨的疲劳寿命和疲劳损伤分布。
轮轨滚动接触弹塑性分析是一个复杂而重要的问题。
通过引入弹塑性力学理论和数值方法,我们能够更准确地描述轮轨滚动接触过程中的应力分布、变形情况以及疲劳损伤等问题,为轮轨系统的设计和优化提供有力支持。
基于有限元的有轨电车弹性车轮模态分析

基于.限无D./电车禪(车給樓态5析颖1 '2民3(1 •上海市轨道交通设备发展有限公司#200245,上海;2.上海有轨电车工程技术研究中心#200125,上海;3 •同济大学铁道与城市轨道交通研究院#201804,上海〃第一作者,高级工程师)摘 要 有轨电车通常采用结构中间嵌有橡胶块的弹性车轮,其在降低车内外噪声及减小车 件的振动与噪声等方面 有 的效果。
在弹性车轮建模方法及对橡胶材模型研究的基 ,建立了相同直径的有轨电车弹性 车轮 性车轮有限元模型,并采用适用于对称特征值问题的Block Lanczos 方法对这两种车轮进行模态分析。
结果表明,在相同模态振 ,弹性车轮的模 率较刚性车轮的模 率低。
弹性车轮具有较好的减振降噪振能力。
关键词 有轨电车;弹性车轮;橡胶块;模态分析中图分类号U482.1.03DOI :10. 16037/j. 1007 -869x. 2020. S1.025Modal Analysio of Tramcar Elastic WheeiBased on Fiyity Element MethodLYU Yuanying # ZHANG JiminAbstract Tramcar usually adopts elastic wheels with rubberblocks embedded in the middle of the structure # in order to a-chievebe t e:application e f ectin educing thenoiseinsideandoutsida the vehicle # as wel l as the viprakon of the vehiclestructure. In this paper # based on researches of the elastic wheal modeling method and the rubber maWkai constitutivemodal # a finite element modal of elastic wheal and rigid wheal with the sama diameter is established. Block Lanczos method@uitabeeforearge-@caee@ymmetriceigenvaeueprobeem iu@ed toconduct moda eana ey@i of the two ******************@uet shows that at the same modal shape # the modal frequency of e-asticwhee7issignificanty 7owerthan thatofrigid whee7# therefore # theeasticwhee7hasabe t ervibration and noisere duction e f ect # and thebe t erhigh-frequency vibration iso ationabiity.Keywordstramcar ; easticwhee7; rubberb7ock ; moda7analysisFirst-suthor> s addrssShanghai Rail TranspoiationEquipmentCo. # Ltd. # 200245 # Shanghai # China弹性车轮是一种分体式车轮,目前主要应用于在城市地面上行驶的有轨电车车辆。
基于环模型的轮胎滚动接触有限元分析_郭孔辉

误 差/% 2.1 1.0 0.67 1.4 2.1 2.2 1.75 1.4 1.25
线性弹性特性并对模型参数进行修正。本文借鉴
了 Mousseau方法[5],建立 薄 膜 和 曲 梁 耦 合 模 型,
利用结构参数计算得到胎侧单元的径向力为
弯曲附加力
[( ) ] T=
烇1 r2
-rr10烉1+EcIos2烋θ+r薄︷ P膜0力
图3轮胎轴荷以及加载点位移的瞬态响应fig3variationoftirewheelloadnandradialdeformationmatloadingpointwithtimes995吉林大学学报工学版第41卷图4轮胎的瞬态变形轮廓fig4schematicoftransientdeformationconfiguration3动态特性仿真分析及试验验证为了检验轮胎模型的有效性与实用性对轮胎在转毂上以较高速度3060kmh滚动通过障碍物的动态过程进行了仿真分析并与试验结果进行了比较
2 限元建模与仿真分析
(Spring/Damper);④ 胎 冠 部 分 橡 胶 的 压 缩 和 剪 切 模 量 通 过 平 面 应 变 单 元 (Shell)模 拟 。
轮胎模型中的参数包括几何参数与结构参数 以及物理参 数。 几 何 参 数 和 结 构 参 数 包 括:带 束 截 面积 A,有效宽度b,有效半径r,带束层厚度h。 这些参数直接从轮胎设计参数中得到。物理参数 包括:有效密度ρ,径 向 弹 簧 参 数kw,切 向 弹 簧 参 数kv,有效弯曲刚 度 EI,物 理 参 数 从 试 验 模 态 来 预报。
模态 N 0(周 向 ) 1(错 动 ) 2 3 4 5 6 7 8
计算值
68.536 98.342 123.76 147.39 172.93 201.16 231.76 264.50 299.25
基于Cowper-Symonds本构关系的轮轨滚动接触行为有限元分析

基于Cowper-Symonds本构关系的轮轨滚动接触行为有限元分析铁路运输作为一种节能环保的交通运输方式,近年来受到了越来越广泛的关注。
而轮轨间的接触和相互作用则一直是铁路领域内被众多学者所关注的重要课题,这是因为轮对和轨道担任着铁路系统中最重要的角色,严重的轮轨故障必然会导致灾难性事故的发生。
随着列车行驶速度的不断提升,轮轨的损伤也会加剧,尤其是在高速列车的运用中,惯性效应变得不容忽视,材料的应变率效应也将更加显著的体现出来。
然而,由于轮轨接触问题中存在着材料、几何和接触非线性,导致高速轮轨系统的动态接触行为十分的复杂,同时这也是研究该问题的意义所在。
因此,建立了三维轮轨滚动接触模型,并采用显式有限元软件LS-DYNA进行仿真计算,模型中考虑了轮轨接触的材料、几何和接触非线性,并考虑了应变率相关的材料参数,以研究动态轮轨接触行为。
为了给轮轨滚动接触行为仿真分析提供真实、可靠的应变率相关的力学参数,采用HTM5020型高速拉伸试验机开展了D1轮辋钢和U71Mn轨钢在中应变率范围内的动态拉伸力学性能试验,得到了不同应变率下的塑性流动应力-应变响应曲线,建立了基于Cowper-Symonds经验性模型的动态本构关系。
同时还将三维轮轨滚动接触有限元模型拓展运用到轮对通过曲线的工况,考虑了曲线轨道的超高、轮对的横移和侧滚角。
在直道工况下,以列车速度、轴重和材料的应变率效应为影响因素,进行轮轨动态响应的分析;在弯道工况下,以轨道曲线半径、轴重和材料的应变率效应为影响因素,进行轮轨动态响应的分析。
对轮轨动态响应的分析,包含:轮轨接触力、von-Mises等效应力、等效塑性应变、车轴轴心垂向加速度、直道下车轮踏面与轨面初始接触点的横向位移和弯道下车轴轴心横向位移。
分析结果表明:1)轮轨接触力对速度有一定敏感性;随着速度的增大,车轮的von-Mises应力最大值和等效塑性应变最大值有增大的趋势,而钢轨的von-Mises应力最大值和等效塑性应变最大值在不考虑材料的应变率效应时呈现出减小的趋势;车轴轴心垂向加速度和车轮踏面与轨面初始接触点的横向位移最大值会随着速度的增大而减小。
轮轨接触应力的有限元分析

2 计算模型 的建立
按照 机车轮 对 和轨道 的实 际尺 寸建立 计算 模 型 。我 闰货车 标准轮 径 为 80mm, 4 内燃 机 车标 准轮 为 l 5 m, 0m 分别 对两种 轮径 建立模 型并 做 了 计算 。模 型 中 , 轮选 择 T 0 车 B锥形 踏 面以 及 I 磨 耗形踏 面 , M 轨 道选 择 6 gm 标 准钢轨 , 图 2所 示 。 由于结 构 和载 荷都 是 对称 的 , 模 时 只取 轮 对 的一 半 , 道 也 只 0k/ 如 建 轨 取单 侧 。对于 单侧 车轮 , 结构 和载 荷也 是对称 的 , 以 为 节省计 算 资 源 只选 l2车轮 进 行 建模 和 分 析 , 其 所 /
的局 限性 也愈 加突 出 。这 些解 析解 和 数值 解 根 本 无法 精 确 模 拟车 轮 踏 面 与钢 轨 的真 实 几何 形状 。文 献
[] 1 和文献 [ ] 2 考虑了钢轨真实的几何形状 和边界条件 , 但它们的共 缺点是接触简载假设 为一集 中荷 载, 没有反映真实的轮轨接触行为。现应用 A S S有限元分析软件 讨论轴重 、 径 、 NY 轮 踏面形状 及横移 量 对轮轨 接触应 力 的影 响。
铁路运输属轮轨接触式运输 , 其区别于其他运输方式 的特点是轮轨问 的相互作用。轮轨关 系是车
辆、 轨道 系统 中最基 本 、 复杂 的一 个 问题 , 典型 的接 触 问题 。 最 是
轮轨接触应力的理沦计算 , 过去大多采用解析解 和数值解 , 即将轮轨视为两个无 限弹性半空问。可 是随着铁路技术的发展 , 特别是磨耗 型车轮踏 面的推广使用 , 使用解析解和数值解来解决轮轨关 系问题
维普资讯
第l 9卷
第 3期
石 家 庄 铁 道 学 院 学 报
基于有限元分析的高速列车轮轨耦合振动研究

基于有限元分析的高速列车轮轨耦合振动研究高速列车的开发已经成为现代交通工具的重要方向之一。
高速列车的设计需要考虑到许多因素,其中一个重要因素是轮轨耦合振动。
轮轨耦合振动是指轮和轨道之间的共振运动,它可能导致车辆损坏和运行不稳定。
因此,研究轮轨耦合振动并采取措施来控制和减少振动是高速列车设计中不可或缺的一部分。
有限元分析(FEA)是研究轮轨耦合振动的一种方法。
它可以模拟列车在轨道上的振动,并帮助分析列车运行过程中的各种现象。
有限元分析是一种解决物理问题的数值方法,它将结构分为许多离散的小单元,每个小单元的行为都可以用简单的数学方程表示。
然后,这些方程可以组装成整个结构的方程。
有限元分析可以用于求解振动、热和流体力学等问题。
在进行有限元分析之前,需要对列车模型进行建模。
建模过程包括将列车分解成小单元,并将各个单元的材质和几何属性输入模型。
轨道和地基模型也需要被建模。
之后,需要建立列车-轮对-轨道系统的模型。
这个系统包括轮对、车轮、轮轴、车体和轨道。
有限元分析可以模拟轮轨耦合振动,并预测结构的响应。
但是,这需要一个准确的模型,包括准确的边界条件和初始条件。
一些研究表明,一些轴类构件的外形几何、制造精度、轴箱承载间隙、轴承和油膜、弹性轮胎以及平低度等因素都会影响高速列车的轮轨耦合振动。
这些因素和列车的运行状态形成复杂的相互关系,需要进行综合分析,以精确定位和解决问题。
除了FEA方法,还有其他方法可以用于研究轮轨耦合振动。
例如,可以沿轨道线安装加速度计,以记录列车在不同位置上的振动情况。
这些加速度计数据可以用来验证有限元模型,并为列车设计提供价值信息。
此外,还可以通过模拟列车运行过程来研究轮轨耦合振动。
这种仿真可以提供有关列车加速度和应力的信息,并可以用来改进列车设计。
总之,轮轨耦合振动是高速列车设计中不可或缺的一部分。
有限元分析是研究轮轨耦合振动的一种方法。
通过建立准确的列车模型和运用合适的分析方法,我们可以预测列车在不同条件下的运行情况,并采取有效的措施来控制和减少振动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于有限元理论的轮轨接触力学特性仿真研究郭伟杰;王旭东;刘邱祖【摘要】轮轨接触的力学特性研究对保障列车的安全运行至关重要.选择动车组车轮LMa踏面与标准CHN60钢轨,借助有限元理论,分别计算两种轮径在不同轴重以及不同横移量下的轮轨接触应力变化情况.计算结果表明:随着轴重的增加,轮轨接触应力会增大;当车轮有横移时,发现靠近轮缘侧的轮轨接触应力大于远离轮缘侧的;同种工况下,增大轮径可以适当改善轮轨受力状态.【期刊名称】《制造业自动化》【年(卷),期】2015(037)021【总页数】4页(P58-61)【关键词】轮轨接触;力学特性;轴重;横移;有限元理论【作者】郭伟杰;王旭东;刘邱祖【作者单位】太原理工大学机械工程学院,太原 030024;太原理工大学机械工程学院,太原 030024;太原理工大学机械工程学院,太原 030024【正文语种】中文【中图分类】U2110 引言近年来,中国铁路运输业朝着高速重载的方向发展,对其传动部件的力学性能提出了更高的要求。
传统的Hertz[1]接触理论在计算轮轨接触压力时便于操作,简单易懂,但是该理论是在接触表面光滑,弹性变形等前提下推导的,而实际的轮轨接触过程中会有塑性变形,接触表面有摩擦,Hertz接触理论与实际工况相差较大Cater[2]。
在Hertz接触理论的基础上,推导出轮轨接触的切向应力,但是轮轨接触问题是一种高度非线性行为,传统理论所得结果总会存在偏差。
如今许多学者借助有限元理论来分析轮轨接触问题,张军[3]用有限元参数二次规划法,对多种工况进行弹塑性分析;陶功权[4]利用数值程序CONTACT和有限元模型进行了对比,说明有限元理论适用性更广泛;孙明昌[5]用有限元分析软件ANSYS对弹性轮对进行了应力、变形和模态计算分析。
本文借助有限元理论,分析两种轮径分别在不同轴重和不同横移量下的轮轨接触应力变化。
1 建立有限元模型高速动车组车轮踏面选取LMa型,车轮宽度是135mm,轮径分别取Φ860mm,Φ920mm;钢轨选用CHN60。
由于轮轨接触的对称型,在用Pro/E建模时只取左侧钢轨和左侧轮对的一半模型,这样可以减少网格单元,节省计算时间。
钢轨长度取300mm,轨底坡为1:40,轨距为1435mm,轮对内侧距为1353mm。
有限元单元[6]采用Solid 45,在加载过程中,轮轨接触表面会发生塑性变形,假设轮对和钢轨的材料相同,弹性模量Ee=210GPa,泊松比γ=0.3;屈服极限σs=450MPa,应变强化模量Ep=21GPa,摩擦系数μ=0.2。
网格划分及加载情况如图1所示,根据弹性力学理论[7],接触区域附近的网格应该细化,网格尺寸取0.5mm~1mm[8],远离接触区域,网格尺寸可以大些,这样不会影响计算精度,如图2所示,共产生98725个节点。
图1 轮轨接触有限元模型图2 轮轨接触区周围网格细分2 结果分析轮轨接触过程中接触斑的面积一般只有100mm2~200mm2,然而如此小的接触斑上却承受极大的外载,因此轮轨接触应力很大,这是造成车轮踏面磨损和疲劳的主要原因。
本文主要考察轴重和横移量对接触应力的影响。
2.1 轴重对轮轨接触应力影响参照动车组相关技术参数可知,每个轮对承受的载重约为10t~17t,为了分析轴重对接触应力的影响[9],分别取11t、13t、15t、17t进行分析。
图3为轮轨间最大Mises应力随轴重的变化,图4为轮轨间最大垂向应力随轴重变化。
由两图可知,随着轴重的增加,两种轮径的轮轨接触应力都在变大,并且Φ860mm车轮轮轨最大接触应力始终大于Φ920mm车轮的,这与Hertz接触理论有相同的变化趋势:其中,P(x,y)为接触班上任一点的压应力;p0为轮轨接触斑上的最大压应力;p为轮轨间的垂向力;a,b为椭圆接触斑的长半轴,短半轴。
所以轮径在一定程度上可以改善轮轨受力状态,车轮运营一段时间后,由于疲劳磨耗等原因需要进场返修,进行旋削处理后,车轮半径会变小,会恶化机车的运行品质。
图3 轮轨间最大Mises应力随轴重的变化图4 轮轨间最大垂向应力随轴重变化图5显示了轮轨接触斑面积随轴重变化趋势,由图可知,随着轴重的增加,两种轮径的轮轨接触斑面积都在变大,Φ920m m车轮轮轨接触斑面积增加了38%,Φ860mm车轮的接触斑面积增加了5.6%,Φ920mm车轮轮轨接触斑面积大于Φ860mm车轮的,所以Φ920mm车轮的轮轨接触应力小于Φ860mm车轮的。
图5 轮轨接触斑面积随轴重变化以17t轴重为例,图6中(a)、(b)分别为沿横向截面观测,根据材料力学第四强度理论主要考察轮径Φ860mm,Φ920mm的轮轨接触等效Mises应力云图。
从两图中可知,车轮上最大等效Mises应力距接触面约2mm~4mm,这一区域正是产生微裂纹的危险区域,车轮上沿图中箭头方向接触等效Mises应力先变大再变小,因此在加工制造车轮过程中,要合理分配轮辋内部的硬度。
图6 轴重17t下轮轨接触应力2.2 横移量对轮轨接触应力影响由于磨耗型车轮踏面和钢轨顶面都是由多段圆弧连接而成的,理想状态下车轮与钢轨应该对中接触,但由于列车线路的复杂性(如高低不平顺,垂向不平顺等)使得轮对的对称平面和钢轨的对称平面总有一个横移量,如图7所示:y就是横移量。
已有研究表明较大的横移量会导致轮缘和钢轨接触,使得轮轨间形成两点接触,加剧轮缘磨耗。
本文考察横移量由-3mm~3mm的轮轨接触应力变化,横移量为正值表示钢轨靠近轮缘侧,负值表示钢轨远离轮缘侧。
图7 有横移量的轮轨接触示意图图8显示了轮轨间最大Mises应力随横移量变化,从图中可知两种轮径的最大Mises应力都经历了先变大后变小的过程,轮轨间最大Mises应力都出现在对中接触的位置,这时左右轮轨受力状态相同,有利于两侧车轮的均匀磨耗。
任何一种轮径靠近轮缘侧的轮轨间最大Mises应力大于远离轮缘侧,这是因为靠近轮缘侧车轮踏面接触面上曲率半径变化较大,会直接影响轮轨接触斑面积。
这种情况常见于列车过曲线时,左右车轮不同的受力情况会造成不均匀磨耗。
Φ860m m轮径的最大Mise应力始终大于Φ920mm轮径的,说明在有横移的情况下,不同的轮径受力状态不同。
图9显示了轮轨间最大垂向应力随横移量变化趋势,从图中可知轮轨对中接触时轮轨间最大垂向应力达到最大值,这是因为对中接触时,左右车轮瞬时滚动圆直径差为零,轮轨间无横向分力,垂向力全部由轴重来提供。
Φ860mm轮径的最大垂向应力始终大于Φ920mm轮径的。
对于Φ920mm车轮远离轮缘侧的轮轨间最大垂向应力大于靠近轮缘侧的,而Φ860mm左右两侧车轮的最大垂向应力无明显变化,这是因为Φ860mm车轮轮轨接触斑面积在不同横移量下的变化较小造成的。
图8 轮轨间最大Mises应力随横移量变化图9 轮轨间最大垂向应力随横移量变化图10显示了轮轨间最大剪切应力随横移量变化趋势,从图中可以看出不同横移量下,轮径为Φ860mm的剪切应力变化比较大,并且两种轮径下的剪切应力变化趋势较相似,轮轨对中接触时,剪切应力是最小的,这是因为在无横移量时,左右轮轨几何接触角相等,横向力可以抵消,因此可以认为横向力会影响剪切应力的分布。
图10 轮轨间最大剪切应力随横移量变化考察17t轴重下,不同横移量的轮轨接触应力分布情况。
图11(a)、(b)分别为沿横向截面观测,偏移量L=3mm,Φ860mm,Φ920mm的轮轨接触等效Mises应力云图。
从两图中可知,车轮上最大等效Mises应力在车轮踏面上,车轮上沿箭头方向接触等效Mises应力不断变小,两种轮径在改横移量下的等效应力差别较小。
图11 偏移量L=3mm,轮轨接触应力3 结论1)有限元分析中考虑了材料的弹塑性变形,Hertz接触理论是在小变形和弹性半空间的前提下推导的,但是增加轴重时,两种轮径的受力状态有相同的变化趋势,都在缓慢增加,并且Φ920mm车轮的接触应力小于Φ860mm车轮,说明车轮轮径对轮轨接触状态有一定影响。
2)轮轨对中接触时,接触应力最大,左右两轮受力状态相同。
当车轮有横移量时,发现靠近轮缘侧车轮的接触应力大于远离轮缘侧的车轮,这时左右两车轮受力状态不相同,容易造成偏磨,不利于车轮合理的使用。
3)车轮有横移量时,Φ920mm车轮的接触应力小于Φ860mm车轮,两种轮径在车轮有横移量时,垂向应力变化不明显,而切向应力变化较大,说明轮轨间的切向应力主要受横移量的影响。
参考文献:[1]Hertz,H.über die berührung fester elasticher kürper[J].Journal für und angewandte Mathematik,1882,92:156-173.[2]Carter F W.On the action of a locomotivedrivingwheel[J].Pro.R.Soc.,London,A.1926,112:151-157.[3]张军.轮轨接触问题的弹塑性分析[J].铁道学报,2000,22(3):17-21.[4]陶功权.两种轮轨接触应力算法对比分析[J].工程力学,2013,30(8):229-235.[5]孙明昌.弹性轮对的有限元分析[J].交通运输工程学报,2002,2(4):39-42.[6]曾攀.有限元基础教程[M].北京,高等教育出版社,2009.[7]徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002.[8]卢勇.大功率机车轮轨接触问题研究[D].南昌:华东交通大学,2010.[9]曹明,宋春明,张东生.基于ANSYS的定梁龙门机床横梁静力学特性分析[J].制造业自动化,2015,37(03):87-89.。
