题库学生版-随堂考试-第1-3章时域分析
题库学生版-随堂考试-Answer_1-er_1-3章74186

• 卷积积分
f (t) h(t) yzs (t)
第5题(1分)
A卷:f
(t)
sin
t,
h(t)=
e-t
(t),
则yzs
(t)
_______d
__________
直
接
B卷:f (t) e-t , h(t)= e-t (t),
则yzs (t)
_______d
__________
套 连
续
卷
C卷:f (t
__________
• 卷积积分
f (k) h(k) yzs (k)
第6题(1分)
A卷:f (k
)
sin
k
,
h(k)=
e-k
(k),
则yzs
(k
)
__________
直
接
B卷:f (k ) e-k , h(k)= e-k (k), 则yzs (k ) __________
套 离
散
卷
C卷:f
(k
(t
)
t
2,3 0,
t 6 其他
则f (t) = t2 ( (t 3) (t 6))
C卷:若f
(t
)
e-t , 0,
5
t 8 其他
则f (t) = e-t ( (t 5) (t 8))。
D卷:若f
(t
)
3t 2 ,1 0,
t 6 其他
则f (t) = 3t2( (t 1) (t 6))。
• 系统的性质-稳定性
f (k)
第10题(1分)
y (k)
A卷:
若y(k)=2f (k-1)则系统是稳定的。
时域分析法习题及解答

第三章 时域分析法习题及解答3-1. 假设温度计可用11+Ts 传递函数描述其特性,现在用温度计测量盛在容器内的水温。
发现需要min 1时间才能指示出实际水温的98%的数值,试问该温度计指示出实际水温从10%变化到90%所需的时间是多少?解: 41m i n ,=0.25T T = 3-2. 系统在静止平衡状态下,加入输入信号t t t r +=)(1)(,测得响应为 试求系统的传递函数。
解:2210.90.910(s+1)()=10s (s+10)C s s s s =+-+ 3-3.解: 设()1s Ts φ=+ 3-4. 已知系统结构图如图3-49所示。
试分析参数a 对输出阶跃响应的影响。
解:1()()111KKTs s Kas T Ka s Ts φ+==++++当a>0时,系统响应速度变慢;0Ta K-<<时,系统响应速度变快。
3-5. 设控制系统闭环传递函数为试在[s ]平面上绘出满足下列各要求的系统特征方程式根的可能分布的区域。
1.707.01>>ξ, 2≥n ω 2.05.0>>ξ, 24≥≥n ω 3.5.0707.0>>ξ, 2≤n ω解:①0.707<<1, 2n ξω≥②0<0.5, 24n ξω≤≤≤ ③0.50.707, 2n ξω≤≤≤3-6. 已知某前向通路的传递函数(如图3-50所示)今欲采用负反馈的办法将阶跃响应的调节时间s t 减小为原来的1.0倍,并保证总放大系数不变。
试选择H K 和0K 的值。
解:解得:00.9 =10H K K =3-7. 设一单位反馈控制系统的开环传递函数为 试分别求出当110-=s K 和120-=sK 时系统的阻尼比ξ,无阻尼自然频率n ω,单位阶跃响应的超调量%σ及峰值时间p t ,并讨论K 的大小对系统性能指标的影响。
解: 22()10()1()0.11010G s K Ks G s s s K s s Kφ===+++++ K 增大使%,p t σ↑↓,但不影响调节时间。
第三章 线性系统的时域分析与校正 习题及答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; T t T T d -⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r (即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
线性系统的时域分析习题答案.doc

第 3 章线性系统的时域分析学习要点1控制系统时域响应的基本概念,典型输入信号及意义;2控制系统稳定性的概念、代数稳定判据及应用;3控制系统的时域指标,一阶二阶系统的阶跃响应特性与时域指标计算;4高阶系统时域分析中主导极点和主导极点法;5控制系统稳态误差概念、计算方法与误差系数,减小稳态误差的方法。
思考与习题祥解题思考与总结下述问题。
(1)画出二阶系统特征根在复平面上分布的几种情况,归纳值对二阶系统特征根的影响规律。
(2)总结和n 对二阶系统阶跃响应特性的影响规律。
(3)总结增加一个零点对二阶系统阶跃响应特性的影响规律。
(4)分析增加一个极点可能对二阶系统阶跃响应特性有何影响(5)系统误差与哪些因素有关试归纳减小或消除系统稳态误差的措施与方法。
(6)为减小或消除系统扰动误差,可采取在系统开环传递函数中增加积分环节的措施。
请问,该积分环节应在系统结构图中如何配置,抗扰效果是否与扰动点相关答:( 1)二阶系统特征根在复平面上分布情况如图所示。
Im③j n (0)p1③j n 1 2(0 1)p1 ③( 1) ( 1) n p③③ 20 ( 2 1) n ( 2 1) Ren n n np2③j n1 / 2j n③图二阶系统特征根在复平面上的分布当0 ,二阶系统特征根是一对共轭纯虚根,如图中情况①。
当 01,二阶系统特征根是一对具有负实部的共轭复数根,变化轨迹是以n为半径的圆弧,如图中情况②。
当1 ,二阶系统特征根是一对相同的负实根,如图中情况③。
当1 ,二阶系统特征根是一对不等的负实根,如图中情况④。
(2)和n 是二阶系统的两个特征参量。
是系统阻尼比,描述了系统的平稳性。
当0 ,二阶系统特征根是一对共轭纯虚根,二阶系统阶跃响应为等幅振荡特性,系统临界稳定。
当 01,二阶系统特征根是一对具有负实部的共轭复数根,二阶系统阶跃响应为衰减振荡特性,系统稳定。
越小,二阶系统振荡性越强,平稳性越差;越大,二阶系统振荡性越弱,平稳性越好。
课后习题及答案_第1章时域离散信号和时域离散系统--答案
1 1 h(−1) + δ (0) + δ (−1) = 1 2 2
题 8 解图(1)
题 8 解图(2)
(3) y(n)=x(n)*h(n)
∞
=
=0.5n ∑ R5(m)0.5-mu(n-m)
m = −∞
m = −∞
∑ R5(m)0.5n
∞
-m
u(n-m)
y(n)对于 m 的非零区间为 0≤m≤4,m≤n ① n<0 时,y(n)=0 ② 0≤n≤4 时,
y (n) = 0.5 n
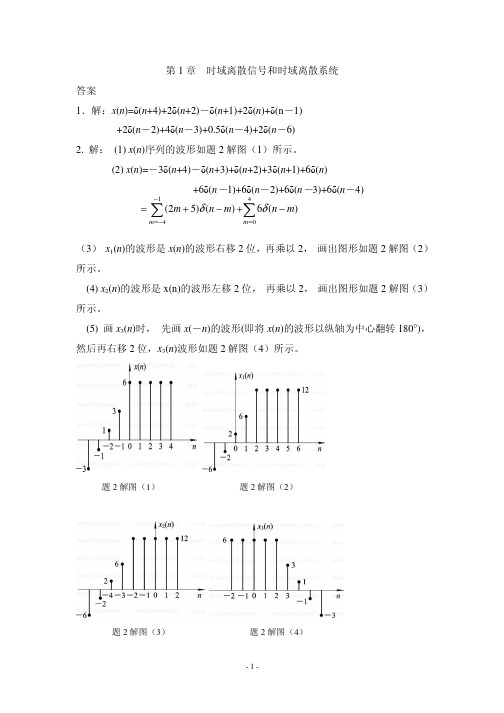
题 2 解图(1)
题 2 解图(2)
题 2 解图(3)
题 2 解图(4)
-1-
2π 14 3 = 3.解: ( 1) 因为 ω= π, 所以 , 这是有理数, 因此是周期序列, 周期 T=14。 7 ω 3
(2)因为 ω=
1 2π ,所以 =16π,这是无理数,因此是非周期序列。 8 ω
4. 解: (1)x(-n)的波形如题 4 解图(1)所示。 (2) 将 x(n)与 x(-n)的波形对应相加,再除以 2,得到 xe(n)。毫无疑问, 这是一个偶对称序列。xe(n)的波形如题 4 解图(2)所示。 (3) 画出 xo(n)的波形如题 4 解图(3)所示。
m= n −4
④ n>7 时, y(n)=0 所以
-6-
y(n)的波形如题 8 解图(1)所示。 (2) y(n)=2R4(n)*[δ(n) - δ(n - 2)]=2R4(n) - 2R4(n - 2)=2[δ(n)+δ(n - 1) - δ(n+4) - δ(n+5)] y(n)的波形如题 8 解图(2)所示。
m = −∞
控制系统的时域分析例题和习题

2
1
T0
10 K
TK0
0.2 2.5
因此有
ts 4.75T0 0.95 1
红河学院自动化系
自动控制原理
3-9 电子心脏起博器心律控制系统结构图如题3-49图所示,其中模仿心脏的传递函
数相当于一纯积分环节。
1.若 0.5 对应最佳响应,问起博器增益 K 应取多大?
2、若期望心速为60次/min,并突然接通起博器,问1s钟后实际心速为多
2.2T
阶跃响应到达并保持 在终值 5%误差带内
3) 求 ts
h(
ts
)
0.95
1
T
T
ets
/T
所需的最短时间
T
T
T
ts T [ln T
ln0.05 ] T [ln T
ln 20 ] T [ 3 ln T
]
红河学院自动化系
自动控制原理
3-5 一种测定直流电机传递函数的方法是给电枢加一定的
+
A4 s+3
按不相等实数极点确定A1 ,A3 ,A4 得:
A1=
-1 2
A3=
2 3
A4=112
A2=
-3 4
A2将=(各2-11待)!定( d系2-1[数Fd(代ss)2(入-1s-上p1 式)2]得) s=:p1 f(t)= =2-tde[-st(-d(sss+43+23e))-]t+s=32-1=+-41312 e-3t
K 应取何值,调节时间 ts 是多少?
解 依题意应取 1,这时可设闭环极点为
s1,2 1 T0 写出系统闭环传递函数
( s )
10 K
3-1-3多次相遇和追及问题-题库学生版

1. 学会画图解行程题2. 能够利用柳卡图解决多次相遇和追及问题3. 能够利用比例解多人相遇和追及问题板块一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的,多人相遇与追及问题虽然较复杂,但只要抓住这个公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.【例 1】 (难度等级 ※)甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步,甲每秒钟跑3.5米,乙每秒钟跑4米,问:他们第十次相遇时,甲还需跑多少米才能回到出发点?【巩固】 (难度等级 ※)甲乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米.如果他们同时分别从直路两端出发,10分钟内共相遇几次?【巩固】 (难度等级 ※)甲、乙两人从400米的环形跑道上一点A 背向同时出发,8分钟后两人第五次相遇,已知每秒钟甲比乙多走0.1米,那么两人第五次相遇的地点与点A 沿跑道上的最短路程是多少米?知识精讲教学目标3-1-3多次相遇和追及问题二、运用倍比关系解多次相遇问题【例 2】(难度等级※※)上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他.然后爸爸立即回家,到家后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?【例 3】(难度等级※※)甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离是多少千米?【巩固】(难度级别※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地4千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地3千米处第二次相遇,求两次相遇地点之间的距离.【巩固】(难度等级※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地7千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地5千米处第二次相遇,求两次相遇地点之间的距离.【巩固】(难度等级※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地6千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地4千米处第二次相遇,求两人第5次相遇地点距B 多远.【巩固】(难度等级※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地7千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地3千米处第二次相遇,求第三次相遇时共走了多少千米.【巩固】(难度等级※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地3千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地2千米处第二次相遇,求第2000次相遇地点与第2001次相遇地点之间的距离.【巩固】(难度等级※※)甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地18千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地13千米处第二次相遇,求AB两地之间的距离.【例 4】(难度等级※※※)如图,甲和乙两人分别从一圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动,当乙走了100米以后,他们第一次相遇,在甲走完一周前60米处又第二次相遇.求此圆形场地的周长.【巩固】(难度等级※※※)如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发反向行走,他们在C点第一次相遇,C离A点80米;在D点第二次相遇,D点离B点6O米.求这个圆的周长.【巩固】A、B是圆的直径的两端,甲在A点,乙在B点同时出发反向而行,两人在C点第一次相遇,在D点第二次相遇.已知C离A有75米,D离B有55米,求这个圆的周长是多少米?三、多次相遇与全程的关系1. 两地相向出发:第1次相遇,共走1个全程;第2次相遇,共走3个全程;第3次相遇,共走5个全程;…………,………………;第N次相遇,共走2N-1个全程;注意:除了第1次,剩下的次与次之间都是2个全程。
自动控制原理随堂练习答案要点

自动控制原理随堂练习答案要点自动控制原理是现代工程技术中的重要学科,它研究如何利用各种控制原理和方法,实现对各种系统的自动控制。
在学习过程中,进行随堂练习是提高理论应用能力的有效方式。
下面是自动控制原理随堂练习的答案要点,供参考:1. 控制系统基本概念- 控制系统:由输入、输出、反馈和控制器等组成的系统。
- 开环控制系统:无反馈的控制系统,输出不受干扰的影响。
- 闭环控制系统:有反馈的控制系统,输出受干扰的影响。
2. 信号与系统- 信号:表示信息或数据的物理量。
- 连续信号与离散信号:连续信号在时间和幅度上都是连续变化的,离散信号在时间和幅度上都是离散变化的。
- 系统:将输入信号转换为输出信号的物理系统。
3. 传递函数与频率响应- 传递函数:描述系统输入与输出关系的函数。
- 频率响应:系统对不同频率信号的响应情况。
4. 时域分析- 系统的单位脉冲响应:系统对单位脉冲信号的响应。
- 系统的单位阶跃响应:系统对单位阶跃信号的响应。
- 系统的零状态响应与零输入响应:零状态响应是指系统对初始状态为零的输入信号的响应,零输入响应是指系统对初始输入为零的非零初始状态信号的响应。
5. 频域分析- 系统的频率响应:描述系统对不同频率输入信号的响应情况。
- 幅频特性图:绘制系统的幅频特性曲线,表示系统对不同频率输入信号的幅度变化。
- 相频特性图:绘制系统的相频特性曲线,表示系统对不同频率输入信号的相位变化。
6. 控制器设计- P控制器:比例控制器,输出与误差成正比。
- I控制器:积分控制器,输出与误差的累积成正比。
- D控制器:微分控制器,输出与误差变化率成正比。
- PID控制器:由P、I和D控制器组成的综合控制器。
7. 稳定性分析- 稳定性:系统在无穷远处的响应是有界的。
- 临界稳定:系统在极限情况下刚好保持稳定。
- 超稳定:系统在极限情况下仍然保持稳定,但响应速度较慢。
- 不稳定:系统在极限情况下不再保持稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h(t)=
e-t
(t),
则yzs
(t)
_______d
__________
• 卷积积分
f (k) h(k) yzs (k)
第6题(1分)
A卷:f (k
)
sin
k
,
h(k)=
e-k
(k),
则yzs
(k
)
__________
B卷:f (k ) e-k , h(k)= e-k (k), 则yzs (k ) __________
5
t 8 其他
则f (t) = _______。
D卷:若f
(t
)
3t 2 ,1 0,
t 6 其他
则f (t) = _______。
E卷:
若f
(t
)
2e-2t 0,
,
3t 其他
7
则f (t) = _______。
• 阶跃序列性质-用阶跃序列表示分段序列
第4题(1分)
A卷:
若f
(k
)
k, 2
D卷: 若y(k)=f (-k),则系统____(是,不是)时不变的。
E卷: 若y(k)=e-k f (k),则系统____(是,不是)时不变的。
• 系统的性质-因果性
f (k)
第9题(1分)
y (k)
A卷:若y(k)=2f (k-1)则系统____(是,不是)因果的。
B卷:若y(k)=k f (k-1)则系统____(是,不是)因果的。
规则:
1.随堂考试共5次,每次满分20 分,5次总和为最终平时成绩. 2.凡参加考试者,至少可得到保 底分10分,请假者可得10分。 3.每生每学期请假不超过3次。 4.每次考试5份不同试卷,按规 定选1套。
本次试卷分配
• 学号:X0,X3 A卷 • 学号:X1,X4 B卷 • 学号:X2,X5 C卷 • 学号:X6,X7 D卷 • 学号:X8,X9 E卷
C卷:f
(k
)
e-k
(k),
h(k)=
e-k
(k),
则yzs
(k
)
__________
D卷:f (k ) sin k, h(k)= e-k (k), 则yzs (k) ______2 , h(k)= e-k (k), 则yzs (k)
__________
第7题(1分)
E卷: 若y(k)= f (k)+1, 则系统____(是,不是)线性的。
• 系统的性质-时不变性
f (k)
第8题(1分)
y (k)
A卷:若y(k)=2f (k-1)则系统____(是,不是)时不变的。
B卷:若y(k)=k f (k-1)则系统____(是,不是)时不变的。
C卷:若y(k)=|f (k-1)|则系统____(是,不是)时不变的。
则yzs (t)
_______d
__________
C卷:f (t
)
e-t
(t),
h(t)=
e-t
(t),
则yzs
(t
)
_______d
__________
D卷: f (t) sin t, h(t)= e-t (t), 则yzs (t)
_______d
__________
E卷:
f
(t)
2t 2 ,
• 系统的性质-线性
f (k)
y (k)
A卷:若y(k)=|f (k)|, 则系统____(是,不是)线性的。
B卷:若y(k)=|f (k-1)|, 则系统____(是,不是)线性的。
C卷:若y(k)= (f (k-1))2, 则系统____(是,不是)线性的。
D卷:若y(k)= 3f (k-1), 则系统____(是,不是)线性的。
• 答卷正面写答案,反面写个人信息, • 班级———;学号—;卷型—;姓名——
• 单位冲击函数性质
A卷: 2t2 (t)dt _____ .
第1题(1分)
B卷: 1 3et (t)dt ______ .
t
C卷: ( )d ______ .
D卷:
et (t)dt
______ .
B卷:
k
若y(k )=
f
(i)则系统____(是,不是)稳定的。
i =0
C卷: 若y(k)=|f (k-1)|则系统____(是,不是)稳定的。
D卷: 若y(k)=f (-k),则系统____(是,不是)稳定的。
E卷: 若y(k)=ek f (k),则系统____(是,不是)稳定的。
E卷: et (t 2)dt ______ .
• 单位冲击序列性质
A卷: n2 (n 1) _______ . n
B卷: (n 1)2 (n 1) _______ . n
n
C卷: (i) _______ . i
第2题(1分)
1
D卷: n3 (n 1) _______ . n
若f
(k)
2e-2k ,3 k 7
0,
其他
则f (k) = _______。
• 卷积积分
f (t) h(t) yzs (t)
第5题(1分)
A卷:f
(t)
sin
t,
h(t)=
e-t
(t),
则yzs
(t)
_______d
__________
B卷:f (t) e-t , h(t)= e-t (t),
0,
k 5 其他
则f (k) = _______。
B卷:若f
(k
)
k
2,3 0,
k 6 其他
C卷:若f
(k
)
e-k , 0,
5
k 其他
8
则f (k) = _______。 则f (k) = _______。
D卷:若f
(k
)
3k 2,1 0,
k 其他
6
则f (k) = _______。
E卷:
E卷: n2 (n 2) _______ . n3
• 阶跃函数性质-用阶跃函数表示分段函数
第3题(1分)
A卷:若f
(t
)
t, 2
0,
t 5 其他
则f (t) = _______。
B卷:若f
(t
)
t
2,3 0,
t 6 其他
则f (t) = _______。
C卷:若f
(t
)
e-t , 0,
C卷: 若y(k)=|f (k-1)|则系统____(是,不是)因果的。
D卷: 若y(k)=f (-k),则系统____(是,不是)因果的。
E卷: 若y(k)=e-k f (k),则系统____(是,不是)因果的。
• 系统的性质-稳定性
f (k)
第10题(1分)
y (k)
A卷: 若y(k)=2f (k-1)则系统____(是,不是)稳定的。
