第六、七章-机械振动与机械波参考答案-2
机械振动和波 试题及答案

一、填空题1、质量为0.10kg 的物体,以振幅1cm 作简谐运动,其角频率为110s -,则物体的总能量为, 周期为 。
2、一平面简谐波的波动方程为y 0.01cos(20t 0.5x)ππ=-( SI 制),则它的振幅为 、角频率为 、周期为 、波速为 、波长为 。
3、一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的倔强系数为 ,振子的振动角频率为 。
4、一横波的波动方程是y = 0.02cos2π(100t – 0.4x)( SI 制)则振幅是_________,波长是_ ,频率是 ,波的传播速度是 。
5、两个谐振动合成为一个简谐振动的条件是 。
6、产生共振的条件是振动系统固有频率与驱动力频率 (填相同或不相同)。
7、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
8、弹簧振子系统周期为T 。
现将弹簧截去一半,仍挂上原来的物体,作成一个新的弹簧振子,则其振动周期为 。
9、作谐振动的小球,速度的最大值为 ,振幅为 ,则振动的周期为 ;加速度的最大值为 。
10、广播电台的发射频率为 。
则这种电磁波的波长为 。
11、已知平面简谐波的波动方程式为 ,则 时,在X=0处相位为 ,在 处相位为 。
12、若弹簧振子作简谐振动的曲线如下图所示,则振幅 ;圆频率初相 。
13、一简谐振动的运动方程为2x 0.03cos(10t )3ππ=+( SI 制),则频率ν为 、周期T 为 、振幅A 为 ,初相位ϕ为 。
14、一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为10.05cos(4)()x t SI ωπ=+和20.05cos(1912)()x t SI ωπ=+,其合成运动的方程x = .15、A 、B 是在同一介质中的两相干波源,它们的位相差为π,振动频率都为100Hz ,产生的波以10.0m/s 的速度传播。
波源A 的振动初位相为3π,介质中的P 点与A 、B 等距离,如图所示。
机械振动与机械波 答案

衡水学院 理工科专业《大学物理B 》机械振动 机械波 习题解答命题教师:杜晶晶 试题审核人:杜鹏一、填空题(每空2分)1、一质点在x 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取坐标原点。
若t =0时质点第一次通过x =-2cm 处且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为23s 。
2、一质点沿x 轴作简谐振动,振动范围的中心点为x 轴的原点,已知周期为T ,振幅为A 。
(a )若t=0时质点过x=0处且朝x 轴正方向运动,则振动方程为cos(2//2)x A t T ππ=-。
(b )若t=0时质点过x=A/2处且朝x 轴负方向运动,则振动方程为cos(2//3)x A t T ππ=+。
3、频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距 0.5 m 。
4、一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是 0.02m ,波长是 2.5m ,频率是 100 Hz 。
5、产生机械波的条件是有 波源 和 连续的介质 。
二、单项选择题(每小题2分)(C )1、一质点作简谐振动的周期是T ,当由平衡位置向x 轴正方向运动时,从1/2最大位移处运动到最大位移处的这段路程所需的时间为( )(A )T /12 (B )T /8 (C )T /6 (D ) T /4( B )2、两个同周期简谐振动曲线如图1所示,振动曲线1的相位比振动曲线2的相位( )图1(A )落后2π (B )超前2π (C )落后π (D )超前π ( C )3、机械波的表达式是0.05cos(60.06)y t x ππ=+,式中y 和x 的单位是m ,t 的单位是s ,则( )(A )波长为5m (B )波速为10m ⋅s -1 (C )周期为13s (D )波沿x 正方向传播( D )4、如图2所示,两列波长为λ的相干波在p 点相遇。
机械振动与机械波(含答案)

25、质量为m 的质点与劲度系数为k 的弹簧构成弹簧振子,忽略一切非保守力做功,则其振动角频率ω26、质量为m 的质点与劲度系数为k 的弹簧构成弹簧振子,忽略一切非保守力做功,则振子位移为振幅A 的4/5时,体系动能占总能量的_9/25___。
27、质量为m 的质点与劲度系数为k 的弹簧构成弹簧振子,忽略一切非保守力做功,若振幅为A ,体系的总机械能为_ kA 2/2 ___。
28、质量为m 的质点与劲度系数为k 的弹簧构成弹簧振子,忽略一切非保守力做功,若振幅为A ,则振子相对于平衡位置位移为A /2时,其速度是最大速度的_。
29、质量为m 的质点与劲度系数为k 1,k 2的串联弹簧构成弹簧振子,忽略一切非保守力做功,则振子的振动角频率。
30、 一质点沿x 轴作简谐振动,振幅A=0.2,周期T=7,t=0时,位移x 0 = 0.1,速度v 0>0,则其简谐振动方程表达式为___x=0.22cos()73t ππ-__________________________________。
31、质量为m 的质点与劲度系数为k 1,k 2的并联弹簧构成弹簧振子,忽略一切非保守力做功,则振子的振动频率ν32、质量为m 的质点与劲度系数为k 1,k 2的并联弹簧构成弹簧振子,忽略一切非保守力做功,则振子的振动角频率ω=____33、两个同方向同频率的简谐振动,其振动表达式分别为:x 1 = 0.3cos(6πt+π/6),x 2=0.3cos(6πt-5π/6)。
它们的合振动的振辐为____0________,初相为____0________。
机械波填空题34、假定两列平面波满足基本的相干条件,波长λ = 8m ,振幅分别为A 1 = 0.1,A 2 = 0.4。
则位相差∆Φ = 2π时,叠加点振幅A=__0.5______________;波程差∆ = 40m 时,叠加点振幅A=_____0.5___________。
高考物理《机械振动和机械波》真题练习含答案

高考物理《机械振动和机械波》真题练习含答案1.[2023·新课标卷]船上的人和水下的潜水员都能听见轮船的鸣笛声.声波在空气中和在水中传播时的()A.波速和波长均不同B.频率和波速均不同C.波长和周期均不同D.周期和频率均不同答案:A解析:声波的周期和频率由振源决定,故声波在空气中和在水中传播的周期和频率均相同,但声波在空气和水中传播的波速不同,根据波速与波长关系v=λf可知,波长也不同,故A正确,B、C、D错误.故选A.2.[2024·浙江1月]如图1所示,质量相等的小球和点光源,分别用相同的弹簧竖直悬挂于同一水平杆上,间距为l,竖直悬挂的观测屏与小球水平间距为2l,小球和光源做小振幅运动时,在观测屏上可观测小球影子的运动.以竖直向上为正方向,小球和光源的振动图像如图2所示,则()A.t1时刻小球向上运动B.t2时刻光源的加速度向上C.t2时刻小球与影子相位差为πD.t3时刻影子的位移为5A答案:D解析:以竖直向上为正方向,根据图2可知,t1时刻,小球位于平衡位置,随后位移为负值,且位移增大,可知,t1时刻小球向下运动,A错误;t2时刻,光源的位移为正值,光源振动图像为正弦式,表明其做简谐运动,根据F回=-kx=ma可知,其加速度方向与位移方向相反,位移方向向上,则加速度方向向下,B错误;根据图2可知,小球与光源的振动步调总是相反,由于影子是光源发出的光被小球遮挡后,在屏上留下的阴影,可知,影子与小球的振动步调总是相同,即t2时刻小球与影子相位差为0,C错误;根据图2可知,t3时刻,光源位于最低点,小球位于最高点,根据光沿直线传播,光源能够在屏上留下影子的位置也处于最高点,影子位于正向最大位移处,根据几何关系有ll+2l =A+AA+x影子,解得x影子=5A,即t3时刻影子的位移为5A,D正确.3.[2024·吉林卷]某同学自制双缝干涉实验装置:在纸板上割出一条窄缝,于窄缝中央沿缝方向固定一根拉直的头发丝形成双缝,将该纸板与墙面平行放置,如图所示.用绿色激光照双缝,能够在墙面上观察到干涉条纹.下列做法可以使相邻两条亮条纹中央间距变小的是()A.换用更粗的头发丝B.换用红色激光照射双缝C.增大纸板与墙面的距离D.减小光源与纸板的距离答案:A解析:由于干涉条纹间距Δx=ldλ可知,换用更粗的头发丝,双缝间距d变大,则相邻两条亮条纹中央间距Δx变小,故A正确;换用红色激光照双缝,波长变长,则相邻两条亮条纹中央间距Δx变大,故B错误;增大纸板与墙面的距离l,则相邻两条亮条纹中央间距Δx 变大,故C错误;减小光源与纸板的距离,不会影响相邻两条亮条纹中央间距Δx,故D错误.故选A.4.[2024·浙江1月](多选)在如图所示的直角坐标系中,xOz平面为介质Ⅰ和Ⅱ的分界面(z轴垂直纸面向外).在介质Ⅰ中的P(0,4λ)处有一点波源,产生波长为λ、速度为v的波.波传到介质Ⅱ中,其速度为2v.图示时刻介质Ⅱ中仅有一个波峰,与x轴和y轴分别交于R 和S点,此时波源也恰好位于波峰.M为O、R连线的中点,入射波与反射波在O点相干加强,则()A .介质Ⅱ中波的频率为2v λB. S 点的坐标为(0,-2 λ)C .入射波与反射波在M 点相干减弱D. 折射角α的正弦值sin α=352 答案:BD解析:波从一种介质到另一种介质,频率不变,故介质Ⅱ中波的频率为f =v λ,A 错误;在介质Ⅱ中波长为λ′=2v f=2 λ,由于图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,故S 点的坐标为(0,-2 λ),B 正确;由于S 为波峰,且波传到介质Ⅱ中,其速度为2 v .图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,则R 也为波峰,故P 到R 比P 到O 多一个波峰,则PR =5λ,则OR =3λ,由于||MO -PM≠2n ·λ2 或(2n +1)λ2 (n =0,1,2,…),故M 点不是减弱点,C 错误;根据n =λ′λ=2 ,则n =sin αOR PR,解得sin α=352 ,D 正确. 5.[2021·天津卷]一列沿x 轴正方向传播的简谐横波,传播速度v =10 m/s ,t =0时位于坐标原点的质点从平衡位置沿y 轴正方向运动,下列图形中哪个是t =0.6 s 时的波形( )答案:B解析:由图中可以看出该波的波长为λ=4 m ,根据v =λT可知该列波的周期为T =0.4 s ,又因为t=0时位于坐标原点的质点从平衡位置沿y轴正方向运动,当t=0.6 s时经历了1.5 T,所以此时位于坐标原点的质点从平衡位置沿y轴负方向运动,结合图像可知B正确.6.[2023·湖南卷]如图(a),在均匀介质中有A、B、C和D四点,其中A、B、C三点位于同一直线上,AC=BC=4 m,DC=3 m,DC垂直AB.t=0时,位于A、B、C处的三个完全相同的横波波源同时开始振动,振动图像均如图(b)所示,振动方向与平面ABD垂直,已知波长为4 m.下列说法正确的是()A.这三列波的波速均为2 m/sB.t=2 s时,D处的质点开始振动C.t=4.5 s时,D处的质点向y轴负方向运动D.t=6 s时,D处的质点与平衡位置的距离是6 cm答案:C解析:由图(b)的振动图像可知,振动的周期为4 s,故三列波的波速为v=λT=4 m4 s=1m/s,A错误;由图(a)可知,D处距离波源C最近的距离为3 m,故开始振动后波源C处的横波传播到D处所需的时间为t C=DC v=3 m1 m/s=3 s故t=2 s时,D处的质点还未开始振动,B错误;由几何关系可知AD=BD=5 m,波源A、B产生的横波传播到D处所需的时间为t AB=ADv=5 m1 m/s=5 s故t=4.5 s时,仅波源C处的横波传播到D处,此时D处的质点振动时间为t1=t-t C =1.5 s由振动图像可知此时D处的质点向y轴负方向运动,C正确;t=6 s时,波源C处的横波传播到D处后振动时间为t2=t-t C=3 s由振动图像可知此时D处为波源C处传播横波的波谷;t=6 s时,波源A、B处的横波传播到D处后振动时间为t3=t-t AB=1 s由振动图像可知此时D处为波源A、B处传播横波的波峰.根据波的叠加原理可知此时D处质点的位移为y=2A-A=2 cm故t=6 s时,D处的质点与平衡位置的距离是2 cm,D错误.故选C.。
大学物理学教程第二(马文蔚)练习册答案6第六章 机械波

解:
6-8 图示为平面简谐波在t=0时刻的波形图,此简谐波 的频率为250Hz,且此图中P点的运动方向向上,求: 第 (1)此波的波动方程;(2)距原点7.5m处质点的运 六 动方程与t=0时该点的振动速度。 y/m 章 解: P点的运动方向向上
习 题 分 析
6-8
波向负方向传播
0.10 0.05 O
6-9
六 章 习 题 分 析
解:
xP 0.2 m
O 0.04
P
0.2 0.4 0.6
x/m
2 0.2 y P 0.04cos[ (t ) ]m 5 0.08 2 2 3 0.04cos[ t ] m 5 2 2 x y 0.04cos[ (t ) ]m 5 0.08 2
第 六 章 习 题 分 析
6-7
y15 A cos 100 t 15 cm 2
y5 A cos 100 t 5 cm 2
解:
15 15.5
5 5.5
2 2 波源振动方程: y0 A cos t cm 2 T 2 x 波动方程:
6-11
6-11 平面简谐波的波动方程为:
第 六 章 习 题 分 析
求:(1)t=2.1s时波源及距波源0.10m两处的相位;(2)离 波源0.80m及0.30m两处的相位差。 解:(1)
y 0.08cos 4 t 2 x (SI 制)
t 2.1s, x 0处, 4 2.1 8.4
x t x y A cos[ (t ) ] A cos[ 2 π ( ) ] u T
) 14-3 已知一波动方程为 y 0.05sin(10 t 2 x)(SI , (1)求波长、频率、波速和周期; (2)说明 x 0 第 六 时方程的意义,并作图表示。
物理学教程(第二版)上册课后答案第六章
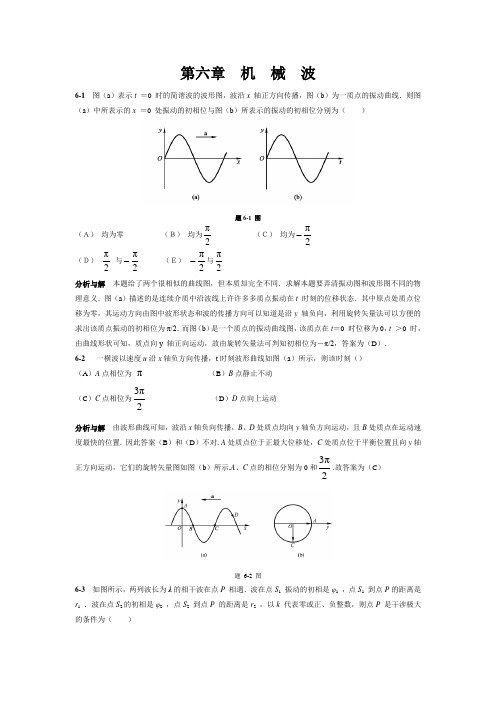
第六章 机 械 波6-1 图(a )表示t =0 时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线.则图(a )中所表示的x =0 处振动的初相位与图(b )所表示的振动的初相位分别为( )题6-1 图(A) 均为零 (B) 均为2π (C) 均为2π- (D) 2π 与2π- (E) 2π-与2π 分析与解 本题给了两个很相似的曲线图,但本质却完全不同.求解本题要弄清振动图和波形图不同的物理意义.图(a )描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态.其中原点处质点位移为零,其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向,利用旋转矢量法可以方便的求出该质点振动的初相位为π/2.而图(b )是一个质点的振动曲线图,该质点在t =0 时位移为0,t >0 时,由曲线形状可知,质点向y 轴正向运动,故由旋转矢量法可判知初相位为-π/2,答案为(D ). 6-2 一横波以速度u 沿x 轴负方向传播,t 时刻波形曲线如图(a )所示,则该时刻()(A )A 点相位为π (B )B 点静止不动 (C )C 点相位为2π3 (D )D 点向上运动分析与解 由波形曲线可知,波沿x 轴负向传播,B 、D 处质点均向y 轴负方向运动,且B 处质点在运动速度最快的位置. 因此答案(B )和(D )不对. A 处质点位于正最大位移处,C 处质点位于平衡位置且向y 轴正方向运动,它们的旋转矢量图如图(b )所示.A 、C 点的相位分别为0和2π3.故答案为(C )题 6-2 图6-3 如图所示,两列波长为λ的相干波在点P 相遇.波在点S 1 振动的初相是φ1 ,点S 1 到点P 的距离是r 1 .波在点S 2的初相是φ2 ,点S 2 到点P 的距离是r 2 ,以k 代表零或正、负整数,则点P 是干涉极大的条件为( )()()()()()()π2/π2A π2/π2A π2A πA 211212121212k r r k r r k k r r =-+-=-+-=-=-λϕϕλϕϕϕϕ 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =,而两列波传到P 点时的两分振动相位差为()λϕϕϕ/π2Δ1212r r ---=,故选项(D )正确.题6-3 图6-4 在波长为λ的驻波中,两个相邻波腹之间的距离为( )(A ) 4λ (B ) 2λ(C ) 43λ (D ) λ分析与解 驻波方程为t λx A y v π2cos π2cos 2=,它不是真正的波.其中λx A π2cos 2是其波线上各点振动的振幅.显然,当Λ,2,1,0,2=±=k k x λ时,振幅极大,称为驻波的波腹.因此,相邻波腹间距离为2λ.正确答案为(B ).6-5 一横波在沿绳子传播时的波动方程为()x y ππ5.2cos 20.0-=,式中y 的单位为m ,t 的单位为s .(1) 求波的振幅、波速、频率及波长;(2) 求绳上质点振动时的最大速度;(3) 分别画出t =1s 和t =2 s 时的波形,并指出波峰和波谷.画出x =1.0 m处质点的振动曲线并讨论其与波形图的不同. 分析 (1) 已知波动方程(又称波函数)求波动的特征量(波速u 、频率υ、振幅A 及波长λ等),通常采用比较法.将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y μ书写,然后通过比较确定各特征量(式中ux 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播).比较法思路清晰、求解简便,是一种常用的解题方法.(2) 讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别.例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即v =d y /d t ;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质 的性质决定.介质不变,波速保持恒定.(3) 将不同时刻的t 值代入已知波动方程,便可以得到不同时刻的波形方程y =y (x ),从而作出波形图.而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程y =y (t ),从而作出振动图.解 (1) 将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较,可得0s m 52m 20001=⋅==-ϕ,.,.u A则 m 0.2/,Hz 25.1π2/====v u λωv(2) 绳上质点的振动速度()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v 则 1max s m 57.1-⋅=v(3) t =1s 和t =2s 时的波形方程分别为()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图(a )所示.x =1.0m 处质点的运动方程为 ()()m π5.2cos 20.0t y -=振动图线如图(b )所示.波形图与振动图虽在图形上相似,但却有着本质的区别.前者表示某确定时刻波线上所有质点的位移情况,而后者则表示某确定位置的一个质点,其位移随时间变化的情况.题6-5 图6-6 波源作简谐运动,其运动方程为()m t πcos240100.43-⨯=y ,它所形成的波形以30m·s-1 的速度沿一直线传播.(1) 求波的周期及波长;(2) 写出波动方程.分析 已知波源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式进行比较,求出振幅A 、角频率ω及初相φ0 ,而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的.再利用题中已知的波速u 及公式ω=2πν =2π/T 和λ=u T 即可求解.解 (1) 由已知的运动方程可知,质点振动的角频率1s π240-=ω.根据分析中所述,波的周期就是振动的周期,故有 s 1033.8/π23-⨯==ωT波长为λ=uT =0.25 m(2) 将已知的波源运动方程与简谐运动方程的一般形式比较后可得A =4.0 ×10-3m ,1s π240-=ω,φ0 =0故以波源为原点,沿x 轴正向传播的波的波动方程为 ()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-6-7 波源作简谐运动,周期为0.02s,若该振动以100m·s-1 的速度沿直线传播,设t =0时,波源处的质点经平衡位置向正方向运动,求:(1) 距波源15.0m 和5.0 m 两处质点的运动方程和初相;(2) 距波源为16.0 m 和17.0m 的两质点间的相位差.分析 (1) 根据题意先设法写出波动方程,然后代入确定点处的坐标,即得到质点的运动方程.并可求得振动的初相.(2) 波的传播也可以看成是相位的传播.由波长λ的物理含意,可知波线上任两点间的相位差为Δφ=2πΔx /λ.解 (1) 由题给条件1s m 100s 020-⋅==u T ,.,可得m 2;s m π100/π21==⋅==-uT λT ω当t =0 时,波源质点经平衡位置向正方向运动,因而由旋转矢量法可得该质点的初相为φ0 =-π/2(或3π/2).若以波源为坐标原点,则波动方程为()[]2/π100π100cos --=x/t A y距波源为x 1 =15.0 m 和x 2 =5.0 m 处质点的运动方程分别为()()π5.5t π100cos π15.5t π100cos 21-=-=A y A y它们的初相分别为φ10 =-15.5π和φ20 =-5.5π(若波源初相取φ0=3π/2,则初相φ10 =-13.5π,φ20 =-3.5π.)(2) 距波源16.0m 和17.0 m 两点间的相位差()π/π2Δ1212=-=-=λϕϕϕx x6-8 图示为平面简谐波在t =0 时的波形图,设此简谐波的频率为250Hz ,且此时图中质点P 的运动方向向上.求:(1) 该波的波动方程;(2) 在距原点O 为7.5 m 处质点的运动方程与t =0 时该点的振动速度.分析 (1) 从波形曲线图获取波的特征量,从而写出波动方程是建立波动方程的又一途径.具体步骤为:1. 从波形图得出波长λ、振幅A 和波速u =λυ;2. 根据点P 的运动趋势来判断波的传播方向,从而可确定原点处质点的运动趋向,并利用旋转矢量法确定其初相φ0 .(2) 在波动方程确定后,即可得到波线上距原点O 为x 处的运动方程y =y (t ),及该质点的振动速度υ=d y /d t .解 (1) 从图中得知,波的振幅A =0.10 m ,波长λ=20.0m ,则波速u =λυ=5.0 ×103 m·s-1 .根据t =0 时点P 向上运动,可知波沿Ox 轴负向传播,并判定此时位于原点处的质点将沿Oy 轴负方向运动.利用旋转矢量法可得其初相φ0 =π/3.故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t A y ϕω(2) 距原点O 为x =7.5m 处质点的运动方程为 ()()m 12π13π5000.10cos y /t +=t =0 时该点的振动速度为 ()-10s m 40.6/12π13sin π50/d d ⋅=-===t t y v题6-8 图6-9 一平面简谐波以速度1s m 08.0-⋅=u 沿Ox 轴正向传播,图示为其在t =0 时刻的波形图,求(1)该波的波动方程;(2)P 处质点的运动方程.题6-9 图分析 (1) 根据波形图可得到波的波长λ、振幅A 和波速u ,因此只要求初相φ,即可写出波动方程.而由图可知t =0 时,x =0 处质点在平衡位置处,且由波的传播方向可以判断出该质点向y 轴正向运动,利用旋转矢量法可知φ=-π/2.(2) 波动方程确定后,将P 处质点的坐标x 代入波动方程即可求出其运动方程y P =y P (t ).解 (1) 由图可知振幅A =0.04 m, 波长λ=0.40 m, 波速u =0.08m·s-1 ,则ω=2π/T =2πu /λ=(2π/5)s-1 ,根据分析已知φ=-π/2,因此波动方程为()m 2π08.05π20.04cos y ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=x t(2) 距原点O 为x =0.20m 处的P 点运动方程为 ()m 2π52π0.04cos y ⎥⎦⎤⎢⎣⎡+= *6-10 一平面简谐波,波长为12 m ,沿O x 轴负向传播.图(a )所示为x =1.0 m 处质点的振动曲线,求此波的波动方程.题6-10图分析 该题可利用振动曲线来获取波动的特征量,从而建立波动方程.求解的关键是如何根据图(a ) 写出它所对应的运动方程.较简便的方法是旋转矢量法.解 由图(a )可知质点振动的振幅A =0.40 m,t =0 时位于x =1.0 m 处的质点在A /2 处并向Oy 轴正向移动.据此作出相应的旋转矢量图(b ),从图中可知3/π0-='ϕ.又由图(a )可知,t =5 s 时,质点第一次回到平衡位置,由图(b )可看出ωt =5π/6,因而得角频率ω=(π/6) rad .s -1 .由上述特征量可写出x =1.0 m 处质点的运动方程为 ()m 3π6π0.04cos y ⎥⎦⎤⎢⎣⎡-=t 将波速1s m 0.1π2//-⋅===ωλT λu 及x =1.0 m 代入波动方程的一般形式()[]0cos ϕω++=u x t A y /中,并与上述x =1.0 m 处的运动方程作比较,可得φ0 =-π/2,则波动方程为()()m 2π10/6π0.04cos ⎥⎦⎤⎢⎣⎡-+=x t y 6-11 平面简谐波的波动方程为()x t y π2π4cos 08.0-=,式中y 和x 的单位为m ,t 的单位为s,求:(1) t =2.1 s 时波源及距波源0.10m 两处的相位;(2) 离波源0.80 m 及0.30 m 两处的相位差. 解 (1)将t =2.1 s 和x =0 代入题给波动方程,可得波源处的相位π4.81=ϕ将t =2.1 s 和x ′=0.10 m 代入题给波动方程,得0.10 m 处的相位为π2.82=ϕ(2)从波动方程可知波长λ=1.0 m .这样,x 1=0.80 m 与x 2=0.30 m 两点间的相位差πΔπ2Δ=⋅=λϕx6-12 为了保持波源的振动不变,需要消耗4.0 W 的功率.若波源发出的是球面波(设介质不吸收波的能量).求距离波源5.0 m 和10.0 m 处的能流密度.分析 波的传播伴随着能量的传播.由于波源在单位时间内提供的能量恒定,且介质不吸收能量,故对于球面波而言,单位时间内通过任意半径的球面的能量(即平均能流)相同,都等于波源消耗的功率P .而在同一个球面上各处的能流密度相同,因此,可求出不同位置的能流密度I =P /S .解 由分析可知,半径r 处的能流密度为2π4/r P I =当r 1 =5.0 m 、r 2 =10.0m 时,分别有22211m W 1027.1π4/--⋅⨯==r P I22222m W 1027.1π4/--⋅⨯==r P I6-13 两相干波波源位于同一介质中的A 、B 两点,如图(a )所示.其振幅相等、频率皆为100 Hz ,B 比A 的相位超前π.若A 、B 相距30.0 m ,波速为u =400 m·s -1 ,试求AB 连线上因干涉而静止的各点的位置.题6-13 图分析 两列相干波相遇时的相位差λϕϕϕr Δπ2Δ12--=.因此,两列振幅相同的相干波因干涉而静止的点的位置,可根据相消条件()π12Δ+=k ϕ获得.解 以A 、B 两点的中点O 为原点,取坐标如图(b )所示.两波的波长均为λ=u /υ=4.0 m .在A 、B 连线上可分三个部分进行讨论.1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r ϕϕϕ因该范围内两列波相位差恒为2π的整数倍,故干涉后质点振动处处加强,没有静止的点.2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r ϕϕϕ显然该范围内质点振动也都是加强,无干涉静止的点.3. 在A 、B 两点的连线间,设任意一点P 距原点为x .因x r -=15B,x r +=15A ,则两列波在点P的相位差为 ()()π1/π2ΔA B A B +=---=x r r λϕϕϕ根据分析中所述,干涉静止的点应满足方程()()π152π1+=+k x x得 ()2,...1,0,k m 2±±==k x因x ≤15 m ,故k ≤7.即在A 、B 之间的连线上共有15 个静止点.6-14 图(a )是干涉型消声器结构的原理图,利用这一结构可以消除噪声.当发动机排气噪声声波经管道到达点A 时,分成两路而在点B 相遇,声波因干涉而相消.如果要消除频率为300 Hz 的发动机排气噪声,则图中弯管与直管的长度差Δr =r 2 -r 1 至少应为多少? (设声波速度为340 m·s -1 )题6-14 图分析 一列声波被分成两束后再相遇,将形成波的干涉现象.由干涉相消条件,可确定所需的波程差,即两管的长度差Δr .解 由分析可知,声波从点A 分开到点B 相遇,两列波的波程差Δr =r 2 - r 1 ,故它们的相位差为()λλϕ/Δπ2/π2Δ12r r r =-=由相消静止条件Δφ=(2k +1)π,(k =0,±1,±2,…)得 Δr =(2k +1)λ/2根据题中要求令k =0 得Δr 至少应为m 57022.//===∆v u r λ讨论 在实际应用中,由于噪声是由多种频率的声波混合而成,因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力.图(b )为安装在摩托车排气系统中的干涉消声器的结构原理图.*6-15 如图所示,x =0 处有一运动方程为t A y ωcos =的平面波波源,产生的波沿x 轴正、负方向传播.MN 为波密介质的反射面,距波源3λ/4.求:(1) 波源所发射的波沿波源O 左右传播的波动方程;(2) 在MN 处反射波的波动方程;(3) 在O ~MN 区域内形成的驻波方程,以及波节和波腹的位置;(4) x >0区域内合成波的波动方程.题6-15 图分析 知道波源O 点的运动方程t A y ωcos =,可以写出波沿x 轴负向和正向传播的方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2.因此可以写出y 1 在MN 反射面上P 点的运动方程.设反射波为y 3 ,它和y 1 应是同振动方向、同振幅、同频率的波,但是由于半波损失,它在P 点引起的振动和y 1 在P 点引起的振动反相.利用y 1 在P 点的运动方程可求y 3 在P 点的运动方程,从而写出反射波y 3 .在O ~MN 区域由y 1 和Y 3 两列同频率、同振动方向、同振幅沿相反方向传播的波合成形成驻波.在x >0区域是同传播方向的y 2 和y 3 合成新的行波.解 (1) 由分析已知:沿左方向和右方向传播的波动方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2(2) y 1 在反射面MN 处引起质点P 振动的运动方程⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=2π3π2cos 43π2π2cos 1t T A t T A y pλλ 因半波损失反射波y 3 在此处引起的振动为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=2ππ2cos ππ23π2cos 3t T A t T A y p设反射波的波动方程为()ϕλ+-=/π2/π2cos 3x T t A y ,则反射波在x =-3λ/4处引起的振动为⎪⎭⎫ ⎝⎛++=ϕπ23π2cos 3t T A y p与上式比较得π2-=ϕ,故反射波的波动方程为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=x λt TA x λt T A y π2π2cos π2π2π2cos 3 (3) 在O ~MN 区域由y 1 和y 3 合成的驻波y 4 为()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=+=t T x λA x λt T A x λt T A y y x t y π2cos π2cos 2π2π2cos π2π2cos ,314 波节的位置:4/2/,2/ππ/π2λλk x k λx +=+=,取k =-1, -2,即x =-λ/4, -3λ/4 处为波节.波腹的位置:2/,π/π2λk x k λx ==,取k =0,-1,即x =0,-λ/2 处为波腹.(4) 在x >0 区域,由y 2 和y 3 合成的波y 5 为()⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=x λt TA x λt T A x λt T A y y x t y π2π2cos 2π2π2cos π2π2cos ,325 这表明:x >0 区域内的合成波是振幅为2A 的平面简谐波.6-16 如图(a )所示,将一块石英晶体相对的两面镀银作电极,它就成为压电晶体,两极间加上频率为ν的交变电压,晶片就沿竖直方向作频率为ν的驻波振动,晶体的上下两面是自由的,故而成为波腹.设晶片d =2.00 mm ,沿竖直方向的声速13s m 1074.6-⋅⨯=u,试问要激起石英片发生基频振动,外加电压的频率应是多少?分析 根据限定区域内驻波形成条件(如图(b )所示),当晶体的上下两面是自由的而成为波腹时,其厚度与波长有关系式 k k d λ2=成立,k 为正整数.可见取不同的k 值,得到不同的k λ,晶体内就出现不同频率k ν的波.对应k =1称为基频,k =2,3,4,…称为各次谐频.解 根据分析基频振动要求2λ=d ,于是要求频率Hz 10685.126⨯===d u u λν题 6-16 图6-17 一平面简谐波的频率为500 Hz ,在空气(ρ=1.3 kg·m -3 )中以u =340 m·s -1 的速度传播,到达人耳时,振幅约为A =1.0 ×10 -6 m .试求波在耳中的平均能量密度和声强.解 波在耳中的平均能量密度2622222m J 1042.6π221--⋅⨯===v A A ρωρω声强就是声波的能流密度,即23m W 10182--⋅⨯==.ωu I这个声强略大于繁忙街道上的噪声,使人耳已感到不适应.一般正常谈话的声强约1.0×10-6W·m -2 左右. 6-18 面积为1.0 m 2 的窗户开向街道,街中噪声在窗口的声强级为80 dB .问有多少“声功率”传入窗内? 分析 首先要理解声强、声强级、声功率的物理意义,并了解它们之间的相互关系.声强是声波的能流密度I ,而声强级L 是描述介质中不同声波强弱的物理量.它们之间的关系为L =lg (I /I 0 ),其中I 0 =1.0 ×10-12 W·m -2为规定声强.L 的单位是贝尔(B ),但常用的单位是分贝(dB ),且1 B =10 dB .声功率是单位时间内声波通过某面积传递的能量,由于窗户上各处的I 相同,故有P =IS .解 根据分析,由L =lg (I /I 0 )可得声强为I =10LI 0则传入窗户的声功率为 P =IS =10L I 0S =1.0 ×10-4 W6-19 一警车以25 m·s -1 的速度在静止的空气中行驶,假设车上警笛的频率为v =800 Hz .求:(1) 静止站在路边的人听到警车驶近和离去时的警笛声波频率;(2) 如果警车追赶一辆速度为15m·s -1 的客车,则客车上人听到的警笛声波的频率是多少? (设空气中的声速u =330m·s -1 )分析 由于声源与观察者之间的相对运动而产生声多普勒效应,由多普勒频率公式可解得结果.在处理这类问题时,不仅要分清观察者相对介质(空气)是静止还是运动,同时也要分清声源的运动状态. 解 (1) 根据多普勒频率公式,当声源(警车)以速度υs =25 m·s -1 运动时,静止于路边的观察者所接收到的频率为s u u vv υμ='警车驶近观察者时,式中υs 前取“-”号,故有Hz 6.8651=-='su u v v υ 警车驶离观察者时,式中υs 前取“+”号,故有 Hz 7.7432=+='s u u v v υ (2) 客车的速度为0υ=15 m·s -1 ,声源(警车)与客车上的观察者作同向运动时,观察者收到的频率为Hz 2.82603=--='su u v v υυ 6-20 蝙蝠在洞穴中飞来飞去,能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz ,当它以声速的401的速度朝着表面平直的岩壁飞去时,试求它听到的从岩壁反射回来的超声波频率为多少?分析 由题意可知,蝙蝠既是波的发出者,又是波的接收者.设超声波的传播速度为u .首先,蝙蝠是声源,发出信号频率为v ,运动速度为40s u =υ,岩壁是接收者,利用多普勒频率公式,即可求得岩壁接收到的信号频率v '.经岩壁反射后频率不变,即岩壁发射信号频率为v ',这时蝙蝠是波的接收者,其运动速度为400u =υ,再次利用多普勒频率公式,可求得蝙蝠接收到的信号频率v ''. 解 将蝙蝠看成波源,则由分析可知,岩壁接收到的信号频率为s υ-='u uvv ,在蝙蝠接收岩壁反射信号时,又将它看成接收者.则蝙蝠接收到的信号频率为kHz 41kHz 3940/1140/11/1/1s 0s 00=⨯-+=-+=-+='+=''v u u v u u v u u v υυυυυ。
第六章 机械波作业及答案

第六章 机械波作业及答案一、选择题1.频率为500Hz 的波,其波速为3601-⋅s m ,在同一波线上位相差为 60的两点的距离为 [ ](A );24.0m (B );48.0m (C );36.0m (D );12.0m2、一平面简谐波的波动方程为)(),3cos(1.0SI x t y πππ+-=,0=t 时刻的波形曲线如图所示,则 [ ](A)O 点的振幅为m 1.0-; (B) 波长为m 3;(C) a,b 两点间位相差为2π; (D) 波速为19-⋅s m .3、图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形.若波的表达式以余弦函数表示,则O 点处质点振动的初相为 [ ](A) 0. (B)π21. (C) π. (D) π23.4、一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是 [ ](A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI).xyOu(C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI).5、一平面简谐波沿x 轴负方向传播.已知 x = x 0处质点的振动方程为0cos()y A t ωϕ=+.若波速为u ,则此波的表达式为 (A) 00cos{[()/]}y A t x x u ωϕ=--+. (B) 00cos{[()/]}y A t x x u ωϕ=--+.(C) 00cos{[()/]}y A t x x u ωϕ=--+.(D) 00cos{[()/]}y A t x x u ωϕ=+-+. [ ]6、如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S , 两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为 [ ](A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C))212cos(2π+π=t A y . (D))1.02cos(22π-π=t A y .二、计算题1 、已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ,x 2 = 25 m 两点处质点的振动方程;(2) 求x 1,x 2两点间的振动相位差;2、某质点作简谐振动,周期为2 s ,振幅为0.06 m ,t = 0 时刻,质点恰好处在负向最大位移处,求S(1) 该质点的振动方程;(2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3) 该波的波长.3、一列平面简谐波在媒质中以波速u = 5 m/s 沿x 轴正向传播,原点O 处质元的振动曲线如图所示.(1) 求解并画出x = 25 m 处质元的振动曲线. (2) 求解并画出t = 3 s 时的波形曲线.4.一横波方程为 )(2cosx ut A y -π=λ, 式中A = 0.01 m ,λ = 0.2 m ,u = 25 m/s ,求t = 0.1 s 时在x = 2 m 处质点振动的位移、速度、加速度.6 一平面简谐波0=t 时的波形如图所示,且向右传播,波速为,2001-⋅=s m u ,试求 (1)o 点的振动表达式; (2)波的表达式;(3)m x 3=处的P 点振动表达式。
北京海淀区高三物理 第六章机械振动和机械波复习总测试

第六章 机械振动和机械波第一节 简谐运动1.作简谐运动的物体每次通过平衡位置时( )A .位移为零,动能为零B .动能最大,势能最小C .速率最大,振动加速度为零D .速率最大,回复力不一定为零2.作简谐运动的物体,当它每次经过同一位置时,一定一样的物理量是( )A .速度B .位移C .回复力D .加速度3.作简谐运动的物体,回复力和位移的关系是图6-1所给四个图像中的( )图6-14.水平放置的弹簧振子先后以振幅A 和2A 振动,稳定后振子从左边最大位移处运动到右边最大位移处的过程中,平均速度分别为v 1和v 2,如此( )A .v 1=2v 2B .2v 1=v 2C .212v vD .v 1=v 25.如图6-2所示,在张紧的绳上挂了a 、b 、c 、d 四个单摆,四个单摆的摆长关系为l c >l b =l d >l a ,先让d 摆摆动起来(摆角小超过5°),如此如下说法中正确的答案是( )图6-2A .b 摆发生振动,其余摆均不动B .所有摆均以一样频率振动C .所有摆均以一样摆角振动D .以上说法均不正确6.如图6-3所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不粘连),并用力向下压球,使弹簧作弹性压缩,稳定后用细线把弹簧拴牢。
烧断细线,球将被弹起,脱离弹簧后能继续向上运动.那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( )图6-3A .球所受合力的最大值不一定大于球的重力值B .在某一阶段内球的动能减小而它的机械能增加C .球刚脱离弹簧时的动能最大D.球刚脱离弹簧时弹簧的弹性势能最小7.如图6-4所示,小球从高处下落到竖直放置的轻弹簧上,在从接触到将弹簧压缩到最短的过程中,如下表示中正确的答案是( )图6-4A.球的加速度的最大值,不一定大于重力加速度gB.球所受弹力的最大值,一定大于其重力的2倍C.小球的动能逐渐减小,而系统的机械能保持不变D.系统的势能先减少后增加8.同一个弹簧振子从平衡位置被分别拉开5cm和2cm,松手后均作简谐运动,如此它们的振幅之比A1∶A2=______,最大加速度之比a1∶a2=______,振动周期之比T1∶T2=______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.两个相干波源的位相相同,它们发出的波叠加后,在下列哪条线上总是加强的?( )
(A)两波源连线的垂直平分线上;(B)以两波源连线为直径的圆周上;
(C)以两波源为焦点的任意一条椭圆上;(D)以两波源为焦点的任意一条双曲线上。
13.平面简谐波 与下面哪列波相干可形成驻波? ( )
第六、七机械振动与机械波
班级学号姓名
一、选择题
1.一弹簧振子,当把它水平放置时,它作简谐振动。若把它竖直放置或放在光滑斜面上,试判断下列情况正确的是 ( )
(A)竖直放置作简谐振动,在光滑斜面上不作简谐振动;
(B)竖直放置不作简谐振动,在光滑斜面上作简谐振动;
C)两种情况都作简谐振动;(D)两种情况都不作简谐振动。
12.一驻波方程为 ,位于 的质元与位于 处的质元的振动位相差为。
三、计算题
1、作简谐振动的小球,速度最大值为3,振幅2,若从速度为正的最大值的某点开始计算时间,(1)求振动的周期;(2)求加速度的最大值;(3)写出振动表达式。
2、如图所示,轻质弹簧的一端固定,另一端系一轻绳,轻绳绕过滑轮连接一质量为m的物体,绳在轮上不打滑,使物体上下自由振动。已知弹簧的劲度系数为k,滑轮的半径为R,转动惯量为J。
(A) ; (B) ;
(C) ; (D) 。
14.两列完全相同的平面简谐波相向而行形成驻波。以下哪种说法为驻波所特有的特征:( )
(A)有些质元总是静止不动; (B)迭加后各质点振动相位依次落后;
(C)波节两侧的质元振动位相相反; (D)质元振动的动能与势能之和不守恒。
二、填空题
1.一弹簧振子作简谐振动,其振动曲线如图所示。则它的周期,其余弦函数描述时初相位 =。
(A) m;
(B) m;
(C) m;
(D) m。
7.一个平面简谐波在弹性媒质中传播,媒质质元从最大位置回到平衡位置的过程中()
(A)它的势能转化成动能;(B)它的动能转化成势能;
(C)它从相邻的媒质质元获得能量,其能量逐渐增加;
(D)把自己的能量传给相邻的媒质质元,其能量逐渐减小。
8.一平面简谐波在弹性媒质中传播时,在传播方向上某质元在某一时刻处于最大位移处,则它的()
4.质量为m的物体和一轻弹簧组成弹簧振子其固有振动周期为T,当它作振幅为A的自由简谐振动时,其振动能量。
5.产生机械波的必要条件是和。
6.一平面简谐波的周期为2.0s,在波的传播路径上有相距为2.0的M、N两点,如果N点的位相比M点位相落后 /6,那么该波的波长为,波速为。
7.处于原点(0)的一波源所发出的平面简谐波的波动方程为 ,其中A、B、C皆为常数。此波的速度为;波的周期为;波长为;离波源距离为l处的质元振动相位比波源落后;此质元的初相位为。
(A)动能为零,势能最大;(B)动能为零,势能也为零;
(C)动能最大,势能也最大;(D)动能最大,势能为零。
9.在同一媒质中两列相干的平面简谐波强度之比是 ,则两列波的振幅之比 为 ()
(A) 4;(B) 2;(C) 16;(D) 1/4。
10.在下面几种说法中,正确的是: ()
(A)波源不动时,波源的振动周期与波动的周期在数值上是不同的;
(1)证明物体作简谐振动;
(2)求物体的振动周期;
(3)设0时,弹簧无伸缩,物体也无初速,写出物体的振动表式。
3、一横波沿绳子传播时的波动表式为 (制)。
(1)求此波的振幅、波速、频率和波长。
(2)求绳子上各质点振动的最大速度和最大加速度。
(3)求0.2m处的质点在1s时的相位,它是原点处质点在哪一时刻的相位?
2.两个简谐振动的振动曲线如图所示,则有( )
(A)A超前 /2; (B)A落后 /2;(C)A超前 ;(D)A落后 。
3.一个质点作简谐振动,周期为T,当质点由平衡位置向x轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的最短时间为: ( )
(A)4; (B)12; (C)6; (D)8。
8.一列强度为I的平面简谐波通过一面积为S的平面,波的传播方向与该平面法线的夹角为 ,则通过该平面的能流是。
9.一平面简谐波沿轴正向传播,波动方程为 ,则 处质点的振动方程为, 处质点的振动和 处质点的振动的位相差为 。
10.一驻波的表达式为 ,两个相邻的波腹之间的距离为。
11.一驻波表式为 (制),在1/6(m)处的一质元的振幅为,振动速度的表式为。
(4)分别画出1s、1.25s、1.50s各时刻的波形。
4、一列沿 正向传播的简谐波,已知 和 时的波形如图所示。(假设周期 )试求
(1) 点的振动表式;
(2)此波的波动表式;
(3)画出 点的振动曲线。
第六、七章:机械振动与机械波参考答案
选择题:1-5:C A B C B 6-10:C C B B C 11-14:A A D C
(B)波源振动的速度与波速相同;
(C)在波传播方向上,任一质点的振动位相总是比波源的位相滞后;
(D)在波传播方向上,任一质点的振动位相总是比波源的位相超前。
11.两相干平面简谐波沿不同方向传播,如图所示,波速均为 ,其中一列波在A点引起的振动方程为 ,另一列波在B点引起的振动方程为 ,它们在P点相遇, , ,则两波在P点的相位差为: ()
2.两个同方向同频率的简谐振动,其合振动的振幅为0.2m,合振动的位相与第一个简谐振动的位相差为π/6,若第一个简谐振动的振幅为 m,则第二个简谐振动的振幅为m,第一、二两个简谐振动的位相差为。
3.有两个相同的弹簧,其倔强系数均为k,(1)把它们串联起来,下面挂一个质量为m的重物,此系统作简谐振动的周期为;(2)把它们并联起来,下面挂一质量为m的重物,此系统作简谐振动的周期为。
填空题:
1、 , 2、0.1, 3、 ,
4、 5、波源,传播机械波的介质 6、24,12
4.分振动方程分别为 和 (制)则它们的合振动表达式为: ( )
(A) ; (B) ;
(C) ; (D) 。
5. 一个平面简谐波沿x轴负方向传播,波速u=10。0处,质点振动曲线如图所示,则该波的表式为()
(A) m;
(B) m;
(C) m;
(D) m。
6.一个平面简谐波沿x轴正方向传播,波速为160,0时刻的波形图如图所示,则该波的表式为()
