高中物理运用割补法解电场强度问题
求解电场强度13种方法(附例题)

求解电场强度方法分类赏析一.必会的基本方法:1.运用电场强度定义式求解例1.质量为m 、电荷量为q 的质点,在静电力作用下以恒定速率v 沿圆弧从A 点运动到B 点,,其速度方向改变的角度为θ(弧度),AB 弧长为s ,求AB 弧中点的场强E 。
【解析】:质点在静电力作用下做匀速圆周运动,则其所需的向心力由位于圆心处的点电荷产生电场力提供。
由牛顿第二定律可得电场力F = F 向 = m r v 2。
由几何关系有r = θs ,所以F = m sv θ2,根据电场强度的定义有 E = q F = qs mv θ2。
方向沿半径方向,指向由场源电荷的电性来决定。
2.运用电场强度与电场差关系和等分法求解例2(2012安徽卷).如图1-1所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O 处的电势为0V ,点A 处的电势为6V ,点B 处的电势为3V ,则电场强度的大小为AA .200/V m B./mC . 100/V m D./m(1)在匀强电场中两点间的电势差U = Ed ,d 为两点沿电场强度方向的距离。
在一些非强电场中可以通过取微元或等效的方法来进行求解。
(2若已知匀强电场三点电势,则利用“等分法”找出等势点,画出等势面,确定电场线,再由匀强电场的大小与电势差的关系求解。
3.运用“电场叠加原理”求解例3(2010海南).如右图2, M 、N 和P 是以MN 为直径的半圈弧上的三点,O 点为半圆弧的圆心,60MOP ∠=︒.电荷量相等、符号相反的两个点电荷分别置于M 、N 两点,这时O 点电场强度的大小为1E ;若将N 点处的点电荷移至P则O 点的场场强大小变为2E ,1E 与2E 之比为BA .1:2B .2:1 C.2 D.4:二.必备的特殊方法:4.运用平衡转化法求解例4.一金属球原来不带电,现沿球的直径的延长线放置N图2一均匀带电的细杆MN ,如图3所示。
金属球上感应电荷产生的电场在球内直径上a 、b 、c 三点的场强大小分别为E a 、E b 、E c ,三者相比( )A .E a 最大B .E b 最大C .E c 最大D .E a = E b = E c【解析】:导体处于静电平衡时,其内部的电场强度处处为零,故在球内任意点,感应电荷所产生的电场强度应与带电细杆MN 在该点产生的电场强度大小相等,方向相反。
高考物理之转换研究对象(用“补偿法”求解电场强度)

高考物理之转换研究对象(用“补偿法”求解电场强度)
转换对象
[典例] 在某平面上有一个半径为r的绝缘带电圆环:
(1)若在圆周上等间距地分布n(n≥2)个相同的点电荷,则圆心处的合场强为多少?
(2)若有一半径同样为r,单位长度带电量为q(q>0)的均匀带电圆环上有一个很小的缺口Δl(且Δl≪r),如图所示,则圆心处的场强又为多少?
[解析] (1)当n分别取2、3、4时圆心处的场强均为零,结合点电荷电场的对称性可知,n个相同的点电荷在圆心处的合场强为零。
(2)可以把均匀带电圆环视为由很多点电荷组成,若将缺口补上,再根据电荷分布的对称性可得,圆心O处的合场强为零,由于有缺口的存在,圆心O处的电场即为缺口相对圆心O的对称点产生的电场,其电场强度为该处电荷(可视为点电荷)在O点的电场强度(包括大
小和方向)。
其电场强度的大小为,方向由圆心O指向缺口。
[答案] (1)合场强为零(2),方向由圆心O指向缺口
【名师点拨】求合场强的两种常用方法
1、对称法
利用带电体电荷分布具有对称性,或带电体产生的电场具有对称性的特点求合场强的方法。
2、补偿法
题给条件建立的模型A不是一个完整的标准模型,这时需要给原来的问题补充一些条件,由这些补充条件建立另一个容易求解的模型B,并且模型A与模型B恰好组成一个完整的标准模型,这样求解模型A的问题就变为求解一个完整的标准模型与模型B的差值问题。
补偿法求电场强度

补偿法求电场强度补偿法是一种求解电场强度的常用方法,它基于超定方程组的思想,利用电场的叠加原理来求解电场强度。
在这篇文章中,我们将介绍补偿法的基本原理,并通过实例来说明如何应用补偿法求解电场强度。
让我们来了解一下补偿法的基本原理。
补偿法的核心思想是将待求点的电场强度表示为已知电荷产生的电场强度与待求点附近的点电荷产生的电场强度之和。
这个思想基于电场的叠加原理,即电荷在空间中产生的电场强度可以相互叠加。
在使用补偿法求解电场强度时,我们通常需要先确定一个基准点,然后计算该基准点附近的点电荷产生的电场强度。
接下来,我们将待求点的电场强度表示为已知电荷产生的电场强度与基准点附近的点电荷产生的电场强度之和。
通过这种方式,我们可以利用已知电荷的电场强度来推导出待求点的电场强度。
为了更好地理解补偿法的应用,让我们通过一个实例来说明。
假设有两个点电荷q1和q2,它们分别位于坐标原点和点P(x, y)处。
我们希望求解点P处的电场强度。
根据补偿法的原理,我们可以将点P处的电场强度表示为点电荷q1和q2产生的电场强度之和。
我们计算点电荷q1产生的电场强度。
根据库仑定律,点P处的电场强度E1可以表示为:E1 = k * q1 / r1^2其中,k是库仑常数,r1是点P与点电荷q1之间的距离。
接下来,我们计算点电荷q2产生的电场强度。
同样地,点P处的电场强度E2可以表示为:E2 = k * q2 / r2^2其中,r2是点P与点电荷q2之间的距离。
我们将E1和E2相加,得到点P处的电场强度E:E = E1 + E2通过这样的计算,我们就得到了点P处的电场强度。
需要注意的是,这个方法适用于任意数量的点电荷,只需将每个点电荷产生的电场强度进行叠加即可。
总结起来,补偿法是一种求解电场强度的常用方法,它基于电场的叠加原理,利用已知电荷的电场强度来推导出待求点的电场强度。
通过计算已知电荷产生的电场强度和待求点附近的点电荷产生的电场强度之和,我们可以得到待求点的电场强度。
高三物理4 用“等效法”和“补偿法”求解电场强度
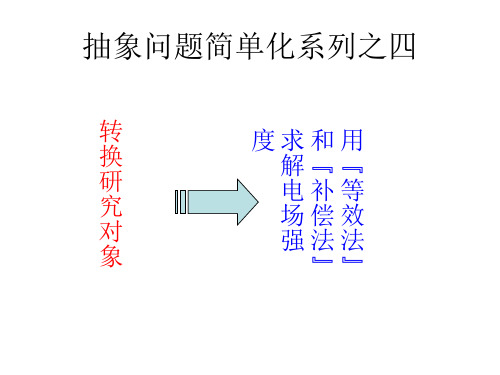
等量异种电荷所形成的电场。所以z轴上
z=h/2处的场强E= 项D正确。
k
q h 2 2
k
q
3h 2
2
k
40q 9h2
,选
• [答案] D
题后悟道
求解合场强常用的四种方法
对称法 补偿法 极限法 微元法
应种电电荷荷的共电同场激。发的。已知静就电迎平刃衡而时解导了体。 内部场强处处为零,则在z轴上z=h/2处的 场强大小为(k为静电力常量)( ) • A.k4q/h2 B.k4q/9h2 • C.k32q/9h2 D.k40q/9h2
图6-1-12
• [解析] 点电荷q和感应电荷所于O点对称的
抽象问题简单化系列之四
转 换 研 究 对 象
度求和用 解““ 电补等 场偿效 强法法 ””
转换对象
• [示 充 荷典,满量例xz为]O<q0y(的的平20点空面13电间是·安荷,无徽置z穷>高于0大的考z导轴空)通如体在荷确上间过图的金周定z为“=6属围其表真-等h板 的 场面处效空1上 电 强,-,法。的 场 的该1”则感 , 情将2导思所在应 无 况电想体电 法 ,, 点电xO荷yq平和面感应上电会荷产形生感应电荷把。研究空对间象任进意行一恰点当 成的处电的场电等场效为皆等是量由异点电荷q和合导理体的表转换面后上,的问感题
高中物理解题方法例话割补法
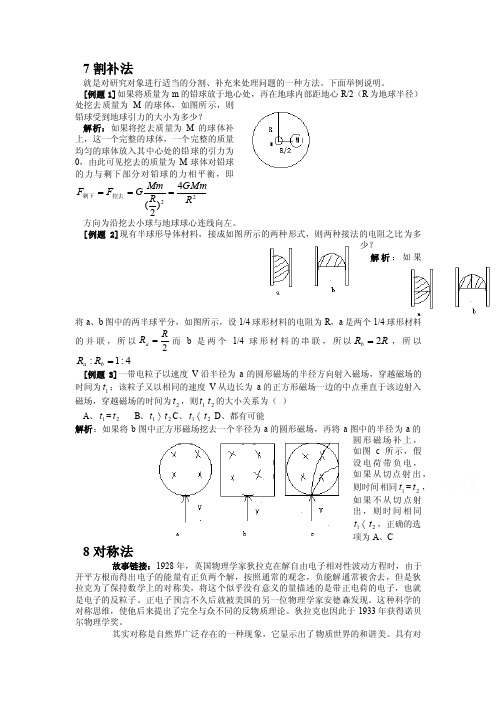
7割补法就是对研究对象进行适当的分割、补充来处理问题的一种方法。
下面举例说明。
[例题1]如果将质量为m 的铅球放于地心处,再在地球内部距地心R/2(R 为地球半径)处挖去质量为M 的球体,如图所示,则铅球受到地球引力的大小为多少?解析:如果将挖去质量为M 的球体补上,这一个完整的球体,一个完整的质量均匀的球体放入其中心处的铅球的引力为0,由此可见挖去的质量为M 球体对铅球的力与剩下部分对铅球的力相平衡,即224)2(R GMmR Mm GF F ===挖去剩下 方向为沿挖去小球与地球球心连线向左。
[例题2]现有半球形导体材料,接成如图所示的两种形式,则两种接法的电阻之比为多少?解析:如果将a 、b 图中的两半球平分,如图所示,设1/4球形材料的电阻为R ,a 是两个1/4球形材料的并联,所以2RR a =而b 是两个1/4球形材料的串联,所以R R b 2=,所以4:1:=b a R R[例题3]一带电粒子以速度V 沿半径为a 的圆形磁场的半径方向射入磁场,穿越磁场的时间为1t ;该粒子又以相同的速度V 从边长为a 的正方形磁场一边的中点垂直于该边射入磁场,穿越磁场的时间为2t ,则1t 2t 的大小关系为( )A 、1t =2tB 、1t 〉2tC 、1t 〈2tD 、都有可能解析:如果将b 图中正方形磁场挖去一个半径为a 的圆形磁场,再将a 图中的半径为a 的圆形磁场补上,如图c 所示,假设电荷带负电,如果从切点射出,则时间相同1t =2t ,如果不从切点射出,则时间相同1t 〈2t ,正确的选项为A 、C8对称法故事链接:1928年,英国物理学家狄拉克在解自由电子相对性波动方程时,由于开平方根而得出电子的能量有正负两个解,按照通常的观念,负能解通常被舍去,但是狄拉克为了保持数学上的对称美,将这个似乎没有意义的量描述的是带正电荷的电子,也就是电子的反粒子。
正电子预言不久后就被美国的另一位物理学家安德森发现。
高中物理:求解电场强度的几种方法

1. 公式法(1)用场强的定义式求电场强度例1:质量为m,电量为q的质点,在静电力作用下以恒定速率v沿圆弧从A点运动到B点其速度方向改变角度为θ(弧度),AB弧长为s,如图1所示,则AB两点间的电势差________,AB弧中点的场强大小________(不计重力)。
图1解析:对带电粒子应用动能定理,所以因带电粒子在静电力作用下做匀速圆周运动,则有,故场强(2)用点电荷的场强公式求电场强度例2:真空中有两个等量异种点电荷,电量大小均为Q,相距r,求连线中点M处场强的大小和方向。
解析:设+Q的场强为,-Q的场强为,则,方向背离;方向指向-Q,所以,方向由+Q指向-Q。
(3)用匀强电场场强公式求电场强度例3:如图2所示,A、B、C三点都在匀强电场中,已知AC⊥BC,∠ABC=60°,BC=20cm,把一个电量的正电荷从A移到B,电场力做功为零,从B移到C,电场力做功,求该匀强电场的电场强度大小和方向。
解析:由于把电荷q从A移到B电场力做功为零,因此,A、B为等势面上的两点,B、C两点间电势差为,由知B点的电势比C点的电势低173V。
根据电场线和等势面的关系知,场强方向垂直于AB连线斜向下。
2. 虚补法例4:如图3所示,在无限大接地金属板上方距板d处有一个+Q点电荷,求金属板表面P点的场强大小。
(已知QP垂直于板面)图3解析:这是一个电荷结构不对称模型,因中学阶段未介绍点电荷与面电荷场强的叠加,似乎无法解决。
若在金属板下方距板d处虚补一个点电荷-Q,则变成了等量异种电荷的对称结构模型,且点电荷+Q、-Q在P点场强的叠加,与点电荷+Q和金属板表面感应负电荷在P点的场强叠加是等效的,很快可得P点的合场强。
说明:当题给模型不对称时,我们可以虚补结构,变不对称为对称。
3. 微元法例5:如图4所示,均匀带电圆环带电量为Q,半径为R,圆心为O,P为垂直于圆环平面的对称轴上的一点,,试求P点的场强。
图4解析:这是一个连续分布的非点电荷电场问题,同学们没有学微积分知识,求解困难。
补偿法求电场强度例题

补偿法求电场强度例题摘要:一、引言- 介绍补偿法求电场强度的基本概念- 说明补偿法求电场强度的优点二、补偿法求电场强度的基本原理- 介绍补偿法的基本原理- 解释电场强度与电势差的关系三、补偿法求电场强度的例题解析- 例题一:二维点电荷的电场强度求解- 例题二:均匀带电圆环的电场强度求解- 例题三:无限长直导线的电场强度求解四、总结- 概括补偿法求电场强度的关键步骤- 强调熟练掌握基本原理的重要性正文:一、引言电场强度是描述电场在某一点作用力的物理量,它在电场问题的分析与计算中具有重要意义。
补偿法是一种常用的求解电场强度的方法,具有简便、直观等优点。
本文将结合例题,详细介绍补偿法求电场强度的基本原理及其应用。
二、补偿法求电场强度的基本原理补偿法是基于电场强度与电势差的关系来求解电场强度的方法。
根据电势差的定义,我们知道沿着某一路径,电势差等于该路径上的电场强度与路径长度的乘积。
因此,我们可以通过测量沿不同路径的电势差,来计算电场强度的大小。
具体操作时,首先选取一个参考点,将其电势设为零,然后测量其他各点相对于参考点的电势差。
根据电势差与路径的关系,可以求出各点的电场强度。
三、补偿法求电场强度的例题解析以下我们通过三个例题,来具体说明补偿法的应用。
例题一:二维点电荷的电场强度求解假设有一个位于坐标原点(0, 0) 的点电荷Q,其电荷量为+2μC。
现要求解该电荷在(x, y) 处的电场强度。
解题步骤:1.选取参考点,设为原点O(0, 0)。
2.测量各点相对于O 点的电势差ΔV(x, y)。
3.根据电势差与电场强度的关系,计算电场强度E(x, y)。
例题二:均匀带电圆环的电场强度求解设有一均匀带电圆环,其半径为R,电荷密度为ρ,圆心位于坐标原点。
现要求解圆环上任意一点P(x, y) 处的电场强度。
解题步骤:1.选取参考点,设为圆环外一点O(a, 0),其中a > R。
2.测量各点相对于O 点的电势差ΔV(x, y)。
补偿法求电场强度例题

补偿法求电场强度例题
(实用版)
目录
1.补偿法求电场强度的概念和原理
2.补偿法的具体步骤和计算方法
3.补偿法在求解电场强度例题中的应用
正文
一、补偿法求电场强度的概念和原理
补偿法是一种求解电场强度的数值方法,它是基于电场线的切线方向与场强方向相切的原理,通过在场强方向上积分电场线的数量来求解场强。
其基本思想是在某一区域内,通过虚拟位移的方式,使电场线与位移方向垂直,从而达到求解电场强度的目的。
二、补偿法的具体步骤和计算方法
1.首先确定需要求解的电场区域,并在该区域内选取一个虚拟的位移方向。
2.通过计算电场线在这个虚拟位移方向上的分量,得到电场强度在该方向上的数值。
3.在整个区域内积分电场强度的分量,得到电场强度的总值。
4.最后,通过总值除以积分面积,就可以得到该区域内的电场强度。
三、补偿法在求解电场强度例题中的应用
假设有一个点电荷 Q,位于原点,我们需要求解距离原点为 r 的球
面上的电场强度。
1.首先,我们选取一个从球心到球面上任意一点的位移方向。
2.然后,我们计算电场线在这个位移方向上的分量,由于电场线的方
向与位移方向垂直,所以电场强度在这个方向上的分量就等于电荷 Q 除以位移的距离。
3.接着,我们在整个球面上积分电场强度的分量,由于球面的面积为4πr^2,所以电场强度的总值就等于 Q 乘以 4πr^2 除以位移的距离。
4.最后,我们用电场强度的总值除以积分面积,就可以得到距离原点为 r 的球面上的电场强度,即 E=Q/(4πε_0r^2),其中ε_0 为真空介电常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中物理运用割补法解电场强度问题
所谓割补法,就是在求解电场强度时根据给出的条件建立起物理模型,如果这个模型是一个完整的标准模型,则容易解决,但有时由题给的条件建立起的模型不是一个完整的标准模型,比如说A不是一个标准的、完整的模型,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且补上的B也必须容易求解,那样待求的A便可从两者的差中获得,这种转换思维角度的方法常常使一些难题的求解变得简单明了。
我们只学到有关点电荷的电场强度、匀强电场的电场强度的计算公式,但不能看成点电荷的带电体产生的电场强度,没有现成公式能用,这时我们就可用割补法使带电体变成标准模型来求解。
例、如图所示,用金属AB弯成半径r=1m的圆弧,但在A、B之间留出宽度d=2cm的间隙,将Q=3.13×10-9C的正电荷分布于金属丝上,求圆心处的电场强度。
分析:我们可以应用割补思维,假设将图中圆环缺口补上,并且它的电荷密度与缺了口的环体原有电荷密度一样,这样就形成了一个电荷均匀分布的完整带电环,环上处于同一直径两端的微小部分可视为两个相对应的点电荷,它们产生的电场在圆心O处叠加后合电场强度为零,根据对称性可知,带电圆环在圆心O处的总电场强度E=0。
至于补上的带电小段,由题给条件
可视作点电荷,它在圆心O处的电场强度E1是可求的,设题中待求电场强度为E2,则E1+E2=E=0,便可求得E2。
本题中如果在A、B之间留出宽度比较大的间隙,则不能运用上面的方法求圆心处的电场强度,因为此时AB段带电体不能当作点电荷来处理,库仑定律不能直接使用。
解析:设原缺口环所带电荷的线密度为,,则补上的金属小段的带电荷量,求出它在O处的电场强度。
设待求的电场强度为E2,因为E1+E2=0,可得E2=-E1=-9×10-2N/C负号表示E2与E1反向,背向球心向左。
