(化工原理)第二节 沉降过程
第3章化工原理中的沉降与过滤

ut
4d (P ) ur 2
3
R
在离心沉降时,如果颗粒与流体的相对运动 属于层流,阻力系数也符合斯托克斯定律:
ut
dP2 (P ) ur2
18
R
离心分离因数:
离心力 离心加速度 KC 重力 重力加速度
3、离心沉降的应用——旋风分离器
旋风分离器动画
文丘里除尘器动画
静电除尘器动画
例3-3:速溶咖啡粉(比重1.05)的直径为60μm, 被250℃热空气带入旋风分离器中,进入时切线速 度为20m/s,在器内的旋转半径为0.5m。求其径向 沉降速度。同样大小的颗粒在同温度的静止空气中 沉降时,其沉降速度应为多少?(设沉降处于层流 区)
9.807
2.66 106 m s 1
检验
Re
值:
Re
dPu0
15106 2.66106 1.005103
998.2
3.96105
1
计算结果表明,与假设相符,故算得的 u0 2.66106ms1 正确。
【例3-2】 某除尘室高2m、宽2m、长5m,用于矿石焙烧炉 的炉气除尘。矿尘的密度为4500kg·m-3,其形状近于圆球。
令 V q,Ve
A
A
qe
q2
2qqe
Kt
K 过滤常数
2、过滤常数的测定
t/q
q2
2qqe
Kt
t q
1 K
q
2 K
qe
α
t 与q线性相关 q
2qe/K
q
tga=1/K
【例 3-4】在100kPa 的恒压下过滤某悬浮液,温度 300 C ,过 滤面积为 40m2 ,并已知滤渣的比阻为11014 m/Kg,x 值 为 0.05Kg/m3 。过滤介质的阻力忽略不计,滤渣不可压缩,试
化工原理 沉降
Ci进、ci出为进、出口气体中粒径 dpi 的颗粒质量浓度g/m3
粒级效率可以准确表示旋风分离器的分离性能。 可以用 i ~ d pi d c 的函数曲线来表示粒级效率:
1.0 0.8 0.6
粒级效率
dc=d50:是粒级效
率恰为50%的颗
0.4
0.2
P P
—— 牛顿公式
沉降速度ut计算方法
计算ut时需先知道所在沉降区域──选择相应式计算。 试差法 设在层流区 计算ut 设在过渡区 no
Re判断
yes
结束
通常微小颗粒的沉降一般属层流区(Stokes区)
沉降速度的影响因素
(1)干扰沉降 发生于颗粒之间距离很小的情况下。多发生于非均 相物系的沉降过程(物系内部有两个以上相)。 当颗粒浓度↑,浮力 ↑ ── ut↓ (2)端效应(器壁效应) 容器壁对颗粒沉降有阻止作用 ,使实际沉降速度 ut<自由沉降速度。当D容器>100dp,可忽略影响。 (3)分子运动 当颗粒直径小到可与流体分子的平均自由程相比拟 时,颗粒可穿过快速运动的流体分子之间,沉降速 度可大于按斯托克斯定律的计算值。
Re<2, gd ——斯托克斯公式 u 18 ζ =24/Re,
2 P P t
过渡区(Allen区) : 2<Re<500, ζ =18.5/Re 0.6
湍流区(Newton区) —— 颗粒较大时
500<Re<×105, ζ ≈0.44
u 1.74
t
d g
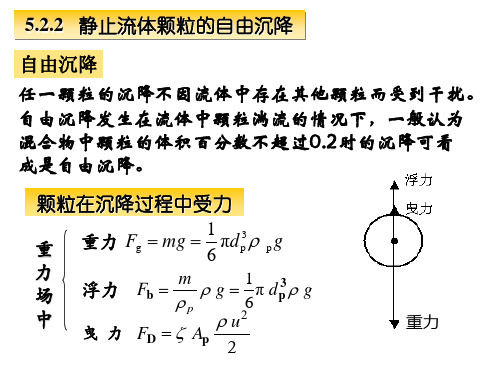
浮力
1 3 Fb g π dp g p 6
m
曳 力 FD Ap
化工原理课件 沉降

t
1 8
1 8 1 .0 0 5 1 0 3
3
计算Rep,核算流型:
R epdpu95 10 61 .9 0 .0 75 9 7 1 0 1 0 3 3 998.20.92442
假设正确,计算有效。
(2)在20 ℃的空气中: 20 ℃空气的密度为1.205kg/m3,粘度为18.1×10-6 Pas
。 m3 / s
,实际上为避免已沉下的尘粒重新被扬起, 往往
u m/ s 取更低 u qV 。降尘室一般用于分离
的粗颗粒。
BH
u
u0.5m/s
dP 50m
• A—降尘室底面积, 。
m2
ABL
u m/ s u •
—颗粒的沉降速度, 。 应根据要分离的最小 颗粒直径 决定。
t
t
d P ,min
5.3.1 重力沉降设备
T↑,气体μ↑,阻力↑ ,除沉不利
T↑,液体μ↓,阻力 ↓,除沉有利
液体粘度约为气体粘度的50倍,故颗粒在液体中的沉降速度比在气体中的小很多。
5.2.2 静止流体中颗粒的自由沉降
3)当流体做水平运动时:
4)当流体以一定的速度向上运动时: 当u>ut时,颗粒向上运动 当u<ut时,颗粒向下运动 当u=ut时,颗粒悬浮在流体中
5.2.1 流体对固体颗粒的绕流
流体与固体颗粒之间的相对运动可分为以下三种情况:
①颗粒静止,流体对其做绕流;
②流体静止,颗粒作沉降运动;
③颗粒与流体都运动,但保持一定的相对运动。
FD
u
流体绕过颗粒的流动
5.2.1 流体对固体颗粒的绕流 (1)两种曳力—表面曳力和形体曳力
5.2.1 流体对固体颗粒的绕流
化工原理:沉降小结

沉降 小结
一、 沉降
1. 定义:利用两相密度的差异,将分均相混合物以分离的单元操作
2. 重力沉降:
1)沉降速度
(斯区 Re<2)
2)沉降设备(降尘室)
生产能力V=u t .A 底 (仅与底面积有关,与高度无关) 3. 离心沉降
1)
沉降速度 Re<2)
2) 沉降设备(旋风分离器) (1) 分离性能 a. 临界直径 b. 分离效率
总效率
粒级效率 (2) 压力降
i
i C C C 0
0-=
η进
出
进,,,i i i i C C C -=η2
1/16D AB c =ζ
二、过滤
1.定义:在外力的作用下,使悬浮液通过多孔介质,将固体颗粒截
留,从而使悬浮液得以分离的单元操作
2.过滤基本方程
或
3.
恒压过滤
4.过滤常数K、q e、V e、θ由实验确定直线)
5.过滤设备
1)间歇操作(板框压滤机、叶压机等)
2)连续操作(转筒真空过滤机)。
化工原理第三章概述、重力沉降

核算流型:
R d e p u t 9 1 5 6 0 1 .9 0 .7 0 1 9 1 5 3 0 7 3 0 9.2 9 0 8 .92 2 4
f(Res,)
【获取方法】当球形度一定时,阻力(曳力)系数ζ 获取方法有如下两种: (1)查取ζ-Re关系曲线图; (2)使用经验公式。
【步骤】(1)根据颗粒的球形度找到对应的 曲线; (2)根据Re找到曲线上的一点; (3)由该点查得ζ ;
s
S Sp
(球形度)
ζ-Re关系曲线图
何谓球形度
s
S Sp
dP ,流体的密度为ρ,则:
Fg
6
dP3Pg
Fb
6
dP3g
Fd A2 u2
dP 2
4
u2
2
当颗粒在流体中做匀速运动(a=0)时,颗粒所 受合力为零,即:
6dP 3Pg 6dP 3gd 4P 22 u20
由此可解出沉降速度:
ut
4gdPP
3
——沉降速度基本计算式
(1)颗粒从静止开始作沉降运动时,分为加速和匀 速两个阶段; (2)对于小颗粒,加速阶段时间很短,通常忽略, 可以认为沉降过程是匀速的。
S——与物体相同体积的球体的表面积; SP——物体的表面积。
【定义】与物体相同体积的球体的表面积和物体的 表面积之比。
(1)此处的雷诺数Re是指:
Re d Pu
计算Re时,dP应为足以表征颗粒大小的长度(特 性尺寸),对球形颗粒而言,就是它的直径。
化工原理中的沉降与过滤

化工原理中的沉降与过滤引言在化工工艺中,沉降和过滤是常用的固液分离方法。
沉降是指根据固液颗粒的重力作用,通过静置使固体颗粒沉降到底部,而将悬浮液体分离出来。
过滤则是通过利用滤介质的孔隙或表面,将悬浮液体中的固体颗粒留下,而使液体通过,从而达到分离固液的目的。
本文将从理论和实际应用两个方面,对化工原理中的沉降与过滤进行介绍。
沉降原理沉降是基于固体颗粒的重力作用,通过静置使固体颗粒沉降到底部,从而实现固液分离的过程。
沉降速度取决于固体颗粒与液体的密度差和粒径大小。
根据Stokes定律,沉降速度与颗粒直径的平方成正比,与液体的粘度成反比。
沉降速度可由下式计算:v = (2/9) * (ρp - ρl) * g * (d^2) / μ其中,v为沉降速度,ρp为颗粒的密度,ρl为液体的密度,g为重力加速度,d为颗粒的直径,μ为液体的动力粘度。
过滤原理过滤是通过滤介质的孔隙或表面,将悬浮液体中的固体颗粒留下,而使液体通过,从而实现固液分离的过程。
滤介质常用的有滤纸、滤筒、滤板等,其孔隙大小决定了能够透过的颗粒大小。
根据Darcy定律,过滤速度与滤介质的孔隙直径的平方成正比,与液体的粘度成反比。
过滤速度可由下式计算:Q = (π/4) * (d^2) * (ΔP/μ) * A其中,Q为过滤速度,d为滤介质的孔隙直径,ΔP为过滤压差,μ为液体的动力粘度,A为过滤面积。
实际应用沉降的应用沉降在化工过程中被广泛应用,常见的应用场景包括:1.污水处理:污水中悬浮的固体颗粒通过沉降实现固液分离,从而达到净化水质的目的。
2.矿石提取:矿石中的有用矿物颗粒通过沉降分离出来,然后进行后续的加工和提取。
3.食品加工:在食品饮料生产中,一些颗粒物质需要通过沉降分离,以获得纯净的液体产品。
4.生物工程:在细胞培养和发酵工艺中,需要将细胞或发酵产物与培养基进行分离。
沉降是一种常用的分离方法。
5.药物制剂:在药物合成和制剂工艺中,沉降用于分离和提取所需的纯净物质。
化工原理 沉降与过滤

(三)压力损失
气体通过旋风分离器的压力损失,可用进 口气体动压的某一倍数表示为
式中的阻力系数用下式计算
ui
2
2
30bh D 2 d LH
四、旋液分离器
旋液分离器是利用离 心力的作用,使悬浮 液中固体颗粒增稠或 使粒径不同及密度不 同的颗粒进行分级。 与旋风分离器相似, 只是液体与颗粒的密 度差较小,为提高分 离的离心力和停留时 间,因此器身做的较 细长。
2、临界粒径dpc:
若在各种不同粒径的尘粒中,有一种粒径的 尘粒能满足L/u=H/ut的条件,此粒径称为 重力降尘室能100%除去的最小粒径,或称 为临界粒径dpc 。
则某些粒径的尘粒,其沉降速度ut大于或等 于qVs/WL,则能全部分离出来。故与临界粒径 dpc相对应的临界沉降速度为utc=qVs/WL 。
分散相或分散物质→非均相物系中,处于分散状态的物质,如悬浮液
中的固体颗粒、乳浊液中的液滴、泡沫液中的气泡;
连续相或分散介质→包围着分散物质且处于连续状态的流体。 根据连续相状态,非均相物质分为两类: 气态非均相物质:如含尘气体、含雾气体等。 液态非均相物质:如悬浮液、乳浊液等。
(二)非均相混合物的分离方式
注: a、由上式可知,当utc与dpc一定时,qVs与底 面积WL成正比,而与高度H无关。 b、当qVs一定时,dpc及utc与降尘室的底面积 WL成反比,而与高度H无关。
3、降尘室的形状:
由以上分析可知,降尘室的生产能力与其高度H无关, 宜做成扁平形。
若qVs不变,使H缩小1/2,则u变为原来的两倍( qVs
连续式增稠器
絮凝剂
溶胶:液体中所含固体颗粒径大小会有差别,含
化工原理-沉降与过滤

三、过滤过程计算
设计型:确定过滤面积 操作型:计算设备生产能力,或确定操作条件
确定恒压过滤面积:例4-6 已知:w、r、ε、Δp、qe=0、V悬、τ 、ρp 、ρ、
V2+2VVe=KA2τ →V、K、τ → V悬、φ、ε、r、Δp 、μ
第四章
第一节 概述
流体通过颗粒层的流动
均相混合物与非均相混合物 液-固 气-固
1、混合物的分类 两相流动物系 2、固定床
流体通过固定床的流动 3、单元操作的应用 固定床反应器 固体悬浮液的过滤
第二节 颗粒床层的特点
一、单颗粒的特性 (大小、形状、表面积) 球形颗粒 dp —球形颗粒直径 非球形颗粒 de —体积当量直径 Ψ —形状系数(球形度)
固体颗粒的流动输送 (气力输送)。 考察两相物系的相对运动应从流体对颗粒运动的阻力着手。
第二节 颗粒的沉降运动
一、流体对颗粒运动的阻力(曳力) 形体阻力 表面阻力 F d =ζ( πdp2 / 4)ρu2/2
阻力(曳力)
式中阻力系数ζ是颗粒相对于流体运动的Ret的函数(可通过 实验测定),当Ret值在不同的范围时的ζ值: 层流区(斯托克斯区) 10-4< Ret < 2 过渡区(阿仑区) 湍流区(牛顿区) 2< Ret <500 ζ=24/ Ret ζ=18.5/ Ret0.5
沉降速度u t表示
* 因 μ气<μ液
,所以 u t 气体中>> u t 液体中
* 沉降速度的确定:
设一种流型 → u t → Ret → 看Ret是否在所设的流型区内
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沉降速度计算—试差法
四、沉降速度的计算
1、试差法
设Rep选公式 ut核算Rep判断
沉降速度计算—摩擦数群法
2、摩擦数群法
3
沉降速度计算—摩擦数群法
ζ是Ret的已知函数,则 ζRet2 也是Ret的已知函数。
ζ-Ret曲线转化为ζRet2Ret曲线
根据已知值,首先算出 ζRet2的值,再用ζRet2- Ret 曲线查出相应的Ret值,然 后根据Ret的定义式反算 出ut,即:
第二节 沉降过程
沉降速度
沉降速度
颗粒的沉降过程应分为两个阶段,起初为加速阶段,而后为等速 阶段
等速阶段里颗粒相对于流体的运动速度ut称为“沉降速度”, “终端速度”。
阻力系数 ζ
二、阻力系数 ζ
定义:颗粒与流体相对运动时的雷诺数
由Re、фs数,查图得ζ
阻力系数 ζ
阻力系数 ζ
气体在器内的运动情况
离心沉降-7
三、旋风分离器的性能 (分离效果、压强降)
( 一)、临界粒径
旋风分离器中能被完全分离下来的最小颗粒直径。
临界粒径的计算式,可在如下简化条件之下 推导出来。
(1)进入旋风分离器的气流严格按螺旋形路线作等速运动,其 切向速度等于进口气速ui
(2) 颗粒向器壁沉降时,必须穿过厚度等于整个进气口宽度B的 气流层,方能到达壁面 而被分离。
作预除尘器使用。 多层降尘室虽能分离较细小的颗粒并节省地
面但出灰不便。
例3-2
例3-2
重力沉降设备–沉降槽
(二)、沉降槽 (过程)
1、沉降槽的构造与操作 又称增浓器或澄清器
重力沉降设备–沉降槽
浓悬浮液的沉聚过程 (自学) 连续沉降槽的直径,小者数米,大者可达
数百米。小槽可用木料或金属制造,大 槽要用混凝土砌筑。小槽耙的转速约 为1r.p.m.,大槽只有0.1r.p.m.左右。
离心沉降-4
在离心沉降时,如果颗粒与流体的相对运动属于滞 流,阻力系数也符合斯托克斯定律:
同一颗粒在同种介质中的离心沉降速度与重力沉降 速度的比值为
比与值重力Kc场也强就度是之颗比粒,所称在为位离置心上分的离惯因性数离心力场强度
离心沉降设备-旋风分离器
二、 旋风分离器的操作原理
结构
离心沉降设备-旋风分离器
重力沉降设备–分级器
(三)、分级器
重力沉降用于分离不同粒径的同种颗粒和不 同密度的颗粒所用设备称为分级器
例3-3
例3-3
例3-3
3-2-2 离心沉降-1
依靠惯性离心力的作用而实现的沉降过 程叫作离心沉降
一、惯性离心力作用下的沉降速度
离心沉降-2
平衡时颗粒在径向上相对于流体的速度 是它在此位置上的离心沉降速度
离心沉降-3
颗粒的离心沉降速度 ur与重力沉降速度 ut 具有相似的关系式,只是将重力场强度 g 改为惯性离心力场强度 uT²/R
区别:
离心力沉降速度ur 不是颗粒运动的绝对速度,而是 绝对速度在径向上的分量,且方向不是向下而是沿 半径向外;
离心沉降速度ur 本身就不是一个恒定的数值,而重 力沉降速度ut 则是不变的。
例3-1
例3-1
重力沉降设备–降尘室
二、重 力 沉 降设备
(一)、降尘室 (过程)
令 l——降尘室的长度,m ; H ——降尘室的高度,m; b ——降尘室的宽度,m; ut —— 颗粒的沉降速度,m;
u —— 气体在降尘室内水平通过的流速,m/s。
重力沉降设备–降尘室
颗粒沉降至室底所 需的时间为:
重力沉降设备–降尘室
如气体处理量为Vs
降尘室的生产能力只与其 沉降面积bl及颗粒 的沉降速度ut有 关,而与降尘室的高度无关。
重力沉降设备–降尘室
因此, 可将降尘室做成多层, 称为多层降尘室
重力沉降设备–降尘室
多层降尘室的生产能力为
Vs ≤(n+1)blut (n为隔板数)
降尘室特点
降尘室结构简单,阻力小, 但体积庞大,分离效率低, 只适用于分离直径在50μm以上的粗粒,一般
离心沉降-8
(3) 颗粒在滞流情况下作自由沉降,其径向沉降速度可用下式 计算
因ρ<<ρs ,故式中的ρ可以略去;又旋转半径R 可取平均值 Rm,则气流中的离心沉降速度为
离心沉降-9
颗粒到达器壁所需的沉降时间为
令气流的有效旋转圈数为Ne,它在器内 运行的距离便是2πRmNe,则停留时间为
离心沉降-10
若某种尺寸的颗粒所需的沉降时间θt恰 等于停留时间θ,该颗粒就是理论上能 被完全分离下来的最小颗粒。
离心沉降-11
临界粒径随分离器尺寸增大而增大,因此分离 效率随分离器尺寸增大而减小,所以当气体处 理量大时,常将若干个小尺寸的旋风分离器 并联使用(称为旋风分离器组),以维持较高的 除尘效率。
Ne的数值一般为0.5~3.0,但对标准旋 风分离器,可取Ne=5。
离心沉降-12
(二)、分离效率
旋风分离器的分离效率有两种表示法,一是 总效率,以η0代表;一是分效率,又称粒级效 率,以ηp代表。
总效率是指进入旋风分离器的全部颗粒中被 分离下来的质量分率,即:
C1——旋风分离器进口气体含尘浓度, g/m³; C2——旋风分离器出口气体含尘浓度, g/m³
曲线(φs=1.0)所示。该曲线可按Re值大 致分为三个区域,各区内的曲线可分别 用相应的关系式来表达
3
3
沉降速度
斯托克斯(Stokes)公式、艾仑(Allen)公 式及牛顿(Newton)公式
影响沉降速度的因素
三、影响沉降速度的因素
1、体积浓度 干扰沉降
2、器壁效应 3、颗粒形状
同一种固体物质,球形或近球形颗粒 比同体积的非球形颗粒的沉降要快一些 4、颗粒粒径
Goto Figure
沉降速度计算—摩擦数群法
令ζ与Ret-1相乘,得
ρ
3
可得ζRet-1- Ret图
由ζRet-1从图中查得 Ret,
用以根据沉降速度ut计 算
颗粒直径d
沉降速度计算—摩擦数群法
Back 14 Back 15
用K判断流型
将层流时的ut代入Ret,有
当Re<1时,在斯托克斯定律区的上限K值为2.62 当Re>1000,在牛顿定律区的下限K值为69.1 可根据K值选用相应的公式,避免试差法
离心沉降-13
粒级效率
C1i ——进口气体粒径在第i 小段范围内的颗粒的浓度,g/m3 Ci2 —— 出口气体中粒径在第i小段范围内的颗粒的浓度,g/m3
