高三数学一轮复习学案:不等式的解法
高考数学一轮复习统考 第7章 不等式 第4讲 基本不等式学案(含解析)北师大版-北师大版高三全册数学

第4讲 基本不等式基础知识整合1.重要不等式a 2+b 2≥012ab (a ,b ∈R )(当且仅当02a =b 时等号成立).2.基本不等式ab ≤a +b2(1)基本不等式成立的条件:03a >0,b >0;(2)等号成立的条件:当且仅当04a =b 时等号成立; (3)其中a +b2叫做正数a ,b 的05算术平均数,ab 叫做正数a ,b 的06几何平均数.3.利用基本不等式求最大、最小值问题 (1)如果x ,y ∈(0,+∞),且xy =P (定值),那么当07x =y 时,x +y 有08最小值2P .(简记:“积定和最小”) (2)如果x ,y ∈(0,+∞),且x +y =S (定值),那么当09x =y 时,xy 有10最大值S 24.(简记:“和定积最大”)1.常用的几个重要不等式 (1)a +b ≥2ab (a >0,b >0); (2)ab ≤⎝⎛⎭⎪⎫a +b 22(a ,b ∈R );(3)⎝ ⎛⎭⎪⎫a +b 22≤a 2+b 22(a ,b ∈R ); (4)b a +a b≥2(a ,b 同号).以上不等式等号成立的条件均为a =b . 2.利用基本不等式求最值的两个常用结论(1)已知a ,b ,x ,y ∈R +,若ax +by =1,则有1x +1y=(ax +by )·⎝ ⎛⎭⎪⎫1x +1y =a +b +by x +ax y≥a +b +2ab =(a +b )2.(2)已知a ,b ,x ,y ∈R +,若a x +b y=1,则有x +y =(x +y )·⎝ ⎛⎭⎪⎫a x +b y =a +b +ay x +bx y≥a+b +2ab =(a +b )2.1.已知a ,b ∈R +,且a +b =1,则ab 的最大值为( ) A .1 B.14 C.12 D.22答案 B解析 ∵a ,b ∈R +,∴1=a +b ≥2ab ,∴ab ≤14,当且仅当a =b =12时等号成立,即ab的最大值为14.故选B.2.已知a ,b ∈(0,1)且a ≠b ,下列各式中最大的是( ) A .a 2+b 2B .2abC .2abD .a +b答案 D解析 ∵a ,b ∈(0,1)且a ≠b ,则显然有a +b >2ab ,a 2+b 2>2ab .下面比较a 2+b 2与a +b 的大小.由于a ,b ∈(0,1),∴a 2<a ,b 2<b ,∴a 2+b 2<a +b .故各式中最大的是a +b .3.下列函数中,最小值为4的是( ) A .y =x +4xB .y =sin x +4sin x(0<x <π)C .y =4e x+e -xD .y =log 3x +log x 3(0<x <1)答案 C解析 A 中x 的定义域为{x |x ∈R ,且x ≠0},函数没有最小值;B 中若y =sin x +4sin x(0<x <π)取得最小值4,则sin 2x =4,显然不成立;D 中由0<x <1,则log 3x ∈(-∞,0),y =log 3x +log x 3=log 3x +1log 3x 没有最小值;C 中y =4e x +e -x =4e x +1e x ≥4,当且仅当4e x =e -x,即x =-ln 2时,函数的最小值为4.故选C.4.(2019·山西晋城模拟)已知a >0,b >0,a +b =2,则y =1a +4b的最小值是( )A.72 B .4C.92 D .5答案 C解析 y =12(a +b )⎝ ⎛⎭⎪⎫1a +4b =12⎝ ⎛⎭⎪⎫5+4a b +b a ≥92⎝ ⎛⎭⎪⎫当且仅当a =23,b =43时等号成立,即1a +4b 的最小值是92.故选C.5.若x ,y 是正数,则⎝ ⎛⎭⎪⎫x +12y 2+⎝ ⎛⎭⎪⎫y +12x 2的最小值是( ) A .3B.72 C .4 D.92答案 C解析 原式=x 2+x y +14y 2+y 2+y x +14x 2≥4.当且仅当x =y =22时取“=”号,即⎝ ⎛⎭⎪⎫x +12y 2+⎝ ⎛⎭⎪⎫y +12x 2的最小值是4. 6.3-aa +6(-6≤a ≤3)的最大值为________.答案 92解析 当a =-6或a =3时,3-aa +6=0;当-6<a <3时,3-a a +6≤3-a +a +62=92, 当且仅当3-a =a +6,即a =-32时取等号.故3-aa +b (-6≤a ≤3)的最大值为92.核心考向突破精准设计考向,多角度探究突破考向一 利用基本不等式求最值 角度1 利用配凑法求最值例1 (1)已知0<x <1,则x (3-3x )取得最大值时x 的值为( ) A.13 B.12 C.34 D.23答案 B解析 ∵0<x <1,∴x ·(3-3x )=13·3x ·(3-3x )≤13⎝ ⎛⎭⎪⎫3x +3-3x 22=34,当且仅当3x =3-3x ,即x =12时,x (3-3x )取得最大值.故选B.(2)设x >0,则函数y =x +22x +1-32的最小值为________.答案 0解析 y =x +22x +1-32=⎝ ⎛⎭⎪⎫x +12+1x +12-2≥2⎝ ⎛⎭⎪⎫x +12·1x +12-2=0,当且仅当x +12=1x +12,即x =12时等号成立.所以函数的最小值为0.通过拼凑法利用基本不等式求最值的策略拼凑法的实质在于代数式的灵活变形,拼系数、凑常数是关键,利用拼凑法求解最值应注意以下几个方面的问题:(1)拼凑的技巧,以整式为基础,注意利用系数的变化以及等式中常数的调整,做到等价变形.(2)代数式的变形以拼凑出和或积的定值为目标. (3)拆项、添项应注意检验利用基本不等式的前提.[即时训练] 1.设a ,b 均大于0,a +b =5,则a +1+b +3的最大值为________. 答案 3 2解析 ∵(a +1+b +3)2=a +1+b +3+ 2a +1b +3=9+2a +1b +3,又2a +1b +3≤a +1+b +3=9⎝ ⎛⎭⎪⎫当且仅当a +1=b +3,即a =72,b =32时取“=”, ∴(a +1+b +3)2≤18, ∴a +1+b +3的最大值为3 2.角度2 利用常数代换法求最值 例2 (1)(2019·绵阳诊断)若θ∈⎝ ⎛⎭⎪⎫0,π2,则y =1sin 2θ+9cos 2θ的取值范围为( )A .[6,+∞)B .[10,+∞)C .[12,+∞)D .[16,+∞)答案 D解析 ∵θ∈⎝⎛⎭⎪⎫0,π2,∴sin 2θ,cos 2θ∈(0,1),∴y =1sin 2θ+9cos 2θ=⎝ ⎛⎭⎪⎫1sin 2θ+9cos 2θ(sin 2θ+cos 2θ)=10+cos 2θsin 2θ+9sin 2θcos 2θ≥10+2cos 2θsin 2θ·9sin 2θcos 2θ=16,当且仅当cos 2θsin 2θ=9sin 2θcos 2θ,即θ=π6时等号成立.故选D. (2)已知a +2b =2,且a >1,b >0,则2a -1+1b的最小值为( ) A .4 B .5 C .6 D .8答案 D解析 因为a >1,b >0,且a +2b =2,所以a -1>0,(a -1)+2b =1,所以2a -1+1b=⎝ ⎛⎭⎪⎫2a -1+1b ·[(a -1)+2b ]=4+4b a -1+a -1b ≥4+24b a -1·a -1b =8,当且仅当4b a -1=a -1b,即a =32,b =14时取等号,所以2a -1+1b的最小值是8,故选D.常数代换法求最值的步骤常数代换法适用于求解条件最值问题.运用此种方法求解最值的基本步骤为: (1)根据已知条件或其变形确定定值(常数). (2)把确定的定值(常数)变形为1.(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积的形式. (4)利用基本不等式求解最值.[即时训练] 2.(2020·正定模拟)若正数x ,y 满足x +3y =5xy ,则3x +4y 的最小值是________.答案 5解析 由x +3y =5xy ,可得15y +35x=1, 所以3x +4y =(3x +4y )⎝ ⎛⎭⎪⎫15y +35x =95+45+3x 5y +12y 5x ≥135+2 3x 5y ·12y 5x =135+125=5,当且仅当x =1,y =12时取等号,故3x +4y 的最小值是5.角度3 利用消元法求最值例3 (1)(2019·江西上饶联考)已知正数a ,b ,c 满足2a -b +c =0,则acb2的最大值为( )A .8B .2 C.18 D.16答案 C解析 因为a ,b ,c 都是正数,且满足2a -b +c =0,所以b =2a +c ,所以ac b 2=ac 2a +c2=ac 4a 2+4ac +c 2=14a c +ca+4≤124a c ·ca+4=18,当且仅当c =2a >0时等号成立,即acb 2的最大值为18.故选C.(2)已知x >54,则函数y =16x 2-28x +114x -5的最小值为________.答案 5解析 令4x -5=t ,则x =t +54(t >0),∴y =t 2+3t +1t =t +1t +3(t >0),又t +1t≥2(当且仅当t =1时,取“=”),∴y 的最小值为5.通过消元法利用基本不等式求最值的方法消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解.有时会出现多元的问题,解决方法是消元后利用基本不等式求解.[即时训练] 3.(2019·安徽阜阳模拟)若直线x a +yb=1(a >0,b >0)过点(1,1),则a +b +3ba的最小值为________. 答案 6解析 因为直线x a +y b =1(a >0,b >0)过点(1,1),所以1a +1b =1,所以b =aa -1>0,所以a >1,所以a +b +3b a =(a -1)+4a -1+2≥4+2=6,当且仅当a =3时等号成立,所以a +b +3ba 的最小值是6.考向二 求参数值或取值范围例4 (1)(2019·山西长治模拟)已知不等式(x +y )·⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则正实数a 的最小值为( )A .2B .4C .6D .8答案 B解析 (x +y )⎝ ⎛⎭⎪⎫1x +a y =1+a ·x y +y x +a ≥1+a +2a =(a +1)2,当且仅当a ·x y =y x,即ax 2=y 2时“=”成立.∵(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,∴(a +1)2≥9.∴a ≥4,即正实数a 的最小值为4.故选B.(2)当0<m <12时,若1m +21-2m ≥k 2-2k 恒成立,则实数k 的取值范围是( )A .[-2,0)∪(0,4]B .[-4,0)∪(0,2]C .[-4,2]D .[-2,4]答案 D解析 因为0<m <12,所以m (1-2m )=12×2m ×(1-2m )≤12×⎣⎢⎡⎦⎥⎤2m +1-2m 22=18⎝ ⎛⎭⎪⎫当且仅当2m =1-2m ,即m =14时取等号,所以1m +21-2m =1m 1-2m ≥8.又1m +21-2m ≥k 2-2k 恒成立,所以k 2-2k -8≤0,所以-2≤k ≤4.所以实数k 的取值范围是[-2,4].故选D.(1)要敏锐地洞察到已知条件与所求式子的联系,并能灵活地进行转化. (2)利用基本不等式确立相关成立条件,从而得到参数的值或取值范围.[即时训练] 4.设a >0,b >0且不等式1a +1b +ka +b ≥0恒成立,则实数k 的最小值等于( )A .0B .4C .-4D .-2答案 C解析 由1a +1b +ka +b≥0得k ≥-a +b 2ab,又a +b 2ab=a b +b a+2≥4(当且仅当a =b 时取等号),所以-a +b2ab≤-4,因此要使k ≥-a +b2ab恒成立,应有k ≥-4,即实数k 的最小值等于-4.故选C.5.(2019·珠海模拟)已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为( ) A .2 B .4 C .6 D .8答案 C解析 解法一:由已知得xy =9-(x +3y ),即3xy =27-3(x +3y )≤⎝⎛⎭⎪⎫x +3y 22,当且仅当x =3y ,即x =3,y =1时取等号,令x +3y =t ,则t >0,且t 2+12t -108≥0,解得t ≥6,即x +3y ≥6.故x +3y 的最小值为6.解法二:∵x +3y =9-xy ≥23xy ,∴(xy )2+23·xy -9≤0,∴(xy +33)(xy -3)≤0,∴0<xy ≤3,∴x +3y =9-xy ≥6,即x +3y 的最小值为6.故选C. 考向三 基本不等式的实际应用例5 (2019·辽宁沈阳质检)某工厂某种产品的年固定成本为250万元,每生产x 千件,需另投入成本为C (x )(万元),当年产量不足80千件时,C (x )=13x 2+10x ;当年产量不小于80千件时,C (x )=51x +10000x-1450.每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L (x )(万元)关于年产量x (千件)的函数解析式; (2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?解 (1)因为每件商品售价为0.05万元,则x 千件商品的销售额为0.05×1000x 万元,依题意得,当0<x <80时,L (x )=(0.05×1000x )-⎝ ⎛⎭⎪⎫13x 2+10x -250=-13x 2+40x -250;当x ≥80时,L (x )=(0.05×1000x )-⎝⎛⎭⎪⎫51x +10000x-1450-250=1200-⎝ ⎛⎭⎪⎫x +10000x . 所以L (x )=⎩⎪⎨⎪⎧-13x 2+40x -250,0<x <80,1200-⎝ ⎛⎭⎪⎫x +10000x ,x ≥80.(2)当0<x <80时,L (x )=-13(x -60)2+950.则当x =60时,L (x )取得最大值L (60)=950万元;当x ≥80时,L (x )=1200-⎝⎛⎭⎪⎫x +10000x ≤1200-2x ·10000x=1200-200=1000⎝⎛⎭⎪⎫当且仅当x =10000x,即x =100时取等号,则当x =100时,L (x )取得最大值1000万元.由于950<1000,所以,当年产量为100千件时,该厂在这一商品的生产中所获利润最大,最大利润为1000万元.有关函数最值的实际问题的解题技巧(1)根据实际问题建立函数的解析式,再利用基本不等式求得函数的最值. (2)设变量时一般要把求最大值或最小值的变量定义为函数. (3)解应用题时,一定要注意变量的实际意义及其取值范围.(4)在应用基本不等式求函数最值时,若等号取不到,可利用函数的单调性求解.[即时训练] 6.某厂家拟在2020年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x 万件与年促销费用m 万元(m ≥0)满足x =3-km +1(k 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2020年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2020年该产品的利润y 万元表示为年促销费用m 万元的函数; (2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大? 解 (1)由题意知,当m =0时,x =1, ∴1=3-k ⇒k =2,∴x =3-2m +1, 每件产品的销售价格为1.5×8+16xx(元),∴2020年的利润y =1.5x ×8+16xx-8-16x -m=4+8x -m =4+8⎝ ⎛⎭⎪⎫3-2m +1-m =-⎣⎢⎡⎦⎥⎤16m +1+m +1+29(m ≥0). (2)∵当m ≥0时,16m +1+(m +1)≥216=8, ∴y ≤-8+29=21,当且仅当16m +1=m +1⇒m =3(万元)时,y max =21(万元). 故该厂家2020年的促销费用投入3万元时,厂家的利润最大为21万元.若a ,b ∈R ,ab >0,则a 4+4b 4+1ab的最小值为________. 答案 4解析 ∵a 4+4b 4≥2a 2·2b 2=4a 2b 2(当且仅当a 2=2b 2时“=”成立), ∴a 4+4b 4+1ab ≥4a 2b 2+1ab =4ab +1ab, 由于ab >0,∴4ab +1ab ≥24ab ·1ab=4 ⎝ ⎛⎭⎪⎫当且仅当4ab =1ab 时“=”成立, 故当且仅当⎩⎪⎨⎪⎧ a 2=2b 2,4ab =1ab 时,a 4+4b 4+1ab的最小值为4. 答题启示利用基本不等式求函数或代数式的最值时一定要注意验证等号是否成立,特别是当连续多次使用基本不等式时,一定要注意每次是否能保证等号成立,并且注意取等号的条件的一致性,因此在利用基本不等式处理问题时,列出等号成立的条件不仅是解题的必要步骤,也是检验转换是否有误的一种方法.对点训练已知a >b >0,求a 2+16b a -b的最小值. 解 ∵a >b >0,∴a -b >0.∴b (a -b )≤⎣⎢⎡⎦⎥⎤b +a -b 22=a 24. ∴a 2+16ba -b ≥a 2+64a 2≥2a 2·64a 2=16. 当a 2=64a 2且b =a -b ,即a =22,b =2时等号成立. ∴a 2+16b a -b 的最小值为16.。
高考数学含绝对值的不等式的解法

三 灵与肉
我站在镜子前,盯视着我的面孔和身体,不禁惶惑起来。我不知道究竟盯视者是我,还是被 盯视者是我。灵
魂和肉体如此不同,一旦相遇,彼此都觉陌生。我的耳边响起帕斯卡尔的话 语:肉体不可思议,灵魂更不可思议,最不可思议的是肉体居然能和灵魂结合在一起。 人有一个肉体似乎是一件尴尬事。那个丧子的母亲终于停止哭泣,端起饭碗,因为她饿了。 那个含情脉脉的姑娘不得不离
您一定愿意静静地听这个生命说:'我愿意静静地听您说话…… '我从不愿把您想像成一个思想家或散文家,您不会为此生气吧。 "也许再过好多年之后,我已经老了,那时候,我相信为了年轻时读过的您的那些话语,我 要用心说一声:谢谢您!" 信尾没有落款,只有这一行字:"生
命本来没有名字吧,我是,你是。"我这才想到查看信 封,发现那上面也没有寄信人的地址,作为替代的是"时光村落"四个字。我注意了邮戳, 寄自河北怀来。
高三第一轮复习
含绝对值不等式的解法
1、绝对值的意义: 其几何意义是数轴的点A(a)离开原点的距离
OA a
a, a 0
a
0,
a
0
a, a 0
2、含有绝对值不等式的解法: (解绝对值不等式的关键在于去掉绝对值的符号)
(1)定义法; (2)零点分段法:通常适用于含有两个及两个以上的绝
卡尔的话:肉体是奇妙的,灵魂更奇妙,最奇妙的是肉体居然能和灵魂 结合在一起。
四 动与静
喧哗的白昼过去了,世界重归于宁静。我坐在灯下,感到一种独处的满足。 我承认,我需要到世界上去活动,我喜欢旅行、冒险、恋爱、奋斗、成功、失败。日子过得
平平淡淡,我会无聊,过得冷冷清清,我会寂寞。但是,我更需要宁静的独处,更喜欢过一 种沉思的生活。总是活得轰轰烈烈热热闹闹,没有时间和自己待一会儿,我就会非常不安, 好像丢了魂一样。 我身上必定有两个自我。一个好动,什么都要尝试,什么都想经历。另一个喜静,
高三数学第一轮复习教案(学生版)
题型1:比较大小
例1.设 ,试比较A=1+a2与B= 的大小。
变式训练:(2010西城二模)若 ,则下列不等式中正确的是( )
A. B. C. D.
题型2:取值范围
题型2:确定取值范围
例2.若 满足 ,求 的取值范围
解:
变式训练:已知-1<a+b<3且2<a-b<4,求2a+3b的取值范围.
一、知识梳理:
1.两实数大小的比较原理:
(差值比较原理)
(1)a-b>0 a>b;
(2)a-b=0 a=b;
(3)a-b<0 a<b.
特别提示(1)在实际问题中a,b可以是含未知数的代数式;
(2)提供了比较两个实数(代数式)大小的方法,也是利用比较法证明不等式的原理。
2.不等式的基本性质:
(1)a>b ________b<a.
推论:a>b>0 ________________- > (n∈N,n>1);
推论:a>b>0 _____________________-an>bn(n∈N,n>1).
(5)a>b,ab>0 _____________ < ,
特别提示:(1)性质5不能弱化条件得a>b < ;
(2)不等式的性质从形式上可分两类:一类是“ ”型;另一类是“ ”型.要注意二者的区别.
⑤若a>b,c>d能否能判定a-c>b-d?
⑥若a>b,c>d,cd≠0是否有
⑦若a>b,c>d是否有a-c>b-d?
⑧若a>b>0,d>c>0是否有
⑨若a>b,ab<0,是否有
⑩若a<b<0是否有(a)a3<b3;(b)a2>b2.
高考一轮复习理科数学课件绝对值不等式的解法及其应用

知识点梳理和归纳总结
01
绝对值不等式的定义 和性质
明确绝对值不等式的概念,掌握其基 本性质,如正数的绝对值是其本身, 负数的绝对值是它的相反数,0的绝 对值是0。
02
绝对值不等式的解法
熟练掌握绝对值不等式的解法,包括 分段讨论法、平方法、几何意义法等 ,能够根据不同的题型选择合适的解 法。
03
绝对值不等式的应用
了解绝对值不等式在解决实际问题中 的应用,如求解最值问题、证明不等 式等。
针对性地进行专项训练和模拟考试
专项训练
针对绝对值不等式的各类题型进行专 项训练,如含参绝对值不等式、绝对 值三角不等式等,提高解题速度和准 确率。
模拟考试
定期进行模拟考试,模拟真实考试环 境,检验自己的备考效果,查漏补缺 。
其他相关定理和性质介绍
绝对值的非负性
对于任意实数x,都有|x|≥0,且 |x|=0当且仅当x=0。
绝对值的单调性
对于任意实数x、y,若x≤y,则 |x|≤|y|。但反之不成立,即若|x|≤|y|
,不能推出x≤y。
绝对值的几何意义
在数轴上,一个数到原点的距离叫 做该数的绝对值。因此,绝对值与 距离、长度等几何概念密切相关。
绝对值不等式分类
03
根据不等号方向分类
可分为严格不等式(如$|x|<a$)和非严 格不等式(如$|x|leq a$)。
根据涉及绝对值个数分类
可分为单一绝对值不等式(如$|x-1|<2$ )和多个绝对值不等式(如$|x1|+|x+2|geq 3$)。
根据解法不同分类
可分为可直接去绝对值符号求解的不等式 和需要讨论绝对值内部表达式正负情况求 解的不等式。
高考数学一轮复习 第7章 不等式 2 第2讲 一元二次不等式及其解法教案 理-高三全册数学教案
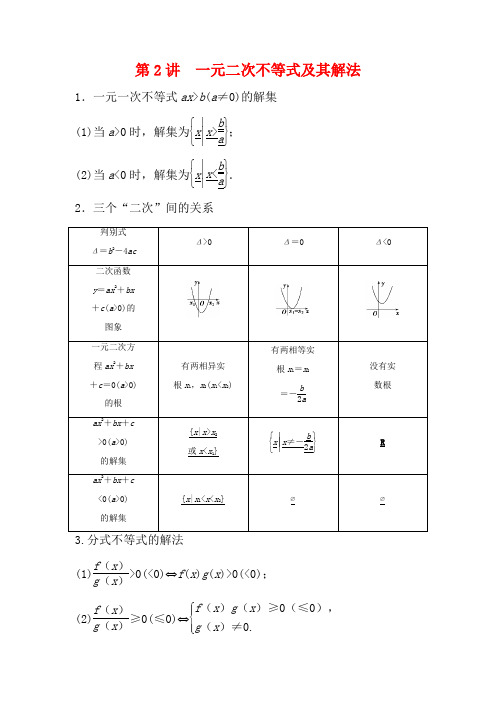
第2讲 一元二次不等式及其解法1.一元一次不等式ax >b (a ≠0)的解集 (1)当a >0时,解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x >b a ;(2)当a <0时,解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <b a .2.三个“二次”间的关系判别式Δ=b 2-4acΔ>0 Δ=0 Δ<0二次函数y =ax 2+bx+c (a >0)的 图象一元二次方 程ax 2+bx +c =0(a >0)的根有两相异实 根x 1,x 2(x 1<x 2)有两相等实根x 1=x 2=-b 2a没有实 数根ax 2+bx +c>0(a >0)的解集{x |x >x 2或x <x 1}⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠-b 2aRax 2+bx +c<0(a >0) 的解集{x |x 1<x <x 2}∅∅(1)f (x )g (x )>0(<0)⇔f (x )g (x )>0(<0);(2)f (x )g (x )≥0(≤0)⇔⎩⎪⎨⎪⎧f (x )g (x )≥0(≤0),g (x )≠0.4.绝对值不等式的解法(1)|f (x )|>|g (x )|⇔[f (x )]2>[g (x )]2;(2)|f (x )|>g (x )⇔f (x )>g (x )或f (x )<-g (x ); (3)|f (x )|<g (x )⇔-g (x )<f (x )<g (x ).判断正误(正确的打“√”,错误的打“×”)(1)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( ) (2)若不等式ax 2+bx +c >0的解集是(-∞,x 1)∪(x 2,+∞),则方程ax 2+bx +c =0的两个根是x 1和x 2.( )(3)若方程ax 2+bx +c =0(a ≠0)没有实数根,则不等式ax 2+bx +c >0的解集为R .( )(4)不等式ax 2+bx +c ≤0在R 上恒成立的条件是a <0且Δ=b 2-4ac ≤0.( )(5)若二次函数y =ax 2+bx +c 的图象开口向下,则不等式ax 2+bx +c <0的解集一定不是空集.( )答案:(1)√ (2)√ (3)× (4)× (5)√(教材习题改编)不等式2x 2-x -3>0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-1<x <32B.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >32或x <-1 C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-32<x <1 D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1或x <-32解析:选B.2x 2-x -3>0⇒(x +1)(2x -3)>0, 解得x >32或x <-1.所以不等式2x 2-x -3>0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >32或x <-1. 不等式x -12x +1≤0的解集为( )A.⎝ ⎛⎦⎥⎤-12,1B.⎣⎢⎡⎦⎥⎤-12,1 C.⎝ ⎛⎭⎪⎫-∞,-12∪[1,+∞)D.⎝⎛⎦⎥⎤-∞,-12∪[1,+∞)解析:选A.由不等式x -12x +1≤0,可得⎩⎪⎨⎪⎧(x -1)(2x +1)≤0,2x +1≠0,解得-12<x ≤1,所以不等式的解集为⎝ ⎛⎦⎥⎤-12,1.设二次不等式ax2+bx +1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-1<x <13,则ab 的值为________. 解析:由不等式ax2+bx +1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-1<x <13,知a <0且ax2+bx +1=0的两根为x 1=-1,x 2=13,由根与系数的关系知⎩⎪⎨⎪⎧-1+13=-b a,-13=1a ,所以a =-3,b =-2,ab =6. 答案:6若不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是__________.解析:因为不等式x 2+ax +4<0的解集不是空集, 所以Δ=a 2-4×4>0,即a 2>16. 所以a >4或a <-4.答案:(-∞,-4)∪(4,+∞)一元二次不等式的解法(高频考点)一元二次不等式的解法是高考的常考内容,题型多为选择题或填空题,难度为中档题.高考对一元二次不等式解法的考查主要有以下三个命题角度:(1)解不含参数的一元二次不等式; (2)解含参数的一元二次不等式;(3)已知一元二次不等式的解集求参数.[典例引领]角度一 解不含参数的一元二次不等式(1)解不等式:-x 2-2x +3≥0;(2)已知函数f (x )=⎩⎪⎨⎪⎧x 2+2x ,x ≥0,-x 2+2x ,x <0,解不等式f (x )>3.【解】 (1)不等式两边同乘以-1,原不等式可化为x 2+2x -3≤0.方程x 2+2x -3=0的解为x 1=-3,x 2=1.而y =x 2+2x -3的图象开口向上,可得原不等式-x 2-2x +3≥0的解集是{x |-3≤x ≤1}.(2)由题意⎩⎪⎨⎪⎧x ≥0,x 2+2x >3或⎩⎪⎨⎪⎧x <0,-x 2+2x >3,解得x >1.故原不等式的解集为{x |x >1}.角度二 解含参数的一元二次不等式(分类讨论思想)解关于x 的不等式:12x 2-ax >a 2(a ∈R ).【解】 因为12x 2-ax >a 2,所以12x 2-ax -a 2>0,即(4x +a )(3x -a )>0. 令(4x +a )(3x -a )=0,解得x 1=-a 4,x 2=a3.①当a >0时,-a 4<a3,解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-a 4,或x >a 3;②当a =0时,x 2>0,解集为{x |x ∈R ,且x ≠0};③当a <0时,-a 4>a3,解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <a 3,或x >-a 4.综上所述:当a >0时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-a 4,或x >a 3;当a =0时,不等式的解集为{x |x ∈R ,且x ≠0};当a <0时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <a 3,或x >-a 4.角度三 已知一元二次不等式的解集求参数已知不等式ax 2-bx -1>0的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-12<x <-13,则不等式x 2-bx -a ≥0的解集是________.【解析】 由题意,知-12,-13是方程ax 2-bx -1=0的两个根,且a <0,所以⎩⎪⎨⎪⎧-12+⎝ ⎛⎭⎪⎫-13=b a,-12×⎝ ⎛⎭⎪⎫-13=-1a ,解得⎩⎪⎨⎪⎧a =-6,b =5.即不等式x 2-bx -a ≥0为x 2-5x +6≥0, 解得x ≥3或x ≤2.【答案】 {x |x ≥3或x ≤2}(1)解一元二次不等式的方法和步骤 (2)解含参数的一元二次不等式的步骤①二次项若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为二次项系数为正的形式.②判断相应方程的根的个数,讨论判别式Δ与0的关系. ③确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式.[通关练习]1.(2018·陕西西安模拟)若集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x x -1≤0,B ={x |x 2<2x },则A ∩B =( ) A .{x |0<x <1} B .{x |0≤x <1} C .{x |0<x ≤1} D .{x |0≤x ≤1}解析:选A.因为A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x x -1≤0={x |0≤x <1}, B ={x |x 2<2x }={x |0<x <2},所以A ∩B ={x |0<x <1},故选A.2.(2018·广东清远一中模拟)关于x 的不等式ax -b <0的解集是(1,+∞),则关于x 的不等式(ax +b )(x -3)>0的解集是( ) A .(-∞,-1)∪(3,+∞) B .(1,3)C .(-1,3)D .(-∞,1)∪(3,+∞)解析:选C.关于x 的不等式ax -b <0的解集是(1,+∞),即不等式ax <b 的解集是(1,+∞),所以a =b <0,所以不等式(ax +b )(x -3)>0可化为(x +1)(x -3)<0,解得-1<x <3,所以所求解集是(-1,3).故选C.3.不等式0<x 2-x -2≤4的解集为________.解析:原不等式等价于⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -2≤4,即⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -6≤0,即⎩⎪⎨⎪⎧(x -2)(x +1)>0,(x -3)(x +2)≤0,解得⎩⎪⎨⎪⎧x >2或x <-1,-2≤x ≤3.借助于数轴,如图所示,原不等式的解集为{x |-2≤x <-1或2<x ≤3}. 答案:[-2,-1)∪(2,3]一元二次不等式恒成立问题(高频考点)一元二次不等式恒成立问题是每年高考的热点,题型多为选择题和填空题,难度为中档题.高考对一元二次不等式恒成立问题的考查有以下三个命题角度:(1)形如f (x )≥0(f (x )≤0)(x ∈R )确定参数的范围; (2)形如f (x )≥0(f (x )≤0)(x ∈[a ,b ])确定参数的范围; (3)形如f (x )≥0(f (x )≤0)(参数m ∈[a ,b ])确定x 的范围.[典例引领]角度一 形如f (x )≥0(f (x )≤0)(x ∈R )确定 参数的范围若不等式(a -2)x 2+2(a -2)x -4<0对一切x ∈R 恒成立,则实数a 的取值范围是________.【解析】 当a -2=0,即a =2时不等式为-4<0, 对一切x ∈R 恒成立.当a ≠2时,则⎩⎪⎨⎪⎧a -2<0,Δ=4(a -2)2+16(a -2)<0,即⎩⎪⎨⎪⎧a <2-2<a <2,解得-2<a <2. 所以实数a 的取值范围是(-2,2]. 【答案】 (-2,2]角度二 形如f (x )≥0(f (x )≤0)(x ∈[a ,b ])确定参数的范围(转化与化归思想)若不等式x 2+mx -1<0对于任意x ∈[m ,m +1]都成立,则实数m 的取值范围是________.【解析】 由题意,得函数f (x )=x 2+mx -1在[m ,m +1]上的最大值小于0,又抛物线f (x )=x 2+mx -1开口向上,所以只需⎩⎪⎨⎪⎧f (m )=m 2+m 2-1<0,f (m +1)=(m +1)2+m (m +1)-1<0, 即⎩⎪⎨⎪⎧2m 2-1<0,2m 2+3m <0, 解得-22<m <0.【答案】⎝⎛⎭⎪⎪⎫-22,0 角度三 形如f (x )≥0(f (x )≤0)(参数m ∈[a ,b ])确定x 的范围求使不等式x 2+(a -6)x +9-3a >0,|a |≤1恒成立的x 的取值范围.【解】 将原不等式整理为形式上是关于a 的不等式(x -3)a +x 2-6x +9>0.令f (a )=(x -3)a +x 2-6x +9,则-1≤a ≤1. 因为f (a )>0在|a |≤1时恒成立,所以(1)若x =3,则f (a )=0,不符合题意,应舍去. (2)若x ≠3,则由一次函数的单调性,可得⎩⎪⎨⎪⎧f (-1)>0,f (1)>0,即⎩⎪⎨⎪⎧x 2-7x +12>0,x 2-5x +6>0,解得x <2或x >4.则实数x 的取值范围为(-∞,2)∪(4,+∞).(1)不等式恒成立问题的求解方法①一元二次不等式在R 上恒成立确定参数的范围时,结合一元二次方程,利用判别式来求解.②一元二次不等式f (x )≥0在x ∈[a ,b ]上恒成立确定参数范围时,要根据函数的单调性,求其最小值,让最小值大于等于0,从而求参数的范围.③一元二次不等式对于参数m ∈[a ,b ]恒成立确定x 的范围,要注意变换主元,一般地,知道谁的范围,就选谁当主元,求谁的范围,谁就是参数.(2)求解不等式恒成立问题的数学思想求解此类问题常利用分类讨论思想及转化与化归思想,如例22是不等式与函数的转化,例23是主元与次元的转化,而例21是对二次项系数是否为0进行讨论.[通关练习]1.若函数y =mx 2-(1-m )x +m 的定义域为R ,则m 的取值范围是________.解析:要使y =mx 2-(1-m )x +m 有意义,即mx 2-(1-m )x +m ≥0对∀x ∈R 恒成立,则⎩⎪⎨⎪⎧m >0,(1-m )2-4m 2≤0,解得m ≥13.答案:m ≥132.若关于x 的不等式4x-2x +1-a ≥0在[1,2]上恒成立,则实数a的取值范围为________. 解析:因为不等式4x-2x +1-a ≥0在[1,2]上恒成立,所以4x-2x +1≥a 在[1,2]上恒成立.令y =4x -2x +1=(2x )2-2×2x+1-1=(2x-1)2-1.因为1≤x ≤2,所以2≤2x≤4.由二次函数的性质可知:当2x=2,即x =1时,y 取得最小值0, 所以实数a 的取值范围为(-∞,0]. 答案:(-∞,0]解分式不等式的关键是先将给定不等式移项,通分,整理成一边为商式,另一边为0的形式,再通过等价转化化成整式不等式(组)的形式进行求解.对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x 轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x 轴下方.另外常转化为求二次函数的最值或用分离参数法求最值. 易错防范(1)对于不等式ax 2+bx +c >0,求解时不要忘记讨论a =0时的情形.(2)当Δ<0时,ax 2+bx +c >0(a ≠0)的解集是R 还是∅,要注意区别.(3)不同参数范围的解集切莫取并集,应分类表述. 1.设集合A ={x |x 2+x -6≤0},集合B 为函数y =1x -1的定义域,则A ∩B 等于( ) A .(1,2) B .[1,2] C .[1,2)D .(1,2]解析:选D.A ={x |x 2+x -6≤0}={x |-3≤x ≤2},由x -1>0得x >1,即B ={x |x >1},所以A ∩B ={x |1<x ≤2}.2.若不等式ax 2+bx +2<0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-12,或x >13,则a -ba 的值为( ) A.56 B.16 C .-16D .-56解析:选A.由题意得ax 2+bx +2=0的两根为-12与13,所以-ba=-12+13=-16,则a -b a =1-b a =1-16=56. 3.不等式x -43-2x<0的解集是( )A .{x |x <4}B .{x |3<x <4}C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32或x >4 D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪32<x <4 解析:选C.不等式x -43-2x <0等价于⎝ ⎛⎭⎪⎫x -32(x -4)>0,所以不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32或x >4.4.若不等式x 2-2x +5≥a 2-3a 对任意实数x 恒成立,则实数a 的取值范围为( ) A .[-1,4]B .(-∞,-2]∪[5,+∞)C .(-∞,-1]∪[4,+∞)D .[-2,5]解析:选A.x 2-2x +5=(x -1)2+4的最小值为4,所以x 2-2x +5≥a 2-3a 对任意实数x 恒成立, 只需a 2-3a ≤4即可,解得-1≤a ≤4.5.(2018·福建龙岩模拟)已知函数f (x )=(ax -1)(x +b ),若不等式f (x )>0的解集是(-1,3),则不等式f (-2x )<0的解集是( )A.⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫12,+∞B.⎝ ⎛⎭⎪⎫-32,12 C.⎝ ⎛⎭⎪⎫-∞,-12∪⎝ ⎛⎭⎪⎫32,+∞D.⎝ ⎛⎭⎪⎫-12,32 解析:选A.不等式f (x )>0的解集是(-1,3),故f (x )<0的解集是{x |x <-1或x >3},故f (-2x )<0的解集为{x |-2x <-1或-2x >3},即⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-32或x >12.6.不等式|x (x -2)|>x (x -2)的解集是________.解析:不等式|x (x -2)|>x (x -2)的解集即x (x -2)<0的解集,解得0<x <2.答案:{x |0<x <2}7.函数y =lg (1-x )-2x 2+12x +32的定义域为________. 解析:由题意,得⎩⎪⎨⎪⎧-2x 2+12x +32>0,1-x >0,即⎩⎪⎨⎪⎧x 2-6x -16<0,1-x >0,解得-2<x <1, 即原函数的定义域为{x |-2<x <1}.答案:(-2,1)8.(2018·江西南昌模拟)在R 上定义运算:x *y =x (1-y ).若不等式(x -y )*(x +y )<1对一切实数x 恒成立,则实数y 的取值范围是________.解析:由题意,知(x -y )*(x +y )=(x -y )·[1-(x +y )]<1对一切实数x 恒成立,所以-x 2+x +y 2-y -1<0对于x ∈R 恒成立.故Δ=12-4×(-1)×(y 2-y -1)<0,所以4y 2-4y -3<0,解得-12<y <32.答案:⎝ ⎛⎭⎪⎫-12,329.若不等式ax 2+5x -2>0的解集是⎩⎨⎧x ⎪⎪⎪⎭⎬⎫12<x <2.(1)求实数a 的值;(2)求不等式ax 2-5x +a 2-1>0的解集.解:(1)由题意知a <0,且方程ax 2+5x -2=0的两个根为12,2,代入解得a =-2.(2)由(1)知不等式为-2x 2-5x +3>0, 即2x 2+5x -3<0,解得-3<x <12,即不等式ax 2-5x +a 2-1>0的解集为⎝⎛⎭⎪⎫-3,12.10.(2018·合肥市第二次教学质量检测)已知函数f (x )=4-|ax -2|(a ≠0). (1)求函数f (x )的定义域;(2)若当x ∈[0,1]时,不等式f (x )≥1恒成立,求实数a 的取值范围.解:(1)要使函数有意义,需4-|ax -2|≥0,即|ax -2|≤4,|ax -2|≤4⇔-4≤ax -2≤4⇔-2≤ax ≤6. 当a >0时,函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-2a≤x ≤6a ;当a <0时,函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪6a≤x ≤-2a .(2)f (x )≥1⇔|ax -2|≤3,记g (x )=|ax -2|,因为x ∈[0,1],所以需且只需⎩⎪⎨⎪⎧g (0)≤3g (1)≤3⇔⎩⎪⎨⎪⎧2≤3|a -2|≤3⇔-1≤a ≤5,又a ≠0,所以-1≤a ≤5且a ≠0.1.已知函数f (x )=-x 2+ax +b 2-b +1(a ∈R ,b ∈R ),对任意实数x 都有f (1-x )=f (1+x )成立,若当x ∈[-1,1]时,f (x )>0恒成立,则b 的取值范围是( ) A .(-1,0) B .(2,+∞)C .(-∞,-1)∪(2,+∞)D .不能确定解析:选C.由f (1-x )=f (1+x )知f (x )的图象关于直线x =1对称,即a2=1,解得a =2.又因为f (x )开口向下,所以当x ∈[-1,1]时,f (x )为增函数,所以f (x )min =f (-1)=-1-2+b 2-b +1=b 2-b -2,f (x )>0恒成立,即b 2-b -2>0恒成立,解得b <-1或b >2.2.(2018·陕西咸阳模拟)已知a ∈Z ,关于x 的一元二次不等式x2-6x +a ≤0的解集中有且仅有3个整数,则所有符合条件的a 的值之和是( ) A .13 B .18 C .21D .26解析:选C.设f (x )=x 2-6x +a ,其图象为开口向上,对称轴是x =3的抛物线,如图所示.若关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则⎩⎪⎨⎪⎧f (2)≤0,f (1)>0,即⎩⎪⎨⎪⎧22-6×2+a ≤0,12-6×1+a >0,解得5<a ≤8,又a ∈Z ,故a =6,7,8.则所有符合条件的a 的值之和是6+7+8=21.3.对于实数x ,当且仅当n ≤x <n +1(n ∈N *)时,[x ]=n ,则关于x 的不等式4[x ]2-36[x ]+45<0的解集为________.解析:由4[x ]2-36[x ]+45<0,得32<[x ]<152,又当且仅当n ≤x <n+1(n ∈N *)时,[x ]=n ,所以[x ]=2,3,4,5,6,7,所以所求不等式的解集为[2,8). 答案:[2,8)4.不等式x 2+8y 2≥λy (x +y )对于任意的x ,y ∈R 恒成立,则实数λ的取值范围为________.解析:因为x 2+8y 2≥λy (x +y )对于任意的x ,y ∈R 恒成立, 所以x 2+8y 2-λy (x +y )≥0对于任意的x ,y ∈R 恒成立,即x 2-λyx +(8-λ)y 2≥0恒成立,由二次不等式的性质可得,Δ=λ2y 2+4(λ-8)y 2=y 2(λ2+4λ-32)≤0,所以(λ+8)(λ-4)≤0, 解得-8≤λ≤4. 答案:[-8,4]5.某商品每件成本价为80元,售价为100元,每天售出100件.若售价降低x 成(1成=10%),售出商品数量就增加85x 成.要求售价不能低于成本价.(1)设该商店一天的营业额为y ,试求y 与x 之间的函数关系式y =f (x ),并写出定义域;(2)若要求该商品一天营业额至少为10 260元,求x 的取值范围.解:(1)由题意得y =100⎝ ⎛⎭⎪⎫1-x 10·100⎝⎛⎭⎪⎫1+850x .因为售价不能低于成本价,所以100⎝⎛⎭⎪⎫1-x 10-80≥0,得x ≤2.所以y =f (x )=20(10-x )(50+8x ),定义域为[0,2].(2)由题意得20(10-x )(50+8x )≥10 260,化简得8x 2-30x +13≤0.解得12≤x ≤134.所以x 的取值范围是⎣⎢⎡⎦⎥⎤12,2.6.设二次函数f (x )=ax 2+bx +c ,函数F (x )=f (x )-x 的两个零点为m ,n (m <n ).(1)若m =-1,n =2,求不等式F (x )>0的解集; (2)若a >0,且0<x <m <n <1a,比较f (x )与m 的大小.解:(1)由题意知,F (x )=f (x )-x =a (x -m )·(x -n ), 当m =-1,n =2时,不等式F (x )>0, 即a (x +1)(x -2)>0.当a >0时,不等式F (x )>0的解集为{x |x <-1,或x >2}; 当a <0时,不等式F (x )>0的解集为{x |-1<x <2}. (2)f (x )-m =a (x -m )(x -n )+x -m =(x -m )(ax -an +1), 因为a >0,且0<x <m <n <1a,所以x -m <0,1-an +ax >0. 所以f (x )-m <0,即f (x )<m .。
高考数学一轮总复习练习不等式的解法 (2)

1.(2019·台州质检)已知关于x 的不等式ax 2-x +c <0的解集为{}x |-1<x <2,则a +c 等于( ) A .-1 B .1 C .-3 D .32.已知函数f (x )=⎝⎛⎭⎫12x,则不等式f (a 2-4)>f (3a )的解集为( ) A .(-4,1) B .(-1,4) C .(1,4)D .(0,4)3.如果方程x 2+(m -1)x +m 2-2=0的两个实根一个小于1,另一个大于1,那么实数m 的取值范围是( ) A .(-2,2) B .(-2,0) C .(-2,1)D .(0,1)4.已知p :-12<a <1,q :对任意的x ∈[-1,1],x 2-ax -2<0,则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.若不等式ax 2+2x +c <0的解集是⎝⎛⎭⎫-∞,-13∪⎝⎛⎭⎫12,+∞,则不等式cx 2+2x +a ≤0的解集是( ) A.⎣⎡⎦⎤-12,13 B.⎣⎡⎦⎤-13,12 C .[-2,3]D .[-3,2]6.若不等式ax -b >0的解集为(-∞,1),则关于x 的不等式bx +3ax -5>0的解集为( )A .(-5,3)B .(-∞,-5)∪(3,+∞)C .(-3,5)D .(-∞,-3)∪(5,+∞)7.(2020·浙江省五校联考)已知关于x 的不等式ax 2-2x +3a <0在(0,2]上有解,则实数a 的取值范围是( ) A.⎝⎛⎭⎫-∞,33 B.⎝⎛⎭⎫-∞,47 C.⎝⎛⎭⎫33,+∞D.⎝⎛⎭⎫47,+∞8.若函数f (x )=2x +12x -a 是奇函数,则使f (x )>3成立的x 的取值范围是( )A .(-1,1)B .(-1,1]C .[0,1)D .(0,1)9.关于x 的不等式x 2-2kx +k 2+k -1>0的解集为{x |x ≠a ,x ∈R },则实数a =________. 10.若x ∈[-1,1]时,关于x 的不等式x 3-1≤ax 2+2ax -a 2恒成立,则实数a 的取值范围是________.11.(2019·嘉兴模拟)已知函数f (x )=⎩⎪⎨⎪⎧-x +1,x <0,x -1,x ≥0,那么不等式x +(x +1)·f (x +1)≤1的解集是( )A .{x |-1≤x ≤ 2-1}B .{x |x ≤1}C .{x |x ≤ 2-1}D .{x |-2-1≤x ≤ 2-1}12.设a ,b 是关于x 的一元二次方程x 2-2mx +m +6=0的两个实根,则(a -1)2+(b -1)2的最小值是( )A .-494B .18C .8D .-613.定义:区间[a ,b ],(a ,b ],(a ,b ),[a ,b )的长度均为b -a ,若不等式1x -1+2x -2≥54的解集是互不相交区间的并集,则该不等式的解集中所有区间的长度之和为( ) A.512 B.125 C.2095D.520920914.定义域为R 的函数f (x )满足f (x +2)=2f (x ),当x ∈[0,2)时,f (x )=))232,0,1,1,1,2,2x x x x x -⎧-∈⎡⎣⎪⎪⎨⎛⎫⎪-∈⎡ ⎪⎣⎪⎝⎭⎩若当x ∈[-4,-2)时,不等式f (x )≥m 24-m +12恒成立,则实数m 的取值范围是( )A .[2,3]B .[1,3]C .[1,4]D .[2,4]15.已知二次函数f (x )=-x 2+2x +3,不等式f (x )≥m 的解集的区间长度为6(规定:闭区间[a ,b ]的长度为b -a ),则实数m 的值是________.16.(2020·浙江省浙南名校联盟联考)已知等比数列{a n }的公比为q ,关于x 的不等式a 2x 2-(a 1+a 3)x +a 2>0有下列说法:①当q >1时,不等式的解集为⎝⎛⎭⎫-∞,1q ,(q ,+∞); ②当0<q <1时,不等式的解集为⎝⎛⎭⎫q ,1q ; ③当a 1>0时,存在公比q ,使得不等式解集为∅; ④存在公比q ,使得不等式解集为R . 上述说法正确的序号是________.答案精析1.A 2.B 3.C 4.A 5.D 6.C 7.A 8.D 9.1 10.⎣⎡⎦⎤0,34 11.C 12.C [因为a ,b 是关于x 的一元二次方程x 2-2mx +m +6=0的两个实根,所以由根与系数的关系得⎩⎪⎨⎪⎧a +b =2m ,ab =m +6,且Δ=4(m 2-m -6)≥0,所以y =(a -1)2+(b -1)2=(a +b )2-2ab -2(a +b )+2=4m 2-6m -10 =4⎝⎛⎭⎫m -342-494,且m ≥3或m ≤-2. 由二次函数的性质知,当m =3时,函数y =4⎝⎛⎭⎫m -342-494取得最小值为8. 即(a -1)2+(b -1)2的最小值为8.] 13.B [不等式1x -1+2x -2≥54,即4(x -2)+8(x -1)-5(x -1)(x -2)4(x -1)(x -2)≥0,化简可得5x 2-27x +264(x -1)(x -2)≤0,∴⎩⎪⎨⎪⎧ 5x 2-27x +26≤0,(x -1)(x -2)>0 或⎩⎪⎨⎪⎧5x 2-27x +26≥0,(x -1)(x -2)<0, 方程5x 2-27x +26=0有两个根x 1=27-20910或x 2=27+20910,则原不等式的解集为⎝ ⎛⎦⎥⎤1,27-20910∪⎝ ⎛⎦⎥⎤2,27+20910,其解集区间的长度为⎝⎛⎭⎪⎫27+20910-2+⎝ ⎛⎭⎪⎫27-20910-1=275-3=125.]14.B [因为当x ∈[-4,-2)时,不等式f (x )≥m 24-m +12恒成立,所以f (x )min ≥m 24-m +12,当x ∈[-4,-2),x +4∈[0,2)时,f (x )=12f (x +2)=14f (x +4)=⎩⎪⎨⎪⎧14[(x +4)2-(x +4)],x +4∈[0,1),-14×34212x +-⎛⎫ ⎪⎝⎭,x +4∈[1,2),当x +4∈[0,1)时,f (x )=14[(x +4)2-(x +4)]≥-14×14=-116,当x +4∈[1,2)时, f (x )=-14×34212x +-⎛⎫⎪⎝⎭≥-14,因此当x ∈[-4,-2)时,f (x )min =-14≥m 24-m +12,所以实数m 的取值范围是1≤m ≤3.] 15.-5解析 根据题意-x 2+2x +3≥m 的解集为[a ,b ],则x =a 和x =b 是方程-x 2+2x +3=m 即x 2-2x +m -3=0的两根, 则a +b =2,ab =m -3,不等式f (x )≥m 的解集的区间长度为6,即b -a =6, 则有(a +b )2-4ab =4-4(m -3)=36, 解得m =-5. 16.③解析 由题意a 1=a 2q ,a 3=a 2q ,不等式a 2x 2-(a 1+a 3)x +a 2>0变为 a 2⎣⎡⎦⎤x 2-⎝⎛⎭⎫1q +q x +1>0, 即a 2(x -q )⎝⎛⎭⎫x -1q >0, 若a 2>0,则(x -q )⎝⎛⎭⎫x -1q >0, 当q >1或-1<q <0时解为x <1q 或x >q ,当0<q <1或q <-1时,解为x <q 或x >1q ,当q =±1时,解为x ≠q ; 若a 2<0,则(x -q )⎝⎛⎭⎫x -1q <0,当q >1或-1<q <0时,解为1q <x <q ,当0<q <1或q <-1时, 解为q <x <1q,当q =±1时,不等式无解. 对照①,②,③,④,只有③正确.。
高中数学一轮复习 一元二次不等式及其解法

(Ⅱ)若 ax2+bx+c≤0 的解集为 R,求实数 c 的取值范围.
Байду номын сангаас解:(Ⅰ)依题意知,-3,2 是方程 ax2+(b-8)x-a-ab=0 的两
-3+2=-b-a 8,
根,且 a<0,则
所以 -3×2=-aa-ab,
a=-3,b=5,则
f(x)=-
1- k1-k2};
当 k=-1 时,不等式的解集为{x|x≠-1};
当 k<-1 时,不等式的解集为 R.
点 拨: 解一元二次不等式的步骤:第一步,将二次项系数化 为正数;第二步,解相应的一元二次方程;第三步,根据 一元二次方程的根,结合不等号的方向画图;第四步,写
出不等式的解集.容易出现的错误有:①未将二次项系数
-2152,所以实数 c 的取值范围为-∞,-2152.
点 拨: 三个“二次”在高考中举足轻重,每年高考中,至
少有三分之一的题目与之相关.直接考查的不多见,以 间接考查为主,贯穿高中数学的始终.其中二次函数居 核心地位.
(1) 已 知 不 等 式 ax2 - 3x + 6>4 的 解 集 为
+2>0 的解集为 R.
(2)若关于 x 的不等式 ax2-x+2a<0 的解集为∅,则
实数 a 的取值范围是________.
解:依题意知,问题等价于 ax2-x+2a≥0 恒成立, 当 a=0 时,-x≥0 不恒成立; 当 a≠0 时,要使 ax2-x+2a≥0 恒成立,
需aΔ>≤0,0,即1a->08,a2≤0,解得 a≥ 42,即 a 的取值
{x|x1<x<x2}
有两相等实根 x1=x2= -2ba
高三数学第一轮复习:4-5 第一章 不等式的基本性质(理)人教实验B版 知识精讲

高三数学第一轮复习:4-5 第一章 不等式的基本性质(理)人教实验B 版【本讲教育信息】一. 教学内容:4-5 / 第一章 / 不等式的基本性质、基本不等式;不等式的解法二. 教学目的:1、巩固不等式的基本性质、拓展基本不等式相关知识;2、掌握一元一次不等式、一元二次不等式及绝对值不等式的解法三. 教学重点、难点基本不等式的知识拓展;绝对值不等式的解法四. 知识分析【不等式的基本性质】1、不等式的基本性质:对于任意的实数a ,b ,有000a b a b a b a b a b a b ->⇔>⎧⎪-=⇔=⎨⎪-<⇔<⎩,这三条基本性质是差值比较法的理论依据.2、不等式的性质包括“单向性”和“双向性”两个方面. 【单向性】(1)c a c b ,b a >⇒>>(2)d b c a d c ,b a +>+⇒>> (3)bc ac 0c ,b a >⇒>> (4)bc ac 0c ,b a <⇒<>(5)bd ac 0d c ,0b a >⇒>>>>(6)n n b a R n ,0b a >⇒∈>>+ 【双向性】(1)000a b a b a b a b a b a b ->⇔>⎧⎪-=⇔=⎨⎪-<⇔<⎩(2)a b b a >⇔<(3)a b a c b c >⇔+>+单向性主要用于证明不等式;双向性是解不等式的基础(当然也可用于证明不等式),由于单向性(3)、(4)的逆命题都成立,所以它们也可用于解不等式,在应用单向性(6)解无理不等式和形如nx a >的高次不等式时,若n 为偶数时要注意讨论. 3、要注意不等式性质成立的条件.例如,在应用“11,0a b ab a b>>⇒<”这一性质时,有些同学要么是弱化了条件,得11a b a b>⇒<,要么是强化了条件,而得110a b a b>>⇒<【基本不等式】定理1 设R b ,a ∈,则ab 2b a 22≥+,当且仅当b a =时,等号成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、考试要求:掌握简单不等式的解法,特别是一元二次不等式,会解简单的分式不等式和含参数的不等式。
二、知识梳理
1.一元二次不等式的一般形式为 或 (a 、b 、c 为常数且a ≠0)任何一个二次项
系数为负数的一元二次不等式都可以通过 化成二次项系数为正数的一
元二次不等式。
2.设方程ax 2+bx+c=0(a>0)的实根为x 1,x 2且x 1≤x 2(有实根时)
则不等式ax 2+bx+c>0(a>0)的解集。
(1)当Δ>0时为 (2)当Δ=0时为
(3)当Δ<0时为
不等式ax 2+bx+c<0 (a>0)的解集。
(1)当Δ>0时为 (2)当Δ=0时为
(3)当Δ<0时为
3.不等式(x-x 1)(x-x 2)>0 当 x 1<x 2时解集为
不等式(x-x 1)(x-x 2)< 0 当x 1<x 2时解集为
不等式ax 2+bx+c>0对任意X ∈R 恒成立的条件是
不等式ax 2+bx+c<0对任意X ∈R 恒成立的条件是 4.()()f x g x >0<=> ()()
f x
g x ≥0<=> 三、基础检测:
⒈(07年福建文科4)“|x|<2”是“x 2-x-6<0”的( )
A 、充分而不必要条件
B 、必要而不充分条件
C 、充要条件
D 、既不充分又不必要条件
⒉(08年福建理科2)设集合A={X|1
x x -<0},B={X|0<x<3}那么“m ∈A ”是“m ∈B ”的( ) A 、充分而不必要条件 B 、必要而不充分条件C 、充要条件 D 、既不充分又不必要条件
⒊(2010全国II ,2)不等式02
3 +-x x 的解集为( ) A.(-∞,2) B.(-∞,+∞) C.(2,+∞) D.(-∞,2)⋃(2,+∞)
⒋(09陕西,1)若不等式2x -x 0≤的解集为M ,函数f(-|x|)的定义域为N ,则M ⋂N 为( ) A.{0,1) B.(0,1) C[0,1] D(-1,0] ⒌(08年北京文科14) 12
x x -+ >1 的解集是 ⒍已知x 2+px+q<0解集为{x|-12<x< 13
},求不等式qx 2+px+1>0的解集 四、典型例题
例1解关于x的不等式
(1)
2
a x
x
-
-
>1,∈R)
例2设a∈R,关于x的方程7x2-(a+13)x+a2-a-2=0有两个实根
x 1,x
2
且0<x
1
<1<x
2
<2,求a的取值范围
例3已知关于x的不等式2x-1>m(x2-1)
⑴是否存在实数m,使不等式对任意x∈R恒成立?并说明理由。
⑵若对于m∈[-2,2]不等式恒成立,求实数x的取值范围。
四、自我测评
⒈关于x的不等式ax2+bx-2>0的解集是(-∞,-1
2
)u(
1
3
,+∞),则ab=( )
A.-24
B.24
C.14
D.-14
⒉(07辽宁理科10)设命题P:log 12
(|x|-3)>0,命题q :x 2-56x+16>0 则p 是q 的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分又不必要条件
⒊函数f(x)=221log (43)
x x -+-的定义域为( ) A.(1,2) B.(-∞,1)u (3,+∞) C.(1,3) D.[1,3]
4.(2010江西,5)不等式02≤-x x 的解集是( )
A.(-∞,2)
B.(-∞,+∞)
C.(2,+∞)
D.(-∞,2)⋃(2,+∞)
5.(08年山东,7)不等式2)
2(52≥-+x x 的解集是( ) A.[-3,21] B.[-21,3] C.[21,1)⋃(1,3) D.[-2
1,1)⋃(1,3]
6.(07年北京理科12)已知集合A={x||x-a|≤1},B={x|x 2-5x+4≥0}若A ∩B=φ,则实数a 的取值范围是 。
7.(08年江西理科16)不等式2
31x x
-+≤12的解集为 8.(11 年上海,6)不等式11 x
的解集为 9.(10年上海,2)不等式04
2 +-x x 的解集是 10.解关于x 的不等式ax 2-2(a+1)x+4>0(a ∈R)
五、课后练习
1.(07年安徽理科5)若A={X ∈Z|2≤22X -<8}B={x ∈R||log 2x |>|}
则A ∩(C R B)的元素个数为( ) A.0 B.1 C.2 D.3
2.对任意x ∈R,不等式(a-2)x 2-(a-2)x-4<0恒成立,则a 的取值范围是( )
A.(-∞,2)
B.(-∞,2 )
C.(-2,2)
D.(-2,2 ]
3.(06年山东理科8)设P:x-x 2-20>0 q:2
1||2x x --<0
则p 是q 的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
4.如果不等式2222463
x mx m x x ++++<1对一切实数x 均成立,则实数m 的取值范围是( ) A.(1,3) B.(-∞,3) C.(- ∞,1)U(2,+ ∞) D.(- ∞,+ ∞)
5.已知函数f(x)=log 2(x 2-ax+3a)在区间[2,+∞)上是增函数,则a 的取值范围是( )
A.(-∞,4)
B.(-4,4 ]
C.(-∞,-4)u[2,+ ∞ )
D.[ -4,2 )
6.不等式0<x-1
x <1的解集是
7.不等式23
4x x --≥0的解集是
8.已知ax 2+2x+c>0的解集为{x|-13<x<1
2},则a+c=
9.(2011广东5)不等式2X 2-X-1>0的解集是( )
A.{x|-2<x<3}
B.{x|x<-2}
C.{x|x<-2 或x>3}
D.{x|x>3}
10.已知关于x 的不等式25
ax x a --的解集为M
(1) 当a=4时,求集合M
(2)若3∈M ,且5∉M ,求实数a 的取值范围。
