一次函数中等腰直角三角形的存在性
一次函数与等腰三角形存在性培优专题

一次函数与等腰三角形存在性培优专题1.已知一次函数1y x=-+的图象与x轴、y轴分别交于点A点、B点,点P在x轴上,并且使以点A、B、P为顶点的三角形是等腰三角形,则这样的点有()A.2个B.3个C.4个D.5个2.已知一次函数443y x=+的图象分别交x轴,y轴于A,B两点,点C在x轴的正半轴上,若ABC△为等腰三角形,则点C的坐标为______________________________________.3.如图,直线OB是一次函数2y x=-的图象,点A的坐标为(02),,在直线OB上找点C,使ACO△为等腰三角形,则点C的坐标是______________________________________.4.一次函数1y x=+的图象交x轴于点A,交y轴于点B,点C在x轴上,且使得ABC△是等腰三角形,符合题意的点C坐标为______________________________________.5.如果一次函数364y x=-+的图象与x轴、y轴分别交于A、B两点,M点在x轴上,并且使得以点A、B、M为定点的三角形是等腰三角形,则M点的坐标为______________________________________.6.如图所示,一次函数4=-+与坐标轴交于A、B两点,点P是线段AB上的一个动点y x(不包含A、B两个端点),C是线段OB上一点,45△是等腰三角形,OPC∠=︒,若OPC试求点P的坐标?7.如图,在平面直角坐标系中,等腰Rt ABC△的顶点A在y轴正半轴上,顶点B在x轴正半轴上,4OB=.OA=,3(1)求点C的坐标;(2)求经过点B,C的一次函数的解析式;(3)在x轴上是否存在点P,使PCB△为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.8.如图,一次函数334y x =-+的图象与x 轴和y 轴分别交于点A 和B ,再将AOB △沿直线CD 对折,使点A 与点B 重合,直线CD 与x 轴交于点C ,与AB 交于点D .连接BC .(1)求点A 和点B 的坐标;(2)求BOC S △;(3)在y 轴上有一点P ,且PAB △是等腰三角形,求出点P 的坐标.9.如图,一次函数364y x =+的图象与x ,y 轴分别交于A ,B 两点,点C 与点A 关于y 轴对称.动点P ,Q 分别在线段AC ,AB 上(点P 与点A ,C 不重合),且满足BPQ BAO ∠=∠. (1)求点A ,B 的坐标及线段BC 的长度;(2)当点P 在什么位置时,APQ CBP △≌△,说明理由;(3)当PQB △为等腰三角形时,求点P 的坐标.10.已知一次函数112y x =-+的图象与x 轴、y 轴分别交于A ,B . (1)求点A 、B 的坐标;(2)如果点C 在一次函数112y x =-+的图象上,并且AOC △是等腰三角形,问满足条件的点C 有几个?并求出所有点C 坐标.11.一次函数2y =+的图象与x 轴、y 轴分别交于点A 、B ,以AB 为边在第二象限内作等边ABC △.(1)求C 点坐标;(2)在第二象限内有一点(1)M m ,,使ABC ABM S S =△△,求M 点坐标;(3)点()0C ',在直线AB 上是否存在一点P ,使ACP △为等腰三角形?若存在,求P 点坐标;若不存在,说明理由.12.在平面直角坐标系xOy 中,点A 、点B 、点C 坐标分别为(50),、(100),、(05) ,. (1)求过B 、C 两点的一次函数解析式;(2)若直线BC 上有一动点()P m n ,,以点O 、A 、P 为顶点的三角形面积和以点O 、C 、P 为顶点的三角形面积相等,求P 点坐标;(3)若y 轴上有一动点Q ,使以点Q 、A 、C 为顶点的三角形为等腰三角形,直接写出Q 点坐标.。
一次函数综合—线段和差、存在性问题

一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P,使PA+PB 值最小。
连AB,与l 交点即为P.两点之间线段最短.PA+PB 最小值为AB.【原理2】作法作图原理在直线l 上求一点P,使PA+PB 值最小.作 B 关于l 的对称点B'连A B',与l 交点即为P.两点之间线段最短.PA+PB 最小值为A B'.【原理3】作法作图原理在直线l 上求一点P,使作直线AB,与直线l的交点即为P.三角形任意两边之差小于第三边.≤AB .PBPA-(1)求线段和最小时动点坐标或直线解析式;(2)求三角形周长最小值;(3)求线段差最大时点的坐标或直线解析式。
3. 口诀:“和小异,差大同”(一)一次函数线段和最小值问题【例题讲解】★★☆例题1.在平面直角坐标系xOy中,y轴上有一点P,它到点(4,3)A,(3,1)B 的距离之和最小,则点P的坐标是()A.(0,0)B.4(0,)7C.5(0,)7D.4(0,)5的值最大 .【原理4】作法作图原理在直线l 上求一点P,使的值最大 .作B 关于l 的对称点B'作直线A B',与l交点即为P.三角形任意两边之差小于第三边.≤A B' .PB PA-PB PA-PB PA-★★☆练习1.如图,在平面直角坐标系中,已知点(2,3)B-,在x轴上存在点P到A,B两点的A,点(2,1)距离之和最小,则P点的坐标是.★★☆练习2.如图,直线34120+-=与x轴、y轴分别交于点B、A两点,以线段AB为边在第一象限x y内作正方形ABCD.若点P为x轴上的一个动点,求当PC PD+的长最小时点P的坐标.★★☆例题2.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,3∆的周长最小时,求点E OB=,D为边OB的中点,若E为x轴上的一个动点,当CDEOA=,4的坐标()A .(3,0)-B .(1,0)C .(0,0)D .(3,0)★★☆练习1.如图,在平面直角坐标系中,点A 、B 的坐标分别为(1,4)和(3,0),点C 是y 轴上的一个动点,连接AC 、BC ,当ABC ∆的周长最小值时,ABC ∆的面积为 .★★☆练习2.如图,在平面直角坐标系中,直线122y x =+与x 轴、y 轴分别交于A 、B 两点,以AB 为边 在第二象限内作正方形ABCD .(1)求点A 、B 的坐标,并求边AB 的长;(2)求点C 和点D 的坐标;(3)在x 轴上找一点M ,使MDB ∆的周长最小,请求出M 点的坐标,并直接写出MDB ∆的周长最小值.(二)一次函数线段差最大值问题【例题讲解】★★☆例题1.已知,如图点(1,1)A,(2,3)B-,点P为x轴上一点,当||PA PB-最大时,点P 的坐标为()A.1(,0)2B.5(,0)4C.1(,0)2-D.(1,0)★★☆练习1.平面直角坐标系中,已知(4,3)A、(2,1)B,x轴上有一点P,要使PA PB-最大,则P点坐标为★★☆练习2.如图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(6,0),点P在一次函数1322y x =+的图象上运动,则PB PA -的最大值为( )A .2B .233C .4D .143【题型知识点总结】一次函数最短路径问题注意事项:1. 根据“和小异,差大同”判断是否需要作对称;2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。
一次函数之等腰直角三角形的存在性 (讲义及答案)

一次函数之等腰直角三角形的存在性(讲义及答案).1. 在正方形网格中,网格线交点称为格点。
已知A、B是两个格点,若点C也是格点且使△ABC为等腰直角三角形,则符合条件的点C只有一个。
2. 做讲义第一题时,先看知识点,再用铅笔计算并将演算保留在讲义上。
如果思路受阻(例如某个点做了2-3分钟),重复上述动作。
如果仍无法解决,重点听课堂讲解。
知识点:1. 解决存在性问题的处理思路①分析不变特征:分析所求图形中的定点、定线、定角等不变特征。
②分类、画图:结合所求图形的形成因素,依据其判定、定义等确定分类,并画出符合题意的图形。
通常先尝试画出其中一种情形,分析解决后,再类比解决其他情形。
③求解、验证:围绕不变特征、画图依据来设计方案进行求解。
验证时,要回归点的运动范围,画图或推理,判断是否符合题意。
注:复杂背景下的存在性问题往往需要研究背景图形,几何背景往往研究点、线、角;函数背景研究点坐标、表达式等。
2. 等腰直角三角形存在性的特征分析及操作要点:三角形的三个顶点分别为直角顶点进行分类,在直角的基础上,再考虑等腰。
通常借助构造弦图模型进行求解。
精讲精练:1. 如图,直线y=-2x+6与x轴、y轴分别交于点A、B。
点P是第一象限内的一个动点,若以A、B、P为顶点的三角形为等腰直角三角形,则点P的坐标为。
2. 如图,直线y=-x+b与x轴、y轴分别交于点A、B。
点C在直线y=-x+b上,且其纵坐标为1。
△___的面积为。
(1)求直线y=-x+b的表达式及点C的坐标。
(2)点P是第二象限内的一个动点,若△ACP是等腰直角三角形,则点P的坐标为。
3. 如图,在平面直角坐标系中,点A的坐标为(2,0)。
点P是y轴正半轴上的一个动点,Q是直线x=3上的一个动点。
若△APQ为等腰直角三角形,则点P的坐标为。
4. 如图,直线y=3x+4与y轴交于点A,点P是直线x=6上的一个动点,点Q是直线y=3x+4上的一个动点,且点Q在第一象限。
一次函数中(特殊三角形)的存在性问题优秀教学设计

辅助策略:借助几何画板,使学生直观形象地观察、操作。
2、教法
演示法:通过几何画板演示两圆一中垂线和外K全等,使学生直观、形象的感知因动点的移动,在何时会出现等腰三角形和等腰直角三角形,思考在没有几何画板的时候,我们自己该如何作图,快速确定动点的位置。
《一次函数中特殊三角形的存在性问题》教学设计
【教学目标】
1、知识与技能
(1)使学生体会定点与动点之间的关系,做到以静制动。
(2)通过数形结合,利用几何法和代数法求一次函数中特殊三角形的存在性问题。
2、过程与方法
(1)借助几何画板探究一次函数中特殊三角形的存在性问题,使学生初步形成正确、科学的分析解决问题的方法。
①设点:设点P(0,m)A(3,0),B(0,4)
②表示三条边:
③列方程:
三、小组讨论
已知A(2,0),B(0,4),在第一象限内是否存在一点P,使得△PAB是等腰直角三角形,若存在请求出点P的坐标;若不存在,请说明理由。
讨论目标:①这样的动点P可能有多少个?如何分类?
②你能不能画出等腰直角三角形?
等腰三角形可以是两条边相等或者两个角相等,在我们所学的知识中,是边好表示,还是角好表示呢?
探究一:用几何法确定动点的位置——两圆一中垂线
例1、已知,A(3,0),B(0,4),在y轴上是否存在一点P,使得△PAB是等腰三角形,若存在,请求出点P的坐标,若不存在,请说明理由
探究二:用代数法确定动点的位置——设点法
实验法:让学生自己动手、在探究过程中,自己发现动点的规律
一次函数之等腰直角三角形的存在性 (讲义及答案).

一次函数之等腰直角三角形的存在性(讲义)➢课前预习1.如图所示的正方形网格中,网格线的交点称为格点.已知A,B 是两个格点,若点C 也是图中的格点,且使得△ABC 为等腰直角三角形,则符合条件的点C 有个.2.用铅笔做讲义第1 题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听.➢知识点睛1.存在性问题的处理思路①分析不变特征分析所求图形中的定点、定线、定角等不变特征.②分类、画图结合所求图形的形成因素,依据其判定、定义等确定分类,并画出符合题意的图形.通常先尝试画出其中一种情形,分析解决后,再类比解决其他情形.③求解、验证围绕不变特征、画图依据来设计方案进行求解;验证时,要回归点的运动范围,画图或推理,判断是否符合题意.注:复杂背景下的存在性问题往往需要研究背景图形,几何背景往往研究点,线,角;函数背景研究点坐标,表达式等.2.等腰直角三角形存在性的特征分析及特征下操作要点:三角形的三个顶点分别为直角顶点进行分类,在直角的基础上,再考虑等腰,通常借助构造弦图模型进行求解.➢精讲精练1.如图,直线y=-2x+6 与x 轴、y 轴分别交于点A,B,点P 是第一象限内的一个动点,若以A,B,P 为顶点的三角形是等腰直角三角形,则点P 的坐标为.2.如图,直线y =-1x +b 与x 轴、y 轴分别交于点A,B,点C 3在直线y =-1x +b 上,且其纵坐标为1,△OAC 的面积为3.3 2(1)求直线y =-1x +b 的表达式及点C 的坐标;3(2)点P 是第二象限内的一个动点,若△ACP 是等腰直角三角形,则点P 的坐标为.3.如图,在平面直角坐标系中,点A 的坐标为(2,0),点P 是y轴正半轴上一个动点,Q是直线x=3 上的一个动点,若△APQ 为等腰直角三角形,则点P 的坐标为.4.如图,直线y=3x+4 与y 轴交于点A,点P 是直线x=6 上的一个动点,点Q 是直线y=3x+4 上的一个动点,且点Q 在第一象限,若△APQ 为等腰直角三角形,则点Q 的坐标为.5. 如图,直线 l 1:y =x +6 与 x 轴、y 轴分别交于点 A ,B ,直线 l 2:y = - 1 x - 3 与 x 轴交于点 A ,点 M 是线段 AB 上的一动点,2过点 M 作 y 轴的平行线交直线 l 2 于点 N ,在 y 轴上是否存在点 P ,使△MNP 为等腰直角三角形?若存在,求出点 P 的坐标;若不存在,请说明理由.【参考答案】➢ 课前预习1. 6➢ 精讲精练1. (9,3),(6,9),( 9 , 9 )2 22. (1) y = - 1 x -1,C (-6,1)3(2)(-2,3),(-5,4),(-4,2)3. (0,1),(0,3),(0,4)4. (2,10),(3,13),( 3 , 17 )2 2 5. 存在,点 P 的坐标为(0, 12 ),(0, - 6 ),(0, 6 )5 5 7。
一次函数背景下的图形存在性问题(原卷版)-2023年中考数学重难点解题大招复习讲义-函数

例题精讲考点一:一次函数中等腰三角形存在性问题【例1】.如果一次函数y=﹣x+6的图象与x轴、y轴分别交于A、B两点,M点在x轴上,并且使得以点A、B、M为定点的三角形是等腰三角形,则M点的坐标为.变式训练【变1-1】.如图,在平面直角坐标系中,直线MN的函数解析式为y=﹣x+3,点A在线段MN上且满足AN=2AM,B点是x轴上一点,当△AOB是以OA为腰的等腰三角形时,则B点的坐标为.【变1-2】.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.(1)求点C的坐标.(2)若P是x轴上的一个动点,直接写出当△OPC是等腰三角形时P的坐标.考点二:一次函数中直角三角形存在性问题【例2】.已知点A、B的坐标分别为(2,2)、(5,1),试在x轴上找一点C,使△ABC为直角三角形.【变2-1】.如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P 是x轴上的一点,且满足△ABP是直角三角形,则点P的坐标是.【变2-2】.如图,已知一次函数y=x﹣2的图象与y轴交于点A,一次函数y=4x+b的图象与y轴交于点B,且与x轴以及一次函数y=x﹣2的图象分别交于点C、D,点D的坐标为(﹣2,﹣4).(1)关于x、y的方程组的解为.(2)求△ABD的面积;(3)在x轴上是否存在点E,使得以点C,D,E为顶点的三角形是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.考点三:一次函数中平行四边形存在性问题【例3】.如图,已知一次函数y=kx+b的图象经过A(1,3),B(﹣2,﹣1)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.变式训练【变3-1】.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.考点四:一次函数中矩形存在性问题【例4】.如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求线段AB的长;(2)求直线CE的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.变式训练【变4-1】.如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2﹣4x+3=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求点H到x轴的距离;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.考点五:一次函数中菱形存在性问题【例5】.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.(1)求点C的坐标;(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M 的坐标;(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.变式训练【变5-1】.如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,﹣2),与直线CD交于点A(m,2).(1)求直线AB的解析式;(2)点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)设P是射线CD上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.1.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为.2.如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标.3.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y 的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为.4.如图,一次函数y=k2x+b的图象与y轴交于点B,与正比例函数y=k1x的图象相交于点A(3,4),且OA=OB.(1)分别求出这两个函数的解析式;(2)求△AOB的面积;(3)点P在x轴上,且△POA是等腰三角形,请直接写出点P的坐标.5.直线l1交x轴于点A(6,0),交y轴于B(0,6).(1)如图,折叠△AOB,使BA落在y轴上,折痕所在直线为l2,直线l2与x轴交于C 点,求C点坐标及l2的解析式;(2)在直线l1上找点M,使得以M、A、C为顶点的三角形是等腰三角形,求出所有满足条件的M点的坐标.6.在平面直角坐标系中,直线y=kx+8k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).(1)求点A的坐标;(2)如图1,将直线AB绕点B逆时针旋转45°交x轴于点C,求直线BC的解析式;(3)在(2)的条件下,直线BC上有一点M,坐标平面内有一点P,若以A、B、M、P 为顶点的四边形是菱形,请直接写出点P的坐标.7.如图,在平面直角坐标系中,一次函数的图象与x轴交于点A(﹣4,0),与y轴交于点B,且与正比例函数y=x的图象交于点C(m,6).(1)求一次函数的解析式;(2)求△BOC的面积;(3)在x轴上是否存在一点P,使得△ABP是等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.8.如图,已知一次函数y=x+m的图象与x轴交于点A(﹣6,0),交y轴于点B.(1)求m的值与点B的坐标(2)问在x轴上是否存在点C,使得△ABC的面积为16?若存在,求出点C的坐标;若不存在,说明理由.(3)问在x轴是否存在点P,使得△ABP为等腰三角形,求出点P坐标.(4)一条经过点D(0,2)和直线AB上的一点的直线将△AOB分成面积相等的两部分,请求出这条直线的函数表达式.9.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P(2,a).(1)求点A、B的坐标;(2)若Q为x轴上一动点,△APQ为等腰三角形,直接写出Q点坐标;(3)点C在直线AB上,过C作CE⊥x轴于E,交直线OP于D,我们规定若C,D,E 中恰好有一点是其他两点所连线段的中点,则称C,D,E三点为“和谐点”,求出C,D,E三点为“和谐点”时C点的坐标.10.如图所示,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4).(1)求△AOB的面积;(2)动点M从A点以每秒1个单位的速度沿x轴向左移动,求△COM的面积S与M的移动时间t之间的函数关系式;(3)当动点M在x轴上移动的过程中,在平面直角坐标系中是否存在点N,使以点A,C,N,M为顶点的四边形为菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.11.如图,直线y=﹣x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且OC=OB.(1)求点A的坐标及直线BC的函数关系式;(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.12.已知,一次函数y=的图象与x轴、y轴分别交于点A、点B,与直线y=相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)求点C到直线l的距离.=S△BCP,求点P的坐标.(3)若S△AOC(4)若点E是直线y=上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,请直接写出点E的坐标.13.如图,在平面直角坐标系xOy中,直线y=﹣x+与y=x相交于点A,与x轴交于点B.(1)求点A,B的坐标;(2)在平面直角坐标系xOy中,是否存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C的坐标;如果不存在,请说明理由;(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.14.如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)(1)求直线AB的函数的表达式;(2)直接写出不等式(kx+b)﹣ax<0的解集;(3)求△AOC的面积;(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P 的坐标.15.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.(1)直接写出k的值为;(2)如图2,C为x轴负半轴上一点,过C点的直线l2:经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QM⊥x轴分别交直线l1、l2于M、N,且MN=2MQ,求t的值;(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.16.如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM 的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.17.如图1,在平面直角坐标系中.直线与x轴、y轴相交于A、B两点,动点C 在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当直线B′C′经过点D时,求点D的坐标;(3)若点P在y轴上,点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,直线AB:y=﹣x+4与x轴、y轴分别交于点A、B,点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D 处.(1)点A的坐标是,点B的坐标是,AB的长为;(2)求点C的坐标;=S△OCD,直接写出点M的坐标.(3)点M是y轴上一动点,若S△MAB(4)在第一象限内是否存在点P,使△PAB为等腰直角三角形,若存在,直接写出点P 的坐标;若不存在,请说明理由.19.如图,直角坐标系中,直线y=kx+b分别与x轴、y轴交于点A(3,0),点B(0,﹣4),过D(0,8)作平行x轴的直线CD,交AB于点C,点E(0,m)在线段OD上,延长CE交x轴于点F,点G在x轴正半轴上,且AG=AF.(1)求直线AB的函数表达式.(2)当点E恰好是OD中点时,求△ACG的面积.(3)是否存在m,使得△FCG是直角三角形?若存在,直接写出m的值;若不存在,请说明理由.20.如图直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0).(1)求k的值.(2)若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时直线AP的解析式.(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.21.如图1,在平面直角坐标系中,O为坐标原点,直线l:y=﹣x+m与x、y轴的正半轴分别相交于点A、B,过点C(﹣4,﹣4)画平行于y轴的直线交直线AB于点D,CD=10(1)求点D的坐标和直线l的解析式;(2)求证:△ABC是等腰直角三角形;(3)如图2,将直线l沿y轴负方向平移,当平移适当的距离时,直线l与x、y轴分别相交于点A′、B′,在直线CD上存在点P,使得△A′B′P是等腰直角三角形.请直接写出所有符合条件的点P的坐标.(不必书写解题过程)22.直线y=kx﹣4与x轴、y轴分别交于B、C两点,且=.(1)求点B的坐标和k的值;(2)若点A时第一象限内的直线y=kx﹣4上的一动点,则当点A运动到什么位置时,△AOB的面积是6?(3)在(2)成立的情况下,x轴上是否存在点P,使△POA是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.23.如图,一次函数y1=x+n与x轴交于点B,一次函数y2=﹣x+m与y轴交于点C,且它们的图象都经过点D(1,﹣).(1)则点B的坐标为,点C的坐标为;(2)在x轴上有一点P(t,0),且t>,如果△BDP和△CDP的面积相等,求t的值;(3)在(2)的条件下,在y轴的右侧,以CP为腰作等腰直角△CPM,直接写出满足条件的点M的坐标.24.如图,在平面直角坐标系中,一次函数y=kx+b的图象与y轴交于点A(0,4),与直线y=﹣x﹣1在第四象限相交于点B,连接OB,△AOB的面积为6.(1)求点B的坐标及直线AB的解析式;(2)已知点M在直线AB右侧,且△MAB是以AB为直角边的等腰直角三角形,请求出符合条件的点M的坐标.25.综合与探究:如图,直线l1:y=x+3与过点A(3,0)的直线l2:y=kx+b(k≠0)交于点C(1,m)与x轴交于点B.(1)求直线l2对应的函数解析式;(2)请直接写出不等式kx+b<x+3的解集;(3)若点N在平面直角坐标系内,则在直线l1上是否存在点F使以A,B,F,N为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.26.一次函数y=kx+(k≠0)的图象与x轴、y轴分别交于A(1,0)、B(0,m)两点.(1)求一次函数解析式和m的值;(2)将线段AB绕着点A旋转,点B落在x轴负半轴上的点C处.点P在直线AB上,直线CP把△ABC分成面积之比为2:1的两部分.求直线CP的解析式;(3)在第二象限是否存在点D,使△BCD是以BC为腰的等腰直角三角形?若存在,请直接写出点D的坐标;若不存在,请说明理由.27.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=k2x的图象交点为C(3,4).(1)求正比例函数与一次函数的关系式.(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标.(3)在y轴上是否存在一点P使△POC为等腰三角形,若存在,求出所有符合条件的点P的坐标.28.在学习一元一次不等式与一次函数的过程中,小新在同一个坐标系中发现直线l1:y1=﹣x+3与坐标轴相交于A,B两点,直线l2:y2=kx+b(k≠0)与坐标轴相交于C,D两点,两直线相交于点E,且点E的横坐标为2.已知OC=,点P是直线l2上的动点.(1)求直线l2的函数表达式;(2)过点P作x轴的垂线与直线l1和x轴分别相交于M,N两点,当点N是线段PM的三等分点时,求P点的坐标;(3)若点Q是x轴上的动点,是否存在以A,E,P,Q为顶点的四边形是平行四边形?若存在,请求出所有满足条件的P点坐标;若不存在,请说明理由.29.(1)认识模型:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;(2)应用模型:①已知直线y=﹣2x+4与y轴交于A点,与x轴交于B点,将线段AB绕点B顺时针旋转90度,得到线段CB,求点C的坐标;②如图3,矩形ABCO,O为坐标原点,B的坐标为(5,4),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x﹣3上的一点,点Q是平面内任意一点.若四边形ADPQ是正方形,请直接写出所有符合条件的点D的坐标.30.如图,四边形OABC为矩形,其中O为原点,A、C两点分别在x轴和y轴上,点B的坐标是(4,6),将矩形沿直线DE折叠,使点C落在AB边上点F处,折痕分别交OC、BC于点E、D,且点D的坐标是(,6).(1)求BF的长度;(2)如图2,点P在第二象限,且△PDE≌△CED,求直线PE的解析式;(3)若点M为直线DE上一动点,在x轴上是否存在点N,使以M、N、D、F为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.。
第4章一次函数-一次函数之等腰直角三角形的存在性(教案)

五、教学反思
今天我们在课堂上探讨了《一次函数之等腰直角三角形的存在性》,整体来看,学生的学习效果还是不错的。但在教学过程中,我也发现了一些值得思考的问题。
首先,我发现有些学生对一次函数图像与等腰直角三角形之间的关系理解不够深入。在讲解过程中,我尽量用生动的例子和形象的比喻来帮助他们理解,但显然,这部分内容对于他们来说还是有一定难度的。在今后的教学中,我需要更加关注这部分学生的需求,尽可能用简单易懂的方式讲解难点,让他们能够真正消化吸收。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解一次函数和等腰直角三角形的基本概念。一次函数是形如y=kx+b的函数,其中k是斜率,b是y轴截距。等腰直角三角形是一种特殊的三角形,它的两条腰相等且与底边成直角。在一次函数图像中,等腰直角三角形的存在性与函数的斜率有关。
2.案例分析:接下来,我们来看一个具体的案例。这个案例将展示如何在一次函数图像中找出等腰直角三角形,以及它如何帮助我们解决实际问题。
-运用逻辑推理和分析数据的能力,解决一次函数图像中等腰直角三角形的定位问题。
举例解释:
-解释斜率为1或-1时,图像上的点与原点的连线和x轴或y轴形成的特殊角度题时,指导学生如何从问题描述中提取关键信息,构建一次函数模型,并利用等腰直角三角形的性质进行解答。
其次,在实践活动环节,学生们的参与度很高,但部分小组在讨论时显得有些拘谨,可能是因为对等腰直角三角形在实际生活中的应用不够了解。在今后的教学中,我会多设计一些与实际生活紧密相关的案例,让学生在实践中更好地理解理论知识。
专题二:一次函数中等腰直角三角形存在性问题方法总结
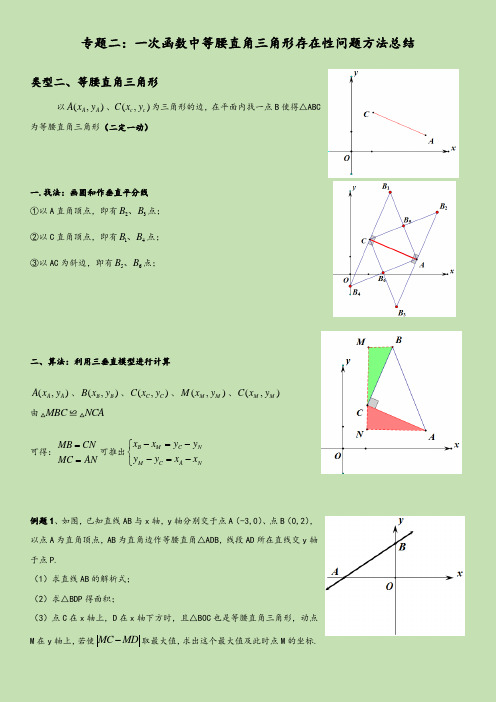
专题二:一次函数中等腰直角三角形存在性问题方法总结类型二、等腰直角三角形以(,)A A A x y 、(,)c c C x y 为三角形的边,在平面内找一点B 使得△ABC为等腰直角三角形(二定一动)一.找法:画圆和作垂直平分线①以A 直角顶点,即有23B B 、点;②以C 直角顶点,即有14B B 、点;③以AC 为斜边,即有56B B 、点;二、算法:利用三垂直模型进行计算(,)A A A x y 、(,)B B B x y 、(,)C C C x y 、(,)M M M x y 、(,)M M C x y由MBC ≌NCA可得:MB CN MC AN ==可推出B M C N M C A Nx x y y y y x x -=-⎧⎨-=-⎩例题1、如图,已知直线AB 与x 轴,y 轴分别交于点A (-3,0)、点B (0,2),以点A 为直角顶点,AB 为直角边作等腰直角△ADB ,线段AD 所在直线交y 轴于点P.(1)求直线AB 的解析式;(2)求△BDP 得面积;(3)点C 在x 轴上,D 在x 轴下方时,且△BOC 也是等腰直角三角形,动点M 在y 轴上,若使MC MD -取最大值,求出这个最大值及此时点M 的坐标.【答案】(1)AB 解析式:2+23y x = (2)①1(1,3)D -- 算法:利用1AOB AID ≅ 设1(,)D m n 20(3)0(3)0m n -=--⎧⎨--=-⎩解得13m n =-⎧⎨=-⎩ 则1(1,3)D -- 同理2(5,3)D -(3)根据题意,如图:12(2,0)(2,0)C C -、(两种情况答案一样,自行分类分析)当11,,C D M 三点共线时,MC MD -取最大值,最大值为11C D 11C D 解析式:36y x =--则M (0,-6)11max 10MC MD C D -==练习:1.已知直线1:l y x b =-+与x 轴交于点A ,直线2416:33l y x =-与x 轴交于点B ,直线12l l 、交于点C ,且C 点的横坐标为1.(1)求直线1l 的解析式和点A 的坐标.(2)直线1l 与y 轴交于点D ,将1l 向上平移9个单位得3l ,3l 与x 轴、y 轴分别交于点E 、F ,点P 为3l 上一动点,连接AP 、BP ,当△ABP 的周长最小时,求△ABP 的周长和点P 的坐标.(3)将1l 绕点C 逆时针旋转,使旋转后的直线4l 过点G (-2,0),过点C 作5l 平行于x 轴,点M 、N 分别为直线4l 、5l 上两个动点,是否存在点M 、点N ,使△BMN 是以点M 为直角顶点的等腰直角三角形,若存在,求出点M 的坐标,若不存在,请说明理由.【答案】解:(1)将1x =代入直线41633y x =-,得4161433y =⨯-=-, 故点C 的坐标为(1,4)-,将C 的坐标(1,4)-代入直线y x b =-+得,41b -=-+, 解得3b =-,∴直线1:3l y x =--,令0y =,则30x --=,解得3x =-,故点A 的坐标为(3,0)-,(2)直线3l 为1l 向上平移9个单位所得,故直线3l 的解析式为:6y x =-+,令0x =,得6y =,令0y =,得6x =,故点E ,点F 的坐标分别为(6,0),(0,6), 直线2416:33l y x =-与x 轴交于点B , 令0y =,得4x =,故B 点的坐标为(4,0),取点B 关于3l 的对称点Q ,设点Q 的坐标为(,)a b ,则线段BQ 的中点坐标为(2a b +,)2b 在直线3l , ∴622b a b +=-+,(1) 且(1)14b a ⋅-=--即14b a =-,(2) 联立(1)(2)得622b a b b +⎧=-+⎪⎪⎨⎪,解得:62a b =⎧⎨=⎩, (6,2)Q ∴,直线AQ 的解析式:2293y x =+, 当ABP ∆的周长最小时,即AP BP +最小, 连接AQ ,交直线3l 于点P ,此时AP BP +最小,最小值为22(63)(20)85AQ =++-=,7AB =,此时ABP ∆的周长为785+,由22936y x y x ⎧=+⎪⎨⎪=-+⎩解得48111811x y ⎧=⎪⎪⎨⎪=⎪⎩, P ∴点坐标为48(11,18)11, (3)设4l 的解析式:y mx n =+,将(1,4)C -,(2,0)G -,代入y mx n =+得,024m n m n =-+⎧⎨-=+⎩,解得4383m n ⎧=-⎪⎪⎨⎪=-⎪⎩, 4l ∴的解析式为:4833y x =--, 1︒当点M 在直线4l 的上方时,设点(,4)N n -,点48(,)33M s s --, 过点N ,B 分别作y 轴的平行线,过点M 作x 轴的平行线,三条直线分别交于R ,S 两点,如图则R ,S 的坐标分别为48(,)33n s --,48(4,)33s --, RM s n ∴=-,48433RN s =--,4MS s =-,4833SB s =--, 90NMB ∠=︒,90NMR SMB ∴∠+∠=︒,90BMS MBS ∠+∠=︒,90S R ∠=∠=︒,MB MN =,()MNR MBS AAS ∴∆≅∆,RM SB ∴=,RN SM =, 即4833s n s -=--,484433s s --=-, 解得8s =-,16n =-,∴点M 的坐标为(8,8)-,2︒当点M 在直线4l 的下方时,设点(,4)N n -,点48(,)33M s s --, 过点N ,B 分别作y 轴的平行线,过点M 作x 轴的平行线,三条直线分别交于R ,S 两点,如图则R ,S 的坐标分别为48(,)33n s --,48(4,)33s --, RM n s ∴=-,48433RN s =+-,4MS s =-,4833SB s =+, 90NMB ∠=︒,90NMR SMB ∴∠+∠=︒,90BMS MBS ∠+∠=︒,NMR MBS ∴∠=∠,90S R ∠=∠=︒,MB MN =,()MNR MBS AAS ∴∆≅∆,RM SB ∴=,RN SM =,即4833n s s -=+,484433s s +-=-, 解得407s =,16n =, ∴点M 的坐标为40(7,72)7-, 综上点M 的坐标为(8,8)-或40(7,72)7-,练习2:7.(2020春•官渡区期末)如图,在平面直角坐标系中,直线13:4l y x =与直线2:(0)l y kx b k =+≠相交于点(,3)A a ,直线2l 与y 轴交于点(0,5)B -. (1)求直线2l 的函数解析式;(2)将OAB ∆沿直线2l 翻折得到CAB ∆,使点O 与点C 重合,AC 与x 轴交于点D .求证:四边形AOBC 是菱形;(3)在直线BC 下方是否存在点P ,使BCP ∆为等腰直角三角形?若存在,直接写出点P 坐标;若不存在,请说明理由.【答案】解:(1)直线3?:4l y x =与直线?:l y kx b =+相交于点(,3)A a , (4,3)A ∴, 直线交?l 交y 轴于点(0,5)B -,5y kx ∴=-,把(4,3)A 代入得,345k =-,2k ∴=,∴直线2l 的解析式为25y x =-;(2)22345OA =+=,OA OB ∴=,将OAB ∆沿直线?l 翻折得到CAB ∆,OB OC ∴=,OA AC =,OA OB BC AC ∴===,∴四边形AOBC 是菱形;(3)如图,过C 作CM OB ⊥于M ,则4CM OD ==,5BC OB ==,3BM ∴=,(4,2)C ∴-, 过1P 作1PN y ⊥轴于N , BCP ∆是等腰直角三角形, 190CBP ∴∠=︒,1MCB NBP ∴∠=∠, 1BC BP =,BCM ∴∆≅△1()PBN AAS , 4BN CM ∴==, 1(3,9)P ∴-;同理可得,2(7,6)P -,37(2P ,11)2-. 综上所述,点P 的坐标是(3,9)-或(7,6)-或7(2P ,11)2-.。
