三角形的中位线经典练习题及其答案
三角形的中位线基础题30道选择题附详细答案

9.5 三角形的中位线基础题汇编(1)...2=...7+9.5 三角形的中位线基础题汇编(1)参考答案与试题解析一.选择题(共30小题)1.(2014•河北)如图,△ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC=()2.(2014•北海)如图△ABC中,D、E分别是边AB、AC的中点,已知DE=5,则BC的长为()3.(2014•泸州)如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为()4.(2014•宜昌)如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()MN=MN=AB5.(2014•牡丹江一模)如图,⊙O的半径为5,弦AB=8,点C在弦AB上,且AC=6,过点C作CD⊥AB交OB 于点D,则CD的长为()AB=4EO=1.5=47.(2013•怀化)如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是()AB8.(2013•昆明)如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()BC EF=则新三角形的周长为AC BC EF=(∴等边三角形的中位线长是:12.(2013•巴中)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、CD的中点且EF=6,则AD+BC的值是()EF=.C D.×(14.(2013•德庆县二模)已知△ABC的三边长分别为3cm,4cm,5cm,D,E,F分别为△ABC各边的中点,则△DEF15.(2013•潮安县模拟)如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为()DAB=4BC=216.(2013•南岗区三模)如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为()DPG=ANAP=AC=17.(2012•台州)如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为()18.(2012•聊城)如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论不正确的是()D=BC=19.(2012•佛山)依次连接任意四边形各边的中点,得到一个特殊图形(可认为是一般四边形的性质),则这个图AC EF=AC EF=AC.cm ∴相似比是21.(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为()BC AC EF=AB BC EF=23.(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是()ABAC24.(2012•德城区三模)如图,在△ABC中,BC=6,M、N分别是AB、AC的中点,则MN等于()DMN=25.(2012•黄埔区一模)如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为()AD=BD=AC BCAB=2AC=2BC=226.(2012•长宁区一模)如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为()D.AD=,的周长为边长的.27.(2012•盐田区二模)如图,▱ABCD的对角线AC、BD相交于点O,E是BC边的中点,OE=1.那么AB=().29.(2011•黔南州)如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()+2BE=CE=AB=3AC=330.(2011•义乌市)如图,DE是△ABC的中位线,若BC的长为3cm,则DE的长是()BC。
人教版八年级数学下册三角形的中位线练习题含答案.pdf

18 证明;连接 BD, ∵E,F,G,H 分别是 AB,BC,CD,DA 的中点
EH 平行且等于 BD/2 ,FD 平行且等于 BD/2 ∴EH 平行且等于 FD ∴四边形 EFGH 是平行四边形。
7/7
6/7
26 证明:连接 AC ,取 AC 的中点 M,连接 ME 、MF ∵M 是 AC 的中点, E 是 DC 的中点 ∴ME 是△ ACD 的 中位线 ∴ME = AD/2,PE ∥AH ∴∠ MEF =∠ AHF ( 同位角 相等) 同理可证: MF =BC/2, ∠MFE =∠ BGF (内错角 相等) ∵AD = BC ∴ME = MF ∴∠ MFE =∠ MEF ∴∠ AHF =∠ BGF
26.已知:如图,在四边形 ABCD 中, AD=BC, E、F 分别是 DC、 AB 边的中点, FE 的延长线分别与 AD、 BC 的延长线交于 H 、 G 点. 求证:∠ AHF =∠ BGF .
4/7
答案 : 1 两边中点 。 2 平行,第三边的一半。 3 3。 4 中线,中位线 。 5 8,5;互相平分。 6 4。 7 7。 8 6.5。 9 B 。 10 D. 11D .12C .13A. 14∵ AE = BE
A,B 间的距离,但绳子不够长,一位
1/7
同学帮他想了一个主意:先在地上取一个可以直接到达
A,B 的点 C,找到 AC,BC的中点 D,E,并且测出 DE
的长为 10m,则 A, B 间的距离为( )
A . 15m B . 25m C . 30m D . 20m
11.已知△ ABC的周长为 1,连结△ ABC的三边中点构成第二个三角形, ?再连结第二个三角形的三边中点构成第
(2021年整理)三角形的中位线练习题含答案

(完整)三角形的中位线练习题含答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)三角形的中位线练习题含答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)三角形的中位线练习题含答案的全部内容。
三角形的中位线练习题三角形中位线定义: 。
符号语言:在△ABC 中,D 、E 分别是AB 、AC 的中点, 则:线段DE 是△__ __三不同点:①三角形中位线的两个端点都是三角形边的中点。
②三角形中线只有一个端点是边的中点,另一端点是三角形一个顶点。
相同点:都是一条线段,都有三条。
三角形中位线定理: 。
符号语言表述:∵DE 是△ABC 的中位线(或AD=BD,AE=CE ) ∴DE //21BC练习1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4。
如图△ABC 中,D 、E 分别是AB 、 AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)如果EF =4cm ,那么BC =__cm 如果AB =10cm ,那么DF =___cmEDA E D(2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm,5cm,6cm ,则连结三边中点所围成的三角形的周长是_________cm .8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm ,4cm ,则原三角形的周长为( ) A .4。
完整版三角形的中位线经典练习题及其答案
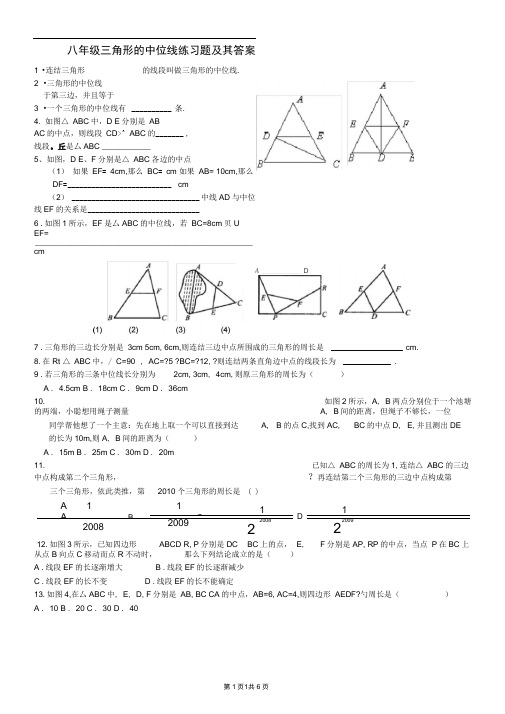
八年级三角形的中位线练习题及其答案1 •连结三角形2 •三角形的中位线于第三边,并且等于3 •一个三角形的中位线有__________ 条.4. 如图△ ABC中,D E分别是ABAC的中点,则线段CD>^ ABC的_______ ,线段。
丘是厶ABC ___________5、如图,D E、F分别是△ ABC各边的中点(1)如果EF= 4cm,那么BC= cm 如果AB= 10cm,那么DF= __________________________ cm(2) ________________________________ 中线AD与中位线EF的关系是____________________________6 .如图1所示,EF是厶ABC的中位线,若BC=8cm贝UEF=_________________________________________________cm7 .三角形的三边长分别是3cm 5cm, 6cm,则连结三边中点所围成的三角形的周长是 __________________ cm.8.在Rt △ ABC中,/ C=90°, AC=?5 ?BC=?12, ?则连结两条直角边中点的线段长为 ____________ .9 .若三角形的三条中位线长分别为2cm, 3cm, 4cm,则原三角形的周长为()A . 4.5cmB . 18cmC . 9cmD . 36cm10. 如图2所示,A, B两点分别位于一个池塘的两端,小聪想用绳子测量A, B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A, B的点C,找到AC, BC的中点D, E,并且测出DE 的长为10m,则A, B间的距离为()A . 15mB . 25mC . 30mD . 20m11. 已知△ ABC的周长为1,连结△ ABC的三边中点构成第二个三角形,?再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( )A 1 1 1 1A、 B C D、2008 2009 20082 2009212.如图3所示,已知四边形ABCD R, P分别是DC BC上的点,E,F分别是AP, RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是()A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长不能确定13.如图4,在厶ABC中, E, D, F分别是AB, BC CA的中点,AB=6, AC=4,则四边形AEDF?勺周长是()A . 10B . 20C . 30D . 40A__________ D的线段叫做三角形的中位线.14. 如图所示,口ABCD的对角线AC, BD相交于点O, AE=EB求证:OE// BC.15. 已知矩形ABCD中,AB=4cm, AD=10cm,点P在边BC上移动,点E、F、G、H 分别是AB、AP、DP、DC的中点.求证:EF+GH=5cm;16 .如图所示,在△ ABC中,点D在BC上且CD=CA CF平分/ ACB AE=EB求证:EF=1BD.217.如图所示,已知在口ABCD中, E, F分别是AD, BC的中点,求证:MN/ BC.18.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、arc CD、DA的中点.求证:四边形EFGH是平行四边形.19.如图,点E, F, G, H分别是CD, BC, AB , DA的中点。
三角形中位线专项训练(30道)(解析版)

专题9.7 三角形中位线专项训练(30道)【苏科版】1.(2021秋•淅川县期末)如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为()A.2B.5C.7D.9【分析】根据三角形的中位线定理得出EF=12DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,N与A重合时,DN最小,从而求得EF的最大值为6.5,最小值是2.5,可解答.【解答】解:连接DN,∵ED=EM,MF=FN,∴EF=12DN,∴DN最大时,EF最大,DN最小时,EF最小,∵N与B重合时DN最大,此时DN=DB=√AD2+BD2=√52+122=13,∴EF的最大值为6.5.∵∠A=90°,AD=5,∴DN≥5,∴EF≥2.5,∴EF长度的可能为5;故选:B.2.(2021秋•渝中区校级期末)如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为()A.1B.2C.3D.4【分析】根据等腰三角形的性质得到AD=DC,根据三角形中位线定理解答即可.【解答】解:∵CB=6,BF=2,∴FC=6﹣2=4,∵BA=BC,BD⊥AC,∴AD=DC,∵AE=EF,∴DE是△AFC的中位线,∴DE=12FC=12×4=2,故选:B.3.(2021秋•龙岗区校级期末)如图,四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是()A.AD+BC>2EF B.AD+BC≥2EF C.AD+BC<2EF D.AD+BC≤2EF【分析】取AC的中点G,连接EF,EG,GF,根据三角形中位线定理求出EG=12BC,GF=12AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.【解答】解:如图,取AC的中点G,连接EF,EG,GF,∵E,F分别是边AB,CD的中点,∴EG,GF分别是△ABC和△ACD的中位线,∴EG=12BC,GF=12AD,在△EGF中,由三角形三边关系得EG+GF>EF,即12BC+12AD>EF,∴AD +BC >2EF ,当AD ∥BC 时,点E 、F 、G 在同一条直线上,∴AD +BC =2EF ,所以四边形ABCD 中,E ,F 分别是边AB ,CD 的中点,则AD ,BC 和EF 的关系是AD +BC ≥2EF .故选:B .4.(2021秋•荆门期末)如图,△ABC 的周长为20,点D ,E 在边BC 上,∠ABC 的平分线垂直于AE ,垂足为N ,∠ACB 的平分线垂直于AD ,垂足为M ,若BC =8,则MN 的长度为( )A .32B .2C .52 D .3【分析】证明△BNA ≌△BNE ,得到BE =BA ,AN =NE ,同理得到CD =CA ,AM =MD ,求出DE ,根据三角形中位线定理计算即可.【解答】解:在△BNA 和△BNE 中,{∠NBA =∠NBE BN =BN ∠BNA =∠BNE,∴△BNA ≌△BNE (ASA )∴BE =BA ,AN =NE ,同理,CD =CA ,AM =MD ,∴DE =BE +CD ﹣BC =BA +CA ﹣BC =20﹣8﹣8=4,∵AN =NE ,AM =MD ,∴MN =12DE =2,故选:B .5.(2021秋•宛城区期中)如图,在△ABC 中,∠A =90°,AC >AB >4,点D 、E 分别在边AB 、AC 上,BD =4,CE =3,取DE 、BC 的中点M 、N ,线段MN 的长为( )A .2.5B .3C .4D .5【分析】如图,作CH ∥AB ,连接DN ,延长DN 交CH 于H ,连接EH ,首先证明CH =BD ,∠ECH =90°,解直角三角形求出EH ,利用三角形中位线定理即可解决问题.【解答】解:作CH ∥AB ,连接DN 并延长交CH 于H ,连接EH ,∵BD ∥CH ,∴∠B =∠NCH ,∠ECH +∠A =180°,∵∠A =90°,∴∠ECH =∠A =90°,在△DNB 和△HNC 中,{∠B =∠NCH BN =CN ∠DNB =∠HNC,∴△DNB ≌△HNC (ASA ),∴CH =BD =4,DN =NH ,在Rt △CEH 中,CH =4,CE =3,∴EH =√CH 2+CE 2=√42+32=5,∵DM =ME ,DN =NH ,∴MN =12EH =2.5,故选:A .6.(2021•丹东模拟)如图,在△ABC 中,CE 是中线,CD 是角平分线,AF ⊥CD 交CD延长线于点F ,AC =7,BC =4,则EF 的长为( )A .1.5B .2C .2.5D .3【分析】延长AF 、BC 交于点G ,证明△ACF ≌△GCF ,根据全等三角形的性质得到CG =AC =7,AF =FG ,求出BG ,根据三角形中位线定理解答即可.【解答】解:延长AF 、BC 交于点G ,∵CD 是△ABC 的角平分线,∴∠ACF =∠BCF ,在△ACF 和△GCF 中,{∠ACF =∠GCF CF =CF ∠AFC =∠GFC =90°,∴△ACF ≌△GCF (ASA ),∴CG =AC =7,AF =FG ,∴BG =CG ﹣CB =3,∵AE =EB ,AF =FG ,∴EF =12BG =1.5,故选:A .7.(2021•碑林区校级模拟)如图,AD 为△ABC 的角平分线,BE ⊥AD 于E ,F 为BC 中点,连接EF ,若∠BAC =80°,∠EBD =20°,则∠EFD =( )A .26°B .28°C .30°D .32°【分析】延长BE 交AC 于G ,证△ABE ≌△AGE (ASA ),得BE =GE ,再由三角形中位线定理得EF ∥GC ,则∠EFD =∠C ,然后求出∠ABC =∠ABE +∠EBD =70°,即可解决问题.【解答】解:延长BE 交AC 于G ,如图所示:∵AD 平分∠BAC ,∠BAC =80°,∴∠BAE =∠GAE =12∠BAC =40°,∵BE ⊥AD ,∴∠BEA =∠GEA =90°,∵AE =AE ,∴△ABE ≌△AGE (ASA ),∴BE =GE ,∵F 为BC 的中点,∴EF 是△BCG 的中位线,∴EF ∥GC ,∴∠EFD =∠C ,∵∠BEA =90°,∴∠ABE =90°﹣∠BAE =90°﹣40°=50°,∴∠ABC =∠ABE +∠EBD =50°+20°=70°,∴∠EFD =∠C =180°﹣∠BAC ﹣∠ABC =180°﹣80°﹣70°=30°,故选:C .8.(2021秋•广饶县期末)如图,AD 是△ABC 的中线,E 是AD 的中点,F 是BE 延长线与AC 的交点,若AC =4,则AF =( )A .85 B .43 C .1 D .23 【分析】取EF 的中点H ,连接DH ,根据三角形中位线定理得到DH =12FC ,DH ∥AC ,证明△AEF ≌△DEH ,根据全等三角形的性质得到AF =DH ,计算即可.【解答】解:取EF 的中点H ,连接DH , ∵BD =DC ,BH =HF ,∴DH =12FC ,DH ∥AC ,∴∠HDE =∠F AE ,在△AEF 和△DEH 中,{∠AEF =∠DEH AE =DE ∠EAF =∠EDH,∴△AEF ≌△DEH (ASA ), ∴AF =DH ,∴AF =12FC , ∵AC =4,∴AF =43,故选:B .9.(2021春•平邑县期末)如图,在△ABC 中,AB =8,AC =6,AD 、AE 分别是其角平分线和中线,过点C 作CG ⊥AD 于F ,交AB 于G ,连接EF ,则线段EF 的长为( )A .1B .2C .32D .12【分析】证明△AFG ≌△AFC ,得到GF =FC ,根据三角形中位线定理计算即可.【解答】解:∵AD 是∠BAC 的角平分线,∴∠GAF =∠CAF ,∵CG ⊥AD ,∴∠AFG =∠AFC =90°,在△AFG 和△AFC 中,{∠AFG =∠AFC AF =AF ∠FAG =∠FAC,∴△AFG≌△AFC(ASA),∴GF=FC,AG=AC=6,∴GB=AB﹣AG=2,∵GF=FC,BE=EC,∴EF=12GB=1,故选:A.10.(2021春•宽城县期末)如图,E,F是四边形ABCD两边AB,CD的中点,G,H是对角线AC,BD的中点,若EH=6,则以下结论不正确的是()A.BC=12B.GF=6C.AD=12D.EH∥GF【分析】先判定EH为△ABD的中位线,GF为△ADC的中位线,然后根据三角形中位线性质对各选项进行判断.【解答】解:∵点E为AB的中点,点H为BD的中点,∴EH为△ABD的中位线,∴EH=12AD,EH∥AD,∵点F为CD的中点,点G为AC的中点,∴GF为△ADC的中位线,∴GF=12AD,GF∥AD,∴GF=EH=6,AD=2EH=12,EH∥GF,所以A选项符合题意,B选项、C选项和D 选项不符合题意.故选:A.二.填空题(共10小题)11.(2021秋•莱阳市期末)如图,D、E分别为△ABC的边AB、AC的中点.连接DE,过点B作BF平分∠ABC,交DE于点F.若EF=4,AD=7,则BC的长为22.【分析】根据三角形中位线定理得到DE ∥BC ,DE =12BC ,BD =AD =7,根据平行线的性质、角平分线的定义得到∠DBF =∠FBC ,根据等腰三角形的判定定理得到DF =BD =7,计算即可.【解答】解:∵D 、E 分别为△ABC 的边AB 、AC 的中点,∴DE ∥BC ,DE =12BC ,BD =AD =7,∴∠DFB =∠FBC ,∵BF 平分∠ABC ,∴∠DFB =∠DBF ,∴∠DBF =∠FBC ,∴DF =BD =7,∴DE =DF +EF =11,∴BC =2DE =22,故答案为:22.12.(2021秋•让胡路区校级期末)如图,△ABC 的周长为64,E 、F 、G 分别为AB 、AC 、BC 的中点,A ′、B ′、C ′分别为EF 、EG 、GF 的中点,△A ′B ′C ′的周长为 16 .如果△ABC 、△EFG 、△A ′B ′C ′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n 个三角形的周长是 27﹣n .【分析】根据E 、F 、G 分别为AB 、AC 、BC 的中点,可以判断EF 、FG 、EG 为三角形中位线,利用中位线定理求出EF 、FG 、EG 与BC 、AB 、CA 的长度关系即可求得△EFG 的周长是△ABC 周长的一半,△A ′B ′C ′的周长是△EFG 的周长的一半,以此类推,可以求得第n 个三角形的周长.【解答】解:∵如图,△ABC 的周长为64,E 、F 、G 分别为AB 、AC 、BC 的中点, ∴EF 、FG 、EG 为三角形中位线,∴EF =12BC ,EG =12AC ,FG =12AB ,∴EF +FG +EG =12(BC +AC +AB ),即△EFG 的周长是△ABC 周长的一半.同理,△A ′B ′C ′的周长是△EFG 的周长的一半,即△A ′B ′C ′的周长为14×64=16.以此类推,第n 个小三角形的周长是第一个三角形周长的64×(12)n ﹣1=27﹣n故答案是:27﹣n .13.(2021春•安徽月考)如图,在四边形ABCD 中,AD =BC ,∠DAB =50°,∠CBA =70°,P 、M 、N 分别是AB 、AC 、BD 的中点,若BC =6,则△PMN 的周长是 9 .【分析】根据三角形中位线定理得到PM ∥BC ,PM =12BC =3,PN ∥AD ,PN =12AD =3,根据等边三角形的判定和性质定理解答即可.【解答】解:∵P 、M 分别是AB 、AC 的中点,∴PM ∥BC ,PM =12BC =3,∴∠APM =∠CBA =70°,同理可得:PN ∥AD ,PN =12AD =3,∴∠BPN =∠DAB =50°,∴PM =PN =3,∠MPN =180°﹣50°﹣70°=60°,∴△PMN 为等边三角形,∴△PMN 的周长为9,故答案为:9.14.(2021秋•长春期中)如图所示,在△ABC 中,BC >AC ,点D 在BC 上,DC =AC =10,且AD BD =32,作∠ACB 的平分线CF 交AD 于点F ,CF =8,E 是AB 的中点,连接EF ,则EF 的长为 4 .【分析】根据等腰三角形的性质得到F 为AD 的中点,CF ⊥AD ,根据勾股定理得到DF =√CD 2−CF 2=6,根据三角形的中位线定理即可得到结论.【解答】解:∵DC =AC =10,∠ACB 的平分线CF 交AD 于F ,∴F 为AD 的中点,CF ⊥AD ,∴∠CFD =90°,∵DC =10,CF =8,∴DF =√CD 2−CF 2=6,∴AD =2DF =12,∵AD BD =32,∴BD =8,∵点E 是AB 的中点, ∴EF 为△ABD 的中位线,∴EF =12BD =4,故答案为:4.15.(2021•商丘四模)如图,四边形ABCD 中,点E 、F 分别为AD 、BC 的中点,延长FE交CD 延长线于点G ,交BA 延长线于点H ,若∠BHF 与∠CGF 互余,AB =4,CD =6,则EF 的长为 √13 .【分析】根据三角形的中位线定理和勾股定理解答即可.【解答】解:连接BD ,取BD 的中点M ,连接EM ,FM ,∵E 、F 分别为AD 、BC 的中点,M 为BD 的中点,∴EM ,MF 分别为△ADB 、△BCD 的中位线,∴EM ∥AB ,MF ∥DC ,EM =12AB =2,MF =12DC =3,∵MF ∥DC ,∴∠FGC =∠EFM ,∵EM ∥AB ,∴∠FEM =∠FHB ,∵∠BHF 与∠CGF 互余,∴∠CGF +∠BHF =∠EFM +∠FEM =90°,∴∠EMF =180°﹣∠EFM ﹣∠FEM =90°,∴△EMF 是直角三角形,∴EF=√EM2+FM2=√22+32=√13,故答案为:√13.16.(2021•香坊区校级开学)如图,在△ABC中,E是AB的中点,D是AC上一点,连接DE,BH⊥AC于H,若2∠ADE=90°﹣∠HBC,AD:BC=4:3,CD=2,则BC的长为6.【分析】如图,延长AC至N,使CN=BC,连接BN,由等腰三角形的性质可得∠ADE =∠N,可证DE∥BN,由三角形中位线定理可得AD=DN,即可求解.【解答】解:如图,延长AC至N,使CN=BC,连接BN,∵2∠ADE=90°﹣∠HBC,∠BCA=90°﹣∠HBC,∴∠BCA=2∠ADE,∵CN=BC,∴∠N=∠CBN,∴∠BCA=∠N+∠CBN=2∠N,∴∠ADE=∠N,∴DE∥BN,又∵E是AB的中点,∴DE是△ABN的中位线,∴AD=DN,∵AD:BC=4:3,∴设AD=DN=4x,BC=CN=3x,∴CD=DN﹣CN=x=2,∴BC=6,故答案为6.17.(2021春•牡丹区期末)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=13,AC=8,则DF的长为 2.5.【分析】延长CF交AB于点G,判断出AF垂直平分CG,得到AC=AG,根据三角形中位线定理解答.【解答】解:延长CF交AB于点G,∵AE平分∠BAC,∴∠GAF=∠CAF,∴AF垂直平分CG,∴AC=AG,GF=CF,又∵点D是BC中点,∴DF是△CBG的中位线,∴DF=12BG=12(AB﹣AG)=12(AB﹣AC)=2.5,故答案为:2.5.18.(2021春•洛阳期末)如图,D是△ABC的边BC的中点,AE平分∠BAC,BE⊥AE于点E,且AB=10cm,DE=2cm,则AC的长为6cm.【分析】延长AC 、BE 交于点F ,证明△AEB ≌△AEF ,根据全等三角形的性质得到AF =AB =10cm ,BE =EF ,根据三角形中位线定理计算即可.【解答】解:延长AC 、BE 交于点F ,∵AE 平分∠BAC ,∴∠BAE =∠CAE ,在△AEB 和△AEF 中,{∠BAE =∠FAE AE =AE ∠AEB =∠AEF =90°,∴△AEB ≌△AEF (ASA ),∴AF =AB =10(cm ),BE =EF ,∵BD =DC ,DE =2cm ,∴CF =2DE =4(cm ),∴AC =AF ﹣CF =6(cm ),故答案为:6.19.(2021春•盐湖区校级期末)如图,在四边形ABCD 中,AB =CD ,M 、N 、P 分别是AD 、BC 、BD 的中点,若∠MPN =130°,则∠NMP 的度数为 25° .【分析】根据中位线定理和已知,易证明△PMN 是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN 的度数.【解答】解:在四边形ABCD 中,M 、N 、P 分别是AD 、BC 、BD 的中点,∴PN ,PM 分别是△CDB 与△DAB 的中位线,∴PM =12AB ,PN =12DC ,PM ∥AB ,PN ∥DC ,∵AB =CD , ∴PM =PN ,∴△PMN 是等腰三角形,∵∠MPN=130°,∴∠PMN=180°−130°2=25°.故答案为:25°.20.(2021春•虹口区校级期末)如图,在△ABC中,BM、CN平分∠ABC和∠ACB的外角,AM⊥BM于M,AN⊥CN于N,AB=10,BC=13,AC=6,则MN= 4.5.【分析】延长AM交BC于点G,根据BM为∠ABC的平分线,AM⊥BM得出∠BAM=∠G,故△ABG为等腰三角形,所以AM=GM.同理AN=DN,根据三角形中位线定理即可求得MN.【解答】解:延长AM交BC于点G,延长AN交BC延长线于点D,∵BM为∠ABC的平分线,∴∠CBM=∠ABM,∵BM⊥AG,∴∠ABM+∠BAM=90°,∠MGB+∠CBM=90°,∴∠BAM=∠MGB,∴△ABG为等腰三角形,∴AM=GM.BG=AB=10,同理AN=DN,CD=AC=6,∴MN为△ADG的中位线,∴MN=12DG=12(BC﹣BG+CD)=12(BC﹣AB+AC)=12(13﹣10+6)=4.5.故答案为:4.5.三.解答题(共10小题)21.(2019春•岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.【分析】连接DE,FG,由BD与CE为中位线,利用中位线定理得到ED与BC平行,FG与BC平行,且都等于BC的一半,等量代换得到ED与FG平行且相等,进而得到四边形EFGD为平行四边形,利用平行四边形的性质即可得证.【解答】证明:连接DE,FG,∵BD,CE是△ABC的中线,∴D,E是AB,AC的中点,∴DE∥BC,DE=12BC,同理:FG∥BC,FG=12BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.22.(2021秋•桓台县期末)如图,在四边形ABCD中,E,F分别是AD,BC的中点.(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.【分析】(1)取BD的中点P,利用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理来求EF的长度;(2)如图,取BD的中点P,连接EP、FP.用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理即可得到结论.【解答】(1)解:如图,取BD的中点P,连接EP、FP.∵E,F分别是AD、BC的中点,AB=6,CD=8,∴PE ∥AB ,且PE =12AB =3,PF ∥CD 且PF =12CD =4.又∵∠ABD =30°,∠BDC =120°,∴∠EPD =∠ABD =30°,∠DPF =180°﹣∠BDC =60°,∴∠EPF =∠EPD +∠DPF =90°,在直角△EPF 中,由勾股定理得到:EF =√EP 2+PF 2=√32+42=5,即EF =5;(2)证明:如图,取BD 的中点P ,连接EP 、FP .∵E ,F 分别是AD 、BC 的中点,∴PE ∥AB ,且PE =12AB ,PF ∥CD 且PF =12CD .∴∠EPD =∠ABD ,∠BPF =∠BDC ,∴∠DPF =180°﹣∠BPF =180°﹣∠BDC ,∵∠BDC ﹣∠ABD =90°,∴∠BDC =90°+∠ABD ,∴∠EPF =∠EPD +∠DPF =∠ABD +180°﹣∠BDC =∠ABD +180°﹣(90°+∠ABD )=90°,∴PE 2+PF 2=(12AB )2+(12CD )2=EF 2,∴AB 2+CD 2=4EF 2.23.(2021秋•莱州市期末)已知:如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,且AC =BD ,E 、F 分别是AB 、CD 的中点,EF 分别交BD 、AC 于点G 、H .求证:OG =OH .【分析】取BC 边的中点M ,连接EM ,FM ,则根据三角形的中位线定理,即可证得△EMF 是等腰三角形,根据等边对等角,即可证得∠MEF =∠MFE ,然后根据平行线的性质证得∠OGH =∠OHG ,根据等角对等边即可证得.【解答】解:取BC边的中点M,连接EM,FM,∵M、F分别是BC、CD的中点,∴MF∥BD,MF=12BD,同理:ME∥AC,ME=12AC,∵AC=BD∴ME=MF∴∠MEF=∠MFE,∵MF∥BD,∴∠MFE=∠OGH,同理,∠MEF=∠OHG,∴∠OGH=∠OHG∴OG=OH.24.(2021春•抚州期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.(1)求证:CE=DE;(2)若点F为BC的中点,求EF的长.【分析】(1)根据ASA证明△AEC和△AED全等,进而利用全等三角形的性质解答即可;(2)根据勾股定理得出AB,进而利用三角形中位线定理解答即可.【解答】(1)证明:∵AE平分∠CAB,∴∠CAE=∠BAE,∵CE⊥AE,∴∠AEC =∠AED =90°,在△AEC 和△AED 中,{∠CAE =∠DAE AE =AE ∠AEC =∠AED,∴△AEC ≌△AED (ASA ),∴CE =DE ;(2)在Rt △ABC 中,∵AC =6,BC =8,∴AB =√AC 2+BC 2=√62+82=10,∵△AEC ≌△AED ,∴AD =AC =6,∴BD =AB ﹣AD =4,∵点E 为CD 中点,点F 为BC 中点,∴EF =12BD =2.25.(2021春•秦都区期末)如图,在△ABC 中,AB =AC ,点D 、E 分别是边AB 、AC 上的点,连接BE 、DE ,∠ADE =∠AED ,点F 、G 、H 分别为BE 、DE 、BC 的中点.求证:FG =FH .【分析】根据等腰三角形的判定定理得到AD =AE ,根据线段的和差得到BD =CE ,根据三角形的中位线定理即可得到结论.【解答】证明:∵∠ADE =∠AED ,∴AD =AE ,∵AB =AC ,∴AB ﹣AD =AC ﹣AE ,即BD =CE ,∵点F 、G 、H 分别为BE 、DE 、BC 的中点,∴FG 是△EDB 的中位线,FH 是△BCE 的中位线,∴FG =12BD ,FH =12CE ,∴FG =FH .26.(2021春•泰兴市月考)如图,在四边形ABCD 中,AB =CD ,E 、F 分别是BC 、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.【分析】连接BD,取BD的中点H,连接HE,HF,根据三角形的中位线的性质得到FH∥BM,FH=12AB,EH∥CN,EH=12CD,根据平行线的性质得到∠BME=∠HFE,∠CNE=∠HEF,根据等腰三角形的性质得到∠HFE=∠HEF,等量代换即可得到结论.【解答】证明:连接BD,取BD的中点H,连接HE,HF,∵E、F分别是BC、AD的中点,∴FH∥BM,FH=12AB,EH∥CN,EH=12CD,∴∠BME=∠HFE,∠CNE=∠HEF,∵AB=CD,∴FH=EH,∴∠HFE=∠HEF,∴∠BME=∠CNE.27.(2021春•沈北新区期末)如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=12CF.【分析】过D 作DG ∥AC ,可证明△AEF ≌△DEG ,可得AF =DG ,由三角形中位线定理可得DG =12CF ,可证得结论.【解答】证明:如图,过D 作DG ∥AC ,则∠EAF =∠EDG ,∵AD 是△ABC 的中线,∴D 为BC 中点, ∴G 为BF 中点,∴DG =12CF ,∵E 为AD 中点,∴AE =DE ,在△AEF 和△DEG 中,{∠EAF =∠EDG AE =DE ∠AEF =∠DEG,∴△AEF ≌△DEG (ASA ), ∴DG =AF ,∴AF =12CF .28.(2021春•莆田期末)如图,已知四边形ABCD 的对角线AC 与BD 相交于点O ,且AC=BD ,M 、N 分别是AB 、CD 的中点,MN 分别交BD 、AC 于点E 、F .你能说出OE 与OF 的大小关系并加以证明吗?【分析】此题要构造三角形的中位线,根据三角形的中位线定理进行证明.【解答】解:相等.理由如下:取AD 的中点G ,连接MG ,NG ,∵G 、N 分别为AD 、CD 的中点, ∴GN 是△ACD 的中位线,∴GN =12AC ,同理可得,GM=12BD,∵AC=BD,∴GN=GM=12AC=12BD.∴∠GMN=∠GNM,又∵MG∥OE,NG∥OF,∴∠OEF=∠GMN=∠GNM=∠OFE,∴OE=OF.29.(2021春•城固县期末)如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD 的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.【分析】根据三角形中位线定理得到EG=12AC,EG∥AC,FG=12BD,FG∥BD,根据平行线的性质、等腰三角形的性质和判定定理证明结论.【解答】证明:∵E,G为AB、BC中点,∴EG=12AC,EG∥AC,∴∠FEG=∠OQP,同理,FG=12BD,FG∥BD,∴∠EFG=∠OPQ,∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP,∴OP=OQ.30.(2021春•三水区期末)如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.【分析】(1)由中点性质及AB=AC,得到BD=EC,再由中位线性质证明FG∥BD,GF=12BD,FH∥EC,FH=12EC,从而得到FG=FH;(2)由(1)FG∥BD,FH∥EC,再由∠A=90°,可证FG⊥FH;(3)由(1)FG∥BD,∠A=80°,可求得∠FKC,再由FH∥EC,可求得∠GFH的度数.【解答】(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点∴BD=EC∵点F,G,H分别为BE,DE,BC的中点∴FG∥BD,GF=12 BDFH∥EC,FH=12 EC∴FG=FH;(2)证明:由(1)FG∥BD又∵∠A=90°∴FG⊥AC∵FH∥EC∴FG⊥FH;(3)解:延长FG交AC于点K,∵FG∥BD,∠A=80°∴∠FKC=∠A=80°∵FH∥EC∴∠GFH=180°﹣∠FKC=100°。
(完整版)三角形的中位线经典练习题及其答案

八年级三角形的中位线练习题及其答案1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4。
如图△ABC 中,D 、E 分别是AB 、AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)如果EF =4cm ,那么BC =__cm 如果AB =10cm ,那么DF =___cm(2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm ,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm . 8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm,4cm,则原三角形的周长为( ) A .4。
5cm B .18cm C .9cm D .36cm10.如图2所示,A ,B 两点分别位于一个池塘的两端,小聪想用绳子测量A ,B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A ,B 的点C ,找到AC ,BC 的中点D,E ,并且测出DE 的长为10m ,则A ,B 间的距离为( )A .15mB .25mC .30mD .20m11.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形,•再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、22009112.如图3所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减少 C .线段EF 的长不变 D .线段EF 的长不能确定13.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6,AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .4014.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .15.已知矩形ABCD 中,AB =4cm ,AD =10cm ,点P 在边BC 上移动,点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点。
三角形的中位线基础题30道解答题

9.5 三角形的中位线基础题汇编(3)BCBC=3DE=6中点重合)EF=EF=CE=,求BCD=EM=(9.5 三角形的中位线基础题汇编(3)参考答案与试题解析一.解答题(共30小题)1.如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.四边形EGFH是平行四边形吗?请证明你的结论.2.请写出“如图,在△ABC中,若DE是△ABC的中位线,则DE=BC”的逆命题.判断逆命题的真假,并说明你的理由?BC3.在四边形ABCD中,BD、AC相交于点O,AC=BD,E、F分别是AB、CD的中点,连接EF,分别交AC、BD 于点M、N.判断△MON的形状,并说明理由.EG=4.如图,在△ABC中,AD⊥BC于点D,E、F、G分别是BC、AC、AB的中点,若AB=BC=3DE=6,求四边形DEFG的周长.BC=3DE=6BC=3DE=6EF=×BC=×,AB=×=GF+DG+DE+EF=+3+2+3=.5.如图,在△ABC中(AB≠AC),M为BC的中点,AD平分∠BAC交BC于D,BE⊥AD于E,CF⊥AD于F,求证:ME=MF.MF=ME=GBME=6.△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:AC=3AF.7.如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.BE=NZ BE=MY8.如图,AB为⊙O的一条弦,CD为直径(C不与A、B及中点重合),作CE⊥AB于E,DF⊥AB于F,问CE﹣DF的值是否变化?为什么?9.△ABC中,D为CB的延长线上一点,BE是∠ABD的角平分线,AE⊥BE,F是AC的中点,试说明:EF∥BC,且EF=(AB+BC).EF=10.如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.GE=GF=CDAB GF=CD11.已知,如图,AB=AC=BE,CD为△ABC中AB边上的中线,求证:CE=2CD.12.如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点.(1)求证:AF∥DE;(2)当AC=6,AB=10时,求BE的长.==,,BE=13.在四边形ABCD中,AB∥CD,E、F是AD、BC中点.求证:EF=(AB+CD),EF∥CD.EF=DM=14.如图,已知△ABC中,点D是BA上一点,BD=AC,E,F分别是BC,DA的中点,EF和CA的延长线相交于点G.求证:AG=AF.15.如图,AD是△ABC的中线,E,F,G分别是AB,AD,DC的中点,求证:EG与DF互相平分.ACED=16.已知:如图,点B是AD的中点,点E是AB的中点,AB=AC 求证:CE=CD.ACBE=CDCE=17.在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.EF=EF=EF=18.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.BC=519.已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求的值.(用多种方法解答);或过BF=DM==20.在△ABC中,D是AB的中点,DC⊥AC且tan∠BCD=,求tanA的值.BCD=,设,即BCD==ABBE=CE=AC.21.已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.22.已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=(AB﹣AC).CF=CF23.如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.24.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.PM=PN=ADBC PN=AD25.如图,△ABC中,BM平分∠ABC,AM⊥BM,垂足M点,点N为AC的中点,AB=10,BC=6,求MN长度.MN=26.已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?27.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.EF=28.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE=EB.求证:OE∥BC.29.△ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=(AB+AC).BF=CE=30.如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少?BCBC BCDG+EH+FI=BC+BC=。
(完整版)三角形的中位线习题归类(绝对经典-绝对震撼)

三角形的中位线习题全面归类一、 直接应用1. 如图1所示,EF 是△ABC 的中位线,若BC=8cm , 则EF=_______cm .2.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点 所围成的三角形的周长是_________cm .3.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角 边中点的线段长为_______.4.若三角形的三条中位线长分别为2cm ,3cm ,4cm , 则原三角形的周长为_______.5.如图2所示,A ,B 两点分别位于一个池塘的两端, 小聪想用绳子测量A ,B 间的距离,但绳子不够长,一 位同学帮他想了一个主意:先在地上取一个可以直接到 达A ,B 的点C ,找到AC ,BC 的中点D ,E ,并且测出DE 的长为10m ,则A ,B 间的距离为_______.6.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形, •再连结第二个三角形的三边中点构成第三个三角形,依此类推, 第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、2200917.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6, AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .408.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .9.如图所示,在△ABC 中,点D 在BC 上且CD=CA , CF 平分∠ACB ,AE=EB ,求证:EF=12BD .10.如图所示,已知在□ABCD 中,E ,F 分别是 AD ,BC 的中点,求证:MN ∥BC .11.已知:如图,E 为□ABCD 中DC 边的延长线上的一点, 且CE =DC ,连结AE 分别交BC 、BD 于点F 、G ,连结AC 交BD 于O ,连结OF .求证:AB =2OF .12.如图,△ABC 中,AD=41AB ,AE=41AC ,BC=16.求DE 的长.(角平分线的垂线必有等腰三角形)13.如图,在△ABC 中,已知AB=6,AC=10,AD 平分 ∠BAC ,BD ⊥AD 于点D ,E•为BC 中点.求DE 的长.14.如图,AD 是△ABC 的外角平分线,CD ⊥AD 于D ,E 是BC 的中点. 求证:(1)DE ∥AB ; (2)DE=21(AB+AC )如图17,BE 、CF 是△ABC 的角平分线,AN ⊥BE 于N ,AM ⊥CF 于M .BGA EFH DC求证:MN ∥BC .二、中点寻线,线组形(多个中点)1.如图,在四边形ABCD 中,点E 是线段AD 上的任意一点 ,G F H ,,分别是BE BC CE ,,的中点. 证明四边形EGFH 是平行四边形;2.如图,在四边形ABCD 中,AD=BC ,点 E ,F ,G 分别是AB ,CD ,AC 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲三角形的中位线1 .连结三角形 的线段叫做三角形的中位线.2 .三角形的中位线 于第三边,并且等于3 . 一个三角形的中位线有 条.4 .如图△ ABC 中,D E 分别是 AR AC 的中点,则线段 CDb^4ABC 的,线段DE 是4ABC5、如图,D E 、F 分别是^ ABC 各边的中点 (1)如果 EF= 4cm,那么BC 的 cm如果 AB= 10cm,那么 DF 的 cm(2)中线AD 与中位线EF 的关系是6.如图1所示,EF 是4ABC 的中位线,若 BC=8cm 贝U EF=cm.⑴ (2) (3) ⑷7 .三角形的三边长分别是 3cm, 5cm, 6cm,则连结三边中点所围成的三角形的周长是 cm. 8 .在Rt^ABC 中,/ C=90° , AC=?5 ?BC=?12, ?则连结两条直角边中点的线段长为 . 9 .若三角形的三条中位线长分别为 2cm, 3cm, 4cm,则原三角形的周长为()A .B . 18cmC . 9cmD . 36cm10 .如图2所示,A, B 两点分别位于一个池塘的两端,小聪想用绳子测量A, B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达 A, B 的点C,找到AC,BC 的中点D,E,并且测出DE的长为10m,则A, B 间的距离为()A . 15mB . 25mC . 30mD . 20m11 .已知△ ABC 的周长为1,连结△ ABC 的三边中点构成第二个三角形,?再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是A 、200820092008 2 20092 12.如图3所示,已知四边形 ABCD R, P 分别是DQ BC 上的点,E, F 分别是AP, RP 的中点,当点P 在BC 上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是()A .线段EF 的长逐渐增大B .线段EF 的长逐渐减少C .线段EF 的长不变D .线段EF 的长不能确定13.如图 4,在4ABC 中,E, D, F 分别是 AB, BG CA 的中点,AB=6,AC=4,贝U 四边形AEDF?勺周长是()20 C . 30 D . 4014.如图所示, □ ABCD 的对角线 AC, BD 相交于点 O, AE=EB 求证:OE// BC.15.已知矩形ABCD中,AB=4cm, AD=10cm,点P在边BC上移动,点E、F、G、H 分别是AB、AP、DP、DC的中点.求证:EF+GH=5cm;16.如图所示,在^ ABC中,点D在BC上且CD=CA CF平分/ ACB AE=EB求证:1 EF=-BD.217.如图所示,已知在DABCN, E, F分别是AD, BC的中点,求证:MN/ BC.四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.EFGH是平行四边形.18.已知:如图,求证:四边形19.如图,点E, F, G, H分别是CD, BC, AB, DA的中点。
求证:四边形EFGH是平行四边形。
EDHE<A\G F20.已知:△ ABC的中线BD、CE交于点O, F、G分别是OB、OC的中点. 求证:四边形DEFG是平行四边形.21.如图5,在四边形ABCD中,点E是线段AD上的任意一点(E与A, D不重合),G, F, H分别是BE, BC, CE的中点.证明四边形EGFH是平行四边形;22如图,在四边形ABCD中,AD=BC,点E, F, G分别是AB , CD, AC的中点。
求证:△ EFG是等腰三角形。
23.如图,在^ ABC中,已知AB=6, AC=1Q A叶分/ BAC BD!AD于点D, E劝BC中点.求DE的长.24.已知:如图,E为DABCD中DC边的延长线上白一点,且CE=DC,连结AE 分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB = 2OF.25.已知:如图,在DABCD中,E是CD的中点, F是AE的中点,FC与BE交于G.求证:GF = GC.26.已知:如图,在四边形ABCD中,AD = BC, E、的延长线F分别是DC、AB边的中点,FE的延长线分别与AD、BC 交于H、G点.求证:/ AHF =/ BGF .三角形的内角和定理旧市学校李姿慧教学目标1.知识与技能:⑴掌握三角形内角和定理的证明。
⑵初步体会添加辅助线证题,培养学生观察、猜想和论证的能力2.过程与方法:经历探索三角形内角和定理的过程,初步体会思维的多样性,给学生渗透化归的数学思想。
3.情感态度与价值观:通过师生的共同活动,培养学生的逻辑思维能力,进而激发学生的求知欲和学习的积极主动性。
使学生主动探索,敢于实验,勇于发现,合作交流。
教学重点三角形内角和定理的证明及其简单的应用。
教学难点在三角形内角和定理的证明过程中如何添加辅助线。
教学用具多媒体、三角板、学生每人准备一个纸片三角板。
教学过程一、引入新课分享小故事:《内角三兄弟之争》在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”老二很纳闷.同学们,你们知道其中的道理吗?从而引出本节课的课题《三角形的内角和定理》二、合作探究1、[师]现在,我们来看两个电脑的动画演示,验证这个结论是不是正确的。
动画演示一图 6-39[师]先将△ ABC 中的/ A 通过平移和旋转到如上图所示的位置,再将图中的/ 移到上图所示的位置。
拖动点A,改变/\ ABC 的形状,三角形的三个内角和总等于180°2.动画演示二[师]先将三角形纸片(图(1)) 一角折向其对边,使顶点落在对边上,折线与对边平行 (图(2)),然后把另外两角相向对折,使其顶点与已折角的顶点相重合(图(3) (4)。
)[师]由电脑的动画演示可知:/A 、/B 、/C 拼成的角总是一个平角,由此得到三角形的三个内角之和等于 180。
[让学生直观感受,调动其研究兴趣]我们通过观察与实验的方法猜想得到的结论不一定正确可靠,要判定一个数学结论 正确与否,需要进行有根有据的推理、证明。
这就是我们这节课所要研究的内容。
3、定理证明[师]接下来我们来证明这个命题:三角形的三个内角之和等于180°。
这是一个文字命题,证明时需要先做什么呢[生]需要先画出图形、根据命题的条件和结论,结合图形写出已知、求证。
章前面几节作为基础,学生有能力画图,写已知,求证。
[师]很好!怎样证明呢?[联想前面撕角拼角的方法,学生能想到。
化的数学思想方法,把新知识化为旧知识。
][生]添加辅助线,延长 BC 到点D,过点C 作CE// AB, / A=Z ACE / B=Z ECD 进而将三个内角拼成平角。
[通过以上分析、研究,让学生讲解依据:根据平行线的性质,B 通过平[有本让学生体会转利用同位角,内错角把三角形三内角转化为一个平角。
使学生亲身参与数学研究的过程,并在过程中体会数学研究的乐趣。
][实验法]已知:△ ABC 求证:/ A+/ B+/ C=180°证明:延长BC到点D,过点C作CE// AB••• CEE// AB/ A=Z ACE(两直线平行,内错角相等)/ B=/ECD两直线平行,同位角相等)••• / ACE吆ECD廿BCA=180/ A+Z B+Z BCA=180 (等量代换)[教师引导,要把三角形三个内角转化为上述两种角,就要在原图形上添加一些线, 这些线叫做辅助线,在平面几何里,辅助线常画成虚线,添辅助线是解决问题的重要思想方法。
]4、探究讨论:五个学生为一组,探索三角形内角和定理的其它证法分析、证明方法。
[师]现在,各组派一名代表说明证明的思路。
[学生自己得出的猜想和证明会更让他们乐于接受,而方法也在此过程中渗透给了学生。
]证法1.[生1]过点A作直线PQ// BG使三个角凑到“ A处。
[通过分析、研究, 让不同做法的学生讲解依据。
]根据平行线的性质,利用内错角,把三角形三内角转化为一个平角。
证明:过点A作直线PQ/ BC••• PQ// BCB=Z PAB(两直线平行,内错角相等)/ C=Z QAC的直线平行,内错角相等)••• / PAB+Z QAC廿BAC=180. • / B+/ C+/ BAC=180 (等量代换)证法2:[生5]过点A作AD// BG有/ C=Z 2,将三个内角拼成一对同旁内角。
证明:过点A作射线AQ// BCC=Z QAC两直线平行,内错角相等)/QAC廿BAC吆B=180° (两直线平行,同旁内角互补••• / BAC+Z B+Z C=180° (等量代换)[师]同学们讨论得真棒。
我们由180°联想到一平角等于180°,一对邻补角之和图6-39等于180 °,两直线平行,同旁内角互补。
由此,大家提供了这么多的的证明方法,说明你们能学以致用。
接下来,我们做练习以巩固三角形内角和定理。
[ 根据以上几种辅助线的作法,选择一种, 师生合作,写出示范性证明过程。
其余由学生自主完成证明过程。
目的是培养学生的思维能力和推理能力。
进一步搞清作辅助线的思路和合乎逻辑的分析方法,充分让学生表述自己的观点,这个过程对培养学生的能力极为重要,依据不充分时,学生可争论,师生共同小结。
]三、例题讲解【例】在^ ABC中,/ A=55° , / B=25° ,求/ C的度数。
变式一:/ A=40° , / B比/ C大30°,求/ B、/ C的度数。
变式二:/ A的度数是/ B的度数的3倍,/ C比/ B大15° ,求/ A、/ R /C的度数。
[ 学生自主探索,教师巡视、诊断,让学生上台板演,学生辨析,教师小结。
][ 使学生灵活应用三角形内角和定理。
用代数方法解决几何问题(方程思想)是重要的方法。
]四、随堂练习1.(苏州•中考)△ ABC的内角和为()A.180° B .360° C .540° D .720°2.在直角三角形ABC中,一个锐角为40。
,则另一个锐角是。
.3.(济宁•中考)若一个三角形三个内角度数的比为 2 : 3 : 4,那么这个三角形是()C. 钝角三角形D. 等边三角形五、师生共同小结本节课你们收获了什么?六、课外作业1.教材课后练习1、2、2.学法大视野第三课时教学反思三角形的有关知识是“空间与图形”中最为核心、最为重要的内容,它不仅是最基本的直线型平面图形,而且几乎是研究所有其它图形的工具和基础而三角形内角和定理又是三角形中最为基础的知识,也是学生最为熟悉且能与小学、中学知识相关联的知识,看似简单,但如果处理不好,会导致学生有厌烦心理。
