将军饮马的六种模型

合集下载

将军饮马问题的11个模型及例题

将军饮马问题的11个模型及例题将军饮马问题是一个经典的逻辑问题，涉及到将军如何用有限数量的马和酒到达目的地。

本文将介绍将军饮马问题的11个模型及相应的例题。

1. 直线模型将军与目的地之间没有障碍物，可以直线前进。

此时，将军只需将马拉到目的地即可。

例题1：将军与目的地之间距离为10公里，马的速度为每小时5公里，将军能否在2小时内到达目的地？2. 单个障碍物模型在将军与目的地之间存在一个障碍物，将军可以绕过该障碍物。

例题2：将军与目的地之间距离为15公里，马的速度为每小时4公里，障碍物位于距离将军起点5公里处，将军能否在3小时内到达目的地？3. 多个障碍物模型在将军与目的地之间存在多个障碍物，将军需要逐一绕过这些障碍物。

例题3：将军与目的地之间距离为20公里，马的速度为每小时6公里，障碍物位于距离将军起点分别为5公里、10公里和15公里的位置，将军能否在4小时内到达目的地？4. 跳跃模型将军可以让马跳过障碍物，从而直接到达目的地。

例题4：将军与目的地之间距离为12公里，马的速度为每小时8公里，将军在距离起点6公里处设置一个障碍物，将军能否在2小时内到达目的地？5. 限时模型将军需要在规定的时间内到达目的地。

例题5：将军与目的地之间距离为30公里，马的速度为每小时10公里，将军需要在3小时内到达目的地，是否可能？6. 守备模型目标地点有守备军，将军需要巧妙规避守备军。

例题6：将军与目的地之间距离为25公里，马的速度为每小时7公里，目的地有一支守备军位于距离目标地点10公里处，将军能否在4小时内到达目的地？7. 短平快模型将军不借助马匹，直接徒步走到目的地。

例题7：将军与目的地之间距离为8公里，将军的步行速度为每小时2公里，将军能否在4小时内到达目的地？8. 时间窗模型将军只能在规定时间范围内到达目的地。

例题8：将军与目的地之间距离为18公里，马的速度为每小时6公里，将军需要在3小时到4小时之间到达目的地，是否可能？9. 兵变模型将军需要利用敌军马匹达到目的地。

初中数学之将军饮马的6种模型(培优)

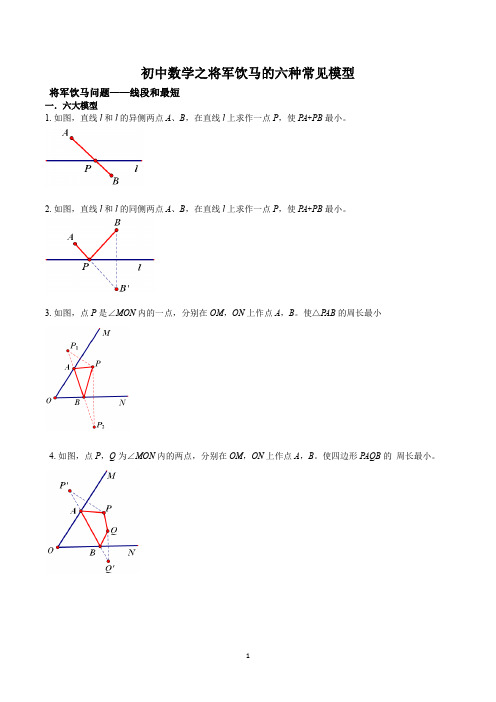
初中数学之将军饮马的六种常见模型将军饮马问题——线段和最短一．六大模型1.如图，直线l和l的异侧两点A、B，在直线l上求作一点P，使P A+PB最小。

2.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使P A+PB最小。

3.如图，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△P AB的周长最小4.如图，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形P AQB的周长最小。

5.如图，点A是∠MON外的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小6. .如图，点A是∠MON内的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小二、常见题目类型一、三角形1．如图，在等边△ABC中，AB= 6，AD⊥BC，E是AC上的一点，M是AD上的一点，AE=2，求EM+EC 的最小值解：∵点C关于直线AD的对称点是点B，∴连接BE，交AD于点M，则ME+MD最小，过点B作BH⊥AC于点H，则EH = AH–AE = 3–2 = 1，BH=在直角△BHE中，BE2．如图，在锐角△ABC中，AB =BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是____．解：作点B关于AD的对称点B'，过点B'作B'E⊥AB于点E，交AD于点F，则线段B'E长就是BM＋ＭＮ的最小值在等腰Rt△AEB'中，根据勾股定理得到，B'E = 43．如图，△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，则这个最小值解：作AB关于AC的对称线段AB'，过点B'作B'N⊥AB，垂足为N，交AC于点M，则B'N= MB'+MN = MB+MN. B'N的长就是MB+MN的最小值，则∠B'AN = 2∠BAC= 60°，AB' = AB = 2，∠ANB'= 90°，∠B' = 30°。

初中数学将军饮马问题的六种常见题型汇总

初中数学将军饮马问题的六种常见模型将军饮马问题——线段和最短一．六大模型1.如图，直线l和l的异侧两点A、B，在直线l上求作一点P，使P A+PB最小。

2.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使P A+PB最小。

3.如图，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△P AB的周长最小4.如图，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形P AQB的周长最小。

5.如图，点A是∠MON外的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小第 1 页共10 页第 2 页共 10 页 6. .如图，点A 是∠MON 内的一点，在射线ON 上作点P ，使P A 与点P 到射线OM 的距离之和最小二、常见题目【1】、三角形1．如图，在等边△ABC 中，AB = 6，AD ⊥BC ，E 是AC 上的一点，M 是AD 上的一点，AE =2，求EM +EC 的最小值解： ∵点C 关于直线AD 的对称点是点B ，∴连接BE ，交AD 于点M ，则ME +MD 最小，过点B 作BH ⊥AC 于点H ，则EH = AH – AE = 3 – 2 = 1，BH =22BC CH -=2263-=33在直角△BHE 中，BE =22BH EH - =22(33)1+=272．如图，在锐角△ABC 中，AB =42，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM +MN 的最小值是____．解：作点B 关于AD 的对称点B '，过点B '作B 'E ⊥AB 于点E ，交AD 于点F ，则线段B 'E 长就是BM ＋ＭＮ的最小值在等腰Rt △AEB '中，根据勾股定理得到，B 'E = 43．如图，△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，则这个最小值解：作AB关于AC的对称线段AB'，过点B'作B'N⊥AB，垂足为N，交AC于点M，则B'N = MB'+MN = MB+MN. B'N的长就是MB+MN的最小值，则∠B'AN = 2∠BAC= 60°，AB' = AB = 2，∠ANB'= 90°，∠B' = 30°。

初中数学最值问题六种模型

初中数学最值问题有六种模型，包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。

1. 将军饮马模型：当两定点A、B在直线l同侧时，在直线上找一点P，使PA+PB最小。

可以理解为两点之间线段最短。

连接AB交直线l于点P，点P即为所求作的点。

2. 一箭穿心模型：在直线l上找M、N两点（M在左），使得AM+MN+NB最小，且MN=d。

将点A向右平移d个单位到A′，作A′关于直线l的对称点A"，连接A"B交直线l 于点N，将点N向左平移d个单位到M，点M、N即为所求。

3. 费马点模型：在三角形ABC中，若D、E分别是AB、AC 上的点，则DE的延长线与BC的延长线交于费马点处，此时三角形周长最小。

4. 阿氏圆模型：以给定点A为圆心，给定距离r为半径画圆，与已知直线l相交于两点B、C，连接两点B、C并延长交于D。

则D点的轨迹是以A为圆心，r为半径的圆。

这个圆被称为阿氏圆。

5. 胡不归模型：在直角三角形ABC中，AB=c，AC=b，BC=a，AD为BC边上的高。

若点P在BC边上，问是否存在点P使得DP垂直于BC边？如果存在，求出点P的位置；
如果不存在，请说明理由。

6. 瓜豆原理模型：在一条直线上有若干个点，每个点都有一个到直线的距离，问如何选择若干个点使得这些点到直线的距离之和最小？瓜豆原理告诉我们，选择任意两个相邻的点并连接它们与直线的交点，然后选择第三个点与前两个点的距离之和最小即可。

以上是初中数学最值问题的六种模型，希望对解决这类问题有所帮助。

将军饮马模型

、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦? 一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题.将军每天从军营A 出发，先到河边饮马，然后再去河岸同侧的军营B 开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它. 从此以后，这个被称为“将军饮马” 的问题便流传至今.【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1:在定直线I上找一个动点P,使动点P到两个定点A与B的距离之和最小，即PA+PB最小.作法：连接AB 与直线I 的交点Q,Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB 最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB,与直线I的交点Q P为直线I上任意一点例2 :在定直线I上找一个动点P,使动点P到两个定点A与B的距离之和最小即PA+PB 的和最小.关键:找对称点作法：作定点B关于定直线I的对称点C,连接AC，与直线I的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC,与直线I的交点Q P为直线I上任意一点，在"PAC中，由三角形三边关系可知：AP+P&AC （当且仅当PQ重合时取=）2.两动一定型例3 :在/ MON 的内部有一点A,在0M上找一点B,在ON上找一点C,使得△ BAC周长最短.作法：作点A关于0M的对称点A',作点A关于ON的对称点A''，连接A' A',与0M交于点B,与ON 交于点C,连接AB AC, △ABC即为所求.原理：两点之间，线段最短例4:在/MON的内部有点A和点B,在OM上找一点C,在ON上找一点D,使得四边形周长最短.作法：作点A关于OM的对称点A,作点B关于ON的对称点B'，连接A B '，与交于点C,与ON交于点D,连接AC, BD AB,四边形ABCD即为所求.原理：两点之间，线段最短3.两定两动型最值例5:已知A B是两个定点，在定直线I上找两个动点M与N,且MN长度等于定长d （动点M位于动点N 左侧），使AM+MN+N 的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A,作A'关于直线I的对称点A'',连接A''B,交直线I于点N,将点N 向左平移长度d, 得到点M作法二：作点A关于直线I的对称点A,将点A1向右平移长度d得到点A2,连接A B ,交直线I于点Q, 将点Q向左平移长度d,得到点Q。

中考数学：'将军饮马'所有模型及变式——终极篇

中考数学：'将军饮马'所有模型及变式——终极篇以微课堂初中精品微课，数学奥林匹克国家一级教练执教。

一、模型展现(1)直线型模型1：在直线l上求作点P，使PA＋PB最小．原理：两点之间，线段最短．PA＋PB最小值即为AB长．模型2：在直线l上求作点P，使PA＋PB最小．原理：和最小，同侧转异侧．两点之间，线段最短．模型3：在直线l上求作点P，使|PA－PB|最大．原理：两边之差小于第三边，|PA－PB|最大值即为AB长．模型4：在直线l上求作点P，使|PA－PB|最大．原理：差最大，异侧转同侧．两边之差小于第三边．变式：在直线l上求作点P，使l平分∠APB，与此作法相同．模型5：在直线l上求作点P，使|PA－PB|最小．原理：|PA－PB|最小为0，中垂线上的点到线段两端的距离相等．(2)角型模型6：在OA，OB上求作点M，N，使△PMN周长最小．原理：作两次对称，两点之间，线段最短．模型7：在OA，OB上求作点M，N，使四边形PQMN周长最小．原理：P，Q分别作对称，两点之间，线段最短．模型8：在OA，OB上求作点M，N，(1)使PM＋MN最小．(2)使PN＋MN最小．原理：先连哪个点，就先做关于那个点所在射线的对称点．垂线段最短．模型9：P，Q为OA，OB的定点，在OA，OB上求作点M，N，使PN＋NM ＋MQ最小．原理：两点之间，线段最短，PN＋NM＋MQ最小值即为P’Q’的长．(3)平移型模型10：在直线l上求作点M，N，使MN＝a，且AM＋MN＋NB最小．原理：将l上的MN转化到B’B．(问题情境：将军从军营A出发，去河边l饮马，饮马完在河边牵马散步a米，回军营B．可以转化为饮完马，直接去军营B，在到达之前散步．)模型11(造桥选址)：直线l1∥l2，在l1上求作点M，在l2上求作点N，使MN⊥l1，且AM＋MN ＋NB最小．原理：将MN转化为AA’．(可以理解为在A处先走过桥的路，再直达点B．)二、典型例题例1：(模型2)从点A(0，2)发出的一束光线，经x轴反射，过点B(4，3)，求从点A到点B所经过的路径长．解析：例2：(模型4)已知点A(1，3)、B(3，－1)，点M在x轴上，当AM－BM最大时，点M的坐标为______解析：例3：(模型10)如图，当四边形PABN的周长最小时，a＝______解析：例4：(模型11)解析：例5：(结合勾股)如图，在等边△ABC中，AB＝6，N为AB上一点，且AN＝2，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM、MN，则BM＋MN的最小值是_____解析：小结：所有类型已归纳完，更多内容，详见八上11讲期中专题一将军饮马类题型全覆盖暑假特辑10《轴对称》之“将军饮马”（上）暑假特辑11《轴对称》之“将军饮马”（下）本讲思考题：已知点A(－3，－4)和B(－2，1)．(1)试在y轴上求一点P，使PA＋PB的值最小(2)试在y轴上求一点P，使|QA－QB|的值最大(3)若C(0，m)，D(0，m－2)，当m为何值时，四边形ABCD的周长最小．答案：(1) P (0，－1)(2) Q (0，11)(3) m = －0.2End欢迎收看《以微课堂》微课，欢迎收看《以微课堂》微课，作者简介：四星级重点中学高级教师、数学名师。

将军饮马模型

将军饮马模型LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】将军饮马问题将军饮马问题=轴对称问题=最短距离问题（轴对称是工具，最短距离是题眼）。

所谓轴对称是工具，即这类问题最常用的做法就是作轴对称。

而最短距离是题眼，也就意味着归类这类的题目的理由。

比如题目经常会出现线段 a+b 这样的条件或者问题。

一旦出现可以快速联想到将军饮马问题，然后利用轴对称解题。

1.将军饮马故事“将军饮马”问题是数学问题中的经典题目，主要转化成“两点之间线段最短问题”原题：如图，一位将军，从A地出发，骑马到河边给马饮水，然后再到B地，问怎样选择饮水的地点，才能使所走的路程最短？AB模型一：一条定直线，同侧两定点在直线l的同侧有两点A,B,在L上求一点P，使得PA+PB值最小。

一般做法：作点 A（B）关于直线的对称点，连接 A’B，A’B 与直线交点即为所求点。

A’B即为最短距离。

理由：A’为 A 的对称点，所以无论 P 在直线任何位置都能得到 AP=A’P。

所以 PA+PB=PA’+PB。

这样问题就化成了求 A’到 B 的最短距离，直接相连就可以了。

例一：某供电部门准备在输电主干线L上连接一个分支线路，分支点为M，同时向新落成的A、B两个居民小区送电。

已知两个居民小区A、B分别到主干线的距离AA1=2千米，BB1=1千米，且A1B1=4千米。

（1）如果居民小区A、B位于主干线L的两旁，如图（1）所示，那么分支点M 在什么地方时总路线最短最短线路的长度是多少千米（2）如果居民小区A、B位于主干线L的同旁，如图（2）所示，那么分支点M 在什么地方时总路线最短此时分支点M与A1的距离是多少千米模型二：一条定直线，一定点，一动点如图，已知直线L 和定点A ，在直线K 上找一点M，在直线L 上找一点P ，使得AP+PB 值最小。

模型三：一定点，两条定直线如图，在∠OAB 内有一点 P ，在 OA 和 OB 各找一个点 M 、N ，使得△PMN 周长最短（题眼）。

将军饮马的六种模型

将军饮马的六种模型将军饮马问题是一个经典的最优化问题，常见的有六种模型。

一、六大模型1.给定直线l和直线l的异侧两点A、B，在直线l上求一点P，使PA+PB最小。

2.给定直线l和直线l的同侧两点A、B，在直线l上求一点P，使PA+PB最小。

3.给定∠MON内一点P，在OM、ON上分别作点A、B，使△PAB的周长最小。

4.给定∠MON内的两点P、Q，在OM、ON上分别作点A、B，使四边形PAQB的周长最小。

5.给定∠MON外的一点A，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

6.给定∠MON内的一点A，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

二、常见题目Part1、三角形1.在等边△ABC中，AB=6，AD⊥BC，E是AC上的一点，M是AD上的一点，AE=2，求EM+EC的最小值。

解：连接BE，交AD于点M，则ME+MD最小。

过点B作BH⊥AC于点H，则EH=AH–AE=3–2=1.在直角△BHE中，BE=√(BH^2+HE^2)=√(3^2+1^2)=√10.因此，EM+EC=BE+BC-2AE=√10+6-2×2=√10+2.2.在锐角△ABC中，AB=√2，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？解：作点B关于AD的对称点B'，过点B'作B'E⊥AB于点E，交AD于点F，则线段B'E长就是BM+MN的最小值。

在XXX△AEB'中，根据勾股定理得到，B'E=√2.因此，XXX√2.3.在△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN值最小，则这个最小值是多少？解：作AB关于AC的对称线段AB'，过点B'作B'N⊥AB，垂足为N，交AC于点M，则B'N=MB'+MN=MB+MN。

中考复习专题：中考中“将军饮马”问题的常见模型及典型例题课件(共38张PPT)

x （1）求a，b的值；
（2）点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时.
①求直线PQ的解析式；②求四边形PABQ周长的最小值。
y
y
B．
A
Q
PO
x
B ． B′
A
Q
PO
x
A′
中考复习专题：中考中“将军饮马” 问题的常见模型及典型例题课件(共38张PPT)
中考复习专题：中考中“将军饮马” 问题的常见模型及典型例题课件(共38张PPT)
典例探究
例7
如图，已知点A（
1 2
，y1），B（2，y2）为反比例函数
y
1 的图 x
象上的两点，动点P（x，0）在x轴正半轴上运动，当AP-BP最大时，点
P的坐标是（ D ）
A、（ 1 ，0） B、（ 1 ，0） 2
C、（ 3 ，0） 2
D、（ 5 ，0） 2
y
A
y x 5 2
B
O
P
P
x
中考复习专题：中考中“将军饮马” 问题的常见模型及典型例题课件(共38张PPT)
梳理体系
【将军饮马问题模型5】同侧两点差的最值问题
A
B l
P （1）
|PA-PB|最大问题
A
B
P
l
（2）
|PA-PB|最小问题
中考复习专题：中考中“将军饮马” 问题的常见模型及典型例题课件(共38张PPT)
中考复习专题：中考中“将军饮马” 问题的常见模型及典型例题课件(共38张PPT)
y A
D E OC B x
y
A
C
D
E
C′O C

初中数学,“将军饮马”的七大模型.doc

初中数学，“将军饮马”的七大模型让我们先来了解“将军饮马”这个故事。

古希腊亚里山大里亚城有一位久负盛名的学者，名叫海伦。

有一天，有位将军不远千里专程前来向海伦求教一个百思不得其解的问题：如图，将军A从出发到河边饮马，然后再到B地军营视察，显然有许多走法．问怎样走路线最短呢？精通数理的海伦稍加思索，便作了完善的回答．这个问题后来被人们称作“将军饮马”问题．下面我们来看看数学家是怎样解决的．海伦发现这是一个求折线和最短的数学问题．根据公理：连接两点的所有线中，线段最短．若A、B在河流的异侧，直接连接AB，AB与l的交点即为所求．若A、B在河流的同侧，根据两点间线段最短，那么显然要把折线变成直线再解．将军饮海伦解决本问题时，是利用作对称点把折线问题转化成直线现在人们把凡是用对称点来实现解题的思想方法叫对称原理，即轴对称思想轴对称的两个图形有如下性质：①关于某条直线对称的两个图形是全等形；②对称轴是任何一对对应点所连线的垂直平分线；③两个图形关于某条直线对称，如果他们的对应线段或延长线相交，那么交点在对称轴上．将军饮马的数学问题，考察的知识点：“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。

解题总思路：找点关于线的对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查。

共有七大模型：模型1，PA+PB最小模型2，PA-PB最小模型3，PA-PB最大【变形】异侧时，也可以问：在直线l上是否存在一点P 使得直线l为∠APB的角平分线模型4，周长最短模型5，“过河”最短距离模型6，线段和最小模型7，在直角坐标系的运用题目巩固1.如图，直线l 和l 的异侧两点A、B，在直线l 上求作一点P，使PA+PB 最小。

2.如图，直线l 和l 的同侧两点A、B，在直线l 上求作一点P，使PA+PB 最小。

3.如图，点P 是∠MON 内的一点，分别在OM，ON 上作点A，B。

使△PAB 的周长最小4.如图，点P，Q 为∠MON 内的两点，分别在OM，ON 上作点A，B。

专题07 将军饮马模型(解析版)

专题07.将军饮马模型将军饮马模型在考试中，无论是解答题，还是选择、填空题，都是学生感觉有困难的地方，也恰是学生能力区分度最重要的地方，主要考查转化与化归等的数学思想。

在各类考试中都以中高档题为主。

在解决几何最值问题主要依据是：①两点之间，线段最短；②垂线段最短，涉及的基本方法还有：利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等。

希望通过本专题的讲解让大家对这类问题有比较清晰的认识。

··模型1、将军饮马--两定一动求线段和的最小值【模型探究】A，B为定点，m为定直线，P为直线m上的一个动点，求AP+BP的最小。

（1）如图1，点A、B在直线m两侧：辅助线：连接AB交直线m于点P，则AP+BP的最小值为AB.（2）如图2，点A、B在直线同侧：辅助线：过点A作关于定直线m的对称点A’，连接A’B交直线m于点P，则AP+BP的最小值为A’B.图1图2例1．（2022·江苏·八年级专题练习）要在街道旁修建一个奶站，向居民区A、B提供牛奶，小聪根据实际情况，以街道旁为x轴，测得A点的坐标为(0，3)，B点的坐标为(6，5)，则从A、B两点到奶站距离之和的最小值是____．【答案】10【分析】作A点关于x轴的对称点A'，连接A'B与x轴交于点P，连接AP，则A'B即为所求．【详解】解：作A点关于x轴的对称点A'，连接A'B与x轴交于点P，连接AP，∵AP＝A'P，∴AP+BP∵A（0，3），∴A'（0∴P点到A、B的距离最小值为【点睛】本题考查轴对称求最短距离，熟练掌握轴对称求最短距离的方法，会根据两点坐标求两点间距离例2．（2022·江苏·八年级专题练习）如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE＝2，则EM＋CM的最小值为（）C．D．A B．【点睛】本题考查轴对称求最短距离，熟练掌握轴对称求最短距离的方法，灵活运用勾股定理是解题关键．例3．（2022·江苏·八年级专题练习）如图所示，在ABC 中，AB AC =，直线EF 是AB 的垂直平分线，D 是BC 的中点，M 是EF 上一个动点，ABC 的面积为12，4BC =，则BDM 周长的最小值是_________．【点睛】本题主要考查了线段垂直平分线的性质，三线合一定理，解题的关键在于能够根据题意得到当A、M、D三点共线时，AM+DM最小，即为AD．例4．（2023·湖北洪山·八年级期中）如图，将△ABC沿AD折叠使得顶点C恰好落在AB边上的点M处，D 在BC上，点P在线段AD上移动，若AC＝6，CD＝3，BD＝7，则△PMB周长的最小值为___．【答案】18【分析】首先明确要使得△PMB周长最小，即使得PM+PB最小，再根据翻折的性质可知PM=PC，从而可得满足PC+PB最小即可，根据两点之间线段最短确定BC即为最小值，从而求解即可．【详解】解：由翻折的性质可知，AM=AC，PM=PC，∴M点为AB上一个固定点，则BM长度固定，∵△PMB周长=PM+PB+BM，∴要使得△PMB周长最小，即使得PM+PB最小，∵PM=PC，∴满足PC+PB最小即可，显然，当P、B、C三点共线时，满足PC+PB最小，如图所示，此时，P点与D点重合，PC+PB=BC，∴△PMB周长最小值即为BC+BM，此时，作DS⊥AB于S点，DT⊥AC延长线于T点，AQ⊥BC延长线于Q点，由题意，AD为∠BAC的角平分线，∴DS=DT，∵1122ACDS AC DT CD AQ==，1122ABDS AB DS BD AQ==，∴11221122ABDACDAB DS BD AQSS AC DT CD AQ==，即：AB BDAC CD=，∴763AB=，解得：AB=14，∵AM=AC=6，∴BM=14-6=8，∴△PMB周长最小值为BC+BM=3+7+8=18，故答案为：18．【点睛】本题考查翻折的性质，以及最短路径问题等，掌握翻折的基本性质，利用角平分线的性质进行推理求解，理解并熟练运用两点之间线段最短是解题关键．例5．（2023·江阴市八年级月考）某班级在探究“将军饮马问题”时抽象出数学模型：直线l 同旁有两个定点A 、B ，在直线l 上存在点P ，使得PA PB +的值最小．解法：如图1，作点A 关于直线l 的对称点A '，连接A B '，则A B '与直线l 的交点即为P ，且PA PB +的最小值为A B '．请利用上述模型解决下列问题：（1）几何应用：如图2，ABC ∆中，90C ∠=︒，2AC BC ==，E 是AB 的中点，P 是BC 边上的一动点，则PA PE +的最小值为；（2）几何拓展：如图3，ABC ∆中，2AC =，30A ∠=︒，若在AB 、AC 上各取一点M 、N 使CM MN +的值最小，画出图形，求最小值并简要说明理由．【答案】（110；（23【分析】（1）作点A 关于BC 的对称点A′，连接A′E 交BC 于P ，此时PA+PE 的值最小．连接BA′，先根据勾股定理求出BA′的长，再判断出∠A′BA=90°，根据勾股定理即可得出结论；（2）作点C 关于直线AB 的对称点C′，作C′N ⊥AC 于N 交AB 于M ，连接AC′，根据等边三角形的性质解答．【详解】解：（1）如图2所示，作点A 关于BC 的对称点A′，连接A′E 交BC 于P ，此时PA+PE 的值最小．连接BA′．由勾股定理得，22BC AC +2222+2，∵E 是AB 的中点，∴BE=122，∵90C ∠=︒，2AC BC ==，∴∠A′BC=∠ABC=45°，∴∠A′BA=90°，∴PA+PE 的最小值=A′E=22'A B BE +()()22222+1010；（2）如图3，作点C关于直线AB的对称点C′，作C′N⊥AC于N交AB于M，连接AC′，则C′A=CA=2，∠C′AB=∠CAB=30°，∴△C′AC为等边三角形，∴∠AC′N=30°，∴AN=12C′A=1，∴CM+MN的最小值为2221 3．【点睛】本题考查的是轴对称--最短路线问题、勾股定理、等边三角形的判定和性质、含30°角的直角三角形的性质、垂线段最短，解这类问题的关键是将所给问题抽象或转化为数学模型，把两条线段的和转化为一条线段．模型2、将军饮马--两动一定求线段和的最小值【模型探究】已知定点A位于定直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.辅助线：过点A作关于定直线m、n的对称点A’、A’’，连接A’A’’交直线m、n于点P、Q，则PA+PQ+QA 的最小值为A’A’’.例1．（2022·江苏·无锡市八年级期末）如图，已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP ＝4，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于4，则α＝（）A．30°B．45°C．60°D．90°【答案】A【分析】设点P关于OA的对称点为C，关于OB的对称点为D，当点E、F在CD上时，△PEF的周长为PE+EF+FP=CD，此时周长最小，根据CD=4可得出△COD是等边三角形，进而可求出α的度数．【详解】解：如图，作点P关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F．此时，△PEF的周长最小．连接OC，OD，PE，PF．∵点P与点C关于OA对称，∴OA垂直平分PC，∴∠COA=∠AOP，PE=CE，OC=OP，同理，可得∠DOB=∠BOP，PF=DF，OD=OP．∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α，OC=OD=OP=4，∴∠COD=2α．又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=4，∴OC=OD=CD=4，∴△COD是等边三角形，∴2α=60°，∴α=30°．故选：A．【点睛】本题主要考查了最短路径问题，本题找到点E和F的位置是解题的关键．要使△PEF的周长最小，通常是把三边的和转化为一条线段，运用三角形三边关系解决．例2．（2022·江苏九年级一模）如图，Rt△ABC中，∠C=90°，AC=3，BC=4，D，E，F分别是AB，BC，AC边上的动点，则△DEF的周长的最小值是（）A．2.5B．3.5C．4.8D．6【答案】C【分析】如图作D关于直线AC的对称点M，作D关于直线BC的对称点N，连接CM，CN，CD，EN，FM，DN，DM．由∠MCA=∠DCA，∠BCN=∠BCD，∠ACD+∠BCD=90°，推出∠MCD+∠NCD=180°，可得M、B、N 共线，由DF+DE+EF=FM+EN+EF，FM+EN+EF≥MN，可知当M、F、E、N共线时，且CD⊥AB时，DE+EF+FD的值最小，最小值=2CD，求出CD的值即可解决问题．【详解】解：如图，作D关于直线AC的对称点M，作D关于直线BC的对称点N，连接CM，CN，CD，EN，FM，DN，DM．∴DF =FM ，DE =EN ，CD =CM ，CD =CN ，∴CD =CM =CN ，∵∠MCA =∠DCA ，∠BCN =∠BCD ，∠ACD +∠BCD =90°，∴∠MCD +∠NCD =180°，∴M 、C 、N 共线，∵DF +DE +EF =FM +EN +EF ，∵FM +EN +EF ≥MN ，∴当M 、F 、E 、N 共线时，且CD ⊥AB 时，DE +EF +FD 的值最小，最小值为MN =2CD ，∵CD ⊥AB ，∴12•AB •CD =12•AB•AC ，∴CD =•AB AC AB =125=2.4，∴DE +EF +FD 的最小值为4.8．故选：C ．【点睛】本题考查了轴对称-最短问题、两点之间线段最短、垂线段最短等知识，解题的关键是灵活运用轴对称以及垂线段最短解决最短问题，属于中考选择题中的压轴题．例3．（2023春·贵州毕节·七年级统考期末）如图所示，30AOB ∠= ，点P 为AOB ∠内一点，8OP =，点,M N 分别在,OA OB 上，求PMN ∆周长的最小值．【答案】PMN ∆周长的最小值为8【分析】作P 关于OA 、OB 的对称点12P P 、，连结1OP、2OP ，即可快速找到解题思路.【详解】如图，作P 关于OA 、OB 的对称点12P P 、，连结1OP、2OP ，12PP 交OA 、OB 于M 、N ，此时PMN ∆周长最小，根据轴对称性质可知1PM PM =，2P N PN =，1212PM N PM M N PN PP ∴∆=++=，且1AO P AO P ∠=∠，2BO P BO P ∠=∠，12260POP AOB ∠=∠=︒，128O P O P O P ===，12PPO ∆为等边三角形，1218PP OP ==即PMN ∆周长的最小值为8.【点睛】本题应用知识比较隐晦，分别考查了轴对称图形和等边三角形，需要认真分析，充分联系所学知识，方可正确解答.例4.（2023.山东八年级期末）如图所示，在四边形ABCD中，∠A＝90º，∠C＝90º，∠D＝60º，AD＝3，AB＝，若点M、N分别为边CD，AD上的动点，则△BMN的周长最小值为（）A. B. C.6 D.3【答案】C【解析】作点B关于CD、AD的对称点分别为点B'和点B''，连接B'B''交DC和AD于点M和点N，连接MB、NB；再DC和AD上分别取一动点M’和N’（不同于点M和N），连接M'B，M'B'，N’B和N'B''，如图1所示：∵B'B''＜M'B'＋M'N'＋N'B"，B'M'＝BM'，B"N'＝BN'，∴BM'＋M'N'＋BN'＞B'B"，又∵B'B"＝B'M＋MN＋NB"，MB＝MB'，NB＝NB''，∴NB＋NM＋BM＜BM'＋M’N'＋BN'NB＋NM＋BM时周长最小；连接DB，过点B'作B'H⊥DB''于B’’D的延长线于点H，如图示2所示：在Rt△ABD中，AD＝3，AB＝，，∴∠2＝30º，∴∠5＝30º，DB＝DB''，又∵∠ADC＝∠1＋∠2＝60º，∴∠1＝30º，∴∠7＝30º，DB'＝DB，∴∠B'DB''＝∠1＋∠2＋∠5＋∠7＝120º，DB'＝DB''＝DB，又∵∠B'DB"＋∠6＝180º，∴∠6＝60º，∴HD＝，HB'＝3，在Rt △B'HB''中，由勾股定理得：B'B"＝，NB ＋NM ＋BM ＝6，故选C.模型3、将军饮马--两动两定求线段和的最小值【模型探究】A ，B 为定点，在定直线m 、n 上分别找两点P 、Q ，使PA +PQ +QB 最小。

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型角型平移型)(练习无答案)

将军饮马所有模型及变式——终极篇一、模型展现(1)直线型模型1：在直线l上求作点P，使PA＋PB最小．原理：两点之间，线段最短．PA＋PB最小值即为AB长．模型2：在直线l上求作点P，使PA＋PB最小．原理：和最小，同侧转异侧．两点之间，线段最短．模型3：在直线l上求作点P，使|PA－PB|最大．原理：两边之差小于第三边，|PA－PB|最大值即为AB长．模型4：在直线l上求作点P，使|PA－PB|最大．原理：差最大，异侧转同侧．两边之差小于第三边．模型5：在直线l上求作点P，使|PA－PB|最小．原理：|PA－PB|最小为0，中垂线上的点到线段两端的距离相等．(2)角型模型6：在OA，OB上求作点M，N，使△PMN周长最小．原理：作两次对称，两点之间，线段最短．模型7：在OA，OB上求作点M，N，使四边形PQMN周长最小．原理：P，Q分别作对称，两点之间，线段最短．模型8：在OA，OB上求作点M，N，(1)使PM＋MN最小．(2)使PN＋MN最小．原理：先连哪个点，就先做关于那个点所在射线的对称点．垂线段最短．模型9：P，Q为OA，OB的定点，在OA，OB上求作点M，N，使PN＋NM＋MQ最小．原理：两点之间，线段最短，PN＋NM＋MQ最小值即为P’Q’的长．(3)平移型模型10：在直线l上求作点M，N，使MN＝a，且AM＋MN＋NB最小．原理：将l上的MN转化到B’B．(问题情境：将军从军营A出发，去河边l饮马，饮马完在河边牵马散步a米，回军营B．可以转化为饮完马，直接去军营B，在到达之前散步．)模型11(造桥选址)：直线l1∥l2，在l1上求作点M，在l2上求作点N，使MN⊥l1，且AM＋MN＋NB 最小．原理：将MN转化为AA’．(可以理解为在A处先走过桥的路，再直达点B．)二、典型例题例1：(模型4)已知点A(1，3)、B(3，－1)，点M在x轴上，当AM－BM最大时，点M的坐标为______解析：例2：(模型11)解析：例3：(结合勾股)解析：练习反馈：1.在直线l上求作点P，使l平分∠APB，与此作法相同．2. 从点A(0，2)发出的一束光线，经x轴反射，过点B(4，3)，求从点A到点B 所经过的路径长．3.已知点A(－3，－4)和B(－2，1)．(1)试在y轴上求一点P，使PA＋PB的值最小(2)试在y轴上求一点P，使|QA－QB|的值最大(3)若C(0，m)，D(0，m－2)，当m为何值时，四边形ABCD的周长最小．4. 如图，在等边△ABC中，AB＝6，N为AB上一点，且AN＝2，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM、MN，则BM＋MN的最小值是_____5.如图，当四边形PABN的周长最小时，a＝______。

将军饮马问题的11个模型及例题

将军饮马问题的11个模型及例题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（将军饮马问题的11个模型及例题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为将军饮马问题的11个模型及例题的全部内容。

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1。

两点之间，线段最短;2。

三角形两边之和大于第三边，两边之差小于第三边;3。

中垂线上的点到线段两端点的距离相等；4。

垂线段最短。

基本模型1.已知:如图，定点A、B分布在定直线l两侧;要求:在直线l上找一点P,使PA+PB的值最小解:连接AB交直线l于点P，点P即为所求，PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB,即AP´+BP´〉AP+BP∴P为直线AB与直线l的交点时，PA+PB最小.2.已知：如图，定点A和定点B在定直线l的同侧要求：在直线l上找一点P，使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A´，连接A´B交l于P，点P即为所求；理由：根据轴对称的性质知直线l为线段AA´的中垂线，由中垂线的性质得：PA=PA´，要使PA+PB最小,则需PA´+PB值最小，从而转化为模型1.3.已知：如图，定点A、B分布在定直线l的同侧(A、B两点到l的距离不相等）要求：在直线l上找一点P,使︱PA—PB︱的值最大解：连接BA并延长，交直线l于点P,点P即为所求；理由：此时︱PA—PB︱=AB,在l上任取异于点P的一点P´，连接AP´、BP´，由三角形的三边关系知︱P´A-P´B︱<AB，即︱P´A—P´B︱〈︱PA—PB︱4。

将军饮马的六种模型

将军饮马的六种模型将军饮马，是中国古代战争策略中的经典战术之一。

通过观察马，了解将军的心思，进而进行军事决策。

将军饮马虽然源于古代战争，但其思想也可以应用于现代管理和决策中。

在现代社会中，可以将将军饮马的思想应用到各种管理模型中，以期提供全面、客观、有效的决策支持。

本文将介绍六种基于将军饮马思想的模型，并对其应用领域进行简要分析。

一、马的姿态模型在将军饮马中，将军观察马展示出的姿态，来判断敌情。

而在管理和决策中，我们也可以通过观察员工或团队展示的姿态，来了解他们的态度、能力和潜力。

例如，一个员工是否充满自信和积极的态度，是否展示出自主解决问题的能力，这些都可以为管理者提供重要的参考信息。

二、军心模型将军饮马中，将军观察马的冷静与否，来判断士兵们的情绪状态。

同样，在管理中，管理者可以通过观察员工的情绪和表现来判断团队的士气和动力。

如果员工们表现出疲惫、消极或情绪低落，可能需要及时采取措施调整团队心态，提高士气。

三、战术模型将军饮马中，将军观察马的行动方式，来判断敌情并制定战术。

在管理决策中，管理者可以观察员工或团队的行动方式和工作方法，来判断他们的能力和适应性。

通过了解员工的工作方式，可以更好地进行任务分配和资源管理，使团队的工作更加高效。

四、资源模型将军饮马中，将军观察马数量和状态，来判断可用资源。

在管理决策中，管理者需要了解团队的资源情况，包括人力、物资、资金等。

通过了解资源状况，管理者可以更好地进行资源分配，确保团队工作的顺利进行。

五、协调模型将军饮马中，将军观察马是否协调一致，来判断士兵团结力。

在管理中，管理者可以通过观察员工的协作和团队合作能力，来判断团队的团结力和协作效率。

如果员工们能够协同合作、相互支持，将会提升整个团队的工作效果。

六、判断模型将军饮马中，将军通过观察马的各种表现，来综合判断敌情和决策方向。

在管理决策中，管理者也需要通过综合观察员工的各种表现和信息，来做出决策。

通过收集和分析各种信息，管理者能够更准确地判断当前形势，做出合理决策。

将军饮马的六大常见模型

将军饮马问题——线段和最短一．六大模型1.如图，直线l和l的异侧两点A、B，在直线l上求作一点P，使PA+PB最小。

2.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最小。

3.如图，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△PAB的周长最小4.如图，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形PAQB的周长最小。

5.如图，点A是∠MON外的一点，在射线ON上作点P，使PA与点P到射线OM的距离之和最小6. .如图，点A是∠MON内的一点，在射线ON上作点P，使PA与点P到射线OM的距离之和最小DBCDACBAA二、常见题目Part1、三角形1．如图，在等边△ABC 中，AB = 6，AD ⊥BC ，E 是AC 上的一点，M 是AD 上的一点，且AE = 2，求EM+EC 的最小值解：∵点C 关于直线AD 的对称点是点B ，∴连接BE ，交AD 于点M ，则ME+MD 最小，过点B 作BH ⊥AC 于点H ，则EH = AH – AE = 3 – 2 = 1， BH =BC2 - CH2 =62 - 32 = 3 3在直角△BHE 中，BE = BH2 + HE2= (33)2 + 12 = 272．如图，在锐角△ABC 中，AB = 42，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是____．解：作点B 关于AD 的对称点B'，过点B'作B'E ⊥AB 于点E ，交AD 于点F ，则线段B'E 的长就是BM ＋ＭＮ的最小值在等腰Rt △AEB'中，根据勾股定理得到，B'E = 43．如图，△ABC 中，AB=2，∠BAC=30°，若在AC 、AB 上各取一点M 、N ，使BM+MN 的值最小，则这个最小值解：作AB 关于AC 的对称线段AB'，过点B'作B'N ⊥AB ，垂足为N ，交AC 于点M ，则B'N = MB'+MN = MB+MN B'N 的长就是MB+MN 的最小值则∠B'AN = 2∠BAC= 60°，AB' = AB = 2， ∠ANB'= 90°，∠B' = 30°。

初中数学常见模型之将军饮马

将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB 最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.关键：找对称点作法：作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PAC中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM 交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d（动点M位于动点N左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l于点N，将点N向左平移长度d，得到点M。

将军饮马的六种模型

将军饮马问题的11个模型及例题

初中数学之将军饮马的6种模型(培优)

初中数学将军饮马问题的六种常见题型汇总

初中数学最值问题六种模型

将军饮马模型

中考数学：'将军饮马'所有模型及变式——终极篇

将军饮马模型

将军饮马的六种模型

中考复习专题：中考中“将军饮马”问题的常见模型及典型例题 课件(共38张PPT)

初中数学,“将军饮马”的七大模型.doc

专题07 将军饮马模型(解析版)

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型 角型 平移型)(练习无答案)

将军饮马问题的11个模型及例题

将军饮马的六种模型

将军饮马的六大常见模型

初中数学常见模型之将军饮马

中考复习专题：中考中“将军饮马”问题的常见模型及典型例题课件(共38张PPT)

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型角型平移型)(练习无答案)