精品解析:【全国市级联考】广东省中山市2017-2018学年高一上学期期末考试数学试题(原卷版)
2017-2018学年高一数学上学期期末统一考试试题及答案(新人教A版 第34套)

中山市高一级2017-2018学年度第一学期期末统一考试数学科试卷本试卷分第I 卷(选择题)、第II 卷(非选择题)两部分。
共150分,考试时间100分钟。
注意事项:1、答第I 卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上.2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上.3、不可以使用计算器.4、考试结束,将答题卡交回,试卷不用上交.5、参考公式:球的体积公式34,3V R π=球,其中R 是球半径. 锥体的体积公式V锥体13Sh =,其中S 是锥体的底面积,h 是锥体的高. 台体的体积公式V台体1()3h S S '=+,其中,S S '分别是台体上、下底面的面积,h 是台体的高.第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每题5分,共50分,每小题给出的4个选项中,只有一选项是符合题目要求的)1.已知集合{|A x x =是平行四边形},{|B x x =是矩形},{|C x x =是正方形},{|D x x =是菱形},则A .AB ⊆ B .C B ⊆ C .D C ⊆ D .A D ⊆ 2.下列函数中,在区间()0,1上是增函数的是( )A .x y =B .x y -=3C .xy 1=D .42+-=x y3.在同一坐标系中,函数y =x-2与y =log 2 x 的图象是( ).ABCD4.如左图是一个物体的三视图,则此三视图所描述的物体是下列几何 体中的( )正视图左视图俯视图5.已知lg 2,lg3,a b ==则lg 45的值用a ,b 表示为 ( ) A .21b a +-B .12b a +-C .3a b +D .2a b b ++6.若函数22)(23--+=x x x x f 的一个正数零点附近的函数值用二分法逐次计算,得到如下参考数据: 那么方程02223=--+x x x 的一个近似根(精确到0.1)为A .1.2B .1.3C .1.4D .1.57.若213211()(),22a a +-<则实数a 的取值范围是 A .(1,)+∞B .1(,)2+∞C .(,1)-∞D .1(,)2-∞8.已知直线b kx y +=经过一、二、三象限,则有( )A .k<0,b <0B .k<0,b>0C .k>0,b>0D .k>0,b<09.已知两条直线,m n ,两个平面,αβ,给出下面四个命题:①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒④//,//,m n m n αβαβ⊥⇒⊥其中正确命题的序号是( ) A .①③B .②④C .①④D .②③10.若()21231log log log 0a a a x x x ++==>,则123,,x x x 之间的大小关系为( ).A .3x <2x <1xB .2x <1x <3xC .1x <3x <2xD .2x <3x <1x第Ⅱ卷(非选择题 共100分)二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在答题卡的横线上) 11.点(1,1) 到直线:3430l x y ++=的距离为 . 12.某同学利用TI-Nspire 图形计算器作图作出幂函数34()f x x =的图象如右图所示. 结合图象,可得到34()f x x =在区间[1,4]上的最大值为 .ABCD(结果用最简根式表示)13.已知⎩⎨⎧>-≤+=)0(2)0(1)(2x x x x x f ,若()10f x =,则x = .14.过点P (3,0)的直线m ,夹在两条直线03:1=++y x l 与022:2=--y x l 之间的线段恰被点P 平分,那么直线m 的方程为三、解答题:(本大题共 6 小题,共 80分.解答应写出文字说明、证明过程或演算步骤.) 15.(本小题满分12分) (I)求值:022*******log 9log 3log 3log --+;(Ⅱ)设函数f (x )是定义在R 上的偶函数,且)2()(-=x f x f ,当x∈[0,1]时,1)(+=x x f ,求)23(f 的值.16.(本小题满分14分)(I)求两条平行直线01243=-+y x 与068=++y mx 之间的距离; (Ⅱ)求两条垂直直线022=++y x 与024=-+y nx 的交点坐标.17.(本小题满分13分)如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(I)证明:平面BDC 1⊥平面BDC ;(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.18.(本小题满分13分)A 、B 两城相距100km ,在两地之间距A 城x km 处D 地建一核电站给A 、B 两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数25.0=λ.若A 城供电量为20亿度/月,B 城为10亿度/月.(I)把月供电总费用y 表示成x 的函数,并求定义域;B 1 CB A DC 1A 1。
中山市高三年级2017—2018学年度第一学期期末统一考试【解析版】

•【解析】浙江 卫视《汉字风 云会》的观众 定位并非是小 学五年级左右 的孩子,而是 低年龄萌娃, 节目选手主要 是小学五年级 左右的孩子。
实用类文本阅读 目录
Contents
01 - LOREM IPSUM DOLOR LOREM 02 - LOREM IPSUM DOLOR LOREM 03 - LOREM IPSUM DOLOR LOREM 04 - LOREM IPSUM DOLOR LOREM 05 - LOREM IPSUM DOLOR LOREM 06 - LOREM IPSUM DOLOR LOREM
实用类文本阅读 目录
Contents
01 - LOREM IPSUM DOLOR LOREM 02 - LOREM IPSUM DOLOR LOREM 03 - LOREM IPSUM DOLOR LOREM 04 - LOREM IPSUM DOLOR LOREM 05 - LOREM IPSUM DOLOR LOREM
论述类文本阅读
•2.下列对原文论证的相关分析,不正确的一项是(3分) •A.文章主要从包容、血统、行政、心态等不同角度,展开论 述。 •B.文章没有明确指出中华文明的“内”与“外”的具体边界。 •C.文章的论证语气在整体上比较温和,这有利于问题的提出 与讨论。
•D.文章最后回归现实,指出“历史中国”的存在 矛盾和解决路径。【没有指出“解决路径”】
文学类文本阅读
Contents
目录
01 - LOREM IPSUM DOLOR LOREM
02 - LOREM IPSUM DOLOR LOREM
文学类文本阅读
•5.小说反复使用“叮当、叮叮当、叮当……”的声音来描述打铁的过程, 这样写的作用是什么?请简要分析。(5分) •5 . ① 详 写 打 铁 的 过 程 , 渲 染 了 紧 张 、 热 烈 的 氛 围 ( 场 面 、 场 景 、 画 面); •②表现了两位打铁老人对打铁一事的专注,配合默契,技艺高超。 •③突出强调了两个老人对打铁的热爱,同时也表现了他们对往昔生活的 怀念; •④与前文两个老人困乏的生活与无奈形成对比,突出两个老人对打铁的 信仰; •评分细则:①场景,②技艺,③情感,④主旨。答对一点1分,答对两 点3分,答对三点给5分。语言表述不准确,酌情扣分。
广东省中山市2017–2018学年度高二级第一学期期末统一考试生物试题与答案

中山市高二级2017—2018学年度第一学期期末统一考试理科生物试卷本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共12页,满分100分,考试时间90分钟。
注意事项:1.答题前,考生必须将自己的姓名、统考考号和考试科目用铅笔涂写在答题卡上。
2.第I卷共40小题,每小题选出答案后,用铅笔把答题卡上对应的答案标号涂黑,如要改动,必须用橡皮擦干净后,再选涂其他答案。
第II卷则用黑色的钢笔(或圆珠笔)按各题要求答在答题卡相应的位置上。
3.考试结束时,将答题卡交回。
第I卷(选择题,共60分)一、单项选择题(本大题包括40小题,每小题1.5分,共60分)1. 下列有关内环境及稳态的叙述中,不正确...的是A. 不同人的体温,会因年龄、性别等不同而存在微小差异B. 人体内检测到病原体,其内环境稳态不一定被破坏C. 内环境是机体进行正常生命活动和细胞代谢的场所D. 当机体内环境稳态遭到破坏时,必将引起细胞代谢紊乱2. 下列属于人体内环境组成成分的是①尿素、血浆蛋白、淋巴因子②唾液淀粉酶、O2和无机盐③氨基酸、CO2和胰岛素④抗体、神经递质和RNA聚合酶A. ①②B. ①③C. ②④D.③④3.下表是人体细胞内液、组织液和血浆中的部分物质含量的测定数据。
下列相关说法中,错误的是A. ①是血浆,其蛋白质含量减少会导致组织水肿B. ②与③的成分差异与细胞膜的结构和功能有关C. ③中含有较多的蛋白质和K+,可判断是细胞内液D. ①②的pH能够保持稳定是因为HCO3-含量较多4.突触小体不能..完成的生理过程是A. 识别神经递质,提供结合位点B. 突触小泡与细胞膜的融合C. 突触前膜释放神经递质D. 完成“电信号—化学信号”的转变5.可以与突触小体共同构成突触的结构包括①同一神经元的树突②其他神经元的树突③同一神经元的细胞体④其他神经元的细胞体⑤骨骼肌细胞⑥心肌细胞A. ①②③④B. ②③④⑤C. ①③⑤⑥D. ②④⑤⑥6.在一条离体神经纤维的左侧施加电刺激使其兴奋(如图甲),兴奋从该神经元向下一个神经元传递(如图乙)。
中山市高三年级2017—2018学年度第一学期期末统一考试 (答案)

中山市高三年级2017—2018学年度第一学期期末统一考试参考答案及评分细则2018年4月20日1.A.(解析:接受条件是“少数民族势力入主中原建立王朝”,并且“在与中原文化近距离相处和共存一个时期之后”。
)2.D.(解析:没有指出“解决路径”。
)3.C.(解析:原文说“如果一个文明群体被其他文明群体所打败,它自身肯定出现某些保守和停滞的特点,失去了活力,外来的冲击可以使其重新焕发青春”,并没有表达这一意思。
)4.A(解析:“折射出只注重物质而忽视精神追求的深层次社会问题”错,过分拔高主题。
)5.①详写打铁的过程,渲染了紧张、热烈的氛围(场面、场景、画面);②表现了两位打铁老人对打铁一事的专注,配合默契,技艺高超。
③突出强调了两个老人对打铁的热爱,同时也表现了他们对往昔生活的怀念;④与前文两个老人困乏的生活与无奈形成对比,突出两个老人对打铁的信仰;评分细则:①场景,②技艺,③情感,④主旨。
答对一点1分,答对两点3分,答对三点给5分。
语言表述不准确,酌情扣分。
6.①“炉火”是贯穿全文的线索,推动故事情节的发展。
②“炉火”象征着两个老人的一种生活方式和生活态度。
③“炉火”喻指打铁职业,饱含着两个老人对打铁的热爱(喜爱)。
④“炉火”衬托出两个老人内心的热忱与执着。
评分细则:①情节结构,②象征意义,③情感态度,④人物性格。
答对一点2分,答对两点4分,答对其中三点给6分。
语言表述不准确,酌情扣分。
7.C(解析:浙江卫视《汉字风云会》的观众定位并非是小学五年级左右的孩子,而是低年龄萌娃,节目选手主要是小学五年级左右的孩子。
)8.BD(解析:A项中“自然而然形成了汉字文化圈”有误,汉字文化圈的形成有赖于人们积极通过汉字来沟通交流;C项中“提笔忘字”现象的直接原因不是拼音输入法应用过多,而是电子设备长时间使用,手写汉字场景不断减少;E项,根据统计可知,大部分人并不认同“提笔忘字”是社会发展不可避免的结果。
)9.(1)积极向国外介绍汉字,促进不同地域思想文化交流,扩大汉字的国际影响力。
广东省中山市2017–2018学年度高三级第一学期期末统一考试生物试题与答案

中山市高三级2017—2018学年度第一学期期末统一考试理科生物试卷本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共12页。
满分90分。
考试时间90分钟。
注意事项:1. 答第I 卷前,考生务必将自己的姓名、考号、考试科目用铅笔写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
3. 请将第II 卷答案写在答题卷上,考试结束后,监考人员将答题卡收回。
第I 卷(选择题,共36分)一、单项选择题:(每小题只有1个最适宜答案,每小题1.5分,共24小题,计36分)1.下列关于生物体中某些物质和结构的描述,错误..的是 A .内质网是双层膜连接而成的网状结构,是脂质合成的车间B .核糖体是由 rRNA 和蛋白质组成的,是进行蛋白质合成的细胞器C .纤维素是植物细胞壁的成分,其单体和动物糖原的单体是相同的D .胆固醇是构成动物细胞膜的重要成分,在人体内还参与脂质的运输2.将一萝卜去皮后切成大小相同的数个小条,测定长度后随机分成数量相等的几组,然后放在不同浓度的蔗糖溶液中进行实验,一定时间后取出,再次测定每组萝卜条的长度并取平均值,得到右边的关系图。
下列有关叙述正确的是A .a 浓度之前蔗糖进入了细胞B .a 浓度之后原生质层紧贴细胞壁C .a 浓度时,细胞内的蔗糖浓度与外界蔗糖溶液相等D .图中萝卜条长度的变化说明细胞壁具有一定的伸缩性3.下列对实验现象和实验操作的描述中,错误..的是 A .甲基绿使DNA 呈绿色,吡罗红使RNA 呈红色B .用台盼蓝染色,死的动物细胞会被染成蓝色,而活的动物细胞不着色C .在花生子叶薄片上滴苏丹Ⅲ染色后,需要用蒸馏水洗去浮色后再观察D .使用斐林试剂时需将0.1g/mL 的NaOH 溶液与0.05g/mL 的CuSO4溶液等量混合蔗糖溶液浓度初始长度 萝卜条长度 a4.下列图1至图4分别为甲状腺激素分子、双缩脲分子、叶绿素和血红蛋白分子局部结构的结构示意图,据图分析,下列相关叙述正确的是A .甲状腺激素属于蛋白质,所以不能口服B .蛋白质与图2的双缩脲发生作用,产生紫色反应C .血红蛋白主要存在于血浆中,而组织液和淋巴几乎不含有D .植物体缺镁会使该植物的光补偿点升高,光饱和点降低5.图甲是H 2O 2酶活性受pH 影响的曲线,图乙表示在最适温度下,pH =b 时H 2O 2分解产生的O 2量随时间的变化曲线。
中山市高三级2017-2018学年度第一学期期末统一考试(理科)答案
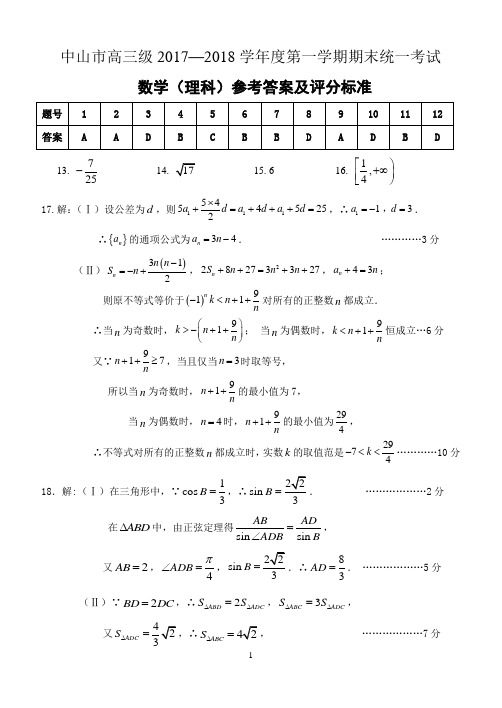
中山市高三级2017—2018学年度第一学期期末统一考试数学(理科)参考答案及评分标准13. 725-14. 15. 6 16. 1,4⎡⎫+∞⎪⎢⎣⎭17.解:(Ⅰ)设公差为d ,则11154545252a d a d a d ⨯+=+++=,∴1 1 3a d =-=,. ∴{}n a 的通项公式为34n a n =-. …………3分(Ⅱ)()312n n n S n -=-+,228273327n S n n n ++=++,43n a n +=;则原不等式等价于()911nk n n-<++对所有的正整数n 都成立. ∴当n 为奇数时,91k n n ⎛⎫>-++ ⎪⎝⎭; 当n 为偶数时,91k n n <++恒成立…6分又∵917n n++≥,当且仅当3n =时取等号, 所以当n 为奇数时,91n n++的最小值为7, 当n 为偶数时,4n =时,91n n ++的最小值为294, ∴不等式对所有的正整数n 都成立时,实数k 的取值范是2974k -<<…………10分18.解:(Ⅰ)在三角形中,∵1cos 3B =,∴sin 3B =. ………………2分 在ABD ∆中,由正弦定理得sin sin AB ADADB B=∠,又2AB =,4ADB π∠=,sin 3B =.∴83AD =. ………………5分(Ⅱ)∵2BD DC =,∴2ABD ADC S S ∆∆=,3ABC ADC S S ∆∆=,又ADC S ∆=ABC S ∆= ………………7分∵1sin 2ABC S AB BC B ∆=⋅,∴6BC =, 在ABC ∆中,由余弦定理得2222cos AC AB BC AB BC ABC =+-⋅∠.∴AC = ………………9分 ∵1sin 2ABD S AB AD BAD ∆=⋅∠,1sin 2ADC S AC AD CAD ∆=⋅∠, 且2ABD ADC S S ∆∆=,∴sin 2sin BAD AC CAD AB∠=⋅=∠ ………………12分19. 解: (1)由弧长计算及扇环面的周长为30米,得()30102(10)x x θ=++-,所以10210xxθ+=+, 100<<x ……3分 (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<.………5分装饰总费用为()9108(10)17010x x x θ++-=+, …………………………7分 所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++, …………9分令17t x =+,则3913243()101010y t t =-+≤,当且仅当t =18时取等号,此时121,11x θ==. 答:当x =1时,花坛的面积与装饰总费用的比最大.……………………………12分 (注:对y 也可以通过求导,研究单调性求最值,同样给分)20. 解:(1)根据题意,学员(1),(2),(4),(6),(9)恰有两项不合格,从中任意抽出2人,所有可能的情况如下:由表可知,全部,故所求概率为610=35. ………………6分(2)由题意可知,该学员顺利完成每1轮测试(或补测)的概率为1×1×1×910×23=35.①由题意,该学员无法通过“科二”考试,当且仅当其测试与3次补测均未能完成5项测试,相应概率为42()5=16625.故学员能通过“科二”考试的概率为1-16625=609625. ………………9分②根据题意,当且仅当该学员通过测试,或未通过测试但通过第1轮补测时X =150,其他情况时均有X =450,而P (X =150)=35+25×35=2125,故X 的分布列为故E (X )=150×2125+450×425=126+72=198(元). ………………12分21. 解:(1)∵底面ABCD 是菱形,∴//AB CD ,又∵AB ⊄面PCD ,CD ⊂面PCD , ∴//AB 面PCD ,又∵A ,B ,E ,F 四点共面,且平面ABEF 平面PCD EF =,∴//AB EF ; ………………4分 (2)取AD 中点G ,连接PG ,GB ,∵PA PD =,∴PG AD ⊥, 又∵平面PAD ⊥平面ABCD ,且平面PAD 平面ABCD AD =,∴PG ⊥平面ABCD ,∴PG GB ⊥, ………………5分 在菱形ABCD 中,∵AB AD =,60DAB ∠=︒,G 是AD 中点,∴AD GB ⊥, ………………6分 如图,建立空间直角坐标系G xyz -,由2PA PD AD ===,得(0,0,0)G ,(1,0,0)A ,B (C -,(1,0,0)D -,P ,又∵//AB EF ,点E 是棱PC 中点, ∴点F 是棱PD 中点,∴(1,22E-,1(,0,)22F -,3(2AF =-uu u r ,1(,2EF =uu u r ,设平面AFE 的法向量为(,,)n x y z =r ,则有00n AF n EF ⎧⋅=⎪⎨⋅=⎪⎩r uu u r r uu u r ,∴z y x⎧=⎪⎨=⎪⎩,不妨令3x =,则平面AFE的一个法向量为n =r, …………9分∵BG ⊥平面PAD ,∴GB =uu u r是平面PAF 的一个法向量,……10分∵cos ,n GB <n GB >n GB⋅===⋅r uu u rr uu u r r uuu r , ………………11分 ∴平面PAF 与平面AFE .………………12分 22.解:(1)因为(1)102af =-=,所以2a =,此时2()ln ,0f x x x x x =-+>, 2121()21(0)x x f x x x x x-++'=-+=> 由()0f x '<,得2210x x -->,又0x >,所以1x >.所以()f x 的单调减区间为(1,)+∞.………………3分(2)方法一:令21()()1)ln (1)12g x f x ax x ax a x =-=-+-+-(, 所以21(1)1()(1)ax a x g x ax a x x-+-+'=-+-=.当0a ≤时,因为0x >,所以()0g x '>. 所以()g x 在(0,)+∞上是递增函数, 又因为213(1)ln11(1)12022g a a a =-⨯+-+=-+>,所以关于x 的不等式()1f x ax ≤-不能恒成立.当0a >时,21()(1)(1)1()a x x ax a x a g x x x-+-+-+'==-, 令()0g x '=,得1x a=. 所以当1(0,)x a∈时,()0g x '>;当1(,)x a∈+∞时,()0g x '<,因此函数()g x 在1(0,)x a ∈是增函数,在1(,)x a∈+∞是减函数.故函数()g x 的最大值为2111111()ln ()(1)1ln 22g a a a a a a a a=-⨯+-⨯+=-. 令1()ln 2h a a a=-, 因为1(1)02h =>,1(2)ln 204h =-<,又因为()h a 在(0,)a ∈+∞是减函数. 所以当2a ≥时,()0h a <.所以整数a 的最小值为2. ………………8分方法二:(2)由()1f x ax -≤恒成立,得21ln 12x ax x ax -+-≤在(0,)+∞上恒成立, 问题等价于2ln 112x x a x x +++≥在(0,)+∞上恒成立. 令2ln 1()12x x g x x x ++=+,只要max ()a g x ≥. 因为221(1)(ln )2()1()2x x x g x x x +--'=+,令()0g x '=,得1ln 02x x --=.设1()ln 2h x x x =--,因为11()02h x x '=--<,所以()h x 在(0,)+∞上单调递减,不妨设1ln 02x x --=的根为0x . 当0(0,)x x ∈时,()0g x '>;当0(,)x x ∈+∞时,()0g x '<, 所以()g x 在0(0,)x x ∈上是增函数;在0(,)x x ∈+∞上是减函数.所以000max 020000011ln 112()()11(1)22x x x g x g x x x x x x +++====++. 因为11()ln 2024h =->,1(1)02h =-<所以0112x <<,此时0112x <<,即max ()(1,2)g x ∈.所以2a ≥,即整数a 的最小值为2. ………………8分 (3)当2a =-时,2()ln ,0f x x x x x =++>由1212()()0f x f x x x ++=,即2211122212ln ln 0x x x x x x x x ++++++=从而212121212()()ln()x x x x x x x x +++=⋅-⋅ 令12t x x =⋅,则由()ln t t t ϕ=-得,1()t t tϕ-'=可知,()t ϕ在区间(0,1)上单调递减,在区间(1,)+∞上单调递增. 所以()(1)1t ϕϕ=≥, 所以21212()()1x x x x +++≥,因此12x x + ………………12分。
【全国市级联考】广东省中山市2017-2018学年高一上学期期末考试数学试题(解析版)

中山市高一级2017-2018学年度第一学期期末统一考试数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 下列四组函数,表示同一函数的是()A. B.C. D.【答案】D【解析】试题分析:A.,对应法则不同;B.,定义域不同;C.,定义域不同;故选D。
考点:本题主要考查函数的概念,构成函数的要素。
点评:解答题,构成函数的要素有定义域、对应法则。
2. 平行于同一平面的两条直线的位置关系是()A. 平行B. 相交C. 异面D. 平行、相交或异面【答案】D考点:平面的基本性质及推论.3. 已知集合,,则()A. B. C. D.【答案】C【解析】,∴故选:C点睛:求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.4. 图中的直线的斜率分别是,则有()A. B. C. D.【答案】D【解析】由图可知:,,,且直线的倾斜角大于直线的倾斜角,所以,综上可知:,故选.5. 设,,则()A. B. C. D.【答案】A【解析】∵,∴故选:A点睛:利用指数函数对数函数及幂函数的性质比较实数或式子的大小,一方面要比较两个实数或式子形式的异同,底数相同,考虑指数函数增减性,指数相同考虑幂函数的增减性,当都不相同时,考虑分析数或式子的大致范围,来进行比较大小,另一方面注意特殊值的应用,有时候要借助其“桥梁”作用,来比较大小.6. 方程在下面哪个区间内有实根()A. B. C. D.【答案】C【解析】令,则在上单调递增,且图象是连续的,又,,,即,由零点定理可知:的零点在内,故选:C7. 一个几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.【答案】D【解析】由题可知对应的几何体为一个底面为等腰直角三角形的直棱柱截去以上底面为底,高为一半的一个三棱锥.......................8. 一圆锥的侧面展开图是一个半圆,则这个圆锥的母线与底面所成角是()A. B. C. D.【答案】C【解析】设圆锥的母线长为R,底面半径为r,则:πR=2πr,∴R=2r,∴母线与底面所成角的余弦值==,∴母线与底面所成角是60°.故选:C.9. 若函数的值域为,则实数的取值范围是()A. B. C. D.【答案】D【解析】函数的值域为,则g(x)=mx2+2(m﹣2)x+1的值域能取到(0,+∞),①当m=0时,g(x)=﹣4x+1,值域为R,包括了(0,+∞),②要使f(x)能取(0,+∞),则g(x)的最小值小于等于0,则,解得:0<m≤1或m≥4.综上可得实数m的取值范围是故选:D.10. 如图,二面角的大小是,线段,,与所成的角为,则与平面所成的角的余弦值是()A. B. C. D.【答案】B【解析】过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D连结AD,易知AD⊥l,故∠ADC为二面角α﹣l﹣β的平面角为60°又由已知,∠ABD=30°连结CB,则∠ABC为AB与平面β所成的角,设AD=2,则AC=,CD=1AB==4,BC=,∴cos∠ABC=.故选:B点睛:(1)求二面角大小的过程可总结为:“一找、二证、三计算。
【全国市级联考word】广东省中山市2018届高三上学期期末考试文数试题

中山市高三级2017-2018学年度第一学期期末统一考试文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合},2|{2R x x x x A ∈-==,},1{m B =,若B A ⊆,则m 的值为( )A . 2B . -1C .-1或2D .2或22.若复数iaiz -+=21(i 是虚数单位)为纯虚数,则实数a 的值为( ) A . 2 B .21 C . 21- D .-23.一名法官在审理一起盗窃案时,四名嫌疑人甲、乙、丙、丁分述如下:甲说:“罪犯在乙、丙、丁三人之中”,乙说:“我没有作案,是丙偷的”,丙说:“在甲和乙中有一个人是罪犯”,丁说:“乙说的是事实”,经调查核实,这四人中只有一人是罪犯,并且得知有两人说的是真话,两人说的是假话,由此可判断罪犯是( )A .甲B . 乙C . 丙D . 丁 4. 阅读如图所示的程序框图,输出的结果s 的值为( ) A . 0 B .23 C. 3 D .23- 5. 若y x ,满足⎪⎩⎪⎨⎧≥≤+-≤+00224y x y y x ,若y x z 2+=,则z 的最大值是( )A . 1B . 4 C. 6 D .86. 李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等. 其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )A .10步,50步B .20步,60步 C. 30步,70步 D .40步,80步7.已知实数22ln =a ,33ln =b ,55ln =c ,则c b a ,,的大小关系是( ) A .c b a << B .b a c << C. a b c << D .c a b << 8. 已知函数)(x f 与)('x f 的图像如图所示,则函数xe xf xg )()(=的递减区间为( ) A . )4,0( B .)4,34(),1,(-∞ C. )34,0( D .),4(),1,0(+∞9.函数14)62sin(2-+=xx x y π的图像大致为( ) A . B .C. D .10. 在正方体1111D C B A ABCD -中,E 是棱1CC 的中点,F 是侧面11B BCC 内的动点,且//1F A 平面AE D 1,则F A 1与平面11B BCC 所成角的正切值t 构成的集合是( )A .}32552|{≤≤t t B .}2552|{≤≤t t C. }322|{≤≤t t D .}222|{≤≤t t 11. 已知131<≤k ,函数k x f x --=|12|)(的零点分别为21,x x )(21x x <,函数12|12|)(+--=k k x g x 的零点分别为43,x x )(43x x <,则)(1324x x x x +-+的最小值为( ) A .1 B .3log 2 C. 6log 2 D .3 12. 已知函数)0(cos4cos sin 3)(2>-=ωωωωx x x x f ,其周期为π,21)(=θf ,则=-++)4()2(πθπθf f ( ) A . 25- B .29- C. 211- D .213-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知54)4cos(=+πα,则=α2sin . 14.已知)2,1(-=a ,)2,0(=+b a ,则=||b .15.某班运动队由足球队员18人、篮球队员12人、乒乓球队员6人组成(每人只参加一项),现从这些运动员中抽取一个容量为n 的样本,若分别采用系统抽样和分层抽样法,则都不用剔除个体;当样本容量为1+n 时,若采用系统抽样法,则需要剔除1个个体,那么样本容量n 为 .16.数列}{n a 的前n 项和n S ,已知511=a ,且对任意正整数n m ,,都有n m n m a a a =+,若对任意*N n ∈,t S n <恒成立,则实数t 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 设等差数列}{n a 的前n 项和n S ,且25655=+=a a S . (1)求}{n a 的通项公式;(2)若不等式)4()1(2782+->++n n n a k n S 对所有的正整数n 都成立,求实数k 的取值范围. 18. 如图,在ABC ∆中,2=AB ,31cos =B ,点D 在线段BC 上. (1)若43π=∠ADC ,求AD 的长; (2)若DC BD 2=,ACD ∆的面积为324,求CAD BAD ∠∠sin sin 的值.19. 某单位拟建一个扇环形状的花坛(如图所示),该扇环面是由以点O 为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成,按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为x 米,圆心角为θ(弧度). (1)求θ关于x 的函数关系式;(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用的比为y ,求y 关于x 的函数关系式,并求出x 为何值时,y 取得最大值?20. 某市小型机动车驾照“科二”考试中共有5项考查项目,分别记作①,②,③,④,⑤.(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并计算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3(3≤)项的概率. (2)如图,某次模拟演练中,教练要求学员甲倒车并转向090,在汽车边缘不压射线AC 与射线BD 的前提下,将汽车驶入指定的停车位,根据经验,学员甲转向090后可使车尾边缘完全落在线段CD 上,且位于CD 内各处的机会相等,若m BD CA 3.0==,m AB 4.2=. 汽车宽度为m 8.1,求学员甲能按教练要求完成任务的概率.21. 如图所示的几何体QPABCD 为一简单组合体,在底面ABCD 中,060=∠DAB ,DC AD ⊥,BC AB ⊥,⊥QD 平面ABCD ,QD PA //,1=PA ,2===QD AB AD .(1)求证:平面⊥PAB 平面QBC ; (2)求该组合体QPABCD 的体积. 22. 已知函数R a x ax x x f ∈+-=,21ln )(2. (1)若0)1(=f ,求函数)(x f 的单调递减区间;(2)若关于x 的不等式1)(-≤ax x f 恒成立,求整数a 的最小值中山市高三级2017—2018学年度第一学期期末统一考试数学(文科)参考答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 AABBCBBDDDBD13. 725-14. 17 15. 6 16. 1,4⎡⎫+∞⎪⎢⎣⎭17.解:(Ⅰ)设公差为d ,则11154545252a d a d a d ⨯+=+++=,∴1 1 3a d =-=,. ∴{}n a 的通项公式为34n a n =-.(Ⅱ)()312n n n S n -=-+,228273327n S n n n ++=++,43n a n +=;则原不等式等价于()911nk n n-<++对所有的正整数n 都成立. ∴当n 为奇数时,91k n n ⎛⎫>-++ ⎪⎝⎭; 当n 为偶数时,91k n n <++恒成立…6分又∵917n n++≥,当且仅当3n =时取等号, 所以当n 为奇数时,91n n++的最小值为7,当n 为偶数时,4n =时,91n n ++的最小值为294, ∴不等式对所有的正整数n 都成立时,实数k 的取值范是2974k -<< 18.解:(Ⅰ)在三角形中,∵1cos 3B =,∴22sin 3B =. 在ABD ∆中,由正弦定理得sin sin AB AD ADB B=∠,又2AB =,4ADB π∠=,22sin 3B =.∴83AD =.(Ⅱ)∵2BD DC =,∴2ABD ADC S S ∆∆=,3ABC ADC S S ∆∆=,又423ADC S ∆=,∴42ABC S ∆=, ∵1sin 2ABCS AB BC B ∆=⋅,∴6BC =, 在ABC ∆中,由余弦定理得2222cos AC AB BC AB BC ABC =+-⋅∠. ∴42AC =, ∵1sin 2ABD S AB AD BAD ∆=⋅∠,1sin 2ADC S AC AD CAD ∆=⋅∠, 且2ABD ADC S S ∆∆=, ∴sin 242sin BAD AC CAD AB∠=⋅=∠19. 解: (1)由弧长计算及扇环面的周长为30米,得()30102(10)x x θ=++-,所以10210xxθ+=+,100<<x …3分 (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<.装饰总费用为()9108(10)17010x x x θ++-=+,所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++,令17t x =+,则3913243()101010y t t =-+≤,当且仅当t =18时取等号, 此时121,11x θ==. 答:当x =1时,花坛的面积与装饰总费用的比最大. (注:对y 也可以通过求导,研究单调性求最值,同样给分)20. 解: (1)根据题意,学员(1),(2),(4),(6),(9)恰有两项不合格,从中任意抽出2人,所有情况如下:学员编号 补测项目 项数 (1)(2) ②③⑤ 3 (1)(4) ②③④⑤ 4 (1)(6) ③④⑤ 3 (1)(9) ①③⑤ 3 (2)(4) ②④⑤ 3 (2)(6) ②③④⑤ 4 (2)(9) ①②⑤ 3 (4)(6) ②③④ 3 (4)(9) ①②④⑤ 4 (6)(9)①③④⑤4由表可知,全部10种可能的情况中,有6种情况补测项数不超过3,由古典概型可知,所求概率为=10635. (2)在线段CD 上取两点B ',D ',使8.1='='D D B B m ,记汽车尾部左端点为M ,则当M 位于线段B A '上时,学员甲可按教练要求完成任务,而学员甲可以使点M 等可能地出现在线段D C '上,根据几何概型,所求概率212.16.08.13.024.28.14.2==-⨯+-=''=D C B A P . 21. 解:(1)证明:因为QD ⊥平面ABCD ,PA QD P ,所以PA ⊥平面ABCD . 又因为BC ⊂平面ABCD ,所以PA BC ⊥,又因为AB BC ⊥,且ABPA A =,所以BC ⊥平面PAB ,又因为BC ⊂平面QBC ,所以平面PAB ⊥平QBC (2)面QDB 将几何体分成四棱锥B PADQ -和三棱锥Q BDC -两部分, 过B 作BO AD ⊥,因为PA ⊥平面ABCD ,BO ⊂平面ABCD , 所以PA BO ⊥,又因为AD OB ⊥,PAAD A =,所以BO ⊥平面PADQ ,即BO 为四棱锥B APQD -的高, 并且3BO =,3PADQ S =梯形, 所133B PADQ PADQV S BO -=⋅=梯形, 因为QD ⊥平面ABCD ,且已知2QD =,BCD ∆为顶角等于120︒的等腰三角形,2BD =,33BDC S ∆=, 所以12339Q BDC BDC V S QD -∆=⋅⋅=, 所以组合体QPABCD 的体积为23113399+=. 22.解:(1)因为(1)102af =-=,所以2a =,此时2()ln ,0f x x x x x =-+>, 2121()21(0)x x f x x x x x-++'=-+=> 由()0f x '<,得2210x x -->,又0x >,所以1x >.所以()f x 的单调减区间为(1,)+∞.(2)方法一:令21()()1)ln (1)12g x f x ax x ax a x =-=-+-+-(, 所以21(1)1()(1)ax a x g x ax a x x-+-+'=-+-=.当0a ≤时,因为0x >,所以()0g x '>. 所以()g x 在(0,)+∞上是递增函数, 又因为213(1)ln11(1)12022g a a a =-⨯+-+=-+>, 所以关于x 的不等式()1f x ax ≤-不能恒成立.当0a >时,21()(1)(1)1()a x x ax a x a g x x x-+-+-+'==-, 令()0g x '=,得1x a=. 所以当1(0,)x a∈时,()0g x '>;当1(,)x a∈+∞时,()0g x '<,因此函数()g x 在1(0,)x a ∈是增函数,在1(,)x a∈+∞是减函数.故函数()g x 的最大值为2111111()ln()(1)1ln 22g a a a a a a a a=-⨯+-⨯+=-. 令1()ln 2h a a a=-, 因为1(1)02h =>,1(2)ln 204h =-<,又因为()h a 在(0,)a ∈+∞是减函数. 所以当2a ≥时,()0h a <. 所以整数a 的最小值为2.方法二:(2)由()1f x ax -≤恒成立,得21ln 12x ax x ax -+-≤在(0,)+∞上恒成立, 问题等价于2ln 112x x a x x +++≥在(0,)+∞上恒成立. 令2ln 1()12x x g x x x ++=+,只要max ()a g x ≥. 因为221(1)(ln )2()1()2x x x g x x x +--'=+,令()0g x '=,得1ln 02x x --=.设1()ln 2h x x x =--,因为11()02h x x '=--<,所以()h x 在(0,)+∞上单调递减,不妨设1ln 02x x --=的根为0x . 当0(0,)x x ∈时,()0g x '>;当0(,)x x ∈+∞时,()0g x '<, 所以()g x 在0(0,)x x ∈上是增函数;在0(,)x x ∈+∞上是减函数.所以000max 020000011ln 112()()11(1)22x x x g x g x x x x x x +++====++. 因为11()ln 2024h =->,1(1)02h =-<所以0112x <<,此时0112x <<,即max ()(1,2)g x ∈.所以2a ≥,即整数a 的最小值为2.中山市高三级2017—2018学年度第一学期期末统一考试数学(文科)参考答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 11 12 答案AABBCBBDDDBD13. 725-14. 17 15. 6 16. 1,4⎡⎫+∞⎪⎢⎣⎭17.解:(Ⅰ)设公差为d ,则11154545252a d a d a d ⨯+=+++=,∴1 1 3a d =-=,. ∴{}n a 的通项公式为34n a n =-. …………3分(Ⅱ)()312n n n S n -=-+,228273327n S n n n ++=++,43n a n +=;则原不等式等价于()911nk n n-<++对所有的正整数n 都成立. ∴当n 为奇数时,91k n n ⎛⎫>-++ ⎪⎝⎭; 当n 为偶数时,91k n n <++恒成立…6分又∵917n n++≥,当且仅当3n =时取等号, 所以当n 为奇数时,91n n++的最小值为7, 当n 为偶数时,4n =时,91n n ++的最小值为294, ∴不等式对所有的正整数n 都成立时,实数k 的取值范是2974k -<<………10分 18.解:(Ⅰ)在三角形中,∵1cos 3B =,∴22sin 3B =. ………………2分 在ABD ∆中,由正弦定理得sin sin AB ADADB B=∠,又2AB =,4ADB π∠=,22sin 3B =.∴83AD =. ………………5分(Ⅱ)∵2BD DC =,∴2ABD ADC S S ∆∆=,3ABC ADC S S ∆∆=,又423ADC S ∆=,∴42ABC S ∆=, ………………7分 ∵1sin 2ABCS AB BC B ∆=⋅,∴6BC =,在ABC ∆中,由余弦定理得2222cos AC AB BC AB BC ABC =+-⋅∠. ∴42AC =, ………………9分 ∵1sin 2ABD S AB AD BAD ∆=⋅∠,1sin 2ADC S AC AD CAD ∆=⋅∠, 且2ABD ADC S S ∆∆=, ∴sin 242sin BAD AC CAD AB∠=⋅=∠ ………………12分19. 解: (1)由弧长计算及扇环面的周长为30米,得()30102(10)x x θ=++-,所以10210xxθ+=+,100<<x …3分 (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<.……5分装饰总费用为()9108(10)17010x x x θ++-=+, ……………………7分 所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++, …9分令17t x =+,则3913243()101010y t t =-+≤,当且仅当t =18时取等号, 此时121,11x θ==. 答:当x =1时,花坛的面积与装饰总费用的比最大. …………………12分 (注:对y 也可以通过求导,研究单调性求最值,同样给分)21. 解: (1)根据题意,学员(1),(2),(4),(6),(9)恰有两项不合格,从中任意抽出2人,所有情况如下:学员编号 补测项目 项数 (1)(2) ②③⑤ 3 (1)(4) ②③④⑤ 4 (1)(6) ③④⑤ 3 (1)(9) ①③⑤ 3 (2)(4) ②④⑤ 3 (2)(6) ②③④⑤ 4 (2)(9) ①②⑤ 3 (4)(6) ②③④ 3 (4)(9) ①②④⑤ 4 (6)(9)①③④⑤4由表可知,全部10种可能的情况中,有6种情况补测项数不超过3,由古典概型可知,所求概率为=10635.………………6分(2)在线段CD 上取两点B ',D ',使8.1='='D D B B m ,记汽车尾部左端点为M ,则当M 位于线段B A '上时,学员甲可按教练要求完成任务,而学员甲可以使点M 等可能地出现在线段D C '上,根据几何概型,所求概率212.16.08.13.024.28.14.2==-⨯+-=''=D C B A P . …………12分21. 解:(1)证明:因为QD ⊥平面ABCD ,PA QD P ,所以PA ⊥平面ABCD .又因为BC ⊂平面ABCD ,所以PA BC ⊥,又因为AB BC ⊥,且AB PA A =,所以BC ⊥平面PAB ,又因为BC ⊂平面QBC ,所以平面PAB ⊥平QBC ……5分(2)面QDB 将几何体分成四棱锥B PADQ -和三棱锥Q BDC -两部分,过B 作BO AD ⊥,因为PA ⊥平面ABCD ,BO ⊂平面ABCD ,所以PA BO ⊥,又因为AD OB ⊥,PA AD A =,所以BO ⊥平面PADQ ,即BO 为四棱锥B APQD -的高, 并且3BO =,3PADQ S =梯形, 所133B PADQ PADQ V S BO -=⋅=梯形,因为QD ⊥平面ABCD ,且已知2QD =,BCD ∆为顶角等于120︒的等腰三角形,2BD =,33BDC S ∆=, 所以12339Q BDC BDC V S QD -∆=⋅⋅=,所以组合体QPABCD 的体积为23113399+=.…………………………12分22.解:(1)因为(1)102af =-=,所以2a =,此时2()ln ,0f x x x x x =-+>,2121()21(0)x x f x x x x x -++'=-+=> 由()0f x '<,得2210x x -->,又0x >,所以1x >.所以()f x 的单调减区间为(1,)+∞.………………4分 O(2)方法一:令21()()1)ln (1)12g x f x ax x ax a x =-=-+-+-(, 所以21(1)1()(1)ax a x g x ax a x x -+-+'=-+-=.当0a ≤时,因为0x >,所以()0g x '>.所以()g x 在(0,)+∞上是递增函数, 又因为213(1)ln11(1)12022g a a a =-⨯+-+=-+>,所以关于x 的不等式()1f x ax ≤-不能恒成立.当0a >时,21()(1)(1)1()a x x ax a x a g x x x-+-+-+'==-,令()0g x '=,得1x a =. 所以当1(0,)x a ∈时,()0g x '>;当1(,)x a ∈+∞时,()0g x '<,因此函数()g x 在1(0,)x a ∈是增函数,在1(,)x a ∈+∞是减函数.故函数()g x 的最大值为2111111()ln ()(1)1ln 22g a a a a a a a a =-⨯+-⨯+=-.令1()ln 2h a a a =-, 因为1(1)02h =>,1(2)ln 204h =-<,又因为()h a 在(0,)a ∈+∞是减函数.所以当2a ≥时,()0h a <. 所以整数a 的最小值为2. ………………12分方法二:(2)由()1f x ax -≤恒成立,得21ln 12x ax x ax -+-≤在(0,)+∞上恒成立,问题等价于2ln 112x x a x x+++≥在(0,)+∞上恒成立. 令2ln1()12x x g x x x ++=+,只要max ()a g x ≥.因为221(1)(ln )2()1()2x x x g x x x +--'=+,令()0g x '=,得1ln 02x x --=. 设1()ln 2h x x x =--,因为11()02h x x '=--<,所以()h x 在(0,)+∞上单调递减,不妨设1ln 02x x --=的根为0x .当0(0,)x x ∈时,()0g x '>;当0(,)x x ∈+∞时,()0g x '<, 所以()g x 在0(0,)x x ∈上是增函数;在0(,)x x ∈+∞上是减函数. 所以000max 020000011ln 112()()11(1)22xx x g x g x xx x x x +++====++. 因为11()ln 2024h =->,1(1)02h =-< 所以0112x <<,此时0112x <<,即max ()(1,2)g x ∈.所以2a ≥,即整数a 的最小值为2. ………………12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中山市高一级2017-2018学年度第一学期期末统一考试
数学试卷
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列四组函数,表示同一函数的是()
A. B.
C. D.
2. 平行于同一平面的两条直线的位置关系是()
A. 平行
B. 相交
C. 异面
D. 平行、相交或异面
3. 已知集合,,则()
A. B. C. D.
4. 图中的直线的斜率分别是,则有()
学§科§网...
A. B. C. D.
5. 设,,则()
A. B. C. D.
6. 方程在下面哪个区间内有实根()
A. B. C. D.
7. 一个几何体的三视图如图所示,则该几何体的体积为()
A. B. C. D.
8. 一圆锥的侧面展开图是一个半圆,则这个圆锥的母线与底面所成角是()
A. B. C. D.
9. 若函数的值域为,则实数的取值范围是()
A. B. C. D.
10. 如图,二面角的大小是,线段,,与所成的角为,则与平面所成的角的余弦值是()
A. B. C. D.
11. 正四面体中,是棱的中点,是点在底面内的射影,则异面直线与所成角的余弦值为()
A. B. C. D.
12. 已知函数在闭区间上的值域为,则满足题意的有序实数对在坐标平面内所对应点组成图形为()
A. B.
C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13. 已知,则__________.
14. 已知两条平行直线分别过点,,且的距离为5,则直线的斜率是__________.
15. 已知函数,若函数有3个零点,则实数的取值范围是__________.
16. 如图,将一边为1的正方体沿相邻三个面的对角线截出一个棱锥,则三棱锥的内切球半径是__________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 求值或化简:
(1);
(2).
18. 如图,正三角形的边长为6,,,点分别在边上,且
,,相交于.
(1)求点的坐标;
(2)判断和是否垂直,并证明.
19. 已知函数.
(1)求函数的定义域;
(2)判断函数的奇偶性,并证明你的结论;
(3)在函数图像上是否存在两个不同的点,使直线垂直轴,若存在,求出两点坐标;若不存在,说明理由.
20. 如图,在四棱锥中,底面,,,,为棱的中点.
(1)求证:;
(2)试判断与平面是否平行?并说明理由.
21. 《中华人民共和国个人所得税法》规定,公民全月工资、薪金(扣除三险一金后)所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额个人所得税计算公式:应纳税额=工资-三险一金=起征点. 其中,三险一金标准是养老保险8%、医疗保险2%、失业保险1%、住房公积金8%,此项税款按下表分段累计计算:
(1)某人月收入15000元(未扣三险一金),他应交个人所得税多少元?
(2)某人一月份已交此项税款为1094元,那么他当月的工资(未扣三险一金)所得是多少元?
22. 设,函数,其中.
(1)求的最小值;
(2)求使得等式成立的的取值范围.。
