华科固体物理考研题
固体物理809真题1997-2012 含部分答案(整理版)
du d 2 u (r ) = 0, > 0, dr dr 2 d 2 u (r ) m(m + 1)α n(n + 1) mα =− + n + 2 = m + 2 ( n − m) > 0 2 dr r0m+ 2 r0 r0
所以 n>m。 三 解：1 根据态密度定义可以给出 g (ω )dω =
α
r
m
+
β
rn
，其中α，β，m,n 均为>0 的常数，试证明此
系统可以处于稳定平衡态的条件是 n>m。 三 已知由 N 个质量为 m，间距为的相同原子组成的一维单原子链的色散关系为
qa ⎛ 4β ⎞ 2 ω = ⎜ ⎟ sin 2 ⎝ m ⎠
1 试给出它的格波态密度 g (ω ) ，并作图表示 2 试绘出其色散曲线形状，并说明存在截止频率 ωmax 的意义 四 半导体材料的价带基本上填满了电子（近满带） ，价带中电子能量表示式
得： g (ω ) =
ωm
ω
2N
π
(ω
2 =
4β m
2
截 止 频 率 是 只 有 频 率 在 ω 到 ω m 之间的格波才能在晶体中传播，其它 频率的格波被强烈衰减，一维单原子 晶格看作成低通滤波器。
L dq （这里 L＝Na） 2π
一维原子链应考虑正负两支 所以 g (ω ) = 2 ×
L 2π
dω L = dq π
dω dq
g（ω）
⎛ 4β ⎞ 将ω = ⎜ ⎟ ⎝ m ⎠
1
2
sin
qa 代入得： 2
1
dω a qa a 2 = ωm cos = (ωm − ω 2 ) 2 dq 2 2 2
华科研究生固体物理第2章习题
第二章习题
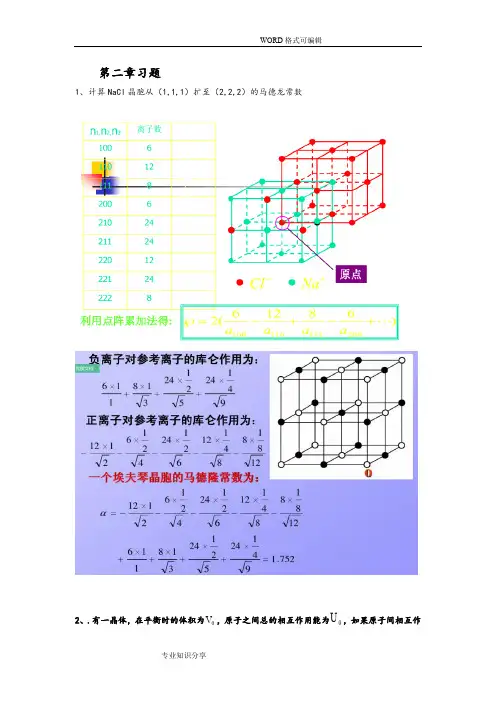
1、计算NaCl 晶胞从（1,1,1）扩至（2,2,2）的马德龙常数
2、.有一晶体，在平衡时的体积为0V ，原子之间总的相互作用能为0U ，如果原子间相互作
用能由下式给出：
n
m
r r r u β
α
+
-
=)(，
试证明弹性模量可由[])9/(00V mn U 给出。
提示：原子间总结合能为)//)(2/()(n m r r N r U βα+-=，体积3ANr V =。
3、.上题表示的相互作用能公式中，若2=m ，10=n ，且两原子构成稳定分子时间距为
10
⨯m，离解能为4eV，试计算α和β之值。
10
3-
4、如果NaCl结构中离子的电荷增加一倍，晶体的结合能及离子间的平衡距离将发生多大的变化？
5、NaCl晶体的体弹模量为2.4×1010Pa，在2×109Pa的气压作用下，晶体中两相邻离子间的距离将缩小百分之几？
6、计算GaAs和氧化铝\氮化铝中离子键的比例。
7、对线型离子晶体，在一条直线链上交替地载有电荷±q 的2N 个离子，最近邻之间的排斥
势能为
n r
b。
（1）试证在平衡间距下 )1
1(42ln 2)(0020n
r Nq r U --=πε
（2）令晶体被压缩，使)1(00δ-→r r ，试证在晶体被压缩单位长度的过程中，（外力）所做功的主项为2)2/1(δC ，其中
0242ln )1(r q n C πε-=
思考题
1.原子结合成晶体时，原子的价电子将重新分布，从而产生不同的结合力。
分析各类晶体
中决定结合类型的主要结合力。
华科固体物理考研题
华科固体物理考研题(共24页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--华中科技大学一九九九年招收硕士研究生入学考试试题 考试科目： 固体物理适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）1.设半径为R 的硬球堆成体心立方晶格，计算可以放入其间隙位置的一个硬球的最大半径r2.已知NaCl 晶体平均每对离子的相互作用能为 2()n q B u r r rα=-+，其中马德隆常数 1.75α=, n = 9，平衡离子间距0 2.82r = Å，求其声学波与光学波之间的频率间隙Δω（Na 的原子量为23, Cl 的原子量为, 1原子质量单位为×2410-克，104.810q -=⨯静电单位电荷）3.已知碳在()铁中的扩散系数D 与温度关系的实验数据为：当温度为200度时，扩散系数D200℃ = 11210/cm -秒；温度为760℃时，D760℃ =-6210/cm 秒，试求扩散过程的激活能Q （千焦耳/摩尔）（气体常数R=焦耳/摩尔·开）4.设N 个电子在边长为L 的正方形框中自由运动，在求解薜定谔方程时所得电子的本征能量220()x y E n n E =+式中，x n ，y n ，为任意正整数，0E 为基态能量，试求绝对零度时系统的费米能F E5.设晶格势场对电子的作用力为L F ，电子受到的外场力为e F ，证明电子的有效质量*m 和电子的惯性质量m 的关系为：*ee L F m F F =+六．已知Na 的费米能 0F E = ，在 T = 0k 下, 测知其电导率σ= ×17110()cm -Ω⋅，试求该温度下Na 的电子的弛豫时间τ.（常数:104.810e cgsu -=⨯, m = ×2810g -，271.0510erg s -=⨯⋅，121.610lev erg -=⨯）华中科技大学 二00一年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学 （除画图题外，所有答案都必须写在答题纸上，写在试题上及草 稿纸上无效，考完后试题随答题纸交回）一、选择题（25分）1.晶体的宏观对称性中有（ ）种基本的对称操作2.金刚石晶格的布拉菲格子为（ ）A.简立方B.体心立方C.面心立方D.六角密排 晶体的结合方式为（）A.离子结合B.共价结合C.金属性结合D.共价结合+离子结合 晶体的配位数是（）晶体中有3支声学波和（）支光学波6.体心立方晶格的晶格常数为a ，其倒格子原胞体积等于（） A.31a B.338a π C.3316aπ D.3332a π 7.周期性势场中单电子本征波函数为（）A.周期函数B.旺尼尔函数C.布洛赫函数D.r k e V18.极低温下，固体的比热Cv 与T 的关系（）A .Cv 与T 成正比 B. Cv 与2T 成正比 C. Cv 与3T 成正比 D. Cv 与T 无关9.面心立方晶格的简约布里渊区是（）A.截角八面体B.正12面体C.正八面体D.正立方体10.位错破坏了晶格的周期性，位错是（）A.点缺陷B.线缺陷C.面缺陷D.热缺陷二、简要回答下列问题（20分）1.简述金属，绝缘体和半导体在能带结构上的差异.2.为什么对金属电导有贡献的只是费米面附近的电子？3.引起固体热膨胀的物理原因是什么？4.什么是金属的功函数，写出两块金属之间的接触电势差12V 与功函数1φ、2φ之间的关系式.三、（15分）一维周期场中电子的波πψax x x 3sin )(=，（a 是晶格常函数是数），试求电子在该状态的波矢。
华科固体物理考研题
华中科技大学一九九九年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）1.设半径为R 的硬球堆成体心立方晶格，计算可以放入其间隙位置的一个硬球的最大半径r2.已知NaCl 晶体平均每对离子的相互作用能为 2()n q B u r r rα=-+，其中马德隆常数 1.75α=, n = 9，平衡离子间距0 2.82r = Å，求其声学波与光学波之间的频率间隙Δω（Na 的原子量为23, Cl 的原子量为35.5, 1原子质量单位为1.67×2410-克，104.810q -=⨯静电单位电荷）3.已知碳在()铁中的扩散系数D 与温度关系的实验数据为：当温度为200度时，扩散系数D200℃ = 11210/cm -秒；温度为760℃时，D760℃ =-6210/cm 秒，试求扩散过程的激活能Q （千焦耳/摩尔）（气体常数R=8.31焦耳/摩尔·开）4.设N 个电子在边长为L 的正方形框中自由运动，在求解薜定谔方程时所得电子的本征能量220()x y E n n E =+式中，x n ，y n ，为任意正整数，0E 为基态能量，试求绝对零度时系统的费米能F E5.设晶格势场对电子的作用力为L F ，电子受到的外场力为e F ，证明电子的有效质量*m 和电子的惯性质量m 的关系为：*ee L F m F F =+六．已知Na 的费米能 0F E = 3.2ev ，在 T = 0k 下, 测知其电导率σ= 2.1×17110()cm -Ω⋅，试求该温度下Na 的电子的弛豫时间τ.（常数:104.810e cgsu -=⨯, m = 9.1×2810g -，271.0510erg s -=⨯⋅，121.610lev erg -=⨯）华中科技大学二00一年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、选择题（25分）1.晶体的宏观对称性中有（ ）种基本的对称操作A.7B.8C.14D.322.金刚石晶格的布拉菲格子为（ ）A.简立方B.体心立方C.面心立方D.六角密排3.GaAs 晶体的结合方式为（）A.离子结合B.共价结合C.金属性结合D.共价结合+离子结合4.NaCl 晶体的配位数是（）A.4B.6C.8D.125.KBr 晶体中有3支声学波和（）支光学波A.6B.3C.6ND.3N6.体心立方晶格的晶格常数为a ，其倒格子原胞体积等于（） A.31aB.338a πC.3316a πD.3332a π 7.周期性势场中单电子本征波函数为（）A.周期函数B.旺尼尔函数C.布洛赫函数D.r k e V1 8.极低温下，固体的比热Cv 与T 的关系（）A .Cv 与T 成正比 B. Cv 与2T 成正比 C. Cv 与3T 成正比 D. Cv 与T 无关9.面心立方晶格的简约布里渊区是（）A.截角八面体B.正12面体C.正八面体D.正立方体10.位错破坏了晶格的周期性，位错是（）A.点缺陷B.线缺陷C.面缺陷D.热缺陷二、简要回答下列问题（20分）1.简述金属，绝缘体和半导体在能带结构上的差异.2.为什么对金属电导有贡献的只是费米面附近的电子？3.引起固体热膨胀的物理原因是什么？4.什么是金属的功函数，写出两块金属之间的接触电势差12V 与功函数1φ、2φ之间的关系式.三、（15分）一维周期场中电子的波函数是πψa x x x 3sin)(=，（a 是晶格常数），试求电子在该状态的波矢。
华科999-20年固体物理考研题
1华中科技大学一九九九年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）1.设半径为R 的硬球堆成体心立方晶格，计算可以放入其间隙位置的一个硬球的最大半径r2.已知NaCl 晶体平均每对离子的相互作用能为 2()n q B u r r rα=-+，其中马德隆常数 1.75α=, n = 9，平衡离子间距0 2.82r =Å，求其声学波与光学波之间的频率间隙Δω（Na 的原子量为23, Cl 的原子量为35.5, 1原子质量单位为1.67×2410-克，104.810q -=⨯静电单位电荷）3.已知碳在()铁中的扩散系数D 与温度关系的实验数据为：当温度为200度时，扩散系数D200℃ = 11210/cm -秒；温度为760℃时，D760℃ =-6210/cm 秒，试求扩散过程的激活能Q （千焦耳/摩尔）（气体常数R=8.31焦耳/摩尔·开）4.设N 个电子在边长为L 的正方形框中自由运动，在求解薜定谔方程时所得电子的本征能量220()x y E n n E =+式中，x n ，y n ，为任意正整数，0E 为基态能量，试求绝对零度时系统的费米能F E5.设晶格势场对电子的作用力为L F ，电子受到的外场力为e F ，证明电子的有效质量*m 和电子的惯性质量m 的关系为：*ee L F m F F =+六．已知Na 的费米能 0F E = 3.2ev ，在 T = 0k 下, 测知其电导率σ= 2.1×17110()cm -Ω⋅，试求该温度下Na 的电子的弛豫时间τ.（常数:104.810e cgsu -=⨯, m = 9.1×2810g -，271.0510erg s -=⨯⋅h ，121.610lev erg -=⨯）3华中科技大学二00一年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、选择题（25分）1.晶体的宏观对称性中有（ ）种基本的对称操作A.7B.8C.14D.322.金刚石晶格的布拉菲格子为（ ）A.简立方B.体心立方C.面心立方D.六角密排3.GaAs 晶体的结合方式为（）A.离子结合B.共价结合C.金属性结合D.共价结合+离子结合4.NaCl 晶体的配位数是（）A.4B.6C.8D.125.KBr 晶体中有3支声学波和（）支光学波A.6B.3C.6ND.3N6.体心立方晶格的晶格常数为a ，其倒格子原胞体积等于（） A.31aB.338a πC.3316a πD.3332a π 7.周期性势场中单电子本征波函数为（）A.周期函数B.旺尼尔函数C.布洛赫函数D.r k e V1 8.极低温下，固体的比热Cv 与T 的关系（）A .Cv 与T 成正比 B. Cv 与2T 成正比 C. Cv 与3T 成正比 D. Cv 与T 无关9.面心立方晶格的简约布里渊区是（）A.截角八面体B.正12面体C.正八面体D.正立方体10.位错破坏了晶格的周期性，位错是（）A.点缺陷B.线缺陷C.面缺陷D.热缺陷二、简要回答下列问题（20分）1.简述金属，绝缘体和半导体在能带结构上的差异.2.为什么对金属电导有贡献的只是费米面附近的电子？3.引起固体热膨胀的物理原因是什么？4.什么是金属的功函数，写出两块金属之间的接触电势差12V 与功函数1φ、2φ之间的关系式.三、（15分）一维周期场中电子的波函数是πψa x x x 3sin)(=，（a 是晶格常数），试求电子在该状态的波矢。
华中科技大学2021年固体物理考研题
华中科技大学2021年固体物理考研题华中科技大学二00七年招收硕士研究生入学考试试题考试科目：固体物理适用专业：微电子学与固体电子学、材料物理与化学、电力电子与传动（除画图题外，所有答案都必须写下在答题纸上，写下在试题上及草稿纸上违宪，考完后试题随其答题纸交还）一、简答下列各题（60分，每小题6分）1.表示硅晶体的晶系、图形类型；晶格常数为a，谋硅原子之间的最近距离。
2.绘出面心立方结构的金属在（110）和（100）面上的原子排列示意图。
3.什么就是马德隆能够？马德隆常数就是由什么因素同意的？4.对于惰性元素晶体，任意两个原子间的相互作用能为:，其中r为原子间距，参数ε、ζ的物理意义是什么？5.什么就是德拜频率？德拜温度？写下德拜温度的典型值范围。
6.按德拜模型，定性说明低温下晶体振动热容对温度的依赖关系。
7.对具备n个初基晶胞的晶体，每个能带能容纳多少电子？18.按自由电子与bloch电子的主要特点，核对下表中。
自由电子bloch电子势场边界条件本征波函数能量9.半导体硅的导带底在布里渊区中的[100]方向，锗的导带底在[111]方向，他们等价的导带底各有多少？10.详述非均衡载流子的无机机理类型。
二、（15分）对于金刚石结构晶体，设原子形状因子为f，推导结构因子s的表达式，并讨论出现x射线衍射峰的条件。
三、（15分后）由2n个电荷为±q的也已负离子等间距交错排序构成的…维链，其最近邻之间的排挤势能为a/rn。
（1）证明在均衡间距r0之下，内能为：；（2）设晶体被压缩，使r0变为r0(1+δ),证明晶体单位长度上，外力所作的功为1cδ，其中2。
四、（15分）对于原子间距为a，由n个原子组成的一维单原子链，在德拜近似下（1）计算晶体振动模式密度；（2）证明在低温极限下，热容正比于温度t;(3)计算绝对零度下总的零点振动能。
2五、（15分）（1）设电子密度为n，按自由电子气体模型推导费米波矢kf的表达式；（2）求与晶格常数为a的面心立方点阵的第一布里渊区内切的费米球所对应的电子密度。
华科固体物理习题解答
2 h3 2 h1 2 h2 k Gh kx ky kz a b c
2 2 2 h h 1 2 2 h 3 Gh 2 ( 12 2 ) 2 2 2 a b c
1 2 k Gh Gh 2
2 2 2 2 h3 h 2 h1 2 h2 h h 3 kx ky k z 2 2 ( 12 2 ) 2 2 a b c a b c
（2）AC晶列的指数
c
C
B
AC OC OA
b
a
A
1 1 [c (a b )] (a b ) a(i j 2k ) 2 2
所以AC晶列的晶列指数为
[112]
第二章 习题 2.1 证明简单六角布喇菲格子的倒格子仍为简单六角布喇菲 格子，并给出其倒格子的晶格常数。 解：在直角坐标系中，简单 六角布喇菲格子的基矢为： 相应的倒格子基矢为：
4 a 3 6 ( ) 2 3 2 x 6 3 3 2 ca 2
(5) 金刚石结构 任意一个原子球有4个最近邻，若原子 以刚性球堆积，则空间对角线四分之一 处的原子与三个面上的面心原子球及顶 角处原子球相切，因此有
3a 8r
晶胞体积为 V a3
晶胞内包含8个原子，所以有：
4 3a 3 8 ( ) 3 3 8 x a3 16
简立方、体心立方、面心立方、六角密积以及金刚石结构 的致密度依次为
6
3 8
2 6
2 6
3 16
a 1.6 基矢为 a1 ai a2 aj a3 ( i j k ) 的晶体为何种结构？ 2
方法1：先计算出原胞体积 V a1 (a2 a3 ) a 3 由原胞体积可推断为体心结构 方法2：由已知的三个基矢构造三个新的基矢
中国科学院物理所考博固体物理试题5套.doc
中国科学院物理所考博固体物理试题5套屮国科学院物理研究所固体物理博士入学试题（2006年）1. 填空题.NaCI石墨铜钠其屮一个的点群与其它不同是•在低温，金刚石比热与温度的关系是•高压晶体体积变小，能带宽度会•石墨屮原子Z间通过键结合成固体。
2. 推导bloch定理；写出理想情况下表面态的波函数的表达式，并说明各项的特点。
3. 推导出一维双原子的色散关系。
4. 在紧束缚近似条件下，求解周期势场屮的波函数和能量木征值。
5. 某面心立方晶体，其点阵常数为aifflj 出晶胞，（1, 1, 1）, （2, 2 , 0 ） , （ 1 , 1 , 3 ）晶面；计算三面的面间距;说明为什么（1，0，0）晶面衍射强度为零。
6. 重费米系统、接触电势、安徳森转变。
7. 为什么金属电子白由程是有限的但又远远大于原子间距？8 .硅木征载流了浓度为9. 6 5 x 1 0 9 cm~3,导带有效密度为2. 8 6x1019 cm-3,若掺入每立方厘米10 16的A s原了，计算载流了浓度。
9 .磁畴1 0 •原激发1 1 .对理想金属可以认为其介电常数虚部为零。
请以A 1为例，给出理想金属对的反射率R随频率的变化（公式、频率值、示意图）1 2.分析说明小角晶界的角度和位错的间距的关系，写出表达式。
1 3.试通过数据说明，为什么处理硅、餡等半导体的可见光吸收时，采用垂真跃迁的近似是合理的。
1 4.试根据超导B=0,推导出超导临界温度和外加磁场的定性关系。
1 5.论述固体内部的位错类型，并且画出示意图。
2004 年第一部分（共6题，选作4题，每题15分，共计60分；如多做，按前4题计分）从成键的角度阐述m-v族和II-VI族半导体为什么可以形成同一种结构:闪锌矿结构。
2. 请导出一维双原了链的色散关系，并讨论在长波极限时光学波和声学波的原了振动特点。
3. 从声子的概念出发，推导并解释为什么在一般晶体屮的低温品格热容量和热导率满足T3关系。
华科研究生固体物理第2章习题
本文档如对你有帮助，请帮忙下载支持！
第二章习题
1、计算NaCl 晶胞从（1,1,1）扩至（2,2,2）的马德龙常数
2、.有一晶体，在平衡时的体积为0V ，原子之间总的相互作用能为0U ，如果原子间相互作用能由下式给出：
n m r r r u βα
+-=)(， 试证明弹性模量可由[])9/(00V mn U 给出。
提示：原子间总结合能为)//)(2/()(n m r r N r U βα+-=，体积3ANr V =。
3、.上题表示的相互作用能公式中，若2=m ，10=n ，且两原子构成稳定分子时间距为10103-⨯m ，离解能为4eV ，试计算α和β之值。
4、如果NaCl 结构中离子的电荷增加一倍，晶体的结合能及离子间的平衡距离将发生多大的变化？
5、NaCl 晶体的体弹模量为2.4×1010Pa ，在2×109Pa 的气压作用下，晶体中两相邻离子间的距离将缩小百分之几？
6、计算GaAs 和氧化铝\氮化铝中离子键的比例。
7、对线型离子晶体，在一条直线链上交替地载有电荷±q 的2N 个离子，最近邻之间的排斥势能为
n r
b 。
（1）试证在平衡间距下 （2）令晶体被压缩，使)1(00δ-→r r ，试证在晶体被压缩单位长度的过程中，（外力）所做功的主项为2)2/1(δC ，其中
思考题
1. 原子结合成晶体时，原子的价电子将重新分布，从而产生不同的结合力。
分析各类晶体
中决定结合类型的主要结合力。
固体物理答案陆栋.pdf
《固体物理学》习题解答( 仅供参考 )参加编辑学生柯宏伟（第一章），李琴（第二章），王雯（第三章），陈志心（第四章），朱燕（第五章），肖骁（第六章），秦丽丽（第七章）指导教师黄新堂华中师范大学物理科学与技术学院2003级2006 年 6 月第一章晶体结构1.氯化钠与金刚石型结构是复式格子还是布拉维格子，各自的基元为何？写出这两种结构的原胞与晶胞基矢，设晶格常数为 a。
解：氯化钠与金刚石型结构都是复式格子。
氯化钠的基元为一个 Na+和一个 Cl－组成的正负离子对。
金刚石的基元是一个面心立方上的Ｃ原子和一个体对角线上的Ｃ原子组成的Ｃ原子对。
由于 NaCl 和金刚石都由面心立方结构套构而成，所以，其元胞基矢都为：⎧⎪a1=a2( j + k)⎪⎪⎨a 2=a2( k + i)⎪⎪⎪a 3=a ( i +j)⎩ 2相应的晶胞基矢都为：⎧a =a i,⎪⎨b =a j,⎪⎩c =a k.2.六角密集结构可取四个原胞基矢a1, a 2,a 3与 a4,如图所示。
试写出O'A1A3、A1 A3 B3 B1、 A2 B2 B5 A5、 A1 A2 A3 A4 A5 A6这四个晶面所属晶面族的晶面指数(h k l m)。
解：(1)．对于O'A1A3面，其在四个原胞基矢上的截矩分别为：１，１，- 1 ，１。
所以，其晶面2( )指数为。
(2)．对于A1A3B3B1面，其在四个原胞基矢上的截矩分别为：１，１，-12，∞。
所以，其晶面指数为(1120)。
(3)．对于A2B2B5A5面，其在四个原胞基矢上的截矩分别为：１，-1，∞，∞。
1所以，其晶面指数为 (1 100)。
(4)．对于 A 1 A 2 A 3 A 4 A 5 A 6 面，其在四个原胞基矢上的截矩分别为：∞ ，∞ ，∞ ，１。
所以， 其晶面指数为 (0001) 。
3. 如将等体积的硬球堆成下列结构，求证球体可能占据的最大体积与总体积的比为：简立方： π6 ；体心立方： 83π；面心立方： 62π ；六角密集： 62π ；金刚石：3π 。
《固体物理》考研真题
南开大学806固体物理往年考研真题一、简答题（每题5分，共30分）1.晶体中可以存在哪些对称元素？讨论对称性有何意义？2.讨论晶格振动时引入了声子的概念，声子与晶体哪些物理性质有关？3.写出布拉格反射公式，并说明各符号的意义。
4.给出晶体中缺陷的基本类型，举例说明缺陷如何影响晶体的性质。
5.金属铯是体心立方结构，每个单胞中有两个单价原子，为什么铯是金属？6.解释倒易空间、倒易格矢、倒易矢量。
二、计算题（每题20分，共120分）1.一维单原子链，原子质量为m ，原子间距为a ，最近邻和次近邻原子间的相互作用力常数分别为和，计算声子的色散关系以及模式密度。
2.对N 个惰性气体原子组成的线性布拉菲点阵，设平均两个原子间的势为：其中和是两个常数，x 是原子间的最近距离，求：A 、原子间的平衡距离B 、每个原子间的平均点阵能C 、平均压缩模量αβ()12602u x x x σσφ⎡⎤⎛⎫⎛⎫=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦σ0φ0x 0u 0B3.某半导体材料，沿方向电子的能量可表示为：其中，a 为晶格周期，计算电子的速度v 以及有效质量，画出在区间以及关系曲线。
4.由二价原子组成的二维晶体，原胞基矢分别为，如果晶格周期势为：（a ）求倒格子原胞的基矢、画出第一布里渊区和第二布里渊区。
（b ）在近自由电子模型下，给出沿方向的第一能带和沿方向的第二能带交叠的条件。
5.（a ）推导绝对零度下金属自由电子费米能的表达式。
（b ）当温度变化是2，费米能如何变化？（c ）体心立方结构的金属钠，其点阵常数为，用自由电子模型计算其费米能。
6.铁为体心立方结构，从其（110）面反射的x 射线布拉格角为22度，x 射线的波长为0.154nm 。
（a ）计算铁的立方晶胞的边长。
（b ）从（111）面反射的x 射线布拉格角为多少？（c ）已知铁的原子量为55.8，计算铁的密度。
(),0,0x k k =()()24212x x E A k a k a π⎡⎤=-⎢⎥⎣⎦0A >m *[]0,a π~x v k ~x m k *,a ai b bj ==()022,2cos cos x y V x y V a b ππ⎡⎤⎛⎫⎛⎫=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦x k y k T ∆0.428a =。
固体物理考研题库
固体物理考研题库固体物理是研究固体物质的物理性质、结构以及它们之间的相互作用的科学领域。
它不仅在物理学中占有重要地位，也是材料科学和电子工程等领域的基础。
以下是一些固体物理考研题库的样例题目，供参考：一、选择题1. 晶体的周期性结构是由哪种对称性定义的？A. 旋转对称性B. 平移对称性C. 反射对称性D. 对称性2. 以下哪个不是固体物理中的晶体缺陷？A. 点缺陷B. 线缺陷C. 面缺陷D. 体缺陷3. 根据布洛赫定理，电子在晶体中的波函数可以表示为：A. ψ(r) = u(r) * e^(ik·r)B. ψ(r) = u(r) * r^2C. ψ(r) = u(r) * sin(kr)D. ψ(r) = u(r) * cos(kr)二、填空题4. 固体的电子能带结构是由_______决定的。
5. 金属的导电性是由于其_______的存在。
三、简答题6. 解释什么是费米-狄拉克统计，并简述其在固体物理中的应用。
7. 简述晶格振动的量子化表述及其对固体热力学性质的影响。
四、计算题8. 假设一个一维单原子链，其原子质量为m，相邻原子间的距离为a。
计算在第一激发态时，链的振动频率。
9. 给定一个立方晶系的固体，其晶格常数为a。
若电子在第一布里渊区内的k点为(π/a, 0, 0)，求电子在该k点的群速度。
五、论述题10. 论述固体中电子的局域化条件以及它们对固体导电性的影响。
11. 讨论不同晶体结构对固体物理性质的影响，例如金属、半导体和绝缘体。
请注意，这些题目只是样例，实际的考研题库可能会包含更复杂和深入的问题。
考生在准备考研时，应该系统地学习固体物理的基础知识，掌握各种物理概念和计算方法，并通过大量练习来提高解题能力。
固体物理经典复习题及答案
固体物理经典复习题及答案一、简答题1.理想晶体答：内在结构完全规则的固体是理想晶体，它是由全同的结构单元在空间无限重复排列而构成的。
2.晶体的解理性答：晶体常具有沿某些确定方位的晶面劈裂的性质，这称为晶体的解理性。
3.配位数答: 晶体中和某一粒子最近邻的原子数。
4.致密度答：晶胞内原子所占的体积和晶胞体积之比。
5.空间点阵(布喇菲点阵)答：空间点阵(布喇菲点阵)：晶体的内部结构可以概括为是由一些相同的点子在空间有规则地做周期性无限重复排列，这些点子的总体称为空间点阵(布喇菲点阵)，即平移矢量123d 、d 、h h h d 中123,,n n n 取整数时所对应的点的排列。
空间点阵是晶体结构周期性的数学抽象。
6.基元答：组成晶体的最小基本单元，它可以由几个原子(离子)组成，整个晶体可以看成是基元的周期性重复排列而构成。
7.格点(结点)答: 空间点阵中的点子代表着结构中相同的位置，称为结点。
8.固体物理学原胞答：固体物理学原胞是晶格中的最小重复单元，它反映了晶格的周期性。
取一结点为顶点，由此点向最近邻的三个结点作三个不共面的矢量，以此三个矢量为边作的平行六面体即固体物理学原胞。
固体物理学原胞的结点都处在顶角位置上，原胞内部及面上都没有结点，每个固体物理学原胞平均含有一个结点。
9.结晶学原胞答：使三个基矢的方向尽可能的沿空间对称轴的方向，以这样三个基矢为边作的平行六面体称为结晶学原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n Ω，其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积。
10.布喇菲原胞答：使三个基矢的方向尽可能的沿空间对称轴的方向，以这样三个基矢为边作的平行六面体称为布喇菲原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n Ω,其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积11.维格纳-赛兹原胞(W-S 原胞)答：以某一阵点为原点，原点与其它阵点连线的中垂面(或中垂线) 将空间划分成各个区域。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
华中科技大学一九九九年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）1.设半径为R 的硬球堆成体心立方晶格，计算可以放入其间隙位置的一个硬球的最大半径r2.已知NaCl 晶体平均每对离子的相互作用能为 2()n q B u r r rα=-+，其中马德隆常数 1.75α=, n = 9，平衡离子间距0 2.82r = Å，求其声学波与光学波之间的频率间隙Δω（Na 的原子量为23, Cl 的原子量为35.5, 1原子质量单位为1.67×2410-克，104.810q -=⨯静电单位电荷）3.已知碳在()铁中的扩散系数D 与温度关系的实验数据为：当温度为200度时，扩散系数D200℃ = 11210/cm -秒；温度为760℃时，D760℃ =-6210/cm 秒，试求扩散过程的激活能Q （千焦耳/摩尔）（气体常数R=8.31焦耳/摩尔·开）4.设N 个电子在边长为L 的正方形框中自由运动，在求解薜定谔方程时所得电子的本征能量220()x y E n n E =+式中，x n ，y n ，为任意正整数，0E 为基态能量，试求绝对零度时系统的费米能F E5.设晶格势场对电子的作用力为L F ，电子受到的外场力为e F ，证明电子的有效质量*m 和电子的惯性质量m 的关系为：*ee L F m F F =+六．已知Na 的费米能 0F E = 3.2ev ，在 T = 0k 下, 测知其电导率σ= 2.1×17110()cm -Ω⋅，试求该温度下Na 的电子的弛豫时间τ.（常数:104.810e cgsu -=⨯, m = 9.1×2810g -，271.0510erg s -=⨯⋅，121.610lev erg -=⨯）华中科技大学二00一年招收硕士研究生入学考试试题考试科目：固体物理适用专业：微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、选择题（25分）1.晶体的宏观对称性中有（）种基本的对称操作A.7B.8C.14D.322.金刚石晶格的布拉菲格子为（）A.简立方B.体心立方C.面心立方D.六角密排3.GaAs晶体的结合方式为（）A.离子结合B.共价结合C.金属性结合D.共价结合+离子结合4.NaCl晶体的配位数是（）A.4B.6C.8D.125.KBr晶体中有3支声学波和（）支光学波A.6B.3C.6ND.3N6.体心立方晶格的晶格常数为a ，其倒格子原胞体积等于（） A.31aB.338a πC.3316a πD.3332a π 7.周期性势场中单电子本征波函数为（）A.周期函数B.旺尼尔函数C.布洛赫函数D.r k e V1 8.极低温下，固体的比热Cv 与T 的关系（）A .Cv 与T 成正比 B. Cv 与2T 成正比 C. Cv 与3T 成正比 D. Cv 与T 无关9.面心立方晶格的简约布里渊区是（）A.截角八面体B.正12面体C.正八面体D.正立方体10.位错破坏了晶格的周期性，位错是（）A.点缺陷B.线缺陷C.面缺陷D.热缺陷二、简要回答下列问题（20分）1.简述金属，绝缘体和半导体在能带结构上的差异.2.为什么对金属电导有贡献的只是费米面附近的电子？3.引起固体热膨胀的物理原因是什么？4.什么是金属的功函数，写出两块金属之间的接触电势差12V 与功函数1φ、2φ之间的关系式.三、（15分）一维周期场中电子的波函数是πψax x x 3sin)(=，（a 是晶格常数），试求电子在该状态的波矢。
四、（20分）由三个原子组成的一维原子链，间距为a ，试求原子的振动频率. 已知：原子的位移和振动频率表示为)(t qna l n Ae X ω-= )2sin(2qa m βω= 五、（20分）设一维晶体的电子能带可以写作其中a 是晶格常数，试求:1.电子在K 状态的速度V(k)；2.能带底和能带顶部电子的有效质量m 底、m 顶。
华中科技大学二00二年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学、材料物理与化学、电力电子与传动（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、选择填空（每题只有一个正确答案，满分15分，每题1.5分）)2cos 81cos 87(ma E(k)22ka ka +-=1. CsCl晶体结构属于（）A.面心立方B.体心立方C.简立方D.六角密积2. 极化子的缺陷类型为（）A.点缺陷B.面缺陷C.线缺陷D.填隙原子3. 对含有N个原胞的一维原子链，用近自由电子模型得出简约布里渊区可容纳的电子数为（）A.3NnB.3NC.2ND.N4. 金刚石结构中能出现衍射斑点的衍射面指数有（）A.221B.442C.100D.1115. 扩散的微观结构为（）A.空穴机构B.填隙原子机构C.位错机构D.极化子机构6. 晶体中的宏观对称性中有如下几种对立的对称操作（）A.1，2，3，4，6，i，m，4B.1，2，3，4，5，6，7，8,C.1，2，3，4，6，1，2，3，4，6D.2，3，4，2，3，47. 由200个NaCl分子组成的晶体，其声子种类个数为（）A.200B.600C.1200D.4008. 德瓦耳斯力F与分子间距r的关系为（）A.F∝13-rB.F∝12-rC.F∝6-rD.F∝8-r9. 晶体中的有效质量为负意味着（）A.电子逸出晶体B.电子动量减小C.电子动量增加D.电子质量减小10. 晶体中可能的配位数为（）A.12，8，6，4，3，2B.12，8，6，5，4，3C.12，9，8，6，4，2D.12，9，6，5，4，2二、填空题（满分15分）1.硅的结构是（），一个晶胞中含有（）个原子，其固体物理学原胞中含有（）个原子，它的体积是结晶学原胞的（）倍。
2.晶体中存在的几种基本结合类型是（）、（）、（）、（）、（）。
3.在含有N 个原胞的CeCl 晶体中，格波的总支数为（），一个波矢对应有（）支格波，其中（）支声学波，（）支光学波，波矢的总数目为（）。
4.晶体按其对称性可分为（）大晶系，共有（）种布喇菲原胞。
5.晶体中原子扩散的微观机构概括起来有（）、（）和（）。
6.晶体最基本特征是（）。
三、设原子质量为m ，晶格常数为a ，恢复力常数为β，试求由6个原子组成的一维布喇菲格子中的所有振动频率（15分）。
四、已知二维晶格的基失1a ，2a 间的夹角为060，且|1a |=|2a |=a ，求倒格子原胞基失和倒格子原胞体积。
（20分）五、假设某一维晶格其势场函数为V （x ）= -2+m 82 sinx+m 42 sin2x+m22sin3x 求：1.所有禁带宽度值；2.第三能带的宽度；3.第二能带顶部和底部的有效质量。
(15分)六、试用能带论的观点解释满带电子不导电、不满带电子在外加电场作用下能导电，并由此说明金属和绝缘体的导电性。
（10分）七、试画出二维正方格子晶格的第一、第二布里渊区，并说明布里渊区的特点。
（10分）华中科技大学二00三年招收硕士研究生入学考试试题考试科目：固体物理适用专业：微电子学与固体电子学（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、（60分）简要回答以下各题：1.写出NaCl和CsCl晶体的结构类型；2.分别指出简单立方、体心立方和面心立方晶体倒易点阵的结构类型；3.计算面心立方结构（设晶格常数为a）的填充率；4.晶体有哪些基本的结合类型？5.晶体比热理论中的德拜（Debye）近似在低温下与实验符合很好，其物理原因是什么？6.在第一布里渊区围绘出一维单原子点阵的色散关系示意图；7.对于初基晶胞数为N的二维晶体，基元含有两个原子，声学支振动模式和光学声学支振动模式的数目各有多少？8.什么是费米能级？写出金属费米能级的典型值；9.简述Bloch定理，该定理必须采用什么边界条件？10.简述半导体和绝缘体能带中电子填充的特点。
二、（22分）对于惰性元素晶体，任意两个原子间的相互作用能为：⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=6ij 12ij ij 4U γσγσε，其中ε、σ为常数， ij γ为原子间距离。
（1）指出上式中两项的物理意义及来源，并写出该类晶体能的表达式；（2）证明平衡时σ与原子最近邻距离 0γ之比是一个与晶体结构有关的常数。
三、（22分）由N 个相同原子组成的面积为S 的二维正方晶格，在德拜近似下计算比热，并论述在低温极限下比热与2T 成正比。
四、（24分）由N 个自由电子组成的三维气体，处于0K 时（1）证明：动能0U 与费米能级F ε的关系为：F 0N 53U ε=； （2）利用结果（1）证明压强与体积的关系为()V U 032p =。
五、（22分）用紧束缚近似求出面心立方晶格和体心立方晶格s 态原子能级相对应的能带）（k S E 。
华中科技大学二00四年招收硕士研究生入学考试试题 考试科目： 固体物理 适用专业： 微电子学与固体电子学、材料物理与化学、电力电子与传动（除画图题外，所有答案都必须写在答题纸上，写在试题上及草稿纸上无效，考完后试题随答题纸交回）一、（60分，每小题6分）简要回答一下各题1．SC 、BBC 和FCC 结构的惯用晶胞各含几个阵点；这三种结构中阵点的最近邻数目分别是多少？2．算晶格常数为a 的FCC 点阵（111）面的面密度。
3．证明倒格矢G =h 1b +k 2b +l 3b 与晶面（hkl ）垂直。
4．固体中原子之间的排斥作用取决于什么原因？5．对三维晶体，绘出德拜模型和爱因斯坦模型下的D(ω)～ω示意图。
6. 在高温极限下，频率为ω的格波声子数目对温度的依赖关系如何？ 7. 金属电阻率产生的主要过程有哪些？在低温极限下，金属电阻率主要由什么因素决定？8. 写出金属费米温度和费米速度的典型值。
9. 证明在周期势场作用下单电子哈密顿量与平移算符可对易。
10.在紧束缚近似下，层电子与外层电子相比，哪一个的能带更宽？二、（16分）已知半导体GaAs 具有闪锌矿结构。
Ga 和As 两原子的最近距离为d=2.540A ，求：（1）其晶格常数；（2）Miller 指数为（110）晶面的面间距。
三、（20分）（1）写出离子晶体能的表达式，并指出各项的物理意义；（2）计算正负离子相间排列的一维晶格的马德隆常数。
四、（20分）对于原子间距为a ，由N 个原子组成的一维单原子链，在德拜近似下（1）计算晶格振动频谱和德拜频率；（2）计算在低温极限下的热容。