传热学第五版课后习题答案(1)11页
《传热学》(第五版)中国建筑工业出版社
《传热学》(第五版)中国建筑工业出版社1、冰雹落体后溶化所需热量主要是由以下途径得到：与地面的导热量与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。
2、略3、略4、略5、略6、夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。
（）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。
（）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。
7、热对流不等于对流换热，对流换热 = 热对流 + 热传导热对流为基本传热方式，对流换热为非基本传热方式8、门窗、墙壁、楼板等等。
以热传导和热对流的方式。
9、因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。
当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。
10、11、直线而为时曲线12、 q 首先通过对流换热使炉子内壁温度升高，炉子内壁通过热传导，使内壁温度生高，内壁与空气夹层通过对流换热继续传递热量，空气夹层与外壁间再通过热传导，这样使热量通过空气夹层。
（空气夹层的厚度对壁炉的保温性能有影响，影响的大小。
）13、已知：、℃ ℃ 墙高2、8m，宽3m 求：、、、解：＝℃ ℃14、已知：、、、℃、℃ 求：、、、解：15、已知：、、℃、、求：、℃16、已知:℃、℃、、℃ 求：、、解：17、已知：、、、℃ ℃、、、求：、、解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁即：＝若％％因为：，即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。
18、略第一章导热理论基础思考题与习题（）答案：1、略2、已知：、、、求：、解：由计算可知，双Low-e膜双真空玻璃的导热热阻高于中空玻璃，也就是说双Low-e膜双真空玻璃的保温性能要优于中空玻璃。
《传热学》课后习题答案-第一章
传热学习题集第一章思考题1． 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答：导热和对流的区别在于：物体内部依靠微观粒子的热运动而产生的热量传递现象，称为导热；对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是：在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式，只有在物质存在的条件下才能实现，而辐射可以在真空中传播，辐射换热时不仅有能 量的转移还伴有能量形式的转换。
2． 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩－玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答：① 傅立叶定律：，其中，－热流密度；－导热系数；－沿x方向的温度变化率，“－”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式：，其中，－热流密度；－表面传热系数；－固体表面温度；－流体的温度。
③ 斯忒藩－玻耳兹曼定律：，其中，－热流密度；－斯忒藩－玻耳兹曼常数；－辐射物体的热力学温度。
3． 导热系数、表面传热系数及传热系数的单位各是什么？哪些是物性参数，哪些与过程有关？答：① 导热系数的单位是：W/(m.K)；② 表面传热系数的单位是：W/(m 2.K)；③ 传热系数的单位是：W/(m 2.K)。
这三个参数中，只有导热系数是物性参数，其它均与过程有关。
4． 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时，冷、热流体之间的换热量可以通过其中任何一个环节来计算（过程是稳态的），但本章中又引入了传热方程式，并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答：因为在许多工业换热设备中，进行热量交换的冷、热流体也常处于固体壁面的两侧，是工程技术中经常遇到的一种典型热量传递过程。
5． 用铝制的水壶烧开水时，尽管炉火很旺，但水壶仍然安然无恙。
而一旦壶内的水烧干后，水壶很快就烧坏。
试从传热学的观点分析这一现象。
《传热学》课后习题答案-第一章
传热学习题集第一章思考题1． 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答：导热和对流的区别在于：物体内部依靠微观粒子的热运动而产生的热量传递现象，称为导热；对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是：在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式，只有在物质存在的条件下才能实现，而辐射可以在真空中传播，辐射换热时不仅有能 量的转移还伴有能量形式的转换。
2． 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩－玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答：① 傅立叶定律：，其中，－热流密度；－导热系数；－沿x方向的温度变化率，“－”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式：，其中，－热流密度；－表面传热系数；－固体表面温度；－流体的温度。
③ 斯忒藩－玻耳兹曼定律：，其中，－热流密度；－斯忒藩－玻耳兹曼常数；－辐射物体的热力学温度。
3． 导热系数、表面传热系数及传热系数的单位各是什么？哪些是物性参数，哪些与过程有关？答：① 导热系数的单位是：W/(m.K)；② 表面传热系数的单位是：W/(m 2.K)；③ 传热系数的单位是：W/(m 2.K)。
这三个参数中，只有导热系数是物性参数，其它均与过程有关。
4． 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时，冷、热流体之间的换热量可以通过其中任何一个环节来计算（过程是稳态的），但本章中又引入了传热方程式，并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答：因为在许多工业换热设备中，进行热量交换的冷、热流体也常处于固体壁面的两侧，是工程技术中经常遇到的一种典型热量传递过程。
5． 用铝制的水壶烧开水时，尽管炉火很旺，但水壶仍然安然无恙。
而一旦壶内的水烧干后，水壶很快就烧坏。
试从传热学的观点分析这一现象。
传热学课后习题答案——第一章
【1-2】
解：根据题意可知，这是一个一维稳态传热过程。通过平壁一维稳态导热的热流密度为
由傅里叶公式有，单位时间内热损
每天产生的热损失
燃气炉需要提供的热量
所需费用
【1-4】
解：流动的空气与换热器之间是稳态对流传热。根据牛顿冷却公式
可知，换热面积
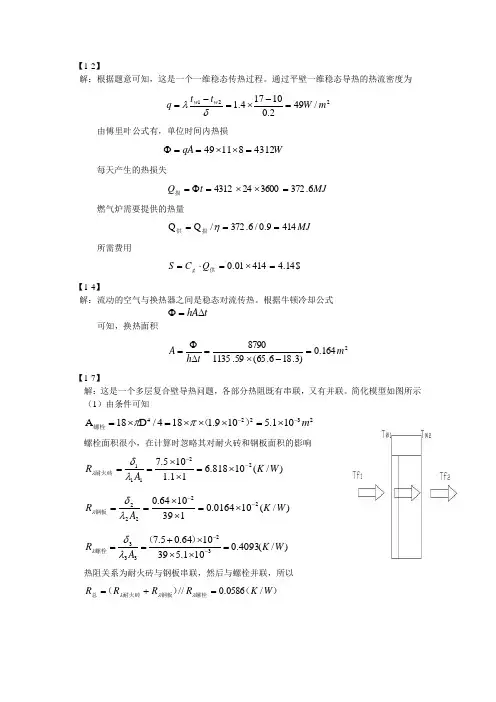
【1-7】
解：这是一个多层复合壁导热问题，各部分热阻既有串联，又有并联。简化模型如图所示
（1）由条件可知
传热学第五课后习题答案
281.976
6
299.714
315.635
329.645
318.162
312.137
277.244
7
298.478
324.570
326.789
330.781
307.593
286.608
8
306.609
322.524
337.566
327.081
318.585
283.567
9
304.747
=0.0424+0.000137×20=0.04514 W/(m·K);
矿渣棉: λ=0.0674+0.000215t W/(m·K)
=0.0674+0.000215×20=0.0717 W/(m·K);
由附录7知聚乙烯泡沫塑料在常温下, λ=0.035~0. 038W/(m·K)。由上可知金属是良好的导热材料，而其它三种是好的保温材料。
4-4 一无限大平壁，其厚度为0.3m，导热系数为 。平壁两侧表面均给定为第三类边界条件，即 ， ； ， 。当平壁中具有均匀内热源 时， 试计算沿平壁厚度的稳态温度分布。（提示：取Δx=0.06m）
方法一 数值计算法
解：这是一个一维稳态导热问题。
（1）、取步长Δx=0.06m，可以将厚度分成五等份。共用六个节点 将平板划分成六个单元体（图中用阴影线标出了节点2、6所在的单元体）。用热平衡法计算每个单元的换热量，从而得到节点方程。
节点5：从左、右两侧通过导热导入的热流量+单元体内热源发出的热流量=0。
节点6：从左边导入的热流量+从右边通过对流输入的热流量+单元体内热源发出的热流量=0。即
将 、 、 、 ， 、 和Δx=0.06m，代入上述六个节点并化简得线性方程组组1：
传热学第五版章熙民_答案第一二三章
2T x 2
x
x
T dx c f dx b U dx T 4
整理得棒温度分布的导热微分方程式：
2T x 2
x
U 4 c T b T （T 取热力学温标） f
从微分方程的形式看，应该需要一个初始条件、两个边界条 件才能获得特解。 边界条件为：1） x 0 时
q q z q I r rdrddzd r r z q r t t t ; q ; q z ； r r z
2t 1 2t 2t I 2 2 2 rdrddzd 2 r r z
q x dt 2 b x dx
q x 0 0 ，无热流量
q x 2 ( 2000 ) 45 0.05 9000 ( W / m 2 )
（2） 将二阶导数代入式（a）
qv d 2t dx
2
2 b 2 ( 2000 ) 45 180000 ( W / m 3 )
整理得：
1-10 从宇宙飞船伸出一根细长散热棒， 以辐射换热将热量散 发到外部空间去，已知棒的发射率（黑度）为 ，导热系数 为 ，棒的长度为 l ，横截面面积为 f ，截面周长为 U ，棒根 部温度为 T0 ，外部空间是绝对零度的黑体，试写出描写棒温 度分布的导热微分方程式和相应的边界条件。 解： 导热微分方程，就是将付立叶定律结合能量守恒定 律（没有功交换时，就是热平衡原理）推出的数学关系式。 如图所示，取一个微元体长度为 dx ，从左边导入的热量
t x 600 K ; t x 400 K ;
解：这是一维的、无内热源的、常物性的、稳态导热问题。 平板内沿厚度方向温度分布呈线性。则 温度梯度： grad t
传热学第五版课后习题答案剖析
传热学习题_建工版V0-14 一大平板，高3m ，宽2m ，厚0.2m ，导热系数为45W/(m.K), 两侧表面温度分别为w1t 150C =︒及w1t 285C =︒ ，试求热流密度计热流量。
解：根据付立叶定律热流密度为：2w2w121t t 285150q gradt=-4530375(w/m )x x 0.2λλ⎛⎫--⎛⎫=-=-=- ⎪ ⎪-⎝⎭⎝⎭ 负号表示传热方向与x 轴的方向相反。
通过整个导热面的热流量为：q A 30375(32)182250(W)Φ=⋅=-⋅⨯=0-15 空气在一根内经50mm ，长2.5米的管子内流动并被加热，已知空气的平均温度为85℃，管壁对空气的h=73(W/m ².k)，热流密度q=5110w/ m ², 是确定管壁温度及热流量Ø。
解：热流量qA=q(dl)=5110(3.140.05 2.5) =2005.675(W)πΦ=⨯⨯ 又根据牛顿冷却公式wf hA t=h A(tt )qA Φ=∆⨯-=管内壁温度为：w f q 5110t t 85155(C)h 73=+=+=︒1-1．按20℃时，铜、碳钢（1.5%C ）、铝和黄铜导热系数的大小，排列它们的顺序；隔热保温材料导热系数的数值最大为多少？列举膨胀珍珠岩散料、矿渣棉和软泡沫塑料导热系数的数值。
解：(1)由附录7可知，在温度为20℃的情况下，λ铜=398 W/(m ·K)，λ碳钢＝36W/(m ·K)， λ铝＝237W/(m ·K)，λ黄铜＝109W/(m ·K). 所以,按导热系数大小排列为: λ铜>λ铝>λ黄铜>λ钢(2) 隔热保温材料定义为导热系数最大不超过0.12 W/(m ·K). (3) 由附录8得知，当材料的平均温度为20℃时的导热系数为: 膨胀珍珠岩散料:λ=0.0424+0.000137t W/(m ·K) =0.0424+0.000137×20=0.04514 W/(m ·K); 矿渣棉: λ=0.0674+0.000215t W/(m ·K) =0.0674+0.000215×20=0.0717 W/(m ·K);由附录7知聚乙烯泡沫塑料在常温下, λ=0.035~0. 038W/(m ·K)。
传热学第五版答案
第一章、一、基本概念主要包括导热、对流换热、辐射换热的特点及热传递方式辨析。
1、冬天，经过在白天太阳底下晒过的棉被，晚上盖起来感到很暖和，并且经过拍打以后，效果更加明显。
试解释原因。
答：棉被经过晾晒以后，可使棉花的空隙里进人更多的空气。
而空气在狭小的棉絮空间里的热量传递方式主要是导热，由于空气的导热系数较小(20℃，1.01325×105Pa 时，空气导热系数为0.0259W/(m ·K)，具有良好的保温性能。
而经过拍打的棉被可以让更多的空气进入，因而效果更明显。
2、夏季在维持20℃的室内工作，穿单衣感到舒适，而冬季在保持22℃的室内工作时，却必须穿绒衣才觉得舒服。
试从传热的观点分析原因。
答：首先，冬季和夏季的最大区别是室外温度的不同。
夏季室外温度比室内气温高，因此通过墙壁的热量传递方向是出室外传向室内。
而冬季室外气温比室内低，通过墙壁的热量传递方向是由室内传向室外。
因此冬季和夏季墙壁内表面温度不同，夏季高而冬季低。
因此，尽管冬季室内温度(22℃)比夏季略高(20℃)，但人体在冬季通过辐射与墙壁的散热比夏季高很多。
根据上题人体对冷感的感受主要是散热量的原理，在冬季散热量大，因此要穿厚一些的绒衣。
3、试分析室内暖气片的散热过程，各环节有哪些热量传递方式？以暖气片管内走热水为例。
答：有以下换热环节及热传递方式(1)由热水到暖气片管到内壁，热传递方式是对流换热(强制对流)；(2)由暖气片管道内壁至外壁，热传递方式为导热；(3)由暖气片外壁至室内环境和空气，热传递方式有辐射换热和对流换热。
4、冬季晴朗的夜晚，测得室外空气温度t 高于0℃，有人却发现地面上结有—层簿冰，试解释原因(若不考虑水表面的蒸发)。
解：如图所示。
假定地面温度为了T e ，太空温度为T sky ，设过程已达稳态，空气与地面的表面传热系数为h ，地球表面近似看成温度为T c 的黑体，太空可看成温度为T sky 的黑体。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
传热学习题_建工版V0-14 一大平板，高3m ，宽2m ，厚0.2m ，导热系数为45W/(m.K), 两侧表面温度分别为w1t 150C =︒及w1t 285C =︒ ，试求热流密度计热流量。
解：根据付立叶定律热流密度为：负号表示传热方向与x 轴的方向相反。
通过整个导热面的热流量为：0-15 空气在一根内经50mm ，长2.5米的管子内流动并被加热，已知空气的平均温度为85℃，管壁对空气的h=73(W/m ².k)，热流密度q=5110w/ m ², 是确定管壁温度及热流量Ø。
解：热流量又根据牛顿冷却公式管内壁温度为：1-1．按20℃时，铜、碳钢（1.5%C ）、铝和黄铜导热系数的大小，排列它们的顺序；隔热保温材料导热系数的数值最大为多少？列举膨胀珍珠岩散料、矿渣棉和软泡沫塑料导热系数的数值。
解：(1)由附录7可知，在温度为20℃的情况下，λ铜=398 W/(m ·K)，λ碳钢＝36W/(m ·K)，λ铝＝237W/(m ·K)，λ黄铜＝109W/(m ·K). 所以,按导热系数大小排列为: λ铜>λ铝>λ黄铜>λ钢(2) 隔热保温材料定义为导热系数最大不超过0.12 W/(m ·K). (3) 由附录8得知，当材料的平均温度为20℃时的导热系数为:膨胀珍珠岩散料:λ=0.0424+0.000137t W/(m ·K)=0.0424+0.000137×20=0.04514 W/(m ·K);矿渣棉: λ=0.0674+0.000215t W/(m ·K)=0.0674+0.000215×20=0.0717 W/(m ·K);由附录7知聚乙烯泡沫塑料在常温下, λ=0.035~0. 038W/(m ·K)。
由上可知金属是良好的导热材料，而其它三种是好的保温材料。
1-5厚度δ为0.1m 的无限大平壁，其材料的导热系数λ＝100W/(m ·K)，在给定的直角坐标系中，分别画出稳态导热时如下两种情形的温度分布并分析x 方向温度梯度的分量和热流密度数值的正或负。
(1)t|x=0=400K, t|x=δ=600K; (2) t|x=δ=600K, t|x=0=400K; 解：根据付立叶定律无限大平壁在无内热源稳态导热时温度曲线为直线，并且x x 02121t t t t t dtx dx x x 0δδ==--∂===∂--x x 0x t t q δλδ==-=- （a ）(1)t|x=0=400K, t|x=δ=600K 时 温度分布如图2-5(1)所示根据式(a), 热流密度xq <0，说明x 方向上的热流量流向x 的反方向。
可见计算值的方向符合热流量由高温传向低温的方向(2) t|x=δ=600K, t|x=0=400K;温度分布如图2-5(2)所示根据式(a), 热流密度x q >0，说明x 方向上的热流量流向x 的正方向。
可见计算值的方向也符合热流量由高温传向低温的方向1-6 一厚度为50mm 的无限大平壁，其稳态温度分布为2t=a+bx （ºC ），式中a=200 ºC, b=-2000 ºC/m 。
若平板导热系数为45w/(m.k),试求：（1）平壁两侧表面处的热流密度；（2）平壁中是否有内热原？为什么？如果有内热源的话，它的强度应该是多大？ 解：方法一由题意知这是一个一维（t t =0y z ∂∂=∂∂）、稳态（t 0τ∂=∂）、常物性导热问题。
导热微分方程式可简化为：2v 2q d tdx λ+= （a ） 因为2t=a+bx ，所以dt2bx dx = （b ） 22d t 2b dx = （c ）（1） 根据式（b ）和付立叶定律x-0q 0=，无热流量（2）将二阶导数代入式（a ）23v 2d tq 2b 2(2000)45=180000w/m dxλλ=-=-=-⨯-⨯ 该导热体里存在内热源，其强度为431.810w /m ⨯。
解：方法二 因为2t=a+bx ，所以是一维稳态导热问题图2-5(2)dt2bx dx= （c ） 根据付立叶定律 （1）x-0q 0=，无热流量（2）无限大平壁一维导热时，导热体仅在边界x=0，及x=δ处有热交换，由（1）的计算结果知导热体在单位时间内获取的热量为()[]in x=0x=area area =q q A 0-(-2b )A δλδΦ-⋅=in area =2b A 0λδΦ< (d)负值表示导热体通过边界散发热量。
如果是稳态导热，证导热体的温度不随时间变化即实现稳态导热。
内热源强度:2-9 某教室的墙壁是一层厚度为240mm 的砖层和一层厚度为20mm 的灰泥构成。
现在拟安装空调设备，并在内表面加一层硬泡沫塑料，使导入室内的热量比原来减少80%。
已知砖的导热系数λ＝0.7W/(m ·K)，灰泥的λ＝0.58W/(m ·K)，硬泡沫塑料的λ＝0.06W/(m ·K)，试求加贴硬泡沫塑料层的厚度。
解: 未贴硬泡沫塑料时的热流密度:1112t q R R λλ=+Δ (1)加硬泡沫塑料后热流密度:121122t q R R R λλλ=++Δ (2)又由题意得,12(180%)q q -= (3)墙壁内外表面温差不变12t t =ΔΔ，将(1)、(2)代入（3）,3δ=0.09056m=90.56mm加贴硬泡沫塑料的厚度为90.56mm.2-19 一外径为100mm ，内径为85mm 的蒸汽管道，管材的导热系数为λ＝40W/(m ·K)，其内表面温度为180℃，若采用λ＝0.053W/(m ·K)的保温材料进行保温，并要求保温层外表面温度不高于40℃，蒸汽管允许的热损失l q =52.3 W/m 。
问保温材料层厚度应为多少？解：根据给出的几何尺寸得到 :管内径1d =85mm=0.085m, 管外径,d2=0.1m, 管保温层外径32d d 20.12δδ=+=+1R λ2R λ•w1t w2ttw 3=40℃时，保温层厚度最小，此时，解得，0.072δ≥m所以保温材料的厚度为72mm.2-24. 一铝制等截面直肋，肋高为25mm ，肋厚为3mm ，铝材的导热系数为λ＝140W/(m ·K)，周围空气与肋表面的表面传热系数为h ＝752w/(m k)。
已知肋基温度为80℃和空气温度为30℃，假定肋端的散热可以忽略不计，试计算肋片内的温度分布和每片肋片的散热量。
解一 肋端的散热可以忽略不计，可用教材式（2-35）、（2-36）、(2-37)求解。
(1) 肋片内的温度分布温度分布为4496[0.472518.9)]ch x =⨯-θ.(2) 肋片的散热量从附录13得，th(ml)=th(0.4725)=0.44单位宽度的肋片散热量解二1、如果肋片上各点的温度与肋基的温度相同，理想的导热量2、从教材图2-17上查肋片效率3、每片肋片的散热量 单位宽度上的肋片散热量为L q 168.8(W/m)=2-27 一肋片厚度为3mm ，长度为16mm ，是计算等截面直肋的效率。
（1）铝材料肋片，其导热系数为140W/(m ﹒K),对流换热系数h=80W/(m ²﹒K);（2）钢材料肋片，其导热系数为40W/(m ﹒K), 对流换热系数h=125W/(m ²﹒K)。
解：（1）铝材料肋片 （2）钢材料肋片例题3-1 一无限大平壁厚度为0.5m ， 已知平壁的热物性参数λ=0.815W/(m .k), c=0.839kJ/(kg.k), ρ=1500kg/m ³, 壁内温度初始时均为一致为18ºC ，给定第三类边界条件：壁两侧流体温度为8 ºC ，流体与壁面之间的表面传热系数h=8.15w/（m ².K ），试求6h 后平壁中心及表面的温度。
教材中以计算了第一项，忽略了后面的项。
计算被忽略掉的的第二项，分析被省略掉的原因。
解：1、例3-1中以计算出平壁的Fo=0.22， Bi=2.5。
因为Fo>0.2, 书中只计算了第一项，而忽略了后面的项。
即2、现在保留前面二项，即忽略第二项以后的项(x,)I(x,6h)II(x,6h)θτθ≈+， 其中3、以下计算第二项II(x,6h )根据Bi=2.5查表3-1，2β=3.7262，2sin 0.5519β=-；cos 3.72620.8339=-a ）平壁中心x=0从例3-1中知第一项I(0m,6h)0.9=，所以忽略第二项时“和”的相对误差为：II(0m,6h )0.01241.4%I(0m,6h )II(0m,6h )0.9+(-0.0124)-==+虽说计算前两项后计算精度提高了，但16.88 ºC 和例3-1的结果17 ºC 相差很小。
说明计算一项已经比较精确。
b ）平壁两侧x=δ=0.5m 从例3-1中知第一项I(0.5m,6h)0.38=，所以忽略第二项时“和”的相对误差为：II(0.5m,6h )0.012.6%I(0.5m,6h )II(0.5m,6h )0.38+0.01==+虽说计算前两项后计算精度提高了，但11.9 ºC 和例3-1的结果11.8 ºC 相差很小。
说明计算一项已经比较精确。
4-4 一无限大平壁，其厚度为0.3m ，导热系数为 k *m w 4.36=λ。
平壁两侧表面均给定为第三类边界条件，即k*m w 60h 21=，C25t f1°=；k*m w 300h 22=，C 215t f2°=。
当平壁中具有均匀内热源35v m /W 102q ×=时， 试计算沿平壁厚度的稳态温度分布。
（提示：取Δx=0.06m ）方法一 数值计算法解：这是一个一维稳态导热问题。
（1）、取步长Δx=0.06m ，可以将厚度分成五等份。
共用六个节点123456t t t t t t 将平板划分成六个单元体（图中用阴影线标出了节点2、6所在的单元体）。
用热平衡法计算每个单元的换热量，从而得到节点方程。
节点1：因为是稳态导热过程所以，从左边通过对流输入的热流量+从右边导入的热流量+单元体内热。
即将 k *m w 4.36=λ、k *m w 60h 21=、C 25t f1°=、k *m w 300h 22=，C215t f2°=、35v m /W 102q ×=和Δx=0.06m ，代入上述六个节点并化简得线性方程组逐步代入并移相化简得： 则方程组的解为:**从迭代的情况看，各节点的温度上升较慢，不能很快得出有效的解。