插值计算EXCEL模板
excel牛顿插值法

excel牛顿插值法
在Excel中,牛顿插值法可以通过手动输入计算公式或使用TREND()函数来实现。
手动输入计算公式的步骤:
1. 打开Excel,输入已知自变量和因变量的值。
2. 根据牛顿插值法的公式,选择一个单元格输入计算公式。
3. 输入完毕后,按回车键,相应的单元格会显示计算结果。
使用TREND()函数的步骤:
1. 打开Excel,输入已知自变量和因变量的值。
2. 点击“公式”选项卡,选择“其他函数”,然后找到“统计”类别下的“TREND”函数。
3. 在“Known_y's”输入框中选择Y值的范围,在“Known_x's”输入框中选择X值的范围,在“New_x's”输入框中输入新的X值。
4. 线性插值的结果将通过TREND函数自动计算出来。
此外,牛顿插值法引入了差商的概念来简化当插值节点增加时的计算过程。
这种方法可以构建一个多项式,该多项式通过所有给定的插值点,并且能够根据差商表来推导出插值多项式的具体形式。
excel内插法计算公式举例

excel内插法计算公式举例好嘞,以下是为您创作的关于“excel 内插法计算公式举例”的文章:在我们日常的工作和学习中,Excel 可是个超级实用的工具。
而内插法计算公式,更是能在很多场景下帮我们解决大问题。
比如说,咱们来假设这么一个情况。
小李是一家公司的销售经理,他负责统计每个月的销售数据。
有一个月,他发现销售业绩的增长呈现出了一种有趣的趋势。
从 1 月到 5 月,销售额分别是 10 万、15 万、20 万、25 万、30 万。
现在他想预测一下 3 月中旬的销售额大概是多少。
这时候,内插法计算公式就派上用场啦!在 Excel 中,内插法的基本原理就是通过已知的数据点,来估算中间未知的数据点。
那具体咋操作呢?先来说说线性内插法。
假设我们有两个已知点 (x1, y1) 和 (x2, y2),要估算位于 x1 和 x2 之间的 x 所对应的 y 值。
计算公式就是:y = y1 + ((x - x1) * (y2 - y1) / (x2 - x1))咱们就拿小李的销售数据来举例。
1 月销售额 10 万(x1=1,y1=10),2 月销售额 15 万(x2=2,y2=15),现在要估算 1.5 月(x=1.5)的销售额 y。
y = 10 + ((1.5 - 1) * (15 - 10) / (2 - 1)) = 10 + (0.5 * 5) = 12.5 万这就得出 1.5 月大概的销售额是 12.5 万。
再来说说多项式内插法。
假如已知三个点 (1, 2)、(2, 5)、(3, 10),要估算 x = 2.5 时的值。
我们先设多项式函数为 y = a*x^2 + b*x + c ,然后把三个已知点代入,得到方程组:2 = a + b + c5 = 4a + 2b + c10 = 9a + 3b + c解这个方程组,得出 a = 1.5,b = -1.5,c = 2所以多项式函数就是 y = 1.5*x^2 - 1.5*x + 2当 x = 2.5 时,y = 1.5 * 2.5^2 - 1.5 * 2.5 + 2 = 8.125通过这些例子,您是不是对内插法的计算公式有点儿感觉啦?回到小李这,他后来发现,用内插法估算出来的销售额,和实际情况虽然不能完全一样,但也能给他提供一个很有参考价值的大概数字,帮助他提前做好一些销售策略的调整。
Excel应用大全如何计算插值?
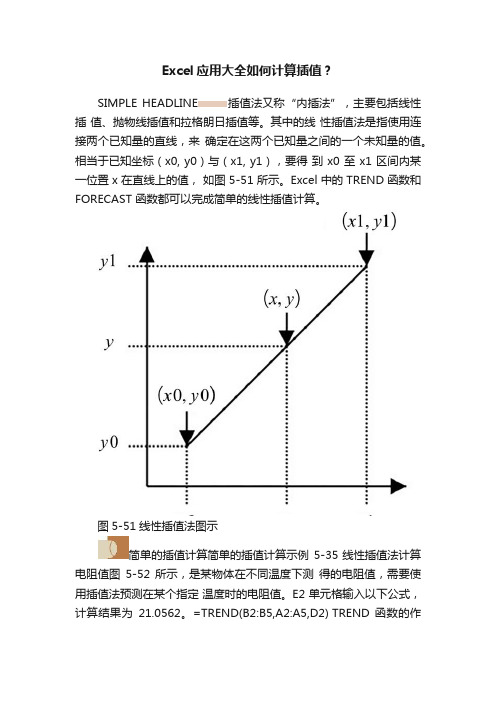
Excel应用大全如何计算插值?SIMPLE HEADLINE插值法又称“内插法”,主要包括线性插值、抛物线插值和拉格朗日插值等。
其中的线性插值法是指使用连接两个已知量的直线,来确定在这两个已知量之间的一个未知量的值。
相当于已知坐标(x0, y0)与(x1, y1),要得到 x0 至 x1 区间内某一位置 x 在直线上的值,如图 5-51 所示。
Excel 中的 TREND 函数和FORECAST 函数都可以完成简单的线性插值计算。
图5-51线性插值法图示简单的插值计算简单的插值计算示例5-35线性插值法计算电阻值图5-52 所示,是某物体在不同温度下测得的电阻值,需要使用插值法预测在某个指定温度时的电阻值。
E2 单元格输入以下公式,计算结果为21.0562。
=TREND(B2:B5,A2:A5,D2) TREND 函数的作用是根据已知x 序列的值和y 序列的值,构造线性回归直线方程,然后根据构造好的直线方程,计算x 值序列对应的y 值序列。
函数语法为:TREND(known_y's,[known_x's],[new_x's],[const]) 第一参数指定已知关系y=mx+b 中的y 值集合。
第二参数指定已知关系y=mx+b 中的 x 值集合。
第三参数指定需要函数 TREND 返回对应 y 值的新 x 值。
第四参数是一个逻辑值,如果为 TRUE 或省略,b 将按正常计算。
如果为 FALSE,b 将被设为 0(零)。
图5-52插值法计算电阻值本例中,TREND 函数的 y 值集合为 B2:B5 单元格区域的电阻值,x 值集合为 A2:A5 单元格区域中的温度值,新 x 值为 D2 单元格中的温度值。
TREND 函数省略第四参数,最终以线性插值法计算出温度为-194 度时对应的电阻值。
使用以下公式也可实现相同的计算。
=FORECAST(D2,B2:B5,A2:A5) FORECAST 函数的作用是根据现有的x 值和 y 值,根据给定的 x 值通过线性回归来预测新的 y 值。
使用excel插值法补齐缺失数据的步骤

使用excel插值法补齐缺失数据的步骤嘿,朋友们!咱今儿来聊聊怎么用 Excel 插值法补齐那些缺失的数据呀!这可真是个有意思的事儿呢。
你想想看,就好比咱拼图,中间缺了几块,那多不完整呀!这数据也是一样,缺了一些,那可不行。
那怎么补上呢?这 Excel 插值法就派上用场啦!首先呢,咱得打开 Excel 表格,找到那些有缺失数据的地方。
就像在茫茫人海中找到那个特别的人一样。
然后呢,选中包含缺失数据的那一列或那一行。
接下来,咱就开始施展魔法啦!在 Excel 里找到那个插值的功能,就像找到了一把神奇的钥匙。
这时候,Excel 就会开始计算啦,根据周围的数据,来推测出缺失的那个值应该是多少。
这就好比是猜谜语,根据一些线索来猜出答案。
比如说,前后的数据都比较大,那缺失的数据很可能也不会小呀;要是前后数据比较小,那缺失的也不会大到哪里去。
你说这是不是很有趣?就像走迷宫一样,一点点找到正确的路径。
然后呀,Excel 就会把补齐的数据给你填好啦,就像是给缺失的拼图块找到了合适的位置。
哎呀呀,你再想想,如果没有这个插值法,那我们面对那些缺失的数据该多头疼呀!就像走路没了方向一样。
但是有了它,我们就能轻松地解决这个问题啦。
而且呀,这插值法还很灵活呢!可以根据不同的情况选择不同的方法。
就像咱穿衣服,不同场合穿不同的衣服,多合适呀!总之呢,学会了用 Excel 插值法补齐缺失数据,那可真是帮了我们大忙啦!让我们的数据变得更加完整、准确。
以后再遇到这种情况,咱就可以轻松应对啦,再也不怕那些缺失的数据捣乱啦!哈哈!。
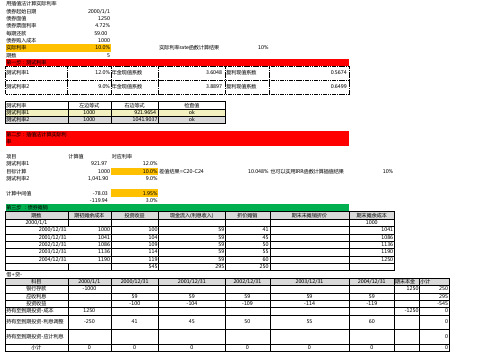
用插值法计算实际利率的excel模拟,CPA持有至到期投资例题2-5
0.5674 0.6499
对应利率 921.97 1000 1,041.90 -78.03 -119.94 12.0% 10.0% 差值结果=C20-C24 9.0% 1.95% 3.0% 投资收益 100 104 109 114 119 545 2000-12-31 59 -100 2001-12-31 59 -104 45 0 现金流入(利息收入) 59 59 59 59 59 295 折价摊销 41 45 50 55 60 250 2002-12-31 59 -109 50 0 2003-12-31 59 -114 55 0 期末未摊销折价 期末摊余成本 1000 1041 1086 1136 1190 1250 10.048% 也可以实用IRR函数计算插值结果 10%
2000-1-1 1250 4.72% 59.00 1000 10.0% 5 12.0% 年金现值系数 9.0% 年金现值系数 左边等式 1000 1000 右边等式 921.9654 1041.9037
实际利率rate函数计算结果
10%
3.6048 复利现值系数 3.8897 复利现值系数 检查值 ok ok
excel滑动平均法插值公式

excel滑动平均法插值公式
滑动平均法是一种常用的数据插值方法,可以用来填补数据中的空缺或缺失值。
该方法通过计算相邻数据点的平均值来估算缺失值,从而实现数据的平滑处理。
在Excel中,使用滑动平均法可以通过以下公式来实现:假设要估算第n个数据点的值,将其前面的m个数据点取平均,即可得到估算值。
具体公式如下:
估算值 = (数据点1 + 数据点2 + ... + 数据点m) / m
其中,数据点1 ~ 数据点m是第n个数据点前面的m个数据点。
滑动平均法的优点在于简单易懂,能够有效地平滑数据曲线,减小噪声的影响。
然而,也需要注意滑动窗口的大小选择,过小的窗口可能导致过度平滑,无法准确反映数据变化;过大的窗口可能导致信息丢失,无法揭示数据的细节。
在实际应用中,滑动平均法可以用于各种数据的插值处理,比如时间序列数据、传感器数据等。
通过对数据进行平滑处理,可以更好地分析数据的趋势和特征,提高数据的可靠性和可解释性。
滑动平均法是一种简单而有效的数据插值方法,在Excel中可以方便地进行实现。
通过合适的滑动窗口大小,可以平滑数据曲线,减小噪声的干扰,从而提高数据分析的准确性和可信度。
无论是在科
学研究、工程设计还是商业分析中,滑动平均法都有着广泛的应用前景。
内插法excel详细计算过程

内插法excel详细计算过程嘿,朋友!你是否在面对内插法在Excel 中的计算时感到一头雾水,仿佛置身于迷雾之中找不到方向?别担心,今天咱就来好好唠唠这内插法在 Excel 里的详细计算过程,保准让你恍然大悟!咱先来说说啥是内插法。
这内插法啊,就好比你在爬一个有很多台阶的楼梯,你知道自己站在某个台阶,也知道上面和下面台阶的位置,然后想准确算出自己在这个楼梯中的具体位置,这时候内插法就派上用场啦!在 Excel 里用内插法,首先你得有两组数据,一组是自变量,就像楼梯的台阶编号;另一组是因变量,好比每个台阶对应的高度。
比如说,你知道在台阶 1 高度是 10 米,台阶 5 高度是 50 米,现在你站在台阶 3,想知道这个位置的高度,这就得靠内插法啦。
那怎么操作呢?打开 Excel 表格,把已知的数据填进去。
比如说,A 列是台阶编号1、2、3、4、5,B 列是对应的高度10、20、?、40、50。
然后呢,在要计算的那个单元格里输入函数。
这函数就像是一把神奇的钥匙,能打开内插法计算的大门。
假设我们用线性内插法,函数可能就长这样:“=FORECAST(3,A1:A5,B1:B5)”。
输入完函数,按下回车键,神奇的事情就发生啦,Excel 就会帮你算出台阶 3 对应的高度。
这是不是有点像魔法?但其实啊,它背后的原理并不复杂。
就好比你在两个已知点之间拉了一条直线,然后根据你所在的位置在这条直线上找到对应的数值。
再举个例子,比如说你知道气温在早上 6 点是 10 度,中午 12 点是30 度,现在想知道 9 点的气温,这不就和刚才的台阶例子一样嘛,用内插法就能轻松搞定。
内插法在很多地方都大有用处呢!比如在数据分析、预测趋势的时候,它就像一个得力的助手,能帮你做出更准确的判断。
所以说,学会内插法在 Excel 中的计算,就像是给你的工具库里添了一件神器,让你在处理数据的时候更加得心应手。
怎么样,是不是觉得没那么难啦?赶紧去试试吧!我的观点结论就是:内插法在 Excel 中的应用虽然一开始可能让人觉得有点复杂,但只要掌握了方法和原理,就能轻松应对各种数据计算和分析的需求,大大提高工作效率。
线性插值excel公式

线性插值excel公式Excel是微软推出的电子表格程序,它能够实现线性插值公式的功能。
线性插值是指在一个给定的点集上,通过线性函数来逼近目标值。
在Excel中,这一功能可以通过线性函数插值(Linest())函数来实现。
Linest()函数的格式是:=LINEST(known_y,[known_x], const , stats)其中,“known_y”是待插值的Y值集合,“known_x”是待插值的X值集合,const参数用于指定是否考虑常数,stats参数用于指定是否显示统计量。
使用线性插值公式来计算斜率和截距。
若已知两组数据{(x1,y1), (x2,y2)},则存在一条直线方程:y=ax+b,其中a和b分别表示斜率和截距,可由下式求得:a=(y2-y1)/(x2-x1) ; b=y1-ax1 ;假设知道如下组数据:(1,2),(2,3),(3,4),(4,5),(5,19)。
则斜率a可以使用LINEST()函数来求得:首先,将数据输入到excel中,如在A1:E1依次输入1、2、3、4、5,在A2:E2依次输入2、3、4、5、19:A1 B1 C1 D1 E11 2 3 4 5A2 B2 C2 D2 E22 3 4 5 19然后,在空间中放入Linest()函数,函数的格式为:=LINEST(A2:E2,A1:E1,FALSE,FALSE),其中FALSE指的是不要考虑常数,也不显示统计量,按下回车,会显示出此函数的结果:F2 G22.0000 -1.0000由此可知,斜率a=2.0000,截距b=-1.0000,于是,y=2x-1就是要求的线性插值公式。
从上面可以看出,线性插值Excel公式是一种有效的工具,可以用于在某一给定的点集上,求得线性函数的方程,这对于分析给定数据、拟合曲线以及求解复杂方程等是非常有用的。
在使用线性插值Excel公式时,需要注意一些问题,如:(1)数据的准确性:一定要保证输入的数据的准确性,否则会影响线性插值的结果。
