2020-2021学年山东省济南市高新区八年级第一学期期中数学试卷(1)
2020-2021学年八年级数学下学期期中考试试题(含答案) (1)

2020-2021学年八年级数学下学期期中考试试题时间:90分钟 满分:120分 考试内容:第十六章至第十八章一、选择题(本大题共10小题,每小题3分,共30分.在每小题的4个选项中,只有一个选项是符合题目要求的)1.(2020江苏连云港赣榆期末,4,★☆☆)若3-m 为二次根式,则m 的取值范围是 ( )A.m<3B.m≤3C.m≥3D.m>32.(2020江苏盐城期末,5,★☆☆)若a>0,则下列二次根式中,属于最简二次根式的是 ( )A.1aB.1a2 C. aD.a 23.(2020上海浦东新区建平中学期末,2,★☆☆)下列计算正确的是 ( )A.-(-3)2=-3B.(- 3 )2=9C.(-3)2=±3 D.9116 =3144.(2019山西忻州期中,1,★☆☆)下列各式化简后,与3的被开方数相同的是 ( )A.12B.18C.19D.235.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D 都在格点上,则下面4条线段的长度为10 的是( A. ABB.BCC. CDD. AD6.如图,在四边形ABCD 中,∠ABC=90°,AB=3,BC =4,CD =12,AD =13,则四边形ABCD 的面积为 ( )A.72B.36C.66D.427.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,则下列说法正确的是 ( )A. CE =BCB. DE =12ABC.∠AED=∠CD.∠A=∠C8.(2020湖南邵阳隆回期末,5,★☆☆)如图,已知直线a∥b∥c,直线d 与直线a,b,c 分别垂直且相交于A,B,C 三点,若AB =2,AC =6,则平行线b 、c 之间的距离是 ( )A.2B.4C.6D.89.(2020四川眉山东坡学校模拟,11,★★☆)如图,已知菱形ABCD 的对角线AC 、BD 的长分别为10cm 、24cm,AE ⊥BC 于点E,则AE 的长是 ( )A.5 3 cmB.2 5 cmC.24013cm D.1201310.(2020四川宜宾叙州期末,12,★★☆)如图正方形ABCO 和正方形DEFO 的顶点A,E,0在同一直线l 上,且EF =2 ,AB =3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD =17 ,④△COF 的面积S △CDF =3,其中正确结论 的个数为 ( )A.1B.2C.3D.4二、填空题(本大题共8小题,每小题4分,共32分)11.(2020湖北武汉东湖高新区期末,11,★☆☆)49=________;1-33 的相反数为________; 3 -2 =________12.(2020福建厦门湖里五缘实验学校期末,13,☆☆)在□ABCD 中,∠C:∠D=5:4,则∠B 的度数为________ 13.已知△ABC 的三边长分别为a,b,c,且a,满足b =5-a +a -5 +12,c =13,则S △A BC =________14.如图,∠CAB=30°,点D 在射线AB 上,且AD =4,点P 在射线AC 上运动,当△ADP 是直角三角形时,PD 的长为 ________15.(2020广东清远英德期末,16,★★☆)如图,在平行四边形ABCD 中,∠C=42°,过点D 作BC 的垂线DF,交AB 于点E,交CB 的延长线于点F,则∠BEF 的度数为________16.如图,正方形ABCD 的边长是2,对角线AC 、BD 相交于点O,点E 、F 分别在边AD 、AB 上,且OE⊥OF,则四边形 AFOE 的面积为________17.(2020湖南娄底期末,18,★★☆)1+13=213,2+14=314,3+15=415,……观察各式,则第n(n≥1)个等式为________________________。
2020-2021学年第一学期八年级数学期中考试卷(及答案)共五套

2020-2021学年第一学期期中考试试卷八年级数学一、选择题(本大题共10小题,每小题2分,共20分)1.下面四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的A .B .C .D .2.在平面直角坐标系中,点P (1,﹣2)的位置在A .第一象限B .第二象限C .第三象限D .第四象限3.等腰三角形两边长分别为2和4,则这个等腰三角形的周长为A .6B .8C .10D .8或104.今年10月环太湖中长跑中参赛选手达到21780人,这个数精确到千位表示约为( ) A .2.2×104B .22000C .2.1×104D .225.如图,在数轴上表示实数7+1的点可能是A .PB .QC .RD .S6.如图是跷跷板的示意图,支柱OC 与地面垂直,点O 是AB 的中点,AB 绕着点O 上下转动.当A 端落地时,∠OAC =20°,跷跷板上下可转动的最大角度(即∠A ′OA )是 A .80° B .60° C .40° D .20°7.如图,将一个三角形纸片ABC 沿过点B 的直线折叠,使点C 落在AB 边上的点E 处,折痕为BD ,则下列结论一定正确的是 A .AD =BDB .AE =ACC .ED +EB =DBD .AE +CB =AB8.由下列条件不能判定△ABC 为直角三角形的是A .a =,b =,c =B .∠A +∠B =∠C C .∠A :∠B :∠C =1:3:2D .(b +c )(b ﹣c )=a 29.如图,已知在△ABC 中,CD 是AB 边上的高线,BE 平分∠ABC ,交CD 于点E ,BC =6,DE =3,则△BCE 的面积等于A .6B .8C .9D .1810.如图,在四边形ABCD 中,AB =AC =BD ,AC 与BD 相交于H ,且AC ⊥BD .①ABPQ RS(第5题)ABCA 'B 'O(第6题)(第7题)∥CD ;②△ABD ≌△BAC ;③AB 2+CD 2=AD 2+CB 2;④∠ACB +∠BDA =135°.其中真命题的个数是A .1B .2C .3D .4二、填空题(本大题共8小题,每空2分,共16分) 11.81的算术平方根是 ▲ .12.在平面直角坐标系中,点P (-1,2)关于x 轴的对称点的坐标为 ▲ . 13.如图,在R t △ABC 中,CD 是斜边AB 上的中线,若AB =20,则CD = ▲ . 14.如图,△ABC 是边长为6的等边三角形,D 是BC 上一点,BD =2,DE ⊥BC 交AB 于点E ,则线段AE = ▲ .15.如图,三个正方形中,其中两个正方形的面积分别是100,36,则字母A 所代表的正方形的边长是 ▲ .16.如图,在△ABC 中,AB =AC ,∠B =66°,D ,E 分别为AB ,BC 上一点,AF ∥DE ,若∠BDE =30°,则∠F AC 的度数为 ▲ .17.如图,数轴上点A 、点B 表示的数分别中1和5,若点A 是线段BC 的中点,则点C 所表示的数是 ▲ .18.已知:如图,ΔABC 中,∠A =45°,AB =6,AC =24,点D 、E 、F 分别是三边AB 、BC 、CA 上的点,则ΔDEF 周长的最小值是 ▲ .AB CD E(第14题)AB CD(第13题)(第15题)ABCDH(第10题)(第9题)A BCF DE(第16题)(第17题)(第18题)FEDCBA三、解答题(本大题共9题,共64分) 19.(8分)(1)计算:()234272-+-; (2)已知:4x 2=20,求x 的值.20.(4分)如图,四边形ABCD 中,AB =BC ,AD =CD ,求证:∠A =∠C .CDBA21.(6分)如图,在△ABC 中,AD ⊥BC ,AB =10,BD =8,∠ACD =45°. (1)求线段AD 的长;(2)求△ABC 的周长.22.(6分)已知点A (1,2a -1),点B (-a ,a -3) . ①若点A 在第一、三象限角平分线上,求a 值.②若点B 到x 轴的距离是到y 轴距离的2倍,求点B 所在的象限.23.(8分)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB ,在图③中已画出点A .按下列要求画图:(1)在图①中,以格点为顶点,AB 为一边画一个等腰三角形ABC ; (2)在图②中,以格点为顶点,AB 为一边画一个正方形;(3)在图③中,以点A 为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .24.(8分)如图,在△ABC 中,AB =AC ,点D 、E 、F 分别在BC 、AB 、AC 边上,且BE =CF ,BD =CE .(1)求证:△DEF 是等腰三角形;(2)当∠A =40°时,求∠DEF 的度数.25.(8分)如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).(1)若点P在AC上,且满足P A=PB时,求出此时t的值;(2)若点P恰好在∠BAC的角平分线上,求t的值.26.(8分)如图,在Rt△ABC中,∠ACB=90°,AD、BE、CF分别是三边上的中线.(1)若AC=1,BC=.求证:AD2+CF2=BE2;(2)是否存在这样的Rt△ABC,使得它三边上的中线AD、BE、CF的长恰好是一组勾股数?请说明理由.(提示:满足关系a2+b2=c2的3个正整数a、b、c称为勾股数.)27.(8分)定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线.(1)如图1,在△ABC中,AB=AC,点D在AC边上,且AD=BD=BC,求∠A的大小;(2)在图1中过点C作一条线段CE,使BD,CE是△ABC的三等分线;在图2中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(3)在△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC 边上,且AD=BD,DE=CE,请直接写出∠C所有可能的值.2020~2021学年度第一学期期中考试八年级数学试题一、选择题(共10小题,每小题3分,共30分) 1.下列图形中不是轴对称图形的是( )2.在平面直角坐标系中,点P (-3,2)在( ) A .第一象限B .第二象限C .第三象限D .第四象限 3.三角形中最大的内角不能小于( ) A .30°B .45°C .60°D .90°4.下列关于两个三角形全等的说法: ① 三个角对应相等的两个三角形全等 ② 三条边对应相等的两个三角形全等③ 有两边和它们的夹角对应相等的两个三角形全等 ④ 有两边和其中一边上的高对应相等的两个三角形全等 正确的说法个数是( ) A .1个 B .2个 C .3个 D .4个 5.在平面直角坐标系中,点P (2,-3)关于x 轴的对称点是( )A .(-2,3)B .(2,3)C .(-2,-3)D .(-3,2) 6.如图所示,∠A =28°,∠BFC =92°,∠B =∠C ,则∠BDC 的度数是( )A .85°B .75°C .64°D .60°7.如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别是D 、E ,AD 、CE 交于点H .已知EH =EB =3,AE =5,则CH 的长是( ) A .1B .2C .53D .358.如图所示的正方形网格中,网格线的交点称为格点,已知A 、B 是两格点,如果C 也是图中的格点,且使得△ABC 为等腰三角形,则点C 的个数是( ) A .6个B .7个C .8个D .9个9.如图,AB =2,BC =AE =6,CE =CF =7,BF =8,四边形ABDE 与△CDF 面积的比值是( ) A .21B .32C .43 D .110.如图,在△ABC 中,BC 的垂直平分线DF 交△ABC 的外角平分线AD 于点D ,DE ⊥AB 于点E ,且AB >AC ,则( ) A .BC =AC +AEB .BE =AC +AEC .BC =AC +AD D .BE =AC +AD二、填空题(本大题共6个小题,每小题3分,共18分)11.若一个多边形的内角和是外角和的2倍,则它的边数是___________12.设△ABC 的三边长分别为a 、b 、c ,其中a 、b 满足|a +b -6|+(a -b +4)2=0,则第三边长c 的取值范围是_____________13.点M (-5,3)关于直线x =1的对称点的坐标是___________14.如图所示,在△FED 中,AD =FC ,∠A =∠F .如果用“SAS ”证明△ABC ≌△FED ,只需添加条件_____________即可15.在△ABC 中,高AD 、BE 所在的直线相交于点G ,若BG =AC ,则∠ABC 的度数是_____16.如图,在Rt △ABC 中,∠C =90°,BC =6,AC =8,一条线段PQ =AB =10,P 、Q 两点分别在AC 和过点A 且垂直于AC 的射线AX 上运动,如果以A 、P 、Q 为顶点的三角形与△ABC 全等,则AP =____________三、解答题(共8小题,共72分)17.(本题8分)解方程组:(1) ⎩⎨⎧=-=-32373y x y x(2) ⎩⎨⎧=-=+5342y x y x18.(本题8分)如图所示,在△ABC 中:(1) 画出BC 边上的高AD 和中线AE(2) 若∠B =30°,∠ACB =130°,求∠BAD 和∠CAD 的度数19.(本题8分)如图,点B 、E 、C 、F 在同一直线上,且AB =DE ,AC =DF ,BE =CF ,请将下面说明△ABC ≌△DEF 的过程和理由补充完整解:∵BE =CF (_____________)∴BE +EC =CF +EC即BC =EF在△ABC 和△DEF 中⎪⎩⎪⎨⎧===__________________BC DF AB )()(∴△ABC ≌△DEF (__________)20.(本题8分)如图所示,D是边AB的中点,△BCD的周长比△ACD的周长大3 cm,BC=8 cm,求边AC的长21.(本题8分)已知,如图所示,CE⊥AB与E,BF⊥AC与F,且BD=CD,求证:(1) △BDE≌△CDF(2) 点D在∠BAC的角平分线上22.(本题10分)如图,设△ABC和△CDE都是等边三角形,并且∠EBD=90°,求证:(1) △ACE≌△BCD(2) 求∠AEB的度数23.(本题10分)如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F(1) 直接写出∠AFC的度数(2) 请你判断并写出FE与FD之间的数量关系(3) 如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD 与AC之间的数量关系并说明理由24.(本题12分)如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E.已知AO=m,BO=n,且m、n 满足(n-6)2+|n-2m|=0(1) 求A、B两点的坐标(2) 若点D为AB中点,求OE的长(3) 如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P 的坐标2020-2021学年八年级(上)期中数学模拟试卷一.选择题(共12小题,满分36分,每小题3分)1.下面的图形中,是轴对称图形的是()A.B.C.D.2.下列因式分解结果正确的是()A.x2+3x+2=x(x+3)+2 B.4x2﹣9=(4x+3)(4x﹣3)C.x2﹣5x+6=(x﹣2)(x﹣3)D.a2﹣2a+1=(a+1)23.利用尺规进行作图,根据下列条件作三角形,画出的三角形不唯一的是()A.已知三条边B.已知两边和夹角C.已知两角和夹边D.已知三个角4.用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;③作射线OC.则射线OC为∠AOB的平分线.由上述作法可得△OCD≌△OCE的依据是()A.SAS B.ASA C.AAS D.SSS5.已知一个三角形有两边相等,且周长为25,若量得一边为5,则另两边长分别为()A.10,10 B.5,10 C.12.5,12.5 D.5,156.若关于x的二次三项式x2+kx+b因式分解为(x﹣1)(x﹣3),则k+b的值为()A.﹣1 B.1 C.﹣3 D.37.如图,已知AB∥CF,E为DF的中点,若AB=8cm,CF=5cm,则BD为()A.2cm B.3cm C.4cm D.1cm8.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=()A.30°B.35°C.45°D.60°9.当x=1时,代数式x3+x+m的值是7,则当x=﹣1时,这个代数式的值是()A.7 B.3 C.1 D.﹣710.如图,△BDC′是将矩形纸片ABCD沿BD折叠得到的,BC′与AD交于点E,则图中共有全等三角形()A.2对B.3对C.4对D.5对11.已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC 对称,点E与点F关于BD对称,AC与BD相交于点G,则()A.1+AB/AD=B.2BC=5CFC.∠AEB+22°=∠DEF D.4AB/BD =12.如图,Rt△ABC中,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,AC=6cm,则BE的长度为()A.10cm B.6cm C.4cm D.2cm二.填空题(共6小题,满分18分,每小题3分)13.如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为.14.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.15.已知:在△ABC中,AH⊥BC,垂足为点H,若AB+BH=CH,∠ABH=70°,则∠BAC= °.16.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=2,则EF= .17.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于.18.我们将1×2×3×…×n记作n!(读作n的阶乘),如2!=1×2,3!=1×2×3,4!=1×2×3×4,若设S=1×1!+2×2!+3×3!+…+2016×2016!,则S除以2017的余数是.三.解答题(共7小题)19.因式分解:(1)9a2﹣4(2)ax2+2a2x+a320.如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1点的坐标;(2)在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.21.如图,已知:A、F、C、D在同一条直线上,BC=EF,AB=DE,AF=CD.求证:BC∥EF.22.若m2﹣2m n+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+()=0,即()2+()2=0.根据非负数的性质,∴m=n=阅读上述解答过程,解答下面的问题,设等腰三角形ABC的三边长a、b、c,且满足a2+b2﹣4a﹣6b+13=0,求△ABC的周长.23.如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.(1)CO是△BCD的高吗?为什么?(2)求∠5、∠7的度数.24.如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,证明:AB=FA+BD;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.25.如图,某学校(A点)与公路(直线L)的距离AB为300米,又与公路车站(D点)的距离AD为500米,现要在公路上建一个小商店(C点),使CA=CD,求商店与车站之间的距离CD的长.参考答案一.选择题1. D.2. C.3. D.4. D.5. A.6. A.7. B.8. B.9. B.10. C.11. A.12. C.二.填空题13. 4.14. 24.15. 75°或35°16. 4.17..18. 2016.三.解答题19.解:(1)9a2﹣4=(3a+2)(3a﹣2)(2)ax2+2a2x+a3=a(x+a)220.解:(1)如图所示,由图可知 A1(﹣4,5);(2)如图所示,点P即为所求点.设直线AB1的解析式为y=kx+b(k≠0),∵A(4,5),B1(﹣1,0),∴,解得,∴直线AB1的解析式为y=x+1,∴点P坐标(0,1),∴△PAB的周长最小值=AB1+AB=+=5+.21.证明:如图,∵AF=CD,∴AF+CF=CD+CF,即AC=DF.∴在△ABC与△DEF中,,∴△ABC≌△DEF(SSS),∴∠BCA=∠EFD,∴BC∥EF.22.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,即(m﹣n)2+(n﹣4)2=0.根据非负数的性质,∴m=n=4,故答案为:n2﹣8n+16;m﹣n;n﹣4;4;已知等式变形得:(a﹣2)2+(b﹣3)2=0,所以a=2,b=3,第一种情况2,2,3,周长=7;第二种情况3,3,2,周长=8.23.解:(1)CO是△BCD的高.理由如下:∵BC⊥CD,∴∠DCB=90°,∴∠1=∠2=∠3=45°,∴△DCB是等腰直角三角形,∴CO是∠DCB的角平分线,∴CO⊥BD(等腰三角形三线合一);(2)∵在△ACD中,∠1=∠3=45°,∠4=60°,∴∠5=30°,又∵∠5=∠6,∴∠6=30°,∴在直角△AOB中,∠7=180°﹣90°﹣30°=60°.24.(本题满分8分)(1)证明:如图1,∵BE⊥CD,即∠BEC=90°,∠BAC=90°,∴∠F+∠FBA=90°,∠F+∠FCE=90°.∴∠FBA=∠FCE.……………………………………………………………(1分)∵∠FAB=180°﹣∠DAC=90°,∴∠FAB=∠DAC.∵AB=AC,∴△FAB≌△DAC.………………………………………………(2分)∴FA=DA.………………………………………………∴AB=AD+BD=FA+BD.………………………………………(4分)(2)如图2,当D在AB延长线上时,AF=AB+BD,…………(6分)理由是:同理得:△FAB≌△DAC,∴AF=AD=AB+BD;如图3,当D在AB反向延长线上时,BD=AB+AF,…………………(8分)理由是:同理得:△FAB≌△DAC,∴AF=AD,∴BD=AB+AD=AB+AF.25.解:∵AB⊥l于B,AB=300m,AD=500m.∴BD==400m.设CD=x米,则CB=(400﹣x)米,x2=(400﹣x)2+3002,x2=160000+x2﹣800x+3002,800x=250000,x=312.5m.答:商店与车站之间的距离为312.5米.2020-2021学年八年级(上)期中数学模拟试卷一.选择题(共10小题,满分30分,每小题3分)1.下列长度的三条线段,能组成三角形的是()A.4cm,5cm,9cm B.8cm,8cm,15cmC.5cm,5cm,10cm D.6cm,7cm,14cm2.下列四个图案中,不是轴对称图案的是()A.B.C.D.3.点M(1,2)关于y轴对称点的坐标为()A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是()A.AB=AC B.∠BAE=∠CADC.BE=DC D.AD=DE5.下列计算正确的是()A.a2+a2=2a4B.2a2×a3=2a6C.3a﹣2a=1 D.(a2)3=a6[来6.只用一种正六边形地砖密铺地板,则能围绕在正六边形的一个顶点处的正六边形地砖有()A.3块B.4块C.5块D.6块7.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC ≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE8.到三角形三个顶点的距离相等的点是三角形()的交点.A.三个内角平分线B.三边垂直平分线C.三条中线D.三条高9.如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有()A.1个B.2个C.3个D.4个10.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是()A.6 个B.7 个C.8 个D.9个二.填空题(共6小题,满分18分,每小题3分)11.计算(2m2n2)2•3m2n3的结果是.12.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.13.等腰三角形的一个外角是80°,则其底角是度.14.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是.15.如图,在Rt△ABC中,斜边AB的垂直平分线交边AB于点E,交边BC于点D,如果∠B=28°,那么∠CAD= 度.16.在等边三角形ABC中,AD是BC边上的高,E为AC的中点P为AD上一动点,若AD=12,则PC+PE的最小值为.三.解答题(共9小题,满分72分)17.(6分)计算:(1)(12a3﹣6a2+3a)÷3a;(2)(x﹣y)(x2+xy+y2).18.(6分)如图,∠A=50°,OB、OC为角平分线,求∠BOC.19.(8分)如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.(1)画出△ABC关于直线BM对称的△A1B1C1;(2)写出AA1的长度.20.(8分)计算:(1)﹣(a2b)3+2a2b•(﹣3a2b)2(2)(a+2b﹣c)(a﹣2b+c)(3)已知6x﹣5y=10,求[(﹣2x+y)(﹣2x﹣y)﹣(2x﹣3y)2]÷4y的值.21.(8分)如图,点D,C在BF上,AB∥EF,∠A=∠E,BD=CF.求证:AB=EF.22.(8分)已知一个等腰三角形的三边长分别为2x﹣1、x+1、3x﹣2,求这个等腰三角形的周长.(1)完成部分解题过程,在以下解答过程的空白处填上适当的内容.解:①当2x﹣1=x+1时,解x= ,此时构成三角形(填“能”或“不能”).②当2x﹣1=3x﹣2时,解x= ,此时构成三角形(填“能”或“不能”).(2)请你根据(1)中两种情况的分类讨论,完成第三种情况的分析,若能构成等腰三角形,求出这个三角形的周长.24.(10分)已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O(1)如图1,求证:AC垂直平分BD;(2)点M在BC的延长线上,点N在AC上,且MD=NM,连接BN.①如图2,点N在线段CO上,求∠NMD的度数;②如图3,点N在线段AO上,求证:NA=MC.25.(10分)已知△ABC是等边三角形,点D,E,F分别是边AB,BC,AC的中点,点M是射线EC上的一个动点,作等边△DMN,使△DMN与△ABC在BC边同侧,连接NF.(1)如图1,当点M与点C重合时,直接写出线段FN与线段EM的数量关系;(2)当点M在线段EC上(点M与点E,C不重合)时,在图2中依题意补全图形,并判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)连接DF,直线DM与直线AC相交于点G,若△DNF的面积是△GMC面积的9倍,AB=8,请直接写出线段CM的长.参考答案与试题解析一.选择题1.【解答】解:A、∵5+4=9,9=9,∴该三边不能组成三角形,故此选项错误;B、8+8=16, 16>15,∴该三边能组成三角形,故此选项正确;C、5+5=10,10=10,∴该三边不能组成三角形,故此选项错误;D、6+7=13,13<14,∴该三边不能组成三角形,故此选项错误;故选:B.2.【解答】解:A、是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项正确;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选:B.3.【解答】解:点M(1,2)关于y轴对称点的坐标为(﹣1,2).故选:A.4.【解答】解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,故A、B、C正确;AD的对应边是AE而非DE,所以D错误.故选:D.5.【解答】解:A、应为a2+a2=2a2,故本选项错误;B、应为2a2×a3=2a5,故本选项错误;C、应为3a﹣2a=a,故本选项错误;D、(a2)3=a6,正确.故选:D.6.【解答】解:因为正六边形的内角为120°,所以360°÷120°=3,即每一个顶点周围的正六边形的个数为3.故选:A.7.【解答】解:A、添加DE=AB与原条件满足SSA,不能证明△ABC≌△DEF,故A选项正确.B、添加DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DEF,故B选项错误.C、添加∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故C选项错误.D、添加AB∥DE,可得∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故D选项错误.故选:A.8.【解答】解:到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点.故选:B.9.【解答】解:∵AB=AC,∠BAC=∠DAE,AE=AD,∴ABE≌△ACD,故①正确.∵ABE≌△ACD,∴∠AEB=∠ADC.∵∠AEB+∠AEF=180°,∴∠AEF+∠ADC=180°,∴∠BFD=180°﹣∠EAD=180°﹣70°=110°,故③正确.∵AE平分∠BAC,∴∠EAC=35°.又∵∠DAE=70°,∴AC平分∠EAD.又∵AE=AD,∴AC⊥EF,AC平分EF.∴AC是EF的垂直平分线,故④正确.由已知条件无法证明BE=EF,故②错误.故选:C.10.【解答】解:如图,分情况讨论:①AB为等腰△ABC的底边时,符合条件的C点有4个;②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.故选:C.二.填空题(共6小题,满分18分,每小题3分)11.【解答】解:原式=4m4n4•3m2n3=12m6n7,故答案是:12m6n7.12.【解答】解:设多边形的边数为n,根据题意,得(n﹣2)•180=3×360,解得n=8.则这个多边形的边数是八.13.【解答】解:与80°角相邻的内角度数为100°;当100°角是底角时,100°+100°>180°,不符合三角形内角和定理,此种情况不成立;当100°角是顶角时,底角的度数=80°÷2=40°;故此等腰三角形的底角为40°.故填40.14.【解答】解:过O作OE⊥AB于E,OF⊥AC于F,连接OA,∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC,∴OE=OD,OD=OF,即OE=OF=OD=4,∴△ABC的面积是:S△AOB+S△AOC+S△OBC=×AB×OE+×AC×OF+×BC×OD=×4×(AB+AC+BC)=×4×21=42,故答案为:42.15.【解答】解:在Rt△ABC中,∠B=28°,∴∠CAB=90°﹣28°=62°,∵DE垂直平分AB,∴AD=BD,∴∠DAB=∠B=28°,∴∠CAD=∠CAB﹣∠DAB=62°﹣28°=34°.故答案为:34.16.【解答】解:如图,连接BE,与AD交于点P,此时PE+PC最小,∵△ABC是等边三角形,AD⊥BC,∴PC=PB,∴PE+PC=PB+PE=BE,即BE就是PE+PC的最小值,∵AD=12,点E是边AC的中点,∴AD=BE=12,∴PE+PC的最小值是12.故答案为12,三.解答题(共9小题,满分72分)17.【解答】解:(1)(12a3﹣6a2+3a)÷3a;=12a3÷3a﹣6a2÷3a+3a÷3a=4a2﹣2a+1;(2)(x﹣y)(x2+xy+y2).=x3+x2y+xy2﹣x2y﹣xy2﹣y3=x3﹣y3.18.【解答】解:∵OB、OC为角平分线,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∵∠ABC+∠ACB=180°﹣∠A,∠OBC+∠OCB=180°﹣∠BOC,∴2∠OBC+2∠OCB=180°﹣∠A,∴180°﹣∠A=2(180°﹣∠BOC),∴∠BOC=90°+∠A=90°+×50°=115°.19.【解答】解:(1)如图所示,△A1B1C1即为所求.(2)由图可知,点A与点A1之间10个格子,所以AA1的长度为10.20.【解答】解:(1)原式=﹣a6b3+2a2b•9a4b2=﹣a6b3+18a6b3=17a6b3(2)原式=[a+(2b﹣c)][a﹣(2b﹣c)]=a2﹣(2b﹣c)2=a2﹣(4b2﹣4bc+c2)=a2﹣4b2+4bc﹣c2(3)当6x﹣5y=10时,∴3x﹣2.5y=5原式=[4x2﹣y2﹣(4x2﹣12xy+9y2)]÷4y=(12xy﹣10y2)÷4y=3x﹣2.5y=522.【解答】解:(1)①当2x﹣1=x+1时,解x=2,此时3,3,4,能构成三角形.②当2x﹣1=3x﹣2时,解x=1,此时1,2,1不能构成三角形.故答案为2,能,1,不能;(2)③当x+1=3x﹣2,解得x=,此时2,,能构成三角形.23.【解答】解:接OA,OB后,可证∠OAP=∠OBP=90°,其依据是直径所对圆周角为直角;由此可证明直线PA,PB都是⊙O的切线,其依据是经过半径外端且垂直于这条半径的直线是圆的切线,证明过程如下:由作图可知OP为⊙C的直径,∴∠OAP=∠OBP=90°,即OA⊥PA、OB⊥PB,∵OA、OB是⊙O的半径,∴OP是⊙O的切线.故答案为:直径所对圆周角为直角,经过半径外端且垂直于这条半径的直线是圆的切线.2020-2021学年八年级(上)期中数学模拟试卷一.选择题(共6小题,满分18分,每小题3分)1.如果三角形的三个内角的度数比是2:3:4,则它是()A.锐角三角形B.钝角三角形C.直角三角形D.钝角或直角三角形2.下列长度的三条线段,能组成三角形的是()A.4cm,5cm,9cm B.8cm,8cm,15cmC.5cm,5cm,10cm D.6cm,7cm,14cm3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是()A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE 5.点M(1,2)关于y轴对称点的坐标为()A.(﹣1,2)B.(﹣1,﹣2) C.(1,﹣2)D.(2,﹣1)6.如右图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选的位置有()A.3个B.4个C.5个D.6个二.填空题(共8小题,满分24分,每小题3分)7.如图,点E在△ABC边BC的延长线上,CD平分∠ACE,若∠A=70°,∠DCA=65°,则∠B的度数是.8.(3分)如图,在△ABC中,∠B=40°,∠C=28°,点D在BA的延长线上,则∠CAD的大小为.9.若一个多边形的内角和比外角和大360°,则这个多边形的边数为.10.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为度.11.在△ABC中,∠C=∠A=∠B,则∠A= 度.12.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是(填上你认为适当的一个条件即可).13.已知点P(3,1)关于y轴的对称点Q的坐标是(a+b,﹣1﹣b),则ab的值为.14.在△ABC中,BC=9,AB的垂直平分线交BC与点M,AC的垂直平分线交BC于点N,则△AMN的周长= .三.解答题(共4小题,满分24分,每小题6分)15.(6分)等腰三角形一腰上的中线,分别将该三角形周长分成30cm 和33cm,试求该等腰三角形的底边长.16.(6分)如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.17.(6分)如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.18.(6分)如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.四.解答题(共3小题,满分21分,每小题7分)19.(7分)已知:如图,△ABC中,D是BC延长线上一点,E是CA 延长线上一点,F是AB上一点,连接EF.求证:∠ACD>∠E.20.(7分)一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数.21.(7分)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠C=40°,求∠BAD的度数;(2)若AC=5,DC=4,求△ABC的周长.五.解答题(共2小题,满分16分,每小题8分)22.(8分)如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE⊥CD;(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有(请写序号,少选、错选均不得分).23.(8分)已知:如图1所示,等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系.六.解答题(共2小题,满分17分)24.(8分)如图1,P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连接PQ交AC于点D.(1)求证:PD=DQ;(2)如图2,过P作PE⊥AC于E,若AB=2,求DE的长.25.(9分)如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C 逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.参考答案一.选择题1. A.2. B.3. B.4. D.5. A.6. B.二.填空题7.60°.8.68°.9. 6.10.37.11. 60.12.【解答】解:∵∠1=∠2,∴∠AEB=∠AEC,又 AE公共,∴当∠B=∠C时,△ABE≌△ACE(AAS);或BE=CE时,△ABE≌△ACE(SAS);或∠BAE=∠CAE时,△ABE≌△ACE(ASA).13. 214. 9三.解答题16.解:在△DFB中,∵DF⊥AB,∴∠FDB=90°,∵∠F=40°,∠FDB+∠F+∠B=180°,∴∠B=50°.在△ABC中,∵∠A=30°,∠B=50°,∴∠ACF=∠A+∠B=30°+50°=80°.18.解:(1)∵AB=AC,∴∠B=∠C=60°,∴∠BAC=60°,∵AD=AE,∴∠ADE=∠AED=70°,∴∠DAE=40°,∴∠BAD=∠BAC﹣∠DAE=20°,∵∠AED=∠CDE+∠C,∴∠CDE=70°﹣60°=10°.(2)结论:α=2β,理由是:设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,∵∠ACB=∠ABC,∴∠ACB=,∵∠ADE=∠AED,∴∠AED=,∴β=∠AED﹣∠ACB=﹣==,∴α=2β;19.证明:∵∠ACD是△ABC的一个外角,∴∠ACD>∠BAC,∵∠BAC是△AEF的一个外角,∴∠BAC>∠E,∴∠ACD>∠E.20.解:根据题意,得(n﹣2)•180=1620,解得:n=11.则这个多边形的边数是11,内角和度数是1620度.21.(1)解:∵EF垂直平分AC,∴AE=CE,∴∠C=∠EAC=40°,∵AD⊥BC,BD=DE,∴AB=AE,∴∠B=∠BEA=2∠C=80°,∴∠BAD=90°﹣80°=10°;(2)由(1)知:AE=EC=AB,∵BD=DE,∴AB+BD=DE+AE=DE+CE=DC,∴C△ABC=AB+BC+AC=2DC+AC=2×4+5=13..25.解:(1)全等的三角形有:△CBD≌△CA1F或△AEF≌△B1ED或△ACD≌△B1CF;证明:∵∠ACB1+∠A1CF=∠ACB1+∠BCD=90°∴∠A1CF=∠BCD∵A1C=BC∴∠A1=∠CBD=45°∴△CBD≌△CA1F;∴CF=CD,∵CA=CB1,∴AF=B1D,∵∠A=∠EB1D,∠AEF=∠B1ED,∴△AEF≌△B1ED,∵AC=B1C,∠ACD=∠B1CF,∠A=∠CB1F,∴△ACD≌△≌△B1CF.(2)在△CBB1中。
山东省济南市高新区2022-2023学年八年级上学期期中考试英语试题(含解析)

山东省济南市高新区2022-2023学年八年级上学期期中考试英语试题学校:___________姓名:___________班级:___________考号:___________10.A.left B.took C.put D.missed 11.A.angry B.surprised C.excited D.meaningless 12.A.at last B.at least C.at most D.at all 13.A.look B.feel C.think D.act 14.A.difficult B.important C.interesting D.comfortable 15.A.Until B.Although C.If D.So二、补全对话单选C.Because I went to the beach.D.Because I visited my uncle. 20.A.Do you need any help?B.Can you help me with my math? C.Are you hard-working?D.Did everyone have a great time?三、阅读单选A.Smoking B.Second-hand SmokeC.No Smoking D.Smoking Is Bad for ChildrenIn my three years of junior high school, I played soccer, basketball, and baseball. I love sports and really enjoy being part of a team. Playing on our school sports teams is the best part of my school life. I think I’m very lucky to have this chance(机会).In fact, many students who love sports don’t have the chance to play on a school team. That’s because, to join a team, you have to try out. And you should do well in tryouts (选拔赛). Some students may be ill that day, or nervous(紧张的), or are just having a bad day, so they don’t play their best and can’t join a team. That is too bad.Also, some students really don’t have the skills to play well. They never join a team, and that isn’t fair (公平的). But remember, this is school and students are here to learn. All students should have the chance to learn sports skills and teamwork by playing on a school sports team.Sports are important for good health. They help students feel good about themselves and their school. They meet and become friends in the teams. Players have fun playing, and their parents have fun watching and cheering for the team. So, sports bring students and parents together, too. These teams are just for fun, so if possible, let’s give every student a chance to play on the school sports team.31.The writer played all the sports, EXCEPT(除了)________.A.soccer B.basketball C.table tennis D.baseball 32.If you want to join sports team, what should you do according to the passage A.Practice every day.B.Do well in sports.C.Do well in tryouts.D.Be good at teamwork.33.What’s the main idea of the 4th paragraph(段落)?A.Joining sports team is good for students.B.Joining sports team makes students tired.C.Sports team isn’t necessary for students.D.It’s difficult to join sports team. 34.Which of the following is NOT true according to the passage?A.The writer loves the sports team very much.B.Students can’t learn sports skills and teamwork from sports team.C.Sports bring students and parents together.D.Not everyone can join sports team.drivers.39.How does the writer feel when Chinese people downplay a compliment?A.Appreciative.B.Uncomfortable.C.Bored.D.Sad. 40.What do we know from the last paragraph?A.The writer only compliments people in the service industry.B.It is not proper(恰当的)to complain about bad service very often.C.Everyone who served the writer got a compliment from him.D.The writer believes that compliments can be very encouraging.四、用所给单词的正确形式填空五、语法填空六、阅读还原7选5E.they will still be your teachers and you should respect(尊敬)them.F.we should obey whatever they ask and finish our homework on time.G.When you consider your teachers as friends, you will have more respect for them.七、看图写短语或句子.A: Where did you go on vacation?....A: What does Mary want to be when she grows up?八、材料作文66.新学期伊始,某英文网站正在征集同学们的新学期打算(New Term’s Resolutions)。
北师大版初中数学八年级上册期中试题(山东省济南市高新区

2018-2019学年山东省济南市高新区八年级(上)期中数学试卷一、选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(4分)在实数,,,,3.14中,无理数有()A.1个B.2个C.3个D.4个2.(4分)一个直角三角形的两条直角边分别是5和12,则斜边是()A.13B.12C.15D.103.(4分)下列函数中,是关于x的一次函数的是()A.y=B.y=2x2+1C.y=3﹣x D.y=4.(4分)如果P(m+3,2m+4)在y轴上,那么点P的坐标是()A.(﹣2,0)B.(0,﹣2)C.(1,0)D.(0,1)5.(4分)下面能满足方程3x+2=2y的一组解是()A.B.C.D.6.(4分)下列各式中,正确的是()A.=﹣2B.(﹣)2=9C.=﹣3D.±=±3 7.(4分)在已知点M(3,﹣4),在x轴上有一点与M的距离为5,则该点的坐标为()A.(6,0)B.(0,1)C.(0,﹣8)D.(6,0)或(0,0)8.(4分)若方程(2a+b)x2+2x+3y a﹣b=4是关于x、y的二元一次方程,则a、b的值是()A.B.C.D.9.(4分)正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x﹣k的图象大致是()A.B.C.D.10.(4分)已知方程组的解为,则2a﹣3b的值为()A.4B.6C.﹣6D.﹣411.(4分)如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是()A.B.C.D.12.(4分)如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣2,4),B (4,2),直线y=kx﹣2与线段AB有交点,则k的值不可能是()A.﹣5B.﹣2C.3D.5二、填空题:(本大题共6个小题,每小题4分,共24分.)13.(4分)已知2x+y=5,请用含x的代数式表示y,则y=.14.(4分)一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B 点,那么它所行的最短路线的长是.15.(4分)如图,若在象棋盘上建立直角坐标系,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),则“兵”位于点.16.(4分)有一个数值转换器,原理如下:当输入x为64时,输出的y的值是.17.(4分)如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y 轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是.18.(4分)对于实数a,b,定义运算“◆”:a◆b=,例如4◆3,因为4>3.所以4◆3==5.若x,y满足方程组,则x◆y=.三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(6分).20.(6分)解方程组:.21.(6分)如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.22.(8分)受气候等因素的影响,今年某些农产品的价格有所上涨.张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元.其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.则甲、乙两种蔬菜各种植了多少亩?23.(8分)如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:(1)在图①中,画一个三角形,使它的三边长都是有理数;(2)在图②中,画一个三边长分别为3,2,的三角形,一共可画这样的三角形个.24.(10分)如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为;(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线L上画出点Q,使△QDE 的周长最小,并求△QDE周长的最小值.25.(10分)甲、乙两年从A城出发匀速行驶至日城,在整个行选过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:(1)A,B两城相距多少千米?(2)分别求甲、乙两车离开A城的距离y与x的关系式.(3)求乙车出发后几小时追上甲车?26.(12分)定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;(2)如图②,在等腰直角△ABC中,AC=BC,∠ACB=90°,点M、N为边AB上两点,满足∠MCN=45°,求证:点M、N是线段AB的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90°试一试.请根据陈老师的提示完成第(2)小题的证明过程;(3)在(2)的问题中,若∠ACM=15°,AM=1,CM=+1.求BM的长.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半.)27.(12分)操作体验(1)如图①,已知△ABC,请画出△ABC的中线AD,并判断△ABD与△ACD 的面积大小关系.(2)如图②,在平面直角坐标系中,△ABC的边BC在x轴上,已知点A(2,4),B(﹣1,0),C(3,0),试确定过点A的一条直线l,平分△ABC的面积,请写出直线l的表达式.综合运用(3)如图③,在平面直角坐标系中,若A(1,4),B(3,2),那么在直线y =﹣4x+20上是否存在一点C,使直线OC恰好平分四边形OACB的面积?若存在,请计算点C的坐标;若不存在,请说明理由.2018-2019学年山东省济南市高新区八年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(4分)在实数,,,,3.14中,无理数有()A.1个B.2个C.3个D.4个【分析】根据无理数是无限不循环小数,可得答案.【解答】解:,是无理数,故选:B.【点评】本题考查了无理数,无理数是无限不循环小数,注意带根号的数不一定是无理数.2.(4分)一个直角三角形的两条直角边分别是5和12,则斜边是()A.13B.12C.15D.10【分析】此题利用勾股定理a2+b2=c2可直接得出答案.【解答】解;由一个直角三角形的两条直角边分别是5和12,利用勾股定理得斜边长为=13.故选:A.【点评】此题主要考查学生对勾股定理的理解和掌握,此题难度不大,是一道基础题.3.(4分)下列函数中,是关于x的一次函数的是()A.y=B.y=2x2+1C.y=3﹣x D.y=【分析】一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数.【解答】解:A、y=不符合一次函数的一般形式,不符合题意;B、y=2x2+1自变量次数不为1,故不是一次函数,不符合题意;C、符合一次函数的一般形式,符合题意;D、y=不符合一次函数的一般形式,不符合题意.故选:C.【点评】本题主要考查一次函数的定义.一次函数解析式的结构特征:k≠0;自变量的次数为1;常数项b可以为任意实数.4.(4分)如果P(m+3,2m+4)在y轴上,那么点P的坐标是()A.(﹣2,0)B.(0,﹣2)C.(1,0)D.(0,1)【分析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P 的坐标即可.【解答】解:∵P(m+3,2m+4)在y轴上,∴m+3=0,解得m=﹣3,2m+4=﹣2,∴点P的坐标是(0,﹣2).故选:B.【点评】解决本题的关键是记住y轴上点的特点:横坐标为0.5.(4分)下面能满足方程3x+2=2y的一组解是()A.B.C.D.【分析】把各选择支代入二元一次方程,验证即可.【解答】解:当x=4,y=2时,方程的左边=14,方程的右边=4,因为方程的左边≠方程的右边,所以A不满足方程;当x=3,y=5时,方程的左边=11,方程的右边=10,因为方程的左边≠方程的右边,所以B不满足方程;当x=2,y=4时,方程的左边=8,方程的右边=8,因为方程的左边=方程的右边,所以C满足方程;当x=1,y=3时,方程的左边=5,方程的右边=6,因为方程的左边≠方程的右边,所以D不满足方程;故选:C.【点评】本题考查了二元一次方程的解,二元一次方程有无数个解,它的解满足方程左右两边相等.6.(4分)下列各式中,正确的是()A.=﹣2B.(﹣)2=9C.=﹣3D.±=±3【分析】由平方根和立方根的定义即可得到.【解答】解:A、应=2,故此项错误;B、应=3,故此项错误;C、应=﹣,故此项错误;D、,故正确;故选:D.【点评】本题考查了平方根和立方根的定义,熟记定义是解题的关键.7.(4分)在已知点M(3,﹣4),在x轴上有一点与M的距离为5,则该点的坐标为()A.(6,0)B.(0,1)C.(0,﹣8)D.(6,0)或(0,0)【分析】到点M的距离为定值的点在以M为圆心,以5为半径的圆上,圆与x 轴的交点即为所求点.【解答】解:该点与M点的距离是5,则这点就是以M点为圆心,以5为半径的圆与x轴的交点,如图:过M作x轴的垂线,垂足是N,则ON=3,MN =4.根据勾股定理就可以求得OM=5,则O就是圆与x轴的一个交点,则O坐标是(0,0);设另一个交点是A,MN⊥OA,则本题满足垂径定理,AN =ON=3.∴点A的坐标是(6,0).故选D.【点评】本题运用了垂径定理,把求点的坐标的问题转化为求线段的长的问题,利用数形结合可以更直观地解题.8.(4分)若方程(2a+b)x2+2x+3y a﹣b=4是关于x、y的二元一次方程,则a、b的值是()A.B.C.D.【分析】根据二元一次方程的定义可得,再解方程组即可.【解答】解:由题意得:,解得.故选:C.【点评】此题主要考查了二元一次方程的定义,关键是掌握二元一次方程需满足三个条件:①首先是整式方程.②方程中共含有两个未知数.③所有未知项的次数都是一次.不符合上述任何一个条件的都不叫二元一次方程.9.(4分)正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x﹣k的图象大致是()A.B.C.D.【分析】根据自正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x﹣k的图象经过第一、三象限,且与y轴的正半轴相交.【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,∴k<0,∵一次函数y=x﹣k的一次项系数大于0,常数项大于0,∴一次函数y=x+k的图象经过第一、三象限,且与y轴的正半轴相交.故选:A.【点评】本题考查了一次函数图象:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).10.(4分)已知方程组的解为,则2a﹣3b的值为()A.4B.6C.﹣6D.﹣4【分析】把原方程组的解代入方程组,求出a,b的值,再代入所求代数式即可.【解答】解:把代入原方程组,得,解得.2a﹣3b=2×﹣3×(﹣1)=6.故选:B.【点评】此题很简单,考查了二元一次方程组的解的定义,所谓“方程组”的解,指的是该数值满足方程组中的每一方程.11.(4分)如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是()A.B.C.D.【分析】根据所给出的图形求出AB、AC、BC的长以及∠BAC的度数,再根据三角形的面积公式列出方程进行计算即可.【解答】解:根据图形可得:AB=AC==,BC==,∠BAC=90°,设△ABC中BC的高是x,则AC•AB=BC•x,×=•x,x=.故选:A.【点评】此题考查了勾股定理,用到的知识点是勾股定理、三角形的面积公式,关键是根据三角形的面积公式列出关于x的方程.12.(4分)如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣2,4),B (4,2),直线y=kx﹣2与线段AB有交点,则k的值不可能是()A.﹣5B.﹣2C.3D.5【分析】当直线y=kx﹣2与线段AB的交点为A点时,把A(﹣2,4)代入y=kx﹣2,求出k=﹣3,根据一次函数的有关性质得到当k≤﹣3时直线y=kx ﹣2与线段AB有交点;当直线y=kx﹣2与线段AB的交点为B点时,把B(4,2)代入y=kx﹣2,求出k=1,根据一次函数的有关性质得到当k≥1时直线y=kx﹣2与线段AB有交点,从而能得到正确选项.【解答】解:把A(﹣2,4)代入y=kx﹣2得,4=﹣2k﹣2,解得k=﹣3,∴当直线y=kx﹣2与线段AB有交点,且过第二、四象限时,k满足的条件为k ≤﹣3;把B(4,2)代入y=kx﹣2得,4k﹣2=2,解得k=1,∴当直线y=kx﹣2与线段AB有交点,且过第一、三象限时,k满足的条件为k ≥1.即k≤﹣3或k≥1.所以直线y=kx﹣2与线段AB有交点,则k的值不可能是﹣2.故选:B.【点评】本题考查了一次函数y=kx+b(k≠0)的性质:当k>0时,图象必过第一、三象限,k越大直线越靠近y轴;当k<0时,图象必过第二、四象限,k越小直线越靠近y轴.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.(4分)已知2x+y=5,请用含x的代数式表示y,则y=﹣2x+5.【分析】本题由二元一次方程2x+y=5,直接移项可得y=﹣2x+5.【解答】解:由二元一次方程2x+y=5,移项可得y=﹣2x+5.【点评】本题主要考查二元一次方程的变形,解题的关键是熟练掌握解二元一次方程的基本步骤.14.(4分)一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B 点,那么它所行的最短路线的长是10.【分析】根据”两点之间线段最短”,将点A和点B所在的两个面进行展开,展开为矩形,则AB为矩形的对角线,即蚂蚁所行的最短路线为AB.【解答】解:如图(1)所示:AB==;如图(2)所示:AB==10.由于>10,所以最短路径为10.【点评】本题的关键是将点A和点B所在的面展开,运用勾股定理求出矩形的对角线.15.(4分)如图,若在象棋盘上建立直角坐标系,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),则“兵”位于点(﹣3,1).【分析】先根据“帥”的位置确定原点的坐标,建立平面直角坐标系,从而可以确定“兵”的位置.【解答】解:根据条件建立平面直角坐标系:由图得“兵”的坐标为:(﹣3,1).故答案为:(﹣3,1).【点评】本题考查了平面坐标系的建立,在平面直角坐标系中确定点的位置,本题难度较小.16.(4分)有一个数值转换器,原理如下:当输入x为64时,输出的y的值是2.【分析】由图中的程序知:输入x的值后,当是无理数时,y=;若的值是有理数,将的值再取算术平方根,直至输出的结果为无理数,也就求出了y的值.【解答】解:由题意,得:x=64时,=8,8是有理数,将8的值代入x中;当x=8时,=2,2是无理数,故y的值是2.故答案为:2.【点评】本题考查了实数的运算,弄清程序的计算方法是解答此类题的关键.17.(4分)如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y 轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是x=2.【分析】一次函数y=ax+b的图象与x轴交点横坐标的值即为方程ax+b=0的解.【解答】解:∵一次函数y=ax+b的图象与x轴相交于点(2,0),∴关于x的方程ax+b=0的解是x=2.故答案为x=2.【点评】本题主要考查了一次函数与一元一次方程的关系.任何一元一次方程都可以转化为ax+b=0 (a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.18.(4分)对于实数a,b,定义运算“◆”:a◆b=,例如4◆3,因为4>3.所以4◆3==5.若x,y满足方程组,则x◆y=60.【分析】根据二元一次方程组的解法以及新定义运算法则即可求出答案.【解答】解:由题意可知:,解得:∵x<y,∴原式=5×12=60故答案为:60【点评】本题考查二元一次方程组的解法,解题的关键是熟练运用二元一次方程组的解法以及正确理解新定义运算法则,本题属于基础题型.三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(6分).【分析】本题比较简单,解答本题只需将二次根式化为最简,然后合并同类二次根式即可得出的答案.【解答】解:原式=3﹣+2=.【点评】本题考查二次根式的加减运算,属于基础题,比较简单,解答本题时注意先化简再合并,要细心运算,避免出错.20.(6分)解方程组:.【分析】可以先消x,也可以先消y,分别是xy的系数相等或互为相反数即可.【解答】解法一:①×2+②得5x=10(3分)解得:x=2(4分)将x=2代入①得y=﹣2(5分)∴方程组的解为(6分)解法二:由①得y=2x﹣6③(3分)将③代入②得x+2(2x﹣6)=﹣2解得:x=2(4分)将x=2代入③得y=﹣2(5分)∴方程组的解为(6分)【点评】本题考查了二元一次方程组的解法根据方程的特点,选加减消元法或代入消元法.21.(6分)如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.【分析】连接AC,先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,最后利用三角形的面积公式求解即可.【解答】解:连接AC,如下图所示:∵∠ABC=90°,AB=3,BC=4,∴AC==5,在△ACD中,AC2+CD2=25+144=169=AD2,∴△ACD是直角三角形,=AB•BC+AC•CD=×3×4+×5×12=36.∴S四边形ABCD【点评】本题考查的是勾股定理、勾股定理的逆定理及三角形的面积,根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键,难度适中.22.(8分)受气候等因素的影响,今年某些农产品的价格有所上涨.张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元.其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.则甲、乙两种蔬菜各种植了多少亩?【分析】等量关系为:甲种蔬菜亩数+乙种蔬菜亩数=10;甲种蔬菜总获利+乙种蔬菜总获利=13800.【解答】解:设甲、乙两种蔬菜的种植面积分别为x、y亩.依题意可得:,解这个方程组得:.故甲、乙两种蔬菜各种植了4、6亩.【点评】解题关键是弄清题意,找到合适的等量关系.23.(8分)如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:(1)在图①中,画一个三角形,使它的三边长都是有理数;(2)在图②中,画一个三边长分别为3,2,的三角形,一共可画这样的三角形16个.【分析】(1)画一个边长3,4,5的三角形即可;(2)由勾股定理容易得出结果.【解答】解:(1)∵=5,∴△ABC即为所求,如图1所示:(2)如图2所示:∵=2,=,∴△ABC,△DBC,…,都是符合条件的三角形,一共可画这样的三角形16个;故答案为:16.【点评】本题考查了正方形的性质、勾股定理、作图﹣﹣应用与设计作图;熟记勾股定理是解决问题的关键.24.(10分)如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′(3,5)、C′(5,﹣2);(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a);(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线L上画出点Q,使△QDE 的周长最小,并求△QDE周长的最小值.【分析】(1)借助网格,根据轴对称的定义画出各点关于直线的对称点,即可解答.(2)由(1)中坐标得出规律,即可求出P(a,b)关于第一、三象限的角平分线l的对称点P'的坐标.(3)作出D点的对称点D′,连接D′E,与直线L的交点即为所求点Q,利用勾股定理可得周长.【解答】解:(1)如图,由点关于直线y=x轴对称可知:B'(3,5),C'(5,﹣2),故答案为:(3,5)、(5,﹣2)(2)由(1)的结果可知,坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a),故答案为:(b,a);(3)由(2)得,D(1,﹣3)关于直线l的对称点D'的坐标为(﹣3,1),连接D'E交直线l于点Q,此时点Q到D、E两点的距离之和最小,D'E==,DE==,∴△QDE周长的最小值+.【点评】本题主要考查作图﹣轴对称变换和轴对称﹣最短路线问题,解题的关键是熟练掌握轴对称变换的定义和性质.25.(10分)甲、乙两年从A城出发匀速行驶至日城,在整个行选过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:(1)A,B两城相距多少千米?(2)分别求甲、乙两车离开A城的距离y与x的关系式.(3)求乙车出发后几小时追上甲车?【分析】(1)根据函数图象可以解答本题;(2)根据图象中的信息分别求出甲乙两车对应的函数解析式,(3)根据(2)甲乙两车对应的函数解析式,然后令它们相等即可解答本题.【解答】解:(1)由图可知,A、B两城相距300千米;(2)设甲对应的函数解析式为:y=kx,300=5k,解得,k=60,即甲对应的函数解析式为:y=60x,设乙对应的函数解析式为y=mx+n,解得:m=100,n=﹣100,即乙对应的函数解析式为y=100x﹣100;(3)解方程组得:,2.5﹣1=1.5,即乙车出发后1.5小时追上甲车.【点评】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.26.(12分)定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;(2)如图②,在等腰直角△ABC中,AC=BC,∠ACB=90°,点M、N为边AB上两点,满足∠MCN=45°,求证:点M、N是线段AB的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90°试一试.请根据陈老师的提示完成第(2)小题的证明过程;(3)在(2)的问题中,若∠ACM=15°,AM=1,CM=+1.求BM的长.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半.)【分析】(1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可.(2)只要证明△MCN≌△MCN'以及∠NAM=90°即可.(3)如图,过N作于NH⊥CM于H.结合图中相关线段的和差关系和直角三角形的性质求得MN=2.由(2)得结论BN2+AM2=MN2,BN=.则BM=BN+MN.【解答】(1)解:①当MN为最大线段时,∵点M、N是线段AB的勾股分割点,∴BN===;②当BN为最大线段时,∵点M、N是线段AB的勾股分割点,∴BN===,综上所述:BN=或;(2)①证明:连接MN′,∵∠ACB=90°,∠MCN=45°,∴∠BCN+∠ACM=45°,∵∠ACN'=∠BCN,∴∠MCN'=∠ACN′+∠ACM=∠BCN+∠ACM=45°=∠MCN,在△MCN和△MCN′中,,∴△MCN≌△MCN'(SAS),∴MN'=MN,∵∠CAN′=∠CAB=45°,∴∠MAN′=90,AN′2+AM2=MN′2,即BN2+AM2=MN2,∴点M、N是线段AB的勾股分割点;(3)如图,过N作于NH⊥CM于H.则∠NHM=90°,∠NMH=60°,设HM=x,则MN=2x,HN=x.得x+x=+1,∴x=1,∴MN=2.由(2)得结论BN2+AM2=MN2,BN=.∴BM=BN+MN=2+.【点评】本题考查几何变换综合题,需要掌握等腰三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质等知识,利用旋转法添加辅助线是解决问题的关键.27.(12分)操作体验(1)如图①,已知△ABC,请画出△ABC的中线AD,并判断△ABD与△ACD 的面积大小关系.(2)如图②,在平面直角坐标系中,△ABC的边BC在x轴上,已知点A(2,4),B(﹣1,0),C(3,0),试确定过点A的一条直线l,平分△ABC的面积,请写出直线l的表达式.综合运用(3)如图③,在平面直角坐标系中,若A(1,4),B(3,2),那么在直线y =﹣4x+20上是否存在一点C,使直线OC恰好平分四边形OACB的面积?若存在,请计算点C的坐标;若不存在,请说明理由.【分析】(1)过A作AE⊥BC于点E,则可表示出△ABD和△ACD的面积,可比较其大小关系;(2)由(1)可知直线l应过BC的中点F,由B、C的坐标可求得F点的坐标,利用待定系数法可求得直线l的表达式;(3)由条件可知直线OC过AB的中点G,由AB的坐标可求得G的坐标,利用待定系数法可求得直线OC的解析式,联立两直线解析式可求得C点坐标.【解答】解:(1)如图①,过A作AE⊥BC于点E,∵AD为BC边上的中线,∴BD=CD,∴BD •AE =CD •AE ,即S △ABD =S △ACD ;(2)如图②,设BC 的中点为F ,∵直线l 平分△ABC 的面积,∴由(1)可知直线l 过点F ,∵B (﹣1,0),C (3,0),∴F (1,0),设直线l 的表达式为y =kx +b ,把A 、F 的坐标代入可得,解得,∴直线l 的表达式y =4x ﹣4;(3)如图③,连接AB 交OC 于点G ,∵直线OC 恰好平分四边形OACB 的面积,∴直线OC 过AB 的中点,即G 为AB 的中点,∵A (1,4),B (3,2),∴G (2,3),设直线OC解析式为y=ax,则3=2a,解得a=,∴直线OC表达式为y=x,联立两直线解析式可得,解得,∴存在满足条件的点C,其坐标为(,).【点评】本题为一次函数的综合应用,涉及待定系数法、三角形的中线、三角形的面积等知识.在(1)中表示出两三角形的面积是解题的关键,在(2)中确定出直线l过BC的中点是解题的关键,在(3)中求得直线OC的解析式是解题的关键.本题考查知识点较多,综合性较强,但难度不大.。
2020-2021学年山东省济南市济阳区八年级(下)期中数学试卷(解析版)
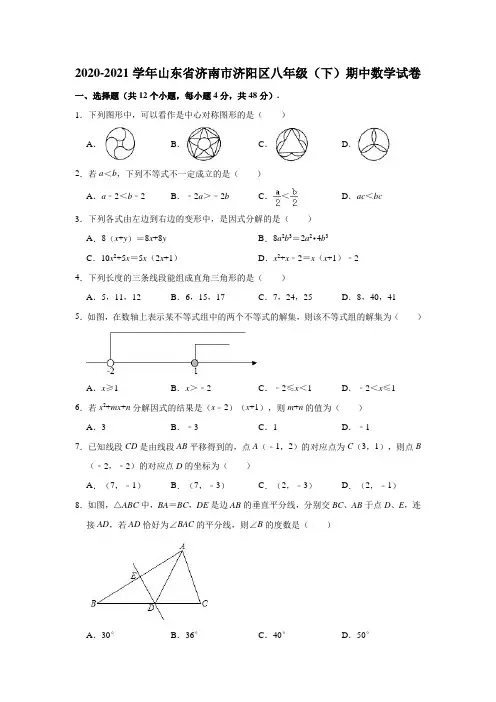
2020-2021学年山东省济南市济阳区八年级(下)期中数学试卷一、选择题(共12个小题,每小题4分,共48分).1.下列图形中,可以看作是中心对称图形的是()A.B.C.D.2.若a<b,下列不等式不一定成立的是()A.a﹣2<b﹣2B.﹣2a>﹣2b C.<D.ac<bc3.下列各式由左边到右边的变形中,是因式分解的是()A.8(x+y)=8x+8y B.8a2b3=2a2•4b3C.10x2+5x=5x(2x+1)D.x2+x﹣2=x(x+1)﹣24.下列长度的三条线段能组成直角三角形的是()A.5,11,12B.6,15,17C.7,24,25D.8,40,415.如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为()A.x≥1B.x>﹣2C.﹣2≤x<1D.﹣2<x≤16.若x2+mx+n分解因式的结果是(x﹣2)(x+1),则m+n的值为()A.3B.﹣3C.1D.﹣17.已知线段CD是由线段AB平移得到的,点A(﹣1,2)的对应点为C(3,1),则点B (﹣2,﹣2)的对应点D的坐标为()A.(7,﹣1)B.(7,﹣3)C.(2,﹣3)D.(2,﹣1)8.如图,△ABC中,BA=BC,DE是边AB的垂直平分线,分别交BC、AB于点D、E,连接AD,若AD恰好为∠BAC的平分线,则∠B的度数是()A.30°B.36°C.40°D.50°9.如果x2+kxy+9y2是一个完全平方式,那么k的值为()A.6B.﹣6C.±6D.1810.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次停止,那么x的取值范围是()A.8<x≤22B.8≤x<22C.22<x≤64D.8<x≤6411.如图所示,直线l1:y=kx+b与直线l2:y=mx+n交于点P(﹣2,3),不等式kx+b≤mx+n的解集是()A.x>﹣2B.x≥﹣2C.x<﹣2D.x≤﹣212.如图,正方形ABCD中,点E、F分别在线段BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N,下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③BE=2,DF=3,则S△AEF=15;④若AB=6,BM=3,则MN=5.其中结论正确的个数是()A.4B.3C.2D.1二、填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)13.用适当的符号表示:m的相反数与2的和是非负数:.14.分解因式:x2﹣9=.15.若x=2是关于x的不等式2x﹣a<0的一个解,则a的取值范围为.16.现规定一种新运算,a※b=2a﹣b,其中a、b为常数.已知关于x的不等式k※x≤3的解集在数轴上表示如图,则k的值为.17.如图,△ABC绕点A顺时针旋转某个角度得到△ADE.已知∠DAC=60°,∠BAE=100°,BC、DE相交于点F,BC、AD相交于点G,则∠DFB的度数为度.18.如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是.三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.解不等式3x+1>2(x﹣1),并写出它的负整数解.20.解不等式组,并把解集在数轴上表示出来.21.因式分解:(1)﹣2ax2+4ax﹣2a;(2)(2a﹣1)2﹣3(1﹣2a).22.已知:如图,∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:△OEF是等腰三角形.23.光明中学团委组织七年级和八年级共60名学生参加环保活动,七年级学生平均收集15个废弃塑料瓶,八年级学生平均收集20个废弃塑料瓶,为了保证所有收集塑料瓶总数不少于1000个,至少需要多少八年级学生参加活动?24.如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)将△ABC先向下平移6个单位长度,再向右平移2个单位长度,画出两次平移后的△A1B1C1,并写出点B1的坐标;(2)若△ABC和△A2B2C2关于原点O成中心对称,画出△A2B2C2,并写出点B2的坐标;(3)将△A1B1C1绕某点旋转一定角度可以得到△A2B2C2,则其旋转中心的坐标是.25.“五一”假期即将来临,甲、乙两家旅行社为了吸引更多的顾客,分别推出了赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:一律按原价的七五折优惠.已知这两家旅行社的原价均为每人600元.(1)若团体人数为6人,选择旅行社更优惠(直接写出“甲”或“乙”);(2)设团体有x(x>4)人,甲、乙两家旅行社的收费分别为y甲,y乙元,请分别写出y,y乙与x之间的关系式;甲(3)随着团体人数的变化,哪家旅行社的收费更优惠?26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个因式分解的等式.(1)图1中大正方形的面积用两种方法可分别表示为、;(2)你得到的因式分解等式是:;(3)观察图2,可以发现代数式2a2+5ab+2b2可以因式分解为;(4)通过不同的方法表示同一个几何体的体积,也可以探求相应的因式分解等式.如图3是棱长为(a+b)的正方体,被如图所示的分割线分成8块.①用不同方法计算这个正方体体积,就可以得到一个因式分解的等式,这个等式是:;②已知a+b=5,ab=2,利用上面的规律求a3+b3的值.27.【问题背景】如图1,等腰直角△ABC中,AB=AC,∠BAC=90°,则边BC与边AB的数量关系为BC=AB.(1)如图2,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则得到边BC与边AB的数量关系为.【迁移应用】(2)如图3,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,①求证:△ADB≌△AEC.②求AD、BD、CD之间的数量关系.【拓展延伸】(3)如图4,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=6,连接BD并延长,交AC于点F.若∠CBF=15°,∠BAD=30°,则四边形AEFD的面积为.参考答案一、选择题(共12个小题,每小题4分,共48分).1.下列图形中,可以看作是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的性质得出图形旋转180°,与原图形能够完全重合的图形是中心对称图形,分别判断得出即可.解:A.旋转180°,与原图形能够完全重合是中心对称图形;故此选项符合题意;B.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;故选:A.2.若a<b,下列不等式不一定成立的是()A.a﹣2<b﹣2B.﹣2a>﹣2b C.<D.ac<bc【分析】根据不等式的性质逐个判断即可.解:A.∵a<b,∴a﹣2<b﹣2,故本选项不符合题意;B.∵a<b,∴﹣2a>﹣2b,故本选项不符合题意;C.∵a<b,∴<,故本选项不符合题意;D.当c≤0时,不能从a<b推出ac<bc,故本选项符合题意;故选:D.3.下列各式由左边到右边的变形中,是因式分解的是()A.8(x+y)=8x+8y B.8a2b3=2a2•4b3C.10x2+5x=5x(2x+1)D.x2+x﹣2=x(x+1)﹣2【分析】根据因式分解的定义逐个判断即可.解:A.从左边到右边的变形是整式乘法,不属于因式分解,故本选项不符合题意;B.不属于因式分解,故本选项不符合题意;C.从左边到右边的变形属于因式分解,故本选项符合题意;D.从左边到右边的变形不属于因式分解,故本选项不符合题意;故选:C.4.下列长度的三条线段能组成直角三角形的是()A.5,11,12B.6,15,17C.7,24,25D.8,40,41【分析】根据勾股定理的逆定理,可以判断各个选项中的三条线段能否构成直角三角形,本题得以解决.解:52+112≠122,故选项A不符合题意;62+152≠172,故选项B不符合题意;72+242=252,故选项C符合题意;82+402≠412,故选项D不符合题意;故选:C.5.如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为()A.x≥1B.x>﹣2C.﹣2≤x<1D.﹣2<x≤1【分析】根据数轴得出答案即可.解:从数轴可知:这个不等式组的解集是x≥1,故选:A.6.若x2+mx+n分解因式的结果是(x﹣2)(x+1),则m+n的值为()A.3B.﹣3C.1D.﹣1【分析】先根据多项式乘以多项式法则进行计算,再根据已知条件求出m、n的值,最后求出答案即可.解:(x﹣2)(x+1)=x2+x﹣2x﹣2=x2﹣x﹣2,∵二次三项式x2+mx+n可分解为(x﹣2)(x+1),∴m=﹣1,n=﹣2,∴m+n=﹣1+(﹣2)=﹣3,故选:B.7.已知线段CD是由线段AB平移得到的,点A(﹣1,2)的对应点为C(3,1),则点B (﹣2,﹣2)的对应点D的坐标为()A.(7,﹣1)B.(7,﹣3)C.(2,﹣3)D.(2,﹣1)【分析】先根据点A的对应点C的坐标得出平移的方向和距离,据此利用点的平移规律可得答案.解:由点A(﹣1,2)的对应点为C(3,1),知线段AB向右平移4个单位、向下平移1个单位即可得到CD,∴点B(﹣2,﹣2)的对应点D的坐标为(﹣2+4,﹣2﹣1),即(2,﹣3),故选:C.8.如图,△ABC中,BA=BC,DE是边AB的垂直平分线,分别交BC、AB于点D、E,连接AD,若AD恰好为∠BAC的平分线,则∠B的度数是()A.30°B.36°C.40°D.50°【分析】设出∠B的度数,然后利用垂直平分线和角平分线的性质表示出∠BAC和∠C 的度数,利用三角形内角和定理列出方程求解即可.解:设∠B=x°,∵DE是边AB的垂直平分线,∴DB=DA,∴∠DAB=∠B=x°,∵AD平分∠BAC,∴∠BAC=2∠BAD=2x°,∵BA=BC,∴∠C=∠BAC=2x°,在△ABC中,根据三角形的内角和定理得:x+2x+2x=180,解得:x=36,∴∠B的度数是36°,故选:B.9.如果x2+kxy+9y2是一个完全平方式,那么k的值为()A.6B.﹣6C.±6D.18【分析】利用完全平方公式的结构特征判断即可求出k的值.解:∵x2+kxy+9y2是一个完全平方式,∴k=±6,故选:C.10.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次停止,那么x的取值范围是()A.8<x≤22B.8≤x<22C.22<x≤64D.8<x≤64【分析】由程序运行一次的结果小于等于190、运行两次的结果大于190,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围.解:依题意,得:,解得:22<x≤64.故选:C.11.如图所示,直线l1:y=kx+b与直线l2:y=mx+n交于点P(﹣2,3),不等式kx+b≤mx+n的解集是()A.x>﹣2B.x≥﹣2C.x<﹣2D.x≤﹣2【分析】观察函数图象,写出直线l1:y=kx+b不在直线l2:y=mx+n上方的自变量的取值范围即可.解:如图所示,直线l1:y=kx+b与直线l2:y=mx+n交于点P(﹣2,3),所以,不等式kx+b≤mx+n的解集是x≤﹣2,故选:D.12.如图,正方形ABCD中,点E、F分别在线段BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N,下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③BE=2,DF=3,则S△AEF=15;④若AB=6,BM=3,则MN=5.其中结论正确的个数是()A.4B.3C.2D.1【分析】根据旋转的性质得到BH=DF,AH=AF,∠BAH=∠DAF,得到∠EAH=∠EAF =45°,根据全等三角形的性质得到EH=EF,∠AEB=∠AEF,于是得到BE+BH=BE+DF =EF,故①正确;过A作AG⊥EF于G,根据全等三角形的性质得到AB=AG,于是得到点A到线段EF的距离一定等于正方形的边长,故②正确;求出EF=BE+DF=5,设BC=CD=n,根据勾股定理即可得到S△AEF=15,故③正确;把△ADN绕点A顺时针旋转90°得到△ABQ,再证明△AMQ≌△AMN(SAS),从而得MQ=MN,再证明∠QBM =∠ABQ+∠ABM=90°,设MN=x,再由勾股定理求出x即可.解:如图,把△ADF绕点A顺时针旋转90°得到△ABH,由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,∵∠EAF=45°,∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°,∴∠EAH=∠EAF=45°,在△AEF和△AEH中,,∴△AEF≌△AEH(SAS),∴EH=EF,∴∠AEB=∠AEF,∴BE+BH=BE+DF=EF,故①正确;过A作AG⊥EF于G,∴∠AGE=∠ABE=90°,在△ABE与△AGE中,,∴△ABE≌△AGE(AAS),∴AB=AG,∴点A到线段EF的距离一定等于正方形的边长;故②正确;∵BE=2,DF=3,∴EF=BE+DF=5,设BC=CD=n,∴CE=n﹣2,CF=n﹣3,∴EF2=CE2+CF2,∴25=(n﹣2)2+(n﹣3)2,∴n=6(负值舍去),∴AG=6,∴S△AEF=×6×5=15.故③正确;如图,把△ADN绕点A顺时针旋转90°得到△ABQ,连接QM,由旋转的性质得,BQ=DN,AQ=AN,∠BAQ=∠DAN,∠ADN=∠ABQ=45°,∵∠EAF=45°,∴∠MAQ=∠BAQ+∠BAE=∠DAN+∠BAE=90°﹣∠EAF=45°,∴∠MAQ=∠MAN=45°,在△AMQ和△AMN中,,∴△AMQ≌△AMN(SAS),∴MQ=MN,∵∠QBM=∠ABQ+∠ABM=90°,∴BQ2+MB2=MQ2,∴ND2+MB2=MN2,∵AB=6,∴BD=AB=12,设MN=x,则ND=BD﹣BM﹣MN=9﹣x,∴32+(9﹣x)2=x2,解得:x=5,∴MN=5,故④正确,故选:A.二、填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)13.用适当的符号表示:m的相反数与2的和是非负数:﹣m+2≥0.【分析】根据相反数的定义以及非负数的定义求解即可.解:m的相反数与2的和是非负数表示为:﹣m+2≥0.故答案为:﹣m+2≥0.14.分解因式:x2﹣9=(x+3)(x﹣3).【分析】本题中两个平方项的符号相反,直接运用平方差公式分解因式.解:x2﹣9=(x+3)(x﹣3).故答案为:(x+3)(x﹣3).15.若x=2是关于x的不等式2x﹣a<0的一个解,则a的取值范围为a>4.【分析】解不等式得出x<,根据2是该不等式的一个解知>2,解之可得答案.解:∵2x﹣a<0,∴2x<a,∴x<,∵x=2是关于x的不等式2x﹣a<0的一个解,∴>2,∴a>4.故答案为:a>4.16.现规定一种新运算,a※b=2a﹣b,其中a、b为常数.已知关于x的不等式k※x≤3的解集在数轴上表示如图,则k的值为1.【分析】根据k※x≤3得出2k﹣x≤3,求出不等式的解集是x≥﹣3+2k,根据数轴得出﹣3+2k=﹣1,再求出k即可.解:∵k※x≤3,∴2k﹣x≤3,∴﹣x≤3﹣2k,∴x≥﹣3+2k,从数轴可知:﹣3+2k=﹣1,解得:k=1,故答案为:1.17.如图,△ABC绕点A顺时针旋转某个角度得到△ADE.已知∠DAC=60°,∠BAE=100°,BC、DE相交于点F,BC、AD相交于点G,则∠DFB的度数为20度.【分析】由旋转的性质得到∠B=∠D,∠BAC=∠DAE,求出∠BAD,再由三角形的外角性质即可求解.解:由旋转的性质得:∠B=∠D,∠BAC=∠DAE,∵∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,∴∠BAD=∠CAE,∵∠DAC=60°,∠BAE=100°,∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣60°)=20°,∵∠B=∠D,∠AGF=∠DFB+∠D=∠BAD+∠B,∴∠DFB=∠BAD=20°.故答案为:20.18.如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是130或100或160.【分析】由旋转的性质得出BD=AB=BC,分三种情况:①当DA=DC时;②当AD=AC时;③当CA=CD时;分别求出m的值即可.解:由旋转的性质得:BD=AB=BC,∵△ADC为等腰三角形,∴分三种情况:①当DA=DC时,∠ABD=∠CBD=(360°﹣∠ABC)=130°,∴m=130;②当AD=AC时,∠ABD=∠ABC=100°,∴m=100;③当CA=CD时,∠CBD=∠ABC=100°,∴∠ABD=360°﹣100°﹣100°=160°,∴m=160;综上所述:m所有可能的取值为130或100或160;故答案为:130或100或160.三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.解不等式3x+1>2(x﹣1),并写出它的负整数解.【分析】不等式去括号,移项合并,把x系数化为1,求出解集,确定出负整数解即可.解:3x+1>2(x﹣1)去括号得:3x+1>2x﹣2,解得:x>﹣3,∴它的负整数解为﹣1,﹣2.20.解不等式组,并把解集在数轴上表示出来.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.解:解①得,x<2,解②得,x≥﹣2,∴原不等式组的解集为﹣2≤x<2,将解集表示在数轴上如下:21.因式分解:(1)﹣2ax2+4ax﹣2a;(2)(2a﹣1)2﹣3(1﹣2a).【分析】(1)提公因式后再利用完全平方公式即可;(2)变形后提公因式即可.解:(1)原式=﹣2a(x2﹣2x+1)=﹣2a(x﹣1)2;(2)原式=(2a﹣1)2+3(2a﹣1)=(2a﹣1)(2a﹣1+3)=2(2a﹣1)(a+1).22.已知:如图,∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:△OEF是等腰三角形.【分析】证明Rt△ABF≌Rt△DCE,根据全等三角形的性质得到∠AFB=∠DEC,根据等腰三角形的判定定理证明结论.【解答】证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE,在Rt△ABF和Rt△DCE中,,∴Rt△ABF≌Rt△DCE(HL)∴∠AFB=∠DEC,∴OE=OF,∴△OEF是等腰三角形.23.光明中学团委组织七年级和八年级共60名学生参加环保活动,七年级学生平均收集15个废弃塑料瓶,八年级学生平均收集20个废弃塑料瓶,为了保证所有收集塑料瓶总数不少于1000个,至少需要多少八年级学生参加活动?【分析】设至少需要x个八年级学生参加活动,则参加活动的七年级学生为(60﹣x)个,由收集塑料瓶总数不少于1000个建立不等式求出其解即可.解:设至少需要x个八年级学生参加活动,则参加活动的七年级学生为(60﹣x)个,由题意,得20x+15(60﹣x)≥1000,解得:x≥20.∴至少需要20个八年级学生参加活动.24.如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)将△ABC先向下平移6个单位长度,再向右平移2个单位长度,画出两次平移后的△A1B1C1,并写出点B1的坐标;(2)若△ABC和△A2B2C2关于原点O成中心对称,画出△A2B2C2,并写出点B2的坐标;(3)将△A1B1C1绕某点旋转一定角度可以得到△A2B2C2,则其旋转中心的坐标是(1,﹣3.【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.(2)分别作出A,B,C的对应点A2,B2,C2即可.(3)对应点连线的交点即为旋转中心.解:(1)如图,△A1B1C1即为所求作,点B1的坐标(﹣3,5).(2)如图,△A2B2C2即为所求作,点B2的坐标(5,﹣1).(3)将△A1B1C1绕某点旋转一定角度可以得到△A2B2C2,则其旋转中心P的坐标(1,﹣3).故答案为:(1,﹣3).25.“五一”假期即将来临,甲、乙两家旅行社为了吸引更多的顾客,分别推出了赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:一律按原价的七五折优惠.已知这两家旅行社的原价均为每人600元.(1)若团体人数为6人,选择乙旅行社更优惠(直接写出“甲”或“乙”);(2)设团体有x(x>4)人,甲、乙两家旅行社的收费分别为y甲,y乙元,请分别写出y,y乙与x之间的关系式;甲(3)随着团体人数的变化,哪家旅行社的收费更优惠?【分析】(1)根据优惠办法求出选择甲、乙两家旅行社的费用即可判断;(2)x>4时,根据甲旅行社的优惠办法,求出y甲的函数关系式,根据乙旅行社的优惠办法写出y乙的函数关系式;(3)分情况讨论列出不等式,然后求解即可.解:(1)若团体人数为6人,选甲:4×600+2×300=3000(元),选乙:6×600×0.75=2700(元);故答案为:乙;(2)y甲=600×4+600××(x﹣4)=300x+1200(x>4);y乙=600×0.75×x=450x(x>4);(3)①当y甲>y乙,300x+1200>450x,∴x<8,∴小于8人选乙;②当y甲=y乙,300x+1200=450x,∴x=8,∴等于8人选甲、乙一样;③当y甲<y乙,300x+1200<450x,∴x>8,∴大于8人选甲.答:团体人数小于8人选乙优惠,团体人数等于8人选甲、乙一样优惠,团体人数大于8人选甲优惠.26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个因式分解的等式.(1)图1中大正方形的面积用两种方法可分别表示为a2+b2+2ab、(a+b)2;(2)你得到的因式分解等式是:a2+b2+2ab=(a+b)2;(3)观察图2,可以发现代数式2a2+5ab+2b2可以因式分解为2a2+5ab+2b2=(2a+b)(a+2b);(4)通过不同的方法表示同一个几何体的体积,也可以探求相应的因式分解等式.如图3是棱长为(a+b)的正方体,被如图所示的分割线分成8块.①用不同方法计算这个正方体体积,就可以得到一个因式分解的等式,这个等式是:a3+b3+3a2b+3ab2=(a+b)3;②已知a+b=5,ab=2,利用上面的规律求a3+b3的值.【分析】(1)用两种方法表示同一个图形面积即可.(2)用两种方法表示同一个图形面积即可.(3)用两种方法表示同一个图形面积即可.(4)①用两种方法表示同一个立体图形体积即可.②将a3+b3用a+b,ab表示即可.解:(1)图1中大正方形的面积为:a2+b2+2ab.又可以表示为:(a+b)2.故答案为:a2+b2+2ab.(a+b)2.(2)由题意得:a2+b2+2ab=(a+b)2.故答案为:a2+b2+2ab=(a+b)2.(3)观察图形2,该图形的面积还可以表示为:(2a+b)(a+2b)∴2a2+5ab+2b2=(2a+b)(a+2b).故答案为:2a2+5ab+2b2=(2a+b)(a+2b).(4)①正方体的体积可以表示为;(a+b)3,又可以表示为:a3+b3+3a2b+3ab2.∴a3+b3+3a2b+3ab2=(a+b)3.②∵a+b=5,ab=2.∴a3+b3=(a+b)3﹣3a2b﹣3ab2=125﹣3ab(a+b)=125﹣30=95.27.【问题背景】如图1,等腰直角△ABC中,AB=AC,∠BAC=90°,则边BC与边AB的数量关系为BC=AB.(1)如图2,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则得到边BC与边AB的数量关系为BC=AB.【迁移应用】(2)如图3,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,①求证:△ADB≌△AEC.②求AD、BD、CD之间的数量关系.【拓展延伸】(3)如图4,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=6,连接BD并延长,交AC于点F.若∠CBF=15°,∠BAD=30°,则四边形AEFD的面积为9+9.【分析】(1)由等腰三角形的性质可得∠B=∠C=30°,BD=CD=BC,由直角三角形的性质可得AB=2AD,BD=AD,可得结论;(2)①由“SAS”可证△ADB≌△AEC;②由全等三角形的性质可得BD=EC,由(1)可知:DE=AD,即可得结论;(3)由直角三角形的性质先求出AF,EH的长,再由面积和差关系可求解.解:(1)BC=AB,理由如下:∵AB=AC,∠BAC=120°,AD⊥BC,∴∠B=∠C=30°,BD=CD=BC,∴AB=2AD,BD=AD,∴BC=2AD,∴BC=AB;(2)①∵∠BAC=∠DAE=120°,∴∠DAB=∠CAE,在△ADB和△AEC中,,∴△ADB≌△AEC(SAS);②DC=BD+AD,理由如下:∵△ADB≌△AEC,∴BD=EC,由(1)可知:DE=AD,∵DC=DE+EC,∴DC=BD+AD;(3)如图4,过点E作EH⊥AC于H,连接EF,∵△ABC是等腰直角三角形,∴AB=AC=6,∠ABC=∠ACB=45°,∵∠CBF=15°,∴∠ABD=30°,又∵∠BAD=30°,∴∠ABD=∠BAD,∠DAF=∠AFD=60°,∴AD=BD,△ADF是等边三角形,∴AD=BD=DF=AF,∵∠ABD=30°,∠BAC=90°,∴BA=AF=6,∴AF=6=AD=BD=DF,∵∠DAE=90°,AD=AE,∴AE=6,∠FAE=30°,∵EH⊥AC,∴EH=AE=3,∵四边形AEFD的面积=S△ADF+S△AEF=S△BAF+S△AEF=××6×6+×6×3=9+9,故答案为:9+9.。
2020-2021学年山东省济南市高新区八年级(上)期中数学试卷(含解析)

2020-2021学年山东省济南市高新区八年级第一学期期中数学试卷一、选择题(共12小题).1.16的算术平方根是()A.﹣4B.±4C.4D.2562.若电影院中“5排8号”的位置,记作(5,8),丽丽的电影票是“3排1号”.则下列有序数对表示丽丽在电影院位置正确的是()A.(3,1)B.(1,3)C.(13,31)D.(31,13)3.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是()A.物体B.速度C.时间D.空气4.下列各组数中是方程x+2y=17的解的是()A.B.C.D.5.下列各式中,是最简二次根式的是()A.B.C.D.6.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y 轴翻折到第一象限,则点C的对应点C′的坐标是()A.(3,1)B.(﹣3,﹣1)C.(1,﹣3)D.(3,﹣1)7.方程组的解为,则被遮盖的前后两个数分别为()A.1、2B.1、5C.5、1D.2、48.已知点(m,n)在第二象限,则直线y=nx+m图象大致是下列的()A.B.C.D.9.点A在数轴上表示的数为﹣,点B在数轴上表示的数为,则A、B之间表示整数的点有()A.5个B.6个C.7个D.8个10.正比例函数y=kx,当x每增加3时,y就减小2,则k的值为()A.B.C.D.﹣11.A,B两地相距30km,甲乙两人沿同一条路线从A地到B地.如图,反映的是两人行进路程y(km)与行进时间t(h)之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有()A.1个B.2个C.3个D.4个12.已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为()A.B.C.D.(1,0)二、填空题(共6小题).13.将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是.14.化简:=.15.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行使过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:t(小时)0123y(升)100928476由表格中y与t的关系可知,当汽车行驶小时,油箱的余油量为40升.16.若|a+b﹣1|+(a﹣b+3)2=0,则a2﹣b2=.17.如图,一次函数y=kx+b的图象经过A(1,2),B(0,1)两点,与x轴交于点C,则△AOC的面积为.18.如图,直线L:y=﹣x+1分别与x、y轴交于M、N两点,若在x轴上存在一点P,使△PMN是以MN为底的等腰三角形,则点P的坐标是.三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(6分)计算:.20.(6分)计算:()()+()2.21.(6分)解方程组:.22.(8分)同学们,学习了无理数之后,我们已经把数的领域扩大到了实数的范围,下面让我们在几个具体的图形中认识一下无理数.(1)如图1,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点P(开始滚动时与点O重合)由原点到达点O′,则OO′的长度就等于圆的周长π,所以数轴上点O′代表的实数就是,它是一个无理数.(2)如图2,在Rt△ABC中,∠C=90°,AC=2,BC=1,根据勾股定理可求得AB =.(3)你能在6×8的网格图中(每个小正方形边长均为1),画出一条长为的格点线段吗?(4)请你在数轴上找到表示﹣的点.23.(8分)先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,形如,如果你能找到两个数m、n,使m2+n2=a,且mn=,则可变形为==|m ±n|,从而达到化去一层根号的目的.例如:====|1﹣|=﹣1仿照上例完成下面各题:①填上适当的数:===||=;②试将化简.24.(10分)如图,已知直线l经过点A(0,﹣1)与点P(2,3).(1)求直线l的表达式;(2)若在y轴上有一点B,使△APB的面积为5,求点B的坐标.25.(10分)某边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.(1)求l1、l2的函数解析式;(2)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A 逃入公海前将其拦截?若能,请求出此时B离海岸的距离:若不能,请说明理由.26.(12分)【定义】若线段AB上所有的点到x轴的距离最大值为W,W就叫线段AB的界值,记作W AB.【理解】如图1,线段AB上所有的点到x轴的最大距离是3,则线段AB的界值W AB=3.【应用】(1)如图2,A(﹣1,﹣3),B(2,﹣1),C(﹣1,1),①w AB=.②平移线段AB,使点A与点C重合,平移后线段的界值w为;【拓展】(2)如图3,A(﹣3,﹣7),B(1,﹣3),将线段AB向上平移m(m>0)个单位长度到线段CD.①当5≤m≤6时,则W CD的取值范围为;②当m>5时,用含m的式子表示W CD;③当3≤W CD≤4时,求m的取值范围.27.(12分)平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于点B、A.(1)点C与点A关于x轴对称,求点C坐标和直线BC的解析式;(2)在(1)的条件下,如图1,直线BC与直线y=﹣x交于E点,点P为y轴上一点,PE=PB,求P点坐标;(3)在(1)的条件下,如图2,点P为y轴上一点,∠OEB=∠PEA,直线EP与直线AB交于点M,求M点的坐标.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.16的算术平方根是()A.﹣4B.±4C.4D.256解:16的算术平方根是:=4.故选:C.2.若电影院中“5排8号”的位置,记作(5,8),丽丽的电影票是“3排1号”.则下列有序数对表示丽丽在电影院位置正确的是()A.(3,1)B.(1,3)C.(13,31)D.(31,13)解:∵“5排8号”的位置,记作(5,8),∴丽丽的电影票是“3排1号”,记作(3,1).故选:A.3.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是()A.物体B.速度C.时间D.空气解:因为速度随时间的变化而变化,故时间是自变量,速度是因变量,即速度是时间的函数.故选:C.4.下列各组数中是方程x+2y=17的解的是()A.B.C.D.解:A、代入方程,得左边=1+14=15≠右边,不是方程的解;B、代入方程,得左边=6+10=16≠右边,不是方程的解;C、代入方程,得左边=﹣3+20=17=右边,是方程的解;D、代入方程,得左边=36﹣20=16≠右边,不是方程的解.故选:C.5.下列各式中,是最简二次根式的是()A.B.C.D.解:A、=,被开方数含分母,不是最简二次根式;B、==3,被开方数中含能开得尽方的因数,不是最简二次根式;C、是最简二次根式;D、==,被开方数含分母,不是最简二次根式;故选:C.6.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y 轴翻折到第一象限,则点C的对应点C′的坐标是()A.(3,1)B.(﹣3,﹣1)C.(1,﹣3)D.(3,﹣1)解:由A点坐标,得C(﹣3,1).由翻折,得C′与C关于y轴对称,C′(3,1).故选:A.7.方程组的解为,则被遮盖的前后两个数分别为()A.1、2B.1、5C.5、1D.2、4解:将x=2代入第二个方程可得y=1,将x=2,y=1代入第一个方程可得2x+y=5∴被遮盖的前后两个数分别为:5,1故选:C.8.已知点(m,n)在第二象限,则直线y=nx+m图象大致是下列的()A.B.C.D.解:∵点(m,n)在第二象限,∴m<0,n>0,∴直线y=nx+m在一、三、四象限.故选:A.9.点A在数轴上表示的数为﹣,点B在数轴上表示的数为,则A、B之间表示整数的点有()A.5个B.6个C.7个D.8个解:因为<<,所以3<<4,所以﹣4<﹣<﹣3,又因为2<<3,所以A、B之间的整数有﹣3,﹣2,﹣1,0,1,2,故选:B.10.正比例函数y=kx,当x每增加3时,y就减小2,则k的值为()A.B.C.D.﹣解:根据题意得y﹣2=k(x+3),y﹣2=kx+3k,而y=kx,所以3k=﹣2,解得k=﹣.故选:D.11.A,B两地相距30km,甲乙两人沿同一条路线从A地到B地.如图,反映的是两人行进路程y(km)与行进时间t(h)之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有()A.1个B.2个C.3个D.4个解:由图象可得,甲始终是匀速行进,乙的行进不是匀速的,故①正确;乙用了5﹣0.5=4.5个小时到达目的地,故②错误;乙比甲迟出发0.5小时,故③正确;甲在出发不到5小时后被乙追上,故④错误;故选:B.12.已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为()A.B.C.D.(1,0)解:作A关于x轴对称点C,连接BC并延长交x轴于点P,∵A(1,1),∴C的坐标为(1,﹣1),连接BC,设直线BC的解析式为:y=kx+b,∴,解得:,∴直线BC的解析式为:y=﹣2x+1,当y=0时,x=,∴点P的坐标为:(,0),∵当B,C,P不共线时,根据三角形三边的关系可得:|PA﹣PB|=|PC﹣PB|<BC,∴此时|PA﹣PB|=|PC﹣PB|=BC取得最大值.故选:A.二、填空题:(本大题共6个小题,每小题4分,共24分)13.将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是(3,2).解:将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是(1+2,2)即(3,2),故答案为:(3,2).14.化简:=3.解:原式===3.故答案为:3.15.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行使过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:t(小时)0123y(升)100928476由表格中y与t的关系可知,当汽车行驶7.5小时,油箱的余油量为40升.解:由题意可得:y=100﹣8t,当y=40时,40=100﹣8t解得:t=7.5.故答案为:7.5.16.若|a+b﹣1|+(a﹣b+3)2=0,则a2﹣b2=﹣3.解:由题意可知:,解得:,∴a2﹣b2=(﹣1)2﹣22=﹣3.故答案为:﹣3.17.如图,一次函数y=kx+b的图象经过A(1,2),B(0,1)两点,与x轴交于点C,则△AOC的面积为1.解:将A(1,2),B(0,1)代入y=kx+b,得:,解得:,∴直线AB的解析式为y=x+1.当y=0时,x+1=0,解得:x=﹣1,∴点C的坐标为(﹣1,0),OC=1,∴S△AOC=OC•y A=×1×2=1.故答案为:1.18.如图,直线L:y=﹣x+1分别与x、y轴交于M、N两点,若在x轴上存在一点P,使△PMN是以MN为底的等腰三角形,则点P的坐标是(,0).解:∵直线L:y=﹣x+1分别与x、y轴交于M、N两点,∴令y=0,求得x=2,令x=0,求得y=1,∴M(2,0),N(0,1),∴MN==,作MN的垂直平分线PQ,交x轴于P,交MN于Q,则△PMN是以MN为底的等腰三角形,∴QM=,∵∠OMN=∠QMP,∠MON=∠PQM=90°,∴△PQM∽△NOM,∴=,即=,∴PM=,∴OP=2﹣=,∴P(,0),故答案为(,0).三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(6分)计算:.解:原式=﹣3+2+2=3﹣.20.(6分)计算:()()+()2.解:原式=3﹣2+3+2+2=6+2.21.(6分)解方程组:.解:原方程组为,①×5+②,得13x=26,∴x=2.将x=2代入①,得y=﹣1.∴原方程组的解为.22.(8分)同学们,学习了无理数之后,我们已经把数的领域扩大到了实数的范围,下面让我们在几个具体的图形中认识一下无理数.(1)如图1,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点P(开始滚动时与点O重合)由原点到达点O′,则OO′的长度就等于圆的周长π,所以数轴上点O′代表的实数就是π,它是一个无理数.(2)如图2,在Rt△ABC中,∠C=90°,AC=2,BC=1,根据勾股定理可求得AB=.(3)你能在6×8的网格图中(每个小正方形边长均为1),画出一条长为的格点线段吗?(4)请你在数轴上找到表示﹣的点.解:(1)OO′=π•1=π,故答案为:π.(2)∵∠C=90°,AC=2,BC=1,∴AB===.故答案为:.(3)如图,线段AB就是要画一条长为的线段.②如图,点A即为所求.23.(8分)先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,形如,如果你能找到两个数m、n,使m2+n2=a,且mn=,则可变形为==|m ±n|,从而达到化去一层根号的目的.例如:====|1﹣|=﹣1仿照上例完成下面各题:①填上适当的数:===|﹣|=﹣;②试将化简.解:①===|﹣|=﹣;故答案为:﹣;﹣;②原式==+.24.(10分)如图,已知直线l经过点A(0,﹣1)与点P(2,3).(1)求直线l的表达式;(2)若在y轴上有一点B,使△APB的面积为5,求点B的坐标.解:(1)设直线l表达式为y=kx+b(k,b为常数且k≠0),把A(0,﹣1),P(2,3)代入得:,解得:,则直线l表达式为y=2x﹣1;(2)设B坐标为(0,m),则AB=|1+m|,∵△APB的面积为5,∴AB•x P横坐标=5,即|1+m|×2=5,整理得:|1+m|=5,即1+m=5或1+m=﹣5,解得:m=4或m=﹣6,则B坐标为(0,4)或(0,﹣6).25.(10分)某边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.(1)求l1、l2的函数解析式;(2)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A 逃入公海前将其拦截?若能,请求出此时B离海岸的距离:若不能,请说明理由.解:(1)设l1的函数解析式是s=kt,10k=5,得k=0.5,即l1的函数解析式是s=0.5t,设l2的函数解析式时s=at+b,,得,即l2的函数解析式是s=0.2t+5;(2),得,∵<12,∴B能追上A,答:B能在A逃入公海前将其拦截,此时B离海岸的距离是海里.26.(12分)【定义】若线段AB上所有的点到x轴的距离最大值为W,W就叫线段AB的界值,记作W AB.【理解】如图1,线段AB上所有的点到x轴的最大距离是3,则线段AB的界值W AB=3.【应用】(1)如图2,A(﹣1,﹣3),B(2,﹣1),C(﹣1,1),①w AB=3.②平移线段AB,使点A与点C重合,平移后线段的界值w为3;【拓展】(2)如图3,A(﹣3,﹣7),B(1,﹣3),将线段AB向上平移m(m>0)个单位长度到线段CD.①当5≤m≤6时,则W CD的取值范围为2≤W CD≤3;②当m>5时,用含m的式子表示W CD;③当3≤W CD≤4时,求m的取值范围.解:【应用】(1)①如图2,∵A(﹣1,﹣3),B(2,﹣1),C(﹣1,1),而3>1,∴w AB=3.故答案为:3;②∵平移线段AB,使点A(﹣1,﹣3)与点C(﹣1,1)重合,∴平移规律是:向上平移4个单位长度,∴B(2,﹣1)的对应点为(2,3),∴平移后线段的界值w为3.故答案为:3;【拓展】(2)如图3,A(﹣3,﹣7),B(1,﹣3),将线段AB向上平移m(m>0)个单位长度到线段CD.假设点A与点C重合,点B与点D重合,则C(﹣3,﹣7+m),D(1,﹣3+m).①∵5≤m≤6,∴﹣2≤﹣7+m≤﹣1,2≤﹣3+m≤3,∴W CD的取值范围为2≤W CD≤3.故答案为:2≤W CD≤3;②∵m>5,∴﹣7+m>﹣2,﹣3+m>2,∴W CD=﹣3+m;③当3≤W CD≤4时,如图,m的取值范围是3≤m≤4或6≤m≤7.27.(12分)平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于点B、A.(1)点C与点A关于x轴对称,求点C坐标和直线BC的解析式;(2)在(1)的条件下,如图1,直线BC与直线y=﹣x交于E点,点P为y轴上一点,PE=PB,求P点坐标;(3)在(1)的条件下,如图2,点P为y轴上一点,∠OEB=∠PEA,直线EP与直线AB交于点M,求M点的坐标.解:(1)∵直线y=2x+4①与x轴、y轴分别交于点B、A.∴A(0,4),B(﹣2,0),∵直线AB与直线BC关于x轴对称,∴C(0,﹣4),设直线BC的解析式为y=kx+b,则,解得,∴直线BC的解析式为y=﹣2x﹣4②;(2)将②与y=﹣x联立并解得,∴E(﹣4,4),∴AE⊥AO,设OP=a,AP=4﹣a,在Rt△BOP和Rt△EAP中,BP2=4+a2,PE2=16+(4﹣a)2,∵PE=PB,∴4+a2=16+(4﹣a)2,解得a=3.5.∴P(0,3.5);(3)①如图,当点P在点A的下方,∵∠OEB=∠PEA,∠AEO=45°,∴∠PEB=45°,过点B作BN⊥BE交直线EP于点N,过点N作NQ⊥OB于Q,过点E作EH⊥OB于点H,∴△EBN为等腰直角三角形,∴EB=BN,∵∠BEH+∠EBH=90°,∠EBH+∠NBQ=90°,∴∠BEH=∠NBQ,又∵∠EHB=∠BQN=90°,∴△EHB≌△BQN(AAS),∴NQ=BH=2,BQ=EH=4,∴N(2,2),由点E、N的坐标得,直线EN的表达式为y=﹣x+③,联立①③并解得,即M(﹣,);②P点在A点的上方,由①知,直线EN的表达式为y=﹣x+,令x=0,则y=,故OP=,则AP=,∴OP=,则点P(0,),由点E、P的坐标得,直线EP的解析式为y=x+④,联立①④并解得,∴M(0.8,5.6).综合以上可得点M的坐标为(﹣,)或(0.8,5.6).。
山东省青岛市青大附中八年级2020-2021学年第一学期期中考试数学试题(pdf版,有答案)
2020-2021学年度第一学期期中质量检测八年级数学试题(满分:120分时间:120分)一、选择题(本大题共8个小题,每题只有一个正确答案,每题3分,共24分)1.9的算术平方根是( )A.3B.3C.±3D.± 32.给出下列四个说法:①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;④三个整数a,b,C是直角三角形的三边长,则2a,2b,2c一定是勾股数,其中正确的是( )A.①②B.②③C.③④D.①④3.下列各式:①2,②13,③8,④27片中,最简二次根式有( )A.1个B.2个C.3个D.4个4.昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭,文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑。
如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(-1,2),则表示弘文阁所在的点的坐标为( )A.(-2,-3)B.(-2,-2)C.(-3,-3)D.(-3,-4) 5.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( )6.如图,已知圆柱的底面直径BC=(),高AB=3,小虫在圆柱表面爬行,从C 点爬到A 点,然后再沿另一面爬回C 点,则小虫爬行的最短路程为( )A.32B.35C.65D.627.如果 2.37-≈1.333,23.7-≈2.872,那么2370-约等于( ) A. 28.72 B. 0.2872 C. 13.33 D. 0.13338.一次函数y1=k1x+a和y2=k2x+b的图象如图所示,下列结论正确的有( )①a>0; ②y1随x的增大而减小;③k1>k2; ④当x<3时,y1<y2 .A.1个B.2个C.3个D.4个二、填空题(本大题共8个小题,每题3分,共24分)9.在平面直角坐标系内,点M(-9,12)到x轴的距离是 .10.在△ABC中,给出以下4个条件:①∠C=90°;②∠A+∠B=∠C;③a:b:c=3:4:5;④∠A:∠B:∠C=3:4:5;从中任取一个条件,可以判定出△ABC是直角三角形的有 .(填序号)11.如果一个整数a的平方根是3x-2和5x+6,则a= .12.如图,AD=1,点A,B在数轴上,点A表示-1,点B表示2,者以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M表示的数为 .第12题图 第13题图13.如图,矩形ABCD中,AB=6,BC=8,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积是 .14.在平面直角坐标系中,直线y=2x-2不动,将坐标系向上平移了3个单位长度后得到新的平面直角坐标系,此时该直线对应的函数关系式为 .15.课间,小聪拿老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度(每块砖的厚度相等)为 cm.第15题图 第16题图16.如图,在直角坐标系中,已知点P0的坐标为(2,2),将线段OP0按逆时针方向旋转45°,再将其长度伸长为0P0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OP n(n为正整数),则点P2021的坐标为 .三、作图题(本大题满分6分)17.如图,△ABC在直角坐标系内的位置如图,且C点坐标是(-2,1).(1)则点A的坐标 和点B的坐标 ;(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称;(3)请直接写出△A1B1C1的面积.四、解答题(本大题共7个小题,满分66分) 18.计算题(本小题共四个小题,每题4分,共16分)(1)32+312−2 (2)34×678−42(3)(5−3)7+(11+3)(11−3) (4)26+12×3−121219.(本小题满分6分)已知如图,四边形ABCD 中,∠B=90°,AB=B,BC=6,CD=24,AD=26,求这个四边形的面积.20.(本小题满分6分)观察下列各式:①f(1)=2−12;②f(2)= 3−22;③f(3)= 2−32;④f(4)= 5−22;… 回答下列问题:(1)利用你观察到的规律直接写出f(n)= ; (2)计算(22018+2)[f 1+f 2+f 3+⋯+f 2017].21.(本小题满分8分)在平面直角坐标系中,有A(-2,a+1),B(a-1,4),C (b-2,b)三点.(1)当点C在y轴上时,求点C的坐标;(2)当AB∥x轴时,求A,B两点间的距离;(3)当CD⊥x轴于点D,且CD=1时,求点C的坐标.22.(本小题满分10分)甲、乙两人相约周末登崂山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且当乙提速后,乙的登山上升速度是甲登山上升速度的3倍,且根据图象所提供的信息解答下列问题:(1)乙在A地时距地面的高度b为 米;t的值为 ;(2)请求出甲在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式;(3)已知AB段对应的函数关系式为y=30x-30,则登山多长时间时,甲、乙两人距地面的高度差为70米?(直接写出答案)23.(本小题满分10分)阅读材料解答问题:自主学习:在平面直角坐标系中,对于任意两点的“非常距离”给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.例如:如图1所示,点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点)问题解决:(1)计算:平面直角坐标系中两点A(-1,0),B(2,3)的“非常距离”.应用拓展:(2)已知点C(67,0),点D为y轴上的一个动点;①若点C与点D的“非常距离”为3,则点D的坐标为 ;②在D点运动过程中,点C与点D的“非常距离”的最小值为 ; 问题延伸:(3)已知:E是直线y=34x+3上的一个动点,如图2,点F的坐标是(0,1),求点E与点F的“非常距离”的最小值及相应点E的坐标.24.(本小题满分10分)如图,在平面直角坐标系中,0为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且∣m−n−3∣+2n−6=0,点P从A出发,以每秒1个单位的速度沿射线A0匀速运动,设点P的运动时间为t秒. (1)求0A、0B的长;(2)连接PB,设△POB的面积为S,用t的式子表示S;(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.2020-2021学年度第一学期期中质量检测八年级数学试题参考答案1 2 3 4 5 6 7 8B C A B B D C B9、12 10、①②③ 11、FGF12、10−113、H3F14、y=2x-5 15、I4I626 16、(0,-22022)17、(1)(0,3)、(-4,4) (2)略 (3)518、(1)G72 (2)62 (3)16−65 (4)619、144 20、(1)f(n)= n+1−n2(2)201721、(1)(0,2) (2)4 (3)(-3,-1)22、(1)30 11 (2)y=10x+100 (3)3 10 1323、(1)3 (2)①(0,3)或(0.-3) ②67(3)8HE(-8H,I3H)24、(1)OA=6,OB=3(2)0≤t≤6时,S=9 - 67t ;t>6时,S=67t - 9(3)存在.t=3或9。
【语文】山东省济南市高新区2023-2024学年八年级上学期期中考试试题(解析版)
C.“何处染嚣尘”用反问手法,抒发诗人超尘脱俗、思归田园的思想感情。
D.全诗采用点面结合、视听结合等手法描写春天,把春意渲染得强烈浓郁。
13.“鸟飞村觉曙,鱼戏水知春”与“几处早莺争暖树,谁家新燕啄春泥”有异曲同工之妙,请分析它们有哪些相似之处。
等到春天和冬天的时候,就可以看见白色的急流回旋着清波,碧绿的潭水倒映着各种景物。极高的山峰上,大多生长着许多奇形怪状的松柏,悬泉瀑布在山峰之间飞流冲荡。水清,树荣,山峻,草盛,的确是趣味无穷。
在秋天,每到天刚放晴的时候或下霜的早晨,树林和山涧显出一片清凉和寂静,经常有猿猴在高处拉长声音鸣叫,声音持续不断,显得非常悲惨凄凉,在空荡的山谷里传来猿叫的回声,声音悲哀婉转,很久才消失。所以三峡中渔民的歌谣唱道:“巴东三峡巫峡长,猿鸣三声泪沾裳。”
B.近年来,济南中央商务区建设取得了重大进展,62座百米以上的高楼鹤立鸡群。
C.他继承了父亲的产业之后,白手起家,驰骋商场,终于有了今日辉煌的成就。
D.无数科学家殚精竭虑,青丝变白发,终于成功破解了这个世界公认的技术难题。
【答案】D
【解析】本题考查成语运用。
A.无所不为:没有不干的事情,指什么坏事都干或干尽了坏事。与句中悄悄修好坏桌椅、悄悄捡起碎纸屑等好行为不符;
故选D。
【2题详解】
本题考查字形。
抑扬顿挫:意思是指声音的大小起伏和停顿转折。
锐不可当:形容勇往直前的气势,不可阻挡。
劳碌:事情多而辛苦。
缅怀:意思是遥念、追思;深情地怀念、追想(已往的人或事)。
故选A。
3.下列句子中加点成语使用恰当的一项是( )
A.有人悄悄修好坏桌椅,有人悄悄捡起碎纸屑,身边的利他之事,同学们无所不为。
2023-2024学年山东省济南市高新区八年级上学期期中考试物理试题
2023-2024学年山东省济南市高新区八年级上学期期中考试物理试题1. 2022年2月15日下午,中国选手苏翊鸣在北京冬奥会单板滑雪男子大跳台决赛中夺冠。
比赛中,他在空中向前运动,如图所示,若认为苏翊鸣是静止的,所选的参照物是()A.场地的跳台B.现场的观众C.自己的头盔D.天上的云朵2.为防止制作油炸食品时烫伤,人们专门制作了如图所示的加长筷子。
根据图片提供的信息,这种筷子的长度最接近()A.B.C.D.3.某同学用同一把刻度尺对同一物体的长度进行了4次测量,结果如下:12.54cm、12.36cm、12.35cm、12.36cm,则该物体的长度应记为()A.12.34cm B.12.35cm C.12.357cm D.12.36cm4.噪声严重影响人们的工作和生活,被称为“隐形杀手”。
控制噪声已成为城市环境保护的重要项目之一。
在医院、学校等部门附近,都有如图所示的标志,以下控制噪声的途径与之相同的是()A.噪声等级显示装置B.摩托车的消声器D.工厂用的防噪声耳C.道路旁的隔声板罩5.如图所示,将正在响铃的手机悬挂于广口瓶内,封闭瓶口,逐渐抽出其中的空气。
对比抽气前后从瓶中传出的响铃声音,下列分析正确的是()A.音调升高B.音调降低C.响度变大D.响度变小6.发生地震时,一些动物能感觉到地震之前发出的声波,而人类虽然会有不同程度的震感却听不到,这是因为地震时发出的次声波()A.响度太小B.频率太低C.传播速度太慢D.具有能量太小7.如图是我国古代的一种计时工具—日晷,通过观察直杆在太阳下影子的位置来计时,这项发明被人类所用达几千年之久。
图中所示情景与日晷工作原理相同的是()A.小孔成像B.水中海岱楼的倒影C.筷子弯折D.雨后彩虹8.如图所示,东南亚地区生活着一种射水鱼,它发现水面上的小昆虫后,能从口中快速喷出一束水柱,将昆虫击落水中,实现捕食.下列光路图能表示射水鱼观察水面上小昆虫的是A.B.C.D.9.“小荷才露尖尖角,早有蜻蜓立上头。
山东省济南市高新区2021-2022学年八年级上学期期中生物试卷
2021-2022学年山东省济南市高新区八年级(上)期中生物试卷1.一朵花中最主要的结构是()A. ①②B. ③⑥C. ⑤⑥D. ④⑤2.将3粒蚕豆种子分别放到盛水烧杯的不同位置,如图所示。
下列分析错误的是()A. 利用该装置可探究水分和空气对种子萌发的影响B. 该装置中①和③可形成一组对照实验,变量是空气C. 该装置中①和②可形成一组对照实验,变量是水D. 该装置中种子数量太少,实验结果的偶然性大3.下列有关生物生殖或发育的叙述,正确的是()A. 利用植物组织培养技术,可以在较短时间内快速培育植物新品种B. 在家蚕的发育过程中,为了提高蚕丝产量,应设法延长蛹时期C. 蚜虫在幼虫期和成虫期对植物都有危害D. 受精的鸟卵由母体产出后,需要经过亲鸟的孵化才开始发育4.如图为植物的根尖结构示意图,下列叙述错误的是()A. ④是生长最快的部位B. ③的细胞具有很强的分裂增生能力C. ②的细胞停止了分裂,开始迅速伸长D. ①是吸收水分及无机盐的主要部位5.玉米是我国重要粮食作物,如图为玉米的一生示意图,下列相关叙述错误的是()A. 由图甲可知,玉米属于雌雄同株植物B. 在玉米种子的纵切面上滴加碘液,图丙中结构2变蓝C. 图乙中的Ⅰ受精后发育成图丙中的7D. 玉米依靠风力完成自花传粉6.有经验的农民在向日葵的开花季节,要为向日葵“别头”(将两个花盘相对),在西瓜开花时节进行“对花”,这样做的目的是()A. 辅助授粉,提高结实率B. 保护花瓣,以免被风吹落C. 保护花蕊,以免被虫咬D. 保护花粉,防止花粉散落7.若樱桃果皮红色(D)对黄色(d)为显性,现将黄果樱桃(dd)的枝条嫁接到红果樱桃(DD)植株上,嫁接的枝条成活后所结果实的颜色及果皮的基因组成是()A. 红色,DDB. 红色,DdC. 黄色,DdD. 黄色,dd8.下列有关实验描述错误的是()A. 在“观察花的结构”实验中,用显微镜观察雄蕊及雌蕊等内部结构B. 在“观察种子的结构”实验中,用放大镜观察种子中胚的结构C. 在“观察枝芽的结构”实验中选取较大的枝芽,用放大镜观察内部结构D. 在“观察鸡蛋的结构”实验中,用探针小心挑破卵黄膜后,使卵黄流出9.图中植物的繁殖属于有性生殖的是()A. 马铃薯B. 草莓C. 玉米D. 落地生根10.下列哪一成语或诗句描述了昆虫生殖发育过程中的产卵行为()A. 蜻蜓点水B. 金蝉脱壳C. 作茧自缚D. 秋蝉鸣树间11.《红楼梦》中的宝黛爱情悲剧让人唏噓不已,下列有关说法正确的是()A. 如果贾宝玉和林黛玉结婚,他们的后代一定会有遗传疾病B. 如果放到当代,贾宝玉和林黛玉自由恋爱,他们结合符合《婚姻法》C. 正常婚配的夫妇生育出具有遗传病的后代的几率为零D. 禁止近亲结婚主要是为了减少隐性致病基因导致的遗传病12.“黄梅时节家家雨,青草池塘处处蛙”,每年的春末夏初是池塘、河边最热闹的时候,下列说法正确的是()A. 青蛙的个体发育起点为蝌蚪B. 青蛙生殖发育过程中有求偶、抱对等生殖行为C. 两栖动物的生殖和发育可以摆脱对水的依赖D. 既能生活在水中又能生活在陆地上的动物就是两栖动物13.与两栖类动物相比,鸟类繁殖成活率较高,其主要原因是()①体内受精②卵生③卵内有丰富的营养物质④有孵卵与育雏行为⑤卵有卵壳保护⑥卵的数量巨大A. ①②③⑤B. ①②③⑥C. ①③④⑤D. ②④⑤⑥14.如图是某地男女生身高增长速度曲线图,据图分析,下列选项正确的是()A. 身高突增是青春期形态发育的显著特点之一B. 男孩的身高增长速度总是比女孩快C. 女孩的身高开始突增的年龄比男孩晚1~2年D. 青少年的身高突增只与性激素有关15.下列各项中属于不可遗传变异的是()A. 大蒜在无光条件下,长成蒜黄B. 视觉正常的夫妇生下了患色盲的儿子C. 通过染色体数目改变培育的无子西瓜D. 利用航天技术培育的太空南瓜16.刚孵出的雏鸟分为早成雏和晚成雏,在你熟悉的下列四种鸟中,哪一种是晚成雏()A. .鸡B. 鹅C. 鸵鸟D. 麻雀17.如图是染色体组成示意图,下列相关叙述错误的是()A. 图中①在同种生物的体细胞内数目相同、形态相似B. 图中①的化学成分主要包括②和③C. 图中③是由一条长链盘旋而成的规则的双螺旋结构D. 图中④是与遗传特征相关的片段,叫做基因18.下列选项中,都属于遗传病的是()A. 色盲、佝偻病、坏血病B. 唇裂、血友病、白化病C. 先天性愚型、侏儒症、龋齿D. 艾滋病、巨人症、猫叫综合征19.已知蝉是以植物中的有机物汁液为食的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前
2020至2021学年第一学期期中学业水平测试
高新初中数学八年级试题
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷共2页,满分为48分;第Ⅱ卷共4页,满分为102分.本试题共6页,满分为150分.考试时间为120分钟.答卷前,考生务必用0.5毫米黑色墨水签字笔将自己的考点、姓名、准考证号、座号填写在答题卡上和试卷规定的位置上.考试结束后,将本试卷和答题卡一并交回.本考试不允许使用计算器.
第I卷(选择题共48分)
注意事项:第Ⅰ卷为选择题,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效.一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.16的算术平方根是
A.B.C.4D.256
2.若电影院中“5排8号”的位置,记作,丽丽的电影票是“3排1号”.则下列有序数对表示丽丽在电影院位置正确的是
A.B.C.D.
3.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是
A.物体B.速度C.时间D.空气
4.下列各组数中是方程的解的是
A.B.C.D.
5.下列各式中,是最简二次根式的是
A.B.C.D.
6.如图,的顶点都在正方形网格格点上,点的坐标为.将沿轴翻
折到第一象限,则点的对应点的坐标是
A.B.
C.D.
7.方程组的解为,则被遮盖的前后两个数分别为
A.1、2B.2、3C.5、1D.2、4
8.已知点在第二象限,则直线图象大致是下列的
A.B.C.D.
9.点在数轴上表示的数为,点在数轴上表示的数为,则、之间表示整数的点有
A.5个B.6个C.7个D.8个
10.正比例函数,当每增加3时,就减小2,则的值为
A.B.C.D.
11.,两地相距,甲乙两人沿同一条路线从地到地.如图,反映的是两人行进路程与行进时间之间的关系,
①甲始终是匀速行进,乙的行进不是匀速的;
②乙用了5个小时到达目的地;
③乙比甲迟出发0.5小时;
④甲在出发5小时后被乙追上.
以上说法正确的个数有
A.1个B.2个
C.3个D.4个
12.已知,如图点,,点为轴上一点,当最大时,点的坐
标为
A.B.
C.D.
第Ⅱ卷(非选择题共102分)
注意事项:
1.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
2.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤.
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13.将一点向右平移2个单位得到一个对应点,则点的坐标是.
14.化简:.
15.某汽车生产厂对其生产的型汽车进行油耗试验,试验中汽车为匀速行驶,在行使过程中,油箱的余油量
...(升与行驶时间(小时)之间的关系如下表:(小时)0123
(升100928476
由表格中与的关系可知,当汽车行驶小时,油箱的余油量为40升.
16.若,则.
17.如图,一次函数的图象经过,两点,与轴交于点,则
的面积为.
第17题图第18题图18.如图,直线L:y=−12x+1分别与x、y轴交于M、N两点,若在x轴上存在一点P,使△PMN是以MN为底的等腰三角形,则点P的坐标是.
三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(本题6分)计算:.
20.(本题6分)计算:
21.(本题6分)解方程组:
22.(本题8分)同学们,学习了无理数之后,我们已经把数的领域扩大到了实数的范围,下面让我们在几个具体的图形中认识一下无理数.
(1)如图1,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点(开
始滚动时与点重合)由原点到达点,则的长度就等于圆的周长,所以数轴
上点代表的实数就是,它是一个无理数.
图1图2
(2)如图2,在中,,,,根据勾股定理可求得.
(3)你能在的网格图中(每个小正方形边长均为,画出一条长为的格点线段
吗?
(4)请你在数轴上找到表示的点.
23.(本题8分)先阅读下列材料,再解决问题:
阅读材料:数学上有一种根号内又带根号的数,形如,如果你能找到两个数、
,使,且,则可变形为,从而达到化去一层根号的目的.
例如:
仿照上例完成下面各题:
①填上适当的数:
=
②试将化简.
24.(本题10分)如图,已知直线经过点与点.
(1)求直线的表达式;
(2)若在轴上有一点,使的面积为5,求点的坐标.
25.(本题10分)某边防局接到情报,近海处有一可疑船只正向公海方向行驶,边防局迅速派出快艇追赶(如图.图2中、分别表示两船相对于海岸的距离(海里)
与追赶时间(分之间的关系.
(1)求、的函数解析式;
(2)当逃到离海岸12海里的公海时,将无法对其进行检查.照此速度,能否在
逃入公海前将其拦截?若能,请求出此时离海岸的距离:若不能,请说明理由.
26.(本题12分)
【定义】
若线段上所有的点到轴的距离最大值为,就叫线段的界值,记作.
【理解】
如图1,线段上所有的点到轴的最大距离是3,则线段的界值.
【应用】
(1)如图2,,,,
①.
②平移线段,使点与点重合,平移后线段的界值为;
【拓展】
(2)如图3,,,将线段向上平移个单位长度到线段.
①当时,则的取值范围为;
②当时,用含的式子表示;
③当时,求的取值范围.
27.(本题12分)平面直角坐标系中,直线与轴、轴分别交于点、.
(1)点C与点A关于轴对称,求点C坐标和直线的解析式;
(2)如图1,直线与直线交于点,点为轴上一点,,求点坐
标;
(3)如图2,点为轴上一点,,直线与直线交于点,求
点的坐标.。
