小学几何图形基本概念及计算公式
几何图形计算公式大全

几何图形计算公式大全在几何学中,几何图形的计算公式是非常重要的,它们可以帮助我们计算图形的各种属性,比如面积、周长、体积等。
本文将为大家整理几何图形的计算公式大全,希望能对大家的学习和工作有所帮助。
一、基本图形的计算公式。
1. 正方形,正方形的面积计算公式为,A = a²,其中a为正方形的边长;周长计算公式为,P = 4a。
2. 长方形,长方形的面积计算公式为,A = l w,其中l为长,w为宽;周长计算公式为,P = 2(l + w)。
3. 圆形,圆的面积计算公式为,A = πr²,其中π为圆周率,r为圆的半径;周长计算公式为,C = 2πr。
4. 三角形,三角形的面积计算公式为,A = 1/2 b h,其中b为底边长,h为高;周长计算公式为,P = a + b + c。
5. 正方体,正方体的体积计算公式为,V = a³,其中a为边长;表面积计算公式为,S = 6a²。
二、特殊图形的计算公式。
1. 梯形,梯形的面积计算公式为,A = 1/2 (a + b) h,其中a和b为上下底长,h为高;周长计算公式为,P = a + b + c + d。
2. 圆柱,圆柱的体积计算公式为,V = πr²h,其中r为底面半径,h为高;表面积计算公式为,S = 2πr² + 2πrh。
3. 锥形,锥形的体积计算公式为,V = 1/3 πr²h,其中r为底面半径,h为高;表面积计算公式为,S = πr² + πrl,其中l为斜高。
4. 球体,球体的体积计算公式为,V = 4/3 πr³,其中r为半径;表面积计算公式为,S = 4πr²。
三、复合图形的计算公式。
1. 复合图形的面积计算公式,首先将复合图形分解为基本图形,然后分别计算各个基本图形的面积,最后将各个基本图形的面积相加即可得到复合图形的总面积。
2. 复合图形的周长计算公式,同样的方法,将复合图形分解为基本图形,然后分别计算各个基本图形的周长,最后将各个基本图形的周长相加即可得到复合图形的总周长。
《小学数学公式定律大全》
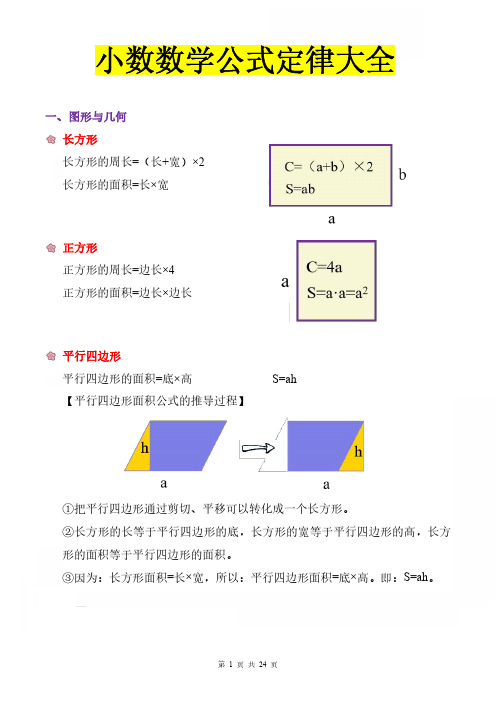
小数数学公式定律大全一、图形与几何长方形长方形的周长=(长+宽)×2长方形的面积=长×宽正方形正方形的周长=边长×4正方形的面积=边长×边长平行四边形平行四边形的面积=底×高S=ah【平行四边形面积公式的推导过程】①把平行四边形通过剪切、平移可以转化成一个长方形。
②长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,长方形的面积等于平行四边形的面积。
③因为:长方形面积=长×宽,所以:平行四边形面积=底×高。
即:S=ah。
三角形三角形的面积=底×高÷2S=ah÷2三角形的内角和=180度=180°【三角形面积公式的推导过程】①用两个完全一样的三角形可以拼成一个平行四边形。
②平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,三角形面积等于和它等底等高的平行四边形面积的一半③因为:平行四边形面积=底×高,所以:三角形面积=底×高÷2。
即:S=ah÷2。
梯形梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2【梯形面积公式的推导过程】①用两个完全一样的梯形可以拼成一个平行四边形。
②平行四边形的底等于梯形的上底和下底的和,平行四边形的高等于梯形的高,梯形面积等于平行四边形面积的一半。
③因为:平行四边形面积=底×高,所以:梯形面积=(上底+下底)×高÷2。
即:S=(a+b)h÷2。
圆直径=半径×2d=2r半径=直径÷2r=d÷2圆的周长=圆周率×直径=圆周率×半径×2C=πd=2πr圆的面积=圆周率×半径×半径S=πrr=πr2【画图说明圆面积公式的推导过程】分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
几何中的立体图形基本概念

几何中的立体图形基本概念一、立体图形的定义与分类1.定义:立体图形是三维空间中的图形,具有长度、宽度和高度。
a)立体几何图形的分类:锥体、柱体、球体、平面立体图形等。
b)根据表面特征分类:直纹立体图形、曲面立体图形等。
二、常见立体图形的基本性质与特征a)定义:底面为平面,顶点在底面上的图形。
i)圆锥:底面为圆,侧面为曲面。
ii)棱锥:底面为多边形,侧面为三角形。
iii)所有锥体的侧面积相等。
iv)锥体的体积与底面半径和高度有关。
b)定义:底面为平行四边形的立体图形。
c)分类:棱柱、圆柱等。
i)柱体的底面积相等。
ii)柱体的体积与底面积和高度有关。
d)定义:所有点与中心点距离相等的立体图形。
πR³。
i)球体的表面积和体积公式为:S=4πR²,V=43ii)球体的直径等于两倍的半径。
4.平面立体图形:a)定义:由平面图形旋转而成的立体图形。
b)分类:圆柱、圆锥、棱柱等。
c)性质:平面立体图形的表面积和体积与平面图形的性质有关。
三、立体图形的计算方法a)圆锥体积公式:V=1πR²h。
3b)棱锥体积公式:V=13Bh ,其中B 为底面积。
c)棱柱体积公式:V=Bh ,其中B 为底面积。
d)圆柱体积公式:V=πR²h 。
e)体积公式:V=43πR³。
f) 表面积公式:S=4πR²。
四、立体图形的实际应用a)应用:漏斗、沙堆等。
b)应用:柱子、烟囱等。
c)应用:球体、地球等。
4. 平面立体图形:a) 应用:各种容器、家具等。
通过以上知识点的学习,学生可以对几何中的立体图形有更深入的了解,并能够运用所学知识解决实际问题。
习题及方法:1.习题:计算一个底面半径为3cm ,高为4cm 的圆锥体的体积。
答案:V=13πR²h=13π×3²×4=12πcm³解题思路:根据圆锥体的体积公式V=13πR²h ,将给定的数值代入公式计算。
几何——第一讲 几何基本概念与简单图形
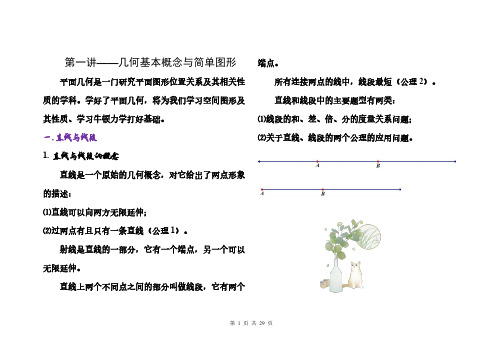
(2)点 A、B 在直线 m 同侧:
第 4 页 共 29 页
(3)两个点都在内侧:
形式二:已知点 A 位于直线 m、n 的内侧, 在直线 m、n 上分别求点 P、Q,使得三角形 APQ 的周长最短。
3. 台球两次碰壁模型 形式一:已知点 A、B 位于直线 m、n 的内侧,在
直线 n、m 上分别求点 D、E 点,使得围成的四边形 ADEB 的周长最短。
果它们有一个公共点,我们就说他们相交,它们是相交 直线,这个公共点叫做它们的交点。
相交关系中最重要的是垂直相交,与垂直有关的知 识,有以下两个重要的结论: ⑴过一点有且仅有一条直线与已知直线垂直; ⑵直线外一点与直线上各点连结的所有线段中,垂线段 最短。
两条直线相交,可形成两组对顶角,它们分别相等, 也可以形成邻补角,即一条直线与端点在这条直线上的 一条射线组成的两个角。也就是说,邻补角是具有特殊 位置关系的两个互补角,一个角的邻补角有且只有两个。
如果两个角的和是一个平角,这两个角叫做互为补角; 如图(b): BDC ABD A ACD
如果两个角的和是一个直角,这两个角叫做互为余角。
第 8 页 共 29 页
⑶“8 字形”模型 如图(c): A B C D
⑷“内角平分线”模型 点 P 是 ABC 和 ACB 的角平分线的交点。 如图(d): BPC 90 1 A
第 20 页 共 29 页
四、面积初步
由于多边形可以分割成若干个三角形,所以多边形
在中学数学里,面积是非常重要的内容,除简单的 的面积可转化为三角形面积来研究。
面积计算外,还要学会使用“等积变换”的思想方法来处
关于三角形的面积,有以下几个重要性质:
理几何问题。
⑴等底等高的两个三角形面积相等;
图形与几何的知识点

图形与几何的知识点在数学中,图形与几何是一门重要的学科。
它涉及到平面图形和立体图形的性质、分类以及相关的计算方法。
本文将详细介绍一些图形与几何的知识点。
一、二维图形1. 点、线、面在几何中,点是最基本的图形,它没有大小和维度,只有位置。
线由无数个点连接而成,它有长度但没有宽度。
面是由无数个线组成的,具有长度和宽度。
2. 常见的平面图形- 线段:两个点之间的部分。
线段的长度可以通过两个点的坐标计算得出。
- 直线:无数个点连成的一条无限延伸的线段。
- 射线:有一个起点,无限延伸的线段。
- 角:由两条线段的公共起点和终点组成。
角可以根据其度数分为锐角、直角和钝角。
- 三角形:由三条线段组成的图形。
三角形的分类有很多种,如等边三角形、等腰三角形等。
- 四边形:由四条线段组成的图形。
它的种类繁多,如矩形、正方形、长方形等。
3. 图形的周长与面积周长是指封闭图形的边界长度,可以通过将每条边的长度相加得到。
面积是指图形所围成的平坦区域的大小,可以通过相应的公式计算得到。
常见图形的周长和面积计算公式如下:- 线段的长度就是其本身的长度。
- 圆的周长和面积分别由半径决定,周长为2πr,面积为πr²。
- 三角形的面积可以通过底边和高的乘积再除以2得到。
- 矩形的周长为2(a+b),面积为a×b,其中a和b分别为矩形的两条边的长度。
二、三维几何1. 空间几何的基本概念- 点:在三维空间中,点是最基本的图形,具有位置但没有大小。
- 线段:连接两个点的部分,有起点和终点。
- 面:由无数个线段组成,具有长度和宽度。
- 体:由无数个面组成,具有长度、宽度和高度。
2. 常见的立体图形- 球体:由三维空间中所有到一个固定点的距离相等的点组成。
它的表面积公式为4πr²,体积公式为(4/3)πr³,其中r为半径。
- 圆柱体:由两个平行圆面和连接它们的侧面组成。
它的侧面积公式为2πrh,底面积为πr²,体积为πr²h,其中r为底面半径,h为高度。
小学数学认识几何形的菱形

小学数学认识几何形的菱形在小学数学学习中,我们学习了许多形状和图形,其中菱形是一种常见而重要的几何形。
菱形具有特殊的性质和特征,对孩子们的几何认识和思维发展有着重要的影响。
本文将介绍菱形的基本概念、特征及其相关的数学知识。
一、菱形的基本概念菱形是指四边形的一种特殊形式,其定义如下:四边形的四条边相等,对角线互相垂直且互相平分的形状就是菱形。
菱形的定义可以使用下面的公式来表达:ABCD是一个菱形,当且仅当AB=BC=CD=DA,且对角线AC与BD互相垂直且平分。
二、菱形的特征菱形具有一些独特的特征,如下所述:1. 对角线相等:在菱形中,对角线AC与BD相等,即AC=BD,这是菱形的重要性质之一。
2. 对角线垂直:菱形的对角线AC与BD相互垂直,垂直是指两条线段相交时互相成直角。
3. 对角线平分:菱形的对角线AC与BD相互平分,即对角线AC平分BD,对角线BD平分AC。
4. 边长相等:在菱形中,四条边的长度相等,即AB=BC=CD=DA。
由于菱形具有以上特征,学习菱形对于小学生来说非常重要,可以培养他们观察、分析和推理的能力。
三、菱形的相关数学知识菱形作为一种常见的几何形状,与其他几何概念和数学知识有着密切的联系。
以下是菱形相关的数学知识点:1. 菱形的面积:菱形的面积可以通过底和高的乘积来计算。
假设菱形的对角线分别为d1和d2,那么菱形的面积可以计算为面积 = 0.5 * d1 * d2。
2. 菱形的周长:菱形的周长可以通过四条边的长度之和来计算,即周长 = AB + BC + CD + DA。
3. 菱形与平行四边形的关系:菱形可以看作是一种特殊的平行四边形,在平行四边形的基础上,菱形还具有垂直对角线且对角线相等的特点。
4. 菱形的旋转对称性:菱形具有旋转对称性,即通过将菱形绕菱形中心点旋转180度,可以得到完全相同的菱形。
通过学习菱形的相关知识,小学生可以不仅了解菱形的基本概念和特征,还可以将其与其他几何形状进行比较和联系,提高他们的几何思维和推理能力。
几何图形的公式,面积,周长,体积

几何图形的公式,面积,周长,体积几何图形与几何学中的其他概念一样,可以追溯到古希腊。
古希腊学者埃洛克斯(Eudoxus)以及对科学有重大贡献的亚里士多德(Aristotle)都是著名的几何学家。
自古以来,几何图形一直被用来表示几何学中的概念。
几何图形都有其独特的形状,大小或平行性,可以被用来描述空间结构。
在几何图形的概念中,每一种图形都有其公式、面积、周长和体积,这些概念可以被使用来对几何图形做出准确的描述。
公式是描述几何图形形状和大小的方法,许多几何图形有自己的公式,例如三角形的面积公式,或者圆形的周长公式。
公式可以用来计算几何图形的面积,周长或体积。
面积是指几何图形的表面积,它是空间对象的一个基本概念。
它定义为平面上某多边形的内部所包含的单位面积。
计算面积的方法有多种,通常有公式和实际测量,这取决于所使用的几何图形。
周长是指几何图形的轮廓线长度,它也是一个空间对象的基本概念。
周长可以是任何多边形,如矩形、三角形或圆形。
其计算方法也可以有公式或实际测量,具体取决于所使用的几何图形。
体积是指几何图形的实体空间,它是三维空间中的一个重要概念。
体积通常可以通过计算面积乘以深度来计算,其方法同样可以是公式或者实际测量。
从上面可以看出,几何图形有其独特的公式、面积、周长和体积,它们都可以用来对几何图形进行准确的描述。
因此,在学习几何学时,学生必须学会识别和使用几何图形的公式、面积、周长和体积等概念,以便正确进行几何计算和应用。
古希腊学者将几何图形用来描述空间结构,这使得人们可以更好地理解空间中几何概念。
几何学和几何图形之间的关系对许多学科来说至关重要,例如数学、物理、化学和工程学,都使用几何学来提高理解力。
几何图形的公式、面积、周长和体积是几何学中非常重要的概念。
它们可以被用来描述几何图形,在理解和计算几何问题时可以提供重要信息。
几何图形是几何学的基础,它们对每一位学习几何学的人都有重要意义。
图形的所有知识点

图形的所有知识点图形是数学中的一个重要概念,它在几何学、代数学以及其他数学学科中扮演着重要的角色。
在本文中,我们将探讨图形的各种类型和相关概念,以帮助您更好地理解和应用图形知识。
一、基本概念与术语图形是由点和线组成的几何形状。
它由以下基本概念和术语组成:1. 点:图形中最基本的元素,通常用大写字母表示,例如 A、B、C。
2. 线:由两个点之间的直接路径组成,可以是直线、曲线或弧线。
3. 线段:连接两个点的部分,用小写字母表示,例如 AB。
4. 射线:从一个点开始,通过另一个点的路径,表示为以起始点为中心的一个方向。
5. 平行线:在同一平面上不相交且始终保持相同距离的线。
6. 垂直线:形成直角交叉的两条线。
7. 角:由两条射线共享一个公共起点组成。
8. 多边形:由线段组成的封闭图形,例如三角形、四边形和多边形。
二、图形的类型图形可以根据其形状和性质进行分类。
下面是一些常见的图形类型:1. 三角形:由三条线段组成的多边形。
2. 四边形:由四条线段组成的多边形。
3. 圆:由一个固定中心点和与该中心点距离相等的所有点组成的图形。
4. 正多边形:所有边相等且所有角均相等的多边形。
5. 平行四边形:拥有两组平行线的四边形。
6. 梯形:拥有两条平行线段的四边形。
三、图形的性质与公式图形的性质和公式帮助我们计算其各种属性,例如面积、周长和体积。
在下面,我们将介绍一些常见的图形性质和相关公式:1. 三角形:三角形的面积可以通过以下公式计算:面积 = 底边长 ×高 / 2。
周长等于三条边长的和。
2. 四边形:四边形的面积可以通过以下公式计算:面积 = 对角线之积 / 2。
周长等于四条边长的和。
3. 圆:圆的面积可以通过以下公式计算:面积= π × 半径的平方。
圆的周长可以通过以下公式计算:周长= 2 × π × 半径。
4. 矩形:矩形的面积可以通过以下公式计算:面积 = 长 ×宽。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学几何图形基本概念及计算公式
轴对称图形:如果一个图形沿着一条直线对折,直线左右的两部分能够完全重合,那么这个图形就叫做轴对称图形.这条直线叫做对称轴.长方形(2条对称轴),正方形(4条对称轴),等腰三角形(1条),等边三角形(3条),等腰直角三角形(1条),等腰梯形(1条),圆(无数条).
点:线和线相交于点.
直线:某点在空间中或平面上沿着一定方向和相反方向运动,所画成的图形,叫做直线.直线是向相反方向无限延伸的,所以它没有端点,不可以度量. (可以用表示直线上任意两点的大写字母来记:直线AB,也可以用一个小写字母来表示:直线a)
射线:由一个定点出发,向沿着一定的方向运动的点的轨迹,叫做射线.这个定点叫做射线的端点,这个端点也叫原点.射线只有一个端点,可以向一端无限延长,不可以度量.(射线可以用表示他端点,和射线上任意一点的两个大写字母表示:射线OA)
线段:直线上任意两点间的部分,叫做线段.这两点叫做线段的端点,线段有长度,可以度量.(线段可以用两个端点的大写字母表示:线段AB,也可以用一个小写字母表示;线段a)线段的性质:在连接两点的所有线中,线段最短.
角:从一点引出两条射线所组成的图形,叫做角.这两条射线的公共端点,叫做角的顶点.组成角的两条射线,叫做角的边. 角的大小与夹角两边的长短无关. 角的分类:
直角:90度的角叫做直角
平角:一条射线由原来的位置,绕它的端点按逆时针方向旋转,到所成的角的终边和始边成一直为止,这时所成的角叫做平角.或者角的两边的方向相反,且同在一条直线上时的角叫做平角,平角是180度.
锐角:小于90度的角叫做锐角
钝角:大于90度的角叫做钝角
垂直与平行:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行. 如果两条直线相交成
直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足.
点到直线的距离:从直线外一点作这条直线的垂线,这点和垂足之间的线段长度,叫做点到直线的距离.从直线外一点到这条直线所画的垂线段最短.
平行线间的距离:从一条直线上的一点向它的平行线作一条垂线,这点到垂足之间的线段的长度,叫做平行线间的距离.平行线间的距离处处相等.即,平行线间的垂线的长度都相等.
三角形:由三条线段围成的图形(每相邻两条线段的的端点相连)叫做三角形.从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底.三角形具有稳定性. 三角形边的性质:
1、三角形任何两边的长度和大于第三边.
2、三角形的任何两边的差小于第三边.三角形三个内角的度数和叫做三角形的内角和.三角形的内角和是180度.
三角形的分类: 1、按边分:三条边都不相等的三角形,叫不等边三角形;三条边中有两条边相等的三角形,叫等腰三角形. 三条边都相等的三角形,叫做等边三角形,也叫正
三角形. 2、按角分:三个角都是锐角的三角形,叫做锐角三角形. 有一个角是直角的三角形,叫做直角三角形. 有一个角是钝角的三角形,叫做钝角三角形. 三角形的面积:三角形的面积=底×高÷2 通常用S表示三角形的面积,用a 表示底,用h表示高.那么:S=ah÷2 或 S=1/2ah 长方形:对边相等,四个角都是直角的四边形,叫做长方形.长方形的长边叫做长方形的长,短边叫做长方形的宽.长方形的对边相等,并且四个角都是直角;对角线长度相等,又互相平行分. 周长:图形一周的长度就是图形的周长. 长方形的周长:长方形的周长=(长+宽)×2 通常用C表示周长,a表示长,b 表示宽,那么C=(a+b)×2 长方形的面积:长方形的面积=长×宽字母公式:S=a×b 正方形:长和宽相等的长方形,叫做正方形.正方形的每条边都叫做边长.正方形的四条边的长度都相等,四个角都是直角.正方形又是特殊的长方形.对角线的长度相等,又互相垂直且平分. 正方形的周长:正方形的周长=边长×4 字母公式:C=4a 正方形的面积:正方形的面积=边长×边长字母公式:S=a×a或S=a的平方平行四边形:两组对边分别平行的四边形,叫做平行四边形.平行四边行对边相等,对角相等平行四边形的任意一组对边间的距离,叫做平行四边形的高,和高垂直的一边,叫做平行四边行的底. 平行四边形的面积:平行四边形的面积=底×高用字母表示:S=a×h 菱形:有一组邻边相等的平行
四边形,叫做菱形.菱形的四条边都相等,对角相等. 梯形:只有一组对边平行的四边形,叫做梯形.在梯形中,互相平行的一组对边,分别叫做梯形的上底和下底.不平行的一组对边,叫做梯形的腰.梯形的两底之间的距离,叫做梯形的高. 等腰梯形:两腰相等的梯形,叫做等腰梯形. 直角梯形:一条腰垂直于底的梯形,叫做直角梯形. 梯形的面积:梯形的面积=(上底+下底)×高÷2 梯形的面积=中位线×高,用a表示上底,b表示下底, h表示高.那么, 用字母表示:S=1/2(a+b)h 圆:在平面上,以一个定点为中心,以一定长度为距离而运动一周形成的轨迹,叫做圆周,简称圆.这个定点叫做圆心,圆心通常用字母O表示.连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示.通过圆心,并且两端都在圆上的线段叫做直径.一般用字母d表示. 圆的性质:在同一个圆内,所有的半径都相等,所有的直径都相等;直径等于半径的2倍
圆周率:圆的周长与这个圆的直径长度的比,叫做圆周率.圆周率是一个固定的值,用希腊字母“π”表示.它是一个无限不循环小数,但在实际应用中,一般取它的近似值,即π=3.14. 约在2000年前中国的古代数学著作《周髀算经》中就有“周三径一”的说法,意思是说圆的周长是它直径的3倍.约1500年前,中国有一位伟大的数学家和天文学家祖冲
之,他计算出圆周率应在:3.1415926和3. 1415927之间,
成为世界上第一个把圆周率值精确到7位小数的人.他的这
项伟大成就比国外数学家得出这样精确的数值的时间,至少
要早1000年.现在人们用计算机算出的圆周率,小数点后面
已经达到上亿位. 圆的周长:圆的周长=圆周率×直径用
字母示:C=πd 或 C=2πr 圆的面积:圆的面积=圆周率×
半径的平方字母公式:S=πr的平方环形的面积:即圆环.
两个半径不相等的同心圆的圆周之间所夹的平面部分,叫做
环形.面积等于外圆的面积减去内圆的面积. 扇形:由圆
心角和圆心角所对的弧围成的图形,叫做扇形. 扇形面积:
扇形面积等于所在圆的面积除以360,再乘以圆心角的度数值.用n表示圆心角的度数,那么:S=πr的平方/360×n. 体积:物体的占空间的大小,叫做物体的体积. 容积:容器
所能容纳物质的体积的大小,叫做容器的容积. 长方体:
长方体是由6个长方形(特殊情况也有两个相对的面是正方形)围成的立体图形.在一个长方体中,有6个面,12条棱,8
个顶点,相对的面完全相同,相对的棱长度相等. 相交于一
个顶点的三条棱的长度分别叫做长方形的长,宽,高. 长方
体的表面积:长方体6个面的面积总和叫做它的表面积.长
方体表面积=(长×高+长×宽+宽×高)×2 长方体的体积:长方体的体积=长×宽×高或长方体的体积=底面×积高
通常用V表示体积,a表示长,b表示宽,h表示高,S表示底面
积.那么,V=abh 或 V=sh 正方体:长、宽、高都相等的长方体,叫做正方体(也叫立方体).正方体六个面都是正方形,12条棱长度都相等,6个面的面积都相等.正方体是特殊的长方体. 正方体的表面积:正方体的表面积=棱长×棱长×6 正方体的体积:正方形的体积=棱长×棱长×棱长字母公式 V=a ×a×a或 V=a的立方. 圆柱:用长方形的一边作轴,并旋转360度,所得的几何体,叫做圆柱,简称圆柱.圆柱的上下两个面是相等的圆,叫做圆柱的底面;两个底面之间的距离叫做圆柱的高;曲面部分称为侧面.圆柱的侧面展开是一个长方形(或正方形)长就是圆柱的底面周长,宽就是圆柱的高. 圆柱的表面积:圆柱的表面积=2底面积×底面周长×高圆柱的体积:圆柱的体积=底面积×高字母公式 V=sh 圆锥:用直角三角形的一条直角边为轴,把它旋转360度,所得的几何体,叫做直圆锥,简称圆锥.圆锥的底面是圆形;圆锥的顶点到底面的距离,叫做圆锥的高;圆锥的体积:圆锥的体积=1/3底面积×高字母公式 V=1/3sh。
