人教版七年级下册数学课课练 第五章相交线与平行线 5.1 相交线
七年级数学下册第5章相交线与平行线5.1相交线第2课时课件新版新人教版
ห้องสมุดไป่ตู้
归纳总结
垂直概念：两条直线相交所成的四个角中，有一个角是 直角时，叫做这两条直线互相垂直．两条直线互相垂直， 其中的一条直线叫做另一条直线的垂线，它们的交点叫 做垂足．
如图，AB ⊥CD，垂足为Ｏ．记作：AB ⊥CD于点Ｏ．
符号语言：因为AB ⊥CD， 所以∠AOC=90°． 反之，因为∠AOC=90°， 所以AB⊥CD．
探究思考1
思考1：两条直线垂直和相交是什么关系？ 垂直是相交的特殊情况
思考2：能否认为在同一平面内，两条直线的位置关系 有3种：相交，平行，垂直？ 不能，因为垂直是相交的特殊情况 思考3：如何判定两条射线垂直？两条线段呢？ 两条线段垂直、两条射线垂直、线段与射线垂直、线 段与直线垂直、射线与直线垂直，都是指它们所在的 直线垂直． 思考4：你能举出一些生活中与垂直有关的实例吗？
垂线．
AP B
P B A
探究思考3
问题：在灌溉时，要把河中的水引到农田P处，如何 挖掘能使渠道最短？
探究思考4
如图所示，比较图中PO，PA1，PA2，PA3，PA4...的 长短，这些线段中，最短的是哪一条？
谢谢 观看
35º, 145º, 145º （2）当a与b所成角α为90 º时，其余角的分别为多少？
均为90º
问题导入
取两根木条a，b，将它们钉在一起，固定木条a，转动 木条b． （3）在木条b的转动过程中，什么量也随之发生改变？
a与b所成的角也随之发生改变 （4）木条b与a成90º的位置有几个？此时，木条b与a所 在的直线有什么位置关系？
学习目标
重点： （1）理解垂线、垂线段的概念，理解点到直线的
距离的概念，掌握垂线的性质； （2）通过利用垂线的性质解决简单的实际问题，
人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案
初一数学人教版七年级下册第五章订交线与平行线5．1订交线同步练习题1. 以下说法中正确的选项是 ()A．不相等的角必定不是对顶角B．互补的两个角是邻补角C．互补且有一条公共边的两个角是邻补角D．两条直线订交所成的角是对顶角2. 以下说法正确的选项是 ()A．在同一平面内，过直线外一点向该直线画垂线，垂足必定在该直线上B．在同一平面内，过线段或射线外一点向该线段或射线画垂线，垂足必定在该线段或射线上C．过线段或射线外一点不必定能画出该线段或射线的垂线D．过直线外一点与直线上一点画的一条直线与该直线垂直3. 已知∠α和∠ β的对顶角，若∠ α＝60°，则∠ β的度数为 ()A ．30°B．60°C．70°D．150°4.如图，直线 AB ，CD 订交于点 O，由于∠ 1＋∠ 3＝180°，∠ 2＋∠ 3＝180°，因此∠ 1＝∠ 2，其推理依照是 ()A ．同角的余角相等B．对顶角相等C．同角的补角相等D．等角的补角相等5. 如图， OB⊥CD 于点 O，∠ 1＝∠ 2，则∠ 2 与∠ 3 的关系是 () A．∠2＝∠3B．∠2 与∠3 互补C．∠ 2 与∠ 3 互余D．不可以确立第1页/共4页6.如图，从地点 P 到直线公路 MN 共有四条小路，若用同样的速度行走，能最快抵达公路 MN 的小路是 ()A ．PA B．PB C．PC D．PD7.如图是一跳远运动员跳落沙坑时留下的印迹，则表示该运动员成绩的是()A ．线段 1 的长B．线段 AP2的长APC．线段 BP3的长D．线段 CP3的长8.如图，已知直线 a， b 被直线 c 所截，则∠ 1 和∠ 2 是一对 ()A ．对顶角B．同位角C．内错角D．同旁内角9.如图，已知直线 b，c 被直线 a 所截，则∠ 1 与∠ 2 是一对 ()A ．同位角B ．内错角C．同旁内角D．对顶角10.如图，直线 AB ，CD 订交于点 O，若∠ AOD ＝28°，则∠ BOC＝__________，∠AOC＝ ___________．11.如下图， OA⊥OB，∠ AOC ＝120°，则∠ BOC 等于 ______度．12.自来水企业为某小区 A 改造供水系统，如下图，沿路线 AO 铺设管道和BO主管道连接(AO⊥BO)，路线最短、工程造价最低，其依据是__________________．13. 如下图，∠ B 与 ____________是直线 _________和直线 _______被直线________所截得的同位角．14.如下图，内错角共有 ____对．15.如下图，当剪刀口∠ AOB 增大 20°时，∠ COD 增大________ ，其依据是_________________．16. 如图，已知 AB ，CD 订交于点 O，OE⊥AB ，∠EOC＝28°，则∠ AOD ＝____第2页/共4页度．17.如图， BC⊥ AC，CB＝8 cm，AC ＝6 cm，点 C 到 AB 的距离是 4.8 cm，那么点 B 到 AC 的距离是 ____ cm，点 A 到 BC 的距离是 ____ cm，A，B 两点间的距离是 ____ cm.18.如图，直线 AB ，CD，EF 订交于点 O.(1)写出∠ COE 的邻补角；(2)分别写出∠ COE 和∠ BOE 的对顶角；(3)假如∠ BOD＝60°，∠ BOF＝90°，求∠ AOF 和∠ FOC 的度数．119. 如图，O 为直线 AB 上一点，∠AOC＝3∠BOC，OC 是∠ AOD 的均分线．判断 OD 与 AB 的地点关系，并说明原因．20.如图，点 A 表示毛毛雨家，点 B 表示小樱家，点 C 表示小丽家，她们三家恰巧构成一个直角三角形，此中 AC ⊥BC，AC＝900 米，BC＝1 200 米，AB ＝1 500 米．(1)试说出毛毛雨家到街道BC 的距离以及小樱家到街道AC 的距离．(2)画出表示小丽家到街道AB 距离的线段．21.如图，直线 a，b 被直线 l 所截，已知∠ 1＝ 40°，试求∠ 2 的同位角及同旁内角的度数．参照答案：1---9AABCC BBDA10. 28°152°11.3012.垂线段最短13. ∠FAC AC BC FB第3页/共4页14.815.20°对顶角相等16.6217. 861018.解： (1)∠COE 的邻补角为∠ COF 和∠ EOD.(2)∠COE 和∠ BOE 的对顶角分别为∠ DOF 和∠ AOF.(3)由于∠ BOF＝90°，因此∠AOF＝ 180°－90°＝90°.又由于∠ AOC＝∠ BOD＝60°，因此∠ FOC＝∠ AOF＋∠A OC＝90°＋60°＝150°.19.解：OD⊥AB. 原因：由于 OC 均分∠ AOD ，因此可设∠ AOC＝∠ COD ＝x°，1而∠ AOC ＝3∠BOC ，因此∠ BOC ＝ 3∠AOC ＝ 3x° .由于∠ AOC ＋∠ BOC＝180°，因此 x＋3x＝180，因此 x＝45，因此∠ AOD ＝2∠COD＝90°，即 OD⊥AB.20.解：(1)毛毛雨家到街道 BC 的距离为 900 米，小樱家到街道 AC 的距离为 1200米．(2)过点 C 作 CD⊥AB 于点 D.线段 CD 的长表示小丽家到街道AB 的距离，图略．21.解：∵∠ 1＝40°，∴∠ 3＝∠ 1＝40°，4＝180°－∠ 1＝140°，即∠ 2的同位角是 140°，∠ 2 的同旁内角是 40°.第4页/共4页。
七年级数学下册第5章相交线与平行线5.1相交线5.1.2垂线教学课件新版新人教版
A
跳远成绩怎么表示？
l
解：过P点作PA⊥l于
P
A
点A ，垂线段PA的长度
就是该同学的跳远成绩.
拓展应用1
如图：在铁路旁边有一 张庄，现在要建一火车站， 为了使张庄人乘火车最方便 （即距离最近），请你在铁 路上选一点来建火车站，并 说明理由.
垂线段最短
张庄
N
拓 展 应 用2
如图：要把水渠中的水引到水池C 中，在渠岸的什么地方开沟，水沟的 长度才能最短？ 请画出图来，并说明理由.
垂线.
B
则所画直线AB是过
点A的直线l的垂线.
A
l
1放：放直尺，直尺的一边要与已知直线重合； 2靠：靠三角板，把三角板的一直角边靠在直尺 3上移；：移动三角板到已知点；
4画线：沿着三角板的另一直角边画出垂线.
探究：
(1)画已知直线l的垂线能画几条？ (2)过直线l上的一点A画l的垂线， 这样的垂线能画几条？ (3)过直线l外的一点B画l的垂线， 这样的垂线能画几条？
5、点到直线的距离 从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.
谢谢 观看
直线外一点到这条直线的垂线段的长度， 叫做点到直线的距离.
特别强调：
垂线段是垂线上的一部分，它是线段， 一端是一个点，另一端是垂足.
P
A
B
D
点到直线的距离：
直线外一点到这条直线的垂线段的长度，叫
做点到直线的距离.
P
例如：如图，PA⊥l于点A，垂线段
PA的长度叫做点P到直线l的距离.
l
例：如图，是一个同学跳远的位置
第五章 相交线与平行线
5.1 相交线
5.1.2垂线
观察：
七年级数学下册 第五章 相交线与平行线 5.1 相交线 5.
5.1 相交线
5.1.2 垂 线
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解垂线的有关概念、性质及画法；（重点） 2.知道垂线段和点到直线的距离的概念，并会应用
其解决问题. （重点、难点）
导入新课
情境引入 观察下面图片，你能找出其中相交的直线吗？它
们有什么特殊的位置关系？
符号语言： ②性质：∵ AB⊥CD ,（已知）
∴ ∠AOD=90° .（垂直的定义） (∠AOC=∠BOC=∠BOD=90°)
典例精析
例1(1)如图1，若直线m、n相交于点O,∠1＝90°,则m⊥n；
(2)若直线AB、CD相交于点O，且AB⊥CD，则 ∠BOD =__9_0_°__；
(3)如图2，BO⊥AO，∠BOC与∠BOA的度数之比 为1∶5，那么∠COA＝_7_2_°_,∠BOC的补角为162°.
如图，从A点向已知直线 l 画一条垂直的线段和 几条不垂直的线段.
说一说：
1.线段AB, AC, AD , AE谁最短？
A
2.你能用一句话表示这个结论吗？
B CD
l E
总结归纳
连接直线外一点与直线上各点的所有线段中垂 线段最短.简单说成：垂线段最短.
A
特别规定：
l D
线段AD的长度叫做点A到直线l的距离.
把互相垂直的两条直线的交点 叫作垂足（如图中的O点）.
C l
O mB
D
垂线的基本性质与判定
如图，当直线AB与CD相交于O点，∠AOD=90°
时，AB⊥CD，垂足为O.
A
D
符号语言：
O
①判定：∵∠AOD=90°,（已知）
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.2 垂线第1课时 垂线课件 新版新人教
线
画法
利用三角尺或量 角器画：一靠、 二过、三画
如图，直线 AB，CD 相交于 O 点，OM⊥AB 于O.
（1）若∠1 =∠2，求∠NOD； （2）若∠BOC = 4∠1，求∠AOC 与∠MOD.
解：（1）因为 OM ⊥ AB ， 所以∠1 + ∠AOC = 90°. 又∠1 = ∠2，所以∠2 + ∠AOC = 90°，所 以∠NOD = 180°-（∠2 + ∠AOC）= 180°90°= 90°.
（2）由已知条件∠BOC = 4∠1，即 90°+∠1 = 4∠1，可 得∠1 = 30°，所以∠AOC = 90°- 30° = 60°，所以由对顶角相等可得∠BOD = 60°，所 以∠MOD = 90°+∠BOD = 150°.
结束
语 七年级数学下册 第五章 相交线与平行线5.1 相交
线5.1.2 垂线第1课时 垂线课件 （新版）新人教版 -七年级数学下册第五章相交线与平行线5.1相交 线5.1.2垂线第1课时垂线课件新版新人教版
复习课件
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.2 垂线第1课时 垂线 课件 （新版）新人教版-七年级数学下册第五章相交线与平行线5.1相交线
5.1.2垂线第1课时垂线课件新版新人教版
相交线5.1.2 垂线第1课时 垂线课件 （ 新人教版-七年级数学下册第五章相交 行线5.1相交线5.1.2垂线第1课时垂线课 版新人教版
解：A、B、C 三点在同一直线上. ∵AB ⊥ l ，BC ⊥ l . 且交点都为 B . ∴A、B、C 三点在同一直线上（在同一平面 内，过一点有且只有一条直线与已知直线垂直）.
课堂小结
定义
当两条直线相交所成的四个角中 有一个角为 90°时，这两条直线
人教版数学七年级下 第5章 相交线平行线配套 课时练习
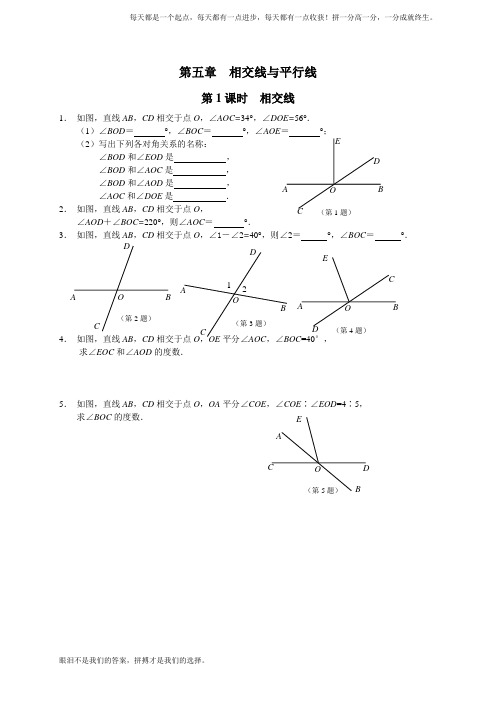
第五章 相交线与平行线第1课时 相交线1． 如图，直线AB ，CD 相交于点O ，∠AOC=34°，∠DOE=56°．（1）∠BOD ＝ °，∠BOC ＝ °，∠AOE ＝ °；（2）写出下列各对角关系的名称：∠BOD 和∠EOD 是 ， ∠BOD 和∠AOC 是 ， ∠BOD 和∠AOD 是 ，∠AOC 和∠DOE 是 ．2． 如图，直线AB ，CD 相交于点O ， ∠AOD ＋∠BOC=220°，则∠AOC ＝ °． 3． 如图，直线AB ，CD 相交于点O ，∠1－∠2=40°，则∠2＝ °，∠BOC ＝ °．4． 如图，直线AB ，CD 相交于点O ，OE 平分∠AOC ，∠BOC =40°，求∠EOC 和∠AOD 的度数．5． 如图，直线AB ，CD 相交于点O ，OA 平分∠COE ，∠COE ∶∠EOD =4∶5，求∠BOC 的度数．A B C D E O（第1题）AB C D O （第2题）CAB DO （第3题） 1 2 ABD CE O （第4题） BCD AE O（第5题）1． 如图，直线AB ，CD 相交于点O ，OE ⊥AB ，垂足是O ，∠DOE ＝55°，则∠BOC 的度数为（ ）A ．40°B ．45°C ．30°D ．35°2． 如图，直线EF ⊥AB 于点E ， CD 是过点E 的直线，且∠AEC =120°，则∠DEF ＝ °． 3． 如图，∠ABD ＝90°．(1)点B 在直线 上，点D 在直线 外；(2)直线 与直线 相交于点A ，点D 是直线 与直线 的交点，也是直线 与直线 的交点，又是直线 与直线 的交点； (3)直线 ⊥ ，垂足为点 ；(4)过点D 有且只有 条直线与直线AC 垂直． 三、解答题4． 如图，点P 在∠AOB 的内部，点M 在∠AOB 的外部，点Q 在射线OA 上，利用三角板按以下要求画图：（1）过点P 画OA 的垂线，再画OB 的垂线； （2）过点Q 画OB 的垂线； （3）过点M 画OA 的垂线．5． 如图，直线AB ，CD ，EF 相交于点O ，且AB ⊥CD ，∠1=30°，求∠2、∠COF 、∠4、∠5的度数．6．直线AB ，CD 相交于点O ，OE ⊥AB 于点O ，∠COE =40°，求∠BOD 的度数．（第2题）A B FE D C ·Q A B O（第4题）·M·P（第3题）A B C D （第5题）AB DCO EF123 45 CO A B D E（第1题）1．如图，P 是直线l 外一点，A ，B ，C 在直线l 上，且P B ⊥l ，那么下列说法错误的是（ ）A ．线段BP 叫做点P 到直线l 的距离B ．PA ，PB ，PC 三条线段中，PB 最短 C ．PB 是点P 到直线l 的垂线段D ．线段AB 的长是点A 到直线PB 的距离2． AC ⊥l 2，AB ⊥l 1，则点A 到直线l 1的距离是线段 的长度．3． 如图，∠AOB ＝90°，所以AB BO ；若OA =3cm ，OB =2cm ，则点A 到OB 的距离是 cm ，点B 到 OA 的距离是 cm ；点O 与AB 上各点连接的所 有线段中 最短．4． 如图，直线a 上有一点M ，直线b 上有一点N ， 用三角板画图：（1）画点M 到直线b 的垂线段； （2）画点N 到直线a 的垂线段．5． 在如图所示的各个三角形中，分别画出AB 边上的高，并量出三角形顶点C 到直线AB 的距离．6．已知：如图，EF ⊥OA ，CD ⊥OB ．用简单的推理，说明：（1）∠CDE ＝∠O ；（2）∠CDF +∠O =180°．ABC A BCAB C ab ·M · N （第4题）B AODC（第6题）FE C P A B l （第1题） A B O （第3题）第4课时 同位角、内错角、同旁内角1． 如图，∠1与∠2不是同位角的是 （ ）2． 如图，∠1与∠2不是同旁内角的是 （ ）3． 如图，∠1和∠3是 角，∠2和∠3是 角，∠1和∠2是 角，∠1和∠4是 角，∠2和∠5是 角． 4． 如图，直线BD 上有一点C ，则： （1）∠1和∠ABC 是 角，它是直线 和 直线 被直线______所截而成的；（2）∠2和∠BAC 是 角，它是直线 和直线 被直线______所截而成的；（3）∠3和∠ABC 是 角，它是直线 和直线 被直线______所截而成的； （4）∠ABC 和∠ACD 是 角，它是直线 和直线 被直线______所截而成的；（5）∠ABC 和∠BCE 是 角，它是直线 和直线 被直线______所截而成的；5．如图，当AB ，CD 被BD 所截时，内错角是______________________________； 当AD ，BC 被BD 所截时， 内错角是______________________________．三、解答题6．如图，试找出图中与∠1是同位角的所有的角．1 2 A ． 12 1 22 1B ．C ．D ．2 1 2 1 2 12 1 B ． A ． C ． D ． 214 35 （第3题）21 3 DC B A E（第4题） A B DC （第5题） （第6题）B 1ACF GD E H第5课时 平行线1．下列说法：①过一点有且只有一条直线垂直于已知直线；②过一点有且只有一条直线平行于已知直线；③与同一条直线平行的两直线必平行；④与同一条直线相交的两直线必相交，其中正确有 （ ）A ．1个B ．2个C ．3个D ．4个 2．在同一平面内的两条直线的位置关系有 。
七年级数学下册 第五章 相交线与平行线 5.1 相交线 5.1.1 相交线课件 (新版)新人教版
知2－练
2 如图，小强和小丽一起玩跷跷板，横板AB绕O 上下转动，当小强从A到A′的位置时， ∠AOA′＝45°，则∠BOB′的度数为____4_5_°__， 理由是_____对__顶__角__相__等_____.
知2－练
3 如图，直线AB，CD交于点O，下列说法中，错 误的是( C ) A．∠AOC与∠BOD是对顶角 B．∠AOE与∠BOE是邻补角 C．∠DOE与∠BOC是对顶角 D．∠AOD与∠BOC都是∠AOC的邻补角
相交线
1 课堂讲解 邻补角的定义及性质
对顶角的定义及性质
2 课时流程
逐点 导讲练
课堂 小结
课后 作业
北京立交桥
相交线
平行线
知识点 1 邻补角的定义及性质
A
D
O
B C
如果两条直线只有一个公共点，就说这两条直线相交. 该公共点叫做两直线的交点直线AB、CD相交于点O.
A
2
D
1O3
4
B
C
∠1和∠2也是直线AB、CD相交得到的，它 们不仅有一个公共顶点O，还有一条公共边OA， 像这样的两个角叫做邻补角 . ∠2与∠3，∠3与∠4，∠1与∠4都是邻补角.
知2－讲
对顶角：有一个公共顶点一 个角的两边是另一个角的 两边的反向延长线，那么 这两个角互为对顶角.
C
2O
B
1 （ （ ）3
）
4 A
D
知2－讲
对顶角
两条直线相交出现对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
对顶角是成对出现的
C
2
1O
A
D
对顶角的性质: 对顶角相等. 为什么?
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.1 相交线课件 (新版)新人教版
（5）对顶角有__∠__1_和__∠__3_，__∠__2_和__∠__4_，_
∠5和__∠__7_，__∠__6_和__∠__8_______.
2.如图，直线AB、CD 相交于点O，∠AOE＝ 90°，如果∠1＝20°，那么∠2＝__2_0_°__，∠3＝ __7_0_°__，∠4＝_1_6_0_°__.
基础巩固
随堂演练
1. 如图，直线 c 分别与直线 a、b 相交形成 8 个
角，写出图中满足下列条件的角. （1）∠1 的邻补角有_∠__2_，__∠__4_；
（2）∠3 的邻补角有_∠__2_，__∠__4_；
（3）∠5 的邻补角有_∠__6_，__∠__8_；
（4）∠7 的邻补角有_∠__6_，__∠__8_；
误区一 不能准确判断对顶角 1.下列图形中，∠1 与∠2 是对顶角的是（ ）
错解 A或C或D 正解 B
错因分析 不理解互为对顶角的条件：（1）有公 共顶点；（2）角的两边互为反向延长线. A，C 或 D 中的∠1 和∠2 不符合对顶角的条件.判断对顶角 一定要抓住对顶角形成的前提条件是两直线相交.
（1）若∠EOC ＝ 70°，求∠BOD 的度数； （2）若∠EOC∶∠EOD ＝ 2∶3，求∠BOD 的度数.
解：（1）因为 OA 平分∠EOC ，所以∠AOC = 1 ∠EOC = 35°，
2 又因为∠BOD 是∠AOC 的对顶角，所以
∠BOD =∠AOC = 35°；
（2）因为∠EOC 是∠EOD 的邻补角，且
（3）因为∠BOD 是∠AOC 的对顶角，所以 ∠BOD =∠AOC = 50°；
因为∠COB 是∠AOC 的邻补角，所以 ∠COB =180°-∠AOC = 130°.
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.2 垂线第2课时 垂线段课件 新版新人
（1）设汽车行驶到公路 AB 上点 M 的位置时， 距离加油站 C 最近；行驶到点 N 的位置时，距离加 油站 D 最近，请在图中分别画出点 M、N 的位置；
C
A
B
D
（2）当汽车从 A 出发向 B 行驶时，在公路 AB 的哪一段路上距离 C、D 两加油站都越来越近？ 在哪一段路上距离加油站 D 越来越近，而离加油 站 C 却越来越远？
册同第学五们章，相下交课线休与息平十行分线钟5.1。相现交在线是休 5.1.2息垂时线间第，2课你时们垂休线息段一课下件眼新睛版，新人
教版
看看远处，要保护好眼睛哦~站起来
动一动，久坐对身体不好哦~
综合运用
3.一辆汽车在直线形的公路 AB 上由 A 向 B 行 驶，C、D 是分别位于公路 AB 两侧的加油站.
垂线性质2：连接直线外一点与直线上各点的所 有线段中，垂线段最短． 简单说成：垂线段最短．
点到直线的距离：直线外一点到这条直线的垂线 段的长度，叫做点到直线的距离．
（5）如果图中的比例尺为 1:100 000，水渠 大约要挖多长？
（6）你能列举生活中类似的实例吗？
练习
如图，三角形 ABC 中，∠C＝90°. （1）分别指出点 A 到直 线 BC，点 B 到直线 AC 的距离 是哪些线段的长A？C BC （2）三条边 AB、AC、 BC 中哪条边最长？为什么？ AB 理由：连接线段外一点与线段上各点的
（1）不考虑其他因素，请你画图确定蓄水池 H 点的位置，使它到四个村庄距离之和最小；
（2）计划把河水引入蓄水池 H 中，怎样开渠 最短并说明根据.
解：（1）∵两点之间线段最短， ∴连接AD，BC 交于 H ，则 H 为蓄水池位 置，它到四个村庄距离之和最小.
人教版七年级数学下册 第五章 相交线与平行线 5.1.1 相交线 课后练习
人教版七年级数学下册 第五章 相交线与平行线 5.1.1 相交线 课后练习一、选择题1．如图，25AOB ︒∠=，90AOC ︒∠=，点B ，O ，D 在同一直线上，则COD ∠的度数为（ ）A ．65B ．25C ．115D ．1552．如图，直线AD ，BE 被直线BF 和AC 所截，则∠1的同位角和∠5的内错角分别是（ ）A ．∠4，∠2B ．∠2，∠6C ．∠5，∠4D ．∠2，∠43．如图，直线AB 和CD 交于点O ，OA 平分∠EOC ，若∠EOC ＝70°，则∠BOD 的度数为（）A ．70°B ．35°C ．30°D ．110°4．如图，下列说法中不正确的是（ ）A ．1∠和3∠是同旁内角B ．2∠和3∠是内错角C ．2∠和4∠是同位角D ．3∠和5∠是对顶角5．如图有四条互相不平行的直线l1、l2、l3、l4所截出的七个角，关于这七个角的度数关系，下列结论正确的是（）A．∠2=∠4+∠7B．∠3=∠1+∠7C．∠1+∠4+∠6=180°D．∠2+∠3+∠5=360°6．下面四个图形中∠1与∠2为互为对顶角的说法正确的是（）A．都互为对顶角B．图1、图2、图3中的∠1、∠2互为对顶角C．都不互为对顶角D．只有图3中的∠1、∠2互为对顶角7．如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC︰∠EOD=2︰3，则∠BOD的度数为（）A．36°B．40°C．35°D．45°8．如图，直线AB，CD 交于点O，则图中互为补角的角对数有（）A．1 对B．2 对C．3 对D．4 对9．如图所示，已知直线AB 、CD 相较于O ，OE 平分∠COB ，若∠EOB=55°，则∠BOD 的度数是（ ）A ．20B ．25°C ．30°D ．70°10．三条互不重合的直线的交点个数可能是（ ）A ．0、1、3B ．0、2、3C ．0、1、2、3D ．0、1、2二、填空题11．如图，1∠与2∠是对顶角，110α∠=+︒，250∠=︒，则α=______．12．小明用一副三角板自制对顶角的“小仪器”，第一步固定直角三角板ABC ，并将边AC 延长至点P ，第二步将另一块三角板CDE 的直角顶点与三角板ABC 的直角顶点C 重合，摆放成如图所示，延长DC 至点F ，PCD ∠与ACF ∠就是一组对顶角，若30ACF ∠=，则PCD ∠=__________，若重叠所成的(090)BCE n n ∠=<<，则PCF ∠的度数__________．13．如图，直线AB ，CD 相交于点O ，OA 平分∠EOC ，∠EOD=120°，则∠BOD=__________°．14．平面内不过同一点的n 条直线两两相交，它们交点个数记作n a ，并且规定10a =，则2a =__________，1n n a a --=____________．15．如图,已知直线AB,CD 相交于点O,OE 平分∠COB,若∠EOB=55°,则∠BOD=_________.三、解答题16．如图，直线AB ，CD 相交于点O ，OA 平分∠EOC ．（1）∠AOC 的对顶角为______，∠AOC 的邻补角为______；（2）若∠EOC ＝70°，求∠BOD 的度数；（3）若∠EOC ：∠EOD ＝2：3，求∠BOD 的度数．17．如图，直线AB 和CD 相交于点O ．（1）∠1的邻补角是____________，对顶角是___________；（2）若∠1＝40°，求出∠2，∠3，∠4的度数．18．如图所示，已知直线AB 、CD 相交于点O ，OE 、OF 为射线，∠AOE=90°，OF 平分∠AOC ，∠AOF+∠BOD=57°，求∠EOD 的度数19．如图，直线a ，b 相交．（1）若170∠=︒，求2∠，3∠，4∠的度数；（2）若1:24:5∠∠=，求2∠，3∠，4∠的度数．20．如图所示，直线AB 、CD 相交于点O ，OE 是∠BOD 的平分线，∠AOE ＝140°．猜想与说理：（1）图中与∠COE 互补的角是 ．（2）因为∠AOD ＋∠AOC ＝180°，∠BOC ＋∠AOC ＝180°，所以根据 ，可以得到∠AOD ＝∠BOC ． 探究与计算：（3）请你求出∠AOC 的度数．联想与拓展：（4）若以点O 为观测中心，OB 为正东方向，则射线OC 的方向是 ．21．如图，已知直线AB 和CD 相交于点O ，∠COE ＝90°，OF 平分∠AOE ．（1）写出∠BOE 的余角；（2）若∠COF 的度数为29°，求∠BOE 的度数．22．如图所示，直线AB 、CD 、EF 相交于点O ，90BOC AOC AOD BOD ∠=∠=∠=∠=︒，OG 平分AOE ∠，2AOF DOF ∠=∠，求：（1）∠BOE的度数；∠的度数．（2）FOG23．如图，直线AB、CD相交于点O、OE平分、BOD、OF平分、COE、、1）若、AOC=76°，求、BOF的度数；、2）若、BOF=36°，求、AOC的度数；、3）若|、AOC、、BOF|=α°，请直接写出、AOC和、BOF的度数．（用含的代数式表示）【参考答案】1．C 2．B 3．B 4．C 5．B 6．D 7．A 8．D 9．D 10．C11．40°12．30°180°－n°13．30°n-.14．1.115．70°16．（1）∠BOD，∠BOC或∠AOD；（2）∠BOD＝35°；（3）∠BOD＝36°．17．（1）∠2和∠4，∠3（2）∠2＝140°，∠3＝40°，∠4＝140°18．∠EOD=128°19．（1）2110∠=︒，370∠=︒，4110∠=︒；（2）2100∠=︒，380∠=︒，4100∠=︒ 20．（1）∠BOE 和∠DOE ；（2）同角的补角相等；（3）∠AOC ＝80°；（4）北偏西10° 21．（1）∠BOD 和∠AOC （2）58°22．（1）60︒；（2）120︒23．（1）∠BOF=33°；（2）∠AOC=72°；(3) ∠AOC=2x=（3607）°﹣47α°，∠BOF=（3607）°+37α°．。
新人教数学七下：第5章相交线平行线配套课时练习答案
参考答案与提示第五章相交线与平行线第1课时相交线1 (1) 34° 146 ° 90° (2)互为余角，互为对顶角，互为邻补角，互为余角2. 110 °3. 110 ° 70°4. 70°, 40°5. 140 °第2课时垂线(1)1 . (1) DB , AC；(2) AD、AC , AD、DB , DB、CD , CD、AD ； (3) DB、AC , B ； (4) 一4. 略5 •/ 2= 60 ° Z COF= 120 ° Z 4= 60 ° / 5 = 90 °6•分两种情况，/ BOD= 50 或130 °第3课时垂线(2)1 . C 2. AB 3•>, 3, 2,垂线段4•略5•略6•略第4课时同位角、内错角、同旁内角1. B2. D 3 .对顶，同位，内错，同位，同旁内角4・(1 )同位角，AB、CE , AC ； (2)内错角，AB、CE，AC ; ( 3)同旁内角，AB、AC，BC;( 4)同位角，AB、AC，BD ; ( 5)同旁内角，AB、CE，BC 5. Z ABD 与Z CDB，Z ADB 与Z CBD 6. Z EBH、Z FCH、Z GDF、Z GEF 第5课时平行线1. B 2 .相交或平行3 .平行，平行于同一条直线的两条直线互相平行4.平行公理5. 11丄12 6.Z ADE =Z ABC，Z AED =Z ACB 11.略7. 0、1、2、3第6课时平行线的判定(1)1 . A 2.同位角相等，两直线平行；AB II CD，内错角相等，两直线平行3.( 1) AF //CE，内错角相等，两直线平行；(2)Z 3，同位角相等，两直线平行4.Z 1= Z 2，Z 2= Z 3，AB // CD，内错角相等，两直线平行5.( 1)因为AB丄EF，CD丄EF，所以Z ABE =Z CDE=90°.所以AB // CD (同位角相等，两直线平行). (2)因为Z ABE =Z MBE + Z仁90 °，Z CDE =Z NDE+ Z 2=90°，Z 1 = Z 2，所以Z MBE =Z NDE .所以BM // DN (同位角相等，两直线平行)6.略第7课时平行线的判定(2)1 . C 2.( 1) AD、BC，内错角相等，两直线平行；(2) AB、CD，内错角相等，两直线平行；(3) AD、BC，同旁内角互补，两直线平行；(4) AB、CD，同旁内角互补，两直线平行3.对顶角相等，等量代换，Z 2+ Z 3=180° ,AB // CD，同旁内角互补，两直线平行4.略5. Z FAE= Z B 或Z DAB = Z B 或Z EAC = Z C 或Z DAC+ Z C=180°或Z EAB + Z B=180°第8课时平行线的性质1 . C2 . C 3. C 4 4. 34°5. 85°6. 40 7. 50，40 8.略第9课时命题、定理1 . C 2. B 3 .题设，结论 4 .两个角是直角，它们都相等5. 如果两个角相等，那么它们的补角相等6.两个角都是锐角，它们的和大于钝角，假7.题设，结论9. 150° 10 (1)如果一个角是锐角，那么这个角的补角大于它的余角；(2)如果有两条直线是平行线一组同位角的平分线，那么它们平行；(3)如果一个角是平角的一半，那么这个角是直角；(4)在同一平面内，如果两条直线不平行，那么它们一定相交11 .略第10课时平移1 . D 2. C 3. B 4. 50，60，60 5. BB1，CC1，DD1 6.略7.略第11课时相交线平行线复习1 . C 2. B 3. C 4. C 5 . C 6 . B 7 . C 8 . A 9 . 10 10.I 11.I 12 . DC、EC，AB，同位角13 . 56 14 .如果两个角相等，那么它们的余角相等15 . ( 2)( 6) 16 . 3cm，平行，平行17 . Z BGD，内错角相等，两直线平行，Z F，内错角相等，两直线平行，平行于同一直线的两条直线平行，Z F，两直线平行，同旁内角互补18 .略19 .略20 .平行21 . Z D =45 ° Z C = 45 ° Z B = 135 ° 22 . 125 °23 .略。
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.3 同位角、内错角、同旁内角课件 新版
6. 如图，画 AE⊥BC，CF⊥AD，垂足分别为 E，F.
F
E
解：AE 和 CF 如图中虚线所示.
7. 如图，用量角器画∠AOB 的平分线 OC， 在 OC 上任取一点，比较点 P 到 OA，OB 的距离 的大小.
P C
解：∠AOB 的平分线 OC 如图中虚线 所示；P 到 OA、OB 的距离相等.
（2）共有 2 对同旁内角．
例 如图，直线 DE、BC 被直线 AB 所截， （1）∠1 和∠2，∠1 和∠3，∠1 和∠4 各是 什么位置关系的角？
∠1 与 ∠2 是内错角， ∠1 与∠3 是同旁内角， ∠1 与∠4 是同位角．
例 如图，直线 DE、BC 被直线 AB 所截，
（2）如果∠1＝∠4，那么∠1 和∠2 相等吗？
复习课件
七年级数学下册 第五章 相交线与平行线5.1 相交线5.1.3 同位角、内错角 、同旁内角课件 （新版）新人教版-七年级数学下册第五章相交线与平行线
5.1相交线5.1.3同位角内错角同旁内角课件新版新人教版
七年级数学下册 第五章 相交线与平行线5.1 相交
线5.1.3 同位角、内错角、同旁内角课件 （新版）
1．能说出同位角、内错角、同旁内角的概念. 2．能结合图形正确找出同位角、内错角、同旁 内角.
探究新知
三条直线相交可以分为哪些情况？ 对三条直线相交按交点的个数分为三种情况：
（1）三条直线交点的个数有一个，即三条直
线交于一点；
l
a b
（2）三条直线交点的个数有两个，即两条 直线平行且被第三条直线所截；
新人教版-七年级数学下册第五章相交线与平行线
5.1相交线5.1.3同位角内错角同旁内角课件新版新
人教版
人教版初一数学七年级下册第5章相交线与平行线5.1相交线同步训练题含答案
人教版初一数学七年级下册第5章相交线与平行线5．1相交线同步训练题含答案1. 以下说法正确的选项是( )A．垂线最短B．对顶角相等C．两点之间直线最短D．过一点有且只要一条直线垂直于直线2. 如图，直线AB，CD相交于点O，假定∠1＋∠2＝100°，那么∠BOC等于( )A．130° B．140° C．150° D．160°3. 如图，能表示点到直线的距离的线段共有( )A．2条 B．3条 C．4条 D．5条4. 如图，直线a，b被直线c所截，那么以下说法中错误的选项是( ) A．∠1与∠2是邻补角 B．∠1与∠3是对顶角C．∠2与∠4是同位角 D．∠3与∠4是内错角5. 如图，直线AB，CD相交于点O，以下条件中，不能说明AB⊥CD的是( ) A．∠AOD＝90° B．∠AOC＝∠BOCC．∠BOC＋∠BOD＝180° D．∠AOC＋∠BOD＝180°6. 如图，∠F的内错角有_____________．7. 如下图，AB交CD于点O，∠AOC＝60°，那么∠AOD的度数为_______．8. 如图，直线l1，l2被直线l3所截，那么图中同位角有_____对．9. 图所示，一个破损的扇形零件，应用图中的量角器可以量出这个扇形零件的圆心角的度数，测量的依据是_________．10. 如图，要把小河里的水引到田地A处，那么作AB⊥l，垂足为点B，沿AB 挖水沟，水沟最短，理由是______________．11. 如图，直线AB，CD相交于点O，OE平分∠BOC，∠COE＝65°，那么∠BOD ＝________°.12. 两条直线都与第三条直线相交，∠1和∠2是内错角，∠3和∠2是邻补角．(1)依据上述条件，画出契合题意的图形；(2)假定∠1∶∠2∶∠3＝1∶2∶3，求∠1，∠2，∠3的度数．13. 如图，直线AB，CD相交于点O，过点O作两条射线OM，ON，且∠AOM＝∠CON＝90°.(1)假定OC平分∠AOM，求∠AOD的度数；(2)假定∠1＝∠BOC，求∠AOC和∠MOD.参考答案：1---11 BADDC6. ∠AEF和∠ADF7. 120°8. 49. 对顶角相等10. 垂线段最短11. 5012. 解：(1)如图：(2)由∠1∶∠2∶∠3＝1∶2∶3，设∠1＝x°，∠2＝2x°，∠3＝3x°.由∠2与∠3是邻补角，得∠2＋∠3＝2x°＋3x°＝180°，解得x＝36，2x＝72，3x＝108.所以∠1＝36°，∠2＝72°，∠3＝108°.13. 解：(1)由于∠AOM＝∠CON＝90°，OC平分∠AOM，所以∠1＝∠AOC＝45°，所以∠AOD＝180°－∠AOC＝180°－45°＝135°.(2)由于∠AOM＝90°，所以∠BOM＝180°－90°＝90°.由于∠1＝∠BOC，所以∠1＝∠BOM＝30°，所以∠AOC＝90°－30°＝60°，∠MOD＝180°－30°＝150°.。
人教版七年级数学下册《5.1相交线》同步练习（含答案）
人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步练习一、单选题（共10题；共30分）1.如图所示，∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个2.如图，下列说法不正确的是（）A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角D. ∠1和∠4是内错角3.如图所示，∠1和∠2是对顶角的是（）A. B. C. D.4.下列说法中正确的个数为（）①两条直线相交成四个角，如果有两个角相等，那么这两条直线垂直；②两条直线相交成四个角，如果有一个角是直角，那么这两条直线垂直；③一条直线的垂线可以画无数条；④在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直．A. 1B. 2C. 3D. 45.如图，∠1=15°，∠AOC=90°，点B，O，D在同一直线上，则∠2的度数为（）A. 75°B. 15°C. 105°D. 165°6.如图所示，下列说法错误的是（）A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角D. ∠C和∠3是同位角7.如图，三条直线相交于点O．若CO⊥AB，∠1=56°，则∠2等于（）A. 30°B. 34°C. 45°D. 56°8.在下列语句中，正确的是（）．A. 在平面上，一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9.如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（）①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题（共10题；共30分）11.如图，直线AB，CD相交于点O，EO⊥AB，垂足为点O，若∠AOD=132°，则∠EOC=________12.如图，已知直线AB与CD相交于点O，OA平分∠COE，若∠DOE=70°，则∠BOD=________．13.如图，∠1和∠2是________角，∠2和∠3 是________角。
七年级数学下册第5章相交线与平行线5.1相交线5.1.1相交线教学课件新版新人教版
两个角互为邻补角.
对顶角：如果一个角的两
边是另一个角的两边的反 向延长线，那么这两个角 互为对顶角.
C 2（O 1（） ）3
A4
B D
练习1、下列各图中∠1、∠2是对顶角 吗？为什么？
1( )2
1( )2
1( )2
练习2、下列各图中∠1、∠2是邻补角 吗？为什么？
1( （2
1( 2
1( 2
探究与发现3
C
2
A
1
B
O3
4
D
∠1 与∠3在数量上又有什么关系呢？
对顶角相等
已知：直线AB与CD相交于O 点(如图)，说明∠1=∠3, ∠2=∠4的理由.
C 1（2（）O）3 B A4 D
解：因为直线AB与CD相交于O点，
所以∠1+∠2=180°, ∠2+∠3=180°.
所以∠1=∠3.
同理可得∠2=∠4.
例1. 如图，直线a，b相交，∠1=40°， 求 ∠2，∠3，∠ 4的度数.
练习：
(1)如图1，两条直线ＣＤ，ＥＦ相交，在这个图形中，有对顶角
__２__对，邻补角__４__对.
(2)如图1，三条直线ＡＢ，ＣＤ，ＥＦ两两相交，在这个图形中，
有对顶角__6__对，邻补角__1_2_对. (3)如图1，三条直线ＡＢ，ＣＤ，ＥＦ相交于一点，在这个图形
中，有对顶角__6__对，邻补角__1_2_对.
大桥上的钢梁和钢索
棋盘上的横线和竖线
第五章 相交线与平行线
5.1 相交线
5.1.1相交线
观察与联想
C
2
A
1 43
B
D
有一个公共点的两条直线形成相交直线.
初中数学人教版七年级下册第五章 相交线与平行线5.1.1相交课件(共25张PPT)
A.40°
B.50°
C.85°
D.60°
)
(第5题)
【点拨】
因为直线AB与CD相交于点O，所以∠BOD＝∠AOC.因
为∠AOC＝50°，所以∠BOD＝50°.故选B.
4.如图，直线AB，CD相交于点O，若∠1＝80°，
∠2＝30°，则∠AOE的度数为(
A.30°
B.50°
C.60°
B )
D.80°
条公共边，“补”指的是两个角的数
量关系是互补.
3. 邻补角与补角的区别：
(1)互为邻补角是互为补角的特殊情况. 互为邻补角的两个
角除具备两角互补这一数量关系外，还要具备两角相邻
的位置关系.
(2)一个角的邻补角有两个，但一个角的补角可以有多个.
1-1. 下列选项中∠ 1与∠ 2 互为邻补角的是( D )
• •
关系，一个角的对顶角只有一个.
• •
2. 性质：对顶角相等.
特别提醒：(1)两个角互为对顶角，它们一定相等；
(2)相等的两个角不一定是对顶角.
2-1. [中考·安顺] 如图，直线a，b相交于点O，如果∠ 1＋
∠ 2=60°，那么∠ 3 是( A )
A. 150°
B. 120°
C. 60°
D. 30°
因为∠BOD＝60°，所以∠AOC＝∠BOD
＝60°，
所以∠FOC＝∠AOF＋∠AOC＝90°＋60°
＝150°.
相交线
定义
性质
邻
补
角
相交线
对
顶
角
定义
性质
于点O.
(1)写出∠COE的邻补角；
【解】∠COE的邻补角为∠COF和∠EOD.
人教版七年级下册数学精品作业课件(RJ) 第五章 相交线与平行线 相交线
6．下列各图中，∠1与∠2是对顶角的是(D )
7．下列语句正确的是(D ) A．顶点相对的两个角是对顶角 B．有公共顶点并且相等的两个角是对顶角 C．两条直线相交，有公共顶点的两个角是对顶角 D．两条直线相交，有公共顶点且没有公共边的两个角是对顶角
8．如图，当剪子口∠AOB增大15°时，∠COD增大____1度5 ．
数学 七年级下册 人教版
第五章 相交线与平行线
5．1 相交线
5．1.1 相交线
1．下面各图中，∠1与∠2是邻补角的是(D )
2．如图，直线a与直线b相交于点O，则∠1的度数是( D) A．64.5° B．55.5° C．40° D．44.5°
第2题图
3．下列说法中错误的是C( ) A．互为邻补角的两个角一定是互补的角 B．互补的两个角不一定是邻补角 C．相邻的两个角一定是邻补角 D．两条直线相交形成的四个角中，一个角有两个邻补角 4．如图，O是直线AB上一点，∠1＝3∠COB，则∠1＝1_3_5_°_．
第4题图
5．如图，直线AB，CD相交于点O，∠AOE＝2∠AOC，若∠1＝38°， 求∠DOE的度数．
解：∵∠1＝38°，∴∠BOC＝180°－∠1＝142°. ∴∠AOC＝180°－∠BOC＝38°.∵∠AOE＝2∠AOC， ∴∠AOE＝76°.∴∠DOE＝180°－∠1－∠AOE＝180°－38°－76°＝66°
第10题图
第11题图
12．如图，三条直线交于同一点，则∠1＋∠2＋∠3＝_1_8_0_°．
第12题图
13．如图，直线AB和CD相交于点O. (1)若∠1＋∠3＝50°，则∠3＝_2_5_°_； (2)若∠1∶∠2＝2∶3，则∠3＝_7_2_°__； (3)若∠2－∠3＝70°，则∠3＝__5_5_°__．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.1相交线课堂练习
1.(易错题)下列选项中,∠1与∠2互为对顶角的是( )
2.如图所示,∠1与∠2互为邻补角的是( )
3.(东光县期中)当光线从空气射人水中时，光线的传播方向发生了改变,这就是折射现象.如图,∠1的对顶角是( )
A.∠AOB
B.∠BOC
C.∠AOC
D.都不是
4.如图,已知∠AOB.
(1)请画出并写出∠AOB的对顶角;
(2)写出图中其他的对顶角和所有的邻补角.
5.已知直线AB,CD交于点0.若∠AOC=35°,则∠BOD的度数为( )
A.30°
B.35°
C.55°
D.145°
6.如图,∠a的度数为( )
A.135°
B.125°
C.115°
D.105°
7.如图,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,当OC的位置发生变化时(不与直线AB重合),那么∠EOF的度数( )
A.不变,都等于90°
B.逐渐变大
C.逐渐变小
D.无法确定
8.如图所示,三条直线相交于点O,则∠1+∠2+∠3等于.
9. (教材例题变式)如图,直线a,b相交,∠1= 135°，求∠2,∠3,∠4的度数.
10.如图,点O是直线AB上的任意一点,OC,OD,OE是过点O的三条射线,若∠AOD=∠COE= 90°，则下列说法:①与∠AOC互为邻补角的角只有一个;②与∠AOC互为补角的角只有一个;③与∠AOC互为邻补角的角有两个;④与∠AOC互为补角的角有两个.其中正确的是( )
A.②③
B.①②
C.③④
D.①④
11.下列语句正确的是( )
A.若两个角是对顶角,则这两个角相等
B.若两个角相等,则这两个角是对顶角
C.若两个角不是对顶角,则这两个角不相等
D.相等的角都是对顶角
12. (西城区期末)如图，直线AB,CD相交于点O,∠EOD=90.若∠AOE=2∠A0C,则∠DOB的度数为()
A.25°
B.30°
C.45°
D.60°
13.如图，直线AB,CD相交于点O,则∠BOD = .
14.如图,将长方形纸片折叠,使A点落在A'处,BC为折痕,BD为∠A'BE的平分线,则∠CBD的度数为
15. (核心素养●问题解决)古城黄冈的旅游资源十分丰富，“桃林春色,
柏子秋波”便是其八景之一,你能设计出一种测量“柏子古塔”外墙底部的底角(图中∠ABC)大小的方案吗?并说明理由.
16.如图,已知直线AB,CD相交于点O,OA平分∠COE,∠COE :∠EOD=4 : 5,求∠BOD的度数.
17. (原创题)如图,直线AB,CD相交于点O,∠AOE=∠BOE,OB平分∠DOF.若∠DOE= 50°,求∠DOF的度数.
18. (核心素养●勇于探究)观察下图,寻找对顶角及邻补角.
(1)图①中共有对对顶角，对邻补角;
(2)图②中共有对对顶角，对邻补角;
(3)图③中共有对对顶角，对邻补角;
(4)根据_上面的规律,直线条数与对顶角对数之间的关系为:若有n条直线相交于一点,则可形成对对顶角，对邻补角.
答案：
1.D
2.D
3.A
4.
5.B
6.A
7.A
8.180°
9.解:因为∠1与∠2是邻补角且∠1= 135° ,所以∠2= 45°又∠1与∠3,∠2与∠4是对顶角，所以∠.4=∠2=45°，∠3=∠1= 135°
10.D
11.A
12.B
13.60°
14.90°
15.解:方案一:如图，延长AB至点D，量出∠CBD的度数，再由邻补角的定义，求出∠ABC的度数.方案二:如图，分别延长AB. CB至点D, E,量出∠DBE的度数，再根据对顶角相等，可得出∠ABC的度数.
16.
17.
18.(1)2 ,4(2)6,12 (3)n(n-1) 2n(n-1)。