921384-数据统计分析-勘误表
1984年第1期 第2期勘误表

1984年第1期第2期勘误表在出版过程中,勘误表是一份非常重要的文献,它记录了出版物中的错误信息,为读者提供了正确的信息和解释。
1984年第1期和第2期也不例外,这两期的勘误表是非常重要的。
本文将探讨这两期勘误表的内容,并对其意义进行分析和评价。
1984年第1期和第2期的勘误表录有几种类型的错误,包括排版错误、文字错误和名字错误。
排版错误指的是文本在出版过程中排版有误,如标点符号、字体等问题。
文字错误则是出版物中的文字有误,如拼写错误、错别字等。
名字错误则是出版物中人名或地名的错误。
在这两期的勘误表中,有几个错误特别引人注目。
首先,这两期的勘误表纠正了一些重要的排版错误,如错误的页码和章节标题。
这些错误会直接影响读者阅读体验,因此及时更正是非常重要的。
其次,这两期的勘误表纠正了一些重要的文字错误。
其中许多错误导致了对原始文本的误解,例如字符丢失或错误的术语使用。
这些错误可能会对读者造成不必要的困惑或误导。
最后,这两期的勘误表还更正了一些名字错误。
这些错误可能会对作品或作者的形象造成不良影响,因此及时更正是非常重要的。
总的来说,勘误表是一份非常重要的文献,它为读者提供了正确的信息和解释。
在这些错误被纠正之前,读者可能会因误解或混淆而感到困惑,但是勘误表能够消除这些问题,并为读者提供更好的阅读体验。
因此,我们认为,1984年第1期和第2期的勘误表具有重要的意义。
这些勘误表纠正了出版物中的错误,防止了误解或混淆,为读者提供了正确的信息和解释。
我们建议出版商在未来的出版过程中继续注意和记录错误,并及时纠正,在保证出版物质量的同时,为读者提供更佳的阅读体验。
此外,勘误表对于出版商和作者来说也具有重要的意义。
勘误表不仅可以帮助作者纠正错误,还可以帮助出版商改进出版过程。
通过勘误表,出版商可以发现自己的错误,改进出版流程,提高出版物的质量,从而提高读者的满意度和信任度。
此外,勘误表也可以帮助作者在作品中保持学术和研究的严谨性。
《概率论与数理统计》本科教材勘误表
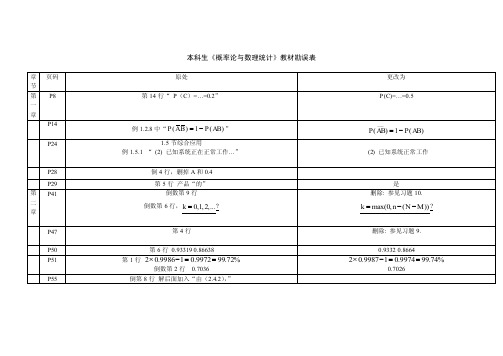
P( AB) 1 P( AB)
(2) 已知系统正常工作
___
P28 P29 第 二 章 P41
是 删除: 参见习题 10.
k max(0, n ( N M )) ?
删除: 参见习题 9. 0.9332 0.8664
P47 P50 P51 P55
第4行 第 6 行 0.93319 0.86638 第 1 行 2 0.9986 1 0.9972 99.72% 倒数第 2 行 0.7036 倒第 8 行 解后面加入“由(2.4.2) , ”
f ( x, y )
P72 第 10 行 P77
1 21 2
2 ( x 1 )( y 2 ) ( y 2 ) 2 1 ( x 1 ) exp 2 2 2 2 2 ( 1 ) 1 1 1 2 2
2
2. (2)
建议删除。
七 章
) 1 ( x , x e f ( x, , ) 0, 其他
( 0, 和未知) ;
倒数第 4 行, 的概率 依概率
X lim P n x n / n
P125 P126
6. 假设某生产线上组装每件成品的时间服从指数分布, 统计资料表明该生产线每件 6.假设某生产线上组装每件成品的时间服从指数分布,统计资料表明 成品的组装时间平均为 15 分钟,各件产品的组装时间相互独立。 该生产线每件成品的组装时间平均为 10 分钟,各件产品的组装时间相 互独立。
问: 参数λ 为平均寿命 400 小时的倒数 空消耗 1 千瓦电将损失 0.12 元。 而当用户用电量超过供电量时, 公司需 要从别处补电, 每 1 千瓦电反而赔 0.20 元。求在指定时间内,该公司获 利润的期望值。
讲义勘误表3

(1 , 7] B.( 7 , 7] C( 1 , 7] D( 7 , 7]
2
2
2
2
603
푠 b 修改为 b
611
B 选项改为-i
748
修改为 㔠
(l) 푠 B B修改为 푠 B 773
(2)C 选项修改为 l −
B
774
AAl푠c
(l)lilililiB,a 修改为 lililil, B,a
750
815
正投影点 E 改为 D
题目本身没问题,只是这道题有三问,没区分好
827
第一根红线那是第二问,第二根红线,是第三问
题目修改为:
859
将直线 ⸱ 푠 绕原点逆时针旋转 90 度,再向右平移 1 个单位,求该直线
901
若 MF2 MF2 改为 MF1 = MF2
(1) 抛物线为⸱B 푠
908
(2) D 选项改为-
420
条件为砀l 푠 li砀B 푠 Bi砀 B 푠 砀
428
问题修改为:它的最小项是第几项?
439
图:
440
最后一行的 : 的冒号,修改为“,”
443
446
449
区间修改为[0, ]
469
516
点 P 为该平面内以动点
541
修改为
点 P 为该平面内一动点
558
选项改为
(
,
2
)
23
选项修改为
559
M、等级(N)修改为: 284
i
294
“两个两点”修改为“两个零点”
301
题前加“已知函”
303
前补充
0,π2
304
统计学第八版贾俊平指导书勘误

统计学第八版贾俊平指导书勘误第八版《统计学》贾俊平指导书勘误全解析序号: 1在统计学领域,贾俊平教授的第八版《统计学》指导书被广泛认可为一本经典之作。
然而,就像任何一本重要的参考书籍一样,难免会有一些错误或疏忽之处。
在本文中,我将全面评估第八版《统计学》贾俊平指导书中的勘误,探讨这些错误或疏忽对于读者的影响,并分享个人对于该主题的观点和理解。
序号: 2在评估贾俊平指导书的勘误之前,让我们先简要回顾统计学的基本概念。
统计学是一门关于数据收集、分析和解释的学科,旨在帮助我们理解和解释现实世界中的现象和变化。
在现代社会中,统计学在各个领域都起着重要的作用,从医学研究到市场调查,从环境科学到经济学,都依赖于统计学的方法和理论。
序号: 3回到贾俊平指导书的勘误上来,我们不能忽视这些错误对读者的影响。
一个错误的公式或解释可能导致读者产生误解,进而影响他们对统计学的理解和应用。
及时发现和纠正这些错误对于保持学科的准确性和可靠性至关重要。
序号: 4在第八版《统计学》贾俊平指导书的勘误中,我注意到了一些重要的错误和疏忽。
在第三章的公式3.2中,分母的符号应为负号而非正号,这个错误可能会导致读者在计算中产生错误结果。
在第五章的表格5.3中,有一个数据单元的数值缺失,这可能会造成读者对该表格的误解。
这些错误和疏忽可能会对读者的学习和应用产生不必要的困扰,因此应该尽快进行勘误和修正。
序号: 5然而,尽管贾俊平指导书中存在一些错误和疏忽,我仍然认为这本书是一本优秀的参考书。
贾俊平教授对统计学的深入理解和干货满满的解释使其成为一本不可或缺的学习资料。
当我们阅读该指导书时,我们应该保持批判性思维并对其中的错误进行评估和修正,以确保我们真正理解统计学的核心概念和原则。
序号: 6总结回顾一下,第八版《统计学》贾俊平指导书的勘误虽然存在一些错误和疏忽,但这并不否定其作为一本经典参考书的价值。
作为读者,我们应该保持对这些错误的警惕,并主动寻找并修正其中的错误。
数据检查勘误表
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
注:1、如勘误内容较多填写不下,请复印勘误表或另附纸并加盖学校公章(未盖公章则此表无效,将不予勘误);
数据检查勘误表
编号:
单位名称
联系老师:
各系公章
(未盖公章则此表无效)
内容描述:请核对照片上相关信息,将照片上的错误信息
填在左侧(请同时提供照片上的身份证号,便于准确查询),正
确信息填在右侧。
联系电话:
邮箱:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
2、填写勘误表时,请将正确和错误的信息信息同时填写(望能同时提供两项信息,如:身份证号和姓名),以便查找、更正;
数据透析表的数据异常检测与数据修正技巧

数据透析表的数据异常检测与数据修正技巧数据透析表(Data Mart)是指针对特定业务领域进行局部化、专门化的数据组织形式。
它是数据仓库的一个分支,通过聚焦于某一具体业务领域,提供了一种便捷的方式来存储和分析数据。
然而,由于数据的复杂性和多样性,数据透析表往往会面临数据异常的问题。
在本文中,我们将探讨数据透析表的数据异常检测与数据修正技巧。
首先,数据异常的形式多种多样,包括但不限于缺失值、异常值、重复值和不一致值等。
针对缺失值,我们可以采取以下几种方法进行处理。
首先,可以使用插值法进行填补。
插值法根据已有数据的特征来推断缺失值,并进行适当的填充。
常用的插值方法有线性插值、多项式插值和随机森林插值等。
其次,可以使用均值、中位数或众数等代替缺失值。
最后,可以通过建立模型来预测缺失值,例如使用线性回归、决策树或支持向量机等进行预测。
对于异常值的检测和修正,我们可以采用如下策略。
首先,可以使用基于统计学的方法来检测异常值,例如Z-score、Tukey方法和箱线图方法等。
这些方法基于数据的分布特征进行异常值的判定,可以有效地找出数据中的异常观测点。
其次,可以使用基于机器学习的方法来检测异常值,例如使用聚类算法或离群点检测算法。
这些方法基于数据的聚类特性或离群点判定规则来判断异常值,能够更全面地捕捉数据中的异常。
除了异常值,重复值也是数据透析表中常见的问题。
重复值的存在可能导致数据分析时的偏差和误差,因此需要进行有效的修正。
对于重复值的检测,可以采用基于唯一标识符的方法,例如检查数据中的主键或唯一字段是否有重复值。
对于发现的重复值,可以采取删除、合并或更新等操作进行修正。
需要注意的是,在进行修正操作时要尽量保证数据的完整性和准确性。
此外,不一致值也是数据透析表中常见的问题。
不一致值是指数据之间存在逻辑矛盾或不符合业务规则的情况。
对于不一致值的检测,可以采用基于规则的方法,例如定义业务规则并检查数据是否符合规则。
统计错误分析

4定量资料统计分析方面存在的统计学错误4.1忽视t检验和方差分析的前提条件4.1.1忽视t检验的前提条件例16原文题目:重症急性胰腺炎并发肝功能不全的临床研究。
实验数据见表5[4]。
原文作者用t检验分析此资料。
请问:这样做正确吗?表5两组患者血清淀粉酶、肌酐和乳酸脱氢酶水平的比较(略)*P<0.05,与重症急性胰腺炎肝功能不全组比较。
对差错的辨析与释疑对表5数据进行方差齐性检验,可发现2组患者的血清淀粉酶和肌酐指标不能满足方差齐性的要求,故不能采用t检验进行分析,须采用相应的非参数检验方法。
4.1.2忽视方差分析的前提条件例17原文题目:川芎嗪对心室快速起搏心力衰竭实验犬心房颤动及心房纤维化的影响。
原作者将健康杂种犬21只,随机分为3组:正常对照组、充血性心力衰竭模型组和川芎嗪治疗组,每组7只[1 3]。
请问:用配对设计定量资料的t检验处理此定量资料合适吗?对差错的辨析与释疑原作者用配对t检验处理此设计下的定量资料是错误的。
此实验分3组,应为单因素三水平设计定量资料,应在检查是否符合方差分析的3个前提条件“独立性”、“正态性”和“方差齐性”后,根据情况选用合适的分析方法。
根据原文陈述,原作者在进行统计分析时,将充血性心力衰竭模型组和川芎嗪治疗组在模型建立之前所测得的血液标本指标,均归入正常对照组进行统计学分析,意在增大正常对照组的样本含量,严格地说,这样做违反了方差分析的“独立”条件。
4.2误用t检验处理均数间的多重比较例18原文题目:姜黄素抑制晶状体上皮细胞增殖的信号转导机制。
原作者实验共分3组:空白对照组、模型组、姜黄素组,实验数据见表6[5]。
统计分析时计量资料均数用x±s表示,组间比较采用t检验。
请问:统计分析方法选用得正确吗?表6姜黄素对重组人表皮生长因子诱导的小牛晶状体上皮细胞增殖细胞内C a2+、c AMP和cGMP浓度的影响(略)**P<0.01,与空白对照组比较;△△P<0.01,与模型组比较。
数据结构教材勘误表
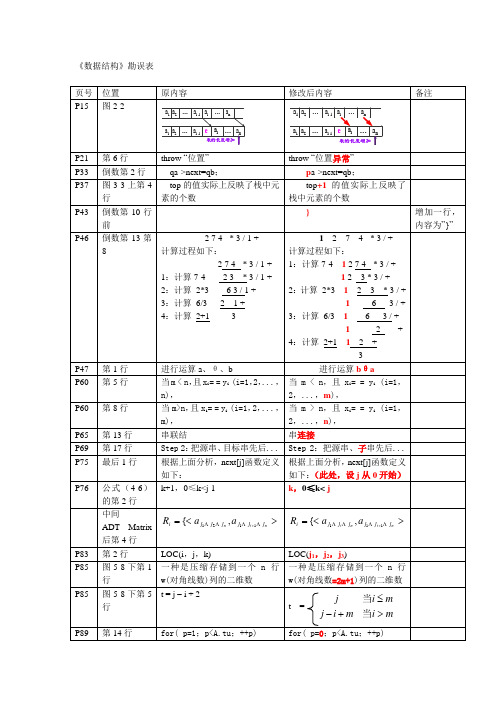
a1 a2 … ai-1 ai … an a1 a2 … ai-1 e ai … an
表的长度增加
修改后内容
a1 a2 … ai-1 ai … an a1 a2 … ai-1 e ai
备注
… an
表的长度增加
P21 P33 P37 P43 P46
for(col=0;col<A.nu ;++col) 0≤i<n,0≤j<m
p 1
A[i][k ] B[k ][ j ]
k 1
p
A[i][k ] B[k ][ j ]
k 0
108 108 108 117 119 123 132
15 18 倒数第 5 行 第一句 文字倒数第 4 行 图 6-13(c) 算法 6.6, 算法 6.13
……仍为 m 阶 B-树 //在 m 阶 B-树*t 上结点…… ……信息,以及指向…… ……解决以下两个问题: ……不同的符号在各位上…… ……位作为哈希地址。 ……稳定性:对任意…… ……进行排序,若相同…… ……将第 i 个记录后移: r[i+1]=r[i] 插入排序……的算法是简 单…… for(int j=i-1;j>=high+1;--j) 记录后移 L.key[j+1]=L.key[j]; L.key[high+1]=L.key[0]; 选择排序的思想是每一…… ……因此,它的空间复杂度为 O(1)。 Step1:……中的元素建大顶堆 不超过式(9-10) : ……,即 //
(ki1,ki2,……,kid)<……
P243 P243 P244 P246 P247 P248 P257 P257 P258 P258 P261
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P:78倒数第11行
79.0%/90.3%),
23.2%/42.8%),
P:78倒数第7行
…如图4.18所示,…有77.8%是
…如图4.17所示,…有21%是
P:78倒数第6行
…占57.2%。…的1.34倍(RR=78.8
…占9.7%。…人的2.16倍(RR=21.0
Percent
Frequency
Percent
CLUSTER 1
403
26.3%
421
26.7%
2
576
37.6%
604
38.3%
3
552
36.1%
554
35.1%
Combined
1531
100.0%
1579
100.0%
勘误表
错误改Βιβλιοθήκη 为P:34第1行在管理人员中,
在总员工中,
P:34第2行
基层管理者占5%,
基层管理者占15%,
P:78倒数第14行
…如图4.17所示,…有21%是
…如图4.18所示,…有77%是
P:78倒数第13行
…占9.7%。…人数的2.16倍
…占57.2%。…人数的1.34倍
P:78倒数第12行
21%/9.7%…人数的87%
…(Sig.)小于或等于
P:96第15行
的概率小于…
的概率大于…
P:114表6.2下1行
…620~640 640以上合计
…620~660 660以上合计
P:152第3行
Salary=-18 149.7+…
Salary=-16 149.7+…
P:174第5行
…+0.418+0.467=…
…+0.418+0.351+0.467=…
cohort患肝炎=
P:79第四表2行中
患肝炎
喝酒
第四表5、7、9行
喝酒的%
患肝炎的%
第六表5、6行中
cohort患肝炎=
cohort喝酒=
P:81图4.19三行
213151 21315100 2 1 3 1 5 1 0
21315 21315000 2 1 3 1 5 0 0
P:96第13行
…(Sig.)大于或等于
P:174第6行
…+0.649=0.951,exp(0.951)=…
…+0.649+0.767=-0.951,exp(-0.951)=…
P:312表下1行
选择Transform→timeSeries→
选择Analyze→timeSeries→
P:246的第一表改变为:
Female
Male
Frequency
P:78倒数第5行
57.2%...54%(RR=23.2%/42.8%)
9.7%...87.5%(RR=79.0%/90.3%)
P:78倒数第3行
这和图4.17所示…。图4.18中
这和图4.18所示…。图4.17中
P:79第一表2行中
喝酒
患肝炎
第一表5、7、9行
患肝炎的%
喝酒的%
第三表5、6行中
cohort喝酒=
