Matlab for西安电子科技大学1-2
matlab全套教程西电

2021/3/4
3
课程安排
课堂教学:共24学时实401、402、403)
学习成绩: 1)上机实验成绩占30%; 2)考勤 10% ; 3) 考试60% (随堂考试)。
主要参考书 ➢ 《精通MATLAB 6.5》张志涌 等编著,北航出版,2003年 ➢ 《高等应用数学问题的Matlab求解》 薛定宇等著,清华大学出
2021/3/4
6
1 Matlab概述
内容
Matlab发展历史 Matlab产品家族(Matlab family of products)体系 Matlab 语言的特点。
目的
全面了解 Matlab软件包 激发对Matlab软件的学习兴趣。
2021/3/4
7
1.1 MATLAB的历史及影响
MATLRAeBal-TToiPmorleobcoWexsoessriknsghBolpo是ck一很set种可等实能,时已详代有见码人M生A将T成你LA工要B具做在,的线它应帮能用助够程文根序据作成工具箱了。 MATLS成Aim实BuCl时ino档k应m模p。用i型le程r生序成。程序源代码,并打包、编译所生成的源代码生 Simulink Stateflow从是现基有于的有Si限mu状lin态k 机和理Sta论te针flo对w自复动杂生成C语言程序代码的功能、
• 70年代中期,Cleve Moler博土及其同事在美国国家基金会 的帮助下,开发了LINPACK和EISPACK的FORTRAN语言 子程序库,这两个程序库代表了当时矩阵运算的最高水平。
• 到了70年代后期,身为美国新墨西哥州大学计算机系系主
任的CIeve Moler,在给学生上线性代数课时,为了让学生
由这些模块产品之间的关系可以图1.1表示。
西电MATLAB大作业

MATLAB大作业班级:021131 姓名:XXX 学号:02113XXX实验一傅里叶变换一试验要求信号在传输过程中,由于受信道或环境等客观因素的影响,在接收端得到的是噪声环境下的信号。
利用FFT函数对这一信号进行傅里叶分析,确定原始有用信号的频率。
已知:采样率:fs=100MHz,有用信号频率:f0=10MHz,样本数:1024点,信噪比:S/N=5dB。
二设计思路1、根据已知条件产生一个有用信号2、根据已知的信噪比产生一个高斯噪声3、将产生的有用信号和高斯噪声叠加,将此信号视为被噪声污染的信号4、调用FFT函数对被噪声污染的信号进行快速傅里叶变换5、对比图象并结合已知条件,得出原始有用信号的频率设计思路如下图:三程序代码clear allclose allclcfs=100e6; %采样率fs=100Mhzf0=10e6; %有用信号频率f0=10MhzN=1024; %样本数N=1024n=0:N-1;t=[0:N-1]/fs; %时间序列input=2*sin(2*pi*f0*t)+sin(2*pi*f0*t)-1; %输入信号subplot(2,2,1),plot(t,input); %有用信号随时间变化的输振幅xlabel('时间');ylabel('振幅');title('输入信号');grid on;am=2; %有用信号的最大幅度p=10^(5/20); %信噪比:S/N=5dBb=am/10^(p/20); %b为噪声信号最大幅度,p=20*log10(am/b)noise=b*randn(1,N); %高斯噪声信号subplot(2,2,2),plot(t,noise); %绘出随时间变化的噪声信号的振幅xlabel('时间');ylabel('振幅');title('噪声信号');grid on;sig=input+noise; %被噪音污染的信号subplot(2,2,3),plot(t,sig); %绘出随时间变化的被噪声信号污染后的信号的振幅xlabel('时间');ylabel('振幅');title('被噪声信号污染后的信号');grid on;y=fft(sig,N); %对被噪声信号污染后的信号进行快速傅里叶变换mag=abs(y); %求得傅里叶变换后的振幅f=n*fs/N; %频率序列subplot(2,2,4),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('傅里叶变换后的信号');grid on;四实验结果及结果分析1、实验结果2、结果分析由“傅里叶变换后的信号”图知有用信号的频率是1×107Hz=10MHz=f0,符合实验设定的事实,实验成功。
matlab实验1-2

MATLAB简介
MATLAB是一套功能强大的工程技术人员必 备的高端数学类科技应用软件 产生的背景:
matlab语言是由美国的Clever Moler博士 于1980年开发的,设计者的初衷是为解 决“线性代数”课程的矩阵运算问题
MATLAB= matrix + laboratory 矩阵实验室
图
具有底层绘图功能——句柄绘图
使用plot函数可随时将计算结果可视化
4.图形化程序编制功能
动态系统进行建模、仿真和分析的 软件包 用结构图编程,而不用程序编程
只需拖几个方块、连几条线,即可 实现编程功能
5.丰富的MATLAB工具箱
MATLAB主工具箱 符号数学工具箱 SIMULINK仿真工具箱 控制系统工具箱 信号处理工具箱 图象处理工具箱 通讯工具箱 系统辨识工具箱 神经元网络工具箱 金融工具箱
M文件的编程工作方式是在命令窗口中调用 M文件,从而执行文件中的多条指令,M文 件是由MATLAB命令行构成的文本文件, 以.m为后缀名。当用户在命令窗口中输入M 文件的文件名按回车后,系统将收索该文 件并逐条执行该文件中的命令。它又分为 两种形式:命令M文件和函数M文件,分别 简称为命令文件和函数文件
经济学、化学和生物学等计算问题的所有其他领 域中的教学与研究
MATLAB 工作环境
在工具栏下的大窗口就是MATLAB的主窗 口,在大窗口里设置右4个小窗口(这是桌面 平台的默认设置): “Workspace”、 “Current Directory”、 “Command History”、 “Command Windows
(整理)自动控制大作业--西安电子科技大学--matlab实现,运行完美实现

自动控制技术大作业学院电子工程学院学号学生姓名授课老师源程序:ft = 30;M=1;B=5;K=20;tspan = [0,5];x0= [0,0];options = odeset('AbsTol',[1e-6;1e-6]);[T,X]=ode45('xt4odefile',tspan,x0,options);figure(1)subplot(3,1,1),plot(T,X(:,1),'r'),title('位移随时间变化曲线'),grid on subplot(3,1,2),plot(T,X(:,2),'b'),title('速度随时间变化曲线'),grid on subplot(3,1,3),plot(X(:,2),X(:,1),'m'),title('位移随速度变化曲线'),grid ona = 1/M*(ft-B*X(:,2)-K*X(:,1));i = 1;while (abs(a(i))>0.0001|(abs(X(i,2))>0.0001))i = i+1;enddisp('系统到达稳态时的时间、速度和加速度及对应的位移分别为:'); result = sprintf('时间t=%4.2f\n',T(i));disp(result);result = sprintf('速度v=%9.6f\n',X(i,2));disp(result);result = sprintf('加速度a=%9.6f\n',a(i));disp(result);result = sprintf('位移d=%6.4f\n',X(i,1));disp(result);其中xt4odefile.m 文件为function xt = odefileC(t,x); ft = 30;M=1;B=5;K=20;xt = [x(2);1/M*(ft-B*x(2)-K*x(1))]; end输出:系统到达稳态时的时间、速度和加速度及对应的位移分别为: 时间 t=4.47速度 v=-0.000087加速度 a=-0.000060位移 d=1.50000.51 1.52 2.53 3.54 4.55012位移随时间变化曲线00.51 1.52 2.53 3.54 4.55-505速度随时间变化曲线-0.500.51 1.52 2.53 3.5012位移随速度变化曲线源程序:num=[2,5,7];den=[1,6,10,6];[z,p,k]=tf2zp(num,den)[r,a,b]=residue(num,den)输出:z =-1.2500 + 1.3919i-1.2500 - 1.3919ip =-3.7693-1.1154 + 0.5897i-1.1154 - 0.5897ik =2r =2.2417-0.1208 - 1.0004i-0.1208 + 1.0004ia =b =[]结论:零点为-1.2500 + 1.3919i ,-1.2500 - 1.3919i ;极点为-3.7693 ,-1.1154 + 0.5897i,-1.1154 - 0.5897i ;增益为2源程序:num=[6.3223,18,12.811];den=[1,6,11.3223,18,12.811];t=0:0.005:20;[y,x,t]=step(num,den,t);plot(t,y);grid ontitle('单位阶跃响应曲线')xlabel('t')ylabel('c(t)')r10=1;while y(r10)<.1; r10=r10+1;end;r90=1;while y(r90)<.9; r90=r90+1;end;rise_time=(r90-r10)*0.005[ymax,tp]=max(y);peak_time=(tp-1)*.005max_overshoot=ymax-1s=4001;while y(s)>.98&y(s)<1.02;s=s-1;end; setting_time=(s-1)*.005输出:rise_time =0.5750peak_time =1.6700max_overshoot =0.6182setting_time =10.0300246810121416182000.20.40.60.811.21.41.61.8单位阶跃响应曲线tc (t )源程序:num=[1 1];den=[1 5 6 0]; sys1=tf(num,den) subplot(3,1,1) step(sys1) subplot(3,1,2) rlocus(num,den)title('系统的根轨迹曲线') r=rlocus(num,den,20.575) a=[1];b=[1 0.8989];sys2=tf(a,b)sys=series(sys1,sys2)%系统串联subplot(3,1,3)step(sys)输出:Transfer function:s + 1-----------------s^3 + 5 s^2 + 6 sr =-2.0505 + 4.3225i -2.0505 - 4.3225i -0.8989Transfer function:1----------s + 0.8989Transfer function:s + 1-------------------------------------s^4 + 5.899 s^3 + 10.49 s^2 + 5.393 s00.511.522.53x 104500010000Step ResponseTime (sec)A m p l i t u d e-3.5-3-2.5-2-1.5-1-0.500.5-10010系统的根轨迹曲线Real Axis I m a g i n a r y A x i s00.51 1.52 2.53x 104500010000Step ResponseTime (sec)A m p l i t u d e源程序:w=logspace(-1,3,1000); %比例环节 num0=0.01; den0=1;g0=tf(num0,den0); bode(g0,w) title('比例环节') grid%二阶积分环节 num1=1; den1=[1,0,0];g1=tf(num1,den1); figure(2)bode(g1,w)title('二阶积分环节') grid%二阶微分环节num2=[1,0.01,1]; den2=1;g2=tf(num2,den2); figure(3)bode(g2,w)title('二阶微分环节') grid%振荡环节num3=1;den3=[0.25,0.01,1]; g3=tf(num3,den3); figure(4)bode(g3,w)title('振荡环节')grid%总:num=0.01*[1,0.01,1]; den=[0.25,0.01,1,0,0]; g=tf(num,den); figure(5)bode(g,w)title('原总波特图') grid输出:-41-40.5-40-39.5-39M a g n i t u d e (d B )10-110101102103-1-0.500.51P h a s e (d e g )比例环节Frequency (rad/sec)-150-100-5050M a g n i t u d e (d B )10-110101102103-181-180.5-180-179.5-179P h a s e (d e g )二阶积分环节Frequency (rad/sec)-50050100150M a g n i t u d e (d B )10-1101011021034590135180P h a s e (d e g )二阶微分环节Frequency (rad/sec)-150-100-5050M a g n i t u d e (d B )10-110101102103-180-135-90-450P h a s e (d e g )振荡环节Frequency (rad/sec)-150-100-50M a g n i t u d e (d B )10-110101102103-180-135-90-450P h a s e (d e g )原总波特图Frequency (rad/sec)源程序:num=[0,20,20,10];den=conv([1,1,0],[1,10]); nyquist(num,den)输出:-1-0.500.51 1.52-20-15-10-55101520Nyquist DiagramReal AxisI m a g i n a r y A x i s源程序:num=[2000,2000];den=conv([1 0.5 0],[1 14 400]); nichols(num,den) v = [-270 -90 -40 40]; axis(v) ngrid输出:-270-225-180-135-90-40-30-20-10102030406 dB3 dB 1 dB 0.5 dB0.25 dB0 dBNichols ChartOpen-Loop P hase (deg)O p e n -L o o p G a i n (d B )源程序:num = [0 2000 2000]; den = conv([1 0.5 0],[1 14 400]); h=tf(num,den); bode(h);num = [0 2000 2000]; den = conv([1 0.5 0],[1 14 400]); h=tf(num,den);[gm,pm,wg,wc]=margin(h)输出:gm =2.7493pm =73.3527wg =19.8244 wc =5.3477-150-100-50050100M a g n i t u d e (d B )10-210-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)源程序:num=[0 0 0 1];den=conv([.5 1 0],[1 1]); sysp=tf(num,den) sys=feedback(sysp,1) w=logspace(-1,1); bode(sys,w)grid on;[mag,phase,w]=bode(sys,w);[Mp,k]=max(mag);resonant_peak=20*log10(Mp)resonant_fre=w(k)n=1;while 20*log10(mag(n))>-3;n=n+1;end; bandwidth=w(n)输出:Transfer function:1---------------------0.5 s^3 + 1.5 s^2 + sTransfer function:1-------------------------0.5 s^3 + 1.5 s^2 + s + 1resonant_peak =5.2388resonant_fre =0.7906bandwidth =1.2649-60-40-2020M a g n i t u d e (d B )10-110101-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)3.1A源程序:num = [1 2 3]; den = [1 3 3 1]; [A,B,C,D] = tf2ss(num,den)输出:A =-3 -3 -11 0 00 1 0B =1C =1 2 3D =3.2B源程序:Z=[-1 -3];P=[0 -2 -4 -6];K=4;[A,B,C,D]=zp2ss(Z,P,K)输出:A =-10.0000 -4.8990 0 04.8990 0 0 0-6.0000 -4.2866 -2.0000 00 0 1.0000 0B =11C =0 0 0 4D =3.1C源程序:A=[0 1;1 -2];B=[0;1];C=[1 3];D=1;[num,den]=ss2tf(A,B,C,D); tf(num,den)[z,p,k]=ss2zp(A,B,C,D);zpk(z,p,k)输出:Transfer function:s^2 + 5 s-------------s^2 + 2 s - 1Zero/pole/gain:s (s+5)--------------------(s+2.414) (s-0.4142)源程序:A1=[0 1;-1 -2];B1=[0;1];C1=[1 3];D1=[1];A2=[0 1;-1 -3];B2=[0;1];C2=[1 4];D2=[0];[A,B,C,D]=series(A1,B1,C1,D1,A2,B2,C2,D2) [A,B,C,D]=parallel (A1,B1,C1,D1,A2,B2,C2,D2) [A,B,C,D]=feedback (A1,B1,C1,D1,A2,B2,C2,D2) [A,B,C,D]=feedback (A1,B1,C1,D1,A2,B2,C2,D2,+1)输出:串联连接A =0 1 0 0-1 -3 1 30 0 0 10 0 -1 -2B =11C =1 4 0 0D =并联连接A =0 1 0 0-1 -2 0 00 0 0 10 0 -1 -3B =11C =1 3 1 4D =1单位负反馈连接A =0 1 0 0-1 -2 -1 -40 0 0 11 3 -2 -7B =11C =1 3 -1 -4D =1单位正反馈连接A =0 1 0 0-1 -2 1 40 0 0 11 3 0 1B =11C =1 3 1 4D =1源程序:A=[0,-2;1,-3];t=.2;F=expm(A*t) %转移矩阵B=[2;0];C=[0,3];D=[0];x0=[1,1];t=[0,.2];u=0*t;[y,x]=lsim(A,B,C,D,u,t,x0)输出:F =0.9671 -0.2968 0.1484 0.5219 y =3.0000 2.0110 x =1.0000 1.00000.6703 0.6703结论:t=0.2时,系统响应为6703.0)0()0(21==x x ,y (0.2)=2.0110源程序:A=[-3,1;1,-3]; B=[1,1;1,1]; C=[1,1;1,-1]; D=[0];Qc=ctrb(A,B) Qo=obsv(A,C) Rc=rank(Qc) Ro=rank(Qo)输出:Qc =1 1 -2 -21 1 -2 -2Qo =1 11 -1-2 -2-4 4Rc =1Ro =2结论:能控性矩阵和能观性矩阵的秩分别为1,2,又系统阶次是2,故系统是不可控的,是可观测的。
电子科大数字信号处理(dsp)matlab作业
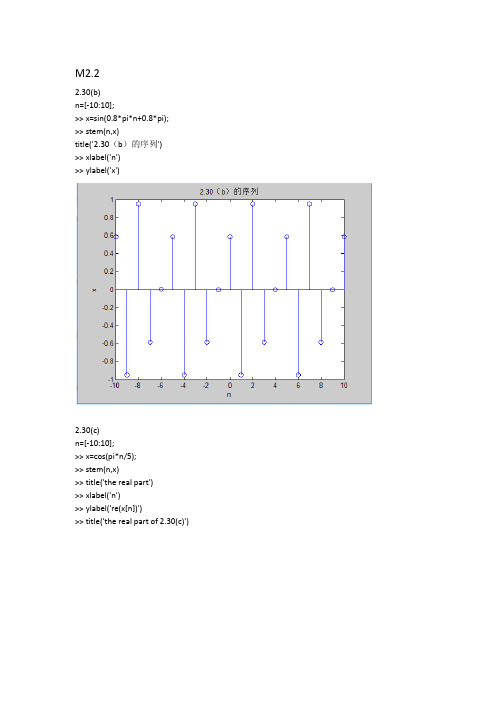
M2.22.30(b)n=[-10:10];>> x=sin(0.8*pi*n+0.8*pi); >> stem(n,x)title('2.30(b)的序列')>> xlabel('n')>> ylabel('x')2.30(c)n=[-10:10];>> x=cos(pi*n/5);>> stem(n,x)>> title('the real part')>> xlabel('n')>> ylabel('re(x[n])')>> title('the real part of 2.30(c)')x=sin(pi*n/10);>> stem(n,x)>> title('the imaginary part of 2.30(c)')>> xlabel('n')>> ylabel('im(x[n])')2.30(d)n=[-20:20];>> x=3*cos(1.3*pi*n)-4*sin(0.5*pi*n+0.5*pi);>> stem(n,x)>> title('2.30(d)的序列')>> xlabel('n')>> ylabel('x[n]')2.30(e)n=[-20:20];>> x=5*cos(1.5*pi*n+0.75*pi)+4*cos(0.6*pi*n)-sin(0.5*pi*n); >> stem(n,x)>> title('2.30(e)的序列')>> xlabel('n')>> ylabel('x[n]')M2.7编写的程序如下% Program M2.7% Computation the discreet time system of exercise 2.40alpha=input('alpha=');y0=1;y1=0.5*(y0+(alpha/y0));while abs(y1-y0)>0.0001y2=0.5*(y1+(alpha/y1));y0=y1;y1=y2;enddisp('y[n]收敛于根号alpha=');y2运行结果如下:alpha=9y[n]收敛于根号alpha=y2 =3.0000alpha=30y[n]收敛于根号alpha=y2 =5.4772经两组数据对比,知已用仿真证明,n趋于无穷时,Y[n]收敛于根号下alpha。
matlab1-2

2、语句生成数组
(1)用线性等间距生成向量矩阵(start:step:end) 》a=[1:2:10] 其中start为起始值,step为步长,end a= 为终止值。当步长为1时可省略step参 1 3 5 7 9 数;另外step也可以取负数。 (2)a=linspace(n1,n2,n) •在线性空间上,行矢量的值从n1到n2,数据个数为n, 缺省n为100。 》a=linspace(1,10,10) a= 1 2 3 4 5 6 7 8 9 10
n=input('Please input n: ')
二、矩阵的输入 1、在命令窗口中输入
》a=1; b=2; c=3; 》x=[5 b c; a*b a+c c/b] x= 5.000 2.000 3.000 2.000 4.000 1.500 》y=[2,4, 5 3 6 8] y=
245 368 • 矩阵生成不但可以使用纯数字(含复数),也可以使用变量 (或者说采用一个表达式)。矩阵的元素直接排列在方括号 内,行与行之间用分号隔开,每行内的元素使用空格或逗号 隔开。大的矩阵可以用分行输入,回车键代表分号。
点线
点划 线 虚线
四、 Matlab 语言规则
Matlab 区分大小写,它的命令和函数全是小写的 一行可以输入几个命令,用分号“;” 或逗号“,”隔开 续行符: “…”(三个点),如果语句很长,可用续行符 将一个语句写成多行。续行符的前最好留一个空格。 注释符: “%”,其后面的内容为注释,对 Matlab 的计 算不产生任何影响
基本数学函数
abs(x) max(x) sqrt(x) log(x) sign(x) conj(x) real(x) 绝对值 最大值 开平方 自然对数 符号函数 求复数的共轭 取复数的实部 sum(x) 求和 min(x) 最小值 exp(x) 以e为底的指数 log10(x) 以10为底的对数 mod(x,y) 两整数相除的余数 imag(x) 取复数的虚部
最速下降法求最优解西安电子科技大学matlab结课大作业

西安电子科技大学课程论文数学软件与实验最速下降法求最优解姓名:方正阳学号:07117020班级:07117107112016、最速下降法求最优解1 2 n,然后MATLAB 结课大作业摘要:最速下降法,又称为梯度法,是一种重要的无约束最优化方法。
它是 1847年由著名数学家 Cauchy 给出的,其他解析方法或是它的变形,或是受它 启发而得到,因此它是最优化方法的基础。
该法将 n 维问题转化为一系列 不断迭代过程中沿负梯度方向用一维搜索方法寻优的问题,本次程序设计 利用最速下降法算法,反复迭代,最终收敛于局部最优点,即为解出的二 元函数的无约束非线性规划问题 minf(x,y)。
引言:最优化理论作为运筹学中的一个重要理论方法,在工业生产,金融经济活 动,工商管理,国防建设,计算机应用中,都有着重要的应用。
最优化理论 通过给出生产活动中的各类实际问题的数学模型,通过最优化方法,寻求 该问题的最优解或满意解。
最速下降算法是最优化理论中常见的一个重要 算法,理论证明:最速下降算法在一定条件下是收敛的,它能够有效地求 解一部分无约束最优化问题。
一、 实验目的熟悉最速下降法算法思想和步骤,用 MATLAB 语言编程最速下降法 求最优值。
二、 实验要求在最优化计算方法中,要求解 y = f (x 1, x 2 , , x n ) 的局部最小值,可以采用如下的方法进行迭代计算:先给出初始点 x 0 = (x 0 , x 0 , , x 0)根据其梯度方向 ∇f (x 0),计算一元函数 y (λ1 ) = min f (x λ≥0 0-λ⋅∇f (x 0 )) ,并1 0 0得到x = x -λ1 ⋅∇f (x ) 。
如此反复迭代,最终收敛于局部最优点。
实现 该算法,求 的最优值,a,b,c,d 自定(非 0)三、 实验假设考虑到参数的随机性、代表性,验证程序的正确性、典型性,在此 我们从两个角度出发,一是在 abcd 值确定的情况下改变初始搜索位置 x0,看函数最优解是否相同;二是初始搜索位置 x0 相同,abcd 值不同的 情况下,看函数最优解是否相同。
2021年MATLAB实验报告一西安邮电大学

西安邮电学院《Matlab》实验报告(一)- 年第 1 学期自动化专业:自动0903 班级:学号:姓名:年9月28日MATLAB语言实验项目实验一熟悉MATLAB集成环境与基本运算一、实验目1.熟悉启动和退出MATLAB软件办法、熟悉MATLAB软件运营环境。
2.熟悉MATLAB命令窗口构成。
3.熟悉MATLAB基本操作。
4.掌握建立矩阵办法。
5.掌握MATLAB各种表达式书写规则以及惯用函数使用。
二、实验设备及条件计算机一台(MATLAB Rb软件环境)。
三、实验原理1.MATLAB启动MATLAB系统启动有三种常用办法:1)使用Windows“开始”菜单。
2)运营MATLAB系统启动程序matlab.exe。
3)运用快捷方式。
2.MATLAB系统退出要退出MATLAB系统,也有三种常用办法:1)在MATLAB主窗口File菜单中选取Exit matlab 命令。
2)在MATLAB命令窗口输入Exit或Quit命令。
3)单击MATLAB主窗口“关闭”按钮。
3.MATLAB协助窗口进入协助窗口可以通过如下三种办法:1)单击MATLAB主窗口工具栏中help按钮。
2)在命令窗口中输入helpwin、helpdesk或doc。
3)选取help菜单中“matlab help”选项。
4.MATLAB协助命令1)help命令在MATLAB命令窗口直接输入help命令将会显示当前协助系统中所包括所有项目,即搜索途径中所有目录名称。
同样,可以通过help加函数名来显示该函数协助阐明。
2)lookfor命令help命令只搜索出那些核心字完全匹配成果,lookfor命令对搜索范畴内m 文献进行核心字搜索,条件比较宽松。
3)模糊查询顾客只要输入命令前几种字母,然后按tab键,系统就会列出所有以这几种字母开头命令。
5.赋值语句1)变量=表达式2)表达式6.矩阵建立1)直接输入法:将矩阵元素用方括号括起来,按矩阵行顺序输入各元素,同一行各元素之间用空格或逗号分开,不同行元素之间用分号分开。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y=ax3+x
a=3 a=2 a=1 a=0 a=-1 a=-2 a=-3
a=-3,-2,…?
另一个程序
x=-2:0.1:2; for a=-3:3 plot(x,a*x.^3+x) hold on end grid on axis([-2,2,-3,3])
y=ax3+x
a=3 a=2 a=1 a=0 a=-1 a=-2 a=-3
在同一窗口中设置多个坐标系
t=0:0.1:3*pi figure(1) subplot(4,1,1) y1=sin(t); plot(t,y1) subplot(4,1,2) y3=sin(3*t)/3; plot(t,y3) subplot(4,1,3) y5=sin(5*t)/5; plot(t,y5) subplot(4,1,4) plot(t,y1+y3+y5)
MATLAB在矩阵运算方面被认为是世界上最好的软件
引入了数据阵列类型,并提供工具函数
向量(行向量,列向量) 二维矩阵 多维矩阵(矩阵分页) 结构阵列 单元阵列 为系统的数学模型的建立、测试、仿真提供平台
是理工科学生必须掌握的基本工具
出色的绘图功能
例1:绘制曲线
y=e
-x2
其中, x∊[-2,2],每隔0.1取1个点 x=-2 : 0.1 : 2 ; % x为向量 y=exp(-x.^2); plot(x,y)
电位三维立体图
等位线及电场分布图
MATLAB模拟电流元的电磁波方向图
电流元辐射的方向 图,表示电磁场在 某方向上的强弱
对于电流元:
F(x)=sin(θ)
MATLAB在信号与系统中的应用
连续信号的研究
如产生单位脉冲、单位阶跃信号 信号的冲击向应
离散信号的研究
离散傅里叶变换 数字滤波器设计
利:在信号与系统中的应用
在同一窗口中显示多个波形
t=0:0.1:3*pi;
y1=sin(t); y3=sin(3*t)/3; y5=sin(5*t)/5;
plot( t,y1,
t,y3,
t,y5,
t,y1+y3+y5 )
多次叠加逼近方波(K=10)
MATALAB图象处理的应用介绍
图象文件的读取,存储,显示,打印 图象的调色板应用 图象过滤处理
x y为向量
例2:绘制三维图形
y=e
-x2
z=e
-x2-y2
plot(x, y)
其中, x∊[-2,2] y∊[-2,2] … z=exp(-x.^2-y.^2) mesh(x,y,z)
y=e
plot(x, y)
-x2
z=e
-x2-y2
mesh(x,y,z)
例3:考虑下列函数的图形
z=X*e
-x2-y2
MATLAB除基本系统外,还有两个重要的模块
MATLAB基本系统
Toolbok
针对不同的应用领域, MATLAB提供了大量的实用函数, 称为“工具箱”
Simulink
系统仿真: DSP、 通信系统、控制统、 …
MATLAB的工具箱函数
Toolbook(工具箱)是一组一组的函数集合 信号处理工具箱(Signal Processing Toolbox) 图像处理工具箱(Image Processing Toolbox) 定点运算工具箱(Fixed-point Blockset) 控制系统工具箱(Control Toolbox) 模糊系统工具箱(Fuzzy Toolbox) 地理信息处理工具箱(Mapping Toolbox) 通讯工具箱(Communications Toolbox) … (P302)
例:
三次抛物线的方程为 y=ax3+x 当参数a分别为-3、-2、-1、0、 1、2、3时 在同一坐标绘制其波形图, 试探讨参数a对其图形的影响. 其中 X∈[-2,2],步长0.1
x=-2:0.1:2; y=zeros(7,length(x)) i=0 for a=-3:3 i=i+1 y(i,:)=a*x.^3+x end plot(x,y(1:7,:)) axis([-2 2 -3 3]) grid on
MATLAB可方便的处理虚数
二次曲面的方程如下
要求讨论参数a,b,c对其形状的影响, 并画出其图形.
注意在给定了x,y值求z时,若有开方运算, 会出现虚数.(如X=5i)
a=5i,b=4,c=3,d=1
a=5,b=4,c=3,d=1
a=5i,b=4i,c=3,d=1
MATLAB在物理学中的应用
MATALAB 几条 C语言 几十条 汇编语言 3000多条
例. 无需复杂算法的矩阵运算 计算 C=A2X3 * B3X2
% m 文件 运行结果: A=[ 1 2 3 4 5 6]; C= B=[ 1 2 22 28 3 4 49 64 5 6 ]; C=A*B 不需要深究其算法,
无法比拟的矩阵运算
MATLAB特点与应用
MATLAB是一种矩阵语言
它以矩阵为最基本的运算单元 如,所有变量都是矩阵型的 工作空间 A=12; B=[1 2 3]; C=‘ABC’ ; D=[ ]
语言简练而功能强大
● 编程效率高,程序员不必过多的研究算法, ●一条MATLAB语句相当于其他高级语言中 几十条几百条甚至几千条语句
可用MATLAB研究普通物理中的各种问题: 物体的运动轨迹 力的分解与合成 电磁场中电场分布与磁场分布 光与波的振动
例:电磁场中的电场分布
在普通物理中,已知空间电位分布的表示式为: V=V(x,y,z) 则空间的电场等于电位场的负梯度: 计算电场强度并画出等电位线和电场方向.
为X,Y,Z方向的单位向量, MATALAB是靠数值微分的方法进行运算, 并绘出图形.
… z=x.*exp(-x.^2-y.^2) mesh(x,y,z)
可设置曲面的线型
可设置曲面的线型
网格
网格加舞台
z=x*e
流水线
-x2-y2
三维曲线
可设置不同的颜色
网格 着色
z=x*e
平滑
-x2-y2
改变调色板
可设置不同的材质,光源和视角
瓷砖 陶瓷
改变调色板
改变视角
实用工具箱拓宽了应用领域
THE END
图象文件的显示
MATLAB由X光数据画出的人体 骨骼图
图象的调色板应用
对图片进行过滤
noice
原始图形
添加噪声后 的噪声
MATLAB 过滤处理
原始图形
添加噪声后 的噪声
MATLAB的在线演示
在命令窗口中打开菜单 help/demos
弹出演示窗口
在线演示
显示M文件
作业题:P30 1.1 MATLAB的主要 特点是什么? 1.6 练习使用 MATLAB的集成环境, 熟悉系统提供的各 种工具.
例: 利用基波及其奇次谐波合成方波
多次叠加逼近方波
t=0:0.1:3*pi figure(1) y1=sin(t); plot(t,y1) figure(2) y3=sin(3*t)/3; plot(t,y3) figure(3) y5=sin(5*t)/5; plot(t,y5) figure(4) plot(t,y1+y3+y5)
MATLAB的特点归纳
主要体现在以下几个方面:
强大的运算能力 出色的图形功能 丰富的Toolbook函数 系统仿真
MATLAB的应用
几乎涵盖了当今所有领域
数据处理与分析(图象处理,数学分析) 电子线路设计与仿真 工业制造 自动控制 建筑设计 医学研究
MATLAB在高等数学中的应用
由于数学模型非常明确,MATLAB在高等数 学中的应用是非常便利的. 求解函数的极限、导数 数值积分 空间解析几何的研究 数列和级数 线性代数
