负数移位运算讲解
负数运算法则公式(一)

负数运算法则公式(一)负数运算法则公式在数学中,我们经常会遇到负数的运算。
负数运算法则是指一系列针对负数的运算规则和公式。
本文将列举常用的负数运算法则公式,并且通过举例进行解释说明。
1. 两个负数相加当两个负数相加时,我们可以先忽略负号,将其视为正数相加,最后再加上负号。
具体公式如下:(-a) + (-b) = -(a + b)例如,计算 -3 + (-5) 的结果,首先将两个负数视为正数相加,得到 3 + 5 = 8,最后再加上负号,所以 -3 + (-5) = -8。
2. 正数与负数相加当一个正数与一个负数相加时,我们可以按照绝对值较大的数的符号进行运算,并取绝对值较大的数的绝对值减去绝对值较小的数的绝对值的结果的符号。
具体公式如下:a + (-b) = a - b例如,计算 7 + (-4) 的结果,我们取绝对值较大的 7 的符号,即正号,并取绝对值较大的 7 的绝对值减去绝对值较小的 4 的绝对值的结果的符号,所以 7 + (-4) = 7 - 4 = 3。
3. 负数相减当两个负数相减时,我们可以先将其转化为加法运算,即将减法转化为加上相反数。
具体公式如下:(-a) - (-b) = (-a) + b = b - a例如,计算 -9 - (-2) 的结果,我们将减法转化为加上相反数,即 -9 - (-2) = -9 + 2 = -7。
4. 负数与正数相乘当一个负数与一个正数相乘时,我们可以忽略负号,将其视为正数相乘,最后再加上负号。
具体公式如下:(-a) * b = -(a * b) = a * (-b)例如,计算 -5 * 2 的结果,首先将两个数的绝对值相乘,得到5 * 2 = 10,最后再加上负号,所以 -5 * 2 = -(5 * 2) = -10。
5. 除以负数当一个数除以一个负数时,我们可以先将负数转化为其相反数,然后进行正常的除法运算。
具体公式如下:a / (-b) = -a / b例如,计算 8 / (-4) 的结果,我们将负数 -4 转化为其相反数4,然后进行正常的除法运算,即 8 / (-4) = -8 / 4 = -2。
负数移位运算

负数移位运算
负数移位运算是指对于负数在二进制表示下进行移位运算。
在进行负数移位运算时,需要将负数转化为补码表示。
移位运算分为左移和右移两种。
左移运算会将二进制表示向左移动指定的位数,空缺的位数用0填充。
在负数移位运算中,如果左移后最高位为1,则表示结果为负数,需要将结果转化为补码表示。
例如,对于-4进行左移1位,得到的结果为-8。
右移运算会将二进制表示向右移动指定的位数,空缺的位数用0或1填充,取决于移位前数值的符号。
在负数移位运算中,右移运算会保留符号位。
例如,对于-4进行右移1位,得到的结果为-2。
需要注意的是,由于负数的二进制表示采用补码表示,因此在进行移位运算时,需要注意符号位的处理。
同时,由于移位运算可能会改变数值的符号,因此在实际应用中,需要根据具体情况进行处理。
- 1 -。
移位运算详解

System.out.println("2右移1位后的原码(相当于除2)");
System.out.println("0000000000000000000000000000000"
+ Integer.toBinaryString(2 >>> 1));
System.out.println("0000000000000000000000000000000"
+ Integer.toBinaryString(2 >>> 1));
System.out.println("################");
System.out.println("负数有符号右移的步骤");
移位运算详解
1
下面是负-2的补码,也是负数的内存中实际存储的形式。
11111111111111111111111111111110
下面是-2的反码:
11111111111111111111111111111101
下面是正2的原码:
前面省略30个0:……10
-2
##################
2的编码(原码)
负数a无符号右移(为正)后的编码(补码-并直接补0)
01000000111111101000000000000000
负数a的编码(补码)
10000001111111010000000000000000
负数a右移(仍然为负)的编码(补码)
11000000111111101000000000000000
位运算符的用法

位运算符的用法位运算符是计算机程序设计中常用的一种运算符,主要用于处理二进制数据,例如计算机存储器中的字节数据。
位运算符可以帮助开发人员在一定程度上操作和调整内存中的字节数据,从而提升程序的执行效率。
位运算符的用法可以用一下几种方式来分类:1. 位移运算:位移运算是指通过移动某个位上的二进制数据来调整内存中的字节数据。
常用的位移运算符有左移运算符(“)和右移运算符(“>>”)。
2. 位反向运算:位反向运算将某个位上的二进制数据翻转过来,例如将0变成1,将1变成0。
常用的位反向运算符有取反运算符(“~”)和翻转位运算符(“^”)。
3. 位与、或、异或运算:位与、或、异或运算可以用于比较两个二进制数据的区别。
常用的位与、或、异或运算符分别为“&”、“|”、“^”。
4.合赋值运算:组合赋值运算可以用于组合多个位上的二进制数据,常用的组合赋值运算符有“&=”、“|=”、“^=”。
位运算符在计算机程序设计中有很多用途,比如可以用于定义内存中的字节数据,也可以用于进行条件判断,还可以用于比较两个数据是否相等。
因此,在计算机程序设计中,位运算符有着十分重要的作用。
尽管位运算符具有许多用途,但是要注意位运算符的操作都是基于二进制数据的,它只能操作字节数据的最小单位,而不能操作整型数据,因此不能直接使用位运算符来进行十进制或其他进制的计算。
另外,在使用位运算符时,也要注意不同的运算符有着不同的作用,而且运算的结果也是不同的,因此,使用位运算符时需要特别注意运算符的用法,避免出现错误的结果。
总的来说,位运算符在计算机程序设计中有着重要的作用,其用法非常复杂,开发人员在使用时需要特别小心,以免出现错误的结果。
移位

定点数运算定点数运算包括移位、加、减、乘、除几种。
一、移位运算1.移位的意义移位运算在日常生活中常见。
例如15米可写作1500厘米,单就数字而言,1500相当于小数点左移了两位,并在小数点前面添了两个0;同样15也相当于1500相对于小数点右移了两位,并删去了小数点后面的两个0。
可见,当某个十进制数相对于小数点左移n位时,相当于该数乘以10n;右移n位时,相当于该数除以10n。
计算机中小数点的位置是事先约定的,因此,二进制表示的机器数在相对于小数点作n位左移或右移时,其实质就便该数乘以或除以2n(n=1,2...n)。
移位运算又叫移位操作,对计算机来说,有很大的实用价值,例如,当计算机没有乘(除)运算线路时,可以采用移位和加法相结合,实现乘(除)运算。
计算机中机器数的字长往往是固定的,当机器数左移n位或右移n位时,必然会使其n位低位或n位高位出现空位。
那么,对空出的空位应该添补0还是1呢这与机器数采用有符号数还是无符号数有关,对有符号的移位叫算术移位。
2.算术移位规则对于正数,由于[x]原=[x]补=[x]反=真值,故移位后出现的空位均以0添之。
对于负数,由于原码、补码和反码的表示形式不同,故当机器数移位时,对其空位的添补规则也不同。
下表列出了三种不同码制的机器数(整数或小数均可),分别对应正数或负数,移位后的添补规则。
必须注意的是:不论是正数还是负数,移位后其符号位均不变,这是算术移位的重要特点。
不同码制机器数移位后的空位添补规则码制添补代码正数原码、补码、反码0原码0负数补码左移添0右移添1反码1由上表可得出如下结论:(1)机器数为正时,不论左移或右移,添补代码均为0。
(2)由于负数的原码其数值部分与真值相同,故在移位时只要使符号位不变,其空位均添0。
(3)由于负数的反码其各位除符号位外与负数的原码正好相反,故移位后所添的代码应与原码相反,即全部添1。
(4)分析任意负数的补码可发现,当对其由低位向高位找到第一个“1”时,在此“1”左边的各位均与对应的反码相同,而在此“1”右边的各位(包括此“1”在内)均与对应的原码相同,即添0;右移时困空位出现在高位,则添补的代码应与反码相同,即添1。
正数负数复习正负数的平移和旋转

正数负数复习正负数的平移和旋转正负数是数学中的基本概念,我们在日常生活中经常会用到。
了解正负数的平移和旋转对于数学的学习和应用都非常重要。
本文将重点介绍正负数的平移和旋转的基本概念和应用。
一、正负数的平移正负数的平移是指在数轴上对数进行左右移动。
正数的平移是指向右移动,负数的平移是指向左移动。
平移的距离由数的绝对值决定,如果平移的距离是一个正数a,则正数平移a个单位,负数平移-a个单位。
举例来说,如果有一个正数3,向右平移2个单位,则结果为正数5;如果有一个负数-5,向左平移3个单位,则结果为负数-8。
平移的另一个应用是求两个数之间的差值。
假设有两个数a和b,a、b都是正数。
如果b大于a,则两数之间的差值等于b向左平移a个单位后的值。
如果b小于a,则两数之间的差值等于a向右平移b个单位后的值。
例如,有两个数a=6和b=3,b小于a。
我们可以将a向右平移3个单位,得到9,这样两个数之间的差值就是9-3=6。
二、正负数的旋转正负数的旋转是在数轴上对数进行顺时针或逆时针旋转。
正数的旋转方向为逆时针,负数的旋转方向为顺时针。
旋转的角度由数的绝对值决定,如果旋转的角度是一个正数a,则正数逆时针旋转a度,负数顺时针旋转-a度。
举例来说,如果有一个正数5,逆时针旋转30度,则结果为5*cos(30°)+5*sin(30°);如果有一个负数-8,顺时针旋转60度,则结果为-8*cos(60°)-8*sin(60°)。
旋转的另一个应用是求两个数之间的夹角。
假设有两个数a和b,a、b都是正数。
如果b大于a,则两数之间的夹角等于b逆时针旋转a度后的值。
如果b小于a,则两数之间的夹角等于a顺时针旋转b度后的值。
例如,有两个数a=45和b=60,b大于a。
我们可以将b逆时针旋转45度,得到60*cos(45°)+60*sin(45°),这样两个数之间的夹角就是旋转后的值。
负数移位运算讲解
C語言中負數移位運算講解
“<<”、“>>”為移位運算符。
“<<”為左移位運算符,即數據字節中的每個二進制位同時向左移位。
如“x<<n”表示x中的每個二進制位同時向左移動n位。
“>>”為右移位運算符,即數據字節中的每個二進制位同時向右移位。
如“x>>n”表示x中的每個二進制位同時向右移動n位。
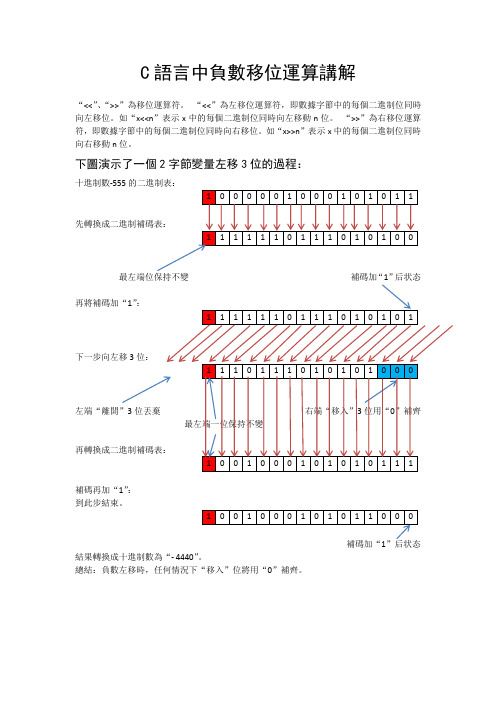
下圖演示了一個2字節變量左移3位的過程:
十進制數-555
最左端位保持不變補碼加“1”后状态
補碼再加“1”:
到此步結束。
結果轉換成十進制數為“- 4440”。
總結:負數左移時,任何情況下“移入”位將用“0”補齊。
“>>”右移位運算可分為兩種情況:一種是移入“0”的叫邏輯右移;一種是移入“1”的叫算術右移。
負數右移用到的是算術右移。
下圖演示了一個2字節變量右移3位的過程:
十進制數-555
最左端位保持不變補碼加“1”后状态
再將補碼加“
下一步向右移
左端“移入”
補碼再加“1”:
到此步結束。
結果轉換成十進制數為“- 70”。
總結:負數右移時,任何情況下“移入”位將用“1”補齊。
注:二進制表最左端的二進制位表示符號位,“+”用“0”表示,“-”用“1”表示。
javascript中负数算术右移、逻辑右移的奥秘探索

javascript中负数算术右移、逻辑右移的奥秘探索javascript中负数的算术右移和逻辑右移都⼗分的让⼈迷惑,特别是逻辑右移>>>,你会发现即使⼀个很⼩的负数,右移之后,也会得到⼀个⽆⽐巨⼤的数,这是为什么呢?原来在逻辑右移中符号位会随着整体⼀起往右移动,这样就是相当于⽆符号数的移动了,最后得到的就是⼀个正数,因为符号位不存在了。
⾸先逻辑右移产⽣的⼀定是32位的数,然后负数的符号位为1,这意味着从第32位到符号位的位置全部由1填充,这样的数能不⼤吗例如-1,逻辑右移0位表现形式就是1111 1111 1111 1111 1111 1111 1111 1111 ,这样的数是当作正数来对待的!所以将-1逻辑右移N位,最后的结果都是全为1!左移运算保留数字的符号位。
例如,如果把 -2 左移 5 位,得到的是 -64,⽽不是 64。
“符号仍然存储在第 32 位中吗?”是的,不过这在 ECMAScript 后台进⾏,开发者不能直接访问第 32 个数位。
即使输出⼆进制字符串形式的负数,显⽰的也是负号形式(例如,-2 将显⽰ -10。
)有符号右移运算符由两个⼤于号表⽰(<$lt;)。
它把 32 位数字中的所有数位整体右移,同时保留该数的符号(正号或负号)。
有符号右移运算符恰好与左移运算相反。
例如,把 64 右移 5 位,将变为 2:var iOld = 64; //等于⼆进制 1000000var iNew = iOld >> 5; //等于⼆进制 10 ⼗进制 2同样,移动数位后会造成空位。
这次,空位位于数字的左侧,但位于符号位之后。
ECMAScript ⽤符号位的值填充这些空位,创建完整的数字,如下图所⽰:⽆符号右移运算符由三个⼤于号(>>>)表⽰,它将⽆符号 32 位数的所有数位整体右移。
对于正数,⽆符号右移运算的结果与有符号右移运算⼀样。
⽤有符号右移运算中的例⼦,把 64 右移 5 位,将变为 2:⽆符号右移运算⽤ 0 填充所有空位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C語言中負數移位運算講解
“<<”、“>>”為移位運算符。
“<<”為左移位運算符,即數據字節中的每個二進制位同時向左移位。
如“x<<n”表示x中的每個二進制位同時向左移動n位。
“>>”為右移位運算符,即數據字節中的每個二進制位同時向右移位。
如“x>>n”表示x中的每個二進制位同時向右移動n位。
下圖演示了一個2字節變量左移3位的過程:
十進制數-555
最左端位保持不變補碼加“1”后状态
補碼再加“1”:
到此步結束。
結果轉換成十進制數為“- 4440”。
總結:負數左移時,任何情況下“移入”位將用“0”補齊。
“>>”右移位運算可分為兩種情況:一種是移入“0”的叫邏輯右移;一種是移入“1”的叫算術右移。
負數右移用到的是算術右移。
下圖演示了一個2字節變量右移3位的過程:
十進制數-555
最左端位保持不變補碼加“1”后状态
再將補碼加“
下一步向右移
左端“移入”
補碼再加“1”:
到此步結束。
結果轉換成十進制數為“- 70”。
總結:負數右移時,任何情況下“移入”位將用“1”補齊。
注:二進制表最左端的二進制位表示符號位,“+”用“0”表示,“-”用“1”表示。
