巧求阴影部分面积
小学数学求阴影面积9种万能解法

小学数学求阴影面积9种万能解法!
其实,小学数学并不难,都是一些基础知识,要说稍难的也就几何基础和应用题。
那今天我就先讲讲让学生们头疼的几何,下次再和大家一起来分析分析应用题。
我们知道几何知识的教学是运用实物、图形等直观教具、学具,让学生通过观察、分析、比较来发现几何形体的特征,掌握有关的知识。
重视直观教学,加强动手操作,发展学生的空间观念,是几何教学的重要规律。
在数学几何考试中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算,一般我们称这样的图形为不规则图形。
对于这类不规则图形,考试常考的就是求图形中的阴影面积。
“几何”问题不仅是小学数学的重点,到了初高中数学学习中也占很大比重,内容是循序渐进的,所以基础一定要打好。
下面这9种方法就是我今天分享给大家的内容,家长们赶紧收藏让孩子在单元考试前好好掌握吧!相信只要孩子掌握了这9种求面积的方法,数学考试再也不怕了!。
六年级阴影面积计算技巧和方法

六年级阴影面积计算技巧和方法嘿呀!今天咱们就来好好聊聊六年级阴影面积计算的那些技巧和方法!首先呢,咱们得明白啥是阴影面积。
哎呀呀,简单说就是图形中那些被阴影盖住的部分,咱们得想办法算出它的大小。
第一种方法,直接计算法!哇,这个方法可简单啦!如果阴影部分是个规则的图形,像正方形、长方形、三角形呀,那咱们就可以直接用对应的面积公式来算。
比如说三角形的面积就是底乘以高除以2 呢。
这是不是挺容易的?接下来,是割补法!哎呀呀,这个方法有点巧妙哦!如果阴影部分的形状不太规则,咱们就可以把它分割成几个规则的图形,或者给它补上一块,变成一个咱们熟悉的规则图形,然后再去计算。
比如说一个不规则的阴影图形,咱们可以把它分割成一个三角形和一个梯形,分别算出它们的面积,再相加或者相减,就能得到阴影部分的面积啦!还有呢,就是等量代换法!哇塞,这个方法可神奇啦!有时候,咱们可以通过找到图形之间的等量关系,把要求的阴影面积转换成我们能计算的图形面积。
比如说,两个三角形等底等高,那它们的面积就相等呀,就可以相互替换来计算阴影面积。
再说说添加辅助线法!嘿,这个方法可有用啦!当图形看起来很复杂,不好计算的时候,咱们就可以巧妙地添加一些辅助线,把图形分成几个部分,这样就能更清楚地看出阴影部分和其他部分的关系,从而计算出阴影面积。
还有一个很重要的方法,就是重叠法!哎呀呀,这个有点难理解,我给您好好讲讲。
比如说两个图形有一部分重叠在一起,形成了阴影部分,咱们可以先分别算出两个图形的面积,再减去重叠部分的面积,剩下的就是阴影部分的面积啦!在实际计算阴影面积的时候,咱们要仔细观察图形的特点,灵活运用这些方法。
有时候,可能需要同时使用几种方法呢!哎呀,计算阴影面积可真是个有趣又有点挑战的事情呀!您瞧瞧,这些方法是不是很实用呢?只要多练习,多思考,计算阴影面积对咱们六年级的同学来说,就不再是难题啦!哇,加油呀,同学们!相信大家都能掌握这些技巧,在数学的海洋里畅游!怎么样,您对这些方法清楚了吗?是不是感觉数学也没那么难啦?。
巧求阴影部分的面积

巧求阴影部分的面积求平面图形阴影部分的面积是近年中考的一个热点,其图形多数是由一些基本图形(如三角形、平行四边形、梯形、扇形、圆等)进行组合、重叠而成的。
因此,解此类问题时,要仔细观察和分析图形,明确该图形是由哪些简单而规则的图形组合而成,或是通过观察把不规则的图形转化为规则图形,利用整体思想迅速获解,学会分解和组合图形,明确要计算图形的面积,可以通过哪些图形的和或差得到,切勿盲目计算。
现举例谈谈几种主要的方法:一、利用平移巧求阴影部分的面积例:如图,大半圆O 与小半圆O 1相切于点C ,大半圆的弦AB 与小半圆相切于点F ,且AB ∥CD ,AB=4㎝,求阴影部分的面积。
点评:1、如果直接求阴影部分的面积,必须要知道大半 圆O 与小半圆O1的半径,而从已知条件无法求出。
2、将小半圆O 1沿CD 平移将两个半圆变为同心 圆,将阴影部分面积变为半圆环的面积。
3、连结OF ,利用切线及勾股定理,可求出大圆半径的平方与小圆半径的平方的差。
解:将半圆O 1向右迁移,使点O 1与点O 重合。
∴S 阴=S 半圆O-S 半圆O1∴S 阴=21π(OB 2-OF 2)=21π·BF 2 ∵AB=4㎝ ∴BF=2㎝∴S 阴=2π(㎝2)二、利用对称性巧求阴影部分面积例2:如图,在△ABC 中,AB=AC=5,BC=6,点E 、F 是中线AD 上两点,则图中阴影部分的面积是( )A CA 6B 12C 24D 30 点评:本题是一道无规则的阴影面积的求解问题,及轴对称图形的性质得BC=DC=3,AD ⊥BC ,S △ABC =S △EFB 又AD 2=AB 2-BD 2=52-32 ∴AD=4所以,S 阴=S △ABD =21×3×4=6,故选A 三、利用代数法巧求阴影部分的面积。
例3:如图:正方形ABCD 的边长为a ,分别以A 、B 、C 、D 为圆心,以a 为半径画弧,求阴影部分的面积。
运用整体思维巧求阴影面积

运用整体思维巧求阴影面积作者:栗先妹来源:《新课程·上旬》 2015年第6期粟先妹(广西壮族自治区桂林市临桂县教育局教研室)在小学高年级数学《求平面组合图形阴影部分面积》解题中,碰到不能按常规的方法解决问题时要突破思维定式。
合理运用“整体思维”,往往可以化繁为简,化难为易,巧妙地求出阴影部分面积。
例1.图1圆的面积是31.4平方分米,那么,阴影部分面积是多少平方分米?分析与解:该题是求三角形的面积,多数学生受思维定式的影响,只想求出这个三角形的底和高(即:圆的半径r),而本题所提供的条件只能求出r2=10,由于小学还没有学习开方的知识,因此解题思路陷入了困境,没有办法求出r的值,也就无法求出阴影部分面积是多少平方分米。
要解决这个问题,我们不妨引导学生“运用整体思维,把r2=10整体代入三角形的面积计算公式”:S阴=1/2ah=1/2r2(a=h=r)=1/2×10(r2=31.4÷3.14=10)=5(平方分米)例2.如图2,正方形的边长是4厘米,AB=CD=2厘米,O是正方形内任意一点。
求阴影部分的面积是多少平方厘米。
分析与解:根据已知条件,上下两个阴影三角形的底AB=CD=2厘米。
但是因为这两个三角形的公共顶点O是正方形内任意一点,所以两个三角形的高是无法确定的,因此,按常规的方法:“先分别求出两个三角形的面积,再求它们的和”是不可能找到问题的答案的。
如果我们转换一种思维的方式:从整体观察图形,我们可以发现上下两个三角形的高之和正好是正方形的边长,这就是h上+h下=4厘米。
由此可得:S阴=S上+S下=1/2×AB×h上+1/2×BC×h下=1/2×2×h上+1/2×2×h下=h上+h下=4(平方厘米)例3.如图3,圆的面积是36平方米,求阴影部分的面积一共是多少?分析与解:解这道题目时,让学生感到困惑的是阴影部分是由两个不规则图形和一个不知道半径的扇形组合而成,也就是各个图形均无法直接找到公式计算其面积,显然,通过求各部分的面积之和来求阴影部分的面积一共是多少,这条路就行不通了。
(完整版)求阴影部分面积的几种常用方法

总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,下图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,下图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为|:四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求下图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如下图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如下图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如下图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求下图(1)中阴影部分的面积,可将左半图形绕B 点逆时针方向旋转180°,使A与C 重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求下图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
专题8 巧求圆中阴影部分的面积(含答案)

专题8 巧求圆中阴影部分的面积【知识解读】求与圆有关的阴影部分的面积,能考查同学们的观察能力、随机应变能力和综合运用数学知识的能力,解答此类问题要注意观察和分析图形的形成,学会分解和组合图形,消除思路中的“阴影”,明确要计算图形的面积,可以通过哪些图形的和或差得到,就能给解决问题带来一片光明,切勿盲目计算;下面介绍几种常用的解法.培优学案【典例示范】等积变换法:是在不改变图形面积的前提下,利用“等底、等高的两个三角形的面积相等”,将不规则图形转化为规则图形的面积来求解的方法.例1 如图1-8-1,点P 是半径为1的⊙O 外一点,OP =2,P A 切⊙O 于点A ,弦AB ∥OP ,连接PB ,则图中阴影部分的面积是.图181AB OP图182ABCDEMNO【跟踪训练】如图1-8-2,AB 是⊙O 的直径,MN 是⊙O 的切线,C 为切点,过点A 作AD ⊥MN 于点D ,交⊙O 于点E .已知AB =6,BC =3,求图中阴影部分的面积.【解答】和差法:是指将阴影部分看作两个规则图形的和或差.例2 如图1-8-3,扇形OAB 中,∠AOB =60°,扇形半径为4,点C 在BC 上,CD ⊥OA ,垂足为点D ,当CD =OD 时,图中阴影部分的面积为.图183BCD图184CEF【跟踪训练】如图1-8-4,在等腰直角三角形ABC 中,∠C =90°,点D 为AB 的中点,已知扇形EAD 和扇形FBD 的圆心分别为点A 、点B ,且AC =2,则图中阴影部分的面积为(结果不取近似值).割补法:是在不改变图形面积的前提下,通过割补,将发散的图形面积集中在一起,把不规则的图形凑合成规则图形的方法.例3 如图1-8-5,半径为2cm ,圆心角为90°的扇形OAB 中,分别以OA ,OB 为直径作半圆,则图中阴影部分的面积为cm 2.图185ABO图186A 'O 'O ABC【跟踪训练】如图1-8-6,将半圆O 绕直径AB 的端点B 逆时针旋转30°,得到半圆O ′,A ′B 交直径AB 于点C ,若BC =23,则图中阴影部分的面积为 .【提示】连接O ′C ,A ′C ,将阴影部分的面积通过割补,转化为△BO ′C 的面积加上扇形O ′AC 的面积.特殊位置法:是在不改变题意的前提下,通过取特殊位置,将图形特殊化,以方便求解.例4 如图1-8-7,一个半径为r 的圆形纸片在边长为a (a >3r )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“接触不到的部分”的面积是()A .23r πB 233π- C .()233r πD .2r π【提示】解答本题的关键是搞清楚圆形纸片“不能接触到的部分”的面积,即圆形纸片与正三角形的相邻两边都相切时,两切点与正三角形的一个顶点形成的曲边三角形的面积.图187图188【跟踪训练】如图1-8-8,一张半径为1的圆形纸片在边长为a (a ≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触到的部分”的面积是() A .2a π-B .()24a π-C .πD .4π-整体代换法:是指在解答过程中,可将某些不易求的且不发生变化的量看作整体处理. 例5 如图1-8-9,在Rt △ABC 中,∠C =90°,CA =CB =4,分别以A ,B ,C 为圆心,以12AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是.图189CBA【提示】直接求阴影部分的面积是不可能的,根据题意结合图形,知阴影部分的面积等于直角三角形的面积减去三个扇形的面积,其中A ,B 两个扇形的面积无法直接求出,但若把它们看作一个“整体”,则问题易求.【跟踪训练】1.如图1-8-10,正方形的边长a ,以各边为直径在正方形内画半圆,则图中阴影部分的面积为 . 【提示】图中阴影部分的面积可以看作四个半圆的面积之和与正方形的面积之差.CBAOFEDCBA2.如图1-8-11,⊙A ,⊙B ,⊙C 两两不相交,且半径都是2cm ,则图中三个扇形(即阴影部分)面积之和是 cm 2.【提示】图中3个扇形正好拼成一个圆心角为180°的大扇形。
巧算阴影部分的面积
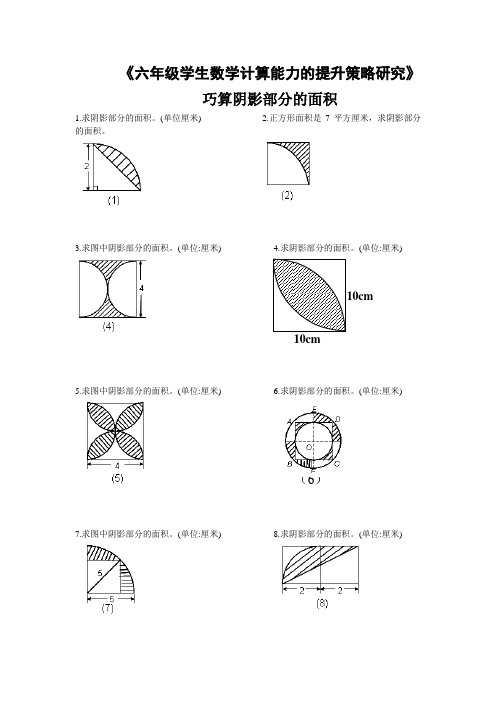
《六年级学生数学计算能力的提升策略研究》
巧算阴影部分的面积
1.求阴影部分的面积。
(单位厘米)
2.正方形面积是7平方厘米,求阴影部分的面积。
3.求图中阴影部分的面积。
(单位:厘米)
4.求阴影部分的面积。
(单位:厘米)
10cm
5.求图中阴影部分的面积。
(单位:厘米)
6.求阴影部分的面积。
(单位:厘米)
(6)
7.求图中阴影部分的面积。
(单位:厘米) 8.求阴影部分的面积。
(单位:厘米)
9.求图中阴影部分的面积。
(单位:厘米) 10.求阴影部分的面积。
(单位:厘米)
(10)
11.求图中阴影部分的面积。
(单位:厘米) 12.求阴影部分的面积。
(单位:厘米) 13.求图中阴影部分的面积。
(单位:厘米) 14.求阴影部分的面积。
(单位:厘米)
15.三角形ABC是直角三角形,阴影部分甲比阴影部分16.求图中阴影部分的面积。
(单位:厘米)乙面积大28平方厘米,AB=40厘米。
求BC的长度。
(15)
(15)。
巧用数学方法 妙求阴影面积

巧用数学方法妙求阴影面积作者:潘兰芳来源:《读写算·基础教育研究》2017年第09期在教学中经常会遇到求阴影部分面积的问题,有些问题,看似无从下手,但认真分析会发现其图形多数是由一些基本图形比如三角形、平行四边形、梯形、扇形、圆等进行组合、重叠而成的。
因此,明确该图形是由哪些简单而规则的图形组合而成,是解决问题的关键。
适当而又巧妙地运用数学思想方法,往往能顺利求解。
一、和差法如图1,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)解析:连接AD,因为△ABC是等腰直角三角形,故∠ABD=45°,再由AB是圆的直径得出∠ADB=90°,故△ABD也是等腰直角三角形,所以AD=BD,S阴影=S△ABC﹣S△ABD﹣S弓形AD由此可得出结论.S阴影=S△ABC﹣S△ABD﹣S弓形AD=24-4π总结:利用基本图形的面积的和与差求出阴影图形的面积.二、整体法如图2,有5个半径都是1的圆,顺次连接5个圆心得五边形ABCDE,则图中阴影部分的面积之和为_____________解析:图中五个扇形的半径虽然已知,但却无求出每个扇形的圆心角的度数可运用整体思想,把这五个扇形拼在一起考虑. 即五个扇形拼在一起可拼成一个整圆和一个半圆. S阴影=32π·12=32π总结:利用整体思想求阴影部分的面积.三、等积变换法如图3,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π).解析:连接OD,根据切线的性质可知∠ODC=90°,因此可证得AC//OD,然后根据平行的性质和圆的半径可证AD是∠CAB的平分线;連接OE、ED,可证得△OAE为等边三角形,然后根据圆周角定理可得∠ADE=30°,由题意可得∠OAD=30°,可证得ED//AB,再由同底等高可知S△AED=S△OED,然后把求阴影部分的面积转化为求扇形ODE的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如下图:正方形边长为2厘米,求阴影部分面积。
思路引导:把“叶形”平均分成2份,然后拼成下面的图形。
即一个半圆减去一个三角形。
列式:2÷2=1(厘米)
1/2×3.14×12-2×1÷2
=1.57-1
=0.57(平方厘米)
2、如下图,已知正方形面积为18平方厘米,求阴影部分的面积。
思路引导:很容易看出,要求阴影部分的面积只要用正方形的面积-圆的面积,但求圆的面积比较困难,因为我们不知道圆的半径,看似可以求出正方形的边长,就可以知道圆的直径了,但小学没有学过开方。
因此,我们只能想别的办法,用设未知数的方法试一试。
设圆的半径为r,那么正方形的面积=2r×2r=18,于是得到下面的等式:
2 r×2r=18
4r2=18
4r2=18÷4
r2=4.5
图中圆的面积:3.14×r2=3.14×4.5=14.13(平方厘米)
阴影部分的面积:18-14.13=3.87(平方厘米)
3、如下图正方形的面积是18平方厘米。
求图中阴影部分的面积。
思路引导:很容易看出图中阴影部分面积=正方形面积-四分之一圆的面积,然而我们发现圆的面积无法计算,因为我们不知道圆的半径或者直径,虽然说求出正方形的边长就能知道圆的直径,可是小学阶段没有学习开方,这条路子也行不通。
很容易联想到上面一题的做法,我们设圆的半径为r,那么正方形的面积=r×r=18,于是有下面的等式:
r×r=18
r2=18
阴影部分面积:18-1/4×3.14×18
=18-14.13
=3.87(平方厘米)
4、如右图:正方形的边长6分米,求图中阴影部分的面积。
怎么计算阴影部分的面积?
思路引导:观察图形,如果把空白的四部分剪下,组合在一起,可以拼成一个半径是3分米的圆形,这样图中的四块阴影部分的面积就可以从正方形面积中减去这个圆的面积求出。
列式: 6×6-3.14×32
=36-3.14×9
=36-28.26
=7.74(平方厘米)
5、图中阴影部分的面积是多少平方厘米?
思路引导:如果直接计算图中阴影部分的面积,几乎是不可能的。
仔细观察我们发现用四分之一大圆的面积(或者大扇形面积)减去右面空白处的面积,就容易求出阴影部分的面积了。
所以阴影部分面积=1/4大圆的面积-(长方形面积-1/4小圆面积)=1/4大圆面积+1/4小圆面积-长方形面积。
列式:1/4×3.14×52+1/4×3.14×22-5×2
=1/4×3.14×(52+22)-5×2
=1/4×3.14×(25+4)-5×2
=1/4×3.14×29-10
=22.765-10
=12.765(平方厘米)
6、求下图S形水泥弯路面的面积。
(单位:米)
思路引导:把左图中水泥弯路面左边的甲部分向右平移2米,使S形水泥路面的两条边重合,便转化为右图,S形水泥路面的面积转化为右图中的阴影部分的面积。
S形水泥路的面积是:30×2=60(平方米)
我来帮他解答
糟了,图太不清楚了。
给点提示:橄榄形区域,我把中间鼓起的部分面积设为S1,两个尖头的面积设为S2。
所以橄榄形区域面积为S1+2*S2
后面的,AFGC的面积减去阴影部分面积等于月牙尖端的面积。
两倍月牙尖端的面积加上S2等于内切圆与正方形所围成的那个角的面积。
这又是一个方程。
两个方程联立可得S1、S2。
阴影部分面积就是内切圆面积减去S1啦!
一定要采纳啊!!!。
