气体扩散.ppt分解
合集下载
第04章大气污染扩散模型环境保护概论ppt课件

平衡浓度为:
第六节 区域大气环境质量模型
多源大气环境质量模型 区域内大气中某一点的污染物浓度等于背景浓度和各
污染源对该点浓度的贡献值之和:
《制定地方大气污染物排放标准的技术方法》中排放总量 限值的计算方法
第七节 厂址的选择和烟囱的设计
如果用y0表示烟流半宽度,z0表 示烟流半高度,则有:
封闭型扩散模式
计算简化:
熏烟型扩散模式
假设: D 换成hf(垂向均匀分布);q只包括进入混合层部分,
则仍可用上面公式
熏烟型扩散模式
第五节 城市及山区扩散模式
城市大气扩散模式
1.线源扩散模式
风向与线源垂直时
边缘效应
城市大气扩散模式
2.面源扩散模式
城市大气扩散模式
2. 面源扩散模式(续)
简化为点源的面源扩散模式(续) 形心上风向距x0处有一虚拟点源,其烟流在形心处宽度正好
与正方形宽度相等
烟流宽度:中心线到浓度为中心处距离的两倍
(正态分布:
)
确定 、 之后即可按点源计算面源浓度
城市大气扩散模式
2. 面源扩散模式(续)
窄烟流模式
某点的污染物浓度主要取决于上风向面单元的源强,上风向 两侧单元对其影响很小
定状态,σ较大,即σ与稳定度密切相关。
扩散参数的确定
P-G曲线法
P-G曲线:Pasquill常规气象资料估算;Gifford制成图表
方法要点
将大气稳定度分为6个等级: A — 极不稳定,B —不稳定,C — 弱不稳定, D — 中性,E — 弱稳定,F —稳定。
太阳辐射
稳定级别 下风距离
P-G曲线图 P-G 表
Eutrophication)
Acid Rain
第六节 区域大气环境质量模型
多源大气环境质量模型 区域内大气中某一点的污染物浓度等于背景浓度和各
污染源对该点浓度的贡献值之和:
《制定地方大气污染物排放标准的技术方法》中排放总量 限值的计算方法
第七节 厂址的选择和烟囱的设计
如果用y0表示烟流半宽度,z0表 示烟流半高度,则有:
封闭型扩散模式
计算简化:
熏烟型扩散模式
假设: D 换成hf(垂向均匀分布);q只包括进入混合层部分,
则仍可用上面公式
熏烟型扩散模式
第五节 城市及山区扩散模式
城市大气扩散模式
1.线源扩散模式
风向与线源垂直时
边缘效应
城市大气扩散模式
2.面源扩散模式
城市大气扩散模式
2. 面源扩散模式(续)
简化为点源的面源扩散模式(续) 形心上风向距x0处有一虚拟点源,其烟流在形心处宽度正好
与正方形宽度相等
烟流宽度:中心线到浓度为中心处距离的两倍
(正态分布:
)
确定 、 之后即可按点源计算面源浓度
城市大气扩散模式
2. 面源扩散模式(续)
窄烟流模式
某点的污染物浓度主要取决于上风向面单元的源强,上风向 两侧单元对其影响很小
定状态,σ较大,即σ与稳定度密切相关。
扩散参数的确定
P-G曲线法
P-G曲线:Pasquill常规气象资料估算;Gifford制成图表
方法要点
将大气稳定度分为6个等级: A — 极不稳定,B —不稳定,C — 弱不稳定, D — 中性,E — 弱稳定,F —稳定。
太阳辐射
稳定级别 下风距离
P-G曲线图 P-G 表
Eutrophication)
Acid Rain
气体的扩散原理PPT课件

肺气肿、肺不张、肺叶切除→ 呼吸膜面积↓ → 气体交换↓
第8页/共17页
3.通气/血流比值
(ventilation/perfusion ratio)
概念: 指每分肺泡通气量(VA)和每分肺血流量 (Q)之间的比值(VA/Q) 正常值:
(4.2L/min)/(5L/min )=0.84
第9页/共17页
第14页/共17页
肺气体交换的影响因素
第15页/共17页
三、组织换气
换气驱动力: 血液与组织液间气体分压差
换气结果: 动脉血
静脉血
换气影响因素:
1、距离毛细血管远的细胞获得的O2少 2、组织的血流量减少时组织换气量降低 3、组织代谢率高时气体的扩散速率增大
第16页/共17页
感谢您的观看。
第17页/共17页
人体直立时肺局部的VA/Q 肺上区 肺下区
VA(L/min)0.24 Q(L/min)0.07
0.82 1.29
VA/Q
3.3 0.63
第12页/共17页
(三)肺扩散容量(DL)——自学 概 念:指气体在单位分压差作用下每分钟通过呼
吸膜扩散的体积。
意 义:肺扩散容量是测定呼吸气通过呼
吸膜的能力的一种指标。
∵CO2的扩散系数是O2的20倍,在同等条件下,CO2
的扩散速率是O2的20倍;但在肺中,由于肺泡气和V
血间分压差的不同,CO2的扩散速率实际约为O2的2
倍。
∴肺功能衰竭患者往往第缺6页O/共1显7页著,CO 潴留不明显。
2.呼吸膜
正常呼吸膜非常薄,通透性与面积极大(70-80m2)。
①血液流经肺毛细血管 全长约需0.7s,而完成 气体交换的时间仅需 0.3s(≈前1/3段) ,有气 体交换的时间储备;
第8页/共17页
3.通气/血流比值
(ventilation/perfusion ratio)
概念: 指每分肺泡通气量(VA)和每分肺血流量 (Q)之间的比值(VA/Q) 正常值:
(4.2L/min)/(5L/min )=0.84
第9页/共17页
第14页/共17页
肺气体交换的影响因素
第15页/共17页
三、组织换气
换气驱动力: 血液与组织液间气体分压差
换气结果: 动脉血
静脉血
换气影响因素:
1、距离毛细血管远的细胞获得的O2少 2、组织的血流量减少时组织换气量降低 3、组织代谢率高时气体的扩散速率增大
第16页/共17页
感谢您的观看。
第17页/共17页
人体直立时肺局部的VA/Q 肺上区 肺下区
VA(L/min)0.24 Q(L/min)0.07
0.82 1.29
VA/Q
3.3 0.63
第12页/共17页
(三)肺扩散容量(DL)——自学 概 念:指气体在单位分压差作用下每分钟通过呼
吸膜扩散的体积。
意 义:肺扩散容量是测定呼吸气通过呼
吸膜的能力的一种指标。
∵CO2的扩散系数是O2的20倍,在同等条件下,CO2
的扩散速率是O2的20倍;但在肺中,由于肺泡气和V
血间分压差的不同,CO2的扩散速率实际约为O2的2
倍。
∴肺功能衰竭患者往往第缺6页O/共1显7页著,CO 潴留不明显。
2.呼吸膜
正常呼吸膜非常薄,通透性与面积极大(70-80m2)。
①血液流经肺毛细血管 全长约需0.7s,而完成 气体交换的时间仅需 0.3s(≈前1/3段) ,有气 体交换的时间储备;
《燃气安全技术(第3版)》教学课件第2章燃气的泄露与扩散

泄漏燃气的扩散模型与泄漏燃气物理性质、 泄漏管道系统的周边环境和气候条件有极 大的关系。
泄漏燃气温度、密度与大气温度、密度的 差异及风速和泄漏现场各类障碍物的存在, 使泄漏燃气扩散模拟变得十分复杂。
2.2.1泄漏液体的蒸发
1)闪蒸 液体燃气(如液化天然气、液化石油气)的
沸点通常低于环境温度,当液态燃气从压力 容器中泄漏出来时,由于压力突减,液态燃 气会突然蒸发,称为闪蒸。 闪蒸的蒸发速度由下式计算:
κ-气体的绝热指数,双原子气体取1.4,多原子气体取
1.29,单原子取1.66;
M-燃气的分子量kg/mol;
R-气体常数,8.3144J/(mol.k);
T-气体的温度,K。
当
p0 (
2
k
) k 1
p k 1
时,气体流动属于亚音
速流动,燃气泄漏的质量流量为:
qmG Cdg AP
kM RT
(
k
当Fv<<1时,可认为泄漏的液体不会发生闪蒸, 此时泄漏量按液体泄漏量公式(2.1)计算;泄漏出 来的液体会在地面上蔓延,遇到防液堤而聚集形 成液池;
当 Fv <1时,泄漏量按两相流模型(2.4)计算;
当 Fv =1时,泄漏出来的液体发生完全闪蒸,此 时应按气体泄漏(2.3)处理。
当 Fv >0.2时,可以认为不形成液池。
k
)( 1
p p0
)
2 k
1
(
p p0
)
k 1 k
(2.3)
3)两相流泄漏
在过热液体发生泄漏时,有时会出现液、气两相流 动。均匀两相流的质量泄漏速度可按下式计算:
qm Cd A 2m ( pm pC )
泄漏燃气温度、密度与大气温度、密度的 差异及风速和泄漏现场各类障碍物的存在, 使泄漏燃气扩散模拟变得十分复杂。
2.2.1泄漏液体的蒸发
1)闪蒸 液体燃气(如液化天然气、液化石油气)的
沸点通常低于环境温度,当液态燃气从压力 容器中泄漏出来时,由于压力突减,液态燃 气会突然蒸发,称为闪蒸。 闪蒸的蒸发速度由下式计算:
κ-气体的绝热指数,双原子气体取1.4,多原子气体取
1.29,单原子取1.66;
M-燃气的分子量kg/mol;
R-气体常数,8.3144J/(mol.k);
T-气体的温度,K。
当
p0 (
2
k
) k 1
p k 1
时,气体流动属于亚音
速流动,燃气泄漏的质量流量为:
qmG Cdg AP
kM RT
(
k
当Fv<<1时,可认为泄漏的液体不会发生闪蒸, 此时泄漏量按液体泄漏量公式(2.1)计算;泄漏出 来的液体会在地面上蔓延,遇到防液堤而聚集形 成液池;
当 Fv <1时,泄漏量按两相流模型(2.4)计算;
当 Fv =1时,泄漏出来的液体发生完全闪蒸,此 时应按气体泄漏(2.3)处理。
当 Fv >0.2时,可以认为不形成液池。
k
)( 1
p p0
)
2 k
1
(
p p0
)
k 1 k
(2.3)
3)两相流泄漏
在过热液体发生泄漏时,有时会出现液、气两相流 动。均匀两相流的质量泄漏速度可按下式计算:
qm Cd A 2m ( pm pC )
第八章-扩散

合金中的扩散也是一样,原子总是从化学位高的地方向化 学位低的地方扩散,当各相中同一组元的化学位相等(多 相合金),则达到平衡状态,宏观扩散停止。原子扩散的 真正驱动力是化学位梯度。
F ui x
当化学位降低的方向与浓度降低的方向相反,如溶质原子 的偏聚、调幅分解等,扩散表现为向浓度高的方向进行, 称为上坡扩散。
1.弹性应力作用下的扩散 金属晶体中存在弹性应力梯度时,将造成原子的扩散。 2.晶界的内吸附 如果溶质原子位于晶界上可使体系总能量降低,它们就会
扩散而聚集在晶界上,使得晶界上浓度比晶内高。 3.电场作用下的扩散
第二节 扩散机制
§8.2.1 间隙扩散(Interstitial diffusion)
间隙扩散是小的间隙原子, 扩散时由一个间隙位置跃 迁到另一个间隙位置。间 隙原子换位时,必须从基 体原子之间挤过去,这就 要求间隙原子具有足够的 激活能来克服基体原子造
成的势垒。
图 间隙扩散机制示意图
图 面心立方结构的八面体间隙及(100)间隙
§8.2.2 置换扩散
1.柯肯达尔效应 柯肯达尔(Kirkendall)于1947年首先用实验验证了置换
将伴随有相变过程的扩散,或者有新相产生的扩散称为反 应扩散或者相变扩散。
图 反应扩散时的相图(a)与对应的浓度分布(b)和相分布(c)
图 纯铁的表面氮化 (a)Fe-N相图 (b)相分布 (c)氮浓度分布
第三节 影响扩散的因素
§8.3.1温度
由扩散系数的表达式 D=D0exp(-Q/RT) ,可以看 出,温度对扩散的影响是 很大的。
D0和Q是随成分和晶体结 构变化而变化的,与温度 基本无关,常看作常数。 扩散系数与温度的变化就 是指数关系。
图 Na+在NaCl中的扩散系数
F ui x
当化学位降低的方向与浓度降低的方向相反,如溶质原子 的偏聚、调幅分解等,扩散表现为向浓度高的方向进行, 称为上坡扩散。
1.弹性应力作用下的扩散 金属晶体中存在弹性应力梯度时,将造成原子的扩散。 2.晶界的内吸附 如果溶质原子位于晶界上可使体系总能量降低,它们就会
扩散而聚集在晶界上,使得晶界上浓度比晶内高。 3.电场作用下的扩散
第二节 扩散机制
§8.2.1 间隙扩散(Interstitial diffusion)
间隙扩散是小的间隙原子, 扩散时由一个间隙位置跃 迁到另一个间隙位置。间 隙原子换位时,必须从基 体原子之间挤过去,这就 要求间隙原子具有足够的 激活能来克服基体原子造
成的势垒。
图 间隙扩散机制示意图
图 面心立方结构的八面体间隙及(100)间隙
§8.2.2 置换扩散
1.柯肯达尔效应 柯肯达尔(Kirkendall)于1947年首先用实验验证了置换
将伴随有相变过程的扩散,或者有新相产生的扩散称为反 应扩散或者相变扩散。
图 反应扩散时的相图(a)与对应的浓度分布(b)和相分布(c)
图 纯铁的表面氮化 (a)Fe-N相图 (b)相分布 (c)氮浓度分布
第三节 影响扩散的因素
§8.3.1温度
由扩散系数的表达式 D=D0exp(-Q/RT) ,可以看 出,温度对扩散的影响是 很大的。
D0和Q是随成分和晶体结 构变化而变化的,与温度 基本无关,常看作常数。 扩散系数与温度的变化就 是指数关系。
图 Na+在NaCl中的扩散系数
热传导方程(扩散方程)ppt课件

( x ,t0) ( x )
波方程的Cauchy问题
由泛定方程和相应边界条件构成的定解问题称为 边值问题。
u0, (x,y),
u f (x, y).
Laplace方程的边值问题
由偏微分方程和相应的初始条件及边界条件构成 的定解问题称为混合问题。
uutt0a2(u(xxx,y,uzy)yuzz)0
kn|x0k(x) qnq0
u x
|xl
q0 k
u x |x0
q0 k
xl
若端点是绝热的,则
u u x|xl x x0 0
三、定解问题
定义1 在区域 G[0,) 上,由偏微分方程、初 始条件和边界条件中的其中之一组成的定解问题称为 初边值问题或混合问题。
u ut x,a 02 u xx (x 0),,
注 1、热传导方程不仅仅描述热传导现象,也可以
刻画分子、气体的扩散等,也称扩散方程;
2、上述边界条件形式上与波动方程的边界条件 一样,但表示的物理意义不一样;
3、热传导方程的初始条件只有一个,而波动方 程有两个初始条件。
4、除了三维热传导方程外,物理上,温度的分 布在同一个界面上是相同的,可得一维热传导方
gk1 k
u1.
注意第三边界条件的推导:
研究物体与周围介质在物体表面上的热交换问题
把一个温度变化规律为 u(x, y, z, t)的物体放入 空
气介质中,已知与物体表面接触处的空气介质温度
为 u1(x, y, z, t),它与物体表面的温度u(x, y, z, t)并不
相同。这给出了第三边界条件的提法。
或
u knk1(uu1).
即得到(1.10): ( u nu)|(x,y,z) g(x,y,z,t).
气体扩散.ppt分解共59页

40、学而不思则罔,思而不学则殆。——孔子
气体扩散.ppt分解
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
谢谢!Leabharlann 36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
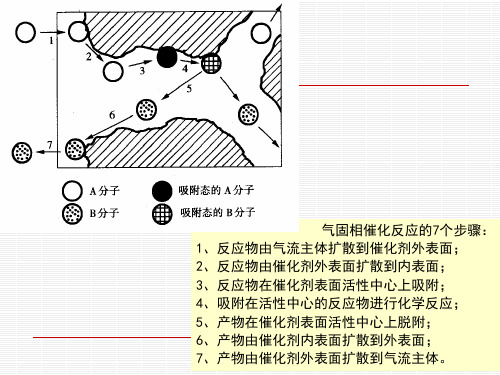
气体在多孔气体中的扩散
内外扩散都有影响时的有效因子
内外扩散都有影响的 内外扩散均有影响时的 反应速率 o 有效因子 扩散无影响时的反应速 率
A kGam cAG cAS kwcAS okwcAG
c AS c AG k 1 w k G am
A kwcAS
r R p , c A c AS dcA r 0, 0 dr
比较薄片催化剂
L
kp De
R p sinh 3r R p cA c AS r sinh3
1 1 1 tanh3 3
6.4.2
内扩散有效因子
d 2c A dr 2 1 dcA k p cA r dr De
圆柱催化剂
Vp ap
kp De
r R p , c A c AS dcA r 0, 0 dr
I 0 2 r R p cA c AS I 0 2
I1 2 I 0 2
特别注意:
< 0.4, 1 > 3.0,
1
6.4.4
2、平行反应
P A
k1
S A
k2
主反应 副反应
n 1 AS
n rA 1 k1cA m rA 2 k2cB
无内扩散影响时,催化剂内浓度就是表面浓度 :
S′
P
kc 1 n m k1cAS k2 cAS 1 k2 c m n AS k1
6.5 内扩散与复合反应选择性的影响 1、两个独立并行的反应
k1 A P C k2 B S W
主反应 副反应
k1 > k2
第六章 扩散

直接应用菲克第二定律解决实际扩散问题,往往很复杂。 但是有两条由菲克第二定律推导出来的结论却十分简单、 有用:
推论 (1)对于同一扩散系统、扩散系数D与 扩散时间t的乘积为一常数。
已知Cu在Al中的扩散系数D, 在500℃和600℃时分别为 4.8×10-14 m2/s和5.3×10-13 m2/s。假如一个工件在600℃ 需要处理10小时,如果在500℃处理,要达到同样的效果 则需要多少小时? (Dt)500 = (Dt)600
三、扩散的热力学分析
1.扩散驱动力 浓度梯度有关的扩散:顺扩散(高浓度→低浓度),逆扩散 (低浓度→高浓度) 热力学:决定组元扩散流向的是化学位 浓度梯度与化学位梯度一致,顺扩散,成分趋于均匀,如铸 锭均匀化 浓度梯度与化学位梯度不一致,逆扩散,成分区域性不均匀, 如共析分解 i, j 两组元系统,组元的体积浓度为 Ci , ni 为组元 i 的摩尔 数,M:组元i的摩尔质量。 C i c M n 则Ci=Mni, i i ,则 n i
渗碳层按齿廓分布的渗碳齿轮
1. 概述
实际上,金属的真空冶炼、材料的提纯、 铸件的凝固和成分均匀化、变形金属的回 复再结晶、相变、化学热处理、粉末冶金 或陶瓷材料的烧结等都受扩散影响 原子或分子的迁移现象称为扩散。扩散的 本质是原子依靠热运动从一个位置迁移到 另一个位置。扩散是固体中原子迁移的唯 一方式。 扩散过程是传质过程。它是一个不可逆过 程,也是体系熵增过程。
§2.2 菲克第二定律
考虑如图所示的扩散系统, 扩散物质沿x方向通过横截面 积为A(=ΔyΔz)、长度为Δx的 微元体,假设流入微元体(x 处)和流出微元体(x+Δx处) 的扩散通量分别为Jx和Jx+Δx, 则在Δt时间内微元体中累积 的扩散物质量为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体动理论
6-1 物质的微观模型 统计规律性
物质结构的微观模型 :
1 、宏观物体是由大量微观粒子 — 分子(或原子 )组成的,分子之间有空隙;
2、分子在不停地作无规则的运动,其剧烈程度与 温度有关; 3、分子之间存在相互作用力。 这些观点就是气体动理论的基本出发点。统计物 理学的任务就是从上述物质分子运动论的基本观点 出发,研究和说明宏观物体的各种现象和性质。
. . . . . . . . . . . . . . . .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . .. .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 i ix 2 ix i
压强P为
dI 1 2 2 P mn vix mn v dSdt 3
理想气体压强公式的简易推导
1 2 引入气体分子平均平动动能 : k mv 2
则又有
2 1 2 2 P n ( mv ) n k 3 2 3
vx v y vz 0
1 2 v v v v 3
2 x 2 y 2 z
二、理想气体压强公式 容器内的气体施加在器壁上的压强,从微观看 是大量气体分子不断与器壁碰撞的结果。每个分子 每次碰撞都给器壁一微小的冲量,大量分子不断碰 撞,表现为一个恒定、均匀、持续的压力。
设贮有理想气体的容器的容积为V,气体分子 的质量为m,分子总数为N,则单位体积内的分子数 为n=N/V。为了便于讨论,将分子分成若干个“等 速组”,即每组内分子具有大小相等、方向相同的 速度vi。将单位体积内速度分别为v1、v2…vi…的分 子数表示为n1、n2 …ni …于是有
四、统计规律
统计规律,是指大量偶然事件整体所遵循的规 律。虽然每个事件都是偶然、无规律的,但总体上 却存在着确定的规律性。伽尔顿板是说明统计规律 的演示实验。 单个小球下落时与哪些铁 钉碰撞,最后落入哪个狭槽完 全是无法预测的偶然事件(随机 事件)。大量小球总体上的分布 有确定的规律性:落入中央狭槽 的小球较多,而落入两端狭槽 的小球较少。重复几次同样实 验,得到的结果都近似相同。
2mvix ni vix dtdS 2ni mv dtdS
2 ix
对于所有可能的速度,全部分子施于dS的总冲量为
dI
vix 0
2n mv dSdt
iห้องสมุดไป่ตู้2 ix
式中限制了vix>0,这是因为vix<0的分子是不可 能与dS相碰的。只要除以2即可去掉vix>0 的限制。 于是有
dI m n v dSdt mnv dSdt
n ni
如图,在器壁上任取一小块面 积dS,设某一分子以速度vi与dS 相碰,碰撞是完全弹性的,所以 Y、Z两个方向的速度分量viy变为 -vix。所以,碰撞一次,分子的 动量变化为
mvix mvix 2mvix
分子施于面元dS的冲量为2mvix。在速度为vi的 分子中,dt时间内能够与dS相碰的分子只是位于以 dS为底、vixdt为高、vi为轴的斜柱体内的那部分。分 子数可表示为ni vixdtdS。因此,速度为vi的“等速组 ”分子施于dS的总冲量为
一、分子的线度与间隙 在标准状态下,气体分子间的距离约为分子直径 的10倍,于是每个分子所占有的体积约为分子本身 的体积的1000倍。因而气体分子可看成是大小可以 忽略不计的质点。 气体分子的间距很大,因而很容易压缩;液体 和固体分子间也有空隙,如:50升水+50升酒精= 97升溶液;在2万个大气压下,液体也会从钢管壁 上渗出等等。 二、分子热运动
6-2 理想气体的压强公式 温度的微观实质
一、理想气体分子的微观模型和统计假设 1.理想气体分子的微观模型 (1)由于气体分子间距较大,分子的大小可以忽 略不计,即可把分子视为质点。
( 2 )气体分子间的相互作用力很弱,可忽略不计 。即认为除碰撞的瞬间外,分子之间以及分子与容 器壁之间都没有相互作用力。
(3)分子之间以及分子与器壁之间的碰撞可视为 完全弹性碰撞。
2.统计假设
(1)容器中各处的分子数密度相同。
(2)分子沿任一方向的运动不比其他方向的运动占 优势,即分子向各个方向运动的几率均等。在任一 时刻,朝着直角坐标系的x、-x、y、-y、z和-z 轴各个方向运动的分子数应相等,并且都等于总分 子数的1/6。 (3)分子速度在各个方向上的分量的各种统计平均 值相等。如:
描述单个分子运动情况的物理量,称为微观量 。例如分子的坐标、速度、动量、能量等,都是微 观量。由于大量气体分子间频繁的碰撞,许多微观 量都是随机量,个别分子的运动规律是无法把握的 。但在平衡态下用于描述系统整体性质的各宏观物 理量(P、T等)均有确定、稳定的值,这说明由大 量分子所组成的系统要遵从确定的统计规律。 本章将要研究的理想气体的压强公式和温度公 式、能量均分定律、麦克斯韦速率分布律等都是统 计规律。从个别分子的力学规律入手,通过对大量 分子求算术平均,建立微观量的统计平均值与宏观 量的联系,从而揭示出宏观量的微观实质,这种方 法称为统计方法。
分子热运动的基本特征是分子的永恒运动和频 繁的相互碰撞。分子热运动具有混乱性和无序性。 分子无规则运动的剧烈程度与温度有关。
三、分子力 分子之间同时存在吸引力 和排斥力。实验证明当分子间 距较大时,存在的引力很小, 随着间距的减小,引力逐渐加 强,当r=r0时,分子力为零, 称r0为平衡位置。r<r0分子力 表现在排斥力,r>r0分子力表 现在吸引力,当r>10r0时,分 子力可以忽略不计。 分子间彼此趋近到分子的直径d时,分子将在强 大的斥力作用下被排斥开,类似小球间“弹性碰撞 ”过程。d的平均值称为分子有效直径,数量级约为 10-10m。
6-1 物质的微观模型 统计规律性
物质结构的微观模型 :
1 、宏观物体是由大量微观粒子 — 分子(或原子 )组成的,分子之间有空隙;
2、分子在不停地作无规则的运动,其剧烈程度与 温度有关; 3、分子之间存在相互作用力。 这些观点就是气体动理论的基本出发点。统计物 理学的任务就是从上述物质分子运动论的基本观点 出发,研究和说明宏观物体的各种现象和性质。
. . . . . . . . . . . . . . . .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . .. .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 i ix 2 ix i
压强P为
dI 1 2 2 P mn vix mn v dSdt 3
理想气体压强公式的简易推导
1 2 引入气体分子平均平动动能 : k mv 2
则又有
2 1 2 2 P n ( mv ) n k 3 2 3
vx v y vz 0
1 2 v v v v 3
2 x 2 y 2 z
二、理想气体压强公式 容器内的气体施加在器壁上的压强,从微观看 是大量气体分子不断与器壁碰撞的结果。每个分子 每次碰撞都给器壁一微小的冲量,大量分子不断碰 撞,表现为一个恒定、均匀、持续的压力。
设贮有理想气体的容器的容积为V,气体分子 的质量为m,分子总数为N,则单位体积内的分子数 为n=N/V。为了便于讨论,将分子分成若干个“等 速组”,即每组内分子具有大小相等、方向相同的 速度vi。将单位体积内速度分别为v1、v2…vi…的分 子数表示为n1、n2 …ni …于是有
四、统计规律
统计规律,是指大量偶然事件整体所遵循的规 律。虽然每个事件都是偶然、无规律的,但总体上 却存在着确定的规律性。伽尔顿板是说明统计规律 的演示实验。 单个小球下落时与哪些铁 钉碰撞,最后落入哪个狭槽完 全是无法预测的偶然事件(随机 事件)。大量小球总体上的分布 有确定的规律性:落入中央狭槽 的小球较多,而落入两端狭槽 的小球较少。重复几次同样实 验,得到的结果都近似相同。
2mvix ni vix dtdS 2ni mv dtdS
2 ix
对于所有可能的速度,全部分子施于dS的总冲量为
dI
vix 0
2n mv dSdt
iห้องสมุดไป่ตู้2 ix
式中限制了vix>0,这是因为vix<0的分子是不可 能与dS相碰的。只要除以2即可去掉vix>0 的限制。 于是有
dI m n v dSdt mnv dSdt
n ni
如图,在器壁上任取一小块面 积dS,设某一分子以速度vi与dS 相碰,碰撞是完全弹性的,所以 Y、Z两个方向的速度分量viy变为 -vix。所以,碰撞一次,分子的 动量变化为
mvix mvix 2mvix
分子施于面元dS的冲量为2mvix。在速度为vi的 分子中,dt时间内能够与dS相碰的分子只是位于以 dS为底、vixdt为高、vi为轴的斜柱体内的那部分。分 子数可表示为ni vixdtdS。因此,速度为vi的“等速组 ”分子施于dS的总冲量为
一、分子的线度与间隙 在标准状态下,气体分子间的距离约为分子直径 的10倍,于是每个分子所占有的体积约为分子本身 的体积的1000倍。因而气体分子可看成是大小可以 忽略不计的质点。 气体分子的间距很大,因而很容易压缩;液体 和固体分子间也有空隙,如:50升水+50升酒精= 97升溶液;在2万个大气压下,液体也会从钢管壁 上渗出等等。 二、分子热运动
6-2 理想气体的压强公式 温度的微观实质
一、理想气体分子的微观模型和统计假设 1.理想气体分子的微观模型 (1)由于气体分子间距较大,分子的大小可以忽 略不计,即可把分子视为质点。
( 2 )气体分子间的相互作用力很弱,可忽略不计 。即认为除碰撞的瞬间外,分子之间以及分子与容 器壁之间都没有相互作用力。
(3)分子之间以及分子与器壁之间的碰撞可视为 完全弹性碰撞。
2.统计假设
(1)容器中各处的分子数密度相同。
(2)分子沿任一方向的运动不比其他方向的运动占 优势,即分子向各个方向运动的几率均等。在任一 时刻,朝着直角坐标系的x、-x、y、-y、z和-z 轴各个方向运动的分子数应相等,并且都等于总分 子数的1/6。 (3)分子速度在各个方向上的分量的各种统计平均 值相等。如:
描述单个分子运动情况的物理量,称为微观量 。例如分子的坐标、速度、动量、能量等,都是微 观量。由于大量气体分子间频繁的碰撞,许多微观 量都是随机量,个别分子的运动规律是无法把握的 。但在平衡态下用于描述系统整体性质的各宏观物 理量(P、T等)均有确定、稳定的值,这说明由大 量分子所组成的系统要遵从确定的统计规律。 本章将要研究的理想气体的压强公式和温度公 式、能量均分定律、麦克斯韦速率分布律等都是统 计规律。从个别分子的力学规律入手,通过对大量 分子求算术平均,建立微观量的统计平均值与宏观 量的联系,从而揭示出宏观量的微观实质,这种方 法称为统计方法。
分子热运动的基本特征是分子的永恒运动和频 繁的相互碰撞。分子热运动具有混乱性和无序性。 分子无规则运动的剧烈程度与温度有关。
三、分子力 分子之间同时存在吸引力 和排斥力。实验证明当分子间 距较大时,存在的引力很小, 随着间距的减小,引力逐渐加 强,当r=r0时,分子力为零, 称r0为平衡位置。r<r0分子力 表现在排斥力,r>r0分子力表 现在吸引力,当r>10r0时,分 子力可以忽略不计。 分子间彼此趋近到分子的直径d时,分子将在强 大的斥力作用下被排斥开,类似小球间“弹性碰撞 ”过程。d的平均值称为分子有效直径,数量级约为 10-10m。
