第2章 Jordan标准型
Jordan标准型总结

第二章 行列式 第一节 引言
9. 矩阵计算:
A P 1 JP Am P 1 J m P; J1m n J 0 1 m J i (i E , m Jm 0 1 可按二项式展开。 0m源自第二章 行列式 第一节 引言
10. r ( A) 1, A ~ J ? , n aii tr ( A). 1 0(n 1 or n重)
i 1 n
0 1 0 (1) tr ( A) 0, A 不可对角化, J 0 0 0 (2) tr ( A) 0, A 可对角化, J
第二章 行列式 第一节 引言
J1 k 12. k , A 0 A ~
注:涉及线性变换或者矩阵的问题,化为相应 Jordan 标准型后可以简化问题。
第二章 行列式 第一节 引言
例题
2005 武汉大学:1,5,7,8 一半题和 Jordan 标准型有关。 例1. 第五题。 (1)设
Er 0
0 1 P AP, 0
0 0 P 1 ( E A B) P E P 1 AP P 1BP B1. 0 E nr
问题化为
0 0 Er 可逆, r ( B 1 0 0 Enr
0 Er B ) r ( B 1 1 0 0
0 ) 。 0
这是因为 B1 的前 r 行和列均线性无关。 (2) 特征值为 n-1 个 0,以及
T T
. 故 A 特征值为 n-1 个 1 和1 T .
1 E B, BT B. 即 B 反对称,从而 B 特征值为 0 或者纯虚数。 2 1 A 特征值实部为 ,于是 0 不是 A 特征值,从而 A 可逆。 2
Jordan标准型

Jordan标准型Jordan标准型是一种非常经典的篮球鞋款,它以其独特的设计和优越的性能而备受球迷和运动员的青睐。
作为一名篮球鞋文档创作者,我将为大家介绍Jordan标准型的特点和优势。
首先,Jordan标准型采用了轻量化的设计,鞋身采用了高质量的材料,既保证了鞋子的耐用性,又减轻了运动员的负担,使得他们在比赛中更加灵活自如。
鞋底采用了高强度的橡胶材料,具有良好的抓地力和耐磨性,可以在不同地面上提供稳定的支撑,让运动员可以更加专注于比赛。
其次,Jordan标准型在缓震性能方面表现出色。
鞋底采用了先进的缓震科技,能够有效地吸收冲击力,减轻脚部的压力,保护运动员的脚部免受受伤。
这种设计不仅能够提高运动员的比赛表现,还能够减少运动中的不适感,让他们能够更加专注于比赛。
此外,Jordan标准型的鞋面设计也非常出色。
采用了透气性良好的材料,能够有效地排出脚部的汗液,保持鞋内干爽舒适。
鞋面的设计也非常时尚,符合现代年轻人的审美需求,不仅在比赛中展现出色,日常穿着也非常合适。
最后,Jordan标准型的品牌影响力也是其优势之一。
作为Nike旗下的明星产品,Jordan标准型凭借着其卓越的品质和独特的设计,深受球迷和运动员的喜爱。
许多知名篮球明星都是Jordan标准型的忠实粉丝,他们的支持也为这款鞋子增添了不少光环。
总的来说,Jordan标准型作为一款经典的篮球鞋,不仅在外观设计上独具匠心,而且在性能表现上也非常出色。
它的轻量化设计、优秀的缓震性能、透气舒适的鞋面以及强大的品牌影响力,使得它成为了众多篮球爱好者和专业运动员的首选。
相信随着篮球运动的不断发展,Jordan标准型将会继续发光发热,为更多的篮球爱好者带来无尽的激情和动力。
线性代数中的Jordan标准型与Jordan分解

线性代数中的Jordan标准型与Jordan分解在线性代数中,Jordan标准型(Jordan Canonical Form)和Jordan 分解(Jordan Decomposition)是两个重要的概念。
它们广泛应用于矩阵理论、线性变换及微分方程等领域。
本文将详细介绍Jordan标准型和Jordan分解,并探讨它们在实际应用中的价值。
1. Jordan标准型Jordan标准型是指一个线性变换或矩阵的标准形式。
对于一个n阶方阵A,如果存在可逆方阵P,使得P逆AP的形式为Jordan标准型,那么A就具有Jordan标准型。
Jordan标准型的特点是,它的主对角线由Jordan块组成,每个Jordan块对应一个特征根,而Jordan块的结构由其几何重数和代数重数决定。
1.1 Jordan标准型的计算方法要计算一个矩阵的Jordan标准型,可以按照以下步骤进行:(1)求出矩阵A的特征多项式;(2)求出A的特征值,即特征多项式的根;(3)对于每个特征值,求出其对应的特征向量;(4)根据特征向量构造Jordan块,并将它们排列在一起形成Jordan矩阵;(5)得到Jordan标准型。
1.2 Jordan标准型的应用Jordan标准型在线性代数的研究中具有重要意义。
它可以用来分析矩阵的性质,如可对角化条件、矩阵的相似性等。
此外,Jordan标准型还可以用来解决微分方程的问题,在微分方程的理论和应用中有广泛的应用。
2. Jordan分解Jordan分解是将一个矩阵分解成若干个Jordan块之和的形式。
对于一个n阶方阵A,如果可以将其分解成 A=S+D,其中S是具有零特征值的Jordan矩阵,D是具有非零特征值的对角矩阵,那么A就具有Jordan分解。
2.1 Jordan分解的计算方法要计算一个矩阵的Jordan分解,可以按照以下步骤进行:(1)求出矩阵A的特征多项式;(2)求出特征值和对应的特征向量;(3)根据特征向量构造Jordan块,并将具有非零特征值的Jordan 块排列在一起形成S;(4)构造对角矩阵D,将每个特征值放在对角线上。
jordan标准型_初等变换法技巧_概述说明

jordan标准型初等变换法技巧概述说明1. 引言1.1 概述在线性代数的学习中,矩阵是一个重要的概念。
通过对矩阵的运算和变换,我们可以更好地理解它们的特征和性质。
而Jordan标准型作为矩阵的一种特殊形式,在代数学和应用领域中扮演着重要角色。
在本篇文章中,我们将介绍Jordan标准型及其相关背景知识,并讨论初等变换法技巧在求解Jordan标准型中的应用。
同时,我们还会对于结果进行分析与说明,并提供实际应用案例的讨论。
最后,我们将探讨Jordan标准型方法存在的局限性,并提出改进方法建议。
1.2 文章结构本文按以下结构展开:首先,在第二部分中,我们将介绍Jordan标准型的定义、背景以及其特征和性质;接着,在第三部分中,我们将概述矩阵初等变换法以及行初等变换法和列初等变换法的技巧;然后,在第四部分中,我们将对结果进行解释与分析,并展示一些实际应用案例;最后,在第五部分中,我们将总结全文内容并对未来发展进行展望。
1.3 目的本文的目的是提供一个关于Jordan标准型和初等变换法技巧的概述,帮助读者理解它们在线性代数中的重要性和应用。
同时,我们也希望通过实际应用案例的讨论以及对方法局限性的探讨,激发读者对于改进方法和未来研究方向的思考。
通过深入学习和理解这些知识,读者可以运用它们解决实际问题,并为相关领域的发展做出贡献。
2. Jordan标准型2.1 定义和背景Jordan标准型是线性代数中一个重要的概念,它用于描述矩阵的特征值和特征向量。
对于n阶方阵A,如果存在一个可逆矩阵P,使得逆矩阵P^-1AP可以化为如下形式:```J = [ J₁0 0 ... 0 ][ 0 J₂0 ... 0 ][ ... ][ 0 0 0 ... Jₙ]```其中J₁, J₂, ..., Jₙ分别是Jordan块(Jordan block),满足以下条件:- 每个Jordan块对应着A的一个互异的特征值。
- 每个Jordan块由特征向量链构成,其中每条链包含多个长度不同但相差为1的特征向量。
第2章矩阵与矩阵的Jordan标准形(详解)
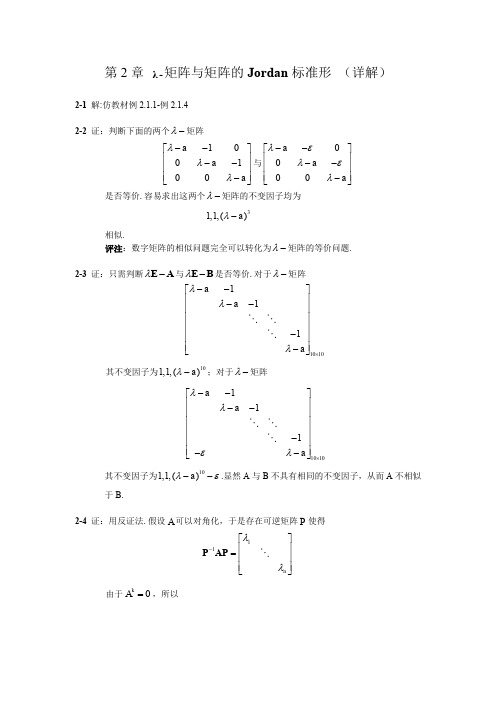
第2章 λ-矩阵与矩阵的Jordan 标准形 (详解)2-1 解:仿教材例2.1.1-例2.1.42-2 证:判断下面的两个λ-矩阵100100a a a λλλ--⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦与0000a a a λελελ--⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦是否等价.容易求出这两个λ-矩阵的不变因子均为31,1,()a λ-相似.评注:数字矩阵的相似问题完全可以转化为λ-矩阵的等价问题.2-3 证:只需判断λ-E A 与λ-E B 是否等价.对于λ-矩阵1010111a a a λλλ⨯--⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦ 其不变因子为101,1,()a λ-;对于λ-矩阵1010111a a a λλελ⨯--⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦ 其不变因子为101,1,()a λε--.显然A 与B 不具有相同的不变因子,从而A 不相似于B.2-4 证:用反证法.假设A 可以对角化,于是存在可逆矩阵P 使得11n λλ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP 由于0kA =,所以11()0k k n λλ-⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦A P P 即10k k n λλ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦由此可知120n λλλ====,故100-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP 这表明0A =,这与0A ≠矛盾.2-5 证:只要证明A 的每一个Jordan 标准形为1211,1i iiii s i n n a a a ⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦J J J J J 那么存在相似变换矩阵P 使得1-=P AP J .因此1k k -==J P A P E于是有111ik k ii k k iiki k k i k i a ka a ka ka a ---⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦J E故i J 必为一阶子块,即s n -.所以A 与对角矩阵相似.2-6证:设A 的若当标准形为11,1ii s i J J J J λλ⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1J Q AQ -=,由2A A =有2J J =,从而i J 都是一阶的,再利用矩阵的初等变换调整对角线上的元素,得证.2-7解:仿教材上的例题.2-8解:仿教材上的例题.2-9 解:用两种方法求解此题.方法一 相似变换矩阵的方法.对于任意一个可逆矩阵P ,矩阵1-PJP 均与矩阵J 相似,从而其Jordan 标准形必为J ,于是任取两个不同的可逆矩阵P ,即可得到两个矩阵A ,B .方法二 矩阵秩的方法.设A (或B )的Jordan 标准形为100021002⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦从而A (或B )的Smith 标准形为211(2)(1)λλ⎡⎤⎢⎥⎢⎥⎢⎥--⎣⎦由此可知A (或B )的行列式因子为2123()1,()1,()(2)(1)D D D λλλλλ===--这样的矩阵A (或B )有很多,取表达式较为简单的矩阵,下列任何一种矩阵都可以200100200*10,*20,*20,**2**2**12**1**2**01*,02*,020********⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦下面分析“*”处元素取何值时才能保证1为主对角元的Jordan 块只有一个,以2为主对角元的Jordan 块也只有一个.根据求矩阵Jordan 标准形的第二种方法(矩阵秩的方法),只要使(2)2r -=A E 或(2)2r -=B E即可.例如20020-1921,010001002⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦均可以.但2001-10020,021051002⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦都不可以. 2-10解(思路)设1Q JQ A -=,其中J 是A 的若当标准形,则1001100A Q J Q -=2-11解: A 的不变因子()()()()123,,133λ(λ+1)λn d d d d λλλλ=====;由A 的初等因子以及E A λ-的秩为n 写出A 的若当标准形J .2-12解:仿教材例题.2-13解: 仿教材例题.2-14 解:因为()10λ=-≠A 1()1λλλλλ--⎡⎤=⎢⎥-+⎣⎦A故 11()1λλλλλ--+⎡⎤=⎢⎥--⎣⎦A 注:n 阶λ-矩阵()λA 的秩为n ,不等价于()λA 可逆,这是与数字矩阵不相同之处.例如1()1λλλ⎡⎤=⎢⎥⎣⎦A 的秩为2,但是它不可逆. 2-15 解:()λA 的元素中有非零常数212221321222122132223221111()2222221101102220031122221111222220010214202,2c c c c c c r r r r c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥←−→⎢⎥⎢⎥=+--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤-+⎢⎥⎢⎥⎢⎥-+-+-⎢⎥⎢⎥⎢⎥+---⎣⎦-++-+-+----A ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦132221222432224323243231000421012100()04214100(3)4100(21)0404003410010104003c c c r c rc c λλλλλλλλλλλλλλλλλλλλλλλ⎡⎤←−→⎢⎥-+-⎢⎥⎢⎥---⎣⎦⎡⎤⎢⎥+⎢⎥-+-⎢⎥⎢⎥-+--⎢⎥⎣⎦⎡⎤-+⎢⎥⎢⎥⎢⎥-+--⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥-++⎣⎦-2-16 解:()λA 的元素有公因子λ,所以额可以用初等变换把左上角元素变成λ3223122222112223322()533515353223c c c r r λλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤-←−→-=⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤+⎡⎤←−→+⎢⎥⎢⎥⎢⎥--⎣⎦⎢⎥⎣⎦A然后用初等变换把公因子λ所在的行、列的其余元素均化为零.2212223122525()320(103)33(5)00(103)r r c c λλλλλλλλλλλλλλλλλλλ⎡⎤+⎡⎤+-⨯+⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦-++⎡⎤⎢⎥--⎣⎦A2-17 解:()λA 的元素无公因子,也无常数元素.用初等变换把矩阵中某一个元素变成常数22212222222123221343221232432110()11100(1)0100()00r r r r r r c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤-++⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥+-+-⎣⎦⎣⎦⎡⎤+-+⎢⎥--+-⎢⎥-++⎢⎥----⎣⎦⎡⎤-++⎢⎥--+-⎢⎥⎢⎥----⎣⎦A剩下的右下角的二阶矩阵有公因子λ,参照2-16用的方法.有32432233224323322223223100()0010000100000100(1)0000110010000(1)c c r r c c r r λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎢⎥--+-⎢⎥⎢⎥----⎣⎦⎡⎤←−→⎢⎥---+⎢⎥⎢⎥----⎣⎦⎡⎤-+⎢⎥---+⎢⎥⎢⎥--⎣⎦⎡⎤-+-+⎢⎥-⎢⎥⎢⎥--⎣⎦-⨯⎡⎤-⨯⎢⎥⎢⎥⎢⎥+⎣⎦A2-18 解:()λA 的元素中有常数.2322123212213323243243212323213(1)1()11(1)1(1)11(1)(+1)1(1)(1)0210100(1)02c c r r r r c c c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤+⎢⎥=+-⎢⎥⎢⎥-⎣⎦⎡⎤+←−→⎢⎥+-⎢⎥⎢⎥-⎣⎦-+⎡⎤+--+⎢⎥----+-⎢⎥⎢⎥-++-++⎣⎦-++----+A 243243210λλλλλλλλ⎡⎤⎢⎥-+-⎢⎥⎢⎥-++-++⎣⎦剩下的二阶矩阵使元素既无公因子又无常数的矩阵,参照2-17的方法可把二阶矩阵初等变换化3232432432233224323222432100()0210100021001000100c c c c λλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎢⎥----+-⎢⎥⎢⎥-++-++⎣⎦⎡⎤-+⎢⎥--+-⎢⎥⎢⎥-++⎣⎦⎡⎤++⎢⎥--+-⎢⎥⎢⎥-++⎣⎦A2324324322324324322234322432432232432100010100010100()0100(1)()100()01000(1)()c c c c c c r r λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤+⎢⎥---⎢⎥⎢⎥-++-++⎣⎦⎡⎤←−→⎢⎥---⎢⎥⎢⎥-++-++⎣⎦⎡⎤--+⎢⎥-⎢⎥⎢⎥-++--+-++⎣⎦⎡-+++--+-++⎤⎢⎥⎢⎥⎢⎥⎣⎦2-19 解:()λA 虽然是对角形,但不是Smith 标准形.2232233222(1)()(1)(1)(1)(1)00(2)0200211(1)(1)c c r r λλλλλλλλλλλλλλλλλλλλλλ+⎡⎤⎢⎥=⎢⎥⎢⎥+⎣⎦+⎡⎤+⎢⎥⎢⎥⎢⎥+⎣⎦+⎡⎤-++⎢⎥++⎢⎥⎢⎥--⎣⎦⎡⎤⎢⎥+⎢⎥⎢⎥+⎣⎦A2-20 解:首先容易求出()λA 的不变因子233342321()(1)(2)(2)()(1)()(1)()1d i i d d d λλλλλλλλλλλλ=-+-=-=-=于是()λA 的Smith 标准形为223331000000(1)0000()00(1)000000(1)(2)(2)00000000i i λλλλλλλλλ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥-+-⎢⎥⎢⎥⎣⎦A对于准对角形矩阵()0()0()λλλ⎡⎤=⎢⎥⎣⎦B A C 为准对角形矩阵,则()λB 与()λC 的不变因子求得()λA 的不变因子,但是能从()λB 与()λC 的初等因子立即得到()λA 的初等因子.2-21 解:方法一 ()λA 行列式因子易得为121()()()1,()()n n n a λλλλλ-=====-D D D D于是()λA 的不变因子为121()()()1,()()n n n d d d d a λλλλλ-=====-因而初等因子只有一个方法二 对()λA 用初等变换求得不变因子为11,1,,1,()n n a λ--个故初等因子为()n a λ-2-22 解:将()λA 之第二行,第三行,,第n 行分别乘以21,,,n λλλ-都加第一行上去,得到1221000()10010()00001n n f a a a a λλλλλ--⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦A 其中 12121()n n n n n f a a a a λλλλλ---=+++++易得 det ()()f λλ=A 故 ()()n f λλ=D 又 1()1n λ-=D 于是 122()()()1n λλλ-====D D D所以 121()()()1,()()n n d d d d f λλλλλ-=====因此()λA 之Smith 标准形为1()1()f λλ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A2-23 解:因为A 的初等因子乘积22(1)1λλλλλ-+是7次多项式,故A 是7阶的.2-24 解:A 是5阶矩阵,答案有如下几种情况:(1)A 的初等因子1,1,2,2,2λλλλλ++---A 的不变因子1,1,2,(1)(2),(1)(2)λλλλλ-+-+-(2)A 的初等因子21,1,2,(2)λλλλ++--A 的不变因子21,1,1,(1)(2),(1)(2)λλλλ+-+-(3)A 的初等因子21,1,(2)λλλ++-A 的不变因子31,1,1,1,(1)(2)λλλ++-(4)A 的初等因子2(1),2,2,2λλλλ+---A 的不变因子31,1,2,2,(2)(1)λλλλ---+(5)A 的初等因子22(1),2,(2)λλλ+--A 的不变因子221,1,1,2,1,(2)(1)λλλλ-+-+(6)A 的初等因子22(1),(2)λλ+-A 的不变因子231,1,1,1,(1)(2)λλ+-2-25 解:先求A 的初等因子.对()λ-E A 运用初等变换可得21261131114(1)λλλλλλ+-⎡⎤⎡⎤⎢⎥⎢⎥-=--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦E A A 的初等因子是21,(1)λλ--故A 的Jordan 标准形是100011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦J2-26 解:100011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦AJ故存在333c ⨯∈P ,满足=AP PJ命 123(,,)=P X X X (1) 把P 代入式(1)得123123100(,,)(,,)011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦AX AX AX X X X (2)比较式(2)两边得1122323,,===+AX X AX X AX X X即 1232()0,()0,()-=-=-=-E A X E A X E A X X在上述每个方程组中只要依次取一个解分别为123,,X X X ,组成123(,,)=P X X X 即可.易见12,X X 是A 的特征值为1的两个线性无关的特征向量.解方程组()0-=E A X可求得两个线性无关的特征向量(1,1,0),(3,0,1)T T =-=ξη若取12,==ξX ηX ,代入32()-=-E A X X ,该方程组无解,这时不能认为P 不存在.因为A 的特征子空间是二维的,即A 的线性无关特征向量不仅是,ξη.例如,只要,S t 满足1≠St 的任意数,,++ξS ηt ξη也是A 的线性无关特征向量.因此,若取12,k ==+X ξX ξη(0)k ≠,k 只要使得方程组32()-=-E A X X 有解.不难知道当1k =时,取2(2,1,1)T=+=X ξη代入32()-=-E A X X 方程组有解为1232331(,)x x x x x =-+-为任意数取它的一个解3(2,0,1)T=X ,就可.于是122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P容易验证有1100011001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP从以上两例可以概括出求Jordan 标准形变换矩阵P 的过程.设A 的Jordan 标准形为J ,则12s ⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎣⎦J J AP PJ P J 其中111i iiii n n λλλ⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦J 把变换矩阵P 按Jordan 块i J 的阶数i n 进行相应的分块,即设12(,,,)S =P P P P其中in n i C⨯∈P ,因此12121212(,,,)(,,,)(,,,)S S S s =⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A P P P P P P J J J P P P J 故 121122(,,,)(,,,)S s S =AP AP AP J P J P J P比较上式两端得i i i =AP P J (1,2,,)i s =对i P 再按列分块12(,,,)i i n n i i i in C ⨯=∈P X X X其中12,,,i i i in X X X 是i n 个线性无关的n 维列向量,代入i i i =AP P J 可得1121221i i i i i i i i i i i n in i in λλλ-=⎧⎪=+⎪⎨⎪⎪=+⎩AX X AX X X AX XX (1,2,,)i s =由第一个方程看到,列向量1i X 是矩阵A 的特征为i λ所对的特征向量.且由1i X 继而可以求得23,,,i i i in X X X .因此,长方形矩阵i P 以至P 都可以求得.由前面例子中可以看到,特征向量1i X 的选取要保证2i X 可以求出,类似地2i X 的选取(因为2i X 的选定并不唯一,只要适当选取一个就可)也要保证3i X 可以求出,如此等等.2-27 解:两种可能性. ①初等因子321,(1),2,(2)λλλλ++--,②初等因子222(1),(1),2,(2)λλλλ++-- (Jordan标准形略).2-28 解:A.若i j λλ≠,则21()()1()2()(1)1()0()i i i i i i i i i n i i i i i h i i i i a rank n rank n rank n n rank h n λλλλ--=--=--=--=-=≥E J E J E J EJ()()(1,2,)l i j j j b rank n l λ-==E J 2()[](1)1[](2)2[]()ii i j i j i j j ii i j i j i j j ihi i j j i j c rank n n n n rank n n n n rank n h n λλλ+++⎛⎫-=-+=+-⎪⎝⎭⎛⎫-=-+=+-⎪⎝⎭⎛⎫-=≥⎪⎝⎭J E J J E J J EJ B .若i j λλ=,不妨设i j n n >,则2()()1()2()0()i j j i i j j i h i j j j a rank n rank n rank h n λλλ-=--=--=≥E J E J EJ21()[](1)(1)2[](2)(2)4[]((1))((1))2[]()()j jii i j i j i j j ii i j i j i j j in i i j i j j j i j j in i i j i j j j i j c rank n n n n rank n n n n rank n n n n n n rank n n n n n n λλλλ++-++⎛⎫-=-+-=+-⎪⎝⎭⎛⎫-=-+-=+-⎪⎝⎭⎛⎫-=--+--=-+⎪⎝⎭⎛⎫-=-+-=-⎪⎝⎭J E J J E J J E J J EJ 12[][(1)]0(1)[](2)[]0j j ij in i i j i j j i j in i i j i j j in i i j j rank n n n n rank n n rank λλλ+++++⎛⎫-=-++⎪⎝⎭=-+⎛⎫-=-+⎪⎝⎭⎛⎫-=⎪⎝⎭J E J J E J J EJ反过来,可以借助(),()kki i i i j j rank rank λλ--E J E J ,[]ik i i j j rank λ+⎛⎫-⎪⎝⎭J E J 得出,i j J J 的阶数,i j n n .由于()()k k i i rank rank λλ-=-E J E A ,因此可以借助计算()ki rank λ-E J 得到Jordan 块的个数,阶数分析,继而可得J 的形状.2-29 解: 4(1)λλ-=-E A234()3,()2()1,()0rank rank rank rank -=-=-=-=E A E A E A E A因此,Jordan 块是4阶1块,即1111111⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A2-30 解:命 123(,,)Tx x x =X ,则方程组可写为126103114d dt --⎡⎤⎢⎥=-=⎢⎥⎢⎥--⎣⎦X X AX 其中 126103114--⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦A 1100011001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP其中 122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 1102112113--⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦P令X =PY 得113322132333222()()()t t t t t t tx k e k e k t k e x k e k t k e x k e k t k e =-+++=++=++其中123,,k k k 为任意常数.2-31 解:先求A 的初等因子,然后求得A 的Jordan 标准形2124⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦J设123(,,)Tααα=P ,且1-=P AP J ,即=AP JP . 于是111211213332(2)02(2)4(4)0ααααααααααα=-==+-=-=-=A E A A E A A E A不难求得1(0,1,0)T α=211(,0,)22T α=-3(1,0,1)T α=11010102100,101111010222-⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦P P于是10121010210021011411010222⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦A10099100100100991999919999100999919999199101210020102100210114110102222202210022100222022⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤-+-+⎢⎥=-⎢⎥⎢⎥-++⎣⎦A2-32 证:由2k =A A 可知A 的特征值只可能是0,k.方法一:由2k =A A 得()0kE A -=A 故秩()A +秩()kE A -n ≤又秩()A +秩()kE A - ≥秩()kE A +-A =秩()k E =n 因此秩()A +秩()kE A -n =若秩()A r =,则A 属于特征值为0的线性无关特征俩向量有r -n 个,A 的属于特征值为k 的线性无关特征向量有n-秩()kE A -=n-[n-秩()A ]=r.所以A 共有(n-r )+r=n 个线性无关特征向量.于是A 可对角化. 方法二:设A 的Jordan 标准形为12(,,,)r diag =J J J J .于是存在可逆矩阵P ,11,--==P AP J A PJP代入2k =A A 可得22,,(1,2,,)i i k k i r ===J J J J .不难验算可知,若2i i k =J J ,i J 必须是一阶Jordan 块.因此A 的Jordan 块(1,2,,)i i r =J 全是一阶的.因此A 与对角矩阵相似.2-33 证:设A 的Jordan 标准形12(,,,)r diag =J J J J ,即存在可逆矩阵P ,满足112(,,,)r diag -==J J J J PAP于是112(,,,)()T T T T T T T r diag -==J J J J P A P这表明TT AJ ,所以如果能证明对于每一个(1,2,,)i i r =都有Ti i J J .则根据相似的传递性便知TA A .事实上,若令00101010i ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P (i P 的阶数=i J 的阶数) 则不难验证1,T i i i i i i -==P P P J P J (证毕)2-34 解:121001011n n a a a a λλλλ-⎡⎤⎢⎥-⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥-+⎣⎦EC 它的不变因子为111(1)1,11,n n n n n a a a λλλ---++++个.2-35 解:2321111(1)(2)584λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥-==⎢⎥⎢⎥⎢⎥⎢⎥---+-⎣⎦⎣⎦E A100004021108002015⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦AJ F052100031⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P为了求Q 需先求FJ 的变换矩阵M ,即=FM MJ设123(,,)βββ=M ,代入=FM MJ 得123123100(,,)(,,)021002ββββββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦F比较两边得1122323,2,2βββββββ===+F F F解之得123(4,4,1),(2,3,1)(1,1,0)T T T βββ=-=-=-于是123421(,,)431110βββ-⎡⎤⎢⎥==--⎢⎥⎢⎥⎣⎦M1111110124-⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦M故1052111318100110111031124214---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦Q PM2-36 解:221111(1)21λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥--=-⎢⎥⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦E A因此100100011001001002⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A J F 122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 为了求Q 需先求F J 的变换矩阵M ,即=FM MJ 设123(,,)βββ=M ,代入=FM MJ 得123123100(,,)(,,)011001ββββββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦F 比较两边得1122323,,βββββββ===+F F F解之得123(1,0,0),(0,1,1)(0,1,0)T T T βββ==-=故123100(,,)011010βββ⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦M 1100001011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦M 于是1122100110001011011124101012--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Q PM2-37 解:(1)A 的初等因子21,(2)λλ+-故A 的不变因子为321,1,34λλ-+ 于是A 的有理标准形为 004100013-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦F(2)A 的初等因子21,(1)λλ-- 故A 的不变因子为21,1,(1)λλ-- 于是A 的有理标准形为100001012⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦F。
jordan标准形

jordan标准形Jordan标准形。
Jordan标准形是指矩阵的一种特殊形式,它可以将任意矩阵通过相似变换转化为Jordan标准形。
Jordan标准形在线性代数和矩阵理论中有着重要的应用,对于矩阵的特征值和特征向量的研究具有重要意义。
本文将介绍Jordan标准形的定义、性质以及如何将一个矩阵转化为Jordan标准形。
首先,我们来定义什么是Jordan标准形。
对于一个n阶矩阵A,如果存在一个可逆矩阵P,使得P^{-1}AP=D,其中D是一个Jordan块对角矩阵,那么我们称D是矩阵A的Jordan标准形。
Jordan块是指形如λI+N的矩阵,其中λ是矩阵的特征值,I是单位矩阵,N是上三角的特殊矩阵。
Jordan标准形的存在性是线性代数中一个重要的结论,它告诉我们任意一个n阶矩阵都可以通过相似变换转化为Jordan 标准形。
接下来,我们来看一下Jordan标准形的性质。
首先,Jordan标准形是唯一的,即对于一个矩阵A,它的Jordan标准形是唯一确定的。
其次,Jordan标准形的对角线上的元素就是矩阵A的特征值。
最后,Jordan标准形的非对角线上的元素对应着矩阵A的特征向量。
这些性质使得Jordan标准形成为了研究矩阵特征值和特征向量的重要工具。
最后,我们来看一下如何将一个矩阵转化为Jordan标准形。
假设我们有一个n阶矩阵A,我们首先需要求出矩阵A的特征值和特征向量。
然后,我们构造出一个可逆矩阵P,它的列向量是矩阵A的特征向量。
接下来,我们可以得到P^{-1}AP,它的对角化矩阵D就是矩阵A的Jordan标准形。
这个过程可以通过线性代数中的特征值分解和相似对角化的理论来实现。
总之,Jordan标准形是线性代数中一个重要的概念,它可以帮助我们研究矩阵的特征值和特征向量。
通过相似变换,我们可以将任意矩阵转化为Jordan标准形,从而更好地理解和分析矩阵的性质。
希望本文的介绍能够帮助读者更好地理解Jordan标准形的定义、性质和转化过程。
Jordan标准形

形式为 1 0 J(( ,,tt)) J 0 0 0 0
形矩阵,其一般形状如
Jordan标准形 J1
J2
Js
i ki ki
Jordan标准形
方阵A的Jordan标准形的求解步骤:
(1)求出n阶方阵A的初等因子源自③用初等变换化 E A 为对角矩阵
diag ( f1 ( ), f n ( )) 再将 f1 ( ), f2 ( ),, fn ( ) 分解成互不相同的一次因
式方幂的乘积,即可得A的初等因子.
E - A 和 E - B 等价.
Jordan标准形
定义 1 设A 是复数域 C 上的 n n 矩阵,
则其特征矩阵(E – A)的不变因子、行列式
因子、初等因子分别称为A的不变因子、行
列式因子、初等因子.
推论1 设 A, B 是复数域 C上两个 n n 矩阵,
则下列命题等价: (1)A 和 B 相似. (2)A 和 B 有相同的各级行列式因子. (3)A 和 B 有相同的不变因子.
形矩阵,其一般形状如
Jordan标准形
0 0 0 0 定义 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 tt 0 t t 的矩阵称为若尔当(Jordan)块,其中 是复数. 0 0 0 1 1 0
Jordan标准形
方阵A的Jordan标准形的求解步骤:
(1)求出n阶方阵A的初等因子
( 1 )n1 ,( 2 )n2 ,,( s )ns
其中 1 , 2 ,, s可能有相同的,指数 n1 , n2 ,, ns 也可能有相同的,且 n1 n2 ns n (2)写出每个初等因子对应的Jordan块
jordan标准形定理

Jordan标准形定理及证明
Jordan标准形定理的主要内容是:每个n阶的复数矩阵A都与一个若尔当形矩阵相似,这个若尔当形矩阵除去其中若尔当块的排列次序是被矩阵A唯一确定的,它称为矩阵A的若尔当标准型。
这个定理可以通过初等因子理论来证明。
具体来说,设a是复数域上的n 维线性空间上的线性变换,在中必定存在一组基,使在这组基下的矩阵是若尔当形,并且这个若尔当形矩阵除去其中若尔当块的排列次序是被唯一决定的。
此外,复数矩阵与对角矩阵相似的充分必要条件是,矩阵的初等因子全为一次的,不变因子都没有重根。
以上内容仅供参考,建议查阅数学专业书籍或咨询专业数学研究人员获取更准确的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T可以对角化T有n个线性无关的特征向量。 dimVi =n dimVi =ki
定理2. 4(p39) T可以对角化T的变换矩阵A可以对角化。
例题2 已知{1,2 ,3 }是空间V3(F) 的基,T是空间上如下定义的线性变换, T( 1 )= 1 T( 2 )=2 2 T( 3 )= 1 +t 2+2 3 讨论:t为何值,T有对角矩阵表示
三、最小多项式
1 定义(P.54, 定义2 . 5)
mA( )是最小多项式
mA( A) =0 mA( )在化零多式
r1 r2 rs
2 mA( )的结构:
设f( )= I–A= ( 1 ) ( 2 ) ( s )
要点:
矩阵A一旦有化零多项式,则有无穷多化零多项式。 g( A )= 0 的决定因素。 存在性问题。
Cayley-Hamilton 定理(P.52, 定理、2 . 7): AFn×n,f ( )= det( I–A),则f ( A )= 0。 Cayley 定理的应用举例: 使Ak ( kn)降阶至不超过n-1次的多项式。 f( 0) 0,则A的逆矩阵可以用多项式表示。 对线性变换T,f ( T)=0,即f( T )为零变换。
矩阵A和JA的特征值相等
J1( 1 ) J 2 ( 2 ) JA J s ( s )
APi Pi J i ( i )
细分矩阵Pi 和 Ji,在Jordan块上,有
Jordan链条{,y2,…,ynj}
( A i I ( A i I ( A i I ( A i I
2 Jordan 矩阵
Jordan矩阵是上三角矩阵 对角矩阵是Jordan 矩阵
3
Jordan 标准形
定理2 . 5 (p41)
含义: Jordan 矩阵可以作为相似标准形。 惟一性:Jordan 子块的集合惟一。
A相似于BJA相似于JB
二、方阵A的Jordan 标准形的求法
目标:求可逆矩阵P和Jordan矩阵JA ,使AP=PJA 分析方法: 在定理 2.5 的基础上逆向分析矩阵JA 和P的构成。 求法与步骤: ks k1 k2 f ( ) I A ( 1 ) ( 2 ) ( s )
推论: 1) 若i是单特征值,则dimVi =1 2) V1+V2+=Vs= V1V2Vs 3) V1V2Vs Vn(F)
二、线性变换矩阵对角化的充要条件
f ( ) I A ( 1 )k1 ( 2 )k2 ( s )k s
15
23 P 1 15
二、矩阵的化零多项式
(Annihilating polynomials of Matrices)
问题:AFn×n , A0,是否存在非零多项式g(), 使 得 g( A )=0? 1. 化零多项式(P.52) 如果 g(A) = 0,则g()被称为矩阵A的化零多项式。
例题3
证明幂等变换(T2=T)有对角矩阵表示。
2.2 Jordan 矩阵介绍
目标:发展一个所有方阵都能与之相似的矩 阵结构----Jordan矩阵。 一、 Jordan 矩阵 1. Jordan 块(p40,定义2.3)
1. 2. 3.
形式: 值 J( ) 确定因素:矩阵的阶数 Jordan 块矩阵的例子: 1 1 1
3. 重要的线性变换
方法:
用矩阵的相似化简研究问题 Jordan化方法
重点:
2.1 线性变换的对角表示
背景: T(1 2 …n) = (1 2 …n)
1. (12 …n) 线性无关
1 2 n
一、变换T的特征值与特征向量 1. 定义(p35 ,定义2.1) 2. 求解分析:(p35 ,定理2.1)
3 矩阵多项式 g(A ) 的计算 方法: Jordan块
J1( 1 ) J 2( ) P 1 A p J k ( ) nn
g ( J1 ) g( J 2 ) P 1 g( A ) p g( J k ) nn
例题1 下列矩阵哪些是Jordan块?
2 1 1 1 0 2 0 2
4 1 0 0 1 0 0 4 0 0 0 1 0 0 4 0 0 0
J1( 1 ) 1) 形式: J 1 ( 2 ) 2) Jordan矩阵举例 3) 特点 元素的结构 J m ( m )
例题1 设 g( ) 4 5 对P38,eg3中的矩阵A,计算g(A)。 解 3 3 2 1
3 2
1
A 7 1
6 2
3 P 2
2
1 P 1 2
1 g( A ) P
) 0 ) y2 ) y3 y 2
特征向量
广义特征向量
) y n j y n j 1
方法步骤:
由特征值i 的代数重数确定主对角线元素是的 i 的 Jordan 矩阵J(i ) 的阶数。 由特征值i 对应的线性无关的特征向量的个数确 定 J(i) 中Jordan 块的个数 由特征向量求得的Jordan 链条的长度确定 Jordan块的阶数 链条中的向量合起来构成可逆矩阵P,Jordan块 构成JA
2 . 性质(定理2 . 7)
• AX = 0 X g(A)X= g(0 )X • P -1 AP =B P -1 g(A)P= g(B)
A1 •A A2 Ak
g( A1 ) g( A2 ) g( A ) g( Ak )
例题1 (p44,例题5)
例题2 (p45,例题6)
例题3 将矩阵A化为Jordan 矩阵。
3 4 0 1 1 0 A 0 0 2 0 0 1 0 0 1 0
例题4 (p46,例题7)
§2.3 最小多项式 (minimal polynomials)
讨论n 阶矩阵多项式的相关问题:
定理2.8:mA( )= ( 1
P.54
)t1 ( 2 )t2 ( s )ts
n1 n2 ns
1 ti ri
定理2.9:mA( )=
( 1 ) ( 2 ) ( s )
ni 是i对应的Jordan块的指数。
3 变换对角矩阵表示的条件 定理2.10:线性变换T可以对角化的充要条 件是T的最小多项式是一次因子的乘积。 例题1 (P.56, eg10) 4×4 ,m ( )=( 1 ) ( 2 )2 例题2 设A R A
矩阵多项式(重点是计算) 矩阵的化零多项式(Cayley 定理) 最小多项式
Jordan标准形的应用
相似不变性 Jordan化的方法
一、矩阵多项式 m m 1 1. 定义 g( ) am am1 a1 a0 m m 1 g( A ) am A am1 A a1 A a0 I
A的特征值就是T的特征值
2. Ti= ii ; L{ i}是不变子空间
A的特征向量是T的特征向量的坐标
例题1(p37 ,例题2.1) 3、 特征向量的空间性质 1) 特征子空间: 2) 特征子空间的性质:(p36 ,定理2.2)
Vi是不变子空间 i j,则ViVi={0} 若i是ki重特征值,则1dimViki
证明JA和JAT的Jordan 块J和JT相似。
证明方法: S 取逆向单位矩阵S, TS 证明:SJ=J 1 1 1
(backward identity )
3、矩阵A ,
T A
, A
HA 和A
设A为n 阶方阵,则下列结果成立:
1. 矩阵A相似于矩阵AT
第1章习题选讲
要点: 线性空间的表示形式:
集合表示形式:Vn(F)={ 满足的性质} 向量生成形式:L{1,2,·,m } · ·
子空间类型:
L{1,2,·,m } · · W1+W2 矩阵AF m×n,两个子空间 不变子空间
1. 线性变换的表示 2. 线性变换的数量关系
线性变换:
求矩阵A的所有可能的Jordan矩阵。
例题3 设
g( ) ( 1 ) ( 2 ) ( 4 )
是矩阵A的化零多项式,证明A可以相似于对角矩 阵。
相似问题中的一些矩阵结果
1. 幂等矩阵、幂零矩阵和乘方矩阵
幂等矩阵(idempotent): A 2 =A
幂零矩阵(nilpotent): A0, k为正整数,Ak=0 乘方矩阵(involutary): A 2 = I
g ( r 1 ) ( ) ( r 1 )! g( ) 2! g ( ) g( )
g( ) ( ) g( ) g 1 2! 1 g( ) g ( ) g( J ) J( ) g( ) 1 r r mr g(J)的结构特点: 由第一行的元素生成
第2章:Jordan标准形介绍
Jordan Canonical Form
第2章:Jordan标准形介绍
问题:
对线性空间中的线性变换T,求一组基{1,2 ,, n} {1,2 ,, n} 和矩阵J ,使 T: J
• 矩阵J 尽可能简单。 • 矩阵J的结构对任何变换可行
内容:
首选A为对角形 线性变换的对角化问题。 建立J 一般的结构 Jordan标准形理论。 Jordan方法及其应用
A为幂等矩阵的充要条件是A相似于矩阵
