线路竖曲线计算公式

竖曲线高程计算公式(一)

竖曲线高程计算公式(一)竖曲线高程计算公式在土木工程和道路设计中，竖曲线是指公路或铁路沿纵向发生变化的曲线。

通过计算竖曲线的高程，我们可以确定道路或铁路的纵向轮廓，确保车辆或列车在垂直方向上的安全行驶。

本文将介绍竖曲线高程计算公式的相关内容，并提供示例说明。

标准竖曲线要素在计算竖曲线高程之前，我们需要了解一些标准竖曲线的要素，包括以下几个参数：1.起点高程（E1）：竖曲线的起点高程，通常为已知值。

2.终点高程（E2）：竖曲线的终点高程，也为已知值。

3.起点纵坡比（G1）：起点的纵向坡度，表示每单位水平距离对应的竖向高度变化。

4.终点纵坡比（G2）：终点的纵向坡度，同样表示每单位水平距离对应的竖向高度变化。

5.曲线长度（L）：竖曲线的水平长度，即起点到终点之间的距离。

6.曲线中点（P）：竖曲线的中点，即起点和终点之间的一半距离。

通常情况下的竖曲线高程计算公式在绝大多数情况下，我们可以使用以下公式来计算竖曲线的高程：E = E1 + G1 * P + (4 * (E2 - E1) - (G1 + G2) * L) *(P / L) * (1 - (P / L))其中，E为竖曲线的任意点的高程。

示例说明我们来通过一个具体的示例来解释竖曲线高程计算公式的应用。

假设一条道路的起点高程为100米，终点高程为150米，起点纵坡比为，终点纵坡比为，曲线长度为200米。

现在我们需要计算该曲线上距离起点100米处的高程。

根据上述公式，我们可以依次计算：•起点到终点的水平距离为200米，因此曲线中点P为100米。

•根据公式，可得到：E = 100 + * 100 + (4 * (150 - 100) - ( + ) * 200)* (100 / 200) * (1 - (100 / 200))化简后计算得到：E = 100 + 3 + (4 * 50 - * 200) * *= 100 + 3 + (200 - 10) *= 100 + 3 +=因此，在距离起点100米处的位置，竖曲线的高程为米。

道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

竖曲线长度计算公式

竖曲线长度计算公式
1、外矢距计算公式: L=T2/2R；
2、切线长计算公式：T=1/2*R*(I前-I后)；
3、凹曲线任一点计算公式：H =E+Abs(Q-C)*I + L；
4、凸曲线任一点计算公式：H =E-Abs(Q-C)*I - L；
说明：
H=所求点高程；
E=竖曲线交点高程；
Q=起点桩号；
C=所求点桩号；
I=线路纵坡坡率。

扩展资料
竖曲线技术指标主要有竖曲线半径和竖曲线长度。

凸形的竖曲线的视距条件较差，应选择适当的半径以保证安全行车的需要。

凹形的竖曲线，视距一般能得到保证，但由于在离心力作用下汽车要产生增重，因此应选择适当的半径来控制离心力不要过大，以保证行车的平顺和舒适。

一般城市干路相邻坡段的坡度小于0.5%或外距小于5cm时，可以不设置竖曲线。

竖曲线的最小半径与设计速度有关，凹形竖曲线最小半径为100M，凸形竖曲线为100M。

竖曲线计算公式

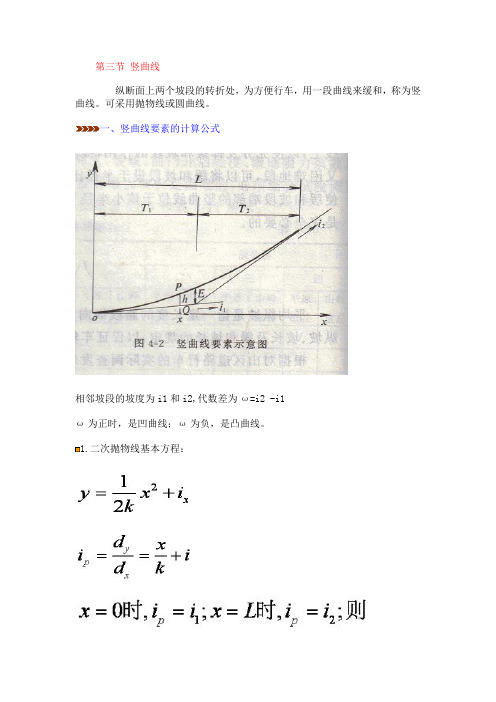
第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：二、竖曲线最小半径（三个因素）1.缓和冲击对离心加速度加以控制。

ν(m/s)根据经验，a=0.5~0.7m/s2比较合适。

我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。

(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时，Lmin = 2ST - 4/ω2.当L≥ST时，ST为停车视距。

以上两个公式，第二个公式计算值大，作为有效控制。

按缓和冲击、时间行程和视距要求（视距为最不利情况）计算各行车速度时的最小半径和最小长度，见表4-13。

表中：（1）一般最小半径为极限最小半径的1.5~2倍；（2）竖曲线最小长度为3s行程的长度。

（二）凹曲线最小半径和长度1.夜间行车前灯照射距离要求：1）L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。

例：设ω＝2%=0.02;则L＝ωＲ竖曲线最小长度Ｌ＝Ｖ/1.2速度Ｖ=120km/h V=40km/h 一般最小半径Ｒ凸17000 700一般最小半径Ｒ凹6000 700 L凸340 14Ｌ凹120 14 例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程＝431.18 - 6.40=424.78m。

道路施工相关计算公式

缓和曲线、竖曲线、圆曲线、匝道（计算公式）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0时sgn(x)=1，当x=0时sgn(x)=0。

切线高程和设计高程计算公式

切线高程和设计高程计算公式竖曲线高程计算公式：
1、外矢距计算公式：L=T2/2R；
2、切线长计算公式：T=1/2*R*（I前-I后）；
3、凹曲线任一点计算公式：H=E+Abs(Q-C)*|+
L;
4、凸曲线任一点计算公式：H=E-Abs(Q-C)*-
L；说明：H=所求点高程；E=竖曲线交点高程；Q=起点桩号；C=所求点桩号；=线路纵坡坡率。

知识点延伸：在线路纵断面上，以变坡点为交点，连接两相邻坡段的曲线称为竖曲线。

竖曲线有凸形和凹形两种。

道路设计高程怎么算？
计算方法：由：A点地面高程+A、B间距×坡度比=B
点地面高程；竖距h=（A、B间距）？？/2R—R为竖曲线
半径；得：B点设计高程=B点地面高程+（-）竖距h—凹曲线时为“+”，凸曲线时为“-”。

高程【elevation】指的是某点沿铅垂线方向到绝对基面的距离，称绝对高程，简称高程。

某点沿铅垂线方向到某假定水准基面的距离，称假定高程。

高程基准是推算国家统一高程控制网中所有水准高程的起算依据，它包括一个水准基面和一个永久性水准原点。

水准基面，通常理论上采用大地水准面，它是一个延伸到全球的静止海水面，也是一个地球重力等位面，实际上确定水准基面则是取验潮站长期观测结果计算出来的。

竖曲线运算步骤及公式讲解

竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号：竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

竖曲线的计算方法

竖曲线铁路线路的纵断面最理想的当然是平道，然而事实上是不可能的，为了适应地形的起伏，以减少工程量，纵断面必须用各种不同的坡面连接而成。

两相邻坡段的连续点谓之变坡点。

相邻坡段的坡度差是两相邻坡段的坡度代数差。

当相邻坡段的坡度差超过允许值时，为了保证行车平顺和安全，应在变坡点处用竖曲线连接起来。

允许不设竖曲线的坡度差允许值是根据车轮不脱轨、车钩不脱钩、列车不撞车和行车平稳等要求进行分析确定的。

一般情况下，竖曲线采用圆曲线，也可以采用抛物线，个别情况下，还可以采用连续短坡曲线。

竖曲线的计算一、圆曲线形竖曲线圆曲线形竖曲线的几何要素和各点设计标高，可按下列公式计算，如图。

R α　x T TyRCα/2　BAi1i21、竖曲线的切线长度TT=R·tan(α/2)=R/2·tanα=R/2·△i‰=R/2000·△i(m) (5-1)式中 R-竖曲线半径(m)；α-竖曲线转角(度)；△i-相邻坡段的坡度代数差(‰)。

R=5000m时， T=2.5△i(m)R=10000m时，T=5.0△i(m)R=15000m时，T=7.5△i(m)R=20000m时，T=10.0△i(m)R=25000m时，T=12.5△i(m)2、竖曲线长度CC≈2T=R/1000·△i(m) (5-2)3、竖曲线纵距yy=x2/2R (m) (5-3)式中 x-竖曲线上计算点至竖曲线起(终)点的横距(m)。

当x=T时，变坡点的纵距Y即为竖曲线的外矢距E。

Y=E=T2/2R=1/2R(C/2)2=C2/8R (5-3.1)4、竖曲线上各点的设计标高H设h为计算点的坡度标高，则H=h±y (5-4)式中的y值，凹形取“+”，凸形取“-”。

【算例一】一凹形竖曲线i1=-4‰，i2=+2‰，△i=6‰，变坡点的里程为K235+165，标高为54.60m，R=15000m，计算竖曲线上各20m点的设计标高。

铁路竖曲线要素计算公式

铁路竖曲线要素计算公式
铁路竖曲线要素计算公式包括：
1.曲线半径：R = (V^2) / (g x tan(α))
其中，R为曲线半径，V为设计速度，g为重力加速度(约等于9.8m/s^2)，α为设定超高角(通常为2-7度)。

2.切线长度：TL = R x sin(α)
其中，TL为切线长度，R为曲线半径，α为设定超高角。

3.过渡曲线长度：GL = R x (cot(α/2) - tan(α/2))
其中，GL为过渡曲线长度，R为曲线半径，α为设定超高角。

4.过渡曲线进入曲线角度：θI = cos^(-1)(cos(α/2) / (1 + GL/R))
其中，θI为过渡曲线进入曲线角度，α为设定超高角，GL为过渡曲线长度，R为曲线半径。

5.过渡曲线退出曲线角度：θO = cos^(-1)(cos(α/2) / (1 -
GL/R))
其中，θO为过渡曲线退出曲线角度，α为设定超高角，GL为过
渡曲线长度，R为曲线半径。

以上是常见的铁路竖曲线要素计算公式，它们用于确定设计时的
曲线半径、切线长度、过渡曲线长度以及进入和退出曲线的角度。

这
些要素的计算是为了确保铁路的行车安全性和乘车舒适性而进行的。

拓展方面，还可以根据需要考虑其他要素，如设计超高、坡度等，以
满足不同的工程要求。

此外，曲线要素计算还可以考虑地形地貌、列
车运行参数、轨道几何要求等方面的因素，以使设计更加综合和实用。

竖曲线坡度计算公式

竖曲线坡度计算公式
竖曲线坡度计算公式，是用于计算道路竖曲线坡度的公式。

竖曲线是指道路在垂直方向上的曲线，它由两条直线和一个圆弧线组成。

竖曲线坡度是指道路在竖曲线上的上下坡度。

竖曲线坡度计算公式需要考虑许多因素，包括道路的设计速度、曲线半径、坡度长度等。

具体的计算公式如下：
1. 计算坡度长度
L = K*v^2/R
其中，L为坡度长度，K为坡度系数（一般为1.5），v为设计速度，R为曲线半径。

2. 计算坡度
G = L/H
其中，G为竖曲线坡度，H为竖曲线高差。

以上就是竖曲线坡度计算公式的具体内容，它是道路设计和施工中必不可少的公式之一。

通过对竖曲线坡度的准确计算，可以确保道路的安全和舒适性，为人们的出行提供更好的保障。

- 1 -。

坐标、高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

线路竖曲线计算公式

竖曲线计算公式
一、公路施工中经常见到线路竖向曲线计算标高的问题，采用近似计算方法以外耻距（E）变化量代替标高增减量计算，设和用于半径（R）大于5000m时，误差为0.2mm。

1、凸曲线：H计算=H起坡点+i×△L起坡点至计算点的距离-（1/conα-1）×R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+（1/conα-1）×R
二、公路施工中经常见到线路竖向曲线计算标高的问题，采用近似计算方法以外变高差（h）变化量代替标高增减量计算，适合用于半径（R）小于5000m时，误差为0.2mm。

1、凸曲线：H计算=H起坡点+ i×△L起坡点至计算点的距离-(△L起坡点至计算点的距离)2/2R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+(△L起坡点至计算点的距离)2/2R
三、计算时考虑是正方计算方向来确定公式变换，如果凹面曲线从坡度终点返算时：坡度值为正值采用2公式时就应为+（- i×△L）。

(整理)高速公路各线形计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路坐标计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道) 坐标计算公式高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

竖曲线运算步骤及公式讲解

竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号：竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。