高等级道路竖曲线的精确计算方法
道路设计平曲线和竖曲线半径如何确定？
道路设计平曲线和竖曲线半径如何确定？1）平曲线与竖曲线应相互重合，且平曲线应稍长于竖曲线。
这种组合是使竖曲线和平曲线对应，最好使竖曲线的起、终点分别放在平曲线的两个缓和曲线内，即所谓的“平包竖”。
对于等级较高的道路应尽量做到这种组合，并使平、竖曲线半径都大一些才显得协调，特别是凹形竖曲线处车速较高，二者半径更应该大一些。
2）平曲线与竖曲线大小应保持均衡所谓均衡，是指平、竖曲线几何要素要大体平衡、匀称、协调，不要把过缓与过急、过长与过短的平曲线和竖曲线组合在一起。
根据德国计算统计，若平曲线半径小于1000m，竖曲线半径大约为平曲线半径的10～20倍时，便可到达均衡的目的。
3）暗弯、明弯与凸、凹竖曲线暗弯与凸形竖曲线及明弯与凹形竖曲线的组合是合理的组合。
对暗与凹、明与凸的组合，当坡差较大时，会给人以错觉：舍弃平坦坡道及近路不走，而故意爬坡、绕弯的感觉。
此种组合在山区难以防止，只要坡差不大，矛盾也不很突出。
4）平、竖曲线应防止的组合设计车速≥40km/h的公路，凸形竖曲线的顶部和凹形竖曲线的底部，不得插入小半径平曲线。
凸形竖曲线的顶部或凹形竖曲线的底部，不得与反向平曲线的顶点重合。
小半径竖曲线不宜与缓和曲线相互重叠。
平面转角小于7？的平曲线不宜与坡度角较大的凹形竖曲线组合在一起。
5）在完全通视的条件下，长上（下）坡路段的平面线形多次转向形成蛇形的组合线形，应竭力防止。
直线上一次变坡是较好的平、纵组合，从美学观点讲以包括一个凸形竖曲线为好，而包括一个凹形线次之；直线中短距离内二次以上变坡会形成反复凸凹的“驼峰”和“凹陷”，看上去线形既不美观也不连贯，宜使驾驶员的视线中断。
道路作为一种线形构造物，应将其视为景观对象来研究。
修建道路会对自然景观产生影响，有时甚至产生一定破坏作用。
而道路两侧的自然景观会影响道路上汽车的行驶，特别是对驾驶员的视觉、心理以及驾驶操作等都有很大影响。
高等级道路竖曲线的精确计算方法
程序使用说明Fx9750、9860系列程序包含内容介绍：程序共有25个，分别是：1、0XZJSCX2、1QXJSFY3、2GCJSFY4、3ZDJSFY5、4ZDGCJS6、5SPJSFY7、5ZDSPFY8、5ZXSPFY9、6ZPJSFY 10、7ZBZFS 11、8JLHFJH 12、9DBXMJJS13、9DXPCJS 14、9SZPCJS 15、GC-PQX 16、GC-SQX17、PQX-FS 18、PQX-ZS 19、ZD-FS 20、ZD-PQX21、ZD-SQX 22、ZD-ZS 23、ZDSP-SJK 24、ZXSP-SJK 25.XGBYCX其中，程序2-14为主程序，程序15-24为子程序，程序25为线性超高与三次抛物线超高修改互换备用程序。
每个主程序都可以单独运行并得到结果，子程序不能单独运行，它是配合主程序运行所必需的程序。
刷坡数据库未采用串列，因为知道了窍门，数据库看起很多，其实很少。
程序1为调度2-8程序；程序2为交点法主线路(含不对称曲线)中边桩坐标正反计算及极坐标放样程序；程序3为主线路中边桩高程计算及路基抄平程序；程序4为线元法匝道中边桩坐标正反计算及极坐标放样程序；程序5为匝道线路中边桩高程计算及路基抄平程序；程序6为任意线型开口线及填筑边线计算放样程序；程序7专为主线路开口线及填筑边线计算放样程序，只需测量任意一点三维数据，即可马上计算出该点相对于中桩法线上的偏移量；程序8专为匝道线路开口线及填筑边线计算放样程序，只需测量任意一点三维数据，即可马上计算出该点相对于中桩法线上的偏移量；程序9为桥台锥坡计算放样程序；程序10为计算两点间的坐标正反算程序；程序11为距离后方交会计算测站坐标程序；程序12为任意多边形面积周长计算程序；程序13为导线近似平差计算程序；程序14为水准近似平差计算程序；程序2-8所用数据库采用的串列，匝道用的File 1；主线用的 File 2。
道路曲线高程计算公式
高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。
道路竖曲线计算
道路竖曲线计算 Hessen was revised in January 2021第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状，通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。
一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。
当 i 1- i 2为正值时，则为凸形竖曲线。
当 i 1 - i 2 为负值时，则为凹形竖曲线。
（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为：Py x 22=若取抛物线参数P 为竖曲线的半径 R ，则有：Ry x 22= Rx y 22=（二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得：==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长： L = R ω3、竖曲线切线长： T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距： E =RT 22⑤竖曲线上任意点至相应切线的距离：Rx y 22=式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；R —为竖曲线的半径，m 。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 （1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。
（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。
竖曲线计算公式及计算方法
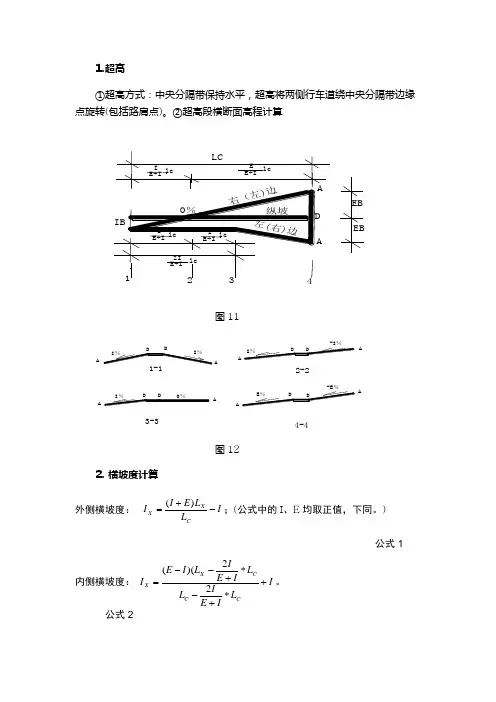
⒈超高①超高方式：中央分隔带保持水平，超高将两侧行车道绕中央分隔带边缘点旋转(包括路肩点)。
②超高段横断面高程计算图11AA AAAAAA2-23-34-4-I％图12⒉横坡度计算外侧横坡度：ILLEIICXX-+=)(；(公式中的I、E均取正值，下同。
)公式 1内侧横坡度：ILIEILLIEILIEICCCXX+*+-*+--=22)((。
公式 2EBEB式中：2 I/(E+I)* L C—在L C段内横坡等于I％的长度,m。
X在区间0～2 I/(E+I)*LC时，横坡度为I；在区间2 I/(E+I)* L C～L C段内时，横坡度为I～E。
I—横坡度设计值，E—超高设计值，L C—缓和曲线长，m。
⒊竖曲线计算公式：W=I1-I2；当w＞0时，为凸曲线；当w＜0时，为凹曲线。
L=R*W；E=T2/2R；H=l2/2r；T=TA=TB=L/2=R*W/2。
式中：H—切线上任一点至竖曲线上的垂直距离；M．l—曲线上相应于H的P点至切点A或B点的距离，M．R—二次抛物线的参数。
(原点处的曲率半径)通常称竖曲率半径，M．I1、I2—切线的斜率，即纵坡度，％．纵坡度(％)，从左向右上坡取“+”，下坡取“-”值．当α很小时，tanα1≈α1=I1, tan α2≈α2=I2。
T—切线长(M)，ZH路线平面图L—竖曲线的曲线长(M)。
竖曲线的计算
竖曲线的计算⼀、设置竖曲线的要求铁路线路所包含的坡度除平坡外，有上坡、下坡。
所谓坡度，即铁路线路的⾼程变化率，⽤千分率表⽰，就是每1000m ⽔平距离⾼程上升或下降的数值，通常⽤符号“+、-、0”依次表⽰上坡、下坡或平坡。
在进⾏纵断⾯设计时，相邻两坡段的交点叫变坡点，两变坡点之间的⽔平距离叫坡段长度。
《铁路线路设计规范》规定：⼯、Ⅱ级铁路相邻坡段坡度的代数差⼤于3％0和Ⅲ级铁路相邻坡段坡度的代数差⼤于4‰时，需⽤竖曲线连接。
竖曲线的形状主要分为圆曲线形和抛物线形两种。
《新建客货共线铁路设计暂⾏规定》规定：纵断⾯宜设计为较长的坡段，相邻坡段的连接宜设计为较⼩的坡度差。
旅客列车设计⾏车速度为200 km／h的路段，最⼩坡段长度不宜⼩于600m，困难条件下最⼩坡段长度不应⼩于400m，且最⼩坡段长度不得连续使⽤2个以上。
旅客列车设计⾏车速度为160km／h的路段，最⼩坡段长度不宜⼩于400m，且最⼩坡段长度不宜连续使⽤2个以上。
竖曲线不得与缓和曲线、相邻竖曲线重叠设置，也不得设在明桥⾯和正线道岔内。
⼆、竖曲线的计算⽅法1.圆曲线形竖曲线计算《铁路线路设计规范》规定：Ⅰ、Ⅱ级铁路竖曲线半径为10000m Tv=5 X △i ，Ⅲ级铁路竖曲线半径为5000m。
Tv=2.5 X △i(1)竖曲线的切线长 Tv=Rv ×tan a/2 = Rv/2 ×tan a= Rv/2000 × △i △i=△i2-△i1 的绝对值Tv－竖曲线的切线长(m)；Rv--竖曲线半径，a----竖曲线转⾓，△i－相邻坡段坡度的代数差(‰)。
(2)竖曲线的曲线长 C≈2T。
(3)竖曲线的纵距竖曲线的纵距即竖曲线上任意点与切线上相邻点的标⾼差，⽤y表⽰，即 y=x2/2Rv式中Y－竖曲线的纵距(m)； x－竖曲线上任意点距竖曲线始点或终点的距离(m)；(4)竖曲线标⾼ H=Hp±y 式中H－竖曲线标⾼(m)； Hp－计算点坡度线标⾼，【例题】某⼀级铁路，有⼀圆曲线形竖曲线(如图3－20所⽰)，竖曲线中点⾥程为K24+400，标⾼为65.7 m，上坡i1=+2‰，下坡i2=-4‰，试计算竖曲线上每20 m点的标⾼。
竖曲线计算方法
竖曲线一、有关规定线路大中修纵断设计有关规定。
1. 设计坡长一般不短于该区段到发线有效长的一半，个别困难地段，应不短于200m。
2. 采用抛物线形竖曲线时，凡相邻坡段的坡段代数差大于2‰时，须设计竖曲线，竖曲线长度每20m的变坡率，凸形应不大于1‰，凹形应不大于0.5‰。
抛物线形竖曲线最好设计在平面曲线两端缓和曲线之外，仅在困难条件下，允许冲迭而不受缓和曲线的限制。
抛物线形竖曲线不能设计在无碴桥梁上。
3. 采用圆曲线形竖曲线时，凡相邻坡段的坡度代数差大于3‰时，须设计竖曲线。
竖曲线半径应根据运营条件采用20000-10000m；困难条件下不小于5000m。
圆曲线形竖曲线不应侵入缓和曲线、道岔及无碴桥梁上。
二、圆曲线形竖曲线的计算竖曲线的几何要素（如下图）及标高的近似计算式如下：切线长度： T=R/2000 ⊿i(m)竖曲线长度： C≈2T(m)竖曲线纵距： y≈x2/2R(m) 式中x——竖曲线横距（m）竖曲线外矢距 E=T2/2R（m）竖曲线标高 H=h±y(m) 式中 h——计算点的路肩设计标高（m）；y——竖曲线上计算点的纵距，凹形竖曲线取“+”，凸竖曲线取“-”形。
不同半径的竖曲线纵距如表竖曲线纵距表y(m)不同半径的竖曲线要素如表竖曲线要素表（m）三、抛物线形竖曲线的计算抛物线形竖曲线在作为竖曲线使用的范围内，曲率变化非常小，在工程实施上与圆曲线形竖曲线无甚差别，即实质上是大半径的圆曲线形竖曲线，其换算半径：R=1000⊿l/r(m)式中 ⊿l ——抛物线形竖曲线的短坡段长度（m ），一般采用20m ； r ——每一短坡段的变坡率（‰）。
⊿l 为20m ，R 与γ的对应关系如表3。
抛物线形竖曲线的几何要素及标高可沿用下列公式计算：⊿i=i 1+i 2 C ’=20⊿i/γ T ≈C ’/2 y ≈γ/40000x 2 E 0≈γ/40000T 2式中 i 1 i 2 ——坡度，用千分率表示； ⊿i ——两相邻坡段的坡度，代数差；y E 0 ——根据表3换算；C ——抛物线形竖曲线长度，取整至m 。
公路测量曲线和竖曲线要素计算方法
1.某山岭区一般二级公路，变坡点桩号为K5＋030，高程为427.68m ，%51=i ，%42-=i ，竖曲线半径R ＝2000m 。
试计算竖曲线各要素以及桩号为k5＋000和K5＋100处的设计高程。
解：⑴计算竖曲线要素09.005.004.012-=--=-=i i ω，为凸形竖曲线。
曲线长20000.09180L R m ω==⨯=切线长m L T 9021802=== 外距2290 2.03222000T E m R ===⨯ ⑵计算设计高程竖曲线起点桩号＝（K5+30）－90=K4+940竖曲线起点高程＝427.68－90×0.05＝423.18m桩号K5+000处：横距m K K x 60)9404()0005(1=+-+= 竖距m R x h 9.040006022211=== 切线高程＝423.18＋60×0.5＝426.18m设计高程＝426.18－0.9＝425.28m桩号K5＋100处：横距m K K x 160)9404()1005(2=+-+= 竖距m R x h 4.6400016022222=== 切线高程＝423.18＋160×0.05＝431.18m设计高程＝431.18－6.4＝424.78m2．某山岭区二级公路，已知JD1、JD2、JD3的坐标分别为（40961.914,91066.103）、（40433.528,91250.097）、（40547.416,91810.392），并设JD2的R=150m ，Ls=40m ，求JD2的曲线要素。
解：⑴计算出JD2、JD3形成的方位角fwj2，︒=--=48966.11528.40433416.40547097.91250392.91810arctan 2fwj 计算出JD1、JD2形成的方位角fwj1， ︒=--=19908.289914.40961528.40433103.91066097.91250arctan1fwj 曲线的转角为α＝360＋fwj2－fwj1＝82.29058°⑵由曲线的转角，计算出曲线的切线长T ，曲线长L 及超距J3322402019.9882240240150s s L L q R =-=-=⨯ 24243340400.444242384241502384150s s L L p R R =-=-=⨯⨯ ︒===639.7150406479.286479.280R L s β 438.151988.19229058.82tan )444.0150(2tan )(=++=++=q p R T α 0150(2)2(82.2905827.639)240290.526180180s RL L ππαβ⨯=-+=-⨯+⨯= 781.49150229058.82sec )444.0150(2sec )(=-+=-+=R p R E α下面总结范文为赠送的资料不需要的朋友，下载后可以编辑删除！祝各位朋友生活愉快！员工年终工作总结【范文一】201x年就快结束，回首201x年的工作，有硕果累累的喜悦，有与同事协同攻关的艰辛，也有遇到困难和挫折时惆怅，时光过得飞快，不知不觉中，充满希望的201x年就伴随着新年伊始即将临近。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
竖曲线上点的里程为:
D Z′= D I - T
D Q ′= D I
D Y ′= D I + T
D P = D Z′+ x P 2. 精确计算公式 如图 2 所示, 在图中建立以水平距离为横坐 标轴 d , 铅垂线为纵坐标轴 H ′的 dO H ′直角坐标 系, A 点 的 坐 标 为 ( dA , 0 ) , Z 点 的 坐 标 为 ( 0, H Z ′) , 竖曲线各元素的精确计算公式如下:
二、计算原理
1. 近似计算公式 如图 1 所示, 设道路纵坡的变坡点为 I , 其设 计高程为 H I, 里程为 D I, 两侧的纵坡度分别为 i1、i2, 竖曲线设计半径为 R , 竖曲线各元素的近似 计算公式如下:
Ξ= i1- i2
L= RΞ
T=
L 2
E=
T2 2R
yP=
x
2 P
2R
H P = H I - (T - x P ) i1- y P
表 1
桩号 (点名)
里程差 m
近似高程 Hm
精确高程 Hm
误差 ∃ mm
辅助计算
6+ 5. 0028 (Z ′)
- 0. 534
53. 51
6+ 500. 814 (Z )
0
53. 747
6+ 540
39. 186
56. 265
56. 270
5
6+ 580
79. 186
58. 383
58. 389
1999 年 第 1 期 测 绘 通 报 23
高等级道路竖曲线的精确计算方法
孙银聪
(福建泉州黎明职业大学 362000)
【摘 要】 本文从竖曲线的严密计算公式入手, 推导竖曲线上点的设计高程和里程的精确计算方法。分析和比较了
近似公式和严密公式的差别及对设计高程和里程的影响。 在道路勘测设计中用本方法可取得精确、方便、迅速的效果, 建议 取代传统的近似方法。
(9)
由式 (9) 可推算出竖曲线上任一与 Z 点的里
程差为 d 的点的纵坐标值 H ′, 则
式中, Α1, Α2 分别为纵坡线与水平线的夹角; Ξ 为变坡角; 3 为切线长; % 为外矢距; d I 为纵坡变 坡点 I 与 Z 点的里程差; dA 为竖圆曲线圆心A 与 Z 点的里程差; H ′为竖圆曲线上任一点的纵坐标 值; d 为竖圆曲线上任一点与 Z 点的里程差; H 为竖圆曲线上任一点的设计高程; ∃H = H ′Z H Z 为 Z 点纵坐标值与 Z 点设计高程之差 (H Z = H I - d I ·i1) ; D 为竖曲线上任一点的里程。
Α1= a rctan i1
(1)
Α2= a rctan i2
(2)
Ξ= Α1- Α2
(3)
T=
R tan
Ξ 2
(4)
E = R ( sec
Ξ 2
-
1)
(5)
d I = T co sΑ1
(6)
dA = R sinΑ1
(7)
H Z ′= R co sΑ1
ቤተ መጻሕፍቲ ባይዱ
(8)
竖曲线在直角坐标系中的方程为
(d - dA ) 2+ H ′2= R 2
58. 865
58. 867
2
6+ 919. 997 (Y ) 6+ 920. 28 (Y ′)
419. 183 419. 466
57. 91
57. 924
四、结 论
采用传统的近似计算公式推算竖圆曲线上点 的设计高程和里程, 存在着一定的误差, 并且随着 道路纵坡的增大而增大。 特别对于大纵坡又有超 高横坡的外边线的竖曲线 (有超高的外边线纵坡 比中线纵坡更大) 以及风景区和校区、别墅区等的 竖曲线 (纵坡常在 10% 左右) , 若用近似方法计 算, 误差更大, 而且没有勘测设计竖圆曲线的变坡 点 N , 直接影响路面施工精度和质量。 而采用本
H = H ′- ∃H D = D Z + d (D Z = D I - d I )
(10)
某山岭重丘的二级公路的纵坡变坡点 I, 其
设计高程 H I = 68. 410 m , 里程 D I = 6+ 710. 280,
(11) 两侧纵坡分别为 7% 和- 5% , 凸形竖曲线的设计
(12)
半径 R = 3 500 m , 其计算结果见表 1。
6
Α1= 4°00′15″
6+ 620
119. 186
60. 043
60. 050
7
Α2= - 2°51′45″
6+ 660
159. 186
61. 246
61. 253
7
Ξ= 6°52′00″
6+ 700
199. 186
61. 992
61. 999
7
T = 209. 979
6+ 710. 28 (Q )
62. 113
62. 291 62. 118
5
∃H = 3437. 709 (Z ′、Y ′、Q ′为 用 近 似公式计算的直圆
6+ 820
319. 186
61. 487
61. 492
5
点 和 圆 直 点、曲 中
6+ 860
359. 186
60. 405
60. 408
3
点)
6+ 900
399. 186
文介绍的方法计算, 计算公式精确严密, 不受坡度 和半径大小的影响, 方便迅速, 又可计算和测设具 有重要作用的竖曲线变坡点N 。采用本方法具有 较高的应用价值和施工实际指导意义。
参考文献
1 陈龙飞, 金其坤编著. 工程测量. 上海: 同济大学出版 社, 1990
2 周荣沾主编. 城市道路设计. 北京: 人民交通出版社, 1988
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
由 式 (10) 可知, 当 d = dA 时, 则里 程 D N = D Z + dA 的 N 点为竖圆曲线的变坡点, 其高程 H N = H N ′- ∃H = R - ∃H = m ax, N 点在现场施工 中具有很重要的指导意义。
三、计算实例
H ′= R 2- (d - dA ) 2 0≤d ≤d Y 并可立即推算点的设计高程和里程
一、引 言
在传统的道路纵断面设计中, 竖曲线元素及 对应桩号里程和设计高程均采用近似公式计算, 在低等级道路及计算工具很落后的时代曾起到过 很大的作用。但是随着高级道路的快速发展, 道路 竖曲线半径的不断加大, 设计和施工的精度要求 越来越高, 因此, 对勘测设计工作提出了很高的要 求。 采用近似的方法进行勘测设计已难以满足高 精度、高效灵活的要求。 为此本文给出了实用、精 确的竖曲线计算公式, 以解决实际工作中存在的 问题。
209. 466
62. 117
E = 6. 239
6+ 710. 342 (Q ′) 6+ 740
209. 528 239. 186
62. 110 62. 281
62. 287
6
dN = dA = 244. 402 H Z ′= 3491. 456
6+ 745. 216 (N ) 6+ 780
244. 402 279. 186
图1
图2
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
24 测 绘 通 报 1999 年 第 1 期