沿程阻力系数测定实验报告
沿程阻力系数测定-实验报告

沿程水头损失实验实验人 XXX 合作者 XXX XX 年XX 月XX 日一、实验目的1.加深了解圆管层流和紊流的沿程损失随平均流速变化的规律,绘制lgh f ~-lg v 曲线; 2.掌握管道沿程阻力系数的量测技术和应用压差计的方法;3.将测得的R e -λ关系值与莫迪图对比,分析其合理性,进一步提高实验成果分析能力。
二、实验设备本装置有下水箱、自循环水泵、[供水阀、稳压筒、实验管道、流量调节阀]三组,计量水箱、回水管、压差计等组成。
实验时接通电源水泵启动,全开供水阀,逐次开大流量调节阀,每次调节流量时,均需稳定2-3分钟,流量越小,稳定时间越长;测流量时间不小于8-10秒;测流量的同时,需测记压差计、温度计[自备,应挂在水箱中]读数。
三根实验管道管径不同,应分别作实验。
三、实验原理由达西公式g v d L h r 22⋅⋅=λ 得222422⎪⎭⎫⎝⎛==d Q L gdh Lv gdh f f πλ=K ×h f /Q 2 另有能量方程对水平等直径圆管可得γ21P P h f -=对于多管式水银压差有下列关系h f =(P 1-P 2)/γw =(γm /γw -1)(h 2-h 1+h 4-h 3)=12.6△h m Δh m = h 2-h 1+h 4-h 3 h f —mmH 2O四、实验结果与分析实验中,我们测量了三根管的沿程阻力系数,三根管的直径分别为10mm ,14mm ,20mm 。
对每根管进行测量时,我们通过改变水的流速,在相距80cm 的两点处分别测量对应的压强。
得到表1至表3中的实验结果。
相关数据说明:水温29.4℃,对应的动力学粘度系数为20.01/cm s ν=流量通过水从管中流入盛水箱的体积和时间确定。
水箱底面积为22020S cm =⨯,记录水箱液面升高12h cm =(从5cm 到17cm 或者从6cm 到18cm )的时间t ,从而计算出流量34800(/)()Sh Q cm s t t s ==; 若管道直径为D ,则水流速度为24Qv Dπ=; 对三根管进行测量时,测量的两点之间距离均为80L cm =; 雷诺数Re vDν=;计算沿程阻力系数:层流164Reλ=;紊流0.2520.316R e λ-= 测量沿程阻力系数:2/f Kh Q λ=,其中25K /8gD L π=,29.8/g m s =第一根管表-1(521110,15.113/D mm K cm s ==)第二根管表-2(522214,81.280/D mm K cm s ==)第三根管表-3(523320,483.610/D mm K cm s ==)通过对三根管的相关计算,我们发现实验测出的沿程阻力系数远远比层流情况下的计算值大,将近大一个数量级。
沿程阻力系数实验报告

沿程阻力系数实验报告沿程阻力系数实验报告引言:沿程阻力系数是描述流体在管道中流动过程中受到的阻力大小的一个重要参数。
准确测量沿程阻力系数对于流体力学研究和工程应用具有重要意义。
本实验旨在通过实验方法测量沿程阻力系数,并探讨其与流速、管道直径等因素的关系。
实验装置:本次实验采用的实验装置主要包括:水泵、流量计、压力计、流量调节阀、管道等。
其中,水泵用于提供流体流动的动力;流量计用于测量流体通过管道的流量;压力计用于测量管道中的压力;流量调节阀用于控制流体流动的速度。
实验步骤:1. 首先,将实验装置按照实验要求进行搭建,并将水泵连接到管道系统中。
2. 打开水泵,调节流量调节阀,使流量计示数稳定在一定数值。
3. 记录流量计示数和压力计示数,并计算流速和压力差。
4. 重复上述步骤,改变流量调节阀的开度,记录不同流速下的流量计示数和压力计示数。
5. 根据实验数据,计算沿程阻力系数。
实验结果:根据实验数据,我们得到了不同流速下的流量计示数和压力计示数。
通过计算,得到了相应的流速和压力差。
进一步分析实验数据,我们得到了不同流速下的沿程阻力系数。
讨论与分析:通过实验结果的分析,我们可以得到以下结论:1. 沿程阻力系数与流速呈正相关关系。
随着流速的增加,沿程阻力系数也会增加。
这是因为流速增加会导致流体分子之间的相互碰撞增加,从而增加了阻力。
2. 沿程阻力系数与管道直径呈反相关关系。
管道直径越大,沿程阻力系数越小。
这是因为管道直径增大会减小单位面积内的流体流速,从而减小了阻力。
3. 沿程阻力系数与流体的黏度有关。
黏度越大,沿程阻力系数越大。
这是因为黏度大的流体分子之间的相互作用力较大,从而增加了阻力。
结论:通过本次实验,我们成功测量了沿程阻力系数,并探讨了其与流速、管道直径、流体黏度等因素的关系。
实验结果表明,沿程阻力系数与流速、管道直径、流体黏度等因素密切相关。
这对于流体力学的研究和工程应用具有重要意义。
致谢:在此,我们要感谢实验指导老师的悉心指导和同组同学的合作。
尼古拉斯实验实验报告

一、实验目的1. 了解尼古拉斯实验的基本原理和方法;2. 掌握通过实验测定沿程阻力系数的方法;3. 分析沿程阻力系数与雷诺数、相对粗糙度的关系;4. 验证尼古拉斯实验结论的正确性。
二、实验原理尼古拉斯实验通过人工粗糙管流实验,研究沿程阻力系数与雷诺数、相对粗糙度的关系。
实验过程中,改变管道直径、粗糙度和流量,测量不同条件下的沿程阻力系数,从而归纳总结出沿程阻力系数的变化规律。
沿程阻力系数f与雷诺数Re和相对粗糙度ε的关系如下:f = f(Re, ε)其中,f(Re, ε)表示沿程阻力系数与雷诺数Re和相对粗糙度ε的函数关系。
三、实验仪器与材料1. 人工粗糙管;2. 流量计;3. 计时器;4. 粗糙度测量仪;5. 计算器。
四、实验步骤1. 根据实验要求,准备不同直径、不同粗糙度的人工粗糙管;2. 调整流量计,控制流量稳定;3. 测量管道直径、粗糙度,计算相对粗糙度ε;4. 在不同流量下,分别测量沿程阻力系数;5. 记录实验数据,进行数据处理和分析。
五、实验结果与分析1. 实验数据:根据实验数据,绘制沿程阻力系数f与雷诺数Re、相对粗糙度ε的关系曲线。
2. 分析:(1)在层流区,沿程阻力系数f与雷诺数Re成反比,与相对粗糙度ε成正比;(2)在光滑管区,沿程阻力系数f与雷诺数Re成反比,与相对粗糙度ε成正比;(3)在湍流过渡区,沿程阻力系数f与雷诺数Re和相对粗糙度ε的关系复杂,需要结合实验曲线进行判断;(4)在湍流粗糙区,沿程阻力系数f与雷诺数Re和相对粗糙度ε的关系呈平方关系。
六、实验结论1. 尼古拉斯实验归纳总结出了流动阻力与雷诺数Re和相对粗糙度ε的关系,将沿程阻力系数的变化归纳为五个区:层流区、光滑管区、湍流过渡区、湍流粗糙区和阻力平方区;2. 实验结果表明,沿程阻力系数与雷诺数Re和相对粗糙度ε之间存在一定的关系,为工程设计和流体力学研究提供了理论依据;3. 尼古拉斯实验为流体力学的研究提供了重要的实验数据,有助于进一步探索流体流动规律。
沿程阻力实验报告
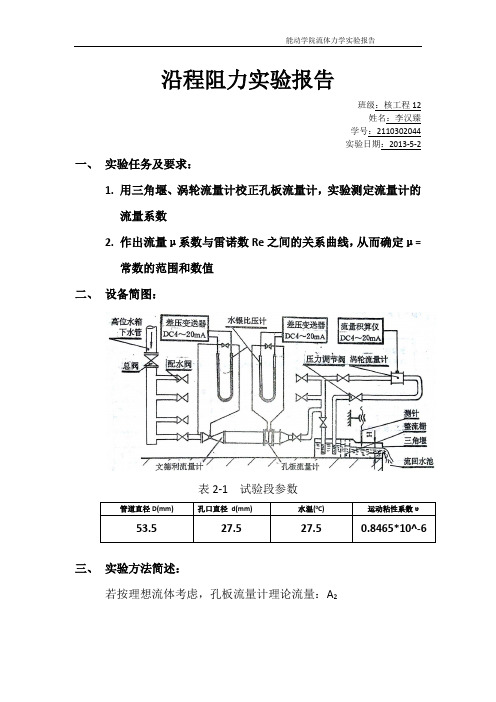
三角堰流量测量:
实验数据处理及计算:
表4-1实验测量数据
序号
孔板比压计
测针读数H(cm)
堰上水头
H=H-H0
H0=12.032
流量Q
(m3/h)
(流量计)
水温
(0C)
运动粘滞系数
X106
(m2/s)
读数1
(cm)
读数2
(cm)
读数差(cm)
1
66.61
37.92
28.69
20.694
8.662
6.119
4.96
27.5
0.8465
6
54.45
51.08
3.37
17.526
5.494
3.85
27.5
0.8465
7
53.9
51.59
2.31
17.182
5.15
3.21
27.5
0.8465
8
53.45
52.1
1.35
16.7
4.668
2.46
26.5
0.8651
表4-2数据处理结果
序号
孔板流量计流量1
11.3
27.5
0.8465
2
62.41
42.32
20.09
20.082
8.05
9.42
27.5
0.8465
3
58.76
46.4
12.36
19.226
7.194
7.4
27.5
0.8465
4
56.89
48.48
8.41
18.693
6.661
6.11
沿程阻力系数测定-实验报告

沿程水头损失实验实验人 XXX 合作者 XXX XX 年XX 月XX 日一、实验目的1.加深了解圆管层流和紊流的沿程损失随平均流速变化的规律,绘制lgh f ~-lg v 曲线;2.掌握管道沿程阻力系数的量测技术和应用压差计的方法; 3.将测得的R e -λ关系值与莫迪图对比,分析其合理性,进一步提高实验成果分析能力。
二、实验设备本装置有下水箱、自循环水泵、[供水阀、稳压筒、实验管道、流量调节阀]三组,计量水箱、回水管、压差计等组成。
实验时接通电源水泵启动,全开供水阀,逐次开大流量调节阀,每次调节流量时,均需稳定2-3分钟,流量越小,稳定时间越长;测流量时间不小于8-10秒;测流量的同时,需测记压差计、温度计[自备,应挂在水箱中]读数。
三根实验管道管径不同,应分别作实验。
三、实验原理由达西公式g v d L h r 22⋅⋅=λ 得222422⎪⎭⎫⎝⎛==d Q L gdh Lv gdh f f πλ=K ×h f /Q 2另有能量方程对水平等直径圆管可得γ21P P h f -=对于多管式水银压差有下列关系h f =(P 1-P 2)/γw =(γm /γw -1)(h 2-h 1+h 4-h 3)=12.6△h m Δh m = h 2-h 1+h 4-h 3 h f —mmH 2O四、实验结果与分析实验中,我们测量了三根管的沿程阻力系数,三根管的直径分别为10mm ,14mm ,20mm 。
对每根管进行测量时,我们通过改变水的流速,在相距80cm 的两点处分别测量对应的压强。
得到表1至表3中的实验结果。
相关数据说明:水温29.4℃,对应的动力学粘度系数为2 0.01/cm s ν=流量通过水从管中流入盛水箱的体积和时间确定。
水箱底面积为2202 0S cm =⨯,记录水箱液面升高12h cm =(从5cm 到17cm 或者从6cm 到18cm )的时间t ,从而计算出流量34800(/)()Sh Q cm s t t s ==; 若管道直径为D ,则水流速度为24Qv Dπ=; 对三根管进行测量时,测量的两点之间距离均为80L cm =; 雷诺数Re vDν=;计算沿程阻力系数:层流164Reλ=;紊流0.2520.316R e λ-=测量沿程阻力系数:2/f Kh Q λ=,其中25K /8gD L π=,29.8/g m s = 第一根管表-1(521110,15.113/D mm K cm s ==)第二根管表-2(522214,81.280/D mm K cm s ==)第三根管表-3(523320,483.610/D mm K cm s ==)通过对三根管的相关计算,我们发现实验测出的沿程阻力系数远远比层流情况下的计算值大,将近大一个数量级。
沿程阻力系数测定-实验报告

沿程阻力系数测定-实验报告实验目的:测定流体在不同管道内流动时的沿程阻力系数,分析流体流动的规律。
实验原理:流体在流动的过程中,由于管道内的摩擦、弯曲等原因,会产生一定的沿程阻力,阻碍流体的流动。
沿程阻力系数是描述阻力大小的物理量,可以反映出流体流动的特性。
测算沿程阻力系数需要通过实验测量不同位置的压力差,计算得出流速和阻力系数,最终得到流体在管道内的流动规律。
实验器材:一台流量计,一根不同内径的水流管,一个流量调节器,一个压力计,一套支架和夹子,水池、水泵等辅助设备。
实验步骤:1. 搭建实验装置,将水泵接入水池,利用泵将水流送入待测管道中。
2. 开始实验前,先测量管道各处的内径和长度,并计算管道的摩擦系数。
3. 将流量计安装在管道的某个位置,调节流量,使其保持在一定的范围。
4. 安装压力计,分别测量流过流量计前后不同位置处的压力差。
5. 根据所测得的数据,计算流体的流速和沿程阻力系数,绘制实验数据图表。
6. 根据实验结果,分析流体的流动规律以及影响沿程阻力系数的因素。
实验结果:通过实验测量,我们得到了不同位置处的压力差、流速和阻力系数等数据,并绘制成图表。
从图表中可以看出,在管道内距离流速计越远的位置,流速逐渐下降,同时沿程阻力系数也逐渐增加。
这说明管道内的摩擦力和阻力对流体的影响逐渐加剧,阻碍了流体的流动。
实验结论:通过本次实验,我们得到了流体在管道内流动时的流速和沿程阻力系数等数据,为研究流体的流动规律提供了实验依据。
我们也发现,管道内的摩擦力和阻力对流体的影响很大,需要注意管道的内径和表面材质等因素。
此外,实验数据也可以为管道设计和流动控制等领域提供参考。
管路沿程阻力测定实验报告st

实验一 管路沿程阻力测定一、实验目的1、掌握流体流经管道时沿程阻力损失的测定方法。
2、测定流体流经直管时的摩擦阻力,确定摩擦系数λ与Re 的关系。
3、测定流体流经管件时的局部阻力,并求出阻力系数ξ。
4、学会压差计和流量计的使用。
二、实验原理流体在管路中流动时,引起的压强损耗包括流体流经直管的沿程阻力以及流体流动方向的改变或因管子大小、形状的改变所引起的局部阻力。
1、沿程阻力液体稳定流动时,阻力损失表现为压强(降低)损耗:12fp p h -=ρ为减少工作量,扩大实验结果的应用范围,采用因次分析法将各个变量综合成准数关系式。
影响阻力损失的因素: a 、流体的性质:密度ρ,粘度μ;b 、管路的几何尺寸:管径d,管长l,管壁粗糙度ε;c 、流动条件:u.经因次分析后,2·2==f P l u h d Δλρ 上式中:λ称为直管摩擦系数,雷诺数Re 在层流时:λ=64/ Re ; 湍流时:λ与Re和ξ/d 有关。
须由实验确定。
2、局部阻力(两种方法) ⑴当量长度法2·2e f l l u h d ⎛⎫ ⎪ ⎪ ⎪⎝⎭+=∑∑λ ⑵阻力系数法流体流经某一管件或阀门的阻力损失用流体在管路中的动能系数p h 表示:2·2p u h =ζ式中:ζ----局部阻力系数,无因次u----小截面管中的平均流速(m/s ) 2/4su V d =π(m/s ) s V ---平均流量(3m /s) p h 应用伯努利方程由液体压差计读数R 求出三、实验装置与流程1、本实验装置及设备主要参数:被测原件:镀锌水管,管长2.0m,管径(公称直径)0.021m;闸阀D=¾。
⑴测量仪表:U压差计(水银指示液);LW-15型涡轮流量计(精度0.5级,量程0.4~4.0m3/ h,仪器编号Ⅰ的仪表常数为599.41(次/升),仪器编号为Ⅱ的仪表常数为605.30(次/升),MMD智能流量仪)。
沿程阻力系数测定实验报告

沿程阻力系数测定实验报告1.1 什么是沿程阻力系数?哎呀,沿程阻力系数听起来有点高深,但其实它就是我们在流体力学中常提到的一个东西。
简单来说,就是流体在管道里流动时,遇到的阻力有多大。
想象一下,你在水管里放了几根铁丝,水流过的时候肯定会受到阻碍,对吧?这个阻碍程度就是沿程阻力系数的体现。
1.2 为什么要测定?那么,为什么我们要搞清楚这个系数呢?这就好比你要知道车的油耗,才能制定出合理的出行计划。
通过测定沿程阻力系数,我们可以预测流体的流动情况,进而优化管道设计,省下很多不必要的麻烦。
2. 实验步骤2.1 准备工作首先,我们得准备一些工具和材料。
流体管道、泵、流量计和压力计这些都是必不可少的。
哦,对了,还得准备好实验室的水源,别让水短缺了,要不然实验就泡汤了!记得在实验开始前,仔细检查一下设备,确保它们都能正常工作,不然可就要浪费时间了。
2.2 实验过程接下来,开始我们的实验吧!首先把水泵启动,让水在管道里流动。
水流过不同长度的管道,咱们要实时记录流量和压力的变化。
每次更换管道长度时,得耐心等待一段时间,确保数据稳定,这样才能得到准确的结果。
哈哈,别急着玩手机哦,专心点!3. 数据分析3.1 结果整理数据收集完毕,咱们就得把这些数字整理成表格。
每一组数据都要清晰明了,不然后续分析可就麻烦了!你会发现,随着管道长度的增加,沿程阻力系数也会逐渐增大,这就像你在跑步时,越跑越累,阻力自然也就多了。
3.2 结论和讨论最后,得出结论了。
我们发现,沿程阻力系数与管道长度成正比关系,真是让人眼前一亮!通过这个实验,不仅让我们对流体流动有了更深入的理解,还能帮助我们在以后的设计中避免不必要的麻烦。
这就像是打游戏时,学会了技能连招,通关自然轻松。
4. 实验心得4.1 体会通过这次实验,我真的感受到了一种探索的乐趣。
流体力学不再是高高在上的学问,而是我们生活中随处可见的现象。
就像喝水时,水是如何顺畅流动的,虽然我们平常不怎么去想,但其实有很多道理在背后。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沿程水头损失实验
实验人 XXX 合作者 XXX XX 年XX 月XX 日
一、实验目的
1.加深了解圆管层流与紊流的沿程损失随平均流速变化的规律,绘制lgh f ~-lg v 曲线;
2.掌握管道沿程阻力系数的量测技术与应用压差计的方法;
3.将测得的R e -λ关系值与莫迪图对比,分析其合理性,进一步提高实验成果分析能力。
二、实验设备
本装置有下水箱、自循环水泵、[供水阀、稳压筒、实验管道、流量调节阀]三组,计量水箱、回水管、压差计等组成。
实验时接通电源水泵启动,全开供水阀,逐次开大流量调节阀,每次调节流量时,均需稳定2-3分钟,流量越小,稳定时间越长;测流量时间不小于8-10秒;测流量的同时,需测记压差计、温度计[自备,应挂在水箱中]读数。
三根实验管道管径不同,应分别作实验。
三、实验原理
由达西公式g v d L h r 22
⋅⋅=λ 得2
22422⎪⎭
⎫
⎝⎛==d Q L gdh Lv gdh f f πλ=K ×h f /Q 2 另有能量方程对水平等直径圆管可得γ
2
1P P h f -=
对于多管式水银压差有下列关系
h f =(P 1-P 2)/γw =(γm /γw -1)(h 2-h 1+h 4-h 3)=12、6△h m
Δh m = h 2-h 1+h 4-h 3 h f —mmH 2O
四、实验结果与分析
实验中,我们测量了三根管的沿程阻力系数,三根管的直径分别为10mm,14mm,20mm 。
对每根管进行测量时,我们通过改变水的流速,在相距80cm 的两点处分别测量对应的压强。
得到
表1至表3中的实验结果。
相关数据说明:
水温29、4℃,对应的动力学粘度系数为2
0.01/cm s ν=
流量通过水从管中流入盛水箱的体积与时间确定。
水箱底面积为2
202
0S cm =⨯,记录水箱液面升高12h cm =(从5cm 到17cm 或者从6cm 到18cm )的时间t ,从而计算出流量
34800(/)()
Sh Q cm s t t s =
=; 若管道直径为D ,则水流速度为2
4Q
v D
π=
; 对三根管进行测量时,测量的两点之间距离均为80L cm =; 雷诺数Re vD
ν
=
;计算沿程阻力系数:层流164Re
λ=
;紊流0.25
20.316R e λ-= 测量沿程阻力系数:2/f Kh Q λ=,其中25
K /8gD L π=,2
9.8/g m s =
第一根管
表-1(52
1110,15.113/D mm K cm s ==)
第二根管
表-2(52
2214,81.280/D mm K cm s ==)
第三根管
表-3(52
3320,483.610/D mm K cm s ==
)
通过对三根管的相关计算,我们发现实验测出的沿程阻力系数远远比层流情况下的计算值大,将近大一个数量级。
实际上,我们实验中的雷诺数在10000-26000,超出层流范围,且在可认为就是在接近紊流或刚达到紊流条件,与紊流情况下算出的层流阻力系数比较相近,但仍略小,所以我们可以认为实验中我们的水流其实就是快接近紊流的。
另外,尽管读数时液面有一定的抖动,但就是对于每一根管算出的沿程阻力系数都比较相
近,因此可认为本实验中读数误差对实验结果没有多大影响。
对三根管的实验结果作lg lg f h v 曲线,结果图-1至图-3所示。
图- 1
图- 2
图- 3
每根管的lg lg f h v 图像,都有较好的线性关系。
管1中,斜率为1、65,可以认为就是紊流
过渡区;管2中斜率为1、93,接近粗管紊流区的斜率值;管3中,斜率为1、60,可以认为就是紊流过渡区。
