八年级数学下册中点四边形规律,中点四边形典型例题及答案解析
(必考题)初中八年级数学下册第十八章《平行四边形》经典练习(答案解析)

一、选择题1.如图,菱形ABCD 中,50A ∠=︒,则ADB ∠的度数为( )A .65︒B .55︒C .45︒D .25︒A解析:A【分析】 由菱形得到AB=AD ,进而得到∠ADB=∠ABD ,再由三角形内角和定理即可求解.【详解】解:∵四边形ABCD 为菱形,∴AD=AB ,∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,故选:A .【点睛】本题考查了菱形的性质,菱形的邻边相等,属于基础题,熟练掌握菱形的性质是解决本题的关键.2.如图,在平行四边形ABCD 中,DE 平分,6,2ADC AD BE ∠==,则平行四边形ABCD 的周长是( )A .16B .18C .20D .24C解析:C【分析】 根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED ,再根据等角对等边的性质可得CE=CD ,然后利用平行四边形对边相等求出CD 、BC 的长度,再求出▱ABCD 的周长.【详解】解:∵DE 平分∠ADC ,∴∠ADE=∠CDE ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,BC=AD=6,AB=CD ,∴∠ADE=∠CED ,∴∠CDE=∠CED ,∴CE=CD ,∵AD=6,BE=2,∴CE=BC-BE=6-2=4,∴CD=AB=4,∴▱ABCD 的周长=6+6+4+4=20.故选:C .【点睛】本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,熟练掌握平行四边形的性质,证明CE=CD 是解题的关键.3.如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,已知6AD =(正方形的四条边都相等,四个内角都是直角),2DF =.则AEF 的面积AEF S =( )A .6B .12C .15D .30C解析:C【分析】 延长CD 到G ,使DG=BE ,连接AG ,易证ADG ABE △≌△所以AE=AG ,BAE=DAG ∠∠ , 证AFG AEG △≌△,所以 GF=EF ,设BE=DG=x ,则EF=FG=x+2,在ECF Rt △中,利用勾股定理得222462x x 解得求出x ,最后求AGF S △问题即可求解.【详解】解:延长CD 到G ,使DG=BE ,连接AG ,在正方形ABCD 中,AB=AD ,90ADB B C ADC ∠=∠=∠=∠=︒ 90ADG B ∴∠=∠=︒,ADG ABE(SAS)∴△≌△,,AG AE BAE DAG ∴=∠=∠,45EAF ∠=︒ ,45DAF BAE ∴∠+∠=︒ ,GAF=45DAG DAF ∴∠∠+∠=︒,GAF=EAF ∴∠∠,又AF=AF ,AFG AEG ∴△≌△(SAS),EF=FG ∴,设BE=DG=x ,则EC=6-x ,FC=4,EF=FG=x+2,在ECF Rt △中,222=FC CE EF +,()()22246=2x x ∴+-+,解得,x=3, GF=DG DF=2+3=5∴+,AEF AGF 11S =S =GF AD=56=1522∴⨯⨯△△, 故选:C .【点睛】 本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,正确构造辅助线,证三角形全等是解决本题的关键.4.如图,在平行四边形ABCD 中,100B D ︒∠+∠=,则B 等于( )A .50°B .65°C .100°D .130°A解析:A【分析】 根据平行四边形的对角相等求出∠B 即可得解.【详解】 解:□ABCD 中,∠B =∠D ,∵∠B +∠D =100°,∴∠B =12×100°=50°, 故选:A .【点睛】本题考查了平行四边形的性质,主要利用了平行四边形的对角相等是基础题.5.如图,已知正方形1234A A A A 的边长为1,延长12A A 到1B ,使得1212B A A A =,延长23A A 到2B ,使得2323B A A A =,以同样的方式得到34,B B ,连接1234,,,B B B B ,得到第2个正方形1234B B B B ,再以同样方式得到第3个正方形1234C C C C ,……,则第2020个正方形的边长为( )A .2020B .2019(5)C .2020(5)D .20205B解析:B【分析】 结合题意分析每个正方形的边长,从而发现数字的规律求解【详解】解:由题意可得:第1个正方形1234A A A A 的边长为012=1=(5)A A∵1212B A A A =∴112A B =∴第2个正方形1234B B B B 221+2=5由题意,以此类推,215C B =2225C B =∴第3个正方形1234C C C C 222(5)(25)5(5)+==…∴第n 个正方形的边长为15)n -∴第2020个正方形的边长为2019(5)故选:B .【点睛】本题考查勾股定理及图形类规律探索,题目难度不大,正确理解题意求解每个正方形边长的规律是解题关键.6.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A .3B .23C .33D .43D解析:D【分析】 根据菱形的性质可得到直角三角形,利用勾股定理计算即可;【详解】如图,AC 与BD 相较于点O ,∵四边形ABCD 是菱形,4AC =,∴AC BD ⊥,2AO =,又∵∠ABC=60゜,∴30ABO ∠=︒,∴24AB AO ==,∴224223BO =-=,∴243BD BO ==;故选D .【点睛】本题主要考查了菱形的性质,结合勾股定理计算是解题的关键.7.如图,在平行四边形ABCD 中,点F 是AB 的中点,连接DF 并延长,交CB 的延长线于点E ,连接AE .添加一个条件,使四边形AEBD 是菱形,这个条件是( )A .BAD BDA ∠=∠B .AB DE =C .DF EF =D .DE 平分ADB ∠D解析:D【分析】先证明△ADF ≌△BEF ,得到AD=BE ,推出四边形AEBD 是平行四边形,再逐项依次分析即可.【详解】解:在平行四边形ABCD 中,AD ∥BC ,∴∠DAB=∠EBA ,∵点F 是AB 的中点,∴AF=BF ,∵∠AFD=∠BFE ,∴△ADF ≌△BEF ,∴AD=BE ,∵AD ∥BE ,∴四边形AEBD 是平行四边形,A 、当BAD BDA ∠=∠时,得到AB=BD ,无法判定四边形AEBD 是菱形,故该选项不符合题意;B 、AB=BE 时,无法判定四边形AEBD 是菱形,故该选项不符合题意;C 、DF=EF 时,无法判定四边形AEBD 是菱形,故该选项不符合题意;D 、当DE 平分ADB ∠时,四边形AEBD 是菱形,故该选项符合题意;故选:D .【点睛】此题考查平行四边形的性质,全等三角形的判定及性质,菱形的判定,熟记平行四边形的性质是解题的关键.8.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .4C解析:C【分析】 根据HL 证明△ADG ≌△FDG ,根据角的平分线的意义求∠GDE ,根据GE=GF+EF=EC+AG ,确定△BGE 的周长为AB+AC.【详解】根据折叠的意义,得△DEC ≌△DEF ,∴EF=EC ,DF=DC ,∠CDE=∠FDE ,∵DA=DF ,DG=DG ,∴Rt △ADG ≌Rt △FDG ,∴AG=FG ,∠ADG=∠FDG ,∴∠GDE=∠FDG+∠FDE =12(∠ADF+∠CDF ) =45°, ∵△BGE 的周长=BG+BE+GE ,GE=GF+EF=EC+AG ,∴△BGE 的周长=BG+BE+ EC+AG=AB+AC ,是定值,∴正确的结论有①③④,故选C.【点睛】本题考查了正方形中的折叠变化,直角三角形的全等及其性质,角的平分线,三角形的周长,熟练掌握折叠的全等性是解题的关键.9.如图,正方形ABCD 的对角线相交于点O ,正方形OMNQ 与ABCD 的边长均为a ,OM 与CD 相交于点E ,OQ 与BC 相交于点F ,且满足DE CF ,则两个正方形重合部分的面积为( )A .212aB .214aC .218a D .2116a B 解析:B【分析】由正方形OMNQ 与ABCD 得∠DOC=∠MOQ=90°可推出∠DOE=∠COF 由AC ,BD 是正方形ABCD 的对角线求得∠ODE=∠OCF=45°,可证△DOE ≌△COF (AAS ),利用面积和差S 四边形FOEC = S △EOC +S △DOE =S △DOC =214a 即可. 【详解】∵正方形OMNQ 与ABCD ,∴∠DOC=∠MOQ=90°,∴∠DOE+∠EOC =90º,∠EOC+∠COF=90º,∴∠DOE=∠COF ,又AC ,BD 是正方形ABCD 的对角线,∴∠ODE=∠OCF=45°,∵DE CF =,∴△DOE ≌△COF (AAS ),∴S 四边形FOEC =S △EOC +S △COF = S △EOC +S △DOE =S △DOC ,∵S △DOC =2ABCD 11=44S a 正方形, ∴S 四边形FOEC =214a . 故选择:B .【点睛】 本题考查正方形的性质,全等三角形的判定与性质,掌握正方形的性质,全等三角形的判定与性质是解题关键.10.如图,Rt Rt ABC BAD △≌△,BC 、AD 交于点E ,M 为斜边的中点,若CMD α∠=,AEB β∠=.则α和β之间的数量关系为( )A .2180βα-=︒B .60βα-=︒C .180αβ+=︒D .2βα=A 解析:A【分析】根据题意可得,CAB DBA ABC BAD ∠=∠∠=∠,再由直角三角形斜边的中线等于斜边的一半,可证CM DM AM BM ===,继而证明()AMC BMD SSS △≌△,解得1802AMC BMD CAM ∠=∠=︒-∠,最后根据三角形内角和180°定理,分别解得αβ、与CAM ∠的关系,整理即可解题.【详解】Rt Rt ABC BAD △≌△,CAB DBA ABC BAD ∴∠=∠∠=∠M 是AB 的中点,11,22CM AB DM AB ∴== CM DM AM BM ∴===∴∠CAM=∠MCA ,Rt Rt ABC BAD △≌△AC BD ∴=()AMC BMD SSS △≌△1802AMC BMD CAM ∴∠=∠=︒-∠CMD α∴=∠180AMC BMD =︒-∠-∠1802(1802)CAM =︒-⨯︒-∠4180CAM =∠-︒90ABC BAD CAM ∠=∠=︒-∠,AEB β=∠=180BAD ABC ︒-∠-∠180(90)(90)CAM CAM =︒-︒-∠-︒-∠2CAM =∠2180βα∴-=︒故选:A .【点睛】本题考查全等三角形的判定与性质、直角三角形斜边中线的性质、等腰三角形的性质、三角形内角和180°等知识,是重要考点,难度较易,掌握相关知识是解题关键.二、填空题11.如图,在ABC 中,10AB AC ==,D 为CA 延长线上一点,DE BC ⊥交AB 于点F .若F 为AB 中点,且12BC =,则DF =__________.8【分析】过点A 作AM ⊥BC 过点A 作AN ⊥BC 交DE 于N 证明△AFN ≌△BFE 得出AN=BE=3再利用勾股定理解答即可【详解】解:∵AB=AC ∴∠B=∠C ∵∴∠C+∠BFE=90∠B+∠BFE=90解析:8【分析】过点A 作AM ⊥BC ,过点A 作AN ⊥BC 交DE 于N ,证明△AFN ≌△BFE ,得出AN=BE=3,再利用勾股定理解答即可.【详解】解:∵AB=AC ,∴∠B=∠C ,∵DE BC ⊥,∴∠C+∠BFE=90,∠B+∠BFE=90°,∵∠BFE=∠AFD ,∠B=∠C ,∴∠BFE=∠AED=∠CDE ,∴AD=AF ,过点A 作AM ⊥BC ,在△ABC 中,∵AB=AC ,∴M 为BC 的中点,∴BM=12BC =6, 在Rt △ABM 中,AM=2222106AB BM -=-=8∵F 为AB 中点,FE ⊥BC , ∴FE 为△ABM 的中位线,BF=AF=12AB =5, ∴AD=AF=5,BE=132BM =, 过点A 作AN ⊥BC 交DE 于N ,∵AF=BF ,∠AFN=∠BFE ,∠ANF=∠BEF=90°,∴△AFN ≌△BFE ,∴AN=BE=3,在Rt △AND 中,DN=2222534AD AN -=-=,∵AD=AF ,AN ⊥DF ,∴DF=2DN=8.故答案为:8.【点睛】本题考查了勾股定理,等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定及性质的运用,正确作出辅助线是解题的关键.12.如图,在菱形ABCD 中,6AC =,5AB =,点E 是直线AB ,CD 之间任意一点,连接AE ,BE ,DE ,CE ,则EAB 和ECD 的面积之和是______.12【分析】连接BD根据菱形对角线的性质利用勾股定理计算BD的长根据两平行线的距离相等所以△EAB和△ECD的面积和等于菱形ABCD面积的一半再利用菱形面积等于对角线积的一半计算可得结论【详解】如图解析:12【分析】连接BD,根据菱形对角线的性质,利用勾股定理计算BD的长,根据两平行线的距离相等,所以△EAB和△ECD的面积和等于菱形ABCD面积的一半,再利用菱形面积等于对角线积的一半计算可得结论.【详解】如图,连接BD交AC于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=12AC=12×6=3,∵AB=5,由勾股定理得:224AB OA-=,∴BD=2OB=8,∵AB∥CD,∴△EAB和△ECD的高的和等于点C到直线AB的距离,∴△EAB 和△ECD 的面积和=12×ABCD S 菱形=12×12×AC×BD=168=124⨯⨯. 故答案为:12. 【点睛】 本题考查菱形的性质,三角形的面积,平行线的性质,熟知平行线的距离相等,得△EAB 和△ECD 的高的和等于点C 到直线AB 的距离是解题的关键.13.如图,在长方形纸片ABCD 中,12AB =,5BC =,点E 在AB 上,将DAE △沿DE 折叠,使点A 落在对角线BD 上的点A '处,则AE 的长为______.【分析】首先利用勾股定理计算出BD 的长再根据折叠可得AD=A′D=5进而得到A′B 的长再设AE=x 则A′E=xBE=12-x 再在Rt △A′EB 中利用勾股定理得出关于x 的方程解出x 的值可得答案【详解】解析:103【分析】首先利用勾股定理计算出BD 的长,再根据折叠可得AD=A′D=5,进而得到A′B 的长,再设AE=x ,则A′E=x ,BE=12-x ,再在Rt △A′EB 中利用勾股定理得出关于x 的方程,解出x 的值,可得答案.【详解】解:∵AB=12,BC=5,∴AD=5,∴22125+=13,根据折叠可得:AD=A′D=5,∴A′B=13-5=8,设AE=x ,则A′E=x ,BE=12-x ,在Rt △A′EB 中:(12-x )2=x 2+82,解得:x=103. 故答案为:103. 【点睛】本题考查了矩形的性质、勾股定理、折叠的性质等知识点,能根据题意得出关于x 的方程是解此题的关键.14.如图,EF 过ABCD 对角线的交点O ,交AD 于E ,交BC 于F ,若ABCD 的周长为19, 2.5OE =,则四边形EFCD 的周长为_____.145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF故四边形的周长=AD+CD+EF根据已知求解即可【详解】解:在平行四边形ABCD中AD∥BCAC与BD互相平分∴AO=OC∠DAC=解析:14.5【分析】根据平行四边形的性质易证三角形全等,进而易得AE=CF,故四边形EFCD的周长=AD+CD+EF,根据已知求解即可.【详解】解:在平行四边形ABCD中,AD∥BC,AC与BD互相平分∴AO=OC,∠DAC=∠ACB,∠AOE=∠COF∴△AOE≌△COF∴AE=CF,OF=OE=2.5∴四边形EFCD的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF=192.5 2×2=14.5.故答案为:14.5.【点睛】本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.15.如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P 不与写B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值等于__________.48【分析】连接由菱形的性质解得再根据勾股定理解得继而证明四边形为矩形得到根据垂线段最短解得当时有最小值最后根据三角形面积公式解题即可【详解】连接四边形是菱形四边形为矩形当时有最小值此时的最小值为故解析:4.8【分析】连接OP ,由菱形的性质解得118,622BO BD OC AC ====,再根据勾股定理解得10BC =,继而证明四边形OEPF 为矩形,得到FE OP =,根据垂线段最短解得当OP BC ⊥时,OP 有最小值,最后根据三角形面积公式解题即可.【详解】连接OP ,四边形ABCD 是菱形,12,16AC BD ==,AC BD ∴⊥118,622BO BD OC AC ==== 22643610BC OB OC ∴=+=+=,,PE AC PF BD AC BD ⊥⊥⊥∴四边形OEPF 为矩形,FE OP ∴=当OP BC ⊥时,OP 有最小值,此时1122OBC S OB OC BC OP =⋅=⋅ 68 4.810OP ⨯∴== EF ∴的最小值为4.8,故答案为:4.8.【点睛】本题考查菱形的性质、矩形的判定与性质、勾股定理、垂线段最短等知识,是重要考点,难度较易,掌握相关知识是解题关键.16.如图,平面直角坐标系中,已知点()9,9A ,点B 、C 分别在y 轴、x 轴上,AB AC ⊥且AB AC =,若B 点坐标为()0,a ,则OC =______(用含a 的代数式表示).18-【分析】过A作AE⊥y轴于EAD⊥x轴于D构造正方形AEOD再证△AEB≌△ADC(SAS)得BE=CD由EB=EO-BO=9-可求CD=9-求出OC=OD+CD=9+9-=18-即可【详解】解析:18-a.【分析】过A作AE⊥y轴于E,AD⊥x轴于D,构造正方形AEOD,再证△AEB≌△ADC(SAS),得BE=CD,由EB=EO-BO=9-a,可求CD=9-a,求出OC=OD+CD=9+9-a=18-a即可.【详解】过A作AE⊥y轴于E,AD⊥x轴于D,A,∵点()9,9AE=AD=OE=OD=9,∠ADO=90º,四边形AEOD为正方形,⊥,∠EAD=90°,∵AB AC∴∠EAB+∠BAD=90°,∠BAD+∠DAC=90°,∴∠BAE=∠CAD,=,AE=AD,∵AB AC∴△AEB≌△ADC(SAS),∴BE=CD,∵EB=EO-BO=9-a,∴CD=9-a,OC=OD+CD=9+9-a=18-a,故答案为:18-a.【点睛】本题考查正方形的判定与性质,三角形全等判定与性质,掌握正方形的判定方法与性质,三角形全等判定的方法与性质是解题关键.17.把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若38CDF∠=︒,则EFD∠的度数是_________.64°【分析】先根据矩形的性质求出∠CFD的度数继而求出∠BFD的度数根据图形折叠的性质得出∠EFD=∠BFE=∠BFD即可得出结论【详解】解:∵ABCD是矩形∴∠DCF=90°∵∠CDF=38°∴解析:64°【分析】先根据矩形的性质求出∠CFD的度数,继而求出∠BFD的度数,根据图形折叠的性质得出∠EFD=∠BFE=12∠BFD,即可得出结论.【详解】解:∵ABCD是矩形,∴∠DCF=90°,∵∠CDF=38°,∴∠CFD=52°,∴∠BFD=180°-52°=128°,∵四边形EFDA1由四边形EFBA翻折而成,∴∠EFD=∠BFE=12∠BFD=12×128°=64°.故答案为:64°.【点睛】本题考查的是矩形折叠问题,掌握轴对称的性质是关键.18.如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若1DE=,则BF的长为__________.【分析】连接FE根据题意得CD=2AE=设BF=x则FG=xCF=2-x 在Rt△GEF中利用勾股定理可得EF2=(-2)2+x2在Rt△FCE中利用勾股定理可得EF2=(2-x )2+12从而得到关于 解析:51-【分析】连接FE ,根据题意得CD=2,AE=5,设BF=x ,则FG=x ,CF=2-x ,在Rt △GEF 中,利用勾股定理可得EF 2=(5-2)2+x 2,在Rt △FCE 中,利用勾股定理可得EF 2=(2-x )2+12,从而得到关于x 方程,求解x 即可.【详解】解:连接EF ,如图,∵E 是CD 的中点,且CE=1∴CD=2,DE=1∵四边形ABCD 是正方形,∴AB=BC=CD=DA=2∴2222215AD DE +=+设BF=x ,由折叠得,AG=AB=2,FG=BF=x ,∴52,在Rt △GFE 中,2222252)EF FG GE x =+=+在Rt △CFE 中,CF=BC-BF=2-x ,CE=1∴22222(2)1EF FC CE x =+=-+∴222252)(2)1x x +=-+解得:=51x ,即51,51【点睛】本题主要考查了折叠的性质、勾股定理.折叠问题主要是抓住折叠的不变量,在直角三角形中利用勾股定理求解是解题的关键.19.如图,点E 是平行四边形ABCD 的边BC 上一点,连结AE ,并延长AE 与DC 的延长线交于点F ,若AB AE =,50F ∠=︒,则D ∠=______︒.65【分析】利用平行四边形的性质以及平行线的性质得出∠F=∠BAE=50°进而由等腰三角形的性质和三角形内角和定理求得∠B=∠AEB=65°利用平行四边形对角相等得出即可【详解】解:如图所示∵四边形解析:65【分析】利用平行四边形的性质以及平行线的性质得出∠F=∠BAE=50°,进而由等腰三角形的性质和三角形内角和定理求得∠B=∠AEB=65°,利用平行四边形对角相等得出即可.【详解】解:如图所示,∵四边形ABCD是平行四边形,∴AB∥DC,∴∠F=∠BAE=50°,.∵AB=AE,∴∠B=∠AEB=65°,∴∠D=∠B=65°.故答案是:65.【点睛】此题主要考查了平行四边形的性质,熟练应用平行四边形的性质得出是解题关键.20.如图,在平行四边形ABCD中,∠ABC=135°,AD=42,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为_____.【分析】连接CE过点C作交AB的延长线于点H设AE=x则BE=8-xCE=AE=x在根据勾股定理即可得到x的值【详解】如图:连接CE过点C作交AB的延长线于点H平行四边形ABCD中设AE=x则BE=解析:20 3【分析】连接CE,过点C作CH AB,交AB的延长线于点H,设AE=x,则BE=8-x,CE=AE=x,在根据勾股定理,即可得到x的值.【详解】如图:连接CE ,过点C 作CH AB ⊥,交AB 的延长线于点H ,平行四边形ABCD 中,135,2ABC AD ∠=︒=45,2CBH BC ∴∠=︒=90,H ∠=︒45,BCH ∴∠=︒4CH BH ∴==设AE=x ,则BE=8-x ,EF 垂直平分AC ,CE AE x ∴==, 在Rt CEH 中,222CH EH EC +=,()222484x x ∴+-+=, 解得:203x =, AE ∴的长为203, 故答案为:203. 【点睛】 本题考查了平行四边形的性质,勾股定理以及线段垂直平分线的性质,解决问题的关键是作辅助线构造直角三角形,利用勾股定理求解.三、解答题21.如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,点E ,F 分别在BD 和DB 的延长线上,且DE BF =,连接AE ,CF .(1)求证:E F ∠=∠;(2)连接AF ,CE ,当BD 平分ABC ∠时,四边形AFCE 是什么特殊四边形?请说明理由.解析:(1)见解析;(2)四边形AFCE 是菱形,理由见解析【分析】(1)根据四边形ABCD 是平行四边形,可以得到AD=CB ,AD ∥BC ,从而可以得到∠ADE=∠CBF ,然后根据SAS 证明△ADE ≌△CBF ,从而得出结论;(2)根据BD 平分∠ABC 和平行四边形的性质,可以证明▱ABCD 是菱形,从而可以得到AC ⊥BD ,然后即可得到AC ⊥EF ,再根据题目中的条件,可以证明四边形AFCE 是平行四边形,然后根据AC ⊥EF ,即可得到四边形AFCE 是菱形.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD=CB ,AD ∥BC ,∴∠ADB=∠CBD ,∴∠ADE=∠CBF ,在△ADE 和△CBF 中,AD CB ADE CBF DE BF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CBF (SAS ),∴∠E=∠F ;(2)当BD 平分∠ABC 时,四边形AFCE 是菱形,理由:∵BD 平分∠ABC ,∴∠ABD=∠CBD ,∵四边形ABCD 是平行四边形,∴OA=OC ,OB=OD ,AD ∥BC ,∴∠ADB=∠CBD ,∴∠ABD=∠ADB ,∴AB=AD ,∴平行四边形ABCD 是菱形,∴AC ⊥BD ,∴AC ⊥EF ,∵DE=BF ,∴OE=OF ,又∵OA=OC ,∴四边形AFCE 是平行四边形,∵AC ⊥EF ,∴四边形AFCE 是菱形.【点睛】本题考查平行四边形的判定与性质、菱形的判定、全等三角形的判定,解答本题的关键是明确题意,利用数形结合的思想解答.22.如图,在四边形ABCD 中,//AB CD ,90A ∠=︒,16cm AB =,13cm BC =,21cm CD =,动点N 从点D 出发,以每秒2cm 的速度在射线DC 上运动到C 点返回,动点M 从点A 出发,在线段AB 上,以每秒1cm 的速度向点B 运动,点M ,N 分别从点A ,D 同时出发.当点M 运动到点B 时,点N 随之停止运动,设运动时间为t (秒). (1)当t 为何值时,四边形MNCB 是平行四边形.(2)是否存在点N ,使NMB △是等腰三角形?若存在,请求出所有满足要求的t 的值,若不存在,请说明理由.解析:(1)5秒或373秒;(2)存在,163秒或72秒或685秒 【分析】 (1)由题意已知,AB ∥CD ,要使四边形MNBC 是平行四边形,则只需要让BM=CN 即可,因为M 、N 点的速度已知,AB 、CD 的长度已知,要求时间,用时间=路程÷速度,即可求出时间;(2)使△BMN 是等腰三角形,可分三种情况,即BM=BN 、NM=NB 、MN=MB ;可利用等腰三角形及直角梯形的性质,分别用t 表达等腰三角形的两腰长,再利用两腰相等即可求得时间t .【详解】解:(1)设运动时间为t秒.∵四边形MNCB是平行四边形,∴MB=NC,当N从D运动到C时,∵BC=13cm,CD=21cm,∴BM=AB-AM=16-t,CN=21-2t,∴16-t=21-2t,解得t=5,当N从C运动到D时,∵BM=AB-AM=16-t,CN=2t-21∴16-t=2t-21,解得t=373,∴当t=5秒或373秒时,四边形MNCB是平行四边形;(2)△NMB是等腰三角形有三种情况,Ⅰ.当NM=NB时,作NH⊥AB于H,则HM=HB,当N从D运动到C时,∵MH=HB=12BM=12(16-t),由AH=DN得2t=12(16−t)+t,解得t=163秒;当点N从C向D运动时,观察图象可知,只有由题意:42-2t=12(16-t)+t,解得t=685秒.Ⅱ.当MN=MB,当N从D运动到C时,MH=AH-AM=DN-AM=2t-t=t,BM=16-t,∵MN2=t2+122,∴(16-t)2=122+t2,解得t =72(秒);Ⅲ.当BM=BN ,当N 从C 运动到D 时,则BH=AB-AH=AB-DN=16-2t ,∵BM 2=BN 2=NH 2+BH 2=122+(16-2t )2,∴(16-t )2=122+(16-2t )2,即3t 2-32t+144=0,∵△<0,∴方程无实根,综上可知,当t=163秒或72秒或685秒时,△BMN 是等腰三角形. 【点睛】 本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.23.如图,平行四边形ABCD 中,,AP BP 分别平分DAB ∠和CBA ∠,交于DC 边上点P , 2.5AD =.(1)求线段AB 的长.(2)若3BP =,求ABP △的面积.解析:(1)5;(2)6【分析】(1)证出AD=DP=2.5,BC=PC=2.5,得出DC=5=AB ,即可求出答案;(2)根据平行四边形性质得出AD ∥CB ,AB ∥CD ,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB 中求出∠APB=90°,由勾股定理求出AP ,从而求得△ABP 的面积.【详解】解:(1)∵AP 平分∠DAB ,∴∠DAP=∠PAB ,∵四边形ABCD 是平行四边形,∵AB ∥CD ,∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP 是等腰三角形,∴AD=DP=2.5,同理:PC=CB=2.5,即AB=DC=DP+PC=5;(2)∵四边形ABCD 是平行四边形,∴AD ∥CB ,AB ∥CD ,∴∠DAB+∠CBA=180°,又∵AP 和BP 分别平分∠DAB 和∠CBA ,∴∠PAB+∠PBA=12(∠DAB+∠CBA )=90°, 在△APB 中,∠APB=180°-(∠PAB+∠PBA )=90°;在Rt △APB 中,AB=5,BP=3,∴AP=2253-=4,∴△APB 的面积=4×3÷2=6.【点睛】本题考查了平行四边形的性质,平行线的性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.24.如图,菱形ABCD 中,60B ∠=︒,点E ,F 分别在BC 和CD 上,BE CF =,求证:AE AF =.解析:证明见解析.【分析】连接AC ,证ABE ACF ≌即可【详解】证明:连接AC ,∵四边形ABCD 是菱形,∴AB BC CD AD ===,AC 平分BCD ∠.∵60B ∠=︒,∴ABC 是等边三角形,∴AB AC =,60∠=∠=∠︒=B BCA ACF . ∴在ABE △与ACF 中,AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩.∴ABE ACF ≌.∴AE AF =.【点睛】本题考查了菱形的性质,全等三角形的判定和性质,证明三角形全等是解此题的关键. 25.已知:平行四边形ABCD 中,点M 为边CD 的中点,点N 为边AB 的中点,联结AM 、CN .(1)求证:AM ∥CN ;(2)过点B 作BH AM ⊥,垂足为H ,联结CH .求证:△BCH 是等腰三角形.解析:(1)见解析;(2)见解析【分析】(1)由四边形ABCD 是平行四边形,根据平行四边形的性质,可得AB ∥CD ,AB=CD ,又由点M 为边CD 的中点,点N 为边AB 的中点,即可得CM=AN ,继而可判定四边形ANCM 是平行四边形,则可证得AM ∥CN .(2)由AM ∥CN ,BH ⊥AM ,点N 为边AB 的中点,可证得BH ⊥CN ,ME 是△BAH 的中位线,则可得CN 是BH 的垂直平分线,继而证得△BCH 是等腰三角形.【详解】解:(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD 且AB CD =.∵点M 、N 分别是边CD 、AB 的中点,∴12CM CD =,1AN AB 2=. ∴CM AN =.又∵AB ∥CD , ∴四边形ANCM 是平行四边形∴AM ∥CN .(2)设BH 与CN 交于点E ,∵AM ∥CN ,BH ⊥AM ,∴BH ⊥CN ,∵N 是AB 的中点,∴EN 是△BAH 的中位线,∴BE=EH ,∴CN 是BH 的垂直平分线,∴CH=CB ,∴△BCH 是等腰三角形.【点睛】此题考查了平行四边形的判定与性质、线段垂直平分线的性质以及等腰三角形的判定.此题难度适中,注意掌握数形结合思想的应用. 26.综合与实践——探究正方形旋转中的数学问题问程情境:已知正方形ABCD 中,点O 是线段BC 的中点,将将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''(点A ',B ',C ',D 分别是点A ,B ,C ,D 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.特例分析:(1)“乐思”小组提出问题:如图1,在正方形绕点O 旋转过程中,顺次连接点B ,B ',C ,C '得到四边形''BB CC ,求证:四边形''BB CC 是矩形;(2)“善学”小组提出问题:如图2.在旋转过程中,当点B '落在对角线BD 上时,设A B ''与CD 交于点M .求证:四边形OB MC '是正方形.深入探究:(3)“好问”小组提出问题:如图3.若点O 是线段BC 的三等分点且2OB OC =,在正方形ABCD 旋转的过程中当线段A D ''经过点D 时,请直接写出''DD OC 的值. 解析:(1)证明见解析;(2)证明见解析;(3)2'='DD OC. 【分析】(1)由旋转性质可得 OB=OB′ ,OC=OC′ ,得到四边形BB′CC′是平行四边形,又 BC=B′ C′ ,得到平行四边形BB′CC′是矩形.(2)先由∠C=∠OB′M=∠B′OC=90°,证明四边形 OB′MC 是矩形 ,再由OC=OB′ 得到四边形 OB′MC 是正方形.(3)过D 作DN ⊥B′C′,证Rt △DNO ≌Rt △DCO(HL),设OC=a ,得到OC′=a ,DD′=2a ,即可求解.【详解】解:(1)由旋转性质可得OB OB '=,OC OC '=.点O 是线段BC 的中点 OB OC ∴=,''∴=OB OC ,OB OC =.∴四边形''BB CC 是平行四边形.又BC B C ''=,∴平行四边形''BB CC 是矩形. (2)证明:四边形ABCD 是正方形,BC CD ∴=,90C ∠=︒.180180904522-∠︒-∴︒∠=∠===︒︒C CBD CDB 由旋转可知,OB OB '=,45''∴∠=∠=︒OB B OBB454590'''∴∠=∠+∠=︒+︒=︒B OC OB B OBB .四边形A B C D ''''是正方形,90'∴∠=︒OB M∴四边形OB MC '是矩形OB OC =,OC=OC′ ,OB′=OB ,∴OC=OB′∴矩形OB MC '是正方形,(3)2'='DD OC .如图,过D 作DN ⊥B′C′可知,∠A′=∠B′=∠B′ND=90°,∠D′=∠C′=∠C′ND=90°,∴四边形DNC′D′为矩形,四边形DNB′A′为矩形,在Rt △DNO 与Rt △DCO 中,∵OD=OD ,DN=DC ,∴Rt △DNO ≌Rt △DCO(HL)设OC=a ,则OB=2OC=2a ,∴ON=OC=OC′=a∴BC=OB+OC=3a ,DD′=NC′=ON+OC′=2a , ∴2DD a OC a'='=2. 【点睛】 本题考查了特殊的四边形,平行四边形,矩形,正方形的性质和判定,解题的关键是熟练掌握特殊的四边形的性质和判定.27.如图,将长方形ABCD 沿着对角线BD 折叠,使点C 落在C '处,BC '交AD 于点E .(1)试判断BDE 的形状,并说明理由.(2)若4AB =,8AD =,求AE 的长.参考答案解析:(1)BDE 是等腰三角形,证明见解析;(2)3AE =.【分析】(1)根据折叠的性质可知EBD DBC ∠=∠,又因为//AD BC ,可知ADB DBC ∠=∠,即推出ADB EBD ∠=∠,所以BE DE =,BDE 为等腰三角形.(2)设AE x =,则8BE DE x ==-,在Rt ABE △中根据勾股定理列出等式,解出x 即可.【详解】(1)BDE 是等腰三角形,理由是:由折叠得:EBD DBC ∠=∠,∵四边形ABCD 是矩形,∴//AD BC ,∴ADB DBC ∠=∠,∴ADB EBD ∠=∠,∴BE DE =,∴BDE 是等腰三角形.(2)设AE x =,则8BE DE x ==-, ∵四边形ABCD 是矩形,∴90A ∠=︒,∴在Rt ABE △中,222AB AE BE +=,即2224(8)x x +=-,解得:3x =,∴3AE =.【点睛】本题考查翻折的性质,矩形的性质,等腰三角形的判定以及勾股定理.根据翻折的性质间接证明出BE DE =是解答本题的关键.28.如图1,正方形ABCD ,E 为平面内一点,且90BEC ∠=︒,把BCE 绕点B 逆时针旋转90︒得BAG ,直线AG 和直线CE 交于点F .(1)证明:四边形BEFG 是正方形;(2)若135AGD ∠=︒,猜测CE 和CF 的数量关系,并说明理由;(3)如图2,连接DF ,若13AB =,17CF =,求DF 的长.解析:(1)见解析;(2)CE=CF ,理由见解析;(3)522【分析】(1)根据正方形的判定定理进行证明即可;(2)证明Rt ADH ≌Rt BAG 得DH AG =,AH=BG ,再证明△DHG 是等腰直角三角形,可得DH=BH=AG ,最后由BEFG 是正方形可得结论;(3)分点F 在AB 右侧和左侧两种情况求解即可.【详解】解:(1)证明:90BEC =︒∠,把BCE 绕点B 逆时针旋转90︒得BAG , BE BG ∴=,90EBG ∠=︒,90BGA ∠=︒,则90BGF ∠=︒,90BEC EBG BGF ∴∠=∠=∠=︒,∴四边形BEFG 是正方形;(2)CE CF =,理由如下:过D 点作DH AF ⊥,垂足为H ,如图,四边形ABCD 是正方形,90BAD ∴∠=︒,AB AD =,90BGA ∠=︒,90DAH BAG ∴∠+∠=︒,90BAG ABG ∠+∠=︒,DAH ABG ∴∠=∠,在Rt ADH 和Rt BAG 中,90,DAH ABG BGA AHD AD AB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩Rt ADH ∴≌()Rt BAG AAS ,DH AG ∴=,∵∠DGH =180°-∠AGD =45°∴在Rt △DHG 中,∠GDH =45°∴DH =GH =AG∴1122AG GH AH BG === 又AG CE =,EF BG =,2EF CE ∴=,CE CF ∴=;(3)①点F 在AB 右侧时,如图,过D 作DK ⊥AG ,交其延长线于K .设正方形BEFG 的边长为x ,则BE x =,17CE x =-,在Rt BEC △中,13BC =,根据勾股定理可得,222BE CE BC +=,即222(17)13x x +-=,解得112x =,25(x =不符合条件,舍去),即12BG BE ==,17125AG CE ==-=,∵四边形BEFG 是正方形,∴∠BAD =90°.∵DK ⊥AG ,∴∠K =90°.∵∠BAG +∠KAD =180°—∠BAD =90°∠ADK +∠KAD =90°∴∠BAG =∠ADK在Rt △ABG 和Rt △DAK 中,90G K AB ADBAG ADK ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩所以Rt△ADK≌Rt BAG,则AK=BG=12,DK=AG=5,∵AF+FK=AK=BG=GF=AG+AF∴FK=AG=5在R t△DFK中,根据勾股定理可得,DF=2252+=DK FK②点F在AB左侧时,如图,过D作DK⊥AG,交其延长线于K.方法同①,可得FK=AG=12,在R t△DFK中,根据勾股定理可得,DF22122+=DK FK综上所述,DF的长为522【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,正方形的性质,勾股定理,熟练掌握相关性质和定理是解本题的关键.。
初二数学四边形试题答案及解析

初二数学四边形试题答案及解析1.如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.【答案】(1)证明见解析;(2)BE=5.【解析】(1)首先由已知证明AF∥EC,BE=DF,推出四边形AECF是平行四边形.(2)由已知先证明AE=BE,即BE=AE=CE,从而求出BE的长;试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形.(2)∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠3=90°﹣∠2,∠4=90°﹣∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=BC=5.【考点】1、平行四边形的判定与性质;2、菱形的性质2.如图,在▱ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.(1)从对称性质看,▱ABCD是_________对称图形;(2)求平行四边形ABCD的周长.【答案】(1)中心;(2)40【解析】(1)根据平行四边形的性质可知:对角线互相平分,所以O为旋转中心,即平行四边形ABCD是中心对称图形;(2)根据平行四边形中对角、对边分别相等,∠B=∠ADC=60°,再根据已知边长,由勾股定理可求出AB、AD的长,进而可求出平行四边形ABCD的周长.试题解析:1)∵四边形ABCD是平行四边形,∴对角线互相平分,∴O为旋转中心,即平行四边形ABCD是中心对称图形,(2)∵四边形ABCD是平行四边形,∴∠B=∠D=60°,AB=CD,AD=BC.∵AE⊥BC,∵BE=4,∴AB=8,∴CD=AB=8,∵CF=2,∴DF=6,∵AF⊥DC,∠D=60°∴在Rt△ADF中,AD=12,∴平行四边形ABCD的周长=2(12+8)=40.【考点】1.平行四边形的性质;2.中心对称图形3.下列性质中,正方形具有而矩形不一定具有的性质是A.对角线互相垂直B.对角线互相平分C.对角线相等D.四个角都是直角【答案】A.【解析】A、正方形的对角线互相垂直平分,矩形的对角线互相平分但不一定垂直,故本选项正确.B、正方形和矩形的对角线都互相平分,故本选项错误;C、正方形和矩形的对角线都相等,故本选项错误;D、正方形和矩形的四个角都是直角,故本选项错误.故选A.【考点】1.正方形的性质2.矩形的性质.4.如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.【答案】3cm.【解析】根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2,然后解方程即可.试题解析:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),∴AF=AD=10,DE=EF,在Rt△ABF中,AB=8,AF=10,∴BF=.∴CF=BC﹣BF=4.设CE=x,则DE=EF=8﹣x,在Rt△CEF中,∵CF2+CE2=EF2,∴42+x2=(8﹣x)2,解得x=3.∴EC的长为3cm.【考点】1.翻折变换(折叠问题);2.矩形的性质;3.勾股定理;4.方程思想的应用.5.ABCD中, ∠A比∠B小200,则∠A的度数为( )A.600B.800C.1000D.1200【答案】B.【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∠A=∠C,∴∠A+∠B=180°,∵∠B-∠A =20°,∴∠B=100°,∴∠A=80°.故选B.【考点】平行四边形的性质.6.矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的周长是()A.6B.C.2(1+)D.1+【答案】C.【解析】本题已知条件涉及矩形的对角线和周长,可考虑用“矩形的对角线相等且相互平分”性质来解.如图所示,∠AOB=120°,AD=2∵ABCD为矩形,∴AD=BC=2,AO=B0=1(矩形的对角线相等且相互平分),∴△AOB为等腰三角形,∠BAO=30°;在Rt△ABD中,∠BAO=30°,AD=2∴AB= ,BD=1,∴矩形ABDC的周长为.【考点】矩形性质.7.如图,在梯形中,为的中点,交于点.(1)求证:;(2)当,且平分时,求的长.【答案】(1)证明详见解析.(2)EF=4.【解析】根据题意构造辅助线,利用中线性质和平行四边形性质即可得出结论.(1)过D作DM∥AB,∵AD∥BC,DM∥AB,∴四边形ABMD为平行四边形,∴BM=AD∵,∴EF∥DM,又∵E为CD的中点∴F为CM中点即MF=CF,∴BF=BM+MF=AD+CF.(2)过E作EH⊥AB,∵BE平分,∴CE=EH=DE(角平分线上一点到角两边的距离相等),在Rt△ADE和Rt△AHE中,DE=EH,AE=AE∴Rt△ADE≌Rt△AHE(SH定理)∴AH=AD=1,同理可得BH=BC=7,∴AB=AH+BH=8∵四边形ABMD为平行四边形,∴DM=AB=8,又∵E、F 分别为CD、CM中点,∴.【考点】1.平行四边形性质;2.角平分线性质;3.全等三角形.8.已知O是口ABCD对角线的交点,△ABC的面积是3,则口ABCD的面积是()A.3B.6C.9D.12【答案】B.【解析】根据平行四边形的性质可知,OD=OB,OA=OC,所以平行四边形的两条对角线把平行四边形分成四个面积相等的三角形,已知△ABC的面积为3,所以平行四边形的面积可求.∵O为▱ABCD对角线的交点,且△ABC的面积为3,∴▱ABCD的面积为2×3=6.故选B.【考点】平行四边形的性质.9.矩形、菱形与正方形都具有的性质是()A.对角线互相垂直B.对角线互相平分C.对角线平分一组对角D.对角线相等【答案】B.【解析】A、矩形对角线不互相垂直,故本选项错误;B、平行四边形的对角线互相平分,以上三个图形都是平行四边形,故本选项正确;C、三个图形中,只有菱形和正方形的对角线平分一组对角,故本选项错误;D、菱形对角线不相等,故本选项错误.故选B.【考点】1.正方形的性质2.菱形的性质3.矩形的性质.10.如图,△ABC中,O是AC上的任意一点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:OE=OF;(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论.【答案】(1)证明见解析;(2)当O运动到AC中点.【解析】(1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;(2)根据矩形的性质可知:对角线且互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,∴OE=OC,OC=OF,∴OE=OF.(2)解:当O运动到AC中点时,四边形AECF是矩形,∵AO=CO,OE=OF,∴四边形AECF是平行四边形,∵∠ECA+∠ACF=∠BCD,∴∠ECF=90°,∴四边形AECF是矩形.【考点】矩形的判定.11.如图,在矩形ABCD中,点E、F分别在AB、DC上,BF∥DE,若AD=12cm,AB=7cm,且AE:EB=5:2,则阴影部分的面积为_______【答案】24cm2.【解析】因为AD=12cm,AB=7cm,且AE:BE=5:2,则AE=5,BE=2,则阴影部分的面积=12×7﹣12×5=24cm2.故答案是24cm2.【考点】矩形的性质.12.如图,在平行四边形ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=6,AD=4,则AE∶EF∶BE为 ( )A.4∶1∶2B.4∶1∶3C.3∶1∶2D.5∶1∶2【答案】A.【解析】∵四边形ABCD是平行四边形∴∠CDE=∠DEA∵DE是∠ADC的平分线∴∠CDE=∠ADE∴∠DEA=∠ADE∴AE=AD=4∵F是AB的中点∴AF=AB=3∴EF=AE-AF=1,BE=AB-AE=2∴AE:EF:BE=4:1:2.故选A.考点: 平行四边形的性质.13.(1)如图1,△ABC的顶点坐标分别为A(-1,0),B(3,0),C(0,2).若将点A 向右平移4个单位,则A、B两点重合;若将点A向右平移1个单位,再向上平移2个单位,则A、C两点重合.试解答下列问题:①填空:将点C向下平移个单位,再向右平移个单位与点B重合;②将点B向右平移1个单位,再向上平移2个单位得点D,请你在图中标出点D的位置,并连接BD、CD,请你说明四边形ABDC是平行四边形;(2)如图2,△ABC的顶点坐标分别为A(-2,-1),B(2,-3),C(1,1).请问:以△ABC的两条边为边,第三边为对角线的平行四边形有几个?并直接写出第四个顶点的坐标.【答案】(1)①2,3;②见解析;(2)有3个,(5,-1),(-1,-5),(-3,3).【解析】(1)①根据平移的规律:上加下减,左加右减即可得出将点C向下平移2个单位,再向右平移3个单位与点B重合;②根据平移的规律:上加下减,左加右减得出将点D的坐标为(4,2),然后根据一组对边平行且相等的四边形是平行四边形证出四边形ABDC是平行四边形;(2)分别以AB,BC,AC为平行四边形的对角线,考虑第四个顶点D的坐标,有三种可能结果.试题解析:(1)①∵B(3,0),C(0,2),∴将点C向下平移2个单位,再向右平移3个单位与点B重合.故答案为2,3;②点D位置如图所示.证明:由图可知AB∥CD,AB=CD,∴四边形ABCD是平行四边形;以△ABC的两条边为边,第三边为对角线的平行四边形共有3个.①以AB、AC为边可作一平行四边形,第四个顶点的坐标为(5,-1);②以CA、CB为边可作一平行四边形,第四个顶点的坐标为(-1,-5);③以BA、BC为边也可作一平行四边形,则第四顶点的坐标为(-3,3).【考点】坐标与图形变化-平移;平行四边形的判定.14.如图所示,平行四边形ABCD的周长是18cm,对角线AC、BD相交于点O,若△AOD与△AOB的周长差是5cm,则边AB的长是_________cm.【答案】2【解析】利用平行四边形的对角线互相平分这一性质,确定已知条件中两三角形周长的差也是平行四边形两邻边边长的差,进而确定平行四边形的边长.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵△AOD的周长=OA+OD+AD,△AOB的周长=OA+OB+AB,又∵△AOD与△AOB的周长差是5cm,∴AD=AB+5,设AB=x,AD=5+x,则2(x+5+x)=18,解得x=2,即AB=2cm.【考点】平行四边形的性质点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.15.在等腰梯形ABCD中,AD∥BC,∠B=45°,若AD=4cm,AB=8cm,试求出此梯形的周长和面积.【答案】(8+20)cm,(48+32)cm2【解析】过A、D点作梯形的高AE、DF,根据等腰直角三角形性质可求得BE、AE的长,从而可以求得结果.过A、D点作梯形的高AE、DF∵等腰梯形ABCD中,∠B=45°,AB=8cm∴BE=AE=4cm∵AD=4cm∴BC=4+8cm∴梯形的周长=(8+20)cm,面积=(AD+BC)×AE=(48+32)cm2.【考点】等腰梯形的性质点评:等腰梯形的性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.16.在梯形ABCD中,AB∥CD,EF为中位线,则△AEF的面积与梯形ABCD的面积之比是______________【答案】1:4【解析】解:过A作AG⊥BC,交EF与H,∵EF是梯形ABCD的中位线,∴AD+BC=2EF,AG=2AH,设△AEF的面积为xcm2,即EF•AH=xcm2,∴EF•AH=2xcm2,∴S梯形ABCD=(AD+BC)•AG=×2EF×2AH=2EF•AH=2×2xcm2=4xcm2.∴△AEF的面积与梯形ABCD的面积之比为:1:4.【考点】梯形的中位线定理点评:本题考查了梯形的中位线定理,比较简单,注意掌握梯形的中位线定理即是梯形的中位线等于上下底和的一半.17.如图所示,在平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于点E.试求∠DAE的度数.【答案】【解析】因为BD=CD,所以∠DBC=∠C=70°,又因为四边形ABCD是平行四边形,所以AD∥BC,所以∠ADB=∠DBC=70°,因为AE⊥BD,所以在直角△AED中,∠DAE即可求出.∵DB=CD,∠C=70°,∴∠DBC=∠C=70°,又∵在▱ABCD中,AD∥BC,∴∠ADB=∠DBC=70°,又∵AE⊥BD,∴∠DAE=90°-∠ADB=90°-70°=20°.【考点】平行四边形的性质,等腰三角形的性质点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.18.如图所示,矩形的边,,它的两条对角线交于点,以、为邻边作平行四边形,平行四边形的对角线交于点,同样以、为邻边作平行四边形,……,依次类推,平行四边形的面积为.【答案】【解析】先根据平行四边形的面积公式分别计算,得到规律,再根据所得的规律求解即可.由题意得平行四边形的面积为平行四边形的面积为所以平行四边形的面积为.【考点】找规律-图形的变化点评:解答此类问题的关键是仔细分析所给图形的特征得到规律,再把这个规律应用于解题. 19.如图在平行四边形ABCD的对角线AC的延长线上取两点E、F,使EA=CF,求证:四边形EBFD是平行四边形.【答案】连接BD,交AC于点O,由四边形ABCD为平行四边形可得AO=CO,BO=DO,又AE=CF,所以EO=FO,即可证得结论.【解析】连接BD,交AC于点O∵四边形ABCD为平行四边形∴AO=CO,BO=DO又∵AE=CF∴EO=FO∴四边形EBFD是平行四边形.【考点】平行四边形的判定和性质点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.20.如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是:(填一个即可)【答案】AB=CD或AD∥BC【解析】两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形. 由题意可补充AB=CD或AD∥BC.【考点】平行四边形的判定点评:本题属于基础应用题,只需学生熟练掌握平行四边形的性判定方法,即可完成.21.已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC=BD时,它是正方形C.当AC⊥BD时,它是菱形D.当∠ABC=900时,它是矩形【答案】B【解析】根据矩形、菱形、正方形的判定方法依次分析各项即可判断.A.当AB=BC时,它是菱形,C.当AC⊥BD时,它是菱形,D. 当∠ABC=900时,它是矩形,均正确,不符合题意;B. 当AC=BD时,无法判定它是正方形,故错误,本选项符合题意.【考点】矩形、菱形、正方形的判定点评:本题属于基础应用题,只需学生熟练掌握矩形、菱形、正方形的判定方法,即可完成. 22.已知EF是梯形ABCD的中位线,且EF=9,上底AB=6,那么下底CD= .【答案】12【解析】因为梯形的中位线长等于上底加下底的和除以2,根据题意,9×2-6=12【考点】梯形的中位线点评:基础题目,学生需要掌握梯形的中位线的运算公式,代入得出答案。
八年级数学下册 中点四边形模型(解析版)
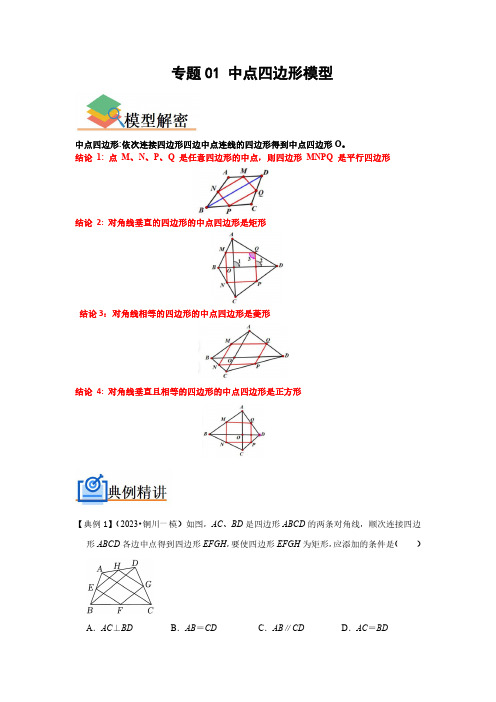
专题01中点四边形模型中点四边形:依次连接四边形四边中点连线的四边形得到中点四边形O。
结论1:点M、N、P、Q是任意四边形的中点,则四边形MNPQ是平行四边形结论2:对角线垂直的四边形的中点四边形是矩形结论3:对角线相等的四边形的中点四边形是菱形结论4:对角线垂直且相等的四边形的中点四边形是正方形【典例1】(2023•铜川一模)如图,AC、BD是四边形ABCD的两条对角线,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A.AC⊥BD B.AB=CD C.AB∥CD D.AC=BD【解答】解:∵E、F、G、H分别为AB、BC、CD、AD的中点,∴EF=AC,EF∥AC,GH=AC,GH∥AC,EH∥BD,∴EF=GH,EF∥GH,∴四边形EFGH为平行四边形,当AC⊥BD时,EF⊥EH,则四边形EFGH为矩形,故选:A.【典例2】(2023春•和平区校级期末)已知在四边形ABCD中,对角线AC与BD相等,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是()A.平行四边形B.矩形C.菱形D.正方形【答案】C【解答】解:如图,E、F、G、H分别是AB、BC、CD、DA的中点,AC=BD,∵E、F分别是AB、BC的中点,∴EF是△ABC的中位线,∴EF=AC,同理:FG=BD,GH=AC,EH=BD,∵AC=BD,∴EF=HG=EH=FG,∴四边形EFGH是菱形.故选:C.【典例3】(2023春•庐江县期末)若顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形一定是()A.矩形C.对角线相等的四边形D.对角线互相垂直的四边形【答案】D【解答】解:由于E、F、G、H分别是AB、BC、CD、AD的中点,根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG,∴四边形EFGH是平行四边形,∵四边形EFGH是矩形,即EF⊥FG,∴AC⊥BD,故选:D.1.(2023春•宿豫区期中)顺次连接对角线相等且垂直的四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【答案】D【解答】解:∵E、F、G、H分别是AB、BC、CD、AD的中点,∴EH∥FG∥BD,EF∥AC∥HG,EF=AC,FG=BD,∴四边形EFGH是平行四边形,∵AC⊥BD,AC=BD,∴EF⊥FG,FE=FG,∴四边形EFGH是正方形,2.(2022秋•辽阳期末)顺次连接矩形四边中点得到的四边形一定是()A.正方形B.矩形C.菱形D.平行四边形【答案】C【解答】解:如图,连接AC、BD.在△ABD中,∵AH=HD,AE=EB,∴EH=BD,同理FG=BD,HG=AC,EF=AC,又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四边形EFGH为菱形.故选:C.3.(2023•佛山模拟)如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、D A的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件是()A.AC⊥BD B.AC=BDC.AC⊥BD且AC=BD D.不确定【答案】B【解答】解:满足的条件应为:AC=BD.理由如下:∵E,F,G,H分别是边AB、BC、CD、DA的中点,∴在△ADC中,HG为△ADC的中位线,所以HG∥AC且HG=AC;同理EF∥AC且EF=AC,同理可得EH=BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,∴四边形EFGH为菱形.故选:B.4.(2023春•涟水县期中)若顺次连接四边形各边中点所得的四边形是菱形,则原四边形()A.一定是矩形B.一定是菱形C.对角线一定互相垂直D.对角线一定相等【答案】D【解答】解:如图,根据题意得:四边形EFGH是菱形,点E,F,G,H分别是边AD,AB,BC,CD的中点,∴EF=FG=CH=EH,BD=2EF,AC=2FG,∴BD=AC.∴原四边形一定是对角线相等的四边形.故选:D.5.(2023春•锡山区校级期中)顺次连接对角线长为6的矩形ABCD四边中点所得的四边形的周长为()A.12B.18C.9D.无法确定【答案】A【解答】解:因为矩形的对角线相等,所以AC=BD=10cm,∵E、F、G、H分别是AB、BC、CD、AD、的中点,∴EH=GF=BD=×6=3,EF=GH=AC=×6=3,故顺次连接矩形四边中点所得的四边形周长为EH+GF+EF+GH=12.故选:A.6.(2023春•南京期中)如图,在四边形ABCD中,E、F、G、H分别是线段AD、BD、BC、AC的中点,要使四边形EFGH是菱形,需添加的条件是()A.AC=BD B.AC⊥BD C.AB=CD D.AB⊥CD【答案】C【解答】解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,∴EF=GH=AB,EH=FG=CD,∵当EF=FG=GH=EH时,四边形EFGH是菱形,∴当AB=CD时,四边形EFGH是菱形.故选:C.7.(2023春•东莞市校级期中)如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点,若AB=5,AD=8,则图中阴影部分四边形EFGH的面积为()A.40B.26C.20D.13【答案】C【解答】解:连接EG、FH,∵四边形ABCD为矩形,∴AB=CD,AD=BC,∠A=90°,∵E、F、G、H分别为边AB、BC、CD、DA的中点,∴EG=AD=8,HF=AB=5,EG⊥HF,=×5×8=20,∴S四边形EFGH故选:C.8.(2022•南召县模拟)如图,在四边形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,则下列说法正确的是()A.在四边形ABCD中,若对角线AC=BD,则四边形EFGH为矩形B.在四边形ABCD中,若对角线AC⊥BD,则四边形EFGH为菱形C.在四边形EFGH中,若对角线EG⊥HF,则四边形EFGH为矩形D.在四边形EFGH中,若对角线EG=HF,且EG⊥HF,则四边形EFGH为正方形【答案】D【解答】解:连接AC、BD,∵E,F分别为边AB,BC的中点,∴EF为△ABC的中位线,∴EF=AC,EF∥AC,同理,HG=AC,HG∥AC,EH=BD,EH∥BD,∴EF=HG,EF∥HG,∴四边形EFGH为平行四边形,当AC=BD时,EF=EH,∴平行四边形EFGH为菱形,故选项A错误;当AC⊥BD时,EF⊥EH,∴平行四边形EFGH为矩形,故选项B错误;在平行四边形EFGH中,若对角线EG⊥HF,则四边形EFGH为菱形,故选项C错误;在平行四边形EFGH中,若对角线EG=HF,且EG⊥HF,则平行四边形EFGH为正方形,故选项D正确.故选:D.9.(2022春•凤凰县期末)顺次连结任意四边形各边中点所得的四边形必定是()A.任意四边形B.平行四边形C.菱形D.矩形【答案】B【解答】解:如图根据中位线定理可得:GF=BD且GF∥BD,EH=BD且EH∥BD,∴EH=FG,EH∥FG,∴四边形EFGH是平行四边形.故选:B.10.(2022春•青白江区校级月考)如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=8,BD=6,则四边形EF GH的面积为()A.48B.24C.32D.12【答案】D【解答】解:∵点E、F分别为四边形ABCD的边AD、AB的中点,∴EF∥BD,且EF=BD=3.同理求得EH∥AC∥GF,且EH=GF=AC=4,又∵AC⊥BD,∴EF∥GH,FG∥HE且EF⊥FG.四边形EFGH是矩形.∴四边形EFGH的面积=EF•EH=3×4=12,即四边形EFGH的面积是12.故选:D.11.(2022春•芜湖期中)如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为()A.B.C.D.【答案】C【解答】解:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即,则周长是正方形ABCD的;顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即正方形ABCD的,则周长是正方形ABCD的;顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即正方形ABCD的,则周长是正方形ABCD的;顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半,即正方形ABCD的,则周长是正方形ABCD的;…故第n个正方形周长是原来的,以此类推:正方形A8B8C8D8周长是原来的,∵正方形ABCD的边长为1,周长为4,∴按此方法得到的四边形A8B8C8D8的周长为,故选:C.12.(2022•旌阳区模拟)如图,在四边形ABCD中,AC=BD=5,点E,F,G,H分别为边AB,BC,CD,DA的中点,连接EG,HF,相交于点O,则EG2+FH2的值为()A.25B.30C.35D.40【答案】A【解答】解:连接EF、FG、GH、HE,∵点E,F,G,H分别为边AB,BC,CD,DA的中点,∴EF=AC=,FG=BD=,GH=AC=,HE=BD=,∴EF=FG=GH=HE,∴四边形EFGH为菱形,∴EG⊥FH,OE=OG,OF=OH,∴OE2+OH2=EH2=,∴EG2+FH2=4OE2+4OH2=25,故选:A.13.(2023春•浦东新区校级期末)顺次连接等腰梯形各边中点所得的四边形的两条对角线为a、b,则等腰梯形的面积为ab.【答案】ab.【解答】解:连接AC、BD,∵E、F分别为AB、BC的中点,∴EF是△ABC的中位线,∴EF=AC,同理可得:GH=AC,EH=BD,GF=BD,∵四边形ABCD为等腰梯形,∴AC=BD,∴EF=FG=GH=EH,∴四边形EFGH为菱形,∵菱形EFGH为对角线分别为a、b,∴等腰梯形ABCD的中位线和高分别为a、b,=ab,∴S等腰梯形故答案为:ab.14.(2023春•南川区期中)如图,已知矩形ABCD的对角线AC的长为18cm,顺次连结各边中点E、F、G、H得四边形EFGH,则四边形EFGH的周长为36cm.【答案】36.【解答】解:∵E、F分别是AB、BC的中点,∴EF是△ABC的中位线,∴EF=AC=×18=9cm,同理FG=BD,HG=AC,EH=BD,∵四边形ABCD是矩形,∴AC=BD,∴EF=FG=GH=HE,∴四边形EFGH是菱形,∴四边形EFGH的周长为9×4=36(cm).故答案为:36.15.(2022春•临海市期末)如图,E,F,G,H分别是四边形ABCD边AB,BC,CD,DA 的中点,若AC=6,BD=4.则四边形EFGH的周长为10.【答案】10.【解答】解:∵E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点,AC=6,BD=4,∴EF是△ABC的中位线,EH是△ABD的中位线,GF是△BDC的中位线,GH是△AD C的中位线,∴EF=AC=×6=3,GH=AC=×6=3,EH=BD=×4=2,FG=BD=×4=2,∴四边形EFGH的周长=EF+FG+GH+EH=3+2+3+2=10,故答案为:10.16.(2022春•克东县期中)如图,E、F、G、H分别是AB、BC、CD、DA的中点,BD=A C.要使四边形EFGH是正方形,BD、AC应满足的条件是AC=BD且AC⊥BD.【答案】AC=BD且AC⊥BD.【解答】解:满足的条件应为:AC=BD且AC⊥BD.理由:∵E,F,G,H分别是边AB、BC、CD、DA的中点,∴在△ADC中,HG为△ADC的中位线,∴HG∥AC且HG=AC;同理EF∥AC且EF=AC,同理可得EH=BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又∵AC=BD,∴EF=EH,∴四边形EFGH为菱形,∵AC⊥BD,EF∥AC,∴EF⊥BD,∵EH∥BD,∴EF⊥EH,∴∠FEH=90°,∴菱形EFGH是正方形.故答案为:AC=BD且AC⊥BD.17.(2023春•盐城期中)阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,D A的中点,依次连接各边中点得到中点四边形EFGH.(1)这个中点四边形EFGH的形状是平行四边形;(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明.【答案】见试题解答内容【解答】解:(1)中点四边形EFGH是平行四边形;理由如下:连接AC,如图1所示:∵E,F,G,H分别是边AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△ACD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形;故答案为:平行四边形;(2)四边形EFGH为菱形.理由如下:连接AC与BD,如图2所示:∵△AMD和△MCB为等边三角形,∴AM=DM,∠AMD=∠CMB=60°,CM=BM,∴∠AMC=∠DMB,在△AMC和△DMB中,,∴△AMC≌△DMB(SAS),∴AC=DB,∵E,F,G,H分别是边AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△ACD的中位线,HE是△ABD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,HE=DB,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形;∵AC=DB,∴EF=HE,∴四边形EFGH为菱形.18.(2023春•姜堰区期中)如图,在四边形ABCD中,点E、F、G、H分别是AB、BC、C D、AD的中点,连接AC、BD.(1)求证:四边形EFGH是平行四边形;(2)当对角线AC与BD满足什么关系时,四边形EFGH是菱形,并说明理由.【答案】(1)证明见解答过程;(2)当AC=BD时,四边形EFGH是菱形,理由见解答.【解答】(1)证明:∵点E、F、G、H分别是AB、BC、CD、AD的中点,∴EF∥AC,EF=AC,HG∥AC,HG=AC,∴EF∥HG,EF=HG,∴四边形EFGH为平行四边形;(2)当AC=BD时,四边形EFGH是菱形,理由如下:由(1)知:四边形EFGH是平行四边形.∵E、H分别是AB、AD的中点,∴EH=BD.又∵EF=AC,∴当AC=BD时,EF=EH,∴平行四边形EFGH是菱形.19.(2022秋•薛城区校级月考)如图,四边形ABCD中,E、F、G、H分别是AB、BC、C D、DA的中点.(1)判断四边形EFGH的形状.并说明理由.(2)当四边形ABCD的对角线添加条件AC⊥BD时,四边形EFGH是矩形.(3)在(2)的条件下,说明四边形EFGH是矩形.【答案】(1)四边形EFGH为平行四边形,理由见解析;(2)AC⊥BD;(3)证明见解答过程.【解答】(1)解:四边形EFGH为平行四边形,理由如下:连接AC、BD,∵E、F、G、H分别是AB、BC、CD、DA的中点,∴EF=AC,EF∥AC,GH=AC,GH∥AC,∴EF=GH,EF∥GH,∴四边形EFGH为平行四边形;(2)解:当AC⊥BD时,四边形EFGH是矩形,故答案为:AC⊥BD;(3)证明:∵E、H分别是AB、DA的中点,∴EH∥BD,∴EF∥AC,EH∥BD,AC⊥BD,∴EF⊥EH,∴平行四边形EFGH为矩形.20.(2022春•工业园区校级期末)如图,四边形ABCD中,点E、F、G、H分别为AB、B C、CD、DA的中点,(1)求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E、F、G、H分别为AB、BC、CD、DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想.【答案】(1)见解析过程;(2)四边形EFGH是菱形,理由见解析过程.【解答】(1)证明:如图1中,连接BD.∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD,∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形;(2)解:四边形EFGH是菱形,理由如下:如图2,连接AC、BD,∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD,在△APC和△BPD中,,∴△APC≌△BPD(SAS),∴AC=BD,∵点E,F,G分别为边AB,BC,CD的中点,∴EF=AC,FG=BD,∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.21.(2022春•咸安区期末)如图,点D,E分别是△ABC的边AB,AC的中点,点O是△A BC内一点,连接OA,OB,OC,点F,G分别是OB,OC的中点,顺次连接点D,F,G,E.(1)求证:四边形DFGE是平行四边形;(2)当OA⊥DE时,求证:四边形DFGE是矩形;(3)若四边形DFGE是正方形,OA与BC之间满足的条件是:OA⊥BC且OA=BC .【答案】(1)证明见解析;(2)证明见解析;(3)若四边形DFGE是正方形,OA与BC之间满足的条件是:OA⊥BC且OA=BC,证明见解析.【解答】(1)证明:∵D、E是AB、AC的中点,∴DE∥BC且DE=BC,∵F、G是OB、OC的中点,∴GF∥BC且GF=BC,∴DE∥GF且DE=GF,∴四边形DFGE是平行四边形;(2)证明:由(1)知,四边形DFGE是平行四边形,如图,连接OA,∵D、G分别是AB、OB的中点,∴DG∥OA,∵OA⊥DE,∴DG⊥DE,∴∠GDE=90°,∴平行四边形DFGE是矩形,所以当OA⊥DE时,四边形DFGE是矩形;(3)解:若四边形DFGE是正方形,OA与BC之间满足的条件是:OA⊥BC且OA=B C,由(2)可知,当OA⊥BC时,四边形DFGE是矩形,∵D、G、F分别是AB、OB、OC的中点,∴DG=AO,GF=BC,∵AO=BC,∴DG=GF,∴矩形DGFE是正方形.故答案为:OA⊥BC且OA=BC.22.(2022春•龙口市月考)已知四边形ABCD是矩形.(1)如图1,E,F,G,H分别是AB,BC,CD,AD的中点,求证:四边形EFGH是菱形;(2)如图2,若菱形EFGH的三个顶点E,F,H分别在边AB,BC,AD上,连接CG.已知BE=2AE=8,CG=2,CF﹣BF=1,求AD的长.【答案】(1)证明见解答过程;(2)14.【解答】(1)证明:如图1,连接AC,BD,∵E,F分别是AB,BC的中点,∴EF∥AC,EF=AC,同理:GH∥AC,GH=AC,EH=BD,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形,∵四边形ABCD是矩形,∴AC=BD,∴EF=EH.∴四边形EFGH是菱形;(2)解:如图2,连接FH,过点G作GM⊥BC交BC的延长线于M,∵四边形ABCD是矩形,∴∠A=90°,AD∥BC.∴∠A=∠M,∠AHF=∠MFH,∵四边形EFGH是菱形,∴FG∥EH,FG=EH,∴∠EHF=∠GFH.∴∠AHE=∠MFG,在△AEH和△MFG中,∴△AEH≌△MFG(AAS),∴GM=AE=4.∵CG=2,根据勾股定理,得CM=2,设BF=x,则CF=x+1,在Rt△GFM中,FG2=(x+1+2)2+16=(x+3)2+16,同理EF2=x2+64,∴(x+3)2+16=x2+64.∴x=,∴BC=2x+1=14,∴AD=BC=14.23.(2022春•崇川区校级月考)如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,有EF⊥GH?请说明你的理由.【答案】见试题解答内容【解答】解:当AB=CD时,有EF⊥GH,连接GE、GF、HF、EH.∵E、G分别是AD、BD的中点,∴EG=AB,同理HF=CD,FG=CD,EH=CD,又∵AB=CD∴EG=GF=FH=EH∴四边形EFGH是菱形.∴EF⊥GH.。
人教版八年级数学下册第十八章四边形典型中点构造专题

⑵求四边形A5B5C5D5的周长.
【解析】⑴由三角形的中位线的性质可以推知,每得到一次四
边形,它的面积变为原来的一半,四边形
的面积为 ;
⑵根据中位线的性质易知,A5B5= A3B3= × A1B1= × × AB,
B5C5= B3C3= × B1C1= × × BC, = .
∴CF//DA且CF=DA,
CF//BD且CF=BD
∴四边形DBCF是平行四边形
∴DF//BC且DF=BC
又
∴DE//BC,且
【点评】教师可以让学生尝试不同方法证明三角形中位线,并复习了平行四边形的判定与性质.
下面方法请做参考.
方法一:如图1,过点 作 的平行线交 延长线于点 ,证明 ,再证四边形 为平行四边形.
【例5】已知:在 中, ,点 在直线 上, 与直线 垂直,垂足为 ,且点 为 中点,连接 、 .
⑴如图1,若点 在线段 上,探究线段 与 及 与 所满足的数量关系,并直接写出你得到的结论;
⑵如图2,若点 在 延长线上,你⑴中的结论是否发生变化?写出你的猜想并证明;
【解析】⑴
⑵结论不变,由题意知 ,∴
⑵取AC中点H连接FH、EH
∴
∵AB=AC、DC=AC
∴AB=CD、EH=FH
∴∠HFE=∠FEH
∵EH∥AB、FH∥CD
∴∠BGE=∠GEH,∠HFE=∠GEB
∴∠BGE=∠BEG
∴∠AGE=∠GEC
∴四边形AGEC是等邻角四边形
⑶存在,如图连接辅助线,同理可证,四边形AGHC为等邻角四边形
思维拓展训练(选讲)
【解析】取 中点 , 中点 ,连接 , , ,
可知 ,又 为梯形 中位线,∴
八年级数学平行四边形30道经典题(含答案和解析)

八年级数学平行四边形30道经典题(含答案和解析)1.如图,平行四边形ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为().A.1B.2C.3D.4答案:B.解析:∵平行四边形ABCD,AE平分∠BAD交BC于点E.∴∠BAE=∠EAD,∠EAD=∠AEB.∴∠BAE=∠AEB.∴AB=BE=3.∴EC=2.所以答案为B.考点:三角形——全等三角形——角平分线的性质定理.四边形——平行四边形——平行四边形的性质.2.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AB的长为().A.13B.14C.15D.16答案:D解析:∵平行四边形ABCD,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.∴四边形ABEF为平行四边形.∴∠FAB+∠ABE=180°,∠FAE=∠EAB,∠ABF=∠FBE. ∴∠BAE+∠ABF=90°,AE⊥BF.∴四边形ABEF为菱形.设AE,BF交点为点O,则点O平分线段AE,BF.在△ABO中,AO2+BO2=AB2,(12AE)2+(12BF)2=AB2.∵BF=12,AB=10.解得AE=16.所以答案为D.考点:三角形——直角三角形——勾股定理.四边形——平行四边形——平行四边形的性质.四边形——菱形——菱形的判定.3.如图,已知平行四边形纸片ABCD的周长为20,将纸片沿某条直线折叠,使点D与点B重合,折痕交AD于点E,交BC于点F,连接BE,则△ABE的周长为.答案:10.解析:依题可知,翻折轴对称BE=DE,△ABE的周长=AB+AE+BE=AB+AD=10.考点:四边形——平行四边形.几何变换——图形的对称——翻折变换(折叠问题).4.下列条件中,不能判断四边形是平行四边形的是().A. AB∥CD,AD∥BCB. AB=CD,AD∥BCC. AB∥CD,AB=CDD. ∠A=∠C,∠B=∠D答案:B.解析:如图:A选项,∵AB∥CD,AD∥BC .∴四边形ABCD是平行四边形,正确,故本选项错误.B选项,根据AB=CD和AD∥BC 可以是等腰梯形,错误,故本选项正确.C选项,∵AB∥CD,AB=CD.∴四边形ABCD是平行四边形,正确,故本选项错误.D选项,∵∠A=∠C,∠B=∠D.∴四边形ABCD是平行四边形,正确,故本选项错误.故选B.考点:四边形——平行四边形——平行四边形的判定.5.阅读下面材料:在数学课上,老师提出如下问题:尺规作图:过直线外一点作已知直线的平行线.已知:直线l及其外一点A.求作:l的平行线,使它经过点A.小云的作法如下:(1)在直线l上任取一点B,以点B为圆心,任意长为半径作弧,交直线l于点C.(2)分别以A,C为圆心,以BC,AB的长为半径作弧,两弧相交于点D.(3)作直线AD.所以直线AD即为所求.老师说:“小云的作法正确.”请回答:小云的作图依据是.答案:两组对边分别相等的四边形是平行四边形;平行四边形对边平行;两点确定一条直线. 解析:两组对边分别相等的四边形是平行四边形;平行四边形对边平行;两点确定一条直线.考点:四边形——平行四边形——平行四边形的判定.尺规作图——过一点作已知直线的平行线.6.如图所示,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=√3.(1)求证:四边形ABDE是平行四边形.(2)求AB的长.答案:(1)证明见解析.(2)AB=√3.解析:(1)∵四边形ABCD是平行四边形.∴AB∥DC,AB=CD.∵AE∥BD.∴四边形ABDE是平行四边形.(2)由(1)知,AB=DE=CD.即D为CE中点.∵EF⊥BC.∴∠EFC=90°.∵AB∥CD.∴∠DCF=∠ABC=60°.∴∠CEF=30°.∴CE=2CF=2√3.∴AB=CD=√3.考点:三角形——直角三角形——含30°角的直角三角形.四边形——平行四边形——平行四边形的性质——平行四边形的判定.7.如图,在矩形ABCD中,E是BC边的中点,沿直线AE翻折△ABE,使B点落在点F处,连结CF并延长交AD于G点.(1)依题意补全图形.(2)连接BF 交AE 于点O ,判断四边形AECG 的形状并证明.(3)若BC =10,AB =203,求CF 的长.答案:(1)画图见解析. (2)四边形AECG 是平行四边形,证明见解析.(3)CF =6.解析:(1)依题意补全图形,如图:(2)依翻折的性质可知,点O 是BF 中点.∵E 是BC 边的中点. ∴EO ∥CG. ∵AG ∥CE.∴四边形AECG 是平行四边形.(3)在Rt △ABE 中.∵BE =12BC =5,AB =203.∴AE =253.∵S △BAE =12AB×BE =12AE×BO.∴BO =4. ∴BF =2BO =8. ∵BF ⊥AE ,AE ∥CG. ∴∠BFC =90°. ∴CF =6.考点:三角形——直角三角形——勾股定理.四边形——平行四边形——平行四边形的判定.几何变换——图形的对称——作图:轴对称变换.8.如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为().A.20B.15C.10D.5答案:D.解析:∵平行四边形的周长为40.∴AB+BC=20.又∵△BOC的周长比△AOB的周长多10.∴BC-AB=10.解得:AB=5,BC=15.故答案为:D.考点:四边形——平行四边形——平行四边形的性质.9.如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′和B C′与AD交于点E,若AB=3,BC=4,则DE的长为.答案:25.8解析:由折叠得,∠CBD=∠EBD.由AD∥BC得,∠CBD=∠EDB.∴∠EDB=∠EBD.∴DE=BE.设DE=BE=x,则AE=4-x.在Rt△ABE中.AE2+AB2=BE2.(4−x)2+32=x2..解得x=258∴DE的长为25.8考点:三角形——直角三角形——勾股定理.四边形——矩形——矩形的性质.几何变换——图形的对称——翻折变换(折叠问题).10.如图,矩形ABCD的对角线AC,BD交于点O,DE∥AC交BA的延长线于点E,点F在BC上,BF=BO,且AE=6,AD=8.(1)求BF的长.(2)求四边形OFCD的面积.答案:(1)BF=5..(2)S四边形OFCD=332解析:(1)∵四边形ABCD是矩形.∴∠BAD=90°.∴∠EAD=180°-∠BAD=90°.∵在Rt△EAD中,AE=6,AD=8.∴DE=√AE2+AD2=10.∵DE∥AC,AB∥CD.∴四边形ACDE 是平行四边形. ∴AC =DE =6.在Rt △ABC 中,∠ABC =90°. ∵OA =OC. ∴BO =12AC =5.∵BF =BO. ∴BF =5. (2)取BC 中点为O.∴BG =CG.∵四边形ABCD 是矩形.∴OB =OD ,∠BCD =90°,CD ⊥BC . ∴OG 是△BCD 的中位线. ∴OG ∥CD .由(1)知,四边形ACDE 是平行四边形,AE =6. ∴CD =AE =6. ∴OG =12CD =3.∵AD =8. ∴BC =AD =8.∴S △BCD =12BC×CD =24,S △BOF =12BF×OG =152. ∴S 四边形OFCD =S △BCD -S △BOF =332.考点:三角形——三角形基础——三角形中位线定理.直角三角形——勾股定理.四边形——平行四边形——平行四边形的性质——平行四边形的判定. 矩形——矩形的性质. 四边形基础——四边形面积.11. 如图,在菱形ABCD 中,∠B =60°,AB =1,延长AD 到点E ,使DE =AD ,延长CD 到点F ,使DF =CD ,连接AC 、CE 、EF 、AF .(1)求证:四边形ACEF是矩形.(2)求四边形ACEF的周长.答案:(1)证明见解析.(2)四边形ACEF的周长为:2+2√3.解析:(1)∵DE=AD,DF=CD.∴四边形ACEF是平行四边形.∵四边形ABCD为菱形.∴AD=CD.∴AE=CF.∴四边形ACEF是矩形.(2)∵△ACD是等边三角形.∴AC=1.∴EF=AC=1.过点D作DG⊥AF于点G,则AG=FG=AD×cos30°=√3.2∴AF=CE=2AG=√3.∴四边形ACEF的周长为:AC+CE+EF+AF=1+√3+1+√3=2+2√3.考点:三角形——等腰三角形——等边三角形的判定.锐角三角函数——解直角三角形.四边形——平行四边形——平行四边形的判定.矩形——矩形的判定.菱形——菱形的性质.四边形基础——四边形周长.12.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别是OA,OB,OC,OD的中点,连接EF,FM,MN,NE.(1)依题意,补全图形. (2)求证:四边形EFMN 是矩形.(3)连接DM ,若DM ⊥AC 于点M ,ON =3,求矩形ABCD 的面积.答案:(1)答案见解析. (2)证明见解析.(3)36√3.解析:(1)(2)∵点 E ,F 分别为OA ,OB 的中点.∴EF ∥AB ,EF =12AB .同理,NM ∥DC ,NM =12DC .∵四边形ABCD 是矩形. ∴AB ∥DC ,AB =DC ,AC =BD. ∴EF ∥NM ,EF =NM.∴四边形EFMN 是平行四边形.∵点E ,F ,M ,N 分别OA ,OB ,OC ,OD 的中点. ∴OE =12OA ,OM =12OC . 在矩形ABCD 中.OA =OC =12AC ,OB =OD =12BD.∴EM =OE +OM =12AC . 同理可证FN =12BD . ∴EM =FN .∴四边形EFMN 是矩形.(3)∵DM ⊥AC 于点M.由(2)可知,OM =12OC. ∴OD =CD . 在矩形ABCD 中.OA =OC =12AC ,OB =OD =12BD ,AC =BD. ∴OA =OB =OC =OD. ∴△COD 是等边三角形. ∴∠ODC =60°. ∵NM ∥DC.∴∠FNM =∠ODC =60°. 在矩形EFMN 中,∠FMN =90°. ∴∠NFM =90°-∠FNM =30°. ∵ON =3.∴FN =2ON =6,FM =3√3,MN =3. ∵点F ,M 分别OB ,OC 的中点. ∴BC =2FM =6√3.∴矩形ABCD 的面积为BC×CD =36√3.考点:直线、射线、线段——直线、射线、线段的基本概念——线段中点、等分点.三角形——三角形基础——三角形中位线定理. 直角三角形——含30°角的直角三角形——勾股定理. 四边形——矩形——矩形的性质——矩形的判定.13. 如图,在平面直角坐标系xOy 中,若菱形ABCD 的顶点A ,B 的坐标分别为(-3,0) ,(2,0),点D 在y 轴正半轴上,则点C 的坐标是 .答案:(5,4).解析:由题意及菱形性质,得:AO=3,AD=AB=DC=5.根据勾股定理,得DO=√AD2−AO2=√52−32=4.∴点C的坐标是(5,4).考点:三角形——直角三角形——勾股定理的应用.四边形——菱形——菱形的性质.14.如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且EF=AE+FC,则边BC的长为().√3A. 2√3B.3√3C. 6√3D.92答案:B.解析:∵四边形ABCD是矩形.∴∠A=90°,AD=BC,AB=DC=3.∵四边形BEDF是菱形.∴EF⊥BD,∠EBO=∠DBF,ED=BE=BF.∴AD-DE=BC-BF,即AE=CF.∵EF=AE+FC,EO=FO.∴AE=EO=CF=FO.∴△ABE≌△OBE.∴AB=BO=3,∠ABE=∠EBO.∴∠ABE=∠EBD=∠DBC=30°.∴在Rt△BCD中,BD=2DC=6.∴BC=√BD2−DC2=3√3.考点:三角形——直角三角形——勾股定理.四边形——矩形——矩形的性质.菱形——菱形的性质.15.如图,在给定的一张平行四边形纸片上作一个菱形.小米的作法是:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM 是菱形.则小米的依据是.答案:一组对边平行且相等的四边形是平行四边形;对角线互相垂直的平行四边形是菱形.解析:根据平行四边形定义可知,一组对边平行且相等的四边形是平行四边形;根据菱形的定义可知对角线互相垂直的平行四边形是菱形,所以答案为一组对边平行且相等的四边形是平行四边形;对角线互相垂直的平行四边形是菱形.考点:四边形——平行四边形——平行四边形的判定.菱形——菱形的判定.16.在数学课上,老师提出如下问题:如图1:将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:如图2:(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D.(2)c点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.老师说:“小明的作法正确.”请回答:小明这样折叠得到菱形的依据是.答案:CD和EF是四边形DECF对角线,而CD和EF互相垂直且平分(答案不唯一).解析:如图,连接DF、DE.根据折叠的性质知,CD⊥EF,且OD=OC,OE=OF.则四边形DECF恰为菱形.考点:四边形——菱形——菱形的判定.几何变换——图形的对称——翻折变换(折叠问题).17.如图,在平行四边形ABCD中,点E,M分别在边AB,CD上,且AE=CM.点F,N分别在边BC,AD上,且DN=BF.(1)求证:△AEN≌△CMF.(2)连接EM,FN,若EM⊥FN,求证:四边形EFMN是菱形.答案:(1)证明见解析.(2)证明见解析.解析:(1)∵四边形ABCD是平行四边形.∴AD=BC,∠A=∠C.∵ND=BF.∴AD-ND=BC-BF.即AN=CF.在△AEN和△CMF中.{AN=CM ∠A=∠C AN=CF.∴△AEN ≌△CMF.(2)由(1)△AEN ≌△CMF.∴EN=FM.同理可证:△EBF ≌△MDB.∴EF=MN.∵EN=FM,EF=MN.∴四边形EFMN是平行四边形.∵EM⊥FN.∴四边形EFMN是菱形.考点:三角形——全等三角形——全等三角形的判定.四边形——平行四边形——平行四边形的性质.菱形——菱形的判定.18.如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC和CE∥AB,两线交于点E.(1)求证:四边形AECD是菱形.(2)若∠B=60°,BC=2,求四边形AECD的面积.答案:(1)证明见解析.(2)S菱形AECD=2√3.解析:(1)∵AE∥DC,CE∥AB.∴四边形AECD是平行四边形.∵Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.∴CD=AD.∴四边形AECD是菱形.(2)连结DE.∵∠ACB=90°,∠B=60°.∴∠BAC=30°.∴AB=4,AC=2√3.∵四边形AECD是菱形.∴EC=AD=DB.又∵CE∥DB.∴四边形ECBD是平行四边形. ∴ED=CB=2.∴S菱形AECD=AC×ED2=2√3×22=2√3.考点:四边形——平行四边形——平行四边形的性质——平行四边形的判定.菱形——菱形的性质——菱形的判定.四边形基础——四边形面积.19.如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于.答案:√2.解析:∵线段AC是正方形ABCD的对角线.∴F对线段AC的对称点永远落在线段DC上.如图所示,做F对线段AC的对称点于F’,连接EF’,EF’的长就是PE+PF的值.根据两平行线的距离定义,从一条平行线上的任意一点到另外一条直线做垂线,垂线段的长度叫两条平行线之间的距离.∴PE+PF的最小值等于垂线段EH的长度.根据平行线间的距离处处相等,可知EH=AD.∵正方形ABCD的面积是2.∴AD=EH=√2.所以答案为√2.考点:几何变换——图形的对称——轴对称与几何最值.20.如图,正方形ABCD的边长为2,点E在AB边上,四边形EFGB也为正方形,设△AFC的面积为S,则().A. S=2B. S=2.4C. S=4D. S随BE长度的变化而变化答案:A.解析:法一:∵AC∥BF.∴S△AFC=S△ABC=2.法二:∵S△AFC=S正方形ABCD+S正方形EFGB+S△AEF-S△FGC-S△ADC.∴设正方形EFGB的边长为a.∴S△AFC=2×2+a2+12a(2−a)−12(2+a)a−12×2×2.=4+a2+a−12a2−a−12a2−2.=2.考点:三角形——三角形基础——三角形面积及等积变换.四边形——正方形.21.将正方形A的一个顶点与正方形的对角线交点重合,如图1位置,则阴影部分面积是正方形A面积的18,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的.(几分之几)答案:12.解析:在图1中,∠GBF +∠DBF =∠CBD +∠DBF =90°.∴∠GBF =∠CBD ,∠BGF =∠CDB =45°,BD =BG. ∴ △FBG ≌△CBD.∴阴影部分的面积等于△DGB 的面积,且是小正方形的面积的14,是大正方形面积的18.设小正方形的边长为x ,大正方形的边长为y. 则有14X 2=18y 2. ∴y =√2x .同上,在图2中,阴影部分的面积是大正方形的面积的14,为14y 2=12x 2.∴阴影部分的面积是正方形B 面积的12.考点:三角形——全等三角形——全等三角形的性质——全等三角形的判定.四边形——正方形——正方形的性质.22. 如图,正方形 的对角线交于O ,OE ⊥AB ,EF ⊥OB ,FG ⊥EB .若△BGF 的面积为1,则正方形ABCD 的面积为 .答案:32.解析:∵两条对角线将正方形分成四个全等的等腰直角三角形.且OE ⊥AB 于点E ,EF ⊥OB 于点F ,FG ⊥EB 于点G. ∴E 为AB 的中点,F 为BO 的中点,G 为EB 的中点. ∴AB =EB =EO =12AB ,EF =BF =FO ,GF =BG =EG =12EB .∴BGAB =14.∴S△BGFS△BAD =(BGAB)2=116.∴S△BAD=16.∴S正方形ABCD=2S△ABD=32.故答案为32.考点:三角形——相似三角形——相似三角形的性质.四边形——正方形——正方形的性质.23.在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.(1)小明发现DG=BE且DG⊥BE,请你给出证明.(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.答案:(1)证明见解析.(2)1+12√14.解析:(1)如图1,延长EB交DG于点H.∵四边形ABCD与四边形AEFG是正方形.∴AD=AB,∠DAG=∠BAE=90°,AG=AE.∴△ABC≌△ABE(SAS).∴∠AGD=∠AEB,DG=BE.∵△ADG中,∠AGD+∠ADG=90°.∴∠AEB+∠ADG=90°.∴△DEH中,∠AEB+∠ADG+∠DHE=180°.∴∠DHE=90°.∴DG⊥BE.(2)如图2,过点A作AM⊥DG交DG于点M.∴∠AMD=∠AMG=90°.∵BD是正方形ABCD的对角线.∴∠MDA=45°.在Rt△AMD中.∵∠MDA=45°,AD=2.∴AM=DM=√2.在Rt△AMG中.∵AM2+GM2=AG2.∴GM=√7.∵DG=DM+GM=√2+√7.∴S△ADG=12×DG×AM=12×(√2+√7)×√2=1+12√14.考点:三角形——全等三角形——全等三角形的性质——全等三角形的判定.直角三角形——勾股定理.四边形——正方形——正方形的性质.24.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,则EF的长为.答案:32.解析:∵DE 为△ABC 的中位线.∴DE =12BC =4,点D 是线段AB 的中点. 又∵∠AFB =90°. ∴DF =12AB =52. ∴EF =DE −DF =32.所以答案为32.考点:三角形——三角形基础——三角形中位线定理.直角三角形——直角三角形斜边上的中线.25. 如图,在四边形ABCD 中,对角线AC ⊥BD ,点E 、F 、G 、H 分别为AB 、BC 、CD 、DA的中点.若AC =8,BD =6,则四边形EFGH 的面积为( ).A. 14B. 12C. 24D.48 答案:B解析:∵点E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点.∴EF =HG =12AC =4,FG =EH =12BD =3,EF ∥HG ,FG ∥EH. ∴四边形EFGH 是平行四边形.∵AC⊥BD.∴EF⊥FG.∴四边形EFGH是矩形.∴四边形EFGH的面积为3×4=12.考点:三角形——三角形基础——三角形中位线定理.四边形——矩形——矩形的判定.四边形基础——四边形面积.26.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB、BC、CA的中点,若CD=6cm,则EF=cm .答案:6.解析:由题意,得:EFAB =12.在Rt△ABC中,D是AB的中点.∴CD=EF=12AB.又∵CD=6.∴EF=CD=6cm.考点:三角形——三角形基础——三角形中位线定理.直角三角形——直角三角形斜边上的中线.27.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点.那么CH的长是.答案:√5.解析:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3.∴AB=BC=1,CE=EF=3,∠E=90°.延长AD交EF于M,连接AC、CF.则AM=BC+CE=1+3=4,FM=EF-AB=3-1=2.∵四边形ABCD和四边形GCEF是正方形.∴∠ACD=∠GCF=45°.∴∠ACF=90°.∵H为AF的中点.AF.∴CH=12在Rt△AMF中,由勾股定理得:AF=√AM2+FM2=√42+22=2√5.∴CH=√5.故答案为:√5.考点:三角形——直角三角形——直角三角形斜边上的中线——勾股定理.四边形——正方形——正方形的性质.28.用两个全等的直角三角形无缝隙不重叠地拼下列图形:①矩形;②菱形;③正方形;④等腰三角形;⑤等边三角形.一定能够拼成的图形是(填序号).答案:①④.解析:由于菱形和正方形中都有四边相等的特点,而直角三角形不一定有两边相等,故两个全等的直角三角形不一定能拼成菱形和正方形.由于等边三角形三个角均为60°,而直角三角形不一定含60°角,故个全等的直角三角形不一定能拼成等边三角形.两个全等的直角三角形一定能拼成矩形和等腰三角形,如图.考点:三角形——等腰三角形——等腰三角形的判定——等边三角形的判定.四边形——矩形——矩形的判定.菱形——菱形的判定——正方形——正方形的判定.29. 边长为a 的菱形是由边长为a 的正方形“形变”得到的,若这个菱形一组对边之间的距离为h ,则称ah 为这个菱形的“形变度”.(1)一个“形变度”为3的菱形与其“形变”前的正方形的面积之比为 . (2)如图,A 、B 、C 为菱形网格(每个小菱形的边长为1,“形变度”为98)中的格点,则△ABC 的面积为 .答案:(1)1:3.(2)12. 解析:(1)如图所示.∵“形变度”为3. ∴ah =3,即h =13a .∴一个“形变度”为3的菱形与其“形变”前的正方形的面积之比为aℎa 2=ℎa =13. (2)在正方形网格中,△ABC 的面积为:6×6−12×3×3-12×3×6−12×3×6=272.由(1)可得,在菱形网格中,△ABC的面积为89×272=12.考点:式——探究规律——定义新运算.三角形——三角形基础——三角形面积及等积变换.四边形——菱形——菱形的性质.30.有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.小南根据学习四边形的经验,对筝形的性质和判定方法进行了探究.下面是小南的探究过程:(1)由筝形的定义可知,筝形的边的性质是:筝形的两组邻边分别相等,关于筝形的角的性质,通过测量,折纸的方法,猜想:筝形有一组对角相等,请将下面证明此猜想的过程补充完整.已知:如图,在筝形ABCD中,AB=AD,CB=CD.求证:___________________________.证明:由以上证明可得,筝形的角的性质是:筝形有一组对角相等.(2)连接筝形的两条对角线,探究发现筝形的另一条性质:筝形的一条对角线平分另一条对角线.结合图形,写出筝形的其他性质(一条即可):.(3)筝形的定义是判定一个四边形为筝形的方法之一.试判断命题“一组对角相等,一条对角线平分另一条对角线的四边形是筝形”是否成立,如果成立,请给出证明:如果不成立,请举出一个反例,画出图形,并加以说明.答案:(1)求证:∠B=∠D.证明见解析.(2)筝形的两条对角线互相垂直.(3)不成立.解析:(1)求证:∠B =∠D .已知:如图,筝形ABCD 中,AB =AD ,CB =CD .求证:∠B =∠D . 证明:连接AC ,如图. 在△ABC 和△ADC 中.{AB =AD CB =CD AC =AC.∴△ABC ≌△ADC . ∴∠B =∠D .(2)筝形的其他性质.①筝形的两条对角线互相垂直. ②筝形的一条对角线平分一组对角. ③筝形是轴对称图形.(3)不成立.反例如图2所示.在平行四边形ABCD 中,AB≠AD ,对角线AC ,BD 相交于点O .由平行四边形性质可知此图形满足∠ABC =∠ADC ,AC 平分BD ,但该四边形不是筝形.考点:四边形——平行四边形.。
中点四边形综合问题重难点培优八年级数学下册尖子生同步培优题典(解析版)【人教版】

八年级数学下册尖子生同步培优题典【人教版】专题18.13中点四边形综合问题(重难点培优)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2019秋•龙岗区期末)如图,四边形ABCD 中,AC BD =,顺次连接四边形各边中点得到的图形是( )A .菱形B .矩形C .正方形D .以上都不对【分析】根据中位线定理证明中点四边形的四边相等,则顺次连接四边形各边中点得到的四边形是菱形. 【解析】E ,F 分别是DC ,AD 的中点, 12EF AC ∴=,//EF AC , 同理,12GH AC =,//GH AC ,12GF BD =, EF GH ∴=,//EF GH ,∴四边形EFGH 是平行四边形,AC BD =,EF GF ∴=,∴平行四边形EFGH 为菱形,故选:A .2.(2021春•宣城期末)下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③四条边相等的四边形是正方形;④顺次连接菱形各边中点形成的四边形一定是矩形.其中正确的个数是( )A .4B .3C .2D .1【分析】根据平行四边形的判定和等腰梯形的判定即可判断①;画出图形,根据菱形的判定即可判断②;根据菱形和正方形的判定即可判断③;根据三角形的中位线性质得出//EF AC '',12EH B D ='',//EH B D '',12FG B D ='',//FG B D '',求出EH FG =,//EH FG ,根据平行四边形的判定得出四边形EFGH 是平行四边形,根据菱形的性质得出AC B D ''⊥'',求出90HEF ∠=︒,根据矩形的判定得出四边形EFGH 是矩形,即可判断④.【解析】①一组对边平行,另一组对边相等的四边形是等腰梯形,不一定是平行四边形,故①错误; ②如图,AC BD ⊥,但是四边形ABCD 不是菱形,即对角线互相垂直的四边形不一定是菱形,故②错误; ③四条边相等的四边形是菱形,不一定是正方形,故③错误;④如图,E 、F 、G 、H 分别是菱形A B C D ''''的边A B ''、B C ''、C D ''、A D ''的中点,//EF AC ∴'',12EH B D ='',//EH B D '',12FG B D ='',//FG B D '', EH FG ∴=,//EH FG ,∴四边形EFGH 是平行四边形,四边形A B C D''''是菱形,∴''⊥'',AC B DEH B D'',//EH AC∴⊥'',EF AC'',//∴⊥,EF EH即90∠=︒,HEF∴四边形EFGH是矩形,故④正确;所以正确的个数是1,故选:D.3.(2020秋•岐山县期中)如图,任意四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA 的中点,连接AC,BD,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若AC BD=,则四边形EFGH为菱形B.若AC BD⊥,则四边形EFGH为矩形C.若AC BD⊥,则四边形EFGH为正方形=,且AC BDD.若AC与BD互相平分,且AC BD=,则四边形EFGH是正方形【分析】连接四边形各边中点所得的四边形必为平行四边形,根据中点四边形的性质进行判断即可.【解析】A.当E,F,G,H是四边形ABCD各边中点,且AC BD===,=时,存在EF FG GH HE故四边形EFGH为菱形,故本选项不符合题意;B、当E,F,G,H是四边形ABCD各边中点,且AC BDEFG FGH GHE∠=∠=∠=︒,⊥时,存在90故四边形EFGH为矩形,故本选项不符合题意;===,⊥,存在EF FG GH HE C、当E,F,G,H是四边形ABCD各边中点,且AC BD=,且AC BD∠=∠=∠=︒,故四边形EFGH为正方形,故本选项不符合题意;90EFG FGH GHED、当E,F,G,H是四边形ABCD各边中点,且AC与BD互相平分,且AC BD=,故四边形EFGH 为菱形,故本选项符合题意;故选:D.4.(2021春•樊城区期末)如果一个四边形的对角线相等,顺次连接该四边形四条边的中点,可以得到( )A.平行四边形B.矩形C.菱形D.正方形【分析】根据三角形中位线定理得到//EF BD,//GH BD,12EF BD=,12GH BD=,12EH AC=,根据菱形的判定定理证明即可.【解析】E、F、G、H分别是边AD、AB、BC、CD的中点,//EF BD∴,//GH BD,12EF BD=,12GH BD=,12EH AC=,//EF GH∴,EF GH=,∴四边形EFGH是平行四边形.如图,连接AC、BD,AC BD=,12EF BD=,12EH AC=,EF EH∴=,∴平行四边形EFGH是菱形,故选:C.5.(2021春•武昌区校级期中)如图,顺次连接四边形ABCD各边中点得到中点四边形EFGH,下列说法中正确的是()A .当AC BD ⊥时,四边形EFGH 为菱形B .当AC BD =时,四边形EFGH 为矩形C .当AC BD ⊥,AC BD =时,四边形EFGH 为正方形D .以上说法都不对【分析】根据三角形中位线定理、平行四边形的判定定理得到四边形EFGH 为平行四边形,根据矩形、菱形、正方形的判定定理判断即可.【解析】点E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,//EF AC ∴,12EF AC =,//GH AC ,12GH AC =,//EH BD ,12EH BD =, //EF GH ∴,EF GH =,∴四边形EFGH 为平行四边形,当AC BD ⊥时,EF EH ⊥,∴四边形EFGH 为矩形,A 选项说法错误;当AC BD =时,EH EF =,∴四边形EFGH 为菱形,B 选项说法错误;当AC BD ⊥,AC BD =时,EF EH ⊥,EF EH =,∴四边形EFGH 为正方形,C 选项说法正确;D 选项说法错误;故选:C .6.(2019•青神县一模)如图,正方形ABCD 四边的中点分别是E 、F 、G 、H ,若四边形EFGH 的面积是2,则正方形ABCD 的周长是( )A .4B .42C .8D .82【分析】根据正方形的性质得到AB BC CD AD ===,求得AE BE BF CF CG DG DH AH =======,根据全等三角形的性质得到EF FG HG EH ===,45AHE DHG ∠=∠=︒,求得90GHE ∠=︒,求得1AE AH ==,得到正方形ABCD 的边长为2,于是得到答案.【解析】正方形ABCD 四边的中点分别是E 、F 、G 、H ,AB BC CD AD∴===,∴=======,AE BE BF CF CG DG DH AH∠=∠=∠=∠=︒,A B C D90∴∆≅∆≅∆≅∆,AEH BFE CGF HDE SAS()∠=∠=︒,AHE DHGEF FG HG EH∴===,45GHE∴∠=︒,90∴四边形EFGH是正方形,四边形EFGH的面积是2,∴四边形EFGH2,∴==,AE AH1∴正方形ABCD的边长为2,∴正方形ABCD的周长是8,故选:C.7.(2019•江油市二模)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是()A.任意一个四边形的中点四边形是菱形B.任意一个平行四边形的中点四边形是平行四边形C.对角线相等的四边形的中点四边形是矩形D.对角线垂直的四边形的中点四边形是正方形【分析】利用三角形中位线定理可得新四边形的对边平行且等于原四边形一条对角线的一半,那么根据一组对边平行且相等的四边形是平行四边形可判定所得的四边形一定是平行四边形.【解析】A、任意一个四边形的中点四边形是平行四边形,故此选项错误;B、任意一个平行四边形的中点四边形是平行四边形,正确;C、对角线相等的四边形的中点四边形是菱形,故此选项错误;D、对角线垂直的四边形的中点四边形是矩形,故此选项错误.故选:B.8.(2019•临沂)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.4【分析】因为一般四边形的中点四边形是平行四边形,当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是正方形,=,且AC BD⊥时,中点四边形是矩形,当对角线AC BD【解析】因为一般四边形的中点四边形是平行四边形,当对角线BD AC⊥时,中点四边形是矩形,当对角线AC BD=,=时,中点四边形是菱形,当对角线AC BD且AC BD⊥时,中点四边形是正方形,故④选项正确,故选:A.9.(2021秋•金水区校级月考)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点,则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;其中正确的个数是()A.0B.1C.2D.3【分析】根据“一般四边形的中点四边形是平行四边形,当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是矩形”进行判断即可.【解析】因为一般四边形的中点四边形是平行四边形,故③错误;当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是矩形,故①②错误,所以正确的有0个,故选:A.10.(2021春•德阳期末)如图,点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是菱形,则AC与BD互相垂直;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.4【分析】先证四边形EFGH是平行四边形,再由菱形、矩形以及正方形的判定分别对各个说法进行判断即可.【解析】E、F、G、H分别是AB、BC、CD、AD的中点,EH∴是ABD∆的中位线,FG是CBD∆的中位线,EF是ABC∆的中位线,//EH BD ∴,12EH BD=,//FG BD,12FG BD=,//EF AC,12EF AC=,//EH FG∴,EH FG=,∴四边形EFGH是平行四边形,①AC BD=,EH EF∴=,∴平行四边形EFGH是菱形,故①错误;②AC BD⊥,EF EH∴⊥,90FEH∴∠=︒,∴平行四边形EFGH 是矩形,故②错误;③若四边形EFGH 是菱形,则AC BD =,故③错误;④对角线AC BD =,且AC BD ⊥时,中点四边形EFGH 是正方形,故④正确,故选:A .二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上 11.(2021春•阿拉尔期末)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是 正方形 .【分析】由三角形中位线定理得//EH BD ,12EH BD =,//FG BD ,12FG BD =,//EF AC ,12EF AC =,则//EH FG ,EH FG =,得四边形EFGH 是平行四边形,再怎EH EF =,则平行四边形EFGH 是菱形,然后证90FEH ∠=︒,即可得出结论.【解析】如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点,EH ∴是ABD ∆的中位线,FG 是CBD ∆的中位线,EF 是ABC ∆的中位线,//EH BD ∴,12EH BD =,//FG BD ,12FG BD =,//EF AC ,12EF AC =, //EH FG ∴,EH FG =,∴四边形EFGH 是平行四边形,AC BD =,EH EF ∴=,∴平行四边形EFGH 是菱形,又AC BD ⊥,EF EH ∴⊥,90FEH ∴∠=︒,∴四边形EFGH 是正方形,故答案为:正方形.12.(2021秋•寿光市期末)下列说法正确的是 A 、C .A .对角线相等的菱形是正方形B .顺次连接对角线互相垂直的四边形的四边中点,所得到的四边形是菱形C .成轴对称的两个图形全等D .有三个角相等的四边形是矩形【分析】利用正方形的判定方法、菱形的判定方法、矩形的判定方法及全等图形的定义分别判断后即可确定正确的答案.【解析】A 、对角线相等的菱形是正方形,正确,符合题意;B 、顺次连接对角线互相垂直的四边形的四边中点,所得到的四边形是矩形,故原命题错误,不符合题意;C 、成轴对称的两个图形全等,正确,符合题意;D 、有四个角相等的四边形是矩形,故原命题错误,不符合题意.故答案为:A 、C .13.(2020春•西华县期末)如图所示,AC 、BD 是四边形ABCD 的两条对角线,且AC BD ⊥,已知10AC =,8BD =,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,则EG 41 .【分析】易证四边形HEFG 是平行四边形,因为AC BD ⊥,所以HG EH ⊥,所以四边形HEFG 为矩形,进而由勾股定理得到22EG HE HG +.【解析】E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,152HG EF AC ∴===,142EH FG BD ===, E ,H ,是AB ,AD 中点,//HE BD ∴,12HE BD =, 同理//FG BD ,12FG BD =, ∴四边形HEFG 是平行四边形, AC BD ⊥,HG EH ∴⊥,∴四边形HEFG 为矩形,22224541EG HE HG ∴=+=+4114.(2020春•孝义市期末)如图,菱形ABCD 的对角线AC ,BD 相交于点O ,依次连接AO ,BO ,CO ,DO 的中点E ,F ,G ,H ,得到四边形EFGH ,点M 是EF 的中点,连接OM ,若10AB =,则OM 的长为 2.5 .【分析】根据菱形的性质得到AC BD ⊥,根据三角形中位线定理得到152EF AB ==,根据直角三角形的性质计算,得到答案.【解析】四边形ABCD 为菱形,AC BD ∴⊥, E 、F 分别为OA 、OB 的中点,152EF AB ∴==, 在Rt EOF ∆中,M 是EF 的中点,1 2.52OM EF ∴==, 故答案为:2.5.15.(2021秋•南海区月考)已知:在四边形ABCD 中,AD BC =,点E ,F ,G ,H 分别是AB ,CD ,AC ,BD 的中点,四边形EHFG 是 菱形 .【分析】由已知条件得出GF是ADC∆的中位线,GE是ABC∆的中位线,EH是ABD∆的中位线,由三角形中位线定理得出//GF EH,GF EH=,得出四边形EGFH是平行四边形,再证出GE EH=,即可得出四边形EHFG是菱形.【解析】证明:点E、F、G、H分别是AB、CD、AC、BD的中点,GF∴是ADC∆的中位线,GE是ABC∆的中位线,EH是ABD∆的中位线,//GF AD ∴,12GF AD=,12GE BC=,//EH AD,12EH AD=,//GF EH∴,GF EH=,∴四边形EGFH是平行四边形,又AD BC=,GE EH∴=,∴四边形EGFH是菱形.故答案是:菱形.16.(2021秋•榆阳区校级月考)点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点,对角线AC,BD交于点O,当四边形ABCD满足对角线垂直且相等条件时,四边形EFGH是正方形.【分析】根据三角形中位线定理得到//EF BD,12EF BD=,//GH BD,12GH BD=,12EH AC=,进而证明四边形EFGH为平行四边形,再根据正方形的判定定理解答即可.【解析】点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点,//EF BD ∴,12EF BD=,//GH BD,12GH BD=,12EH AC=,//EF GH∴,EF GH=,∴四边形EFGH为平行四边形,当AC BD=时,EF EH=,∴平行四边形EFGH为菱形,当AC BD⊥时,EF EH⊥,∴菱形EFGH为正方形,∴当四边形ABCD的对角线垂直且相等时,四边形EFGH是正方形,故答案为:对角线垂直且相等.17.(2021•西城区校级开学)如图,点A,B,C为平面内不在同一直线上的三点,点D为平面内一个动点,线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④中点四边形MNPQ不可能是正方形;所有结论正确的序号是①②③.【分析】根据中点四边形的性质:一般中点四边形是平行四边形,对角线相等的四边形的中点四边形是菱形,对角线垂线的中点四边形是矩形,对角线相等且垂直的四边形的中点四边形是正方形解答.【解析】中点四边形都是平行四边形,对角线相等的四边形的中点四边形是菱形,对角线垂线的中点四边形是矩形,对角线相等且垂直的四边形的中点四边形是正方形,∴存在无数个中点四边形MNPQ是平行四边形,存在无数个中点四边形MNPQ是菱形,存在无数个中点四边形MNPQ是矩形.故答案为:①②③.18.(2020春•新乐市期末)对于任意矩形ABCD ,若M ,N ,P ,Q 分别为边AB ,BC ,CD ,DA 上的中点,下面四个结论中,①四边形MNPQ 是平行四边形;②四边形MNPQ 是矩形;③四边形MNPQ 是菱形; ④四边形MNPQ 是正方形.所有正确结论的序号是 ①③ .【分析】连接AC 、BD ,由三角形中位线定理得出//MN AC ,12MN AC =,//PQ AC ,12PQ AC =,//MQ BD ,12MQ BD =,则//MN PQ ,MN PQ =,MN MQ =,证出四边形MNPQ 是平行四边形,四边形MNPQ 是菱形;①③正确;当AC BD ⊥时,MN MQ ⊥,四边形MNPQ 是矩形,四边形MNPQ 是正方形,②④不正确,即可得出结论.【解析】连接AC 、BD ,如图:四边形ABCD 是矩形,AC BD ∴=,M ,N ,P ,Q 分别为边AB ,BC ,CD ,DA 上的中点,MN ∴是ABC ∆的中位线,PQ 是ACD ∆的中位线,MQ 是ABD ∆的中位线,//MN AC ∴,12MN AC =,//PQ AC ,12PQ AC =,//MQ BD ,12MQ BD =, //MN PQ ∴,MN PQ =,MN MQ =,∴四边形MNPQ 是平行四边形,∴四边形MNPQ 是菱形;故①③正确;当AC BD ⊥时,MN MQ ⊥,四边形MNPQ 是矩形,四边形MNPQ 是正方形.故②④不正确; 故答案为:①③.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020春•工业园区期末)已知:如图,在四边形ABCD 中,AB 与CD 不平行,E ,F ,G ,H 分别是AD ,BC ,BD ,AC 的中点.(1)求证:四边形EGFH 是平行四边形;(2)①当AB 与CD 满足条件 AB CD = 时,四边形EGFH 是菱形;②当AB 与CD 满足条件 时,四边形EGFH 是矩形.【分析】(1)根据三角形中位线定理得到12EG AB =,//EG AB ,12FH AB =,//FH AB ,根据平行四边形的判定定理证明结论;(2)①根据邻边相等的平行四边形是菱形解答;②根据矩形的判定定理解答.【解析】(1)证明:E ,G 分别是AD ,BD 的中点,EG ∴是DAB ∆的中位线,12EG AB ∴=,//EG AB , 同理,12FH AB =,//FH AB , EG FH ∴=,//EG FH ,∴四边形EGFH 是平行四边形;(2)①F ,G 分别是BC ,BD 的中点,FG ∴是DCB ∆的中位线,12FG CD ∴=,//FG CD , 当AB CD =时,EG FG =,∴四边形EGFH 是菱形;②//HF AB , HFC ABC ∴∠=∠,//FG CD ,GFB DCB ∴∠=∠,90ABC DCB∴∠+∠=︒,90HFC GFB∴∠+∠=︒,90GFH∴∠=︒,∴平行四边形EGFH是矩形,故答案为:①AB CD=;②AB CD⊥.20.(2020春•海陵区校级期中)如图,O为BAC∠内一点,E、F、G、H分别为AB,AC,OC,OB 的中点.(1)求证:四边形EFGH为平行四边形;(2)当AB AC=,AO平分BAC∠时,求证:四边形EFGH为矩形.【分析】(1)根据三角形中位线定理推知////EH AO FG,12EH FG AO==,则四边形EFGH是平行四边形.(2)根据平行线的性质和等腰AEF∆的性质推知:90HEF ADE∠=∠=︒,则四边形EFGH为矩形.【解析】证明:(1)EH是ABO∆的中位线,//EH AO ∴,12EH AO=.同理,FG是ACO∆的中位线,//FG OA ∴,12FG AO=.//EH FG∴,EH FG=,∴四边形EFGH是平行四边形.(2)设OA与EF的交点为D,AB AC=,E、F分别为AB,AC的中点,AE AF∴=.AO平分BAC∠,//EH AD,∴∠=∠=︒,HEF ADE90∴四边形EFGH为矩形.21.已知:如图,分别以BM、CM为边,向BMC∆形外作等边三角形ABM、CDM,E、F、G、H分别为AB、BC、CD、DA中点.(1)猜测四边形EFGH的形状;(2)证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?【分析】(1)由题意可猜测四边形EFGH是菱形;(2)首先连接AC,BD,易证得()∆≅∆,即可得AC BDAMC BMD SAS=,又由E、F、G、H分别为AB、===,即可得四边形EFGH是菱形;BC、CD、DA中点,则可证得EF FG GH EH(3)由(2)得:BMC∆形状的改变对上述结论没有影响.【解析】(1)解:四边形EFGH是菱形;(2)证明:连接AC,BD,∆和CDMABM∆是等边三角形,∴=,CM DMAM BM∠=∠=︒,=,60AMB CMD∴∠=∠,AMC BMD在AMC ∆和BMD ∆中,AM BM AMC BMD CM DM =⎧⎪∠=∠⎨⎪=⎩,()AMC BMD SAS ∴∆≅∆,AC BD ∴=,E 、F 、G 、H 分别为AB 、BC 、CD 、DA 中点,12EF GH AC ∴==,12EH FG BD ==, EF FG GH EH ∴===,∴四边形EFGH 是菱形;(3)解:BMC ∆形状的改变对上述结论没有影响.22.(2021春•东莞市期末)如图,在四边形ABCD 中,AC 、BD 是对角线,点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,依次连接E 、F 、G 、H .(1)证明:四边形EFGH 是平行四边形;(2)在四边形ABCD 中,若再补充一个条件: AC BD ⊥ ,则四边形EFGH 是矩形;(3)连接EG 、FH ,求证:222222EG FH EF FG GH HE +=+++.【分析】(1)由中位线定理证明://HG AC ,12HG AC =,//EF AC ,12EF AC =,从而//HG EF ,HG EF =,即可证明四边形EFGH 是平行四边形;(2)若AC BD ⊥,则90DOC ∠=︒,由//EF AC ,//FG BD ,即可得90GFE ∠=︒,故四边形EFGH 是矩形;(3)过H 作HP EG ⊥于P ,过F 作FQ EG ⊥于Q ,Rt HPE ∆中,22222EH HP OE OP OE OP =++-⋅,Rt HPG ∆中,22222HG HP OG OP OG OP =++-⋅,由四边形EFGH 是平行四边形,可得12OE OG EG ==,12OH OF HF ==,故2222222222112222EH HG HP OE OP OE OP HP OG OP OG OP HF EG +=++-⋅+++-⋅=+,同理可得:22221122EF FG HF EG +=+,从而可证明222222EG FH EF FG GH HE +=+++.【解析】(1)H 、G 是AD 、CD 的中点,HG ∴是ACD ∆的中位线,//HG AC ∴,12HG AC =,同理://EF AC ,12EF AC =,//HG EF ∴,HG EF =,∴四边形EFGH 是平行四边形;(2)解:补充的条件是:AC BD ⊥,证明如下:如图:若AC BD ⊥,则90DOC ∠=︒,//EF AC , 90OMF DOC ∴∠=∠=︒,FG 是BCD ∆的中位线,//FG BD ∴,18090GFE OMF ∴∠=︒-∠=︒,由(1)知:四边形EFGH 是平行四边形,∴四边形EFGH 是矩形;故答案为:AC BD ⊥;(3)过H 作HP EG ⊥于P ,过F 作FQ EG ⊥于Q ,如图:Rt HPE ∆中,22222222()2EH HP EP HP OE OP HP OE OP OE OP =+=+-=++-⋅, Rt HPG ∆中,22222222()2HG HP PG HP OG OP HP OG OP OG OP =+=++=++-⋅, 由(1)知:四边形EFGH 是平行四边形,12OE OG EG ∴==,12OH OF HF ==, 2222222222EH HG HP OE OP OE OP HP OG OP OG OP ∴+=++-⋅+++-⋅ 22222()HP OP OE OG =+++222112()()22OH EG EG =++ 22112()22HF EG =⨯+ 221122HF EG =+, 同理可得:22221122EF FG HF EG +=+, 222222EG FH EF FG GH HE ∴+=+++.23.(2021春•集贤县期末)在四边形ABCD 中,AB 、BC 、CD 、DA 的中点分别为P 、Q 、M 、N .(1)如图1,试判断四边形PQMN 怎样的四边形,并证明你的结论;(2)若在AB 上取一点E ,连结DE ,CE ,恰好ADE ∆和BCE ∆都是等边三角形(如图2),判断此时四边形PQMN 的形状,并证明你的结论.【分析】(1)连接AC 、BD .利用三角形中位线定理判定四边形PQMN 的对边平行且相等,易证该四边形是平行四边形;(2)①设ADE ∆的边长是x ,BCE ∆的边长是y ,由于2222213()()2DB x y x x xy y =++=++,2222213()()2AC x y y x xy y =++=++,可得平行四边形PQMN 的对角线相等,从而得出平行四边形PQMN 是菱形;【解析】四边形PQMN 为平行四边形;(1)连接AC 、BD .PQ 为ABC ∆的中位线,//PQ AC ∴,12PQ AC =, 同理//MN AC .12MN AC =. MN PQ ∴=,//MN PQ ,∴四边形PQMN 为平行四边形;(2)四边形PQMN 是菱形;理由如下:设ADE ∆的边长是x ,BCE ∆的边长是y ,2222213()()2DB x y x xy y ∴=++=++,2222213()()2AC x y y x xy y =++=++, 平行四边形PQMN 的对角线相等,∴平行四边形PQMN 是菱形;24.(2021春•泗阳县期末)已知:如图,在四边形ABCD 中,AB 与CD 不平行,E ,F ,G ,H 分别是AD ,BC ,BD ,AC 的中点.(1)求证:四边形EGFH 是平行四边形;(2)当AB CD =,四边形EGFH 是怎样的四边形?证明你的结论.【分析】(1)根据三角形中位线定理得到12EG AB =,//EG AB ,12FH AB =,//FH AB ,根据平行四边形的判定定理证明结论; (2)依据四边形ABCD 是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.【解析】(1)证明:E ,G 分别是AD ,BD 的中点, EG ∴是DAB ∆的中位线,12EG AB ∴=,//EG AB , 同理,12FH AB =,//FH AB , EG FH ∴=,//EG FH ,∴四边形EGFH 是平行四边形;(2)菱形.理由:F ,G 分别是BC ,BD 的中点,FG ∴是DCB ∆的中位线,12FG CD ∴=,//FG CD ,又12EG AB =, ∴当AB CD =时,EG FG =,∴平行四边形EGFH 是z。
【初中数学】人教版八年级下册专题训练(二)中点四边形(练习题)

人教版八年级下册专题训练(二)中点四边形(146) 1.如图,在四边形ABCD中,AC=BD=6,E,F,G,H分别是AB,BC,CD,DA的中点,求EG2+FH2的值.2.四边形ABCD为边长等于1的菱形,顺次连接它的各边中点组成四边形EFGH(四边形EFGH称为原四边形的中点四边形),再顺次连接四边形EFGH的各边中点组成第二个中点四边形……则按上述规律组成的第八个中点四边形的边长等于.3.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.(1)当四边形ABCD是矩形时,四边形EFGH是形,并说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH是正方形?并说明理由.4.如图,在四边形ABCD中,E,F,G,H分别是BC,AD,BD,AC的中点.(1)求证:EF与GH互相平分;(2)当四边形ABCD的边满足条件时,EF⊥GH.5.顺次连接对角线相等的四边形的各边中点,所得四边形是()A.矩形B.平行四边形C.菱形D.任意四边形6.顺次连接菱形各边中点所得到的四边形是()A.梯形B.矩形C.菱形D.正方形7.若四边形的对角线互相垂直,则顺次连接这个四边形各边中点所得的四边形是()A.平行四边形B.矩形C.菱形D.正方形8.如图,顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是(填序号).9.如图,在四边形ABCD中,AD=CD,AB=CB,E,F,G,H分别是AD,AB,CB,CD的中点.求证:四边形EFGH是矩形.10.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形11.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是()A.矩形B.正方形C.对角线相等的四边形D.对角线互相垂直的四边形12.如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB,CD应满足的条件是.13.如图所示,E,F,G,H为四边形ABCD各边的中点,若对角线AC,BD的长都为20,则四边形EFGH的周长是()A.80B.40C.20D.1014.如图,已知E,F,G,H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60∘,则四边形EFGH的面积为cm2.15.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.16.如图,在四边形ABCD中,AC=8,BD=6,且AC⊥BD,E,F,G,H分别是AB,BC,CD,DA 的中点,则EG2+FH2=.参考答案1.【答案】:如图,连接EF ,FG ,GH ,EH ,∵E ,H 分别是AB ,DA 的中点,∴EH 是△ABD 的中位线,∴EH =12BD =3. 同理可得EF ,FG ,GH 分别是△ABC ,△BCD ,△ACD 的中位线, ∴EF =GH =12AC =3,FG =12BD =3,∴EH =EF =GH =FG =3,∴四边形EFGH 为菱形,∴EG ⊥HF ,且垂足为O ,∴EG =2OE ,FH =2OH .在Rt △OEH 中,根据勾股定理得:OE 2+OH 2=EH 2=9,等式两边同时乘4得4OE 2+4OH 2=9×4=36,∴(2OE)2+(2OH)2=36,即EG 2+FH 2=36.【解析】:连接EH,HG,GF,FE ,根据题目条件提供的四个中点,结合中位线的性质,证明四边形EFGH 为菱形,再根据菱形的性质及勾股定理求出结果.2.【答案】:116【解析】:根据题意,结合图形寻找规律:第二、四、六、八个中点四边形为菱形,第一个菱形边长为12,第二个菱形边长为14,第三个菱形边长为18,第四个菱形边长为116,即为第八个菱形的边长3(1)【答案】当四边形ABCD 是矩形时,四边形EFGH 是菱形.理由:∵四边形ABCD 是矩形,∴AC =BD .∵E ,F ,H 分别是AB ,BC ,AD 的中点,∴EF=12AC,EH=12BD,∴EF=EH.同理可得EF=GH=GF,∴四边形EFGH是菱形【解析】:利用矩形及中位线的性质,结合菱形的判定方法进行推导证明.(2)【答案】当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH是正方形.理由:∵E,F分别是四边形ABCD的边AB,BC的中点,∴EF∥AC,EF=12AC,同理,EH∥BD,EH=12BD,GF=12BD,GH=12AC.∵AC=BD,∴EF=EH=GH=GF,∴四边形EFGH是菱形.∵AC⊥BD,∴EF⊥EH,∴菱形EFGH是正方形【解析】:根据三角形的中位线平行于第三边并等于第三边的一半,先判断出AC=BD,又正方形的四个角都是直角,可以得到正方形的邻边互相垂直,然后证出AC与BD垂直,得到四边形ABCD满足的条件.4(1)【答案】证明:连接GE,GF,HF,EH.∵E,G分别是BC,BD的中点,∴EG=12CD.同理FH=12CD,FG=12AB,EH=12AB,∴EG=FH,GF=EH,∴四边形EHFG是平行四边形.∴EF与GH互相平分【解析】:根据题中提供的四个中点,得到几组中位线,利用中位线的性质,及平行四边形的判定方法,推导出四边形EHFG是平行四边形,进而推导出结论(2)【答案】当四边形ABCD的边满足条件AB=CD时,EF⊥GH.【解析】:理由如下:当EF⊥GH时,四边形EGFH是菱形,此时GF=EG.∵EG=12CD,FG=12AB,∴AB=CD.∴当四边形ABCD的边满足条件AB=CD时,EF⊥GH5.【答案】:C【解析】:顺次连接对角线相等的四边形的各边中点,所得四边形是菱形.如图,∵E,F,G,H分别为四边形ABCD各边的中点,∴EH为△ABD的中位线,FG为△CBD的中位线,∴EH∥BD,EH=12BD,FG∥BD,FG=12BD,∴EH∥FG,EH=FG=12BD,∴四边形EFGH为平行四边形.又∵EF为△ABC的中位线,∴EF=12AC.又∵EH=12BD,且AC=BD,∴EF=EH,∴平行四边形EFGH为菱形.故选C.6.【答案】:B【解析】:利用菱形的性质、矩形的判定方法及中位线的性质推导出结果.7.【答案】:B【解析】:如图,在四边形ABCD中,AC⊥BD,连接各边的中点E,F,G,H,则EH∥AC,FG∥AC,EF∥BD,GH∥BD.又因为对角线AC⊥BD,所以GH⊥EH,EH⊥EF,EF⊥FG,FG⊥HG.故可判定该四边形是矩形.故选B.8.【答案】:①④【解析】:如图四边形ABCD,连接AC,BD.∵E,F,G,H分别是四边形各边的中点,∴EF∥AC,HG∥AC,EH∥BD,GF∥BD,∴EF∥GH,EH∥FG,∴四边形EFGH是平行四边形,故①正确.若四边形ABCD是矩形,则AC=BD.∵EF=12AC,EH=12BD,∴EF=EH,∴平行四边形EFGH是菱形,故②错误.若四边形EFGH是菱形,则AC=BD,但四边形ABCD不一定是矩形,故③错误.若四边形ABCD是正方形,则AC=BD,AC⊥BD,∴四边形EFGH是正方形,故④正确.∴正确的叙述是①④.9.【答案】:连接AC,BD,交于点O,如图.∵E,F,G,H分别是AD,AB,CB,CD的中点,∴EF∥BD∥GH,EH∥AC∥FG,EF=GH=12BD,EH=FG=12AC,∴四边形EFGH是平行四边形.∵AD=CD,AB=CB,∴点D,B都在线段AC的垂直平分线上,∴DB垂直平分AC,∴DB⊥AC,OA=OC.∵EF∥DB,∴EF⊥AC.∵FG∥AC,∴EF⊥FG,∴四边形EFGH是矩形【解析】:利用三角形的中位线解题.10.【答案】:D【解析】:若得到的四边形是矩形,那么邻边互相垂直,根据三角形中位线定理,故原四边形的对角线必互相垂直,由此得解.11.【答案】:C【解析】:若得到的四边形是菱形,那么四条边都相等,根据三角形中位线定理,故原四边形的对角线必相等,由此得解.12.【答案】:AB=CD【解析】:若四边形EFGH是菱形,则GH=EH,又根据题中条件所给的四个中点,利用中位线的性质推导出AB=2GH,CD=2EH,所以AB=CD.13.【答案】:B【解析】:∵E,F,G,H是四边形ABCD各边的中点,∴HG=EF=12AC,GF=HE=12BD,∴四边形EFGH的周长=HG+EF+GF+HE=12(AC+AC+BD+BD)=12×(20+20+20+20)=40 14.【答案】:9√3【解析】:连接AC,BD,相交于点O,如图所示, ∵点E,F,G,H分别是菱形四边的中点,∴EH=12BD=FG,EH∥BD∥FG, EF=12AC=HG,∴四边形EHGF是平行四边形.∵菱形ABCD中,AC⊥BD,∴EF⊥EH,∴平行四边形EFGH是矩形.∵四边形ABCD是菱形,∠ABC=60∘,∴∠ABO=30∘.∵AC⊥BD,∴∠AOB=90∘,∴AO=12AB=3cm,∴AC=6cm.在Rt△AOB中,由勾股定理,得OB=√AB2−OA2=3√3cm, ∴BD=6√3cm.∵EH=12BD,EF=12AC,∴EH=3√3cm,EF=3cm,∴矩形EFGH的面积=EF·EH=9√3cm2. 故答案为9√315.【答案】:12【解析】:∵E,F,G,H分别为边AD,AB,BC,CD的中点,∴HE=12AC=4,HE∥AC,GF∥AC,∴HE∥GF.同理,HG∥EF,HG=12BD=3,∴四边形EFGH是平行四边形.∵AC⊥BD,∴∠EHG=90∘,∴四边形EFGH是矩形,∴四边形EFGH的面积为3×4=1216.【答案】:50【解析】:连接HG,EH,EF,FG,∵E,F,G,H分别是AB,BC,CD,DA的中点,∴HG=EF=12AC=4,EH=FG=12BD=3,∵E,H分别是AB,AD的中点,∴HE∥BD,HE=12BD,同理FG∥BD,FG=12BD,∴四边形HEFG是平行四边形.∵AC⊥BD,∴HG⊥EH,∴四边形HEFG为矩形,∴EG2+FH2=EF2+FG2+EF2+EH2=52+52=50。
2020-2021学年人教版八年级数学下册第18章平行四边形解答题典型必练(一)

人教版八年级数学下册第18章《平行四边形》解答题典型必练(一)1.如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为6,求四边形AEDF面积.2.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.(1)求证:四边形EFGH是平行四边形;(2)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.3.如图,在正方形ABCD中,AC,BD相交于点O,E,F分别在OA,OD上,∠ABE =∠DCF.(1)求证:△ABE≌△DCF.(2)若BC=4,AE=3,求BE的长.4.如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)直接写出GF与GC的数量关系:;(2)用等式表示线段BH与AE的数量关系,并证明.5.四边形ABCD是矩形,点P在边CD上,∠PAD=30°,点G与点D关于直线AP对称,连接BG.(1)如图,若四边形ABCD是正方形,求∠GBC的度数;(2)连接CG,设AB=a,AD=b,探究当∠CGB=120°时,a与b的数量关系.6.如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE 关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2,当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论.7.如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.(1)求证:AF⊥EH;(2)连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.8.如图,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC.(1)求证:∠FBC=∠CDF;(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.9.已知AP为正方形ABCD外的一条射线,B′为点B关于直线AP的对称点,连接B′D.如图1所示.(1)如果∠BAP=20°,求∠ADB′的度数的大小.(2)如图2所示,M为射线B′B上一点,且∠BMC=135°.①求证:BB′=CM.②求证:CM∥B′D.10.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图1;图2;(2)若∠PAB=25°,求∠ADF的度数;(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间数量关系,并证明.11.如图,已知正方形ABCD边长为1,点P是射线AD的上的一个动点,点A关于直线BP的对称点是点Q,设AP=x.(1)求当D,Q,B三点在同一直线上时对应的x的值.(2)当△CDQ为等腰三角形时,求x的值.12.在正方形ABCD中,点P是射线CB上一个动点.连接PA,PD,点M,N分别为BC,AP的中点,连接MN交PD于点Q.(1)如图1,当点P在线段CB的延长线上时,请判断△QPM的形状,并说明理由.(2)如图2,正方形的边长为4,点P'与点P关于直线AB对称,且点P'在线段BC上.连接AP',若点Q恰好在直线AP'上,求P'M的长.13.如图,在边长为6的正方形ABCD中,G是边BC的中点,点C关于直线DG的对称点为F,连接GF并延长交AB于点E,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:△ADE≌△FDE;(2)求AE的长;(3)求BH的长;14.如图,经过正方形ABCD的顶点A在其外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F.(1)依题意补全图1.(2)若∠PAB=30°,求∠ADF的度数.(3)如图,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.15.在小学,我们已经初步了解到,正方形的每个角都是90°,每个边都是相等.如图,在正方形ABCD外侧作直线AQ,点D关于直线AQ的对称点为E,连接DE、BE,BE交AD于点F,若∠QAD=15°.(1)求∠ABE的度数;(2)若AB=6,求AF的长.参考答案1.(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ABC+∠BAD=180°,∵AF∥BE,∴∠EBA+∠BAF=180°,∴∠CBE=∠DAF,同理得∠BCE=∠ADF,在△BCE和△ADF中,,∴△BCE≌△ADF(ASA);(2)解:∵点E在▱ABCD内部,,∴S△BEC+S△AED=S▱ABCD由(1)知:△BCE≌△ADF,∴S△BCE=S△ADF,∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S,▱ABCD ∵▱ABCD的面积为6,∴四边形AEDF的面积为3.2.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C.∴在△AEH与△CGF中,,∴△AEH≌△CGF(SAS),∴EH=GF,同理证得△EBF≌△GDH,则EF=GH,∴四边形EFGH是平行四边形;(2)解:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.连接AC,∵CG′=CG=AE,AB∥CG′,∴四边形AEG′C为平行四边形,∴EG′=AC.在△EFG′中,∵EF+FG′>EG′=AC,∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.3.证明:(1)∵四边形ABCD是正方形,∴AB=CD,∠BAE=∠CDF=45°,∵∠ABE=∠DCF,在△ABE与△DCF中,,∴△ABE≌△DCF(ASA);(2)∵四边形ABCD是正方形,∴AB=BC,OA=OB=OC=OD,∠ABC=∠AOB=90°,∵BC=4,∴AB=4,∴AC=,∴OA=OB=4,∵AE=3,∴OE=OA﹣AE=4﹣3=1,在Rt△BOE中,BE=.4.证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,,∴Rt△DFG≌Rt△DCG(HL),∴GF=GC;(2)BH=AE,理由是:证法一:如图,在线段AD上截取AM,使AM=AE,∵AD=AB,∴DM=BE,由(1)知:∠ADE=∠EDF,∠FDG=∠GDC,∵∠ADC=90°,∴∠ADE+∠EDF+∠FDG+∠GDC=90°,∴2∠EDF+2∠FDG=90°,∴∠EDF+∠FDG=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,∴△DEH是等腰直角三角形,∴∠AED+∠BEH=∠AED+∠ADE=90°,DE=EH,∴∠ADE=∠BEH,在△DME和△EBH中,,∴△DME≌△EBH(SAS),∴EM=BH,Rt△AEM中,∠A=90°,AM=AE,∴EM=AE,∴BH=AE;证法二:如图,过点H作HN⊥AB于N,∴∠ENH=90°,由方法一可知:DE=EH,∠1=∠NEH,在△DAE和△ENH中,,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=HN=AE.5.解:(1)连接DG,交AP于点E,连接AG,如图1,∵点G与点D关于直线AP对称,∴AP垂直平分DG,∴AD=AG.∵在△ADG中,AD=AG,AE⊥DG,∴∠PAG=∠PAD=30°,又∵在正方形ABCD中,AD=AB,∠DAB=∠ABC=90°,∴AG=AB,∠GAB=∠DAB﹣∠PAD﹣∠PAG=30°,∴在△GAB中,∠ABG=∠AGB==75°,∴∠GBC=∠ABC﹣∠ABG=15°;(2)连接DG,AG.由(1)可知,在△ADG中,AD=AG,∠DAG=∠PAD+∠PAG=60°,∴△ADG是等边三角形,∴DG=AG=AD,∠DAG=∠ADG=∠DGA=60°,又∵在矩形ABCD中,AB=DC,∠DAB=∠ADC=∠ABC=90°,∴∠DAB﹣∠DAG=∠ADC﹣∠ADG,即∠GAB=∠GDC=30°,∴△GAB≌△GDC(SAS),∴GB=GC.当∠CGB=120°时,点G可能在矩形ABCD的内部或外部.若点G在矩形ABCD的内部,∵在△BGC中,GB=GC,∠CGB=120°,∴∠GBC==30°,∴∠GBA=∠ABC﹣∠GBC=90°﹣30°=60°,在△ABG中,∠AGB=180°﹣∠GAB﹣∠GBA=90°,∴a=b,若点G在矩形ABCD的外部,在△BGC中,∠GBC=30°,∴∠ABG=120°,又∵∠GAB=30°,∴∠AGB=180°﹣30°﹣120°=30°.∴BA=BG,过点B作BH⊥AG,垂足为H,∴AH=AG=b.在Rt△ABH中,∠AHB=90°,∠HAB=30°,∴cos∠HAB==,∴a=b,在Rt△ADP中,∠ADP=90°,∠PAD=30°,∴tan∠PAD==,∴DP=b.所以无论点G在矩形ABCD内部还是点G在矩形ABCD外部,都有DP≤DC,均符合题意.综上,当∠CGB=120°时a与b的数量关系为a=b或a=b.6.解:(1)∵∠ADE=15°,∴∠FDE=15°,∠CDF=60°.∵DC=AD=DF,∴∠CFD=60°.又∠CFD=∠DGC+∠FDE=15°+∠DGC,∴∠DGC=45°;(2)不变,理由如下:∵△ADE与△FDE关于DE对称,∴∠AGD=∠DGF.设∠ADE=x,可得∠FDE=x,∠CDF=90°﹣2x,∵DC=AD=DF,∴∠CFD=45°+x.又∠CFD=∠DGC+∠FDE=x+∠DGC,∴∠DGC=45°;(3)四边形AGFM是正方形;理由:∵∠DAE=∠DFE=90°,点M为DE的中点,∴AM=FM=DM=DE,∴∠ADM=∠DAM,∠MDF=∠DFM,∴∠AME=∠EMF=2∠ADM=2∠MDF=45°,∴∠AMF=90°,∵∠MGF=45°,∴FM=FG,在△ADG与△FDG中,,∴△ADG≌△FDG(SAS),∴AG=FG,∴AM=MF=FG=AG,∵∠AMF=90°,∴四边形AGFM是正方形.7.解:(1)证明:∵点B关于直线AE的对称点为F,∴AB=AF,BE=EF,又∵AE=AE,∴△ABE≌△AFE(SSS),∴∠AFE=∠B=90°,∴AF⊥EH;(2)连接AH,如图:由(1)得AB=AF,AF⊥EH,∴AF=AD,∠D=∠AFH=90°,AH=AH,∴△AFH≌△ADH(HL),∴∠FAH=∠DAH,又∵∠BAE=∠FAE,在正方形ABCD中,∠BAD=90°,∴∠EAH=45°.8.解:(1)∵ABCD为正方形,∴∠DCE=90°.∴∠CDF+∠E=90°,又∵BF⊥DE,∴∠FBC+∠E=90°,∴∠FBC=∠CDF(2)如图所示:在线段FB上截取FM,使得FM=FD.∵∠BDC=∠MDF=45°,∴∠BDM=∠CDF,∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°,∴∠EFG=∠EFC=45°,∴∠CFG=90°,∵CF=FG,∴CG=CF,∴BM=CG,∴BF=BM+FM=CG+DF.补充方法:连接GM,证明四边形BMGC是平行四边形即可.9.(1)解:连接AB',如图1,∵B′为点B关于直线AP的对称点,∴AB=AB',∴∠BAP=∠B'AP=20°,∵四边形ABCD是正方形,∴AB=AD,∴AB'=AD,∴∠AB'D=∠ADB',∵∠B'AD=∠B'AB+∠BAD=90°+40°=130°,∴∠ADB'=25°.(2)证明:①设B'D与AP的交点为N,连接AB',BN.由(1)得:∠1=∠2,∠3=∠4,∵∠1+∠2+∠3+∠4=90°,∴∠1+∠3=45°,∴∠B'NP=45°,∵∠B'NP=∠BNP,∴∠BNP=45°,则△BNB'为等腰直角三角形.∴BB'=BN,∠ANB=135°,∴∠BMC=∠ANB=135°,∵∠5+∠6=45°,∠4+∠5=45°,∴∠4=∠6.在△ANB和△BMC中,,∴△ANB≌△BNC(AAS),∴BN=CM,∴BB'=CM;②∵△BB'N为等腰直角三角形,∴∠NB'B=45°,∴∠NB'B=∠7=45°,∴B'D∥MC.10.解:(1)如图1、图2所示:(2)连接AE,如图3所示:则∠PAB=∠PAE=25°,AE=AB=AD,∴∠AED=∠ADF,∵四边形ABCD是正方形,∴∠BAD=90°,∴∠EAD=90°+25°+25°=140°,∴∠ADF=(180°﹣∠EAD)=20°;(3)连接AE、BF、BD,如图4所示:则EF=BF,AE=AB=AD,∴∠ABF=∠AEF=∠ADF,∴∠BFD=∠BAD=90°,∴BF2+FD2=BD2,∴EF2+FD2=AB2+AD2=2AB2,即EF2+FD2=2AB2.11.解:(1)连接DB,若Q点落在BD上,由AP=x,则PD=1﹣x,PQ=x.∵∠PDQ=45°,∴PD=PQ,即1﹣x=x.∴x=﹣1.(2)①如图2,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.∵△BCQ1为等边三角形,正方形ABCD边长为1,∴Q1F=Q1E=.在四边形ABPQ1中,∵∠ABQ1=30°,∴∠APQ1=150°,∴△PEQ1为含30°的直角三角形,∴PE=Q1E=,∵AE=,∴x=AP=AE﹣PE=2﹣.②如图3,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.∵EF垂直平分CD,∴EF垂直平分AB,∴AQ2=BQ2.∵AB=BQ2,∴△ABQ2为等边三角形.在四边形ABQP中,∵∠BAD=∠BQP=90°,∠ABQ2=60°,∴∠ABP=30°,∴x=AP=.③如图4,连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,∴Q1Q2=,Q1E=,∴EF=.在四边形ABQ3P中,∵∠ABF=∠ABC+∠CBQ3=150°,∴∠EPF=30°,∴EP=EF=.∵AE=,∴x=AP=AE+PE=+2.综上所述,△CDQ为等腰三角形时x的值为2﹣,,2+.12.解:(1)△QPM是等腰三角形,理由如下:延长BC至E,使CE=BP,连接AE,∵PB=CE,∴PB+BC=CE+BC,∴CP=BE,∵四边形ABCD是正方形,∴AB=CD,∠ABC=∠DCB=90°,在△DCP和△ABE中,∴△DCP≌△ABE(SAS)∴∠DPC=∠AEB,∵M是BC的中点,∴MB=MC,∴MB+BP=MC+CE,∴MP=ME,∴M是PE的中点,又∵N是AP的中点,∴MN∥AE,∴∠PMN=∠AEB,∴∠PMN=∠DPC,∴QP=QM,∴△QPM是等腰三角形;(2)延长BC至E,使CE=BP,连接AE,∵M是BC的中点,BC=4,∴BM=CM=2,又∵BP=CE,∴BM+BP=CM+CE,即PM=ME,∴M是PE的中点,且点N是AP中点,13.证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点C关于直线DG的对称点为F,∴△DCG≌△DFG,∴DC=DF=DA,∠DFG=∠C=90°,∴∠DFE=90°,在Rt△ADE和Rt△FDE中,∵,∴Rt△ADE≌Rt△FDE(HL);(2)∵G是边BC的中点,BC=6,∴CG=BG=FG=3,∵△ADE≌△FDE,∴AE=EF,设AE=x,则BE=6﹣x,EG=EF+FG=x+3,∵在Rt△EBG中,BE2+BG2=EG2,∴(6﹣x)2+32=(x+3)2,解得x=2,∴AE=2;(3)如图2,过点H作HN⊥AB于点N,∴∠ENH=90°,由(1)知∠ADE=∠EDF,∠FDG=∠CDG,∵∠ADC=90°,∴2∠EDF+2∠FDG=90°,∴∠EDF+∠FDG=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,△DEH是等腰直角三角形,∴DE=EH,∠ADE=∠NEH,在△DAE和△ENH中,∵,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=.14.解:(1)如图1、图2所示:(2)连接AE,如图3所示:则∠PAB=∠PAE=30°,AE=AB=AD,∴∠AED=∠ADF,∵四边形ABCD是正方形,∴∠BAD=90°,∴∠EAD=90°+30°+30°=150°,∴∠ADF=(180°﹣∠EAD)=15°;(3)连接AE、BF、BD,如图4所示:则EF=BF,AE=AB=AD,∴∠ABF=∠AEF=∠ADF,∴∠BFD=∠BAD=90°,∴BF2+FD2=BD2,∴EF2+FD2=AB2+AD2=2AB2,即EF2+FD2=2AB2.15.解:(1)连接AE,如图1所示:∵点D关于直线AQ的对称点为E,∴AE=AD,AQ垂直平分DE,∴∠EAQ=∠QAD=15°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠BAE=15°+15°+90°=120°,AE=AB,∴∠ABE=(180°﹣120°)=30°;(2)作A⊥BE于M,如图2所示:则∠AMB=∠AMF=90°,∴AM=AB=3,∵∠1=90°﹣30°=60°,∴∠2=90°﹣60°=30°,∴∠FAM=15°+30°=45°,∴△AMF是等腰直角三角形,∴AF=AM=3.。
