黄家英自动控制原理第二版第二章习题答案
自动控制原理简明教程第二版第二章习题答案.ppt

(2) 对微分方程进行非零状态下的拉氏变换;
2 d c ( t ) dc ( t ) 3 2 c ( t ) 2 r ( t ) 2 dt dt
2 s C ( s ) sc ( 0 ) c ( 0 ) 3 { sC ( s ) c ( 0 )} 2 C ( s ) 2 R ( s )
1 L a 1 G G H G G 1 2 1 1 2
与前向通路的P1(增益=-1)对应的余子式Δ1? 与前向通路的P2(增益=G3G2)对应的余子式Δ2?
G H 1 1G 1 2 1
2 1
n G 1 G G H P P G 1 32 121 1 1 22 ( s ) p k k 1 G G H G G k 1 121 12
2-14(a) 试用梅森公式求下图的传递函数C(s)/R(s).
n P G G 1 11 12 ( s ) p kk 1 G G H G G k 1 12 1 12
2-14(a) 试用梅森公式求下图的传递函数C(s)/R(s).
计算输入信号下的闭环传递函数,令N(s)=0,则此时:
第二步:求传递函数 2 C ( s ) s 4 s 2 s 1 2 G ( s ) 1 1 R ( s )( s 1 ) ( s 2 ) ( s 1 ) ( s 2 ) s 1 s 2
第三步:写出复数域的脉冲响应形式
1 2 C ( s ) G ( s )( R s ) G ( s ) 1 s 1s 2 第四步:写出时间域的脉冲响应形式 1 2 1 1 t 2 t c ( t ) L C ( s ) L 1 ( t ) e e 1 s 2 s
自动控制原理黄家英第二版课后答案2.pdf

B2.2 求下列函数的拉氏反变换:
(4)F(s)
(s
s 1)2(s
2)
(4)解:
F(s)
(s
s 1)2 (s
2)
1 (s 1)2
s
2 1
s
2 2
f (t) tet 2et 2e2t
t0
B2.4 在图B2.4所示的电路中电压u1(t)为输入量,试以电压 u2(t)或uC2(t)作为输出量,分别列写该系统的微分方程。
B2.17 解:由梅森公式 :
T
1
n
pkk , 这里n
k 1
4
L1 G2H1,
L2 G4H2 ,
L3 G6H3 ,
L4 G3G4G5H4 ,
L5 G1G 2G 3G4G5G6H5 ,
L6 G7G3G4G5G6H5 ,
L7 G1G8G6H5
L8 G8H1H4,
L9 G7H1G8G6H5 ,
C1R1 )s
1
U c1 (s) U1 (s)
R1R 2C1C2s2
C1R1s 1 (R1C2 R2C2
C1R1 )s
1
R1R2C1C2uc1 (R1C2 R2C2 C1R1 )u c1 uc1 C1R1u 1 u1
B2.8 设系统的微分方程为
试用拉氏变换法进行求解。
B2.8解:
式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) 为中间变量,τ、β、K1和K2均为常数。
试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含
有哪些典型环节?
B2.9(2)解:
G(s)
s2
1 2s 1
自动控制原理课后习题答案第二章

第 二 章2-3试证明图2-5(a)的电网络与(b)的机械系统有相同的数学模型。
分析 首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找出两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列出系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析,可得:o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得:2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出,电网络(a )和机械系统(b )两者参数的相似关系为1112221211,,,K f R K f R C C2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) ;)()(2t t x t x =+(2))。
自动控制原理习题2(含答案)

第二章习题及答案2-1试建立题2-1图所示各系统的微分方程[其中外力)(t F ,位移)(tx 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),f (阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解(a )以平衡状态为基点,对质块m 进行受力分析(不再考虑重力影响),如图解2-1(a)所示。
根据牛顿定理可写出22)()(dt yd m dt dy f t ky t F =--整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++—(b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有)()(111dtdydtdxf x x k -=-(1)对B 点有y k dtdydt dx f 21)(=-(2)联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++(c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs Rs U c r ++=(3)`2)()(Rs Uc s I =(4)联立式(3)、(4),可解得:),可解得: Cs R R R R Cs R R s U s U r c 212112)1()()(+++= 微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1(d )可写出)可写出[]Cs s I s I s I R s U c R R r 1)()()()(++= (5))()(1)(s RI s RI Css I c R c -= (6)[]Css I s I R s I s U c R c c 1)()()()(++= (7)联立式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c |微分方程为微分方程为 rr r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
自动控制原理习题2(含答案)

第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ,位移)(t x 和电压)(t u r 为输入量;位移)(t y 和电压)(t u c 为输出量;k (弹性系数),f (阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解(a )以平衡状态为基点,对质块m 进行受力分析(不再考虑重力影响),如图解2-1(a)所示。
根据牛顿定理可写出22)()(dty d m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++(b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- (1) 对B 点有 y k dtdydt dx f 21)(=- (2) 联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= (3)2)()(R s Uc s I =(4) 联立式(3)、(4),可解得: CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++(d) 由图解2-1(d )可写出[]Css I s I s I R s U c R R r 1)()()()(++= (5) )()(1)(s RI s RI Css I c R c -= (6) []Css I s I R s I s U c R c c 1)()()()(++= (7)联立式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
《自动控制原理》第二版课后习题答案
k (x x ) f ( dx1 dy )
(1)
1
1
dt dt
对B点有
f ( dx1 dy ) k y dt dt 2
(2)
联立式(1)、(2)可得:
dy k1k2 y k1 dx dt f (k1 k2 ) k1 k2 dt
电压。
在正常情况下,炉温等于某个期望值T °C,热电偶的输出电压u f 正好等于给定电压ur 。 此时, ue ur u f 0 ,故u1 ua 0 ,可逆电动机不转动,调压器的滑动触点停留在某 个合适的位置上,使uc 保持一定的数值。这时,炉子散失的热量正好等于从加热器吸取的热
量,形成稳定的热平衡状态,温度保持恒定。
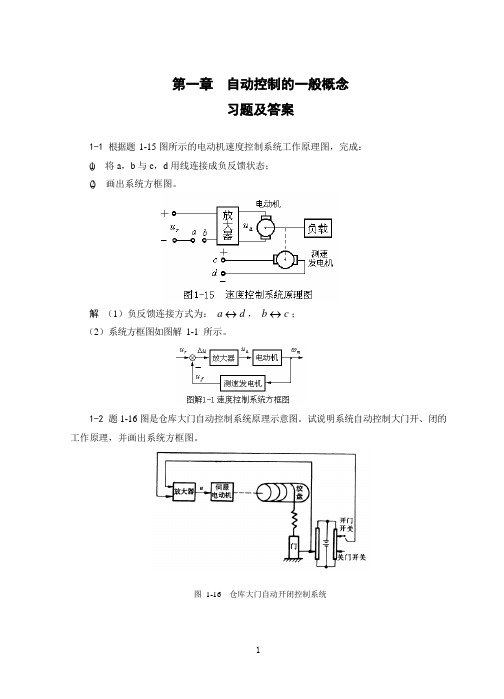
第一章 自动控制的一般概念 习题及答案
1-1 根据题 1-15 图所示的电动机速度控制系统工作原理图,完成: (1) 将 a,b 与 c,d 用线连接成负反馈状态; (2) 画出系统方框图。
解 (1)负反馈连接方式为: a d , b c ;
(2)系统方框图如图解 1-1 所示。
1-2 题 1-16 图是仓库大门自动控制系统原理示意图。试说明系统自动控制大门开、闭的 工作原理,并画出系统方框图。
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下
自动控制原理课后习题答案第二章

解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
自动控制原理第二章课后习题答案(免费)

自动控制原理第二章课后习题答案(免费)自动控制原理第二章课后习题答案(免费)离散系统作业注明:*为选做题2-1 试求下列函数的Z 变换(1)()E z L =();n e t a = 解:01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ (2) ();at e t e -= 解:12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值:(1)112();(1)Tz E z z --=-解: 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- (2)2()(0.8)(0.1)z E z z z =--。
解:211(1)()(1)()0(0.8)(0.1)lim lim lim t z z z z f t z E z z z →∞→→-=-==--2-3* 已知()(())E z L e t =,试证明下列关系成立:(1)[()][];n z L a e t E a=证明:()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ (2)()[()];dE z L te t TzT dz=-为采样周期。
证明:11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以:()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 s
部分分式展开 5 1 −4 Y(s) = + + s+3 s+2 s
∴ y (t ) = −4e −3 t + 5e −2t + 1 , t ≥ 0
已知控制系统的微分方程(或微分方程组) B2.9 已知控制系统的微分方程(或微分方程组)为
式中r(t)为输入量,y(t)为输出量, (t)、 (t)和 式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) r(t)为输入量 为输出量 为中间变量, 均为常数。 为中间变量,τ、β、K1和K2均为常数。 试求: a)各系统的传递函数Y(s)/R(s);(b)各系统含 各系统的传递函数Y(s)/R(s) 试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含 有哪些典型环节? 有哪些典型环节?
在图B2.4所示的电路中电压u (t)为输入量 B2.4所示的电路中电压 为输入量, B2.4 在图B2.4所示的电路中电压u1(t)为输入量,试以电 (t)或 (t)作为输出量 分别列写该系统的微分方程。 作为输出量, 压u2(t)或uC2(t)作为输出量,分别列写该系统的微分方程。
B 2.4解: u 2作为输出,应用网络的 复阻抗法: 作为输出, 复阻抗法: Q U 2 (s ) = U 1 (s ) 1 R1 1 C1s + R2 + 1 C 2s R1 + C1s 1 (R 2 + ) C 2s
B2.8 设系统的微分方程为
试用拉氏变换法进行求解。 试用拉氏变换法进行求解。
B 2.8解: 进行拉氏变换 & s 2 Y(s) - (sy(0) + y(0)) + 5sY(s) - 5y(0) + 6Y(s) =
代入初值整理 2s 2 + 12s + 6 Y(s) = 3 s + 5s 2 + 6s
Y
G 1G 5 + G 1G 2G 3G 4 Y(s ) = R(s ) 1 + G 1G 2 H 1 + G 2G 3 H 2 + G 1G 5 H 3 + G 1G 2G 3G 4 H 3 1 + G 1G 2 H 1 + G 2G 3 H 2 E(s ) = R(s ) 1 + G 1G 2 H 1 + G 2G 3 H 2 + G 1G 5 H 3 + G 1G 2G 3G 4 H 3
x3
x2
x1
B2.23(1)解:取积分器的输出 变量为状态变量
& x1 = x 2 & & x 2 = x 3 + x 3 − 5x 2 x = −2x + x − ( 2x + x ) + r &2 2 3 1 & 3
& x1 = x 2 & x 2 = − x 1 − 3 .5 x 2 + x 3 + 0 . 5 r & x 3 = − x + 0 . 5 x 2 + 0 . 5r
j
-1
0
B2.15 已知控制系统的结构图如图 已知控制系统的结构图如图B2.15所示,试应用结 所示, 所示 构图等效变换法求各系统的传递函数。 构图等效变换法求各系统的传递函数。 B2.15解: 解 R(s) G2(s) Y(s) G1(s)
G2(s) H(s)
R(s)
Y(s) G1(s) G2(s) HG2(s)
G1 + G 2 G (s) = 1 + HG 2
B2.17 求图 求图B2.17所示闭环控制系统的传递函数 所示闭环控制系统的传递函数Φ(s)=Y(s)/R(s) 所示闭环控制系统的传递函数 和Φe(s)=E(s)/R(s)。 。
B2.17 解:由梅森公式 : 1 n T = ∑ p k ∆ k , 这里n = 4 ∆ k =1 L 1 = −G 2 H 1 , L 2 = −G 4 H 2 , L 3 = −G 6 H 3 , L 4 = −G 3 G 4G 5 H 4 , L 5 = − G 1G 2 G 3 G 4 G 5 G 6 H 5 , L 6 = −G 7 G 3 G 4 G 5 G 6 H 5 , L 7 = − G 1G 8 G 6 H 5 L 8 = G 8 H 1H 4 , L 9 = G 7 H 1G 8 G 6 H 5 ,
作为输出, 复阻抗法: u c 2作为输出,应用网络的 复阻抗法: (R 2 + Q U1 (s ) − U1 (s )( 1 1 C1s + 1 R1 ) ) = Uc2
1 + R2 + 1 C 2s C1s + R1 1 C1s + 1 R1 )
(R 2 + = U1 (s )(1 − 1
) = Uc2 1 + R2 + 1 C 2s C1s + R1 U (s ) C1 R 1s + 1 ∴ c1 = U 1 (s) R 1 R 2C1C 2s 2 + ( R 1C 2 + R 2C 2 + C1 R 1 )s + 1
U c 1 (s ) C1 R 1s + 1 ∴ = U 1 (s) R 1 R 2C1C 2s 2 + ( R 1C 2 + R 2C 2 + C1 R 1 )s + 1 && & & R 1 R 2C1C 2u c1 + ( R 1C 2 + R 2C 2 + C1 R 1 )u c1 + u c1 = C1 R 1u1 + u1
图B2.4 电路原理图
[T1T2s 2 + (T1 + T2 )s + 1]U1 (s ) = T1T2s 2 + (T1 + T2 + R 1C 2 )s + 1
其中: T2 = R 2C 2 其中: T1 = R 1C1 , && & && & ∴ T1T2u 2 + (T1 + T2 + R 1C 2 )u 2 + u 2 = T1T2u1 + (T1 + T2 )u1 + u1
G2 G3 H2 H3
G5 + G4 G 2G 3
Y
R
E - G1
G 2G 3 1 + G 1G 2 H 1 G 2G 3 1+ H2 1 + G 1G 2 H 1
G5 + G4 G 2G 3
Y
H3 R
G 1G 5 + G 1G 2G 3G 4 1 + G 1G 2 H 1 + G 2G 3 H 2 + G 1G 5 H 3 + G 1G 2G 3G 4 H 3
已知控制系统的结构图,如图B 18所示 要求: 所示。 B2.18 已知控制系统的结构图,如图B2.18所示。要求:(1) 分别应用结构图等效变换法和梅森公式求各闭环系统的传递 函数Y(s)/R(s) E(s)/R(s); Y(s)/R(s)和 欲使图B 18(a) (a)系统的输 函数 Y(s)/R(s) 和 E(s)/R(s);(2) 欲使图 B2.18(a) 系统的输 Y(s)不受扰动D(s)的影响 试问其条件是什么? 不受扰动D(s)的影响, 出Y(s)不受扰动D(s)的影响,试问其条件是什么?
B2.18解 B2.18解: 求各闭环系统的传递函数Y(s)/R(s)和E(s)/R(s) 求各闭环系统的传递函数Y(s)/R(s)和 Y(s)/R(s) H1 R E - G1 G1 G2 H2 H3 G5 D G3 G4 Y
Байду номын сангаас
H1 G2 R E - G1 G1 G2 H2 H3 G5 D(s) G3 G4 Y
P1 = G 1G 2G 3G 4G 5G 6 , P2 = G 7G 3G 4G 5G 6 , P3 = G 1G 8G 6 , P4 = −G 7 H 1G 8G 6 ,
∆ 1 = 1, ∆2 = 1 ∆ 3 = 1 + G 4H 2 , ∆ 4 = 1 + G 4H 2
G 1G 2 G 3 G 4 G 5 G 6 + G 7 G 3 G 4 G 5 G 6 C(s ) / R(s ) = ∆ (G 1G 8G 6 − G 7 H 1G 8G 6 )(1 + G 4 H 2 ) + ∆
对上式求拉氏变换 1 R(s) = s 1 1 2 3s + 2 Y (s ) = + − = 3 s s + 1 s + 2 s + 3 s2 + 2 s 3s + 2 3s + 2 s3 + 3 s2 + 2 s = ∴ G (s ) = 1 s2 + 3 s + 2 s -2 3 (s + 0.6667) = (s + 2) (s + 1)
第二章 部分习题及解答
B2.2
求下列函数的拉氏反变换: 求下列函数的拉氏反变换:
s (s + 1)2(s + 2)
(4)F(s) =
( 4)解: F (s ) = s 2 2 −1 + − = (s + 1) 2 (s + 2) (s + 1) 2 s + 1 s + 2 t≥0
∴ f (t ) = −te − t + 2e − t − 2e − 2 t
G5 R E - G1 1 1 + G 1G 2 H 1
G2 G3 H2 H3
G4
Y
G5 G 2G 3
