精讲通关7.
二建机电精讲7-建筑电气第一篇

二级建造师机电实务精讲讲义7第三章:机电工程施工技术第一节:建筑给水排水与供暖工程施工技术精讲14:压力试验1、管道压力试验宜采用液压试验,试验前编制专项施工方案,经批准后组织实施。
高层建筑管道应先按分区、分段进行试验,合格后再按系统进行整体试验。
2、室内给水系统、室外管网系统管道安装完毕,应进行水压试验。
水压强度试验压力必须符合设计要求,当设计未注明时,各种材质的给水管道系统强度试验压力均为工作压力的1.5倍,但不得小于0.6MPa。
3、室内给水系统、热水供应系统水压试验检验方法:钢管及复合管道在系统试验压力下10min内压力降不大于0.02MPa,然后降至工作压力检查,压力应不降,不渗不漏;塑料管道系统在试验压力下稳压1h压力降不超过0.05MPa,然后在工作压力1.15倍状态下稳压2h,压力降不超过0.03MPa,连接处不得渗漏。
4、室外给水钢管、铸铁管在系统试验压力下10min内压力降不大于0.05MPa,然后降至工作压力检查,压力应保持不变,不渗不漏;塑料管道系统在试验压力下稳压1h压力降不超过0.05MPa,然后降至工作压力进行检查,压力应保持不变,不渗不漏。
5、供暖系统(热水供应系统)安装完毕,管道保温之前应进行水压试验。
试验压力应符合设计要求。
当设计未注明时,水压试验检验方法:①蒸汽、热水供暖系统,应以系统顶点工作压力加0.1MPa做水压试验,同时在系统顶点的试验压力不小于0.3MPa。
②高温热水供暖系统,试验压力应为系统顶点工作压力加0.4MPa。
③使用塑料管及复合管的热水供暖系统,应以系统顶点工作压力加0.2MPa做水压试验,同时在系统顶点的试验压力不小于0.4MPa。
检验方法:使用钢管及复合管的供暖系统应在试验压力下10min内压力降不大于0.02MPa,降至工作压力后检查,不渗、不漏;使用塑料管的供暖系统应在试验压力下1h内压力降不大于0.05MPa,然后降压至工作压力的1.15倍,稳压2h,压力降不大于0.03MPa,同时各连接处不渗、不漏。
Uint 7 精讲知识点

Uint 7 Where would you like to visit?第一课时Section A一,词汇1.tire (动词)使···疲惫tiring(形容词)累人的,引起疲劳的tired(形容词)感到疲倦的2. education(名词)教育educational(形容词)有教育意义的3. peaceful(形容词)和平的peace(名词)和平;平静4. thrilling(形容词)令人震颤的thrill(动词)使激动,使震颤5. trek(动词)长途跋涉trek(名词)长途跋涉二:短语归纳1.take it easy 从容2.some day/one day 某一天3.somewhere relaxing 令人放松的某个地方4.for example 举例5.in general 一般来说三:句型归纳1.Where do you like to go on vacation?你想要去哪里度假?2.I hope to go to France some day.我希望有一天能去法国。
3.I like the places where the weather is always warm.我喜欢气候总是很暖和的地方。
三:语法would like的用法1.would like后面可直接跟名词作宾语,即would like sth。
2.想要某人做某事:would like sb to do sth。
3.某人想要做某事,sb would like to do sth。
4.某人不想做某事,通常是否定不定式:sb would like not todo sth。
5.含would like的陈述句变成一般疑问句时,需要把would提前。
第二课时Section B & Self check二,词汇1. east(名词)东部eastern(名词)东部的2. outdoor(形容词)户外的outdoors(副词)在户外3. suggestion(名词)建议suggest(动词)建议4. crowd(动词)拥挤crowded(形容词)拥挤的5. relaxing(形容词)令人放松的relax(动词)放松6. exciting(形容词) 令人兴奋的excited(形容词)感到兴奋的短语归纳1. somewhere warm 暖和的地方2. provide sb with sth 给某人提供某物3. in the eastern China 在中国东部4. outdoor activities 户外活动5. need to do sth 需要做某事三,句型归纳1. I would like to go somewhere warm.我想要去暖和的地方。
小学六年级奥数讲义之精讲精练第7讲 转化单位“1”(二)含答案

第7讲 转化单位“1”(二)一、知识要点我们必须重视转化训练。
通过转化训练,既可理解数量关系的实质,又可拓展我们的解题思路,提高我们的思维能力。
二、精讲精练【例题1】甲数是乙数的32,乙数是丙数的43,甲、乙、丙的和是216,甲、乙、丙各是多少?练习1:下面各题怎样计算简便就怎样计算:1、甲数是乙数的65,乙数是丙数的43,甲、乙、丙三个数的和是152,甲、乙、丙三个数各是多少?2、橘子的千克数是苹果的32,香蕉的千克数是橘子的21,香蕉和苹果共有220千克,橘子有多少千克?【例题2】红、黄、蓝气球共有62只,其中红气球的53等于黄气球的32,蓝气球有24只,红气球和黄气球各有多少只?练习2:1、甲数的32等于乙数的65,甲、乙两数的和是162,甲、乙两数各是多少?2、今年8月份,甲所得的奖金比乙少200元,甲得的奖金的32正好是乙得奖金的74,甲、乙两人各得奖金多少元?【例题3】已知甲校学生数是乙校学生数的52,甲校的女生数是甲校学生数的103,乙校的男生数是乙校学生数的5021,那么两校女生总数占两校学生总数的几分之几?练习3:1、在一座城市中,中学生数是居民的51,大学生是中学生数的41,那么占大学生总数的2/5的理工科大学生是居民数的几分之几?2、某人在一次选举中,需43的选票才能当选,计算32的选票后,他得到的选票已达到当选票数的65,他还要得到剩下选票的几分之几才能当选?【例题4】仓库里的大米和面粉共有2000袋。
大米运走52,面粉运作101后,仓库里剩下大米和面粉正好相等。
原来大米和面粉各有多少袋?练习4:1、甲、乙两人各准备加工零件若干个,当甲完成自己的32、乙完成自己的41时,两人所剩零件数量相等,已知甲比乙多做了70个,甲、乙两人各准备加工多少个零件?2、一批水果四天卖完。
第一天卖出180千克,第二天卖出余下的72,第三、四天共卖出这批水果的一半,这批水果有多少千克?【例题5】400名学生参加植树活动,计划每个男生植树20棵,每个女生植树15棵。
【中考备战】2014届中考物理(全国通用)总复习精讲:第7讲 透镜及其应用

实像 填“实像”或“虚像”).这个像再被目镜放大 _____(
一次,我们就可以看到肉眼看不见的小物体了. 8.在望远镜中,物镜的作用是使远处的物体在焦点附 放大 镜,用来把 实 像,目镜的作用相当于一个_____ 近成___
这个像放大.
考点一
透镜
命题点: (1) 透镜和种类; (2) 凸透镜对光线的作用; (3)凹透镜对光线的作用. 例 1(2013· 济宁 ) 下图中画出了光线通过透镜(图中未
的提示进行了操作,终于看到了“缩小”的花朵.关于
小亮看到“放大”花朵后的操作及他看到的“缩小”
花朵,下列说法正确的是(
)
A. 小亮向靠近花朵的方向移动放大镜,看到的是花朵
的正立缩小虚像,像的位置在放大镜与花朵之间
B. 小亮向靠近花朵的方向移动放大镜,看到的是花朵 的倒立缩小实像,像的位置在放大镜与小亮眼睛之间 C. 小亮向远离花朵的方向移动放大镜,看到的是花朵 的正立缩小虚像,像的位置在放大镜与花朵之间
相同条件下,镜头的焦距越大,凸透镜越薄,所成的
像越不容易变形,所以为了使像更大一些,应该利用
长焦距镜头.
答案:(1)凸透镜 (2)上 (3)a d d (4)较大
例4(2013· 杭州)将点燃的蜡烛放在一凸透镜前 1.5倍焦
距的地方,当它向与它同侧的距离透镜3倍焦距的地方
移动时,它所成的像( A.变大 B.变小 C.先变小后变大 )
D.与蜡烛之间的距离变小
解析:本题考查凸透镜成像规律的应用 .凸透镜成实像
时,遵循这样的规律:“物近像远像变大,物远像近
像变小”.当蜡烛从1.5倍焦距的地方向与它同侧的距离 透镜3倍焦距的地方移动时,物距变大,所以像变近变 小.故选B. 答案:B
2023-2024年小学数学五年级上册高频考点精讲精练 第7讲 数学广角—植树问题(人教版含解析)
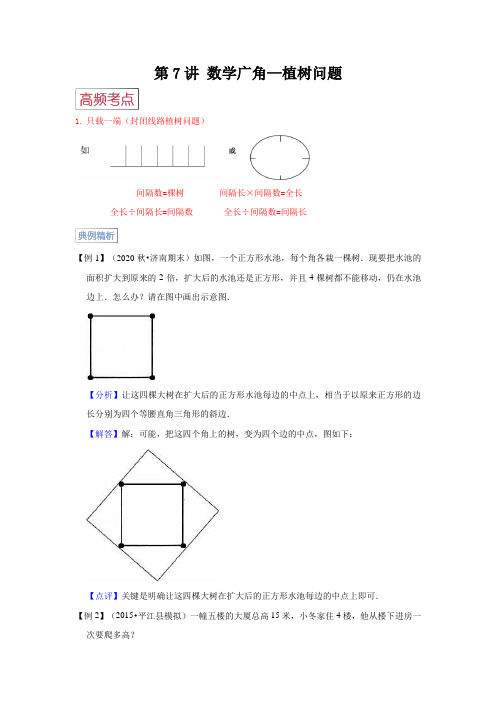
第7讲数学广角—植树问题1.只载一端(封闭线路植树问题)间隔数=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长【例1】(2020秋•济南期末)如图,一个正方形水池,每个角各栽一棵树.现要把水池的面积扩大到原来的2倍,扩大后的水池还是正方形,并且4棵树都不能移动,仍在水池边上.怎么办?请在图中画出示意图.【分析】让这四棵大树在扩大后的正方形水池每边的中点上,相当于以原来正方形的边长分别为四个等腰直角三角形的斜边.【解答】解:可能,把这四个角上的树,变为四个边的中点,图如下:【点评】关键是明确让这四棵大树在扩大后的正方形水池每边的中点上即可.【例2】(2015•平江县模拟)一幢五楼的大厦总高15米,小冬家住4楼,他从楼下进房一次要爬多高?【分析】五层楼总高15米,那么每层的高度是15÷5=3米,小冬家住4楼,他从楼下进房一次要爬4﹣1=3个楼间距,然后用3乘每层的高度即可解决问题.【解答】解:15÷5×(4﹣1)=3×3=9(米)答:他从楼下进房一次要爬9米高.【点评】本题属于植树问题的实际应用,关键是明确:间隔数=层数﹣1.【例3】(2014春•杭州期末)为了保护公园里的一棵千年古树,园林局决定为它做一个圆形防护栏.如果护栏有10个间隔,一共需要打多少根木桩?【分析】根据植树的知识知道,在圆形的周围植树,间隔数就是植树的棵数,而本题中的防护栏是个圆形的,护栏有10个间隔,所以即可得出需要打木桩的根数.【解答】解:因为在圆形的防护栏周围打木桩,有几个间隔就必须打几个木桩,所以如果护栏有10个间隔,一共需要打10根木桩;答:一共需要打10根木桩.【点评】此题属于在圆形的物体周围植树的问题,即在圆形的周围植树,间隔数就是植树的棵数.2.两端都载:如图:间隔数+1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔长+1=棵数全长÷间隔数=间隔长全长÷(棵树-1)=间隔长【例4】(2015•平江县模拟)在一段路的路边每隔20米栽一棵树,包括这段路两端在内栽10棵树,这段路长多少米?【分析】由于从一端到另一端一共栽了10棵树,共有间隔数为:10﹣1=9个;又由于间距是20米,根据总距离=间距×间隔数可以求出这条路的长度,列式为:20×9=180(米);据此解答.【解答】解:根据分析可得,20×(10﹣1)=20×9=180(米);答:这段路长180米.【点评】本题考查了植树问题,知识点是:栽树的棵数=间隔数+1(两端都栽),总距离=间距×间隔数.【例5】(2015春•长春校级期末)工人叔叔要在马路的一侧安装路灯,从头开始每隔4米安一个,共安装了30个,这条路长米.【分析】因为间隔数=路灯的盏数﹣1,所以先求出马路边路灯的间隔数,再乘4即可.【解答】解:(30﹣1)×4=29×4=116(米)答:这条路长116米.故答案为:116.【点评】本题主要考查了间隔数=树的棵数﹣1,再根据基本的数量关系解决问题.【例6】(2015春•务川县期中)小朋友们在路的一边植树,先植一棵树,以后每隔3米植一棵,已经植了9棵,问第一棵和第九棵树相距多少米?【分析】此题属于植树问题中的两端都要栽的情况:间隔数=植树棵数﹣1,据此可得一共有9﹣1=8个间隔,再乘每个间隔的长度3米,即可得出第一棵和第九棵树相距多少米.【解答】解:(9﹣1)×3,=8×3,=24(米);答:第一棵和第九棵树相距24米.【点评】植树问题中:两端都要栽时,间隔数=植树棵数﹣1.3.两端都不载如图:间隔数-1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长全长÷间隔长-1=棵数全长÷(棵树+1)=间隔长【例7】(2016春•魏县校级月考)某木工把一根长4米的圆柱形木料锯成80厘米的小段,需40分钟;如果改锯成50厘米的小段,需要多少时间?【分析】根据题意,先求出长4米的圆柱形木料锯成80厘米的小段需要锯多少次,再求出每锯一次所需要的时间,即可求出锯成50厘米的小段所需要的时间.【解答】解:4米=400厘米,400÷80﹣1=4(次),40÷4=10(分钟),400÷50﹣1=7(次),10×7=70(分钟),答:需要70分钟.【点评】解答此题的关键是,要知道锯木料的次数比锯成的段数少1,再根据题中的数量关系即可解答.【例8】(2015春•永胜县月考)一根钢管,把它锯成7段,需要18分钟,照这样计算,如果锯成16段需要多少分钟?【分析】锯两段只需要锯1次,所以锯成7段,需要锯(7﹣1)次,用18分钟除以这个时间,就是锯一次用的时间;锯16段只需要锯16﹣1=15次,用锯一次用的时间乘上15就是锯成9段需要的时间.【解答】解:18÷(7﹣1)=18÷6=3(分钟)3×(16﹣1)=3×15=45(分钟)答:如果锯成16段需要45分钟.【点评】本题关键是要理解锯1次就可以锯成2段,存在这个关系:锯成的段数=锯的次数+1.【例9】(2013秋•即墨市期末)崂山举行登山大赛,组委会在长达845米的山路中,每隔65米设置一个服务站(起点和终点不设).共设多少个服务站?【分析】先用全程除以间隔的长度,求出一共有多少段,再用段数减去1就是需要设服务站的数量.【解答】解:845÷65﹣1=13﹣1=12(个)答:共设12个服务站.【点评】本题属于植树问题中的两段都不栽的情况:植树的棵数=间隔数﹣1.一.选择题(共8小题)1.(2021秋•盐都区期末)把一根电缆截成2段需要4分钟,如果截成5段需要()分钟.A.10B.20C.162.(2020秋•黔西南州期末)一根绳子长15米,剪了三刀剪成()段.A.3B.4C.53.(2019秋•东海县期中)大上海国际公寓步行街上两边张灯结彩,从这头到那头每隔4米挂一个红灯笼(两端都挂),步行街全长600米,一共挂了多少个红灯笼?()A.150B.151C.302D.3004.(2021秋•巴马县期末)一根钢筋锯成6段,共需30分钟,平均锯一次需要()分钟.A.5B.7C.6D.45.(2015秋•利川市月考)圆形滑冰场的一周全长180m.在这个滑冰场的一周每隔12m安装一盏灯,一共要安装()盏灯.A.14B.15C.166.(2021秋•老城区期末)公园内一条林荫大道全长800米,在它的两侧从头到尾每隔20米放一个垃圾桶,一共需要()个垃圾桶。
高中数学选择性必修三 精讲精炼 7 离散型随机变量的字特征(精练)(无答案)

7.3 离散型随机变量的数字特征(精练)【题组一 均值方差的性质(小题】1.(2021·全国·高二课时练习)已知随机变量ξ的分布列为则()54E ξ+等于( ) A .2.2 B .2.3C .11D .132.(2021·安徽·定远县育才学校高二期末(理))已知随机变量X 的分布列如下:若随机变量31X η=-,则()E η为( ) A .42. B .189. C .53.D .随m 变化而变化3.(2021·全国·高二课时练习)将3个球(形状相同,编号不同)随机地投入编号为1、2、3、4的4个盒子,以ξ表示其中至少有一个球的盒子的最小号码(3ξ=表示第1号,第2号盒子是空的,第3个盒子至少1个球),则()E ξ、(21)E ξ+分别等于( ) A .2516、258B .2516、338 C .32、3D .32、44(2021·全国·高二单元测试)随机变量X 的概率分布为()()()1,2,31aP X n n n n ===+,其中a 是常数,则()E aX =( )A .3881B .139C .152243D .52275.(2021·全国·高二课时练习)若p 为非负实数,随机变量ξ的分布列为则()E ξ的最大值为( ) A .1 B .32C .23D .26.(2021·黑龙江·哈尔滨市第六中学校高二月考)已知一组数据123456,,,,,x x x x x x 的方差是1,那么另一组数据121x -,221x -,321x -,421x -,521x -,621x -的方差是( ) A .1 B .2 C .3 D .47.(2021·全国·高二课时练习)设随机变量X 的方差()1D X =,则()21D X +的值为( ) A .2 B .3 C .4 D .58.(2021·全国·高二课时练习)已知A 1,A 2为两所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为12,该同学一旦通过某所高校的考试,就不再参加其他高校的考试,设该同学通过考试的高校个数为随机变量X ,则D (X )=( ) A .316B .54C .2564D .19649(2021·全国·高二课时练习)若随机变量X 的分布列为P (X =m )=13,P (X =n )=a ,若E (X )=2,则D (X )的最小值等于( ) A .0 B .1 C .4 D .210.(2021·全国·高二课时练习)已知随机变量X 满足D (X )=2,则D (3X +2)=( )A .6B .8C .18D .2011.(2021·全国·高二课时练习)(多选)下列说法正确的有( ) A .离散型随机变量X 的期望()E X 反映了X 取值的平均水平 B .离散型随机变量X 的期望()E X 反映了X 取值的波动水平 C .离散型随机变量X 的方差()D X 反映了X 取值的平均水平 D .离散型随机变量X 的方差()D X 反映了X 取值的波动水平12.(2021·全国·高二学业考试)(多选)已知随机变量ξ满足()103P ξ==,()1P x ξ==,()223P x ξ==-,若203x <<,则( ) A .()E ξ有最大值 B .()E ξ无最小值 C .()D ξ有最大值 D .()D ξ无最小值13.(2021·全国·高二课时练习)(多选)若随机变量X 服从两点分布,且()104P X ==,则( ) A .()()1P X E X == B .()413E X += C .()316D X = D .()414D X +=14.(2021·江苏江都·高二月考)(多选)设随机变量X 的分布列为,其中0ab ≠,则下列说法正确的是( )A .1a b +=B .()E X b =C .()D X 随b 的增大先增大后减小 D .()D X 有最小值15.(2021·福建·浦城县第三中学高二期中)(多选)已知随机变量X 满足(23)7E X +=,(23)16D X +=,则下列选项错误的是( ) A .()72E X =,()132D X = B .()2E X =,()4D X = C .()2E X =,()8D X = D .7()4E X =,()8D X =【题组二 均值方差的应用(解答题】1(2021·全国·高二课时练习)如图所示,是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.(1)求直方图中x 的值;(2)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X 的分布列、数学期望与方差.2.(2021·全国·高二课时练习)中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,是国家重要的空间信息基础设施,我国北斗卫星导航系统不仅对国防安全意义重大,而且在民用领域的精准化应用也越来越广泛.如图是40个城市北斗卫星导航系统与位置服务产业的产值(单位:万元)的频率分布直方图:(1)根据频率分布直方图,求产值小于500万元的城市个数;(2)在上述40个城市中任选2个,设Y 为产值小于500万元的城市个数,求Y 的分布列、期望和方差.3.(2021·全国·高二课时练习)袋中有20个除标号不同外其他完全相同的球,其中标号为0的有10个,标号为n 的有()1,2,3,4n n =个.现从袋中任取一球,ξ表示所取球的标号.求ξ的分布列、数学期望、方差和标准差.4.(2021·全国·高二课时练习)某大学志愿者协会有10名同学,成员构成如下表,表中部分数据不清楚,只知道从这10名同学中随机抽取1名同学,该名同学的专业为数学的概率为25.现从这10名同学中随机选取3名同学参加社会公益活动(每名同学被选到的可能性相同). (1)求m ,n 的值;(2)求选出的3名同学恰为专业互不相同的男生的概率;(3)设ξ为选出的3名同学中是女生或专业为数学的人数,求随机变量ξ的分布列、均值及方差.5.(2021·全国·高二课时练习)某市教育局为了了解高三学生的体育达标情况,随机抽取了100名高三学生的体育成绩进行调研,按成绩(单位:分)分组:第1组[)75,80,第2组[)80,85,第3组[)85,90,第4组[)90,95,第5组[]95,100,得到的频率分布直方图如图所示.现要在成绩较高的第3,4,5组中用分层抽样的方法抽取6名学生进行复查.(1)已知学生甲和学生乙的成绩均在第4组,求学生甲和学生乙至少有1人进行复查的概率;(2)从抽取到的6名学生中随机抽取3名学生接受篮球项目的考核,设第3组中有ξ名学生接受篮球项目的考核,求ξ的分布列、数学期望和方差..6.(2021·全国·高二课时练习)已知在某公司年会上,甲、乙等6人分别要进行节目表演,若采用抽签的方式确定每个人的演出顺序(序号:为1,2,,6),求:(1)甲、乙两人的演出序号至少有一个为奇数的概率;(2)甲、乙两人之间的演出节目的个数ξ的分布列、数学期望与方差.【题组三均值方差做决策】1.(2021·江苏·南京市人民中学高二月考)某地已知6名疑似病人中有1人感染病毒,需要通过血液检测确定该感染人员,血清检测结果呈阳性的即为感染人员,呈阴性表示没感染,拟采用两种方案检测:方案甲;将这6名疑似病人血清逐个检测,直到能确定感染人员为止;方案乙:将这6名疑似病人随机分成2组,每组3人.先将其中一组的血清混在一起检测,若结果为阳性,则表示感染人员在该组中,然后再对该组中每份血清逐个检测,直到能确定感染人员为止;若结果为阴性,则对另一组中每份血清逐个检测,直到能确定感染人员为止.(1)求甲方案所通检测次数X和乙方案所需检测次数Y的概率分布;(2)如果每次检测的费用相同,请预测哪种方案检测总费用较少?并说明理由.2.(2021·全国·高二课时练习)某商店欲购进某种食品(保质期为两天),且该商店每两天购进该食品一次(购进时,该食品是刚生产的).根据市场调查,该食品每份进价8元,售价12元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响.为了解市场的需求情况,现统计该食品在本地区100天的销售量,如下表:(1)根据该食品在本地区100天的销售量统计表,记两天一共销售该食品的份数为ξ,求ξ的分布列与数学期望;(视样本频率为概率)(2)以两天内该食品所获得的利润的数学期望为决策依据,若该商店计划一次性购进32份或33份该食品,试判断哪一种获得的利润更高.3.(2021·全国·高二课时练习)某产品按行业生产标准分成8个等级,等级系数X 依次为1,2,…,8,其中5X ≥为标准A ,35X ≤<为标准B .已知甲厂执行标准A 生产该产品,产品的售价为6元/件;乙厂执行标准B 生产该产品,产品的售价为4元/件.假定甲、乙两厂的产品都符合相应的执行标准. (1)已知甲厂产品的等级系数1X 的分布列如下表所示,且1X 的数学期望()16E X =,求a ,b 的值.(2)为分析乙厂产品的等级系数2X,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:3 5 3 3 8 5 5 6 34 6 3 4 7 53 4 8 5 3 8 3 4 3 4 4 7 5 6 7用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数2X的数学期望.(3)在(1)(2)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?并说明理由.注:①产品的“性价比” 产品的等级系数的数学期望产品的售价;②“性价比”大的产品更具可购买性.4.(2021·全国·高二课时练习)1933年7月11日,中华苏维埃共和国临时中央政府将8月1日作为中国工农红军成立纪念日.中华人民共和国成立后,将此纪念日改称为中国人民解放军建军节.为庆祝建军节,某校举行“强国强军”知识竞赛.该校某班经过层层筛选,还有最后一个参赛名额要在A,B两名学生中产生,该班班委设计了一个测试方案:A,B两名学生各自从6个问题中随机抽取3个问题作答,根据答题情况确定参赛学生.已知这6个问题中,学生A能正确回答其中的4个问题,而学生B能正确回答每个问题的概率均为23,A,B两名学生对每个问题回答的正确与否都是相互独立的.设学生A答对题数为X,学生B答对题数为Y,若让你投票选择参赛选手,你会选择哪名学生?请说明理由.5.(2021·黑龙江·哈尔滨市第六中学校高二月考)在某单位的职工食堂中,食堂每天以2元/个的价格从面包店购进面包,然后以4元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x (单位:个,60110x ≤≤)表示面包的需求量,T (单位:元)表示利润.(1)求T 关于x 的函数解析式;(2)根据直方图估计利润T 不少于120元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量[60,70)x ∈,则取65x =,且65x =的概率等于需求量落入[60,70)的频率),求T 的分布列和数学期望.6.(2021·全国·高二课时练习)某牛奶店每天以每盒3元的价格从牛奶厂购进若干盒鲜牛奶,然后以每盒5元的价格出售,如果当天卖不完,剩下的牛奶作为垃圾回收处理.(1)若牛奶店一天购进50盒鲜牛奶,求当天的利润y (单位:元)关于当天需求量n (单位:盒,n *∈N )的函数解析式;(2)牛奶店老板记录了某100天鲜牛奶的日需求量(单位:盒),整理得下表:以这100天记录的各需求量的频率作为各需求量发生的概率.①若牛奶店一天购进50盒鲜牛奶,X表示当天的利润(单位:元),求X的分布列及均值;②若牛奶店计划一天购进50盒或51盒鲜牛奶,从统计学角度分析,你认为应购进50盒还是51盒?请说明理由.7.(2021·全国·高二课时练习)根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01.该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:方案1:运走设备,搬运费为3800元.方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水.方案3:不采取措施,希望不发生洪水.如果你是工地的负责人,你会采用哪种方案?说明理由.8.(2021·全国·高二课时练习)已知5只动物中有1只患有某种疾病,需要通过血液化验来确定患病的动物,血液化验结果呈阳性的为患病动物.下面是两种化验方案:方案甲:将各动物的血液逐个化验,直到查出患病动物为止.方案乙:先取3只动物的血液进行混合,然后检查,若呈阳性,对这3只动物的血液再逐个化验,直到查出患病动物;若不呈阳性,则检查剩下的2只动物中1只动物的血液.分析哪种化验方案更好.。
2020版高考数学浙江专用新精准大一轮精讲通用版:第九章第7讲抛物线含解析

[基础达标]1.已知点A (-2,3)在抛物线C :y 2=2px (p >0)的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .-43B .-1C .-34D .-12解析:选C.由已知,得准线方程为x =-2,所以F 的坐标为(2,0).又A (-2,3),所以直线AF 的斜率为k =3-0-2-2=-34.2.已知抛物线C 1:x 2=2py (p >0)的准线与抛物线C 2:x 2=-2py (p >0)交于A ,B 两点,C 1的焦点为F ,若△F AB 的面积等于1,则C 1的方程是( )A .x 2=2yB .x 2=2yC .x 2=yD .x 2=22y 解析:选A.由题意得,F ⎝⎛⎭⎫0,p 2,不妨设A ⎝⎛⎭⎫p ,-p 2,B (-p ,-p 2),所以S △F AB =12·2p ·p =1,则p =1,即抛物线C 1的方程是x 2=2y ,故选A.3.(2019·丽水调研)已知等边△ABF 的顶点F 是抛物线C :y 2=2px (p >0)的焦点,顶点B 在抛物线的准线l 上且AB ⊥l ,则点A 的位置( )A .在C 开口内B .在C 上 C .在C 开口外D .与p 值有关解析:选B.设B ⎝⎛⎭⎫-p 2,m ,由已知有AB 中点的横坐标为p2,则A ⎝⎛⎭⎫3p 2,m ,△ABF 是边长|AB |=2p 的等边三角形,即|AF |=⎝⎛⎭⎫3p 2-p 22+m 2=2p ,所以p 2+m 2=4p 2,所以m =±3p ,所以A ⎝⎛⎭⎫3p 2,±3p ,代入y 2=2px 中,得点A 在抛物线C 上,故选B.4.已知抛物线y 2=2px (p >0)的焦点为F ,点P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3)在抛物线上,且2x 2=x 1+x 3,则有( )A .|FP 1|+|FP 2|=|FP 3|B .|FP 1|2+|FP 2|2=|FP 3|2C .|FP 1|+|FP 3|=2|FP 2|D .|FP 1|·|FP 3|=|FP 2|2解析:选C.根据抛物线的定义知|FP 1|=x 1+p 2,|FP 2|=x 2+p 2,|FP 3|=x 3+p 2,所以|FP 1|+|FP 3|=⎝⎛⎭⎫x 1+p 2+⎝⎛⎭⎫x 3+p 2=(x 1+x 3)+p =2x 2+p =2⎝⎛⎭⎫x 2+p2=2|FP 2|. 5. 抛物线y 2=4x 的焦点为F ,准线为l ,经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ,AK⊥l ,垂足为K ,则△AKF 的面积是( )A .4B .3 3C .4 3D .8解析:选C.F (1,0),直线AF :y =3(x -1),代入y 2=4x 得3x 2-10x +3=0, 解得x =3或x =13.由于点A 在x 轴上方且直线的斜率为3,所以其坐标为(3,23).因为|AF |=|AK |=3+1=4,AF 的斜率为3,即倾斜角为60°,所以∠KAF =60°, 所以△AKF 为等边三角形, 所以△AKF 的面积为34×42=4 3. 6.(2019·杭州市高考模拟)设倾斜角为α的直线l 经过抛物线Г:y 2=2px (p >0)的焦点F ,与抛物线Г交于A ,B 两点,设点A 在x 轴上方,点B 在x 轴下方.若|AF ||BF |=m ,则cos α的值为( )A .m -1m +1B .m m +1C .m -1mD .2m m +1解析:选A.设抛物线y 2=2px (p >0)的准线为l :x =-p2.如图所示,分别过点A ,B 作AM ⊥l ,BN ⊥l ,垂足分别为M ,N . 在三角形ABC 中,∠BAC 等于直线AB 的倾斜角α, 由|AF ||BF |=m ,|AF |=m |BF |,|AB |=|AF |+|BF |=(m +1)|BF |, 根据抛物线的定义得:|AM |=|AF |=m |BF |,|BN |=|BF |, 所以|AC |=|AM |-|MC |=m |BF |-|BF |=(m -1)|BF |,在直角三角形ABC 中,cos α=cos ∠BAC =|AC ||AB |=(m -1)|BF |(m +1)|BF |=m -1m +1,故选A.7.已知抛物线y 2=2px (p >0)上一点M 到焦点F 的距离等于2p ,则直线MF 的斜率为________.解析:设M (x M ,y M ),由抛物线定义可得|MF |=x M +p 2=2p ,解得x M =3p2,代入抛物线方程可得y M =±3p ,则直线MF 的斜率为y M x M -p 2=±3pp =±3.答案:±38.已知抛物线C 的方程为y 2=2px (p >0),○·M 的方程为x 2+y 2+8x +12=0,如果抛物线C 的准线与○·M 相切,那么p 的值为________.解析:将○·M 的方程化为标准方程:(x +4)2+y 2=4,圆心坐标为(-4,0),半径r =2,又因为抛物线的准线方程为x =-p2,所以⎪⎪⎪⎪4-p 2=2,p =12或4. 答案:12或49.若点P 在抛物线y 2=x 上,点Q 在圆(x -3)2+y 2=1上,则|PQ |的最小值为________. 解析:由题意得抛物线与圆不相交, 且圆的圆心为A (3,0),则|PQ |≥|P A |-|AQ |=|P A |-1,当且仅当P ,Q ,A 三点共线时取等号, 所以当|P A |取得最小值时,|PQ |最小. 设P (x 0,y 0),则y 20=x 0,|P A |=(x 0-3)2+y 20=x 20-6x 0+9+x 0=⎝⎛⎭⎫x 0-522+114,当且仅当x 0=52时,|P A |取得最小值112,此时|PQ |取得最小值112-1. 答案:112-1 10.(2019·浙江省名校协作体高三联考)抛物线顶点在原点,焦点在x 轴上,且过点(4,4),焦点为F . (1)求抛物线的焦点坐标和标准方程;(2)P 是抛物线上一动点,M 是PF 的中点,求M 的轨迹方程.解:(1)抛物线顶点在原点,焦点在x 轴上,且过点(4,4),设抛物线解析式为y 2=2px ,把(4,4)代入,得16=2×4p ,所以p =2,所以抛物线标准方程为y 2=4x ,焦点坐标为F (1,0).(2)设M (x ,y ),P (x 0,y 0),F (1,0),M 是PF 的中点,则x 0+1=2x ,0+y 0=2y , 所以x 0=2x -1,y 0=2y ,因为P 是抛物线上一动点,所以y 20=4x 0, 所以(2y )2=4(2x -1),化简得y 2=2x -1. 所以M 的轨迹方程为y 2=2x -1.11.已知抛物线y 2=2px (p >0)的焦点为F ,A 是抛物线上横坐标为4,且位于x 轴上方的点,A 到抛物线准线的距离等于5,过A 作AB 垂直于y 轴,垂足为B ,OB 的中点为M .(1)求抛物线的方程;(2)若过M 作MN ⊥F A ,垂足为N ,求点N 的坐标.解:(1)抛物线y 2=2px 的准线为x =-p2,于是4+p2=5,所以p =2.所以抛物线方程为y 2=4x . (2)因为点A 的坐标是(4,4), 由题意得B (0,4),M (0,2). 又因为F (1,0),所以k F A =43,因为MN ⊥F A ,所以k MN =-34.又F A 的方程为y =43(x -1),①MN 的方程为y -2=-34x ,②联立①②,解得x =85,y =45,所以点N 的坐标为⎝⎛⎭⎫85,45.[能力提升] 1.(2019·台州书生中学月考)抛物线y 2=2px (p >0)的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足∠AFB =120°,过AB 的中点M 作抛物线准线l 的垂线MN ,垂足为N ,则|MN ||AB |的最大值为( )A .33B .1C .233D .2解析:选A.过A 、B 分别作抛物线准线的垂线,垂足分别为A 1,B 1,连接AF 、BF ,由抛物线的定义知|MN |=12(|AA 1|+|BB 1|)=12(|AF |+|BF |),在△AFB 中,|AB |2=|AF |2+|BF |2-2|AF ||BF |·cos 120°=|AF |2+|BF |2+|AF ||BF |.所以⎝⎛⎭⎫|MN ||AB |2=14·|AF |2+|BF |2+2|AF ||BF ||AF |2+|BF |2+|AF ||BF | =14⎝⎛⎭⎫1+|AF ||BF ||AF |2+|BF |2+|AF ||BF | =14⎝ ⎛⎭⎪⎫1+1|AF ||BF |+|BF ||AF |+1≤14×⎝⎛⎭⎫1+12+1=13, 当且仅当|AF |=|BF |时取等号,所以|MN ||AB |的最大值为33.2.已知F 为抛物线y 2=x 的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,OA →·OB →=2(其中O 为坐标原点),则△ABO 与△AFO 面积之和的最小值是( ) A .2B .3C .1728D .10解析:选B.设A (x 1,x 1),B (x 2,-x 2), 则S △AFO =12×14x 1=18x 1.由OA →·OB →=2得x 1x 2-x 1x 2=2, 即x 1x 2-x 1x 2-2=0,解得x 1x 2=4, 所以(|OA →|·|OB →|)2=(x 21+x 1)(x 22+x 2)=x 21x 22+x 1x 2·(x 1+x 2)+x 1x 2 =20+4(x 1+x 2),因为cos ∠AOB =OA →·OB→|OA →||OB →|,所以sin ∠AOB =1-cos 2∠AOB=1-⎝⎛⎭⎪⎪⎫OA →·OB →|OA →||OB →|2.所以S △AOB =12|OA →||OB →|sin ∠AOB=12|OA →||OB →|1-⎝⎛⎭⎪⎪⎫OA →·OB →|OA →||OB →|2=12 (|OA →||OB →|)2-(OA →·OB →)2=1216+4(x 1+x 2)=4+(x 1+x 2) =x 1+4+4x 1=x 1+2x 1,所以S △ABO +S △AFO =98x 1+2x 1≥298x 1·2x 1=3,当98x 1=2x 1,即x 1=169时等号成立. 3.如图,正方形ABCD 和正方形DEFG 的边长分别为a ,b (a <b ),原点O 为AD 的中点,抛物线y 2=2px (p >0)经过C ,F 两点,则ba=________.解析:依题知C ⎝⎛⎭⎫a 2,-a ,F ⎝⎛⎭⎫a 2+b ,b ,因为点C ,F 在抛物线上,所以⎩⎪⎨⎪⎧a 2=pa ,b 2=p (a +2b ),两式相除得⎝⎛⎭⎫b a 2-2b a -1=0,解得b a =1+2或ba=1-2(舍). 答案:1+ 2 4.(2019·台州市高考模拟)如图,过抛物线y 2=4x 的焦点F 作直线与抛物线及其准线分别交于A ,B ,C 三点,若FC →=4FB →,则|AB →|=________.解析:分别过A ,B 作准线的垂线,垂足分别为A 1,B 1,则DF =p =2,由抛物线的定义可知FB =BB 1,AF =AA 1, 因为FC →=4FB →,所以DF BB 1=FC BC =43,所以FB =BB 1=32.所以FC =4FB =6, 所以cos ∠DFC =DF FC =13,所以cos ∠A 1AC =AA 1AC =AF AF +6=13,解得AF =3,所以AB =AF +BF =3+32=92.答案:925.已知抛物线x 2=4y 的焦点为F ,P 为该抛物线在第一象限内的图象上的一个动点. (1)当|PF |=2时,求点P 的坐标;(2)求点P 到直线y =x -10的距离的最小值.解:(1)由抛物线x 2=4y 的焦点为F ,P 为该抛物线在第一象限内的图象上的一个动点, 故设P ⎝⎛⎭⎫a ,a24(a >0), 因为|PF |=2,结合抛物线的定义得a 24+1=2,所以a =2,所以点P 的坐标为(2,1). (2)设点P 的坐标为P ⎝⎛⎭⎫a ,a24(a >0), 则点P 到直线y =x -10的距离为⎪⎪⎪⎪a -a 24-102=⎪⎪⎪⎪a 24-a +102.因为a 24-a +10=14(a -2)2+9,所以当a =2时,a24-a +10取得最小值9,故点P 到直线y =x -10的距离的最小值为922.6.(2019·杭州宁波二市三校联考)已知A ,B ,C 是抛物线y 2=2px (p >0)上三个不同的点,且AB ⊥AC .(1)若A (1,2),B (4,-4),求点C 的坐标;(2)若抛物线上存在点D ,使得线段AD 总被直线BC 平分,求点A 的坐标.解:(1)因为A (1,2)在抛物线y 2=2px (p >0)上,所以p =2.所以抛物线方程为y 2=4x . 设C ⎝⎛⎭⎫t 24,t ,则由k AB ·k AC =-1,即-4-24-1·t -2t24-1=-1,解得t =6,即C (9,6). (2)设A (x 0,y 0),B ⎝⎛⎭⎫y 212p ,y 1,C ⎝⎛⎭⎫y 222p ,y 2,则y 20=2px 0, 直线BC 的方程为y -y 1y 2-y 1=x -y 212p y 222p -y 212p ,即(y 1+y 2)y =2px +y 1y 2,由k AB ·k AC =y 1-y 0y 212p -y 202p ·y 2-y 0y 222p -y 202p=-1, 得y 0(y 1+y 2)+y 1y 2+y 20=-4p 2,与直线BC 的方程联立,化简,得(y 1+y 2)(y +y 0)=2p (x -2p -x 0), 故直线BC 恒过点E (x 0+2p ,-y 0).因此直线AE 的方程为y =-y 0p (x -x 0)+y 0,代入抛物线的方程y 2=2px (p >0),得点D 的坐标为⎝⎛⎭⎫2p (x 0+p )2y 20,-2p (x 0+p )y 0. 因为线段AD 总被直线BC 平分, 所以⎩⎨⎧2(x 0+2p )=x 0+2p (x 0+p )2y 20,-2y 0=y 0-2p (x 0+p )y 0,解得x 0=p2,y 0=±p ,即点A 的坐标为⎝⎛⎭⎫p2,±p .。
朱红 一级建造师 建筑工程管理与实务 真题解析(7)
一级建造师建筑工程管理与实务精讲通关主讲老师:朱红4.合同管理与造价控制背景资料(2013年案例四)某新建工程,采用公开招标的方式,确定某施工单位中标。
双方按《建设工程施工合同(示范文本)》(GF-2013-0201)签订了施工总承包合同。
合同约定总造价14250万元,预付备料款2800万元,每月底按月支付施工进度款。
竣工结算时,结算价款按调值公式法进行调整。
在招标和施工过程中,发生了如下事件:【事件一】建设单位自行组织招标。
招标文件规定:合格投标人为本省企业;自招标文件发出之日起15天后投标截止;招标人对投标人提出的疑问分别以书面形式回复给相应提出疑问的投标人。
建设行政主管部门评审招标文件时,认为个别条款不符合相关规定,要求整改后再进行招标。
【事件二】合同约定主要材料按占造价比重55%计,预付备料款在起扣点之后的五个月度支付中扣回。
【事件三】基坑施工时正值雨季,导致停工6天,造成人员窝工损失2.2万元。
一周后出现了罕见特大暴雨,造成停工2天,人员窝工损失1.4万元。
针对上述情况,施工单位分别向监理单位上报了这四项索赔申请。
【事件四】某分项工程由于设计变更导致该分项工程量变化幅度达20%,合同专用条款未对变更价款进行约定。
施工单位按变更指令施工,在施工结束后的下一个月上报支付申请的同时,还上报了该设计变更的变更价款申请,监理工程师不批准变更价款。
【事件五】种植屋面隐藏工程通过监理工程师验收后开始覆土施工,建设单位对隐藏工程质量提出异议,要求复验,施工单位不予同意。
经总监理工程师协调后三方现场复验,经检验质量满足要求。
施工单位要求补偿由此增加的费用,建设单位予以拒绝。
【事件六】合同中约定,根据人工费和四项主要材料和价格指数对总造价按调值公式法进行调整。
各调值因素的比重、基准和现行价格指数如下表:可调项目人工费材料一材料二材料三材料四因素比重0.15 0.30 0.12 0.15 0.08基期价格指数0.99 1.01 0.99 0.96 0.78现行价格指数 1.12 1.16 0.85 0.80 1.05【问题】1.事件一中,指出招标文件规定的不妥之处,并分别写出理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011建设工程法规及相关知识主讲人:刘菁1Z301080 建设工程保险制度1Z301081保险与保险索赔的规定一、保险概述保险合同是指投保人与保险人约定保险权利义务关系的协议。
投保人是指与保险人订立保险合同,并按照保险合同负有支付保险费义务的人。
保险人是指与投保人订立保险合同,并承担赔偿或者给付保险金责任的保险公司。
保险合同在履行中还会涉及被保险人和受益人。
保险合同分为财产保险合同、人身保险合同。
如:建筑工程一切险和安装工程一切险(含第三者责任险)为财产保险合同;意外伤害险为人身保险合同。
1Z301081保险与保险索赔的规定二、保险索赔(一)投保人进行保险索赔须提供必要的有效的证明索赔的证据:保单、建设工程合同、事故照片、鉴定报告以及保单中规定的证明文件。
(二)投保人等应当及时提出保险索赔(三)计算损失大小一个建设工程项目同时由多家保险公司承保,则应当按照约定的比例分别向不同的保险公司提出索赔要求。
1Z301082建设工程保险的主要种类和投保权益一、建筑工程一切险(及第三者责任险)建筑工程一切险是承保各类民用、工业和公用事业建筑工程项目,包括道路、桥梁、水坝、港口等,在建造过程中因自然灾害或意外事故而引起的一切损失的险种。
建筑工程一切险往往还加保第三者责任险。
第三者责任险是指在保险有效期内因在施工工地上发生意外事故造成在施工工地及邻近地区的第三者人身伤亡或财产损失,依法应由被保险人承担的经济赔偿责任。
1Z301082建设工程保险的主要种类和投保权益(一)投保人与被保险人《建设工程施工合同(示范文本)》中规定,工程开工前,发包人应当为建设工程办理保险,支付保险费用。
(二)保险责任范围(1)自然事件:指地震、海啸、雷电、飓风、台风、龙卷风、风暴、暴雨、洪水、水灾、冻灾、冰雹、地崩、山崩、雪崩、火山爆发、地面下陷下沉及其他人力不可抗拒的破坏力强大的自然现象;(2)意外事故:指不可预料的以及被保险人无法控制并造成物质损失或人身伤亡的突发性事件,包括火灾和爆炸。
1Z301082建设工程保险的主要种类和投保权益(三)除外责任(1)设计错误引起的损失和费用;(2)自然磨损、内在或潜在缺陷、物质本身变化、自燃、自热、氧化、锈蚀、渗漏、鼠咬、虫蛀、大气(气候或气温)变化、正常水位变化或其他渐变原因造成的保险财产自身的损失和费用;(3)因原材料缺陷或工艺不善引起的保险财产本身的损失以及为换置、修理或矫正这些缺点错误所支付的费用;(4)非外力引起的机械或电气装置的本身损失,或施工用机具、设备、机械装置失灵造成的本身损失;(5)维修保养或正常检修的费用;1Z301082建设工程保险的主要种类和投保权益(6)档案、文件、账簿、票据、现金、各种有价证券、图表资料及包装物料的损失;(7)盘点时发现的短缺;(8)领有公共运输行驶执照的,或已由其他保险予以保障的车辆、船舶和飞机的损失;(9)除非另有约定,在保险工程开始以前已经存在或形成的位于工地范围内或其周围的属于被保险人的财产的损失;(10)除非另有约定,在本保险单保险期限终止以前,保险财产中已由工程所有人签发完工验收证书或验收合格或实际占有或使用或接收的部分。
1Z301082建设工程保险的主要种类和投保权益(四)第三者责任险(1)在保险期限内,因发生与所保工程直接相关的意外事故引起工地内及邻近区域的第三者人身伤亡、疾病或财产损失;(2)被保险人因上述原因支付的诉讼费用以及事先经保险人书面同意而支付的其他费用。
(五)赔偿金额均不得超过保险单明细表中对应列明的每次事故赔偿限额。
经济赔偿的最高赔偿责任不得超过本保险事明细表中列明的累计赔偿限额。
1Z301082建设工程保险的主要种类和投保权益(六)保险期限起点:保险工程在工地动工或用于保险工程的材料、设备运抵工地之时。
终点:工程所有人对部分或全部工程签发完工验收证书或验收合格,或工程所有人实际占用或使用或接收该部分或全部工程之时终止。
以先发生者为准。
保险期限的起始或终止不得超出保险单明细表中列明的保险生效日或终止日。
1Z301082建设工程保险的主要种类和投保权益二、安装工程一切险(及第三者责任险)(一)保险责任范围自然灾害、意外事故(具体内容与建筑工程一切险基本相同)1Z301082建设工程保险的主要种类和投保权益(二)除外责任其除外责任与建筑工程一切险的第(2)、(5)、(6)、(7)、(8)、(9)、(10)相同,不同之处主要是:(1)因设计错误、铸造或原材料缺陷或工艺不善引起的保险财产本身的损失以及为换置、修理或矫正这些缺点错误所支付的费用;(2)由于超负荷、超电压、碰线、电弧、漏电、短路、大气放电及其他电气原因造成电气设备或电气用具本身的损失;(3)施工用机具、设备、机械装置失灵造成的本身损失。
1Z301082建设工程保险的主要种类和投保权益(三)保险期限基本同建筑工程一切险,此外,一般应包括一个试车考核期。
考核期的保险责任一般不超过3个月。
对于旧机器设备不负考核期的保险责任,也不承担其维修期的保险责任。
1Z301082建设工程保险的主要种类和投保权益【案例】1.背景(P43)2006年3月7日,某养殖公司与某财产保险公司签订了《建筑工程一切险保险合同》,保险项目为该养殖公司的围埝工程,投保金额为3485000元,事故绝对免赔额为50000元;保险期限自2006年3月16日中午12时起至2006年5月5日中午12时止。
双方在合同第13条还特别约定:物质损失部分每次事故赔偿限额为500000元。
2006年3月11日,该养殖公司交付保险公司保险费12455元。
1Z301082建设工程保险的主要种类和投保权益在保险期间,该围埝工程施工于2006年4月15日、4月30日因海上出现大风天气,导致两次海损事故发生,造成一定经济损失。
在理赔过程中,双方就损失赔偿问题未达成一致意见。
该养殖公司起诉到人民法院。
2007年6月15日,一审法院依法委托某工程咨询管理公司对两次海损工程量进行了司法鉴定,同年7月31日得出鉴定结论:两次海损损毁的工程量合计26525.25立方米。
若按照双方提供的工程承包合同单价每立方米41元计算,则海损部分的工程造价为1087535.25元。
原告支付了鉴定费80000元。
1Z301082建设工程保险的主要种类和投保权益2.问题被告是否应当赔偿损失,赔偿额应当是多少?1Z301082建设工程保险的主要种类和投保权益3.分析2006年4月15日、4月30日的最大风速为8级。
两次海损均属人力不可抗拒的破坏力强大的自然现象所致,属于保险责任的范围,被告应按照保险合同的约定承担保险赔偿责任。
法院对两次海损工程量司法鉴定报告书认定程序合法,对该鉴定报告予以采信。
根据鉴定结沦,2006年4月15日第一次海损给原告造成的损失为266336元,减去绝对免赔额50000元,被告应赔偿216336元;2006年4月30日,第二次海损造成的损失为821199.25元,因双方约定了物质损失部分每次事故赔偿限额为500000元,故被告应赔偿损失500000元。
1Z301082建设工程保险的主要种类和投保权益结论:被告赔偿原告2006年4月15日海损损失216336元;被告赔偿原告2006年4月30日海损损失500000元;案件受理费18118元,其他费用4670元,共计22788元,双方各负担一半。
鉴定费80000元,由被告担负。
1Z301082建设工程保险的主要种类和投保权益三、建筑职工意外伤害险施工单位应当为施工现场从事危险作业的人员办理意外伤害保险。
属于强制险。
四、保险经纪人和保险代理人保险代理人是受保险公司的委托,为该保险公司推销保险产品。
——推销员保险经纪人则是受投保人(保险客户)的委托,根据客户的风险情况,为其设计保险方案、制定保险计划,横向比较各保险公司的保险条款优劣,帮助投保人选择适当的保险公司。
——顾问例题解析1.某建筑公司中标了某桥梁工程,依照《建筑法》的规定,该建筑公司必须投保的险种是()。
A.建筑工程一切险B.安装工程一切险C.工程监理责任保险D.建筑意外伤害险[答案] D例题解析2.属于建筑工程一切险承保的是()。
A.因自然灾害导致的工程损毁B.设计错误引起的损失C.意外事故所导致的钢结构安装过程中人员伤亡D.因自然灾害导致工程现场机械损坏[答案] AA为建筑工程一切险的承包范围B为建筑工程一切险的除外责任C为建筑职工意外伤害险D为安装工程一切险的承包范围例题解析3.建筑工程一切险是一种综合性的保险,该险种承保的损失范围是()。
A.信用保险和意外伤害保险B.财产损失保险和第三者责任保险C.财产损失保险和意外伤害保险D.健康保险和责任保险[答案] B例题解析4.某建筑公司承包了某工程,该工程计划于5月15日开工,该建筑公司在5月5日与保险公司签订了建筑职工意外伤害保险合同,5月8日,该建筑公司工作人员在巡视工程现场时发生了意外事故,建筑公司拟向保险公司索赔,此时保险公司承担保险责任的期限起算时间应为()。
A.5月5日B.5月8日C.5月15日D.6月15日[答案] C例题解析5.投保建筑意外伤害险的保险公司,被保险人在建筑施工中遭受意外致残的,被保险人凭一系列()证明文件向保险公司申请给付保险金。
A.保险单及投保单位证明B.被保险人户籍证明及身份证明C.有保险人指定或认可的医疗机构或医师出具的被保险人残疾程度鉴定书D.被保险人所能提供的与确认保险事故性质、原因、伤害程度等有关的其他证明和资料E.保险人认可的医疗机构出具的被保险人死亡证明[答案] ABCD例题解析6.建筑工程意外伤害险承保的范围包括()。
A.工程本身受损B.施工用设施受损C.被保险人从事建筑施工时由于操作不当受伤害致残D.被保险人在施工现场被高空坠物砸死E.场地清理费[答案] CD例题解析7.建筑工程意外伤害险责任免除的情形有()。
A.建筑公司的有关人员故意杀害被保险人B.被保险人在施工现场内酒后驾驶肇事死亡C.被保险人在施工时违反机器操作规程导致截肢D.被保险人在施工现场之外受到意外伤害E.被保险人在施工现场与他人打斗受到重伤[答案] ABDE1Z301090 建设工程法律责任制度1Z301091法律责任的基本种类和特征按照违法行为的性质和危害程度,可以将法律责任分为:违宪法律责任、刑事法律责任、民事法律责任、行政法律责任和国家赔偿责任。
1Z301092建设工程民事责任的种类及承担方式一、民事责任的种类民事责任可以分为违约责任和侵权责任两类。
违约责任:是指合同当事人违反法律规定或合同约定的义务而应承担的责任。
侵权责任:是指行为人因过错侵害他人财产、人身而依法应当承担的责任,以及虽没有过错,但在造成损害以后,依法应当承担的责任。
