Mathematica数学软件系统使用入门
mathematica使用指南

mathematica使用指南Mathematica是一款功能强大的数学软件,具备广泛的应用领域,包括数学、统计学、物理学、工程学等等。
本文将为您提供一份Mathematica的使用指南,帮助您快速入门并提高使用效率。
1. Mathematica简介Mathematica是由Wolfram Research公司开发的一款通用计算软件,它具备数值计算、符号计算、图形绘制等多种功能。
Mathematica基于Wolfram Language语言,用户可以直接在其中编写代码进行计算和分析。
2. 安装与启动首先您需要从Wolfram Research公司官方网站下载Mathematica安装文件,并按照安装向导完成安装过程。
安装完成后,您可以在计算机上找到Mathematica的启动图标,点击即可启动该软件。
3. Mathematica界面介绍Mathematica的主界面由菜单栏、工具栏、输入区域和输出区域组成。
菜单栏提供了各种功能选项,工具栏包含常用工具按钮,输入区域用于输入代码,而输出区域用于显示计算结果。
4. 基本计算在输入区域中,您可以直接输入数学表达式进行计算。
例如,输入"2 + 3",然后按下Enter键即可得到计算结果"5"。
Mathematica支持基本的算术运算、三角函数、指数函数等数学操作。
5. 变量与函数您可以使用Mathematica定义变量并进行计算。
例如,输入"x = 2",然后再输入"y = x^2",按下Enter键后,变量y会被赋值为2的平方,即4。
定义的变量可以在后续计算中使用。
6. 图形绘制Mathematica提供了丰富的图形绘制功能。
您可以使用Plot函数绘制函数曲线,使用ListPlot函数绘制离散数据点,还可以绘制3D图形等等。
通过调整参数和选项,您可以自定义图形的样式和外观。
mathematic使用指南
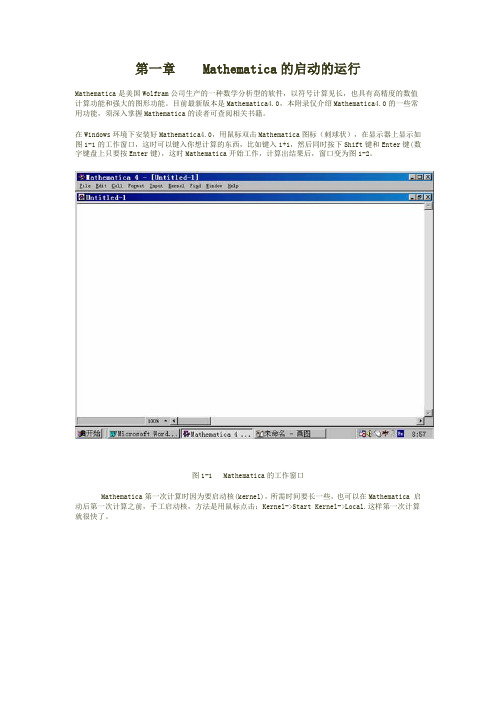
第一章Mathematica的启动的运行Mathematica是美国Wolfram公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
目前最新版本是Mathematica4.0,本附录仅介绍Mathematica4.0的一些常用功能,须深入掌握Mathematica的读者可查阅相关书籍。
在Windows环境下安装好Mathematica4.0,用鼠标双击Mathematica图标(刺球状),在显示器上显示如图1-1的工作窗口,这时可以键入你想计算的东西,比如键入1+1,然后同时按下Shift键和Enter键(数字键盘上只要按Enter键),这时Mathematica开始工作,计算出结果后,窗口变为图1-2。
图1-1 Mathematica的工作窗口Mathematica第一次计算时因为要启动核(kernel),所需时间要长一些,也可以在Mathematica 启动后第一次计算之前,手工启动核,方法是用鼠标点击:Kernel->Start Kernel->Local.这样第一次计算就很快了。
图1-2 完成运算后的Mathematica的窗口图1-2中的“In[1]:=”表示第一个输入;“Out[1]=”表示第一个输出结果。
接下来可键入第二个输入,按这样的方式可利用Mathematica进行“会话式”计算。
要注意的是:“In[1]:= ”和“Out[1]=”是系统自动添加的,不需用户键入。
Mathematica还提供“批处理”运行方式,即可以将Mathematica作为一种算法语言,编写程序,让计算机执行,这在第七章将会作简要介绍。
第二章 Mathematica的基本运算功能2.1 算术运算Mathematica最基本的功能是进行算术运算,包括加(+),减(-),乘(*),除(/),乘方(^),阶乘(!)等。
注意:1 在Mathematica中,也可用空格代表乘号;数字和字母相乘,乘号可以省去,例如:3*2可写成3 2,2*x可写成2x,但字母和字母相乘,乘号不能省去。
Mathematica入门(一)

NUDT
Mathematica入门 入门
表的操作 Join[ t1 , t2] Union[ t1 , t2] 将表 t1 和表 t2连接成一个表 将表 t1 和表 t2 的并集组成一个表
某些特殊属性表的建立 Table[ f , {i,imin , imax , stepi} , { j , jmin , jmax , stepj}]
t1 = 1, 2, 4 t2 = 1, 3, Sin x , Cos x
8 8@ @ <D D 8 <
表元素的操作 t[[n]] 表示表 t 的第 n 个元素(同Part[t , n]的意义 个元素( 的意义) 的意义 t[[i , j]] 表示表 t 中第 i 个子表的第 j 个元素 Length[ t ] 表示表 t 的元素个数
p = x + 2 x y+ y p . x® 1
2
p = x2 + 2 x y + y2 p . x ® 1, y ® 2
8 <
NUDT
Mathematica入门 入门
(5)表 表是存贮多个数、变量或算式等对象的一种数据结构, 表是存贮多个数、变量或算式等对象的一种数据结构,一 个表用一对花括号表示,其成员(元素) 个表用一对花括号表示,其成员(元素)在括号内用逗号 隔开,同一个表的成员可以是不同的数据类型, 隔开,同一个表的成员可以是不同的数据类型,表的成员 还可以是一个表(子表)。 还可以是一个表(子表)。
1
-1.5
-1
-0.5 -0.5
0.5
1
1.5
-2
-1
1
2
-1
-1
-2
NUDT
Mathematica入门 入门
mathematica简明使用教程

mathematica简明使用教程Mathematica是一种强大的数学软件,广泛应用于科学研究、工程计算和数据分析等领域。
本文将简要介绍Mathematica的使用方法,帮助读者快速上手。
一、安装和启动Mathematica我们需要下载并安装Mathematica软件。
在安装完成后,可以通过桌面图标或开始菜单中的快捷方式来启动Mathematica。
二、界面介绍Mathematica的界面分为菜单栏、工具栏、输入区域和输出区域四部分。
菜单栏提供了各种功能选项,工具栏包含了常用的工具按钮,输入区域用于输入代码或表达式,而输出区域则显示执行结果。
三、基本操作1. 输入和输出在输入区域输入代码或表达式后,按下Shift+Enter键即可执行,并在输出区域显示结果。
Mathematica会自动对输入进行求解或计算,并返回相应的输出结果。
2. 变量定义可以使用等号“=”来定义变量。
例如,输入“a = 3”,然后执行,就会将3赋值给变量a。
定义的变量可以在后续的计算中使用。
3. 函数调用Mathematica内置了许多常用的数学函数,可以直接调用使用。
例如,输入“Sin[π/2]”,然后执行,就会返回正弦函数在π/2处的值。
4. 注释和注解在代码中添加注释可以提高代码的可读性。
在Mathematica中,可以使用“(*注释内容*)”的格式来添加注释。
四、数学运算Mathematica支持各种数学运算,包括基本的加减乘除,以及更复杂的求导、积分、矩阵运算等。
下面简要介绍几个常用的数学运算:1. 求导可以使用D函数来求导。
例如,输入“D[Sin[x], x]”,然后执行,就会返回正弦函数的导数。
2. 积分可以使用Integrate函数来进行积分运算。
例如,输入“Integrate[x^2, x]”,然后执行,就会返回x的平方的不定积分。
3. 矩阵运算Mathematica提供了丰富的矩阵运算函数,可以进行矩阵的加减乘除、转置、求逆等操作。
第1讲 Mathematica入门

1. 集合的定义 直接定义: 直接定义 直接用{}将相关元素放在一起就得到一个集 合.例如: 例22 In[1]:= t1={1,2,3,4,5,6} In[2]:= t2={Sin[x],Cos[x]} 语句定义: 可用Range与Table语句来定义集合. 语句定义 Range[imin,imax,di]给出的是一个数的集合,第一项为 imin,最后一项不超过imax,步长为di. 例如: 例23 In[3]:= t3=Range[1,30,3] Out[3]= {1,4,7,10,13,16,19,22,25,28}
除了上面的这种赋值形式(称为即时赋值)以外,还有 一种延迟赋值。 例10 In[4]:= t:=4 延迟赋值并不显示结果,只有调用变量时,才进行计 算并赋值。下面的例子可以看出即时赋值与延迟赋值的 区别。 例11 In[5]:= r=Random[ ]; s={r,r} Out[6]= {0.455181, 0.455181} In[7]:= r:=Random[ ]; s={r,r} Out[8]= {0.967234, 0.526599}
这些常数可以参与运算。
例6 In[1]:= 2*E Out[1]= 2E In[2]:= N[Pi,30] Out[2]= 3.14159265358979323846264338328 函数N[x,n]给出x的n位有效数字。 Mathematica提供了许多数学上的函数,表3给出了 一些常用的数学函数。
例15 In[15]:= x=2.0; u[x_]:=Sin[x]; v[x_]=Sin[x] Out[15]= 0.909297 In[16]:= ?u Global`u u[x_]=Sin[x] In[17]:= ?v Global`v v[x_]=0.909297 可以看出,上例中函数u[x]被定义为Sin[x],而v[x]被 定义为常函数0.909297(=sin2.0).
Mathematica基础教程

Mathematica基础Mathematica自1988年由美国的Wolfram Research公司首次推出,是一个功能强大的常用数学软件, 不但可以解决数学中的数值计算问题, 还可以解决符号演算问题, 并且能够方便地绘出各种函数图形。
常用数学软件之比较,Matlab Mathematica MathCAD Maple:1. Mathematica基本使用(1)在工作区(软件打开初始时,左侧的窗口,上方有untitled-1*)输入命令,按Shift+Enter组合键执行命令;如输入“2+3”,按Shift+Enter执行后,窗口显示In[1]:= 2 + 3Out[1]= 5其中“In[1]:=,Out[1]=”为系统自动添加(不必管),In[1]括号内数字1表示第1次输入。
如果不想显示此次输入的结果,只要在所输入命令的后面再加上一个分号便可。
(2)软件打开初始时,右侧有一个运算符号面板,可以更方便命令输入,如级数,积分,数学符号等。
(3)除可以用直接键盘输入的方法进行输入外, 还可以用打开的方式从磁盘中调入一个已经存在的文件来进行操作。
2. Mathematica的基本语法特征(1)Mathematica中区分大、小写,如Name、name、NAME等是不同的变量名或函数名。
(2)系统所提供的功能大部分以系统函数的形式给出,内部函数一般写全称,而且一定是以大写英文字母开头,如Sin[2]等。
(3)乘法即可以用*,又可以用空格表示,如2 3=2*3=6 ,x y,2 Sin[x]等;乘幂可以用“^”表示,如x^,Tan[x]^y。
(4)自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头。
(5)当赋予变量任何一个值,除非明显地改变该值或使用Clear[变量名]或“变量名=.”取消该值为止,否则它将始终保持原值不变。
(6)一定要注意四种括号的用法:()圆括号表示运算项的结合顺序,如(x+(y^x+1/(2x)));[]方括号表示函数,如Log[x], BesselJ[x,1];{}大括号表示一个“表”(一组数字、任意表达式、函数等的集合),如{2x,Sin[12 Pi],{1+A,y*x}};[[]]双方括号表示“表”或“表达式”的下标,如a[[2,3]]、{1,2,3}[[1]]=1。
mathematica教程
M athematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
假设在Windows环境下已安装好Mathematica4.0,启动Windows后,在“开始”菜单的“程序”中单击,就启动了Mathematica4.0,在屏幕上显示如图的Notebook窗口,系统暂时取名Untitled-1,直到用户保存时重新命名为止输入1+1,然后按下Shif+Enter键,这时系统开始计算并输出计算结果,并给输入和输出附上次序标识In[1]和Out[1],注意In[1]是计算后才出现的;再输入第二个表达式,要求系统将一个二项式展开,按Shift+Enter输出计算结果后,系统分别将其标识为In[2]和Out[2].如图在Mathematica的Notebook界面下,可以用这种交互方式完成各种运算,如函数作图,求极限、解方程等,也可以用它编写像C那样的结构化程序。
在Mathematica系统中定义了许多功能强大的函数,我们称之为内建函数(built-in function), 直接调用这些函数可以取到事半功倍的效果。
这些函数分为两类,一类是数学意义上的函数,如:绝对值函数Abs[x],正弦函数Sin[x],余弦函数Cos[x],以e为底的对数函数Log[x],以a为底的对数函数Log[a,x]等;第二类是命令意义上的函数,如作函数图形的函数Plot[f[x],{x,xmin,xmax}],解方程函数Solve[eqn,x],求导函数D[f[x],x]等。
必须注意的是:如果输入了不合语法规则的表达式,系统会显示出错信息,并且不给出计算结果,例如:要画正弦函数在区间[-10,10]上的图形,输入plot[Sin[x],{x,-10,10}],则系统提示“可能有拼写错误,新符号‘plot’ 很像已经存在的符号‘Plot’”,实际上,系统作图命令“Plot”第一个字母必须大写,一般地,系统内建函数首写字母都要大写。
Mathematica数学软件操作技巧及界面详解

Mathematica数学软件操作技巧及界面详解Mathematica是一款十分强大的数学计算软件,它可以广泛应用于科学、工程和教育等领域。
本文将介绍一些Mathematica的操作技巧,并详细解析其界面设计。
一、Mathematica的基本操作技巧1. 输入和计算Mathematica的主界面提供了一个输入框,我们可以在其中输入各种数学表达式和计算公式。
输入时需要遵循一定的语法规则,比如使用^表示乘方,使用*表示乘法,使用/表示除法等。
在输入完毕后,按下Enter键即可进行计算。
2. 变量定义和赋值在Mathematica中,我们可以使用等号(=)来定义和赋值变量。
比如,我们可以输入"radius = 5"来定义一个名为radius的变量,并将其赋值为5。
之后,我们可以直接使用radius来进行计算。
3. 函数调用Mathematica内置了许多数学函数,比如sin、cos、log等。
我们可以使用这些函数来进行各种数学运算。
调用函数时需要在函数名后加上待计算的参数,比如"sin(0.5)"可以计算出0.5的正弦值。
二、Mathematica的界面详解1. 顶部菜单栏Mathematica的顶部菜单栏包含了许多功能按钮,我们可以通过点击这些按钮来执行相应的操作,比如打开文件、保存文件、进行图像绘制等。
2. 工具栏在Mathematica的工具栏上,我们可以找到常用的绘图工具、格式调整工具和计算选项卡等。
这些工具可以帮助我们更加方便地进行数学计算和图形绘制。
3. 文档窗口Mathematica的文档窗口是我们进行数学计算和编写代码的主要区域。
我们可以在文档窗口中输入数学表达式、编写代码,并且可以将计算结果直接显示在文档窗口中。
4. 侧边栏在Mathematica的侧边栏上,我们可以找到各种各样的面板和选项卡。
这些面板和选项卡提供了对Mathematica的进一步设置和功能扩展,比如图形面板、数据面板和设置面板等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ch1. a Mathematic 概述1.1a Mathematic 的工作环境a Mathematic 的基本系统是用C 语言编写的,因此能够方便的移植到各种计算机系统上。
打开a Mathematic ,可以看到它是一个窗口软件,包括一个执行各种功能的工作条(屏幕顶端)和一个工作区窗口。
激活工作区窗口,输入希望的计算式(如:“3+8-4”),同时按下“Shift ”和“Enter ”键便可执行计算。
使用a Mathematic 的几个注意点:1. 每次使用a Mathematic ,第一次计算时间较长,这是系统在进行初始化工作,从第二次计算开始就很快了。
2. 输入计算公式和普通文本输入一样,系统将把每次输入记录在案,并自动给每个输入记录用“In[n]”编号,计算结果用“Out[n]”编号。
“%”表示上一次计算结果,“%n ”表示“Out[n]”的内容,这样可以减少重复输入。
3. 输完计算式后,同时按下“Shift ”和“Enter ”键,a Mathematic 将完成计算。
4. 必须严格按照系统所规定的格式输入算式,否则将无法完成计算任务,通常给出一段文字,告诉你出错的(可能)原因。
1.2a Mathematic 的基本功能1.基本计算功能,如: In[1]:= 3+8-4 Out[1]= 7In[2]:= 12.5^3 (*即12.53*) Out[2]= 1953.132.强大的符号计算功能a Mathematic 的最大特点是能进行符号计算。
如: (1) 解方程x a x 2=+ In[3]:= Out[3]=I注意,方程的解用“ ”代替了“=”。
(2) 求不定积分dx x e x ⎰sin In[4]:= Out[4]= 注意,不定积分的任意常数C 均省略。
3.绘图功能a Mathematic 有强大的图形功能,可作各种二维、三维图形。
如: (1) 作函数x x y 6.1sin sin +=的二维图形--Graphics (2) 作函数)sin(xy z =的三维图形In[6]:=--phics SurfaceGra1.3从a Mathematic 中获得帮助信息1. 点击工作条中的Help 可获得帮助信息。
特别是下拉菜单“Help Browser ”中的“Mathematica Book ”系统而完整地介绍了本软件的使用方法。
2. 用“?”可获得帮助信息(常用信息)。
如: In[7]:= ?SinSin @z D gives the sine of z.3. 用“??”可获得帮助信息(详细信息)。
如: In[8]:= ??SinSin @z D gives the sine of z.Attributes @S in D =8L istable,NumericFunction,Protected <花括号内的多项内容可到“Help Browser ”中查询,只要在“Go To ”右面的对话框中输入想查询信息的名称后打回车键即可找到相应的信息了。
Ch2. aMathematic的基本命令2.1算术运算1.算术运算用aMathematic运算与用计算器一样简单。
如:In[1]:= 3.55+12.879/(4.33-1.203)^2.3Out[1]=4.4856aMathematic有强大的计算功能,总可以得到精确值。
如:In[2]:= (30000*12345)^9Out[2]=1310723665724312245850482517300821679687500000000000000/ 0000000000000000000000如果想得到近似值,可在输入结尾加上“//N”。
如:In[3]:= (30000*12345)^9//NOut[3]=7731072.1⨯10用“N[ ]”也有相同效果。
如:In[4]:=N[Pi,50] (*表示π的近似值,取50位有效数字*)Out[4]= 3.1415926535897932384626433832795028841971693993751 输入整数时,aMathematic认为是精确值;输入小数时,aMathematic认为是近似值。
如:In[5]:=(30000*12345)^9.0Out[5]=7710.1⨯31072In[6]:= 3/8+2/67217Out[6]=5362.2 常用函数与常数1.2. Pi(圆周率π) E(自然对数的底e) I(虚数单位i) Infinity(+∞) -Infinity(-∞) Degree(π/180)角度 注意,1.a Mathematic 中内部函数和常数须用大写字母开头; 2.函数的自变量应放在方括号内。
例如; In[7]:= Sin[Pi/3]Out[7]=23 (*这是符号解,即3sin的精确解*) In[8]:= N[%,6] (*上述23的近似值,取6位有效数字*)Out[8]= 866025.03.复数 “I ”表示虚数单位i ,如: In[9]:= Log[-737.3]Out[9]= 6.60299+3.14159äa Mathematic 1.赋值与消除赋值有时某些变量(或函数)在计算中重复出现,为避免重复输入,可以先给它们赋值。
如果要对变量赋值可用以下方法: (1)在变量计算前先赋值。
如: In[1]:= x=3; (*分号表示不立即输出*)这时变量x 就已赋值为3,以后遇到x 时,a Mathematic 就认为是3了。
In[2]:= x+x Out[2]= 6(2)在变量计算后赋值。
如:In[3]:= y+2y/.y->3 (*这时y 已赋值为3*) Out[3]= 9In[4]:= x^2+2y Out[4]= 15(3) 定义函数(对函数赋值)a Mathematic 中有很多内部函数,如:Log[x],Sin[x],Abs[x]等;用户也可以自己定义函数,如定义32)(2++=x x x f In[5]:= f[x_]:=x^2+2 x+3这样函数f(x)就定义好了,在定义函数时,等号一般用“:=”,方括号内自变量右边必须有下划线“_”。
下面就可以使用此函数了。
In[6]:= f[2] Out[6]= 7In[7]:= f[t+1]Out[7]= 3+2 (1+t)+(1+t)2In[8]:= Integrate[f[x],{x,0,1}] Out[8]= 313定义分段函数可用Which(或If)命令来完成,如:⎪⎩⎪⎨⎧>≤≤--<-=121112)(x x xx x f In[9]:= f[x_]:=Which[x<-1,-2, x<=1,x,x>1,2]同样可定义多元函数 In[10]:= g[x_,y_,z_]:=Sin[x]+y-zIn[11]:= g[Pi/2,1/2,3] Out[11]= 23-要消除赋值,可用以下方法: (1)赋值x=. 如: In[12]:= x=. In[13]:= x^2+2y Out[13]= x 2+6(2)用函数“Clear ”。
如: In[14]:= Clear[y] In[15]:= x^2+2y Out[15]= x 2+2y清除定义的函数也用 Clear[f]。
In[16]:= Clear[f]2.常用的初等代数符号计算 (1)展开多项式 ExpandIn[17]:= Expand[(x+1)(x^2+2x+2)+2x+5] Out[17]= 7+6x+3x 2+x 3 (2)因式分解 Factor In[18]:= Factor[x^2+2x+1] Out[18]= (1+x)2(3)通分 TogetherIn[19]:= Together[2/(3+x)^2+3x/(3+x)^2+x^2/(3+x)^2]Out[19]= 22x)(3x x 32+++ (4)拆分(把有理分式分解为部分分式之和) Apart In[20]:= Apart[(2-3x+x^3)/(9+3x-5x^2+x^3)] Out[20]= ()()()x 141x 3419x 3512+++-++-+(5)约分 CancelIn[21]:= Cancel[(1+2x+x^2)/(x^2-x-2)] Out[21]=x2x1+-+3.解代数方程a Mathematic 中的方程的等号以双等号“= =”表示。
In[22]:= Solve [x^2+3x-8==0,x]Out[22]= ()()⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+-→⎭⎬⎫⎩⎨⎧--→41321x ,41321xIn[23]:= N[%]Out[23]= {}{}{}1.70156x ,4.70156x →-→ In[24]:= Solve[{x+y-1==0,x-y==0},{x,y}]Out[24]= ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧→→21y ,21x要求5次以上的高次方程,Solve 就无能为力了,可用NSolve 求多项式方程的近似解。
In[25]:= NSolve[x^3-2x^2-4x-7==0,x]Out[25]=8x ®-0.81599-1.12316ä<,8x ®-0.81599+1.12316ä<,8x ®3.63198<也可用命令FindRootIn[26]:= FindRoot[x^3-2x^2-4x-7==0,{x,4}] Out[26]= 8x ®3.63198<其中4表示方程在从4出发求解。
2.4微积分的符号计算与数值计算 1.微分(导数)运算(1)D[f,x] 求导数或偏导数 In[1]:= D[Sin[x],x] Out[1]= Cos[x]In[2]:= D[y+Sin[x](x+y),y]Out[2]= 1+Sin[x](2)D[f,{x,n}] 求n 次(偏)导数 In[3]:= D[x^3+x^2+1,{x,2}] Out[3]= 2+6x(3)D[f,x1,x2] 求混合偏导数 In[4]:= D[(x^2)Sin[y],x,y] Out[4]= 2xCos[y]In[5]:= D[f[x^2,x y],x]Out[5]=y f H 0,1L @x 2,x y D +2x f H 1,0L @x 2,x y D2.积分运算(1)不定积分 ⎰fdx In[6]:= Integrate[x^2,x]Out[6]= 33xa Mathematic 可做几乎所有标准函数的不定积分,但对于“积不出”的可积函数a Mathematic 也不能求。
