中考数学试卷
2024浙江省中考数学真题试卷及答案

2024浙江省中考数学真题试卷一、选择题(每题3分)1.以下四个城市中某天中午12时气温最低的城市是( ).A.北京B.济南C.太原D.郑州2.5个相同正方体搭成的几何体主视图为()A. B.C. D.3.2024年浙江经济一季度GDP 为201370000万元,其中201370000用科学记数法表示为( ) A.920.13710⨯B.80.2013710⨯C.92.013710⨯D.82.013710⨯4.下列式子运算正确的是( ) A.325x x x +=B.326x x x ⋅=C.329()x x =D.624x x x ÷=5.有5位学生参加志愿者,服务次数为:7,7,8,10,13.则这5位学生志愿服务次数的中位数为( ) A.7B.8C.9D.106.如图,在平面直角坐标系中,△ABC 与'''A B C ∆是位似图形,位似中心为点O .若点(3,1)A -的对应点为'(6,2)A -,则点B (-2,4)的对应点'B 的坐标为( )A.(-4,8)B.(8,-4)C.(-8,4)D.(4,-8)7.不等式组2113(2)6x x -≥⎧⎨->-⎩的解集在数轴上表示为( )A.B.C. D.8.如图,正方形ABCD 由四个全等的直角三角形(△ABE ,△BCF ,△CDG ,△DAH )和中间一个小正方形EFGH 组成,连接DE .若AE=4,BE =3,则DE=( )A.5B.6 17 D.49.反比例函数4y x=的图象上有12(,),(4,)P t y Q t y +两点.下列正确的选项是( ) A.当4t <-时,210y y << B.当40t -<<时,210y y << C.当40t -<<时,120y y <<D.当0t >时,120y y <<10.如图,在▱ABCD 中,AC ,BD 相交于点,2,3O AC BD ==过点A 作AE BC ⊥的垂线交BC 于点E ,记BE 长为x ,BC 长为y .当x ,y 的值发生变化时,下列代数式的值不变的是( )A.x y +B.x y -C.xyD.22x y +二、填空题(每题3分)11.因式分解:27a a -=____________. 12.若211x =-,则x =____________. 13.如图,AB 是O 的直径,AC 与O 相切,A 为切点,连接BC .已知050ACB ∠=,则B ∠的度数为___________.14.有8张卡片,上面分别写着数1,2,3,4,5,6,7,8.从中随机抽取1张,该卡片上的数是4的整数倍的概率是_________.15.如图,D ,E 分别是△ABC 边AB ,AC 的中点,连接BE ,DE .若,2AED BED DE ∠=∠=,则BE 的长为_______________.16.如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,53AC BD =.线段AB 与''A B 关于过点O 的直线l 对称,点B 的对应点'B 在线段OC 上,''A B 交CD 于点E ,则△'B CE 与四边形'OB ED 的面积比为___________.三、解答题(17-21每题8分,22,23每题10分,24题12分)17.计算:11()54--18.解方程组:254310x y x y -=⎧⎨+=-⎩.19.如图,在△ABC 中,AD ⊥BC ,AE 是BC 边上的中线,AB =10,AD =6,tan 1ACB ∠=. (1)求BC 的长 (2)求sin DAE ∠的值.20.某校开展科学活动.为了解学生对活动项目的喜爱情况,随机抽取部分学生进行问卷调查.调查问卷和统计结果描述如下:根据以上信息.解答下列问题:(1)本次调查中最喜爱“AI应用”的学生中更关注“辅助学习”有多少人?(2)菜鸡学校共有1200名学生,根据统计信息,估计该校最喜爱“科普讲座”的学生人数. 21.尺规作图问题:如图1,点E是▱ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小明:小丽,你的作法有问题.小丽:哦……我明白了!(1)证明AF∥CE(2)指出小丽作法中存在的问题.22.小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小明跑步时中间休息了两次.跑步机上C档比B档快40米/分,B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程s(米)与小明跑步时间t(分)的函数关系如图所示.时间 里程分段 速度档 跑步里程 小明16:00~16:50不分段 A 档 4000米 小丽 16:10~16:50 第一段B 档 1800米第一次休息第二段 B 档 1200米第二次休息第三段C 档 1600米(1)求A ,B ,C 各档速度(单位:米/分) (2)求小丽两次休息时间的总和(单位:分)(3)小丽第二次休息后,在a 分钟时两人跑步累计里程相等,求a 的值.23.已知二次函数2y x bx c =++(b ,c 为常数)的图象经过点(2,5)A -,对称轴为直线12x =-.(1)求二次函数的表达式(1)若点(1,7)B 向上平移2个单位长度,向左平移(0)m m >个单位长度后,恰好落在2y x bx c =++的图象上,求m 的值(3)当2≤a ≤n 时,二次函数2y x bx c =++的最大值与最小值的差为94,求n 的取值范围. 24.如图,在圆内接四边形ABCD 中,AD<AC ,ADC BAD ∠<∠,延长AD 至点E ,使AE=AC ,延长BA 至点F ,连结EF ,使AFE ADC ∠=∠.(1)若60O AFE ∠=,CD 为直径,求ABD ∠的度数.(2)求证:①EF ∥BC ②EF=BD .2024浙江省中考数学真题试卷答案一、选择题二、填空题 三、解答题. 17.【答案】718.【答案】124x y ⎧=⎪⎨⎪=-⎩19.【答案】(1)14 (2)3720.【答案】(1)32 (2)324 21.【答案】证明略22.【答案】(1)80米/分,120米/分,160米/分 (2)5分 (3)42.523.【答案】(1)23y x x =++ (2)4m = (3)112n -≤≤。
中考数学试卷真题及答案

中考数学试卷真题及答案1. 选择题1) 单选题:A. 若 a + b = 2,a×b = 1,则 a² + b² = ?A) 4 B) 3 C) 2 D) 1B. 如果 6x - 2y = 10 且 3x + 4y = 8,则 x 的值是多少?A) 4 B) 2 C) 1 D) -1C. 已知正方形 ABCD 的边长为 a,若 AB = 2a - 1,则 BC 的长度是多少?A) a + 1 B) a - 1 C) 2a + 1 D) 2a - 12) 多选题:A. 若 a、b、c 为实数,且a ≠ 0,那么下列命题中正确的有:A) 若 a × b = a × c,则 b = c;B) 若 a × b = a × c,则 b - c = 0;C) 若 a × b = a × c,则 b + c = 2a;D) 若 a × b = 0,则 a = 0 或 b = 0;B. 下列四个集合中,至少有一个集合是互斥事件的是:A) A:取到一张黑桃牌;B) B:取到一张红心牌;C) C:取到一张梅花牌;D) D:取到一张方块牌;C. 能同时整除3和7的两位数是:A) 14 B) 21 C) 42 D) 632. 解答题1) 简答题:请问任意一个正方形的对角线长度与边长的关系是什么?请给出你的计算过程。
解答:正方形的对角线可以通过勾股定理来计算。
设正方形的边长为a,则正方形的一个对角线可以看作是边长为 a 的直角三角形的斜边,所以对角线的长度 d 可以表示为d = √(a² + a²),即d = √(2a²)。
然后,我们可以继续化简这个式子:d = √(2a²) = a√2。
因此,任意一个正方形的对角线长度与边长的关系为:对角线长度等于边长乘以根号2。
2) 计算题:已知函数 f(x) = x² - 5x + 6,求 f(x) = 0 的解。
初三中考数学试卷高清版

考试时间:120分钟满分:150分一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √-1B. πC. 2/3D. √92. 若a、b是方程x²-2ax+1=0的两根,则a+b的值为()A. 2B. 1C. 0D. -23. 已知函数f(x)=2x-3,若f(x)的值域为[1,5],则x的取值范围是()A. [2,4]B. [1,3]C. [1,2]D. [2,5]4. 在平面直角坐标系中,点A(2,3),点B(-3,1),则线段AB的中点坐标为()A. (-1,2)B. (1,2)C. (-1,3)D. (1,3)5. 若x²+2x+1=0,则x的值为()A. 1B. -1C. 2D. -26. 在等腰三角形ABC中,AB=AC,∠B=40°,则∠C的度数是()A. 40°B. 50°C. 60°D. 70°7. 已知一次函数y=kx+b的图象经过点(1,2)和点(2,3),则k和b的值分别为()A. k=1, b=1B. k=1, b=2C. k=2, b=1D. k=2, b=28. 在△ABC中,∠A=45°,∠B=60°,则△ABC是()A. 直角三角形B. 钝角三角形C. 锐角三角形D. 等腰三角形9. 若a、b、c是△ABC的三边,且a+b>c,b+c>a,c+a>b,则△ABC一定是()A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形10. 下列各数中,无理数是()A. √4B. √-1C. πD. 2/3二、填空题(每题3分,共30分)11. 若x²-5x+6=0,则x的值为______。
12. 若函数f(x)=x²-4x+4的值域为[0,4],则x的取值范围是______。
13. 在平面直角坐标系中,点P(3,4),点Q(-2,-1),则线段PQ的长度为______。
初中中考数学试卷及答案

一、选择题(每题3分,共30分)1. 下列各数中,不是有理数的是()A. 0.5B. -2.3C. √2D. 1/3答案:C2. 若a=3,b=-1,则下列各式正确的是()A. a+b=2B. a-b=2C. ab=-3D. a/b=-1答案:A3. 在下列函数中,y与x成反比例关系的是()A. y=x+1B. y=2xC. y=3/xD. y=2x+1答案:C4. 已知等腰三角形底边长为6,腰长为8,则其周长为()A. 18B. 20C. 22D. 24答案:D5. 若等差数列的前三项分别为2,5,8,则该数列的公差为()A. 1B. 2C. 3D. 4答案:B6. 下列各数中,属于正数的是()A. -1B. 0C. 1/2D. -1/2答案:C7. 若x=3,则下列各式正确的是()A. x^2=9B. x^3=27C. x^4=81D. x^5=243答案:A8. 已知平行四边形ABCD,若∠A=60°,则∠B的度数为()A. 60°B. 120°C. 180°D. 240°答案:B9. 若等比数列的首项为2,公比为1/2,则该数列的第5项为()A. 1/16B. 1/8C. 1/4D. 1/2答案:A10. 在下列图形中,面积为圆的是()A. 正方形B. 长方形C. 等腰三角形D. 圆答案:D二、填空题(每题3分,共30分)11. 已知a=5,b=-3,则a+b=_________,ab=_________。
答案:2,-1512. 若等差数列的前三项分别为3,6,9,则该数列的公差为_________。
答案:313. 已知等比数列的首项为-2,公比为-1/2,则该数列的第4项为_________。
答案:-1/1614. 若平行四边形ABCD,若∠A=75°,则∠B的度数为_________。
答案:105°15. 若等腰三角形底边长为10,腰长为8,则其周长为_________。
中考数学试卷真题2023全国

中考数学试卷真题2023全国Ⅰ. 选择题1.(必做题)分解质因数,化简计算√6 + √6×√10 - √102.已知 a∶b = 2∶3,b∶c = 3∶4,c∶d = 1∶5,求 a∶c∶d3.如图,矩形 ABCD 的长边 AB = 8cm,短边 AD = 6cm,将矩形沿着其中一条副对角线剪下两个全等三角形 EAD 和 FAE,如图所示,割去部分回形纸制成的圆柱体立体图形如右图所示。
若副对角线 EF = 2.4cm,截得的圆柱体的高为多少?精确到百分位。
Ⅱ. 解答题1.某地日照时间的调查表如下:(表格略)(1)求每个城市日出到日落的时段(小时和分钟)。
(2)根据上述调查表得出的数据,计算该地一年中的日照总时长。
2.如图,平行四边形 ABCD 的边长分别为 AB = 8cm,BC = 6cm,点 E、F、G、H 分别为 CD 的中点、BC 的中点、AB 的中点、AD 的中点。
连接 EF、FG、GH,求证:三角形 EFG 的面积是平行四边形ABCD 面积的 1/5。
3.实数 a、b 满足条件:a + b = 15,a^2 + b^2 = 113,求 a、b 的值。
Ⅲ. 应用题1.某班学生的身高(cm)如下所示:135, 142, 137,140, 139, 138,139, 144, 136,141, 137, 138,144, 136, 136(1)计算学生身高的最大值和最小值。
(2)计算学生身高的中位数。
(3)将数据从小到大排列,计算学生身高的四分位数。
注意:计算四分位数时,如果一个数和小数部分之和正好等于整数部分,保留这个数,其余向下取整。
2.一个凹透镜的焦距为20cm,已知一束平行光线照射到该透镜上,经过折射后放大了 2 倍,求左右的移位量。
3.如图,已知下图中两圆心之间的距离为 8cm,点 P、Q 分别在两圆上。
若 PQ 的长为 4cm,求弧 PAB 的长。
【题目来源】2023年全国卷·中考数学真题【答案解析】上述为2023全国中考数学试卷真题。
2024年苏州市中考数学真题试卷及答案

2024年苏州市中考数学真题试卷一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B 铅笔涂在答题卡相对应的位置上.1. 用数轴上的点表示下列各数,其中与原点距离最近的是( )A. 3-B. 1C. 2D. 32. 下列图案中,是轴对称图形的是( )A. B. C. D. 3. 苏州市统计局公布,2023年苏州市全年实现地区生产总值约为2.47万亿元,被誉为“最强地级市”.数据“2470000000000”用科学记数法可表示为( )A. 102.4710⨯B. 1024710⨯C. 122.4710⨯D. 1224710⨯ 4. 若1a b >-,则下列结论一定正确的是( )A. 1a b +<B. 1a b -<C. a b >D. 1a b +> 5. 如图,AB CD ,若165∠=︒,2120∠=︒,则3∠的度数为( )A. 45︒B. 55︒C. 60︒D. 65︒ 6. 某公司拟推出由7个盲盒组成的套装产品,现有10个盲盒可供选择,统计这10个盲盒的质量如图所示.序号为1到5号的盲盒已选定,这5个盲盒质量的中位数恰好为100,6号盲盒从甲、乙、丙中选择1个,7号盲盒从丁、戊中选择1个,使选定7个盲盒质量的中位数仍为100,可以选择( )A. 甲、丁B. 乙、戊C. 丙、丁D. 丙、戊7. 如图,点A 为反比例函数()10y x x=-<图象上的一点,连接AO ,过点O 作OA 的垂线与反比例()40y x x =>的图象交于点B,则AO BO 的值为( )A. 12 B. 14 C.3 D. 138. 如图,矩形ABCD 中,AB =1BC =,动点E,F 分别从点A,C 同时出发,以每秒1个单位长度的速度沿AB ,CD 向终点B,D 运动,过点E,F 作直线l,过点A 作直线l 的垂线,垂足为G,则AG 的最大值为( )A.B. 2C. 2D. 1二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相对应的位置上.9. 计算:32x x ⋅=___________.10. 若2a b =+,则()2b a -=______.11. 如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是______.12. 如图,ABC 是O 的内接三角形,若28OBC ∠=︒,则A ∠=______.13. 直线1:1l y x =-与x 轴交于点A,将直线1l 绕点A 逆时针旋转15︒,得到直线2l ,则直线2l 对应的函数表达式是______.14. 铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,AB 所在圆的圆心C 恰好是ABO的内心,若AB =则花窗的周长(图中实线部分的长度)=______.(结果保留π)15. 二次函数()20y ax bx c a =++≠的图象过点()0,A m ,()1,B m -,()2,C n ,()3,D m -,其中m,n 为常数,则m n的值为______.16. 如图,ABC ,90ACB ∠=︒,5CB =,10CA =,点D,E 分别在AC AB ,边上,AE =,连接DE ,将ADE 沿DE 翻折,得到FDE ,连接CE ,CF .若CEF △的面积是BEC 面积的2倍,则AD =______.三、解答题:本大题共11小题,共82分.把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔.17. 计算:()042-+- 18. 解方程组:27233x y x y +=⎧⎨-=⎩. 19. 先化简,再求值:2212124x x x x x +-⎛⎫+÷ ⎪--⎝⎭.其中3x =-. 20. 如图,ABC 中,AB AC =,分别以B,C 为圆心,大于12BC 长为半径画弧,两弧交于点D,连接BD ,CD ,AD ,AD 与BC 交于点E .(1)求证:ABD ACD △≌△(2)若2BD =,120BDC ∠=︒,求BC 的长.21. 一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.(1)若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为______(2)若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由) 22. 某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A (羽毛球),B (乒乓球),C (篮球),D (排球),E (足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:根据以上信息,解决下列问题:(1)将图①中的条形统计图补充完整(画图并标注相应数据)(2)图①中项目E 对应的圆心角的度数为______°(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B (乒乓球)的人数. 23. 图①是某种可调节支撑架,BC 为水平固定杆,竖直固定杆AB BC ⊥,活动杆AD 可绕点A 旋转,CD 为液压可伸缩支撑杆,已知10cm AB =,20cm BC =,50cm AD =.(1)如图①,当活动杆AD 处于水平状态时,求可伸缩支撑杆CD 的长度(结果保留根号) (2)如图①,当活动杆AD 绕点A 由水平状态按逆时针方向旋转角度α,且3tan 4α=(α为锐角),求此时可伸缩支撑杆CD 的长度(结果保留根号).24. 如图,ABC 中,AC BC =,90ACB ∠=︒,()2,0A -,()6,0C ,反比例函数()0,0k y k x x=≠>的图象与AB 交于点(),1D m ,与BC 交于点E .(1)求m,k 的值(2)点P 为反比例函数()0,0k y k x x=≠>图象上一动点(点P 在D,E 之间运动,不与D,E 重合),过点P 作PM AB ∥,交y 轴于点M,过点P 作PN x ∥轴,交BC 于点N,连接MN ,求PMN 面积的最大值,并求出此时点P 的坐标.25. 如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠,cos 4ADC ∠=,O 是ACD 的外接圆.(1)求BC 的长(2)求O 的半径.26. 某条城际铁路线共有A,B,C 三个车站,每日上午均有两班次列车从A 站驶往C 站,其中D1001次列车从A 站始发,经停B 站后到达C 站,G1002次列车从A 站始发,直达C 站,两个车次的列车在行驶过程中保持各自的行驶速度不变.某校数学学习小组对列车运行情况进行研究,收集到列车运行信息如下表所示.列车运行时刻表请根据表格中的信息,解答下列问题:(1)D1001次列车从A 站到B 站行驶了______分钟,从B 站到C 站行驶了______分钟 (2)记D1001次列车的行驶速度为1v ,离A 站的路程为1d ;G1002次列车的行驶速度为2v ,离A 站的路程为2d .①12v v =______ ①从上午8:00开始计时,时长记为t 分钟(如:上午9:15,则75t =),已知1240v =千米/小时(可换算为4千米/分钟),在G1002次列车的行驶过程中()25150t ≤≤,若1260d d -=,求t 的值.27. 如图①,二次函数2y xbx c =++的图象1C 与开口向下的二次函数图象2C 均过点()1,0A -,()3,0B .(1)求图象1C 对应的函数表达式(2)若图象2C 过点()0,6C ,点P 位于第一象限,且在图象2C 上,直线l 过点P 且与x 轴平行,与图象2C 的另一个交点为Q (Q 在P 左侧),直线l 与图象1C 的交点为M,N (N 在M 左侧).当PQ MP QN =+时,求点P 的坐标(3)如图①,D,E 分别为二次函数图象1C ,2C 的顶点,连接AD,过点A 作AF AD .交图象2C 于点F,连接EF,当EF AD ∥时,求图象2C 对应的函数表达式.2024年苏州市中考数学真题试卷解析一、选择题.1. 【答案】B2. 【答案】A3. 【答案】C4. 【答案】D5.【答案】B6. 【答案】C7. 【答案】A【解析】解:过A 作AC x ⊥轴于C,过B 作BD x ⊥轴于D①11122ACO S =⨯-=,1422BDO S =⨯=,90ACO ODB ∠=∠=︒ ①OA OB ⊥①90AOC OBD BOD ∠=∠=︒-∠①AOC OBD △∽△ ①2ACO BDO S OA S OB ⎛⎫= ⎪⎝⎭,即2122OA OB ⎛⎫= ⎪⎝⎭ ①12OA OB =(负值舍去) 故选:A .8. 【答案】D【解析】解:连接AC ,BD交于点O ,取OA 中点H ,连接GH ,如图所示:①四边形ABCD 是矩形 ①90ABC ∠=︒,OA OC =,AB CD ①在Rt ABC △中,2AC === ①112OA OC AC === ①AB CDEAO FCO ∴∠=∠ 在AOE △与COF 中 AE CF EAO FCO OA OC =⎧⎪∠=∠⎨⎪=⎩(SAS)AOE COF ∴△≌△ AOE COF ∴∠=∠ E ∴,O ,F 共线 AG EF ⊥,H 是OB 中点 ①在Rt AGO △中,1122GH AO == G ∴的轨迹为以H 为圆心,12为半径即AO 为直径的圆弧.①AG 的最大值为AO 的长,即max 1AG AO ==. 故选:D .二、填空题. 9. 【答案】5x 10. 【答案】411. 【答案】3812. 【答案】62︒13.【答案】y =-14. 【答案】8π【解析】解:如图所示:过点C 作CE AB ⊥①六条弧所对应的弦构成一个正六边形①60,AOB OA OB ∠=︒=①AOB 为等边三角形①圆心C 恰好是ABO 的内心①30CAO CAE CBE ∠∠∠===︒①120ACB ∠=︒①AB =①AE BE ==①2cos30AE AC ==︒①AB 的长为:1202π4π1803⨯⨯= ①花窗的周长为:4π68π3⨯= 故答案为:8π.15. 【答案】35【解析】解:把()0,A m ,()1,B m -,()3,D m -代入()20y ax bx c a =++≠得93c m a b c m a b c m =⎧⎪++=-⎨⎪++=-⎩解得2383a m b m c m ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩①22833y mx x m =-+ 把()2,C n 代入22833y mx mx m =-+ 得2282233n m m m =⨯-⨯+ ①53n m =- ①5533m m m n ==-- 故答案为:35. 16. 103【解析】解:①AE =①设AD x =,AE =①ADE 沿DE 翻折,得到FDE①DF AD x ==,ADE FDE ∠=∠过E 作EH AC ⊥于H,设EF 与AC 相交于M,则90AHE ACB ︒∠=∠=,又A A ∠=∠①AHE ACB ∽ ①EH AH AE BC AC AB==, ①5CB =,10CA =,AB ===①510EH AH ==①EH x =,2AH x ==,则DH AH AD x EH =-== ①Rt EHD 是等腰直角三角形①45HDE HED ∠=∠=︒,则135ADE EDF ∠=∠=︒①1354590FDM ∠=︒-︒=︒在FDM 和EHM 中90FDM EHM DMF HMEDF EH ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩①()AAS FDM EHM ≌ ①12DM MH x ==,3102CM AC AD DM x =--=- 111331*********CEF CME CMF S S S CM EH CM DF x x x x ⎛⎫⎛⎫=+=⋅+⋅=-⋅⨯=-⋅ ⎪ ⎪⎝⎭⎝⎭ 111051025522BEC ABC AEC S S S x x =-=⨯⨯-⨯⋅=- ①CEF △的面积是BEC 面积的2倍①()31022552x x x ⎛⎫-⋅=- ⎪⎝⎭,则23401000x x -+= 解得1103x =,210x =(舍去) 即103AD= 故答案为:103. 三、解答题.17. 218. 【答案】31x y =⎧⎨=⎩ 19. 【答案】2x x +,1320. 【答案】(1)见解析 (2)BC =【小问1详解】证明:由作图知:BD CD =.在ABD △和ACD 中AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,,. ABD ACD ∴≌△△.【小问2详解】解:ABD ACD ≌,120BDC ∠=︒60BDA CDA ∴∠=∠=︒.又BD CD =DA BC ∴⊥,BE CE =.2BD =sin 2BE BD BDA ∴=⋅∠==2BC BE ∴==.21.【答案】(1)14(2)1622. 【答案】(1)见解析 (2)72(3)本校七年级800名学生中选择项目B (乒乓球)的人数约为240人【小问1详解】解:总人数为915%60÷=D 组人数为6061891215----=补图如下:【小问2详解】解:123607260︒⨯=︒ 故答案为:72【小问3详解】解:1880024060⨯=(人). 答:本校七年级800名学生中选择项目B (乒乓球)的人数约为240人.23. 【答案】(1)CD =(2)CD =24. 【答案】(1)2m =,8k(2)PMN S △有最大值92,此时83,3P ⎛⎫ ⎪⎝⎭ 【小问1详解】解: ()2,0A -,()6,0C8AC ∴=.又AC BC =8BC ∴=.90ACB ∠=︒∴点()6,8B .设直线AB 的函数表达式为y ax b =+将()2,0A -,()6,8B 代入y ax b =+,得2068a b a b -+=⎧⎨+=⎩解得12a b =⎧⎨=⎩①直线AB 的函数表达式为2y x =+.将点(),4D m 代入2y x =+,得2m =.()2,4D ∴.将()2,4D 代入k y x=,得8k . 【小问2详解】解:延长NP 交y 轴于点Q,交AB 于点L .AC BC =,90BCA ∠=︒45BAC ∴∠=︒.PN x ∥轴45BLN BAC ∴∠=∠=︒,90∠=︒NQM .PM AB ∥45MPL BLP ∴∠=∠=︒45QMP QPM ∴∠=∠=︒QM QP ∴=.设点P 的坐标为8,t t ⎛⎫⎪⎝⎭,()26t <<,则PQ t =,6PN t =-. MQ PQ t ∴==.()()21119632222PMN S PN MQ t t t ∴=⋅⋅=⋅-⋅=--+. ∴当3t =时,PMN S △有最大值92,此时83,3P ⎛⎫ ⎪⎝⎭. 25. 【答案】(1)4BC =(2)O 【小问1详解】解:BAC BCD ∠=∠,B B ∠=∠BAC BCD ∴∽.BC BA BD BC∴=,即2BC AB BD =⋅ 4AB =为AB 中点12BD AD AB ∴===①216BC AB BD =⋅==4BC ∴=.【小问2详解】解:过点A 作AE CD ⊥,垂足为E,连接CO,并延长交①O 于F,连接AF在Rt AED △中,cos 4DE CDA AD ∠==. 又2AD =1DE =∴.①在Rt AED △中,AE =BAC BCD △∽△AC AB CD BC∴==. 设CD x =,则AC =,1CE CD DE x =-=-. ①在Rt ACE 中,222AC CE AE =+)()2221x ∴=-+,即2280x x +-=解得12x =,24x =-(舍去).2CD ∴=,AC =①AC AC =AFC ADC ∴∠=∠.CF 为①O 的直径90CAF ∴∠=︒.sin sin 4AC AE AFC CDA CF AD ∴∠==∠==.7CF ∴=,即①O的半径为7. 26. 【答案】(1)90,60(2)①56;①75t =或125 【小问1详解】解:D1001次列车从A 站到B 站行驶了90分钟,从B 站到C 站行驶了60分钟 故答案为:90,60【小问2详解】解:①根据题意得:D1001次列车从A 站到C 站共需9060150+=分钟 G1002次列车从A 站到C 站共需356030125++=分钟①12150125v v = ①1256v v =故答案为:56①14v =(千米/分钟),1256v v = 2 4.8v ∴=(千米/分钟).490360⨯=∴A 与B 站之间的路程为360.360 4.875÷=∴当100t =时,G1002次列车经过B 站.由题意可如,当90110t ≤≤时,D1001次列车在B 站停车. ∴G1002次列车经过B 站时,D1001次列车正在B 站停车. ①.当2590t ≤<时,12d d >1212d d d d ∴-=-,()4 4.82560t t ∴--=,75t =(分钟) ①.当90100t ≤≤时,12d d ≥1212d d d d ∴-=-,()360 4.82560t ∴--=,87.5t =(分钟),不合题意,舍去 ①.当100110t <≤时,12d d <1221d d d d ∴-=-,()4.82536060t ∴--=,112.5t =(分钟),不合题意,舍去 ①.当110150t <≤时,12d d <1221d d d d ∴-=-,()()4.825360411060t t ∴--+-=⎡⎤⎣⎦,125t =(分钟). 综上所述,当75t =或125时,1260d d -=.27. 【答案】(1)2=23y x x --(2)点P的坐标为)1,4 (3)25515424y x x =-++ 【小问1详解】解:(1)将()1,0A -,()3,0B 代入2y x bx c =++,得10930b c b c -+=⎧⎨++=⎩解得:23b c =-⎧⎨=-⎩ 1C ∴对应的函数表达式为:223y x x =--【小问2详解】解:设2C 对应的函数表达式为()()()130y a x x a =+-<,将点()0,6C 代入 得:36a -=解得:2a =-.2C ∴对应的函数表达式为:()()213y x x =-+-,其对称轴为直线1312x -+==. 又图象1C 的对称轴也为直线1x =作直线1x =,交直线l 于点H (如答图①)由二次函数的对称性得,QH PH =,NH MH = ①PM NQ =.又PQ MP QN =+,而PQ HP QH =+ PH PM ∴=.设()02PH t t =<<,则点P 的横坐标为1t +,点M 的横坐标为21t +.将1x t =+代入()()213y x x =-+-,得()()222P y t t =-+-将21x t =+代入()()13y x x =+-,得()()2222M y t t =+-.P M y y =,()()()()2222222t t t t ∴-+-=+-即2612t =,解得1t =2t =.∴点P 的坐标为)1,4 【小问3详解】解:连接DE,交x 轴于点G,过点F 作FI ED ⊥于点I,过点F 作FJ x ⊥轴于点J .(如答图①)FI ED ⊥,FJ x ⊥轴,ED x ⊥轴∴四边形IGJF 为矩形IF GJ ∴=,IG FJ =.设2C 对应的函数表达式为()()()130y a x x a =+-<点D,E 分别为二次函数图象1C ,2C 的顶点将1x =分别代入223y x x =--,()()()130y a x x a =+-< 得4,4D E y y a =-=-①()1,4D -,()1,4E a -4DG ∴=,2AG =,4EG a =-.∴在Rt AGD 中,21tan 42AG ADG DG ∠===. AF AD ⊥90FAB DAB ∴∠+∠=︒.又90DAG ADG ∠+∠=︒ADG FAB ∴∠=∠.1tan tan 2FJ FAB ADG AJ ∴∠=∠==. 设()02GJ m m =<<,则FI m =,2AJ m =+. 22m FJ +∴= 21,2m F m +⎛⎫∴+ ⎪⎝⎭. EF AD ∥FEI ADG ∴∠=∠.1tan tan 2FI FEI ADG EI ∴∠=∠== 2EI m ∴=.又EG EI IG =+2242m m a +∴+=- 258m a +∴=-① 点F 在2C 上()()211132m a m m +∴+++-=即()()2222m a m m ++-=. 20m +≠()122a m ∴-=① 由①,①可得()251282m m +--=. 解得10m =(舍去),285m = 54a ∴=-. 2C ∴的函数表达式为()()255515134424y x x x x =-+-=-++.。
2024年云南省中考数学真题试卷附答案

2024年云南省中考数学真题试卷(全卷三个大题,共27个小题,共8页;满分100分,考试用时120分钟)一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)1.中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作100+米,则向南运动100米可记作()A.100米B.100-米C.200米D.200-米2.某市今年参加初中学业水平考试的学生大约有57800人,57800用科学记数法可以表示为()A.45.7810⨯ B.357.810⨯ C.257810⨯ D.578010⨯3.下列计算正确的是()A.33456x x x += B.635x x x ÷= C.()327a a = D.()333ab a b =4.在实数范围内有意义,则x 的取值范围是()A.0x > B.0x ≥ C.0x < D.0x ≤5.某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图(主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是()A.正方体B.圆柱C.圆锥D.长方体6.一个七边形的内角和等于()A.540︒B.900︒C.980︒D.1080︒7.甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人10次射击成绩的平均数x (单位:环)和方差2s 如下表所示甲乙丙丁x 9.99.58.28.52s 0.090.650.162.85根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择()A.甲B.乙C.丙D.丁8.已知AF 是等腰ABC ∆底边BC 上的高,若点F 到直线AB 的距离为3,则点F 到直线AC 的距离为()A.32B.2C.3D.729.两年前生产1千克甲种药品的成本为80元,随着生产技术的进步,现在生产1千克甲种药品的成本为60元.设甲种药品成本的年平均下降率为x ,根据题意,下列方程正确的是()A.()280160x -= B.()280160x -=C.()80160x -= D.()801260x -=10.按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L ,第n 个代数式是()A.2nx B.()1nn x- C.1n nx + D.()1nn x+11.中华文明,源远流长;中华汉字,寓意深广.下列四个选项中,是轴对称图形的为()A.爱B.国C.敬D.业12.在Rt ABC △中,90B Ð=°,已知34AB BC ==,,则tan A 的值为()A.45B.35C.43D.3413.如图,CD 是O 的直径,点A ,B 在O 上.若 AC BC=,36AOC ∠= ,则D ∠=()A.9B.18C.36oD.4514.分解因式:39a a -=()A.()()33a a a -+ B.()29a a + C.()()33a a -+ D.()29a a -15.某校九年级学生参加社会实践,学习编织圆锥型工艺品.若这种圆锥的母线长为40厘米,底面圆的半径为30厘米,则该圆锥的侧面积为()A.700π平方厘米B.900π平方厘米C.1200π平方厘米D.1600π平方厘米二、填空题(本大题共4小题,每小题2分,共8分)16.若关于x 的一元二次方程220x x c -+=无实数根,则c 的取值范围是______.17.已知点()2,P n 在反比例函数10y x=的图象上,则n =__________.18.如图,AB 与CD 交于点O ,且AC BD ∥.若12OA OC AC OB OD BD ++=++,则AC BD=__________.19.某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用.学校数学兴趣小组为给学校提出合理的采购意见,随机抽取了该校学生100人,了解他们喜欢的体育项目,将收集的数据整理,绘制成如下统计图注:该校每位学生被抽到的可能性相等,每位被抽样调查的学生选择且只选择一种喜欢的体育项目.若该校共有学生1000人,则该校喜欢跳绳的学生大约有______人.三、解答题(本大题共8小题,共62分)20.计算:120117sin3062-⎛⎫++--- ⎪⎝⎭.21.如图,在ABC ∆和AED △中,AB AE =,BAE CAD ∠=∠,AC AD =.求证:ABC AED ≌△△.22.某旅行社组织游客从A地到B地的航天科技馆参观,已知A地到B地的路程为300千米,乘坐C型车比乘坐D型车少用2小时,C型车的平均速度是D型车的平均速度的3倍,求D型车的平均速度.23.为使学生更加了解云南,热爱家乡,热爱祖国,体验“有一种叫云南的生活”.某校七年级年级组准备从博物馆a,植物园b两个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等;八年级年级组准备从博物馆a,植物园b,科技馆c三个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等.记选择博物馆a为a,选择植物园b为b,选择科技馆c为c,记七年级年级组的选择为x,八年级年级组的选择为y.(1)请用列表法或画树状图法中的一种方法,求(),x y所有可能出现的结果总数(2)求该校七年级年级组、八年级年级组选择的研学基地互不相同的概率P.24.如图,在四边形ABCD 中,点E ,F ,G ,H 分别是各边的中点,且AB CD ∥,AD BC ∥,四边形EFGH 是矩形.(1)求证:四边形ABCD 是菱形(2)若矩形EFGH 的周长为22,四边形ABCD 的面积为10,求AB 的长.25.A ,B 两种型号的吉祥物具有吉祥如意、平安幸福的美好寓意,深受大家喜欢.某超市销售A ,B 两种型号的吉祥物,有关信息见下表成本(单位:元/个)销售价格(单位:元/个)A 型号35aB 型号42b若顾客在该超市购买8个A 种型号吉祥物和7个B 种型号吉祥物,则一共需要670元;购买4个A 种型号吉祥物和5个B 种型号吉祥物,则一共需要410元.(1)求a ,b 的值(2)若某公司计划从该超市购买A ,B 两种型号的吉祥物共90个,且购买A 种型号吉祥物的数量x (单位:个)不少于B 种型号吉祥物数量的43,又不超过B 种型号吉祥物数量的2倍.设该超市销售这90个吉祥物获得的总利润为y 元,求y 的最大值.注:该超市销售每个吉祥物获得的利润等于每个吉祥物的销售价格与每个吉祥物的成本的差.26.已知抛物线21y x bx =+-的对称轴是直线32x =.设m 是抛物线21y x bx =+-与x 轴交点的横坐标,记533109m M -=.(1)求b 的值(2)比较M 与2的大小.27.如图,AB 是O 的直径,点D ,F 是O 上异于A ,B 的点.点C 在O 外,CA CD =,延长BF 与CA 的延长线交于点M ,点N 在BA 的延长线上,AMN ABM ∠∠=,AM BM AB MN ⋅=⋅.点H 在直径AB 上,90AHD ∠= ,点E 是线段DH 的中点.(1)求AFB ∠的度数(2)求证:直线CM 与O 相切(3)看一看,想一想,证一证以下与线段CE ,线段EB ,线段CB 有关的三个结论:CE EB CB +<,CE EB CB +=,CE EB CB +>,你认为哪个正确?请说明理由.2024年云南省中考数学真题试卷解析一、选择题.1.【答案】B 2.【答案】A 3.【答案】D 4.【答案】B 5.【答案】D 6.【答案】B【解析】解:一个七边形的内角和等于()72180900-⨯︒=︒故选:B .7.【答案】A【解析】由表中数据可知,射击成绩的平均数最大的是甲,射击成绩方差最小的也是甲∴中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲故选:A .8.【答案】C 【解析】解:如图∵AF 是等腰ABC 底边BC 上的高∴AF 平分BAC∠∴点F 到直线AB ,AC 的距离相等∵点F 到直线AB 的距离为3∴点F 到直线AC 的距离为3.故选:C .9.【答案】B 【解析】解: 甲种药品成本的年平均下降率为x 根据题意可得()280160x -=故选:B .10.【答案】D【解析】解:∵按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L ∴第n 个代数式是()1n n x +故选:D .11.【答案】D 12.【答案】C【解析】解:∵90B Ð=°,34AB BC ==,∴tan A =43BC AB =故选:C .13.【答案】B 【解析】解:连接OB∵ AC BC=∴36BOC AOC ∠=∠=︒∴1182D BOC ∠=∠=︒故选:B .14.【答案】A【解析】解:()()()329933a a a a a a a -=-=+-故选:A .15.【答案】C【解析】解:圆锥的底面圆周长为2π3060π⨯=厘米∴圆锥的侧面积为160π401200π2⨯⨯=平方厘米故选:C .二、填空题.16.【答案】1c >17.【答案】5【解析】解: 点()2,P n 在反比例函数10y x=的图象上1052n ∴==故答案为:5.18.【答案】12【解析】解: AC BD∥ACO BDO∴ ∽∴AC BD =12OA OC AC OB OD BD ++=++故答案为:12.19.【答案】120【解析】解:该校喜欢跳绳的学生大约有100012%120⨯=人故答案为:120.三、解答题.20.【答案】2【解析】解:120117sin3062-⎛⎫++--- ⎪⎝⎭1116522=++--2=.21.【解析】证明: BAE CAD∠=∠∴BAE EAC CAD EAC ∠+∠=∠+∠,即BAC EAD∠=∠在ABC 和AED △中AB AE BAC EAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABC AED ∆∆≌.22.【答案】D 型车的平均速度为100km /h【解析】解:设D 型车的平均速度为km /h x ,则C 型车的平均速度是3km /hx根据题意可得,30030023x x-=整理得,6600x=解得100x=经检验100x=是该方程的解答:D型车的平均速度为100km/h.23.【答案】(1)见解析(2)23【解析】【小问1详解】解:由题意可列表如下a ba(),a a(),b ab(),a b(),b bc(),a c(),b c由表格可知,(),x y所有可能出现的结果总数为以上6种【小问2详解】解:由表格可知,该校七年级年级组、八年级年级组选择的研学基地互不相同的情况有4种∴P(七年级年级组、八年级年级组选择的研学基地互不相同)42 63 ==.24.【答案】(1)见解析(2【小问1详解】解:连接BD,ACAB CD ∥,AD BC∥∴四边形ABCD 是平行四边形四边形ABCD 中,点E ,F ,G ,H 分别是各边的中点GF BD ∴∥,HG AC∥ 四边形EFGH 是矩形HG GF∴⊥∴BD AC⊥∴四边形ABCD 是菱形【小问2详解】解: 四边形ABCD 中,点E ,F ,G ,H 分别是各边的中点12GF EH BD ∴==,12HG EF AC == 矩形EFGH 的周长为22∴22BD AC += 四边形ABCD 是菱形即111122BD AC OA OB +=+= 四边形ABCD 的面积为101102BD AC ∴⋅=,即210OA OB ⋅=()2222121OA OB OA OA OB OB +=+⋅+= ∴2212110111OA OB +=-=∴AB ==.25.【答案】(1)4050a b =⎧⎨=⎩(2)564【小问1详解】解:由题知,8767045410a b a b +=⎧⎨+=⎩解得4050a b =⎧⎨=⎩【小问2详解】解: 购买A 种型号吉祥物的数量x 个则购买B 种型号吉祥物的数量()90x -个 且购买A 种型号吉祥物的数量x (单位:个)不少于B 种型号吉祥物数量的43∴()4903x x ≥-解得3607x ≥A 种型号吉祥物的数量又不超过B 种型号吉祥物数量的2倍.∴()290x x ≤-解得60x ≤即360607x ≤≤由题知,()()()4035504290y x x =-+--整理得3720y x =-+ y 随x 的增大而减小∴当52x =时,y 的最大值为352720564y =-⨯+=.26.【答案】(1)3b =-(2)当32M +=时,2M >;当32M =时,2M <.【小问1详解】解:∵抛物线21y x bx =+-的对称轴是直线32x =∴3212b -=⨯∴3b =-【小问2详解】解:∵m 是抛物线21y x bx =+-与x 轴交点的横坐标∴2310m m --=∴213m m-=∴422219m m m -+=∴42111m m =-而231m m =+代入得:()41131123310m m m =+-==+∴()()5423310331033311010933m m m m m m m m m m =⋅=+=+=++=+∴5331093333109109m m M m -+-===∵2310m m --=解得:32m ±=当3132M m +==时,1331313302222M +-=-=>∴2M >当32M m -==时,3302222M --=-=<∴2M <.27.【答案】(1)90︒(2)见解析(3)CE EB CB +=,理由见解析【小问1详解】解:∵AB 是O 的直径,点F 是O 上异于A ,B 的点∴90AFB ∠=︒【小问2详解】证明:∵AM BM AB MN⋅=⋅∴AM MN AB BM=又∵AMN ABM∠∠=∴ABM AMN∽∴AMB N ∠=∠,MAN MAB ∠=∠∵180MAN MAB ∠+∠=︒∴90MAN MAB ∠=∠=︒∴OA CA ⊥∵OA 是半径∴直线CM 与O 相切【小问3详解】我认为:CE EB CB +=正确,理由如下连接,,OA OD BD ,连接OC 交AD 于点G ,如图,则:OA OD =∴点O 在线段AD 的中垂线上∵CA CD=∴点C 在线段AD 的中垂线上∴OC AD ⊥∴90OGA ∠=︒∵AB 是O 的直径∴90ADB ∠=︒∴OGA ADB ∠=∠∴OG BD ∥∴AOC ABD ∠=∠∵90AHD ∠=︒∴90DHB ∠=︒∴tan DH HBD BH ∠=,tan EH HBE BH ∠=∵E 为DH 的中点∴11tan tan 22EH DH HBE HBD BH BH ∠==⋅=∠∵tan ,tan AC AC AOC ABC AO AB ∠=∠=,且12AO AB =∴11tan tan 22AC ABC AOC OA ∠=⋅=∠∵AOC ABD ∠=∠∴tan tan HBE ABC ∠=∠∴HBE ABC ∠=∠∴,,B E C 三点共线∴CE EB CB +=.。
2024年河南省中考数学真题试卷及答案
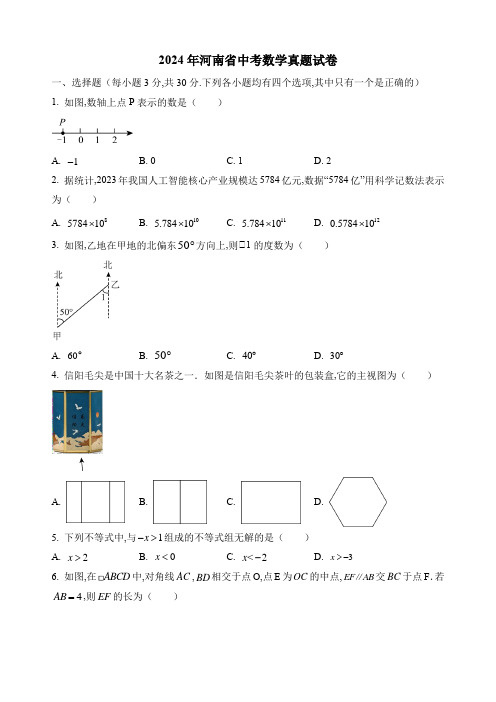
2024年河南省中考数学真题试卷一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 如图,数轴上点P 表示的数是( )A. 1-B. 0C. 1D. 22. 据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为( )A. 8578410⨯B. 105.78410⨯C. 115.78410⨯D. 120.578410⨯ 3. 如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为( )A. 60︒B. 50︒C. 40︒D. 30︒4. 信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A. B. C. D. 5. 下列不等式中,与1x ->组成的不等式组无解的是( )A. 2x >B. 0x <C. <2x -D. 3x >-6. 如图,在ABCD 中,对角线AC ,BD 相交于点O,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为( )A. 12 B. 1 C. 43 D. 27. 计算3()a a a a a ⋅⋅⋅个的结果是( )A. 5aB. 6aC. 3a a +D. 3a a 8. 豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19B. 16C. 15D. 139. 如图,O 是边长为ABC 的外接圆,点D 是BC 的中点,连接BD ,CD .以点D 为圆心,BD 的长为半径在O 内画弧,则阴影部分的面积为( )A. 8π3B. 4πC. 16π3D. 16π10. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I 与使用电器的总功率P 的函数图象(如图1),插线板电源线产生的热量Q 与I 的函数图象(如图2).下列结论中错误的是( )A. 当440W P =时,2A I =B. Q 随I 的增大而增大C. I 每增加1A,Q 的增加量相同D. P 越大,插线板电源线产生的热量Q 越多二、填空题(每小题3分,共15分) 11. 请写出2m 的一个同类项:_______.12. 2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.13. 若关于x 的方程2102x x c -+=有两个相等的实数根,则c 的值为___________. 14. 如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20-,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为___________.15. 如图,在Rt ABC △中,90ACB ∠=︒,3CA CB ==,线段CD 绕点C 在平面内旋转,过点B 作AD 的垂线,交射线AD 于点E .若1CD =,则AE 的最大值为_________,最小值为_________.三、解答题(本大题共8个小题,共75分)16. (1)计算(01 (2)化简:231124a a a +⎛⎫+÷ ⎪--⎝⎭. 17. 为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.技术统计表根据以上信息,回答下列问题.(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误()1⨯-,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好. 18. 如图,矩形ABCD 的四个顶点都在格点(网格线的交点)上,对角线AC ,BD 相交于点E,反比例函数()0k y x x=>的图象经过点A .(1)求这个反比例函数的表达式.(2)请先描出这个反比例函数图象上不同于点A 的三个格点,再画出反比例函数的图象. (3)将矩形ABCD 向左平移,当点E 落在这个反比例函数的图象上时,平移的距离为________.19. 如图,在Rt ABC △中,CD 是斜边AB 上的中线,∥BE DC 交AC 的延长线于点E .(1)请用无刻度的直尺和圆规作ECM ∠,使ECM A ∠=∠,且射线CM 交BE 于点F (保留作图痕迹,不写作法).(2)证明(1)中得到的四边形CDBF 是菱形20. 如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB ∠为最大视角.图1 图2(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB ∠为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m .参考数据 1.73≈). 21. 为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B 两种食品作为午餐.这两种食品每包质量均为50g ,营养成分表如下.(1)若要从这两种食品中摄入4600kJ 热量和70g 蛋白质,应选用A,B 两种食品各多少包? (2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g ,且热量最低,应如何选用这两种食品? 22. 从地面竖直向上发射的物体离地面的高度()m h 满足关系式205h t v t =-+,其中()s t 是物体运动的时间,()0m /s v 是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)小球被发射后_________s 时离地面的高度最大(用含0v 的式子表示).(2)若小球离地面的最大高度为20m ,求小球被发射时的速度.(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s .”已知实验楼高15m ,请判断他的说法是否正确,并说明理由. 23. 综合与实践在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质. 如图2,四边形ABCD 是邻等对补四边形,AB AD =,AC 是它的一条对角线.∠写出图中相等的角,并说明理由∠若BC m =,DC n =,2BCD θ∠=,求AC 的长(用含m,n,θ的式子表示).(3)拓展应用如图3,在Rt ABC △中,90B ,3AB =,4BC =,分别在边BC ,AC 上取点M,N,使四边形ABMN 是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN 的长.2024年河南省中考数学真题试卷答案一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 【答案】A2. 【答案】C3. 【答案】B4. 【答案】A5. 【答案】A6. 【答案】B7. 【答案】D8. 【答案】D9. 【答案】C10. 【答案】C【解析】解∠根据图1知:当440W P =时,2A I =,故选项A 正确,但不符合题意 根据图2知:Q 随I 的增大而增大,故选项B 正确,但不符合题意根据图2知:Q 随I 的增大而增大,但前小半段增加的幅度小,后面增加的幅度大,故选项C 错误,符合题意根据图1知:I 随P 的增大而增大,又Q 随I 的增大而增大,则P 越大,插线板电源线产生的热量Q 越多,故选项D 正确,但不符合题意故选:C .二、填空题(每小题3分,共15分)11. 【答案】m (答案不唯一)12. 【答案】913. 【答案】1214. 【答案】()3,1015.【答案】 ∠. 1 ∠. 1【解析】解:∠90ACB ∠=︒,3CA CB == ∠190452BAC ABC ∠=∠=⨯︒=︒∠线段CD 绕点C 在平面内旋转,1CD =∠点D 在以点C 为圆心,1为半径的圆上∠BE AE ⊥∠90AEB ∠=︒∠点E 在以AB 为直径的圆上在Rt ABE △中,cos AE AB BAE =⋅∠∠AB 为定值∠当cos BAE ∠最大时,AE 最大,cos BAE ∠最小时,AE 最小 ∠当AE 与C 相切于点D,且点D 在ABC 内部时,BAE ∠最小,AE 最大,连接CD ,CE ,如图所示:则CD AE ⊥∠90ADE CDE ∠=∠=︒∠AD ==∠AC AC =∠45CED ABC ==︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =+=+即AE 的最大值为1当AE 与C 相切于点D,且点D 在ABC 外部时,BAE ∠最大,AE 最小,连接CD ,CE ,如图所示:则CD AE ⊥∠90CDE ∠=︒∠AD ==∠四边形ABCE 为圆内接四边形 ∠180135CEA ABC =︒-=︒∠∠∠18045CED CEA =︒-=︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =-=-即AE 的最小值为1故答案为:1;1.三、解答题(本大题共8个小题,共75分) 16. 【答案】(1)9(2)2a +17. 【答案】(1)甲 29(2)甲 (3)乙队员表现更好 18. 【答案】(1)6y x= (2)见解析 (3)92【小问1详解】解:反比例函数k y x =的图象经过点()3,2A ∠23k = ∠6k = ∠这个反比例函数的表达式为6y x =【小问2详解】解:当1x =时,6y =当2x =时,3y =当6x =时,1y =∠反比例函数6y x=的图象经过()1,6,()2,3,()6,1 画图如下:【小问3详解】解:∠()6,4E 向左平移后,E 在反比例函数的图象上∠平移后点E 对应点的纵坐标为4当4y =时,64x=解得32x = ∠平移距离为39622-=.故答案为:92.19. 【答案】(1)见解析(2)见解析【小问1详解】解:如图【小问2详解】证明:∠ECM A∠=∠∠CM AB∥∠∥BE DC∠四边形CDBF是平行四边形∠在Rt ABC△中,CD是斜边AB上的中线∠12 CD BD AB ==∠平行四边形CDBF是菱形.20. 【答案】(1)见解析(2)塑像AB的高约为6.9m 【小问1详解】证明:如图,连接BM.则AMB APB∠=∠.∠AMB ADB∠>∠∠APB ADB ∠>∠.【小问2详解】解:在Rt AHP 中,60APH ∠=︒,6PH =. ∠tan AH APH PH∠=∠tan 606AH PH =⋅︒==∠30APB ∠=︒∠603030BPH APH APB ∠=∠-∠=︒-︒=︒.在Rt BHP △中,tan BH BPH PH ∠=∠tan 306BH PH =⋅︒==∠()4 1.73 6.9m AB AH BH =-==≈⨯≈.答:塑像AB 的高约为6.9m .21. 【答案】(1)选用A 种食品4包,B 种食品2包(2)选用A 种食品3包,B 种食品4包【小问1详解】解:设选用A 种食品x 包,B 种食品y 包根据题意,得7009004600,101570.x y x y +=⎧⎨+=⎩解方程组,得4,2.x y =⎧⎨=⎩答:选用A 种食品4包,B 种食品2包.【小问2详解】解:设选用A 种食品a 包,则选用B 种食品()7-a 包根据题意,得()1015790a a +-≥.∠3a ≤.设总热量为kJ w ,则()70090072006300w a a a =+-=-+.∠2000-<∠w 随a 的增大而减小.∠当3a =时,w 最小.∠7734a -=-=.答:选用A 种食品3包,B 种食品4包.22. 【答案】(1)010v (2)()20m /s(3)小明的说法不正确,理由见解析【小问1详解】解:205h t v t =-+220051020v v t ⎛⎫=--+ ⎪⎝⎭ ∠当010v t =时,h 最大 故答案为:010v 【小问2详解】解:根据题意,得 当010v t =时,20h = ∠20005201010v v v ⎛⎫-⨯+⨯= ⎪⎝⎭∠()020m /s v =(负值舍去)【小问3详解】解:小明的说法不正确.理由如下:由(2),得2520h t t =-+当15h =时,215520t t =-+解方程,得11t =,23t =∠两次间隔的时间为312s -=∠小明的说法不正确.23. 【答案】(1)∠∠ (2)∠ACD ACB ∠=∠.理由见解析;∠2cos m n θ+(3)5或7 【小问1详解】解:观察图知,图∠和图∠中不存在对角互补,图2和图4中存在对角互补且邻边相等 故图∠和图∠中四边形是邻等对补四边形故答案为:∠∠【小问2详解】解:∠ACD ACB ∠=∠,理由:延长CB 至点E,使BE DC =,连接AE∠四边形ABCD 是邻等对补四边形∠180ABC D ∠+∠=︒∠180ABC ABE ∠+∠=︒∠ABE D ∠=∠∠AB AD =∠()SAS ABE ADC ≌∠E ACD ∠=∠,AE AC =∠E ACB ∠=∠∠ACD ACB ∠=∠∠过A 作AF EC ⊥于F∠AE AC = ∠()()1112222m n CF CE BC BE BC DC +==+=+= ∠2BCD θ∠=∠ACD ACB θ∠=∠=在Rt AFC △中,cos CF θAC= ∠cos 2cos CF m n AC θθ+== 【小问3详解】解:∠90B ,3AB =,4BC =∠5AC∠四边形ABMN 是邻等对补四边形 ∠180ANM B ∠+∠=︒∠90ANM =︒当AB BM =时,如图,连接AM ,过N 作NH BC ⊥于H∠22218AM AB BM =+=在Rt AMN 中222218MN AM AN AN =-=- 在Rt CMN 中()()22222435MN CM CN AN =-=--- ∠()()22218435AN AN -=--- 解得 4.2AN = ∠45CN = ∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠1225NH =,1625CH = ∠8425BH =∠BN ==当AN AB =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠BM NM =,故不符合题意,舍去 当AN MN =时,连接AM ,过N 作NH BC ⊥于H∠90MNC ABC ∠=∠=︒,C C ∠=∠ ∠CMN CAB ∽△△ ∠CN MN BC AB =,即543CN CN -= 解得207CN =∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠127NH =,167CH = ∠127BH =∠BN ==当BM MN =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠AN AB =,故不符合题意,舍去综上,BN 的长为5或7.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年中考数学试卷
卷Ⅰ(选择题,共42分)
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列图形具有稳定性的是( )
A .
B .
C .
D . 2.一个整数8155500用科学记数法表示为108.155510⨯,则原数中“0”的个数为( )
A .4
B .6
C .7
D .10
3.图1中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
A .1l
B .2l
C .3l
D .4l
答案:C
4.将29.5变形正确的是( )
A .2229.590.5=+
B .2
9.5(100.5)(100.5)=+- C.2229.5102100.50.5=-⨯⨯+ D .2229.5990.50.5=+⨯+
5.图2中三视图对应的几何体是( )
A .
B . C. D .
6.尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的垂直平分线;Ⅲ.过直线上一点作这条直线的垂线;Ⅳ.作角的平分线.
图3是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A .①-Ⅳ,②-Ⅱ,③-Ⅰ,④-Ⅲ
B .①-Ⅳ,②-Ⅲ,③-Ⅱ,④-Ⅰ
C. ①-Ⅱ,②-Ⅳ,③-Ⅲ,④-Ⅰ D .①-Ⅳ,②-Ⅰ,③-Ⅱ,④-Ⅲ
7.有三种不同质量的物体,“”“”“”其中,同一种物体的质量都相等,现左右
手中同样的盘子上都放着不同个数的物体,只有一组左右质量不.
相等,则该组是( ) A . B . C. D .
8.已知:如图4,点P 在线段AB 外,且PA PB =.求证:点P 在线段AB 的垂直平分线上.
在证明该结论时,需添加辅助线,则作法不.
正确的是( ) A .作APB ∠的平分线PC 交AB 于点C
B .过点P 作P
C AB ⊥于点C 且AC BC =
C.取AB 中点C ,连接PC
D .过点P 作PC AB ⊥,垂足为C
9.为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗
高(单位:cm )的平均数与方差为:13x x ==甲丙,15x x ==乙丁;22 3.6s s ==甲丁,
22 6.3s s ==乙丙.则麦苗又高又整齐的是( )
A .甲
B .乙 C.丙 D .丁
10.图5中的手机截屏内容是某同学完成的作业,他做对的题数是( )
A .2个
B .3个 C. 4个 D .5个
11.如图6,快艇从P 处向正北航行到A 处时,向左转50︒航行到B 处,再向右转80︒继续
航行,此时的航行方向为( )
A .北偏东30︒
B .北偏东80︒
C.北偏西30︒ D .北偏西50︒
12.用一根长为a (单位:cm )的铁丝,首尾相接围成一个正方形.要将它按图7的方式向外等距扩1(单位:cm ), 得到新的正方形,则这根铁丝需增加( )
A .4cm
B .8cm C.(4)a cm + D .(8)a cm +
13.若22222n n n n +++=,则n =( )
D.14
14.老师设计了接力游戏,用合作的方式完成分式化简.规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图8所示: 接力中,自己负责的一步出现错误的是( )
A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
15.如图9,点I 为ABC 的内心,4AB =,3AC =,2BC =,将ACB ∠平移使其顶点与I 重合,则图中阴影部分的周长为( )
16.对于题目“一段抛物线:(3)(03)L y x x c x =--+≤≤与直线:2l y x =+有唯一公共点.若c 为整数,确定所有c 的值.”甲的结果是1c =,乙的结果是3c =或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上)
17.= . 18.若a ,b 互为相反数,则22a b -= .
19.如图101-,作BPC ∠平分线的反向延长线PA ,现要分别以APB ∠,APC ∠,BPC ∠为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.
例如,若以BPC ∠为内角,可作出一个边长为1的正方形,此时90BPC ∠=︒,而90452︒=︒是360︒(多边形外角和)的18
,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图102-所示.
图102-中的图案外轮廓周长是 ;在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 .
三、解答题 (本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
20. 嘉淇准备完成题目:化简:
2268)(652)x x x x ++-++发现系数“”印刷不清楚.
(1)他把“”猜成3,请你化简:22(368)(652)x x x x ++-++;
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
”是几?
21. 老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图111-)和不完整的扇形图(图112-),其中条形图被墨迹掩盖了一部分.
(1)求条形图中被掩盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.
22. 如图12,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
尝试(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x 是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用k (k 为正整数)的式子表示出数“1”所在的台阶数.
23. 如图13,50A B ∠=∠=︒,P 为AB 中点,点M 为射线AC 上(不与点A 重合)的任意一点,连接MP ,并使MP 的延长线交射线BD 于点N ,设BPN α∠=.
(1)求证:APM BPN △△≌;
(2)当2MN BN =时,求α的度数;
(3)若BPN △的外心在该三角形的内部,直.接.
写出α的取值范围. 24. 如图14,直角坐标系xOy 中,一次函数152
y x =-+的图像1l 分别与x ,y 轴交于A ,B 两点,正比例函数的图像2l 与1l 交于点C (,4)m .
(1)求m 的值及2l 的解析式;
(2)求AOC BOC S S -△△的值;
(3)一次函数1y kx =+的图像为3l ,且1l ,2l ,3l 不能..围成三角形,直接..
写出k 的值. 25. 如图15,点A 在数轴上对应的数为26,以原点O 为圆心,OA 为半径作优弧AB ,使点B 在O 右下方,且4tan 3
AOB ∠=.在优弧AB 上任取一点P ,且能过P 作直线//l OB 交数轴于点Q ,设Q 在数轴上对应的数为x ,连接OP .
(1)若优弧AB 上一段AP 的长为13π,求AOP ∠的度数及x 的值;
(2)求x 的最小值,并指出此时直线与AB 所在圆的位置关系;
(3)若线段PQ 的长为12.5,直接..
写出这时x 的值. 26.图16是轮滑场地的截面示意图,平台AB 距x 轴(水平)18米,与y 轴交于点B ,与滑道(1)k y x x
=≥交于点A ,且1AB =米.运动员(看成点)在BA 方向获得速度v 米/秒后,从A 处向右下飞向滑道,点M 是下落路线的某位置.忽略空气阻力,实验表明:M ,A 的竖直距离h (米)与飞出时间(秒)的平方成正比,且1t =时5h =;M ,A 的水平距离是vt 米.
(1)求k ,并用表示h ;
(2)设5v =.用表示点M 的横坐标x 和纵坐标y ,并求y 与x 的关系式(不写x 的取值范围),及13y =时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A 处飞出,速度分别是5米/秒、v 乙米/秒.当甲距x 轴米,且乙位于甲右侧超过米的位置时,直接..写出的值及v 乙的范围.。
