灰色关联分析中分辨系数的选取_申卯兴

合集下载

滤毒过滤器的设计与阻力确定

维普资讯
２Ｏ０７年第３３卷第７期
ＪｌＯ７ｕｙ２Ｏ
工业安全与环保ＩｕｔａＳｆｙａｄＥｖｏｍｎａＰｏｃｏｎｓｉａｅｎｎｉｎｅｔｒｅｔｎｄｒｌｔｒｌｔｉ
・４・９
滤毒过滤器的设计与阻力确定
过滤系统降低排风中毒剂的浓度，使之达到对作业人
［］３邓聚龙．灰色关联系统教程．武汉：华中工学院出版社。９．１０９［］４申卯兴，薛西锋，张小水．灰色关联分析中分辨系数的选取．空军
工程大学学报（自然科学版）２Ｏ，（）６７．，０３４１：８— ｏ
杨华雷丁红梅王洪波胡张雁
（中国人民解放军６６９队湖北枝江４３０）１９部４２Ｏ
摘
法。
要
在危险化学品生产和销毁工厂的通风系统中一定要设置滤毒装置，介绍了滤毒过滤器的设计与阻力确定方
滤毒冗余阻力
关键词
Ｄｅ印ａｄＲｓｓｎｅＤｅｅｍｉａｉｎｏｒｔｒｗｉｘｃＧａｓｉｎｅｉｔｃｔｒｎｌｆｌｅｔＴｏｉｓａｏｄｈ
中，过滤器的组成和冗余是设计中重要的内容和参数。设计
合理既能够节省投资，又能保证设施抗击事故冲击的能力，使装置能够安全平稳地运行。在运行中，过滤器更换时机至
关重要。
１概况
经过分析各种预想事故，系统的冗余性进行研究，对确定了活性炭过滤器和ＨＥＡ过滤器的冗余计算方法，完成了系统

数学建模方法之灰色关联度分析

教育的发达程度国民平均受教育的年限社会治安面貌和社会秩序刑事案件的发案率对于例1中我们确定工资总额为参考数比较数列为计时工资档案工资原始数据的处理原始数据存在量纲和数量级上的差异不同的量纲和数量级不便于比较或者比较时难以得出正确结论
灰色关联度分析
何为灰色关联度分析? 如何运用?
灰色关联度分析
灰色系统是指部分信息已知而部分信息未知的系统，灰色
计算关联度
对各评价对象分别计算其p个指标与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系，称其为关联度，记为
1
P
(k)
P 0i k 1
i 1,2,...,n
如果各指标在综合评价中所起的作用不同，可对关联系数求加权平均值，即
W ' 1 P P 0i k 1
设 X i (xi (1), xi (2),, xn (n)) 为因素 Xi 的行为序列
初值化
X X x x x x x '
(1) ( ' (1), ' (2),..., ' (n)),
i
ii
i
i
i
(1) 0,i 0,1,2,...,m
i
一般地，初值化方法适用于较稳定的社会经济现象的无量纲化，因为这样的数列多数呈稳定增长趋势，通过初值化处理，可使增长趋势更加明显。
均值化
一般说来，均值化方法比较适合于没有明显升降趋势现象的数据处理。
区间化
一般地，三种方法不宜混合、重叠作用，在进行系统因素分析时，可根据实际情况选用其中一个。
对例1中数据做均值化处理
关联系数的计算
设经过数据处理后的参考数列为：
比较数列为：
从几何角度看，关联程度实质上是参考数列与比较数列曲线形状的相似程度。凡比较数列与参考数列的曲线形状接近，则两者间的关联度较大；反之，如果曲线形状相差较大，则两者间的关联度较小。因此，可用曲线间的差值大小作为关联度的衡量标准。

Excel在灰色关联分析中的应用_刘建

职业安全卫生Excel在灰色关联分析中的应用＊刘建　刘丹　刘向远(西南交通大学环境科学与工程学院　成都610031) 摘　要　介绍了灰色关联分析的一般步骤,并对其中分辨率的取值和权重的计算作了初步分析。

在此基础上,通过将灰色关联分析方法编写成Excel VBA程序,并应用于铜锣山隧道出口端隧道水的来源识别,不仅在较大程度上简化了计算,而且也取得了良好的预期成果。

关键词　灰色关联分析　Excel VBA　铜锣山隧道The Application of Excel in Grey Correlation AnalysisLIU Jian　LIU D an　LIU Xiang-yuan(School of Southwes t Jiaotong Univ ers ity　C hengdu610031)Abstract　General steps of grey correlation anal ys is are introduced in this paper,al ong wit h pri mary anal ys is on its identification coefficient and weight.Based on this,an Excel VBA program of grey correlation analysis method is designed to be used t o identify the s ource of water in Tongluoshan Tunnel.It not onl y s implifies the process of calculation to s ome extent,but also gives an good result.Keywords　grey correl ation analys is　Excel VBA　tongl uoshan tunnel 灰色关联的基本思想是根据曲线几何形状的相似程度来判别其联系是否紧密。

两因素三水平用灰色关联法

灰色关联分析法是一种用于比较多个因素之间关联程度的分析方法，其基本思想是通过比较各因素之间的相似程度来评估它们之间的关联程度。

在两因素三水平的情境下，可以使用灰色关联分析法来比较三个水平之间的关联程度。

具体步骤如下：1.确定参考序列和比较序列。

参考序列是用于比较的基准序列，通常选择一个固定值或者已知的最佳水平作为参考序列。

比较序列是待比较的各个因素在不同水平下的观测值序列。

2.数据预处理。

对参考序列和比较序列进行数据预处理，包括数据清洗、缺失值处理、异常值处理等。

3.计算灰色关联度。

根据灰色关联分析法的原理，计算参考序列与各个比较序列之间的灰色关联度。

灰色关联度的计算公式为：(\gamma(x_0, x_i) = \frac{\min_i |x_0(k) - x_i(k)| + \rho \max_i |x_0(k) -x_i(k)|}{|x_0(k) - x_i(k)| + \rho \max_i |x_0(k) - x_i(k)|})其中，(x_0(k))表示参考序列在时刻k的值，(x_i(k))表示第i个比较序列在时刻k 的值，(\min_i |x_0(k) - x_i(k)|)和(\max_i |x_0(k) - x_i(k)|)分别表示第k时刻所有比较序列与参考序列的差的绝对值的最小值和最大值，(\rho)是一个分辨系数，通常取0.5。

4. 判断关联程度。

根据计算出的灰色关联度，判断各个比较序列与参考序列的关联程度。

灰色关联度越接近于1，表示关联程度越高。

通过以上步骤，可以得出各个水平之间的关联程度，从而为决策提供依据。

需要注意的是，灰色关联分析法只是一种定性的分析方法，其结果具有一定的主观性，因此在具体应用时需要根据实际情况进行合理的解释和判断。

(整理)灰色关联度分析法

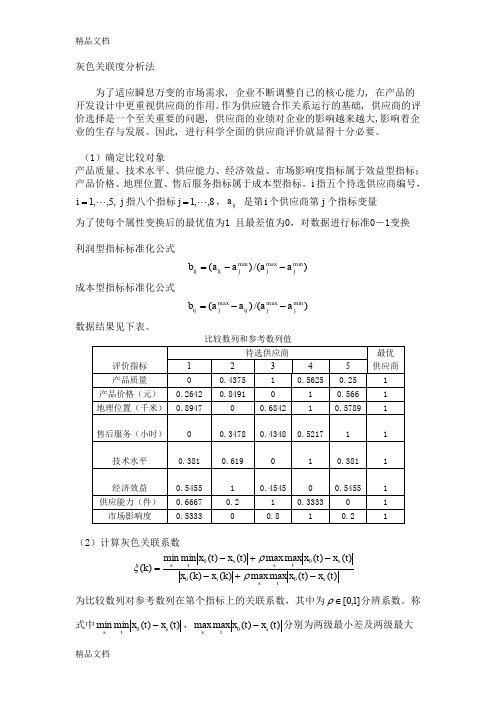
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。

作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。

因此, 进行科学全面的供应商评价就显得十分必要。

（1）确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标；产品价格、地理位置、售后服务指标属于成本型指标。

i 指五个待选供应商编号，,5,,1 =i j 指八个指标8,,1j =，ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0，对数据进行标准0－1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。

（2）计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数，其中为]1,0[∈ρ分辨系数。

称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。

一般来讲，分辨系数ρ越大，分辨率越大；ρ越小，分辨率越小。

在这里ρ取0.5。

（3）计算灰色加权关联度灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。

关联系数和关联度值（4）评价分析根据灰色加权关联度的大小，对各评价对象进行排序，可建立评价对象的关联序，关联度越大其评价结果越好。

灰色系统关联度之分辩系数的研究

灰色系统关联度之分辨系数的研究α吕　锋(武汉工业大学机电科学与工程学院,430070)摘要　本文讨论了灰关联度r i中分辨系数Θ的实质意义,研究了Θ与r i的关系,分析了在不同的系统观测信息下,Θ的取值对关联度的影响,提出了Θ的取值准则并给出了应用实例。

关键词　灰色系统　关联度　分辨系数R esearch on the Iden tificati on Coefficien tof R elati onal Grade fo r Grey SystemL uβFeng(W uhan U n iversity of T echno logy,430070)Abstract　In th is paper,the Iden tificati on Coefficien tΘis discu ssed and it is po in ted ou tthatΘdeno tes the w eigh t of the system w ho leness in R elati onal Grade r i.T he relati on2sh i p s betw eenΘand r i are studied,that is fo llow ing:1.ifΘ1<Θ2,then r i(Θ1)<r i(Θ2);2.ifΘ1>Θ2,then r i(Θ1)>r i(Θ2);w hereΘ1andΘ2are the values ofΘ.T he influence of values ofΘon the R elati onal Spacefo r grey system is also studied under the k inds of i m age sequence of system facto rs.Based on the above all,the m ethod of determ inm ing the values ofΘis p ropo sed,as fo l2low ing:1.if∃m ax>3∃v,thenΕ∃≤Θ≤1.5Ε∃;2.if∃m ax≤3∃v,then1.5Ε∃<Θ≤2Ε∃;F inally,app licati on examp les are given.Keywords　grey system;relati onal grade;iden tificati on coefficien t1　引言灰关联空间是灰色系统的基石,关联度则是灰关联空间的基础,分辨系数的取值直接影响关联度的计算结果,从而影响系统的分析、建模、决策与控制,影响对系统模型G M的评价和预测结果的可信度。

第四章灰色关联度评价法

第四章灰色关联度评价法1982年,华中理工大学邓聚龙教授首先提出了灰色系统得概念,并建立了灰色系统理论.之后,灰色系统理论得到了较深入的研究,并在许多方面获得了成功得应用.灰色系统理论认为,人们对客观事物得认识具有广泛得灰色性,即信息的不完全性和不确定性,因而由客观事物所形成得是一种灰色系统,即部分信息已知、部分信息未知得系统.比如社会系统、经济系统、生态系统等都可以看作是灰色系统..人们对综合评价的对象—被评价事物的认识也具有灰色性,因而可以借助于灰色系统的相关理论来研究综合评价问题.下面首先介绍灰色关联分析方法,然后探讨其在综合评价中应用的一些问题.一、灰色关联分析方法灰色关联分析（GRA）是一种多因素统计分析方法,它是以各因素的样本数据为依据用灰色关联度来描述因素间关系得强弱、大小和次序的.如果样本数据列反映出两因素变化的态势(方向、大小、速度等)基本一致,则它们之间得关联度较大;反之,关联度较小.与传统的多因素分析方法(相关、回归等)相比,灰色关联分析对数据要求较低且计算量小，便于广泛应用.GRA分析得核心是计算关联度,下面通过一个例子来说明计算关联度得思路和方法.表5-3是某地区1990～1995年国内生产总值得统计资料.现在提出这样得问题:该地区三次产业中,哪一产业产值得变化与该地区国内生产总值(GDP)的变化态势更一致呢?也就是哪一产业与GDP的关联度最大呢?这样得问题显然是很有实际意义的.一个很自然的想法就是分别将三次产业产值的时间序列与GDP 的时间序列进行比较,为了能够比较,先对各序列进行无量纲化,这里采用均值化法.各序列得均值分别为:2716,461.5,1228.83,1025.67,表5-3中每列数据除以其均值可表5-3 某地区国内生产总值统计资料(百万元)得均值化序列(如表5-4所示).粗略地想一下,两序列变化的态势是表现在其对应点的间距上.如果各对应点间距均较小,则两序列变化态势的一致性强,否则,一致性弱.分别计算各产业产值与GDP在对应期的间距(绝对差值),结果见表5-5.接下来表5-4表5-5似乎应该是对三个绝对差值序列分别求平均再进行比较,就可以解决问题了.但如果仔细观察表5-5中数据就会发现绝对差值数据序列的数据间存在着较大的数量级差异(最大为0.1857,最小的为0.0006,相差300多倍),不能直接进行综合,还需要对其进行一次规范化.设(max)∆分别表示表5-5中绝对差∆和(min)值)(0t i ∆的最大数和最小数,则(m ax ))((m in)00∆≤∆≤∆≤t i因而1(max ))((max )(min)00≤∆∆≤∆∆≤t i显然(max ))(0∆∆t i 越大,说明两序列i x 和0x 变化态势一致性弱,反之,一致性强,因此可考虑将(max ))(0∆∆t i 取倒反向.为了规范化后数据在[0,1]内,可考虑(max ))((max )(min)0∆∆∆∆t i由于在一般情况下(min)∆可能为零(即某个)(0t i ∆为零),故将上式改进为)((max ))((max )(min)00t t i i ερρ∆=+∆∆+∆∆ρ在0和1之间取值.上式可变形为1995,,1990,3,2,1(max))((max)(min))(00 ==∆+∆∆+∆=t i t t i i ρρε (5-6))(0t i ε称为序列i x 和序列0x 在第t 期的灰色关联系数(常简称为关联系数).由(5-6)式可以看出,ρ取值的大小可以控制(max)∆对数据转化的影响, ρ取较小的值,可以提高关联系数间差异的显著性,因而称ρ为分辨系数.利用(5-6)式对表5-5中绝对差值)(0t i ∆进行规范化,取ρ=0.4,结果见表5-6.以)1990(01ε计算为例:4191.01857.04.01044.01857.04.00006.0)1990(1857.0(max),0006.0(min)01=⨯+⨯+==∆=∆ε 同样可计算出表5-6中其余关联系数.表5-6最后分别对各产业与GDP 的关联系数序列求算术平均可得7209.0)4758.000.17338.05213.07257.08687.0(615760.0)3510.06141.08761.04903.05178.06067.0(614571.0)2881.03696.07055.05808.03796.04191.0(61010101=+++++==+++++==+++++=r r ri r 0称为序列0x 和)3,2,1(=i x i 的灰色关联度.由于010203r r r >>,因而第三产业产值与GDP 的关联度最大,其次是第二产业、第一产业.从上例可以看出,灰色关联分析需要经过以下几个步骤:1.确定分析序列在对所研究问题定性分析的基础上,确定一个因变量因素和多个自变量因素.设因变量数据构成参考序列0X ',各自变量数据构成比较序列1),,,2,1(+='n n i X i 个数据序列形成如下矩阵:(5-7)其中n i N x x x X T i i i i ,,2,1,))(,,2(),1(( ='''=' N 为变量序列的长度.)1(110110)()()()2()2()2()1()1()1(),,,(+⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'''''''''='''n N nnnn N x N x N x x x x x x x X X X无论是时间序列数据、指标序列数据还是横向序列数据都可以用来作关联分析。

灰色关联分析

灰⾊关联分析
灰⾊关联分析法
对于有m个评价对象，n个评价指标的问题，⽤灰⾊关联分析来选择，可以针对⼤量的不确定因素以及相互关系，⽤定性和定量有机结合的⽅式，使原本复杂的决策问题变得更加清晰简单，⽽且计算⽅便，主要是排除了决策者的主观任意性，得出的结论很客观，有⼀定的参考价值。

主要步骤
1. 确定评价对象和评价标准。

（以⼀个评价对象为例）
评价对象为x={x(k)|k=1,2,3,...,n}，评价标准为x0={x(k)|k=1,2,3,...,n}
k是指该评价对象的第k个评价指标
2. 确定各个评价指标的权重
主要是为了最后对求出的各个指标的灰⾊关联系数进⾏总和，若⽆权重也可以直接求平均值
3. 计算灰⾊关联系数
将每⼀个评价对象的评价指标都与评价标准相减并求绝对值，即
令c=|x(k)−x0(k)|
那么我们可以得到⼀个新的矩阵C
取C中的每⼀列中的最⼩值在每⼀⾏中的最⼩值，即两级最⼩差
a=min i min j c ij
再取每⼀列中的最⼤值在每⼀⾏中的最⼤指，即两级最⼤差
b=max i max j c ij
灰⾊关联系数为
ξi(j)=a+ρb c ij+ρb
式中，ρ⼀般取0.5，ρ属于0到1.
4. 计算灰⾊加权关联度
就是计算每⼀个评价对象的灰⾊关联度的加权和
r i=
n
∑
j=1w i∗ξi(j)
灰⾊关联度越⼤则效果越好Processing math: 100%。

(整理)灰色分析

灰色关联分析法（见课件）“灰”表示部分信息清楚，部分信息不清楚，即信息不完全．凡是信息不完全确知的系统都可称为灰色系统．灰色关联分析是灰色系统理论的一个分支．应用灰色关联分析方法对受多种因素影响的事物和现象从整体观念出发进行综合评价是一个被广为接受的方法．一、灰色关联分析的步骤利用灰色关联分析进行综合评价的步骤是：1．根据评价目的确定评价指标体系，收集评价数据设n 个数据序列形成如下矩阵：()()()()()()()()()()⎪⎪⎪⎪⎪⎭⎫⎝⎛'''''''''='''m x m x m x x x x x x x X X X n n nn21212121222111,, 其中m 为指标的个数，()()()()n i m x x x X Ti i i i ,,2,1,,,2,1 ='''='．2．确定参考数据列参考数据列应该是一个理想的比较标准，可以以各指标的最优值（或最劣值）构成参考数据列，也可根据评价目的选择其它参照值．记作()()()m x x x X 0000,,2,)1('''=' 3．对指标数据进行无量纲化无量纲化后的数据序列形成如下矩阵：()()()()()()()()()()⎪⎪⎪⎪⎪⎭⎫⎝⎛=m x m x m x x x x x x x X X X n n n n10101010222111,,, 常用的无量纲化方法有均值化法（见（12－3）式）、初值化法（见（12－4）式）和sxx -变换等．()()()()()().,,2,1,,1,0)412(1)312(11m k n i x k x k x k x m k x k x i ii mk i i i ==-''=-''=∑=；或采用内插法使各指标数据取值范围（或数量级）相同．例如，某地县级医院病床使用率最高为90%，最低为60%，我们可以将90%转化10，60%转化为1，其它可以通过内插法确定其转化值．如80%转化为多少？可进行如下计算：608060901110--=--x 解之得7=x ，即80%转化为7．4．逐个计算每个被评价对象指标序列（比较序列）与参考序列对应元素的绝对差值即 )()(0k x k x i - （ m k ,,1 = n i ,,1 = n 为被评价对象的个数）． 5．确定 )()(min min 011k x k x i mk ni -== 与)()(max max 011k x k x i mk ni -==6．计算关联系数由（12－5）式，分别计算每个比较序列与参考序列对应元素的关联系数．)512)()(max max )()()()(max max )()(min min )(0000--⋅+--⋅+-=（k x k x k x k x k x k x k x k x k i kii i kii kii ρρζm k ,,1 =式中ρ为分辨系数，在（0，1）内取值，ρ越小，关联系数间的差异越大，区分能力越强．通常ρ取0.5．当用各指标的最优值（或最劣值），构成参考数据列计算关联系数时，也可用改进的更为简便的计算方法：)()(max )()()()(max )()(min )(0000k x k x k x k x k x k x k x k x k i ii i ii ii '-'⋅+'-''-'⋅+'-'=ρρζ m k ,,1 =改进后的方法不仅可以省略第三步，使计算简便，而且避免了无量纲化对指标作用的某些负面影响．如果)}({0k x 为最优值数据列，)(k i ζ越大，越好；如果)}({0k x 为最劣值数据列，)(k i ζ越大，越不好．7．计算关联序对各评价对象（比较序列）分别计算其m个指标与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系，并称其为关联序，记为i r 0：∑==mk i i k m r 10)(1ζ n i ,,1 =8．如果各指标在综合评价中所起的作用不同，可对关联系数求加权平均值即∑=⋅='mk i k i k W m r 10)(1ζ m k ,,1 =式中k W 为各指标权重．9．依据各观察对象的关联序，得出综合评价结果．二、灰色关联分析的应用举例利用灰色关联分析对6位教师工作状况进行综合评价1．评价指标包括：专业素质、外语水平、教学工作量、科研成果、论文、著作与出勤． 2．对原始数据经处理后得到以下数值，见表（12— 3 ）表12— 3 教师考评数据3．确定参考数据列：}9,4,8,9,9,9,9{}{0=x4．计算)()(0k x k x i -，见表（12—4 ）．表12— 4 绝对差值)()(0k x k x i -5． )()(m in m in 011k x k x i mk ni -===)0,0,1,0,1,0m in(=0)()(max max 011k x k x i mk ni -===)5,6,6,5,6,7m ax (=76．依据（12－5）式，取5.0=ρ计算，得778.075.0175.00)1(1=⨯+⨯+=ζ000.175.0075.00)2(1=⨯+⨯+=ζ778.0)3(1=ζ636.0)4(1=ζ 467.0)5(1=ζ 333.0)6(1=ζ000.1)7(1=ζ同理得出其它各值，见表（12—5 ）表（12—5） )(k i ζ计算结果7．分别计算每个人各指标关联系数的均值（关联序）：713.07000.1333.0467.0636.0778.0000.1778.001=++++++=r同理 614.002=r ，680.003=r ，599.004=r ，683.005=r ，658.006=r 8．如果不考虑各指标权重（认为各指标同等重要），六个被评价对象由好到劣依次为1号（713.001=r ），5号（683.005=r ），3号（680.003=r ），6号（658.006=r ），2号（614.002=r ），4号（599.004=r ）．。

(整理)灰色关联度分析

第五章灰色关联度分析目录壹、何谓灰色关联度分析 ------------------------- 5-2 贰、灰色联度分析实例详说与练习 ----------------- 5-8负责组员工教行政硕士班二年级周世杰591701017陶虹沅591701020林炎莹591701025第五章灰色关联度分析壹、何谓灰色关联度分析一.关联度分析灰色系统分析方法针对不同问题性质有几种不同做法，灰色关联度分析(Grey Relational Analysis)是其中的一种。

基本上灰色关联度分析是依据各因素数列曲线形状的接近程度做发展态势的分析。

灰色系统理论提出了对各子系统进行灰色关联度分析的概念，意图透过一定的方法，去寻求系统中各子系统(或因素)之间的数值关系。

简言之，灰色关联度分析的意义是指在系统发展过程中，如果两个因素变化的态势是一致的，即同步变化程度较高，则可以认为两者关联较大；反之，则两者关联度较小。

因此，灰色关联度分析对于一个系统发展变化态势提供了量化的度量，非常适合动态(Dynamic)的历程分析。

灰色关联度可分成「局部性灰色关联度」与「整体性灰色关联度」两类。

主要的差别在于「局部性灰色关联度」有一参考序列，而「整体性灰色关联度」是任一序列均可为参考序列。

二.直观分析依据因素数列绘制曲线图，由曲线图直接观察因素列间的接近程度及数值关系，表一某老师给学生的评分表数据数据为例，绘制曲线图如图一所示，由曲线图大约可直接观察出该老师给分总成绩主要与考试成绩关联度较高。

表一某一老师给学生的评分表单位：分/ %由曲线图直观分析，是可大略分析因素数列关联度，可看出考试成绩与总成绩曲线形状较接近，故较具关联度，但若能以量化分析予以左证，将使分析结果更具有说服力。

三. 量化分析量化分析四步曲：1. 标准化(无量纲化)：以参照数列(取最大数的数列)为基准点，将各数据标准化成介于0至1之间的数据最佳。

2. 应公式需要值，产生对应差数列表，内容包括：与参考数列值差(绝对值)、最大差、最小差、ζ（Zeta ）为分辨系数，0＜ζ＜1，可设ζ = 0.5(采取数字最终务必使关联系数计算：ξi （k ）小于1为原则，至于分辨系数之设定值对关联度并没影响，请参考p14例) 3. 关联系数ξi （k ）计算：应用公式 maxoi(k)maxmin )(∆+∆∆+∆=ζζξk i 计算比较数列X i 上各点k 与参考数列X 0 参照点的关联系数，最后求各系数的平均值即是X i 与X 0 的关联度r i 。

Matlab学习系列.灰色关联分析

28. 灰色关联分析一、灰色系统理论简介若系统的内部信息是完全已知的，称为白色系统；若系统的内部信息是一无所知（一团漆黑），只能从它同外部的联系来观测研究，这种系统便是黑色系统；灰色系统介于二者之间，灰色系统的一部分信息是已知的，一部分是未知的。

灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统为研究对象，其特点是：（1）认为不确定量是灰数，用灰色数学来处理不确定量，使之量化，灰色系统理论只需要很少量的数据序列；（2）观测到的数据序列看作随时间变化的灰色量或灰色过程，通过鉴别系统因素之间发展趋势的相似或相异程度，即进行关联度分析；（3）通过累加生成和累减生成逐步使灰色量白化，从而建立相应于微分方程解的模型，从而预测事物未来的发展趋势和未来状态。

二、灰色关联度分析1. 要定量地研究两个事物间的关联程度，可以用相关系数和相似系数等，但这需要足够多的样本数或者要求数据服从一定概率分布。

在客观世界中，有许多因素之间的关系是灰色的，分不清哪些因素之间关系密切，哪些不密切，这样就难以找到主要矛盾和主要特性。

灰因素关联分析，目的是定量地表征诸因素之间的关联程度，从而揭示灰色系统的主要特性。

关联分析是灰色系统分析和预测的基础。

关联分析源于几何直观，实质上是一种曲线间几何形状的分析比较，即几何形状越接近，则发展变化趋势越接近，关联程度越大。

如下图所示：xt曲线A 与B 比较平行，则认为A 与B 的关联程度大；曲线C 与A 随时间变化的方向很不一致，则认为A 与C 的关联程度较小；曲线A 与D 相差最大，则认为两者的关联程度最小。

2. 关联度分析是分析系统中各因素关联程度的方法步骤：(1) 计算关联系数设参考序列为0000{(1),(2),...,()}X x x x n =比较序列为{(1),(2),...,()}, 1,,i i i i X x x x n i m ==比较序列X i 对参考序列X 0在k 时刻的关联系数定义为：0000min min ()() max max ()()()()() max max ()()s s s t s ti i s s tx t x t x t x t k x k x k x t x t ρηρ-+-=-+- 其中，0min min ()()s s tx t x t -和0max max ()()s s t x t x t -分别称为两级最小差、两级最大差，[0,1]ρ∈称为分辨系数，ρ越大分辨率越大，一般采用0.5ρ=对单位不一，初值不同的序列，在计算关联系数之前应首先进行初值化，即将该序列的所有数据分别除以第一数据，将变量化为无单位的相对数值。

灰色关联分析方法(1)

作关联系数 1 ( k )在各个时刻的值的集合，得关联系数序 1
可编辑ppt
13
1 ( 1 ( 1 ) , 1 ( 2 ) , 1 ( 3 ) , 1 ( 4 ) , 1 ( 5 ) , 1 ( 6 ) ) ( 1 , 0 . 9 5 5 , 0 . 8 9 4 , 0 . 8 4 8 , 0 . 6 7 9 , 0 . 5 8 3 )
可编辑ppt
9
[例] 关联系数的计算
给出已出初值化的序列如下：
x0(1,1.1,2,2.25,3,4)
x 1 ( 1 ,1 .1 6 6 ,1 .8 3 4 ,2 ,2 .3 1 4 ,3 )
x 2 ( 1 ,1 .1 2 5 ,1 .0 7 5 ,1 .3 7 5 ,1 .6 2 5 ,1 .7 5 ) x3(1 ,1 ,0 .7 ,0 .8 ,0 .9 ,1 .2 )
1 2.25 2.8
第二步求两级最小差与最大差容第易三求步出计m 算iin关(m ki联nx系0(k数)xi(k))0 m a ix(m k axx0(k)xi(k))2.8 将数据代入关联系数计算公式，得
i(k)x0(k)0 xi0 (k .5 ) 2 0 .8 .52.8 i(可k 1 ).编4 辑1 p.4 pt
x 0 ( k ) 。因此，参考序列x 0 可表示为 x 0 (x 0(1 ),x 0(2 ), x 0(n ))
关联分析中被比较数列常记为 x1,x2, ,xk，类似参考序列x 0 的表
，，示方法，有x 1(x 1(1 ),x 1(2 ), x 1(n ))
x k (x k(1 ),x k(2 ), x k(n ))
例如在社会系统中，人口是一种重要的子系统。影响人口发展变化的有社会因素，如计划生育、社会治安、社会道德风尚、社会的生活方式等。影响人口发展变化的因素还有经济的，如社会福利、社会保险；还有医疗的，如医疗条件、医疗水平等。总之，人口是多种因素互相关联、互相制约的子系统。这些因素的分析对于控制人口、发展生产是必要的。

灰色关联分析(算法步骤)

灰色关联分析（一）灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度[1]。

灰色系统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory)，其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度，来判断因素之间关联程度的方法。

此方法通过对动态过程发展态势的量化分析，完成对系统内时间序列有关统计数据几何关系的比较，求出参考数列与各比较数列之间的灰色关联度。

与参考数列关联度越大的比较数列，其发展方向和速率与参考数列越接近，与参考数列的关系越紧密。

灰色关联分析方法要求样本容量可以少到4个，对数据无规律同样适用，不会出现量化结果与定性分析结果不符的情况。

其基本思想是将评价指标原始观测数进行纲化处理，计算关联系数、关联度以及根据关联度的大小对待评指标进行排序。

灰色关联度的应用涉及社会科学和自然科学的各个领域，尤其在社会经济领域，如国民经济各部门收益、区域经济优势分析、产业结构调整等方面，都取得较好的应用效果。

[2]关联度有绝对关联度和相对关联度之分，绝对关联度采用初始点零化法进行初值化处理，当分析的因素差异较大时，由于变量间的量纲不一致，往往影响分析，难以得出合理的结果。

而相对关联度用相对量进行分析，计算结果仅与序列相对于初始点的变化速率有关，与各观测数据大小无关，这在一定程度上弥补了绝对关联度的缺陷。

[2]灰色关联分析的步骤[2]灰色关联分析的具体计算步骤如下：第一步：确定分析数列。

确定反映系统行为特征的参考数列和影响系统行为的比较数列。

反映系统行为特征的数据序列，称为参考数列。

影响系统行为的因素组成的数据序列，称比较数列。

设参考数列（又称母序列）为Y={Y(k) | k= 1,2,Λ,n}；比较数列（又称子序列）Xi={X i(k) | k = 1,2,Λ,n},i= 1,2,Λ,m。

灰色关联分析法原理及解题步骤

灰色关联分析法原理及解题步骤---------------研究两个因素或两个系统的关联度(即两因素变化大小,方向与速度的相对性)关联程度——曲线间几何形状的差别程度灰色关联分析是通过灰色关联度来分析和确定系统因素间的影响程度或因素对系统主行为的贡献测度的一种方法。

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密1> 曲线越接近,相应序列之间的关联度就越大,反之就越小 2> 灰色关联度越大，两因素变化态势越一致分析法优点它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。

灰色系统关联分析的具体计算步骤如下 1》参考数列和比较数列的确定参考数列——反映系统行为特征的数据序列比较数列——影响系统行为的因素组成的数据序列2》无量纲化处理参考数列和比较数列(1) 初值化——矩阵中的每个数均除以第一个数得到的新矩阵(2) 均值化——矩阵中的每个数均除以用矩阵所有元素的平均值得到的新矩阵(3) 区间相对值化3》求参考数列与比较数列的灰色关联系数ξ(Xi) 参考数列X0比较数列X1、X2、X3……………比较数列相对于参考数列在曲线各点的关联系数ξ(i)称为关联系数，其中ρ称为分辨系数，ρ?(0，1)，常取0.5.实数第二级最小差，记为Δmin。

两级最大差，记为Δmax。

为各比较数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值。

记为Δoi(k)。

所以关联系数ξ(Xi)也可简化如下列公式:4》求关联度ri关联系数——比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。

因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，关联度ri公式如下:5》排关联序因素间的关联程度，主要是用关联度的大小次序描述，而不仅是关联度的大小。

灰色关联分析中分辨系数取值的定量研究

DOI:10.13546/ki.tjyjc.2019.10.002(理论新探灰色关联分析中分辨系数取值的定量研究钱隼驰12,仇蕾u(1.河海大学管理科学研究所；2.江苏省“世界水谷”与水生态文明协同创新中心，南京211100)摘要：灰色关联分析模型作为一种有效的定性比较方法应用于经济、生态、决策方法等多个领域。

在灰色关联度计算中，分辨系数p的不同取值将影响关联度排序的结果。

通常研究中依靠经验对p取值，使 p=0.5 ;或者根据序列的波动情况定性地对p取大值或小值。

为增大关联度之间的分辨率，文章采用了数学推导的方式对p进行定量取值。

实例证明，这种取值方式能提升不同因素关联度之间的分辨率，使比较更准确。

关键词：灰色系统；关联度;分辨系数中图分类号:C931;N941 文献标识码:A文章编号：1002-6487(2019)10-0010-04〇引言1分辨系数在灰色关联分析中的意义灰色关联分析作为灰色系统理论中十分活跃的一个分支'能有效地对系统内不同因素之间的相互影响关系进行定性比较。

灰色关联分析模型自邓聚龙(1982)w提出以来，已经在生态环境与经济发展|3_51、水资源管理161、决策方法171等诸多问题上得到了广泛运用。

它的基本思想是在微观上用点在纵轴上的接近程度来描绘它们之间的联系，进而在宏观上根据序列曲线几何形状的相似程度来判断不同序列之间的关联度，两条曲线的形状越相似，它们的关联度就越大。

在进行灰色关联分析时，涉及到其分辨系数p的取值问题3邓聚龙在灰色系统理论中指出|2|:“分辨系数的取值范围为(〇，1)，一般情况取0.1~0.5,通常取0.5。

其作用在于提高关联系数之间的差异显著性。

”可见关于p的取值并没有明确的规定。

东亚斌'吕锋P l等学者通过理论与算例证明了 p的不同取值将影响因素关联度的排序结果。

由此,许多学者围绕p的取值问题进行了有益的探索申•卯兴|m|通过推演证明了 p值越小，关联度值域越大，分辨率越高，因此他认为p值取0.05为宜。